密炼机是聚合物加工的重要设备,广泛应用于聚合物塑炼和混炼等。密炼机内聚合物流体经历着变形、合并、破裂、混合等一系列行为,其流动和混合机理非常复杂。转子是密炼机的核心部件,是引发流体混合的主要动力来源;转子的几何构型和运行条件是控制混合强度的主要因素。因此,以密炼机转子系统为核心,聚合物流体的混合机理,是调控混炼设备参数和加工参数、实现混炼过程精密控制的重要理论基础。
目前,国内外对于密炼机流体混合机理的研究主要集中在分布混合和分散混合等线性混合表征。Connelly等[1]采用粒子簇分布指数、分离尺度、平均混合效率和瞬时混合效率等参数表征二维混合器的分布混合,采用剪切应力和混合指数表征分散混合。Zhang等[2]采用停留时间分布(RTD)表征聚合物流体分布混合。Domingues等[3]采用Shannon熵和分布混合指数表征聚合物分布混合,采用毛细管数和液滴尺寸变形量表征分散混合强度。Nakayama等[4]采用流体所经历的平均应力和最大应力值来衡量分散混合。聚合物流体线性混合的表征方法已具有相对较高的成熟度,但很难从本质上揭示混炼流体的复杂混合机理。
混沌混合是强化聚合物加工流体层流混合的有效方法,传统混沌混合动力学主要以Poincaré截面和Lyaponuv指数等为研究工具[5~9]。Lee等[6]采用Poincaré截面和Lyaponuv指数对单螺杆挤出机混沌螺杆螺槽展开模型进行了混沌混合研究。Hwang等[7]利用体积输运原理,采用Poincaré截面刻画了混沌单螺杆的流体折叠结构,并利用奇异摄动法给出了不稳定流形。程志飞等[8]采用Poincaré截面和Lyapunov指数对Roller转子密炼机聚合物流体的混沌混合特性进行了研究,以非线性混沌混合的视角对流场混合过程进行了分析。徐百平等[9]对副螺棱轴向往复运动的单螺杆挤出机牛顿流体进行了三维周期性流动和混沌混合进行了数值模拟,计算了示踪剂界面增长,采用Poincaré截面揭示混沌混合存在的区域。
近年来,在传统混沌混合动力学研究的基础上,提出了基于拉格朗日体系的流动结构分析方法。Haller等[10]利用有限时间Lyapunov指数(FTLE)定义了拉格朗日拟序结构(LCS),Shadden等[11]进一步给出了LCS的精确定义,并证明了LCS结构与输运边界之间的相关性。Santitissadeekorn等[12]使用FTLE探究了单转子混合机理,成功的识别了流场的LCS。Robinson等[13]利用速度场,计算了Cam转子密炼机流体的FTLE和LCS,研究了转子构型对LCS的影响。目前,拉格朗日拟序结构分析方法广泛应用于海洋流动、湍流和微流体混合等领域[14~18],而对于聚合物加工流场的研究十分有限。
4WS标准四棱转子是在传统双棱转子的基础上发展起来,具有混炼均匀、混合效率高等优点。本文以4WS转子密炼机为研究对象,利用基于拉格朗日体系的有限时间Lyapunov指数(FTLE)、拉格朗日拟序结构(LCS),结合Poincaré映射和粒子可视化技术,研究了4WS转子密炼机二维流场的混沌混合特性,分析了密炼机二维流场潜在的动力学和几何特性以及4WS转子几何结构对FTLE和LCS的影响。从拉格朗日拟序结构分析视角,分析了密炼机流体输运和混合机理,为密炼机转子的设计提供理论参考。
2 拉格朗日拟序结构对于二维流场,其瞬时变化的速度场可表示为:
| $ \frac{{dx}}{{dt}} = u\left( {x,y,t} \right);\frac{{dy}}{{dt}} = v\left( {x,y,t} \right) $ | (1) |
式中,
| $ {J_T} = \frac{{d{\varphi _T}x{{\left( t \right)}^*}}}{{dx}}\frac{{d{\varphi _T}x\left( t \right)}}{{dx}} $ | (2) |
式中,A*为A的转置。假设在有限时间T上,JT最大和最小特征值
| $ {\text{ln}}{\lambda _{{\text{min}}}}\left( T \right) < 0 < {\text{ln}}{\lambda _{{\text{max}}}}\left( T \right) $ | (3) |
上式说明流体粒子(流体质点)沿轨迹同时存在一个方向的拉伸和另一个方向的压缩。这种依赖时间速度场的轨迹就是双曲轨迹。其中,
| $ {\left\| {\frac{{{\text{d}}{\varphi _{\text{T}}}x\left( t \right)}}{{{\text{d}}x}}} \right\|^2} = {\lambda _{\max }}\left( T \right) $ | (4) |
在时间段T内,x(t)沿轨迹最大拉伸的有限时间Lyapunov指数(FTLE)可表示为[11]:
| $ {\sigma _T}\left( {x\left( t \right)} \right) = \frac{1}{{\left| T \right|}}{\text{ln}}\sqrt {{\lambda _{{\text{max}}}}\left( T \right)} $ | (5) |
由FTLE的定义可知,FTLE是表征相邻流体粒子的运动状态,定义其“脊”结构为拉格朗日拟序结构(LCS)。当时间向前积分时(T > 0),FTLE值越大,则表明在该位置的物质被拉伸得越长,即此时“脊”结构代表稳定流型,成为排斥的LCS。相反,当时间向后积分时(T < 0),则表明该处物质将被压缩,此时“脊”结构则代表非稳定流型,成为吸引的LCS。基于FTLE的LCS是分析非定常流体的有利工具,可以捕捉到流场潜在的力学和几何特性。
3 物理模型及计算方法4WS转子的几何模型如图 1(a)所示,转子最大回转半径为22 mm,两转子中心距为45 mm,密炼机的机筒内壁半径为25 mm,两转子同向逆时针旋转,转子转速为0.5 r×min-1。为了有效的反应流场的瞬时变化,采用GAMBIT软件,利用网格叠加技术(MST)划分网格。为捕捉转子与筒壁之间间隙的流场变化,两转子和筒壁采用2层边界层网格,流道网格划分方法如图 1(b)所示,其中网格数为21879,结点数为22546。密炼机内黏性聚合物流体采用Bird-Carreau本构模型进行表征,需要说明的是,不同的聚合物模型对于本文的定性分析会得到相似的结论,所以本文将不考虑不同聚合物模型的影响。采用Polyflow软件进行密炼机流场计算时,由于部分填充在相交面会对流场产生一些不可预测的扰动,不宜获取具有一般意义的结论,所以流场选取全填充状态。根据流场计算结果,提取出速度场
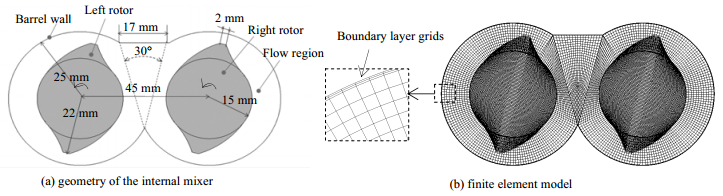
|
图 1 密炼机几何模型和有限元模型 Fig.1 Geometry and finite element model of the internal batch mixer |
积分时间是影响FTLE场中“脊”表现状态的核心要素,当选取优质积分时间,FTLE场中的“脊”结构(LCS)较为明显且结构完整。然而,优质的积分时间段并不是绝对的,对于不同的动力系统、不同的网格密度等,积分时间段的选取也不相同。本文研究的密炼机为封闭式流道结构,流体运动不能穿过筒壁或流进转子,随着转子的转动,原本相近的流体粒子(流体质点,以下简称粒子)必然会相遇。这对于利用Cauchy-Green张量计算的FTLE有一定的影响。由公式(5)可知,当T→∞时,σ→0,这就意味着当选取较长的积分时间时,不同流域的FTLE相差较小,从而使FTLE变得平缓,不易观测“脊”状结构。因此,本文首先对积分时间T的选取进行分析。当两转子的相位角为0°时(见图 1(a)),设定为初始时刻t=0 s,利用有限元网格结点速度,采用4阶Runge-Kutta法,确定出整体流场的速度函数,进而求解相应的流函数;再分别选取不同的积分时间,计算出时间向前的FTLE。
图 2所示为不同积分时间密炼机流场时间向前的FTLE场,其中红色代表较大的FTLE值,蓝色代表较小的FTLE值。从图 2(a)中可以看出,当积分时间T=40 s时,在流道中心位置具有由较大值FTLE所组成的连续曲线,即“脊”状结构-LCS。随着积分时间的增加,中心区域靠近转子附近的较为平缓的“脊”消失,并出现了突变,且脊线长度增加。因此,积分时间选取较短,会导致LCS显示不完整,甚至还会将重要的LCS掩埋。当T=160 s时,LCS基本将整个转子包围,这对于理解全局混合特性具有重要的参考意义。当T=240 s时,LCS表现的更加复杂,很难分辨出主要与次要的LCS,不利于短期全局混合特性的研究,而适于研究局部混合形态。当T=480 s时,由于流体粒子的均匀混合,使得FTLE而趋于平均化,LCS全局混乱且“脊”状结构不再明显,只能作为长时间混合和拉伸形态的参照。需要说明的是,由于初始的数据提取会有一定的误差,在长时间的积分过程中,误差将以指数增长,为了避免误差过大,尽量不要选取过长的积分时间,这也是选取有限时间Lyapunov指数计算LCS的原因。
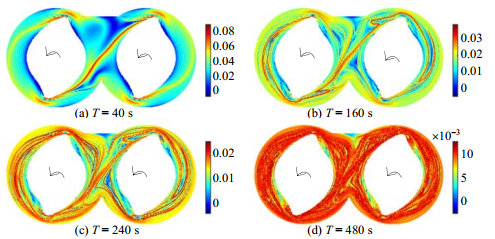
|
图 2 t=0 s时不同积分时间的时间向前FTLE场 Fig.2 Forward time FTLE field in the mixer with different integration times |
LCS是物质线的近似,且随着转子旋转而发生相应的改变[10]。为了详细了解密炼机流场不同时刻的LCS状态,给出了积分时间T=160 s时,不同初始时刻流场的时间向前FTLE场,如图 3所示。从图中可以看到,排斥的LCS随着转子旋转而表现出不同的形状,但是无论形状如何变化,其主要部分总是在中心区域,将混合区划为两个部分。由于排斥的LCS将导致边界两侧的粒子向背离LCS的方向运输,成为流体运动中一个无形边界。通过该边界的流量很小,可以忽略[15]。所以,粒子在排斥的LCS附近会受到较强的拉伸作用,使得在LCS两侧较近的粒子,在某一时间内以指数速度迅速分开,形成了良好的混沌混合开端。
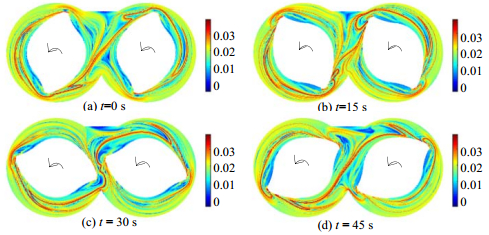
|
图 3 积分时间T=160 s不同初始时刻的时间向前FTLE场 Fig.3 Forward time of FTLE field in the mixer with different initial times at T=160 s |
图 4为积分时间T=−160 s时,不同初始时刻的时间向后的FTLE场。从图中可以清晰的辨识出吸引的LCS。随着时间增加,在吸引LCS附近的流体粒子会逐渐被吸引到该“脊”线上。因此,“脊”线上的流体粒子逐渐被压缩、变细、重新排列。这说明瞬时运动的粒子会按照当时所表现的吸引的LCS轨迹进行运动。此外,在图 4中还可以看到在转子棱边的凹槽附近,会产生类似于马蹄状的扭结,随着转子的转动,扭结被逐渐拉长而最终捏合成一条线,同时在另一转子棱的凹槽附近产生新的扭结,且循环往复。在扭结附近粒子出现折叠现象,使其周围的流体粒子混合更加充分。
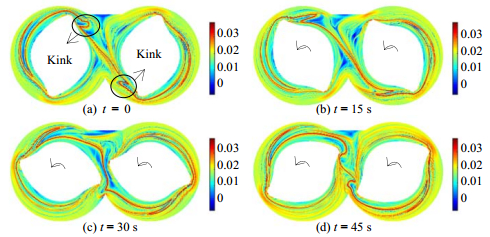
|
图 4 积分时间T=-160 s不同初始时刻的时间向后FTLE场 Fig.4 Backward time of FTLE field in the mixer with different initial times at T=-160 s |
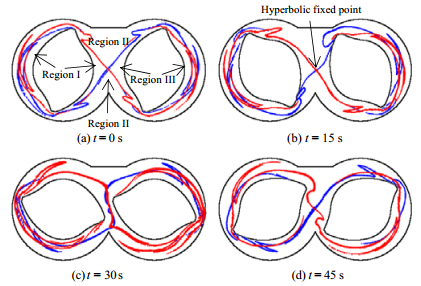
为了便于分析密炼机流场的全局混合特性,将排斥和吸引的LCS共同提取,并绘制于同一流场中。图 5所示为积分时间T=±160 s时,密炼机流场排斥和吸引的LCS分布。需要说明的是,本节研究的主要目的是分析全局混合性态,为了不被细小的LCS所扰乱,只提取了最主要的LCS,即较突出的“脊”。对于数值较小的FTLE“脊”,具体细节将在4.4节中详细分析。
|
图 5 不同初始时刻流场排斥(蓝)和吸引(红)的LCS (T=±160 s) Fig.5 The repelling LCS (blue) and attracting LCS (red) redrawn from the FTLE field with different initial times |
从图 5中可以看到,排斥和吸引的LCS将整个流场分割成了3个不同运动特性的流场区域,即:Ⅰ、Ⅱ、Ⅲ区,其中Ⅰ、Ⅲ区为LCS与转子外壁之间的流体区域,Ⅱ区为LCS与机筒外壁之间的流体区域,其中两个转子被分入不同的区域。由于LCS作为运输的准边界,在运动过程中穿过这个边界的物质是非常少的,在一定程度上可以忽略[12]。这表明流场中的粒子也会按照其边界的变化而被划为三个区域,且各区域之间只有很少的流体交流。位于Ⅱ区被困在转子周围的粒子,由于采用了无滑移边界条件,贴近转子周围的粒子随着转子一同旋转,混合效果相对较差。值得注意的是,在密炼室中心区域存在双曲不动点,粒子团在经过双曲不动点将先沿着非稳定流型的法线方向受到强拉伸;沿着非稳定流型运动时,受到沿非稳定流型法线方向的压缩。这使得初始位置在稳定流型两侧很近的两个粒子在经过双曲不动点之后,会以指数速度分离,这是混沌混合必要条件。
此外,从LCS分布图还可以看出,对于远转子区(Ⅱ区),由于自由流动使得流体粒子能够均匀分布,混合比较充分,仅在贴近机筒壁面区域的粒子存在滞留,混合效果相对较差。反之,在近转子区的流体(Ⅰ、Ⅲ区),由于物质线的封闭,导致流体的输运受到阻碍,加之转子边界的作用,流体的拉伸强度较弱,混合均匀性较差,而近转子区和转子的几何形状有关。因此,近转子区是进行转子优化的重要流域。由于4WS转子棱边独特的凹槽区产生了局部涡流,减小了转子边界上粒子滞留的区域,强化了边界区域的流体混合,使得密炼机的整体混合效率有所提高。
混沌混合的另一标志性是Smale马蹄映射,是双区不动点邻域同宿轨道性态简单模型的康托尔集(Cantor set)[19]。图 6为0~180 s吸引的LCS的变化。由于转子为同步周期性转动,可以看到吸引的LCS形成马蹄映射的整个过程。特别是LCS上的的马蹄结构在多次迭代映射后,将逐渐变细,并在双曲固定点附近趋于非稳定流型。由稳定和非稳定流型相互叠加后,可推断在流域中存在多个同宿点,并形成同宿穿插(Homoclinic transverse),由于混合腔室的空间有限,稳定流型和非稳定流型都被压缩在一起。另外,因为稳定流型和非稳定流型是不变集,且流映射是至少C1微分同胚,说明这些同宿点具有相同的性质,根据Smale-Birkhoff定理[19],接近这些同宿点的不变康托尔集,在Poincaré映射下是混沌的。
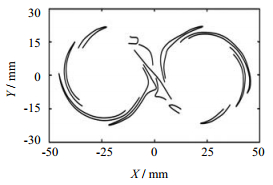
|
图 6 不同时刻稳定流型的变化 Fig.6 Change of stable manifolds with different times |
本节将利用Poincaré截面和LCS结构,分析密炼机流场的局部混合特性。Poincaré截面由不同回归点的集合所组成,对封闭轨线和不动点的研究更为直观[20]。本文选取40个周期的回归点,求出不同时刻的Poincaré截面,对局部混合特性进行深入分析。图 7所示为不同初始时刻的Poincaré截面。从图中可以看到,周期轨道在相空间中大部分处于一种无序的混沌状态,流道的大部分区域属于混沌区。其中,在密炼机最右和最左端的区域粒子分布最为均匀,没有明显的规则区域。此外,在密炼机Poincaré截面中也存在规则区-KAM管、马蹄结构和局部极限环曲线。为了进一步了解上述的特殊区域的混合特性,给出了Poincaré截面的局部放大图,如图 8所示。从图 8(c)中可以看到,规则区的流体粒子具有较为有序的运动。根据KAM定理可知,外部粒子不能穿越KAM管边界而进入到管内部,管内的粒子也不能穿过边界而进入管外部,使得KAM管内粒子独立于外部区域,不与外界产生物质交换。同时,在混沌的中心区域可以清晰可见一些曲线,如图 8(b)所示。由Poincaré截面的特性可知,当t→∞时,周围的流体质点会逐渐靠近这些曲线。这些曲线具有类似极限环的性质,由于转子的扰动使得这些原本封闭的极限环不能闭合,这样的曲线称之为局部极限环曲线。局部极限环曲线的存在阻隔了粒子的运输,减缓了粒子的交换和重叠,使得物质混合的区域变得有限,而减小了全局混沌混合。此外,图 7(a)中还存在一处较为特殊的极限环曲线-马蹄结构,其局部放大图如图 8(a)所示。粒子在极限环的限制作用下,随极限环曲线产生强弯曲,形成了马蹄形结构。虽然粒子的运输性降低了,但流体粒子的折叠作用增加了混合的均匀性。需要说明的是,由于粒子的混沌运动,其混沌结构大部分被众多粒子所掩盖。对于混沌区内部的混合状态、混合边界以及混合机理仍不易看出。

|
图 7 不同时刻密炼机流道Poincaré截面 Fig.7 Poincaré sections in the mixer with different initial times |
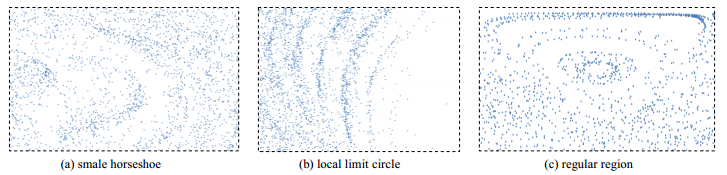
|
图 8 Poincaré截面局部放大图 Fig.8 Magnified Poincaré sections in local flow region |
为了更好的理解混沌区内部的混合机理,给出了物质线随时间演变成马蹄形结构过程,如图 9所示。物质线由于两端的拉伸被分成两段新的物质线,且产生弯曲和折叠现象,如图 9(a)~(d)所示。随着时间的增加,两段物质线的弯曲和折叠程度逐渐增大。当物质线再次回到双曲不动点附近时(见图 9(l)),由于双曲不动点周围的拉伸与压缩的作用,其物质线运动方式由平流压缩变为折叠压缩,并逐步向初始物质线靠拢,再一次压缩为一条物质线,这就是一次马蹄映射的全过程。之后,新生成的物质线再次被拉伸成两段新的物质线而被弯曲折叠,循环往复。
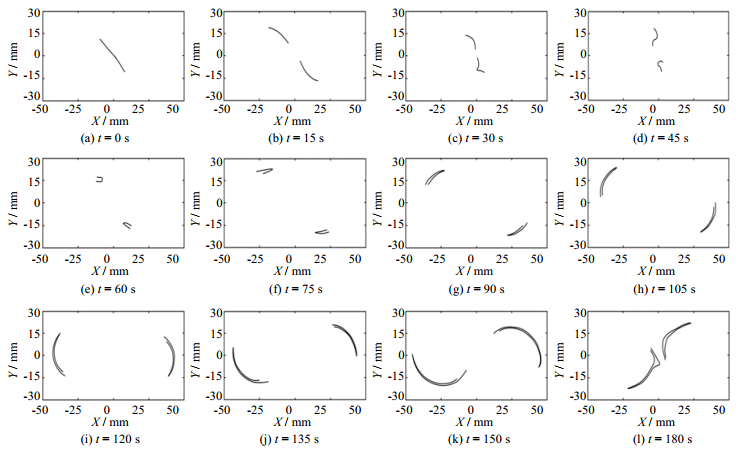
|
图 9 物质线演变成马蹄形结构过程 Fig.9 Processes of material line evolution into horseshoe shaped structures |
选取积分时间T=-240 s,计算密炼机流场时间向后的FTLE场,如图 10所示,较长的积分时间(T=-240 s)可以体现出更多LCS细节。从图 10可以看到,在转子棱边凹槽附近,物质线产生了具有较大弯曲和压缩的扭结(在Poincaré截面中表现为马蹄结构,见图 8(a))。产生扭结的主要原因为:一是流道空间狭小,粒子没有较大扩散的范围而积聚在一起;二是由于转子的“S形”轮廓结构,更容易产生滚压作用,从而得到较大的压缩。随着时间的增加,扭结的弯曲和压缩程度逐渐增大。当转子经过一个周期后,物质线已严重变薄,且在转子凸棱与机筒内壁之间的强压缩作用下,扭结尾部的物质线被截断在远离转子的混合区(Ⅱ区),如图 10(c)所示,这种分离现象使部分属于近转子区域(Ⅰ、Ⅲ区)的粒子,能够进入到远转子区域,有利于不同区域之间的物质交换。这是扭结(马蹄结构)所带来的积极作用,即让远、近转子区域的粒子有了交换的媒介,增强了流体混合的均匀性。由于马蹄结构的循环产生(见图 9),因此,马蹄结构在混沌混合中具有重要的强化作用。
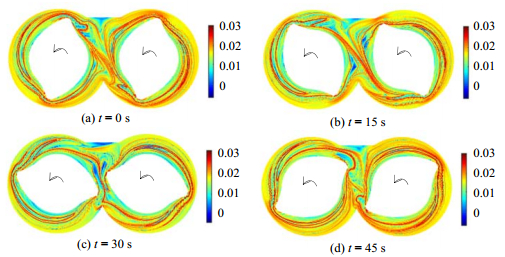
|
图 10 积分时间T=-240 s不同初始时刻时间向后的FTLE场 Fig.10 Backward time of FTLE field in the mixer with different initial times at T=-240 s |
密炼机流道的不同区域呈现出不同的混沌或周期混合特性,为了进一步理解密炼机局部混合特性,在流道中选取了3处典型位置释放流体粒子,进行粒子追踪可视化分析[22],计算结果如图 11所示。图 11(a)为在吸引的LCS内侧(位于Ⅰ区)和外侧区域(位于Ⅱ区)分别释放粒子的可视化结果。从图中可以看到,位于吸引的LCS外侧的蓝色粒子团与LCS内侧的红色粒子团基本上没有相互混合。蓝色粒子团不但比红色粒子团具有更大的拉伸,还伴随着折叠与再拉伸。对于内侧红色粒子团,经过240 s后依然附于转子壁面,不但未与蓝色粒子团发生混合,其自身也仅出现了较小拉伸和折叠现象,混合效果较差。这说明即使初始位置很近的两个粒子团,但位于不同的LCS分割区域,混合效果也有较大的差异。
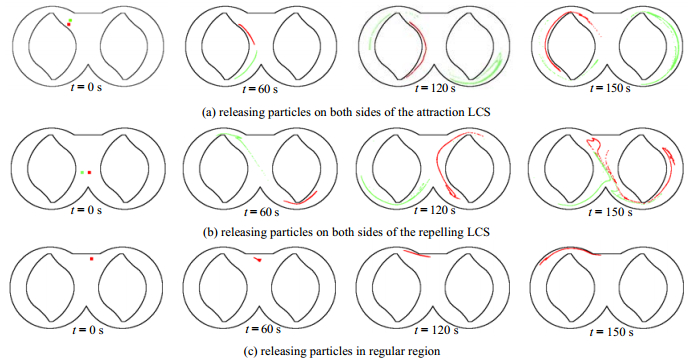
|
图 11 不同区域粒子追踪可视化结果 Fig.11 Particle visualization results in different portions |
其次,对转子中心区域释放粒子,红色和绿色粒子团分别位于靠近双曲不动点两侧的Ⅰ区和Ⅲ区,如图 11(b)所示,通过粒子追踪分析双曲固定点周围流体的混合特性。从图中可以看到,在60 s时,放于双曲不动点两侧的粒子团在非稳定流型的作用下产生了背离运动,并随转子转动而逐渐拉长且在转子凹槽处发生折叠;之后在同宿穿插的作用下,近转子区域与远转子区域出现物质交换;在150 s后,部分回到双曲不动点粒子在稳定流型的影响下,再次被折叠并在稳定流型的附近重新排列和压缩,使混合得到进一步增强。可见双曲固定点的存在极大的提高了混合效率。
最后,讨论规则区内粒子追踪可视化规律,如图 11(c)所示。规则区是通过Poincaré截面所获得的具有周期性混合的区域(见图 8(c)),对应的FTLE值较小,粒子间没有较大的相对位移差。从图 11(c)中可以看到,红色粒子团被放于规则区内部,在60 s时,红色粒子团仍保持在规则区内,无明显变化。在120 s后红色粒子团被逐渐拉伸,并缓慢地贴近机筒壁内侧流动,150 s后这一区域的粒子仍呈连续状分布,无明显的混合现象,因此规则区内流体的混合强度远弱于混沌区。
5 结论采用有限时间Lyapunov指数、拉格朗日拟序结构和Poincaré截面等对4WS转子密炼机流体的混沌混合进行了分析,讨论了转子几何结构对FTLE和LCS分布的影响。
(1) 通过对同一相位不同积分时间的FTLE场可以发现,积分时间过短时,LCS结构显示不明显。当增加积分时间,可逐渐清晰、完整的辨识出LCS。但积分时间过长,LCS结构反而被各种计算误差所产生的复合误差所掩埋。
(2) 吸引和排斥的LCS在全局上形成同宿穿插,在双曲不动点附近产生马蹄形映射,且随时间增加,马蹄形映射重复出现,密炼机流体获得了较好的混沌混合。排斥和吸引的LCS将整个流场分割成了2个不同运动特性的流动区域,其中,在近转子区由于物质线的封闭,而导致流体的输运受到阻碍,因此,近转子区是进行转子优化的重要流域。由于4WS转子棱边特殊的凹槽结构,在近转子区易产生马蹄结构,且随着混合时间的增加,马蹄结构的弯曲和折叠程度逐渐增大,增强了近转子区和远转子区之间的物质交换,强化了流场的混沌混合。
(3) 粒子可视化模拟结果表明,相比于近转子区的粒子,远转子区的粒子会受到更大的拉伸,而且有更好的遍历性。在双曲不动点的附近,近转子区域中的粒子由于受到同宿穿插的影响,使得原本封闭的区域发生了物质交换,从而引起了各区域之间的粒子交换,并在不动点周围的稳定流型上重新排列而获得了较好的混合效果。
(4) 受双曲不动点的影响,在Poincaré截面中,流道中间区域粒子向两侧拉伸,且存在不同层次的分成结构,并其带入到马蹄结构中,得到较好的折叠而达到混沌混合。同时,在整体混沌的情况下,还在密炼机流道的混合区上部存在较低FTLE值的局部规则区-KAM管,以及诸多局部极限环结构,阻隔了粒子的运输,减缓了粒子的交换和重叠,一定程度上减弱了全局混沌混合。
符号说明:
FTLE --有限时间Lyapunov指数
JT --有限时间应变张量
LCS --拉格朗日拟序结构
t --初始时刻
T --积分时间
u(x, y, t) --x方向速度函数
v(x, y, t) --y方向速度函数
x --x方向坐标
y --y方向坐标
φT --流函数
λmax(T) --有限时间应变张量最大特征值
λmin(T) --有限时间应变张量最小特征值
σT(x(t)) --有限时间Lyapunov指数
* --表示矩阵的转置
| [1] | Connelly R K, Kokini J L . Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking[J]. Journal of Food Engineering , 2007, 79 (3) : 956-969. DOI:10.1016/j.jfoodeng.2006.03.017. |
| [2] | Zhang X M, Feng L F, Chen W X , et al. Numerical simulation and experimental validation of mixing performance of kneading discs in a twin screw extruder[J]. Polymer Engineering and Science , 2009, 49 (9) : 1772-1783. DOI:10.1002/pen.v49:9. |
| [3] | Domingues N, Cunha A G, Covas J A . A quantitative approach to assess the mixing ability of single-screw extruders for polymer extrusion[J]. Journal of Polymer Engineering , 2012, 32 (2) : 81-94. |
| [4] | Nakayama Y . Melt-mixing by novel pitched-tip kneading disks in a co-rotating twin-screw extruder[J]. Chemical Engineering Science , 2011, 66 (1) : 103-110. DOI:10.1016/j.ces.2010.10.022. |
| [5] | FU Xin(傅新), LIU Su-fen(刘素芬), RUAN Xiao-dong(阮晓东) . Chaotic mixing characteristics of micromixer based on Lagrngian tracking method(基于拉格朗日跟踪法的微混合器内混沌混合特性)[J]. Journal of Mechanical Engineering(机械工程学报) , 2008, 44 (11) : 64-68. DOI:10.3901/JME.2008.11.064. |
| [6] | Lee T H, Kwon T H . A new representative measure of chaotic mixing in a chaos single-screw extruder[J]. Advances in Polymer Technology , 1999, 18 (1) : 53-68. DOI:10.1002/(ISSN)1098-2329. |
| [7] | Hwang W R, Kwon T H . Chaotic volumetric transports in a single screw extrusion process[J]. Polymer Engineering and Science , 2003, 43 (4) : 783-797. DOI:10.1002/(ISSN)1548-2634. |
| [8] | CHENG Zhi-fei(程志飞), HE Yan-dong(何延东), ZHU Xiang-zhe(朱向哲) , et al. Chaotic mixing of polymer melt in internal mixer with Roller rotors(Roller转子密炼机聚合物流体的混沌混合特性)[J]. Polymer Materials Science & Engineering(高分子材料科学与工程) , 2013, 29 (12) : 128-132. |
| [9] | XU Bai-ping(徐百平), YU Hui-wen(喻慧文), HE Liang(何亮) , et al. Chaotic mixing in single screw extruders with reciprocating baffle(带有扰动副螺棱的单螺杆挤出机内混沌混合)[J]. Journal of Mechanical Engineering(机械工程学报) , 2012, 48 (14) : 70-76. DOI:10.3901/JME.2012.14.070. |
| [10] | Haller G, Yuan G . Lagrangin coherent structures and mixing in two-dimensional turbulence[J]. Physica D-nonlinear Phenomena , 2000, 10 (1) : 99-108. |
| [11] | Shadden S C, Lekien F, Marsden J E . Definition and properties of Lagrangian coherent structures from-finite Lyapunov exponents in two-dimensional aperiodic[J]. Physica D-nonlinear Phenomena , 2005, 212 (3-4) : 271-304. DOI:10.1016/j.physd.2005.10.007. |
| [12] | Santitissadeekorn N, Bohl D, Bollt E M . Analysis and modeling of an experimental device by finite-time Lyapunov exponent method[J]. International Journal of Bifurcation & Chaos , 2009, 19 (3) : 993-1006. |
| [13] | Robinson M J, Cleary P W . The influence of cam geometry and operating conditions on chaotic mixing of viscous fluids in a twin cam mixer[J]. Aiche Journal , 2011, 57 (3) : 581-598. DOI:10.1002/aic.12297. |
| [14] | Prantsa S V . Chaotic Lagrangian transport and mixing in the ocean[J]. European Physical Journal Special Topics , 2014, 223 (13) : 2723-2743. DOI:10.1140/epjst/e2014-02288-5. |
| [15] | Green M A, Rowley C W, Haller G . Detection of Lagrangian coherent structures in three-dimensional turbulence[J]. Journal of Fluid Mechanics , 2007, 572 (1) : 111-120. |
| [16] | Bozorgmagham A E, Ross S D . Atmospheric Lagrangian coherent structures considering unresolved turbulence and forecast uncertainty[J]. Communications in Nonlinear Science & Numerical Simulation , 2015, 22 (1-3) : 964-979. |
| [17] | Rubio G, Borgogno D, Veranda M , et al. Detection of magnetic barriers in a chaotic domain:first application of finite time Lyapunov exponent method to a magnetic confinement configuration[J]. Plasma Physics & Controlled Fusion , 2015, 57 (8) : 1-10. |
| [18] | LEI Peng-fei(雷鹏飞), ZHANG Jia-zhong(张家忠), WANG Zhuo-pu(王琢璞) , et al. Lagrangian coherent structure and transport in unsteady transient flow(非定常瞬态流动过程中的Lagrangian拟序结构与物质运输作用)[J]. Acta Physica Sinica-Chinese Edition(物理学报) , 2014, 63 (8) : 084702. |
| [19] | Verhulst F . Nonlinear differential equations and dynamical systems[M]. 2nd ed. New York: Springer-Verlag, 1996: 120-128. |
| [20] | Teschl G . Ordinary differential equations and dynamical systems[M]. Cambridge: Cambridge University Press, 2004: 82-90. |
| [21] | Farazmand M, Haller G . Computing Lagrangian coherent structures from their variational theory[J]. Chaos , 2012, 22 (1) : 413-419. |
| [22] | WANG Jia-nan(王佳男), WANG Jia-jun(王嘉骏), FENG Lian-fang(冯连芳) , et al. Numerical study on fluids mixing based on droplet flows in serpentine microchannels(弯曲微通道中液滴内混合过程的数值模拟研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2014, 28 (2) : 218-222. |




