在现代工业中,过程安全和产品质量是被关注最多的2个问题。过程监控是提高过程安全和产品质量的重要手段[1]。近年来,基于数据驱动的方法不要求过程模型和相关的专家知识,在过程监控领域越发受到欢迎并取得有效的进展。其中多变量统计过程监控(multivariate statistical process monitoring,MSPM)是目前应用最多的数据驱动方法。该类方法通过多变量分析利用正常历史数据建立基于数据驱动的模型,随后将新数据映射到正常模型中判断新数据是否统计正常。主元分析方法[2](principal component analysis,PCA)和偏最小二乘法[3](partial least squares,PLS)是多变量统计过程监控的主要代表方法。该类算法的思想是将高维数据映射到低维特征空间,提取原始数据的绝大部分信息建立指标进行正常数据与异常数据的判断。但在实际化工生产过程中,过程数据往往呈现非线性、非高斯特性。由于PCA只适用于线性和高斯假设的条件,使得该方法无法在复杂的过程监控中取得好的监控效果。针对以上特点,对于传统方法的改进和新方法的提出得到快速的发展。针对非线性问题,核主元分析[4](kernel principal component analysis,KPCA)、核偏最小二乘[5](kernel partial least squares,KPLS)、近邻保留神经网络[6]等方法相继提出。Kano等[7]将独立主元分析(independent component analysis, ICA)方法应用于过程监控解决非高斯问题。但是目前的MSPM方法,大多在建模前需要对数据进行降维或者对数据进行高斯假设,这使得在对数据进行总体分析时总会缺失一些信息,从而导致一些方法不能完整地描述数据结构。如果不对数据进行降维操作,完全根据数据间的依赖性进行建模将避免有用信息的损失。
近年来,作为概率建模的有效工具,copula方法通过描述变量间的相关性,将联合分布函数和边缘分布函数有效地联系起来,使得该方法在金融、气象等领域得到广泛的应用[8-10]。然而,标准的多变量copula(如Gaussian/Student-t copula)在构建维数较大数据间的依赖性时,缺乏灵活性。为此,Joe[11]提出了pair-copula。该方法是将多变量copula用一系列的二元copula来表示。Pair copula的结构化使得一系列的pair copula可以聚集在不同的树上,Bedford等[12]将此定义为Vine。Vine copula的提出加速了该方法在过程监控领域中的应用。Ren等[13]首先将Vine copula引入化工过程监控领域,利用C-vine模型并结合广义贝叶斯推断概率指标对非高斯、非线性的数据进行监测。周南等[14]利用核密度方法来估计R-vine。由于二元copula族种类众多,这为Vine copula估计数据间的依赖性提供了更灵活的选择。但是目前常用的Vine copula估计方法都是基于参数的方法,所有备选的copula首先使用最大似然估计进行填充,随后利用AIC准则比较来选取最合适的二元copula族。这个过程需要计算出所有备选的copula密度,所需计算的参数众多,使得copula选择甚为复杂。而且常用参数二元copula存在参数假设条件。另一方面,对于复杂的化工数据来说,常用的参数copula族并不能完全描述数据间的依赖性,同时对于D-vine第一棵树变量顺序的确定,目前尚没有统一的选择方法。
目前最常用的Vine copula主要有C-vine和D-vine。相较于C-vine需要根据主导变量确定每棵树的根节点,D-vine直线型结构更加简单且易于建模,因此本文采用D-vine copula结合伯恩斯坦多项式建立一种过程监控模型(pBp-Dvine)。首先根据正常数据计算变量间的校正赤池信息准则(corrected Akaike information criterion,cAIC)值作为权重,结合最近邻算法确定变量顺序,从而确定D-vine第一棵树结构。随后利用惩罚伯恩斯坦多项式估计二元copula函数。根据前一棵树的二元copula值估计下一棵树的二元copula,直至模型确定。利用核密度估计器估计单变量边缘概率密度函数,最后联合copula密度函数构成联合概率密度。并针对化工生产过程,利用pBp-Dvine模型结合高密度区域(HDR),构建广义局部概率指标(GLP)。通过在TE过程和醋酸脱水过程中的应用,表明pBp-Dvine模型在过程监控具有良好性能。
2 D-vine copula理论及其选择方法Copula允许将一个多变量分布分解为单变量边缘和copula结构。Sklar提出,假设d维随机向量
| $F({x_1}, {x_2}, ..., {x_d}) = C({F_1}({x_1}), {F_2}({x_2}), ..., {F_d}({x_d}))$ | (1) |
式中:C(.)称为copula,它可以表示为在
对式(1)两边求导,则可以得到联合概率密度的表达式为
| $f({x_1}, {x_2}, ..., {x_d}) = c({u_1}, {u_2}, ..., {u_d})\prod\limits_{i = 1}^d {{f_i}({x_i})} $ | (2) |
式中:
| $c({u_1}, {u_2}, \cdots , {u_d}) = \frac{{{\partial ^d}C({u_1}, {u_2}, \cdots , {u_d})}}{{\partial {u_1}\partial {u_2} \cdots \partial {u_d}}}$ | (3) |
一旦copula分布函数的形式固定,即可通过极大似然法对式(2)中的参数进行估计,得到多维数据的联合概率密度。然而,对于传统的多变量copula在面临高维数据参数估计过程中可能会出现维度灾难。
2.1 D-vine copula由于标准的多元copula包括多元Gaussian copula、student-t copula,当数据维数升高时,两类多元copula在精确构建数据的依赖性时缺乏灵活性。Joe等人引入了Vine copula。Vine copula是一个分层图模型,它将n维的多元copula密度分解为一系列的二元条件copula的乘积。这个工具对处理非线性、非高斯的数据带来了便利。这里采用D-vine来对多元copula密度进行分解。对于一个n维的多元变量,D-vine模型包括n-1颗树和
| $f(\boldsymbol{x}) = \left( {\prod\limits_{j = 1}^n {{f_j}({x_j})} } \right)\left( {\prod\limits_{j = 1}^{n - 1} {\prod\limits_{i = 1}^{n - j} {{c_{i, i + j|{D_{ij}}}}} } } \right)$ | (4) |
式中:为简化定义,令
D-vine模型是线性结构,模型中变量的顺序决定了D-vine的结构。所以在建模前确定变量的顺序是至关重要的。传统的确定D-vine变量结构的方法是采用相关性大小排序,即
| $\hat i{\rm{ = }}\arg \mathop {\max }\limits_i \sum\limits_{j = 1}^m {\left| {{\tau _{i, j}}} \right|} \begin{array}{*{20}{l}} {} \end{array}(i = 1, 2, ..., m)$ | (5) |
通过求解优化每个结点与其他结点的Kendall秩相关系数和,按照系数和的大小来确定结点的前后顺序。
同时,在确定了变量的顺序后,对于pair copula的估计,常用的方法是采用伪极大似然AIC准则来估计。
| ${\rm{AIC}}: = - 2\sum\limits_{i = 1}^n {{\ln_{}}[c({u_{i, 1}}, {u_{i, 2}}|\theta )]} + 2k$ | (6) |
式中:
在估计每个二元copula时,模型首先要计算所有可获得的二元参数copula的最大似然估计,得到每个二元copula函数的密度值,然后通过计算AIC值求取最小的二元参数copula作为最后的最优待选copula。而这在选择过程中需要计算众多copula参数导致过程复杂,而且对于精确模型的估计需要不断优化AIC准则。同时,利用参数方法对二元copula进行估计时,存在参数假设条件,而且常用的二元参数copula族并不能满足所有的数据依赖性关系。
基于以上问题,Kauermann等[16]提出了半参数估计copula。由于现今的化工生产过程变量过多,且生产工况不时变化,导致实时采出的数据分布变化很快,且数据呈现出非线性、非高斯的性质,使用参数估计方法很难给出满意的效果。而利用惩罚伯恩斯坦多项式来对模型进行估计,伯恩斯坦多项式可以拟合任意的copula函数,同时根据cAIC结合最近邻算法来确定D-vine的顺序是一种新的半参数估计方法。
3 伯恩斯坦多项式D-vine模型构建 3.1 边缘概率密度估计对于边缘概率密度,使用核密度估计器估计各维变量的边缘分布,一个单变量核密度估计器的形式如下:
| ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} _{{X_i}}}({x_i}) = \frac{1}{{nh}}\sum\limits_{j = 1}^n {H\left( {\frac{{{x_i} - {x_{ij}}}}{h}} \right)} $ | (7) |
式中:H为核函数,满足
由式(4)中可以看出,Vine模型的构建等同于一系列二元copula的选择,采用伯恩斯坦多项式作为基函数来估计copula密度:
| ${\tilde c_{_{ij\left| D \right.}}}({u_{i\left| D \right.}}, {u_{j\left| D \right.}};{\boldsymbol{v}^{(i, j\left| D \right.)}}): = \sum\limits_{{k_1} = 0}^K {\sum\limits_{{k_2} = 0}^K {{\phi _{K{k_1}}}({u_{i\left| D \right.}})} } {\phi _{K{k_2}}}({u_{j\left| D \right.}})\boldsymbol{v}_{{k_1}, {k_2}}^{(i, j\left| D \right.)}{\rm{ = \{ }}{\phi _K}{\rm{(}}{u_{i\left| D \right.}}{\rm{)}} \otimes {\phi _K}{\rm{(}}{u_{j\left| D \right.}}{\rm{)\} }}{\boldsymbol{v}^{(i, j\left| D \right.)}}$ | (8) |
式中:
对于式(8)中的条件分布函数
| ${u_{i|D}} = F({x_i}{x_D}) = \frac{{\partial {{\tilde C}_{ir|{D_{ - r}}}}\{ F({x_i}|{x_{{D_{ - r}}}}), F({x_r}|{x_{{D_{ - r}}}})\} }}{{\partial F({x_r}|{x_{{D_{ - r}}}})}} = \sum\limits_{{k_1} = 0}^K {\sum\limits_{{k_2} = 0}^K {{\phi _{K{k_1}}}({u_{i|{D_{{\rm{ - }}r}}}})} } {\phi _{K{k_2}}}({u_{r|{D_{ - r}}}})\boldsymbol{v}_{{k_1}, {k_2}}^{(i, r|{D_{ - r}})}$ | (9) |
式中:
在得到边缘分布函数后,需要通过估计系数向量
| ${l_{ij|D}}({\boldsymbol{v}^{(i, j|D)}}) = \sum\limits_{t = 1}^n {{{\log }_{}}[\{ {\phi _K}({{\tilde u}_{i, t|D}}) \otimes {\phi _K}({{\tilde u}_{j, t|D}})\} {\boldsymbol{v}^{(i, j|D)}}]} $ | (10) |
通过最大化似然式(10),估计出所有的系数向量,从而接连填充出所有的pair copula。高水平的树的系数向量由低水平估计出来的copula参数来估计。
虽然上述估计过程是灵活的,但由于在估计每一个二元copula时需要使用(K+1)2个参数,这使得在估计时可能会发生过拟合,同时为了控制拟合时函数的光滑度,对式(10)引入惩罚项:
| $l_{i j|D i j| D}^{p}\left(\boldsymbol{v}^{(i, j \mid D)}, \lambda^{(i, j \mid D)}\right)=l_{i j \mid D}\left(\boldsymbol{v}^{(i, j \mid D)}\right)-\frac{1}{2} \lambda^{(i, j \mid D)} \boldsymbol{v}^{(i, j \mid D)^{\mathrm{T}}} \boldsymbol{P} \boldsymbol{v}^{(i, j \mid D)}$ | (11) |
式中:
通过设定初始的惩罚参数
D-vine变量的顺序选择至关重要。一旦D-vine第一棵树的结构确定,就确定了整棵树的结构。对于给定的p维变量,首先计算
| $\min \sum\limits_{i=1}^{p-1} \operatorname{cAIC}\left(\tilde{c}_{\pi^{(1)}(i) \pi^{(1)}(i+1)}\right)$ | (12) |
| $ \mathrm{cAIC}\left(\tilde{c}_{\pi^{(1)}(i) \pi^{(1)}(i+1)}\right)=-l_{i, j \mid D}^{p}\left(\boldsymbol{v}^{(i, j \mid D)}, \lambda\right)+\mathrm{d} f(\lambda)+\frac{2 \mathrm{~d} f(\lambda)(\mathrm{d} f(\lambda)+1)}{n-\mathrm{d} f(\lambda)-1} $ | (13) |
式中:
本文中采用最近邻算法[21]计算变量顺序。主要的计算流程如下:
1) 对于p维变量,首先计算
2) 找出最小的cAIC值对应的最小变量,从该变量开始,找到剩余变量中与该变量cAIC值最小的变量连接起来。
3) 从第2个变量开始,依次按照步骤(2)的规则进行计算,直至最后一个变量计算完。
4 基于伯恩斯坦多项式和D-vine模型的过程监控方法 4.1 监测指标针对非线性、非高斯过程,基于概率的过程监测的关键任务是设计出当前样本数据距离正常数据分布的概率性度量指标。目前通用的基于Vine方法的概率指标是基于高密度区域与密度分位数表结合构建的非线性非高斯GLP,通过对正常样本的概率密度的计算,制定密度分位数表,实现对实时数据的监控。
高密度区域是一种适合于任意分布的概率性度量区域,该区域能以尽可能小的体积覆盖给定概率α下的样本空间且区域内每个点的概率密度要大于等于区域外的点的概率密度[22]。对于非高斯过程来说,基于局部马氏距离概率指标已不再适用。根据HDR,可以给出
| $\mathrm{GLP}\left(\boldsymbol{x}_{t}^{\mathrm{monitor}}\right)=P\left(f(\boldsymbol{X}) \geqslant f\left(\boldsymbol{x}_{t}^{\mathrm{monitor}}\right)\right)$ | (14) |
式中:
| $q_{\hat \delta }^y = f({\boldsymbol{x}}_t^{\mathrm{monitor}})$ | (15) |
| $则有~~~{\mathrm{GLP}_{}}({\boldsymbol{x}}_t^{\mathrm{monitor}}) \cong 1 - \hat \delta $ | (16) |
式中:
对于给定的控制限
基于惩罚伯恩斯坦多项式D-vine的过程监控方法分为2个过程:离线建模和在线监控。如图 1所示为整个过程的监控流程图。具体操作步骤如下:
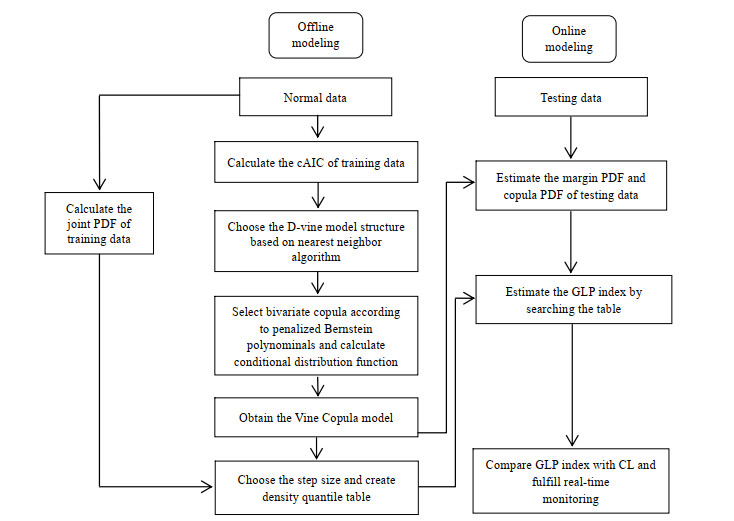
|
图 1 pBp-Dvine过程监控方法流程图 Fig.1 Flow chart of the pBp-Dvine monitoring method |
离线建模:
1) 获得正常操作情况下的训练数据;
2) 利用cAIC准则作为边权重,结合最近邻算法求得最短路径,确定D-vine模型的第一棵树的变量顺序,从而确定整个D-vine模型的结构;
3) 指定伯恩斯坦多项式自由度K,给定初始惩罚参数λ,由式(11)计算系数向量;
4) 由式(9)计算条件分布函数;
5) 由式(8)计算pair copula密度;
6) 其余的二元copula根据式(4)、(5)重复进行。下一棵树的估计过程由上一棵树估计出的pair copula进行迭代计算,直至计算到最后一棵树;
7) 计算训练样本的联合概率密度值,构建密度分位数表。
在线监控:
1) 利用式(16)结合密度分位数表计算当前样本的GLP指标;
2) 判断GLP指标是否超限,完成在线监控过程。
5 应用分析本章通过TE过程和醋酸脱水实例的监测效果验证基于伯恩斯坦多项式的D-vine copula方法的有效性,同时通过与KPCA、D-vine(参数估计)方法的比较来验证所提出方法的有效性。
5.1 TE过程TE仿真平台是由美国Eastman化学公司开发的具有开放性和挑战性的化工模型仿真平台。其产生的数据具有非线性特征,广泛用于测试复杂工业过程的控制和故障监测模型。该过程具有5个主要的操作单元:反应釜、冷凝器、压缩机、气液分离器和汽提塔[23]。TE过程数据集共有52个变量,其中41个为测量变量,11个为操纵变量。41个测量变量中有22个为连续变量。本文中采用22个连续变量来进行建模。TE过程总共21个故障,每个故障有960个样本,前160个为正常状态下的样本,从第161个样本起,加入不同的故障共800个故障样本。
对训练数据进行离线建模,建立静态密度分位数表,随后对测试数据进行在线监控。为了对比方法的有效性,这里对KPCA、D-vine(参数估计)方法进行比较,KPCA的主元个数选择前85%。置信水平均设置为0.99。pBp-Dvine的自由度K=8。其中KPCA的检测结果取自文献[24]。
表 1给出了3种方法的监测结果。表中T2和SPE分别为KPCA在残差子空间和主元子空间的监测指标,所提出的方法在总体上表现出了好的效果。针对故障1、2、6、8、12、13、14,所有方法都能取得相近的检测结果,这表明提出的方法较其他方法在易监测的故障上可以取得同等的检测性能。针对故障3、4、5、9、15、19这些难检测的故障来说,所有方法均不能有效检测出故障,但同比于其他方法,pBp-Dvine仍能给出高于其他方法的检测结果。尤其是对于故障15、19,提出的方法明显高于其他方法的检测水平。针对故障11、16和21,所提出的方法较其他方法得到了较好的提升。总体来说,本文提出的pBp-Dvine方法较其他监测方法的监控性能有所提升。如图 2所示为3种方法对于故障8的监控图。从图中可以看出,所有方法均可以达到好的检测效果。KPCA和D-vine的检测率分别达到了97.38%和97.75%。这说明对于该类故障2种方法可以得到好的检测率,而且2种方法表现出了相似的检测效果,而提出的方法在此基础上可以更早识别出故障,达到更高的检测率(98.88%),高于其他方法。
|
|
表 1 TE过程故障检测率对比分析 Table 1 Comparison of monitoring performance in TE processes |
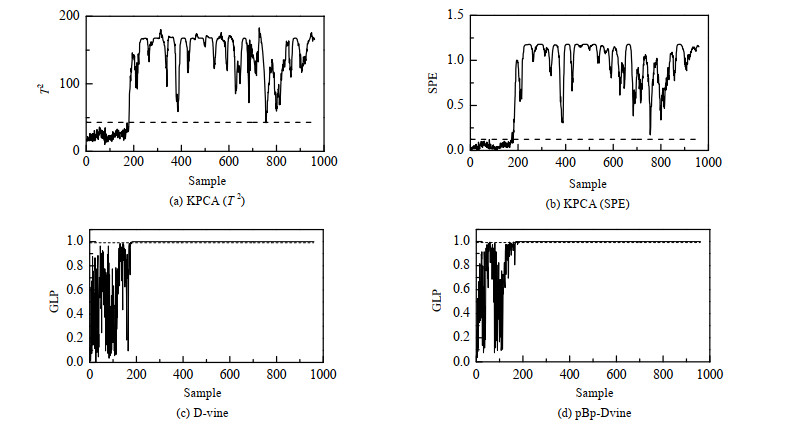
|
图 2 故障8的过程监控图 Fig.2 Fault detection charts of Fault 8 during TE processes |
精对苯二甲酸是重要的有机化工原料。该产物由醋酸作为溶剂,对二甲苯经过催化氧化得到粗对二甲苯酸再经一系列化学操作得到。为了克服普通精馏无法有效将醋酸和水分离,工业上经常采用共沸精馏法,加入共沸剂增加醋酸和水的相对挥发度,从而有效地分离水和醋酸[25]。
醋酸脱水系统由90级塔板和4个进料组成。本文采用温度、压力、流量等连续的21个过程变量对顶部醋酸蒸馏过程进行实时监控。本次试验训练数据样本为500组,测试数据样本为300组。在离线建模阶段,利用500组训练样本进行模型训练。对于测试的300组样本,在开始的前100个时刻,过程处于正常运行状态。在第101时刻顶部醋酸产品含量由不到1.15%上升到1.5%,该过程持续100个时刻。到最后的100时刻,醋酸含量又回复到1.15%以下。
表 2为在控制限CL=0.98条件下,KPCA、D-vine(参数估计)、pBp-Dvine的检测率(FDR)和误报率(FAR)。pBp-Dvine的自由度取为12。
|
|
表 2 醋酸脱水过程的检测率和误报率(CL=0.98) Table 2 Fault detection and false alarm rates of the acetic acid dehydration process |
如图 3所示为醋酸脱水过程的监控图。结合表 2和图 3可以发现,所有方法都可以完全地检测出故障,这说明3种方法可以有效检测出此类故障。由图 3中可以看出,pBp-Dvine方法的误报率是最低的。综合该故障的检测率和误报率,表明本文提出的pBp-Dvine方法在醋酸脱水过程中有良好的监控性能。
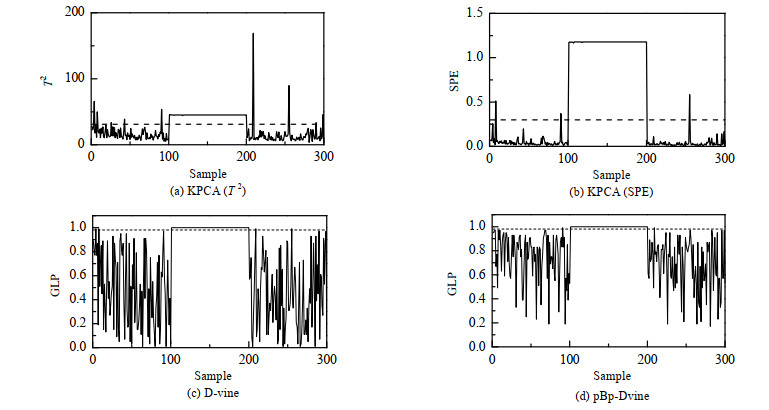
|
图 3 醋酸脱水过程的监控图 Fig.3 Monitoring results of the acetic acid dehydration process |
本文提出了一种基于pBp-Dvine模型的过程监控方法,在过程监控领域取得了不错的监测效果。pBp-Dvine方法首先根据两两变量间的cAIC值作为权重,利用最近邻算法求得最短路径,得到D-vine的第一颗树结构。随后利用惩罚伯恩斯坦多项式估计二元copula函数。该方法在不降维的条件下,在二元copula的估计过程中摒弃参数假设,挖掘出高维变量间的复杂信息,从而获得半参D-vine模型,使得模型估计更灵活。TE过程和醋酸脱水过程证明了pBp-Dvine方法的良好性能。
| [1] |
GE Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562. |
| [2] |
DUNIA R, QIN S J, EDGAR T F, et al. Use of principal component analysis for sensor fault identification[J]. Computers & Chemical Engineering, 1996, 20: S713-S718. |
| [3] |
MACGREGOR J F, JAECKLE C, KIPARISSIDES C, et al. Process monitoring and diagnosis by multiblock PLS methods[J]. AIChE Journal, 1994, 40(5): 826-838. DOI:10.1002/aic.690400509 |
| [4] |
JIA M, XU H, LIU X, et al. The optimization of the kind and parameters of kernel function in KPCA for process monitoring[J]. Computers & Chemical Engineering, 2012, 46: 94-104. |
| [5] |
BOTRE C, MANSOURI M, NOUNOU M, et al. Kernel PLS-based GLRT method for fault detection of chemical processes[J]. Journal of Loss Prevention in the Process Industries, 2016, 43: 212-224. DOI:10.1016/j.jlp.2016.05.023 |
| [6] |
ZHAO H, LAI Z. Neighborhood preserving neural network for fault detection[J]. Neural Networks, 2019, 109: 6-18. DOI:10.1016/j.neunet.2018.09.010 |
| [7] |
KANO M, TANAKA S, HASEBE S, et al. Monitoring independent components for fault detection[J]. AIChE Journal, 2003, 49: 969-976. DOI:10.1002/aic.690490414 |
| [8] |
NELSEN R B. An introduction to copulas [M]. Springer Science & Business Media, 2007.
|
| [9] |
DISSMANN J, BRECHMANN E C, CZADO C, et al. Selecting and estimating regular vine copulae and application to financial returns[J]. Computational Statistics & Data Analysis, 2013, 59: 52-69. |
| [10] |
SHE D, MISHRA A K, XIA J, et al. Wet and dry spell analysis using copulas[J]. International Journal of Climatology, 2016, 36(1): 476-491. DOI:10.1002/joc.4369 |
| [11] |
JOE H. Families of m-variate distributions with given margins and m (m-1)/2 bivariate dependence parameters[J]. Lecture Notes-Monograph Series, 1996, 120-141. |
| [12] |
BEDFORD T, COOKE R M. Vines——a new graphical model for dependent random variables[J]. The Annals of Statistics, 2002, 30(4): 1031-1068. |
| [13] |
REN X, TIAN Y, LI S. Vine copula-based dependence description for multivariate multimode process monitoring[J]. Industrial & Engineering Chemistry Research, 2015, 54(41): 10001-10019. |
| [14] |
周南, 李绍军. 基于核密度估计的R-Vine Copula选择及其在故障检测中的应用[J]. 高校化学工程学报, 2019, 33(2): 443-452. ZHOU N, LI S J. R-Vine Copula selection based on kernel density estimation and its application in fault detection[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 443-452. DOI:10.3969/j.issn.1003-9015.2019.02.024 |
| [15] |
JAWORSKI P, DURANTE F, HARDLE W K, et al. Copula theory and its applications[M]. New York: Springer, 2010.
|
| [16] |
KAUERMANN G, SCHELLHASE C. Flexible pair-copula estimation in D-vines using bivariate penalized splines[J]. Statistics and Computing, 2014, 24(6): 1081-1100. DOI:10.1007/s11222-013-9421-5 |
| [17] |
BOWMAN A W. An alternative method of cross-validation for the smoothing of density estimates[J]. Biometrika, 1984, 71(2): 353-360. DOI:10.1093/biomet/71.2.353 |
| [18] |
SILVERMAN B W. Density estimation [M]. London: Chapman & Hall, 1986.
|
| [19] |
WAND M P, JONES M C. Multivariate plug-in bandwidth selection[J]. Computational Statistics, 1994, 9(2): 97-116. |
| [20] |
HURVICH C M, TSAI C L. Regression and time series model selection in small samples[J]. Biometrika, 1989, 76(2): 297-307. DOI:10.1093/biomet/76.2.297 |
| [21] |
ROSENKRANTZ D J, STEARNS R E, LEWIS I P M. An analysis of several heuristics for the traveling salesman problem[J]. SIAM Journal on Computing, 1977, 6(3): 563-581. DOI:10.1137/0206041 |
| [22] |
HYNDMAN R J. Computing and graphing highest density regions[J]. The American Statistician, 1996, 50(2): 120-126. |
| [23] |
DOWNS J J, VOGEL E F. A plant-wide industrial process control problem[J]. Computers & Chemical Engineering, 1993, 17(3): 245-255. |
| [24] |
REN X, ZHU K, CAI T, et al. Fault detection and diagnosis for nonlinear and non-gaussian processes based on copula subspace division[J]. Industrial & Engineering Chemistry Research, 2017, 56(40): 11545-11564. |
| [25] |
曾根保, 李绍军, 钱锋. 醋酸脱水系统的动态模拟及其控制[J]. 计算机与应用化学, 2008, 25(5): 533-536. ZENG G B, LI S J, QIAN F. Dynamic simulation and control of acetic acid dehydration system[J]. Computers and Applied Chemistry, 2008, 25(5): 533-536. DOI:10.3969/j.issn.1001-4160.2008.05.005 |




