气固循环流化床已广泛应用于化工以及能源等领域,其中气固颗粒的聚集(聚团)是气固流动最重要的特征之一,对气固相间传热和传质都有较大的影响[1-3]。有关循环流化床内颗粒聚团特性如划分聚团标准[4-5],聚团尺寸和聚团分布[6-7]等都有大量的研究。聚团速度是聚团的另一个重要特性,相关的研究不论是实验还是模拟都较多,LIU等[8]模拟结果显示聚团速度在时间和空间分布都呈现出明显的非均匀性。
XU等[9]采用光导纤维和高速相机对提升管内颗粒聚团进行了研究,发现聚团速度是中心大边壁小。聚团速度测量方法主要有光导纤维探头[10-11]和高速数字相机[12-13]等,由于光纤探头测量的范围有限,且探头会干涉气固流动,对聚团测量产生较大的影响,因此许多研究者采用高速数字相机来研究循环流化床内的聚团。高速数字相机不会对流化床内的气固两相流场造成任何的干扰,同时能对床内的二维流动进行高分辨率识别,可以对流化床内的颗粒和聚团的运动提供直接可视化分析,因此本项目采用高速摄像机来探测聚团速度。众所周知,提升管内同时存在向上运动和向下运动的聚团[14-15],然而多数研究者将上下行聚团作为一个整体进行分析,而没有对上行聚团和下行聚团各自的特性进行研究,如上行/下行聚团的数量及其分布,聚团速度大小及分布等。本研究将上行和下行聚团分别进行统计分析,考察上行/下行聚团各自特性。同时,聚团的横向运动对流化床内的径向混合以及径向传热和传质都有影响,然而目前对此研究报道还较少,因此本项目也对聚团的横向速度进行研究。
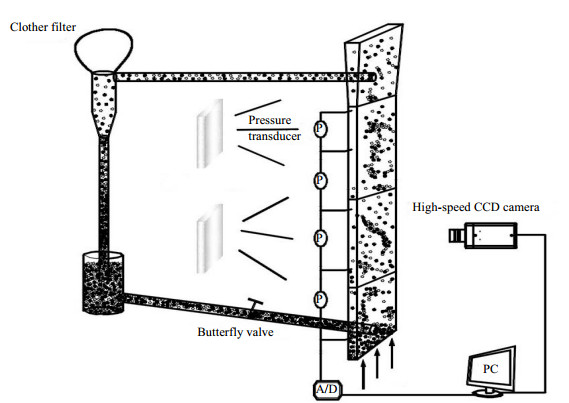
2 实验装置实验是在自行搭建的由透明有机玻璃制造的循环流化床中进行,为方便相机捕捉流化床中的聚团,采用片状二维循环流化床,循环流化床提升管尺寸为150 mm ×15 mm×3 000 mm,装置如图 1所示。试验采用压缩空气为流化气体,表观气速在3.09~4.92 m·s-1;固体物料是石英砂颗粒,平均粒径215 μm,密度为2 500 kg·m-3,颗粒循环流率在20~45 kg·m-2·s-1。
|
图 1 实验装置示意图 Fig.1 Schematic diagram of the experimental setup of a 2D circulating fluidized bed |
循环流化床内气固流动图像的采集是利用加拿大NorPix公司的FR-340-10G高速摄像系统来进行的,高速摄像机设置在提升管的正前方,光源灯固定在提升管的背部,采用100 W的LED灯,分布均匀。为了获得聚团的动态特性,采用较高的采样频率,每秒采集500帧图像,分辨率为2 048×728,采样时长8 s,每次试验采集4 000张图像,选取其中2 000张图片进行处理。
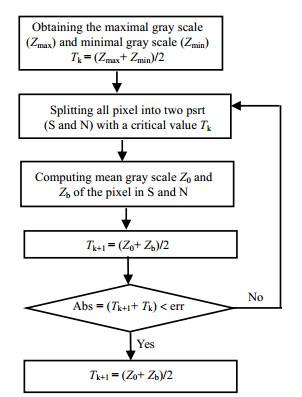
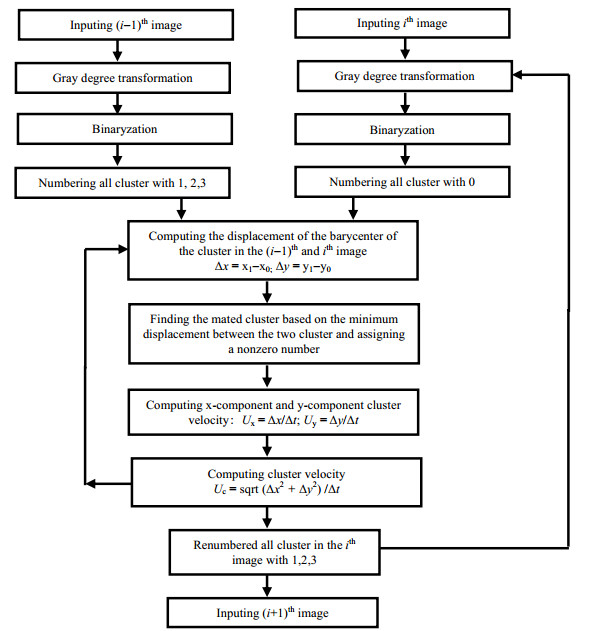
本研究采用迭代寻优法来求取最佳的阀值,计算流程如图 2所示。图像处理过程:首先裁剪出有效区域,并对图像进行均值滤波、腐蚀与膨胀等形态处理,再将数字图像由RGB图转化为灰度图,最后进行二值化将聚团从流场的分离出来,并设定当量直径大于2 mm的黑色区域为聚团,如图 3的黑色区域。其中区分聚团和非聚团区域的阀值是关键,对于流场中运动物体的研究,通常有欧拉方法(EVT)和拉格朗日方法(LVT),由于拉格朗日方法是跟踪物体的运动过程,以运动的物体作为研究对象,通过跟踪物体运动的轨迹线而获得物体的时空特性,其数学表达式如式(1)。本研究通过跟踪记录聚团质心随时间的变化来获得聚团速度,具体过程:首先连续读入相邻两张图片并分离出聚团,对每个聚团进行编号;然后将第1张图中第1个聚团的质心坐标与第2张图中每个聚团的质心坐标求差,其中距离最小的聚团即为同一聚团,将此距离与采样时间间隔相比, 就是该聚团的聚团速度,第1张图片中每个聚团都重复上述步骤就可以获得聚团速度,计算示例结果如图 3所示,图 3中左边图为原始图,右边为处理后的二值图。式(2)~(4)给出一个计算聚团的横向,纵向和整体速度的示例,需要说明的是为了便于观察聚团的移动,这两张图片时间间隔较大,计算的是图片中间聚团的速度。整个图像处理过程采用Matlab语言编程,可以连续计算数千张图片中的上万个聚团的运动速度,其流程框图如图 4所示。
| $\overrightarrow r = \overrightarrow r ({x_0}, {y_0}, t) \Rightarrow \left\{ \begin{gathered} x = x({x_0}, {y_0}, {z_0}, t) \\ y = y({x_0}, {y_0}, {z_0}, t) \\ \end{gathered} \right.$ | (1) |
| ${U_{{\rm{cx}}}} = \frac{{\left| {{x_1} - {x_0}} \right|}}{{\Delta t}} = {0.024_{}}{\rm{m}} \cdot {\rm{ }}{{\rm{s}}^{ - 1}}$ | (2) |
| ${U_{{\rm{cy}}}} = \frac{{\left| {{y_1} - {y_0}} \right|}}{{\Delta t}} = {0.136_{}}{\rm{m}} \cdot {\rm{ }}{{\rm{s}}^{ - 1}}$ | (3) |
| ${U_{\rm{c}}} = \frac{{{y_1} - {y_0}}}{{\left| {{y_1} - {y_0}} \right|}}\frac{{\sqrt {\Delta {x^2} - \Delta {y^2}} }}{{\Delta t}} = {0.138_{}}{\rm{m}} \cdot {\rm{ }}{{\rm{s}}^{ - 1}}$ | (4) |
|
图 2 迭代法计算最佳阈值流程图 Fig.2 Flow chart of optimum threshold calculation via iterative procedure |

|
图 3 聚团速度计算示意图 Fig.3 Schematic diagram of cluster velocity calculation Ug = 4.32 m·s-1, Gs = 30 kg·m-2·s-1 |
|
图 4 拉格朗日法计算聚团速度流程图 Fig.4 Flow chart of cluster velocity calculation by Lagrange approach |
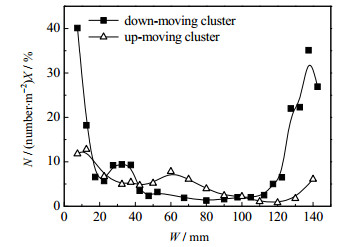
提升管内颗粒聚团既有向上运动,也有向下运动的聚团,其运动规律并不完全一致,因此需要对上行聚团和下行聚团分别进行统计研究。RHODES等[18]实验显示,在边壁区域不但有下行的聚团,也存在上行的聚团,同时在中心区域也存在下行的聚团,即在提升管整个床层都同时存在上行和下行聚团,这与本实验结果一致,如图 5所示。
|
图 5 不同运动方向聚团的径向分布 Fig.5 Radial density distribution of up-moving and down-moving clusters Gs = 30 m·s-1, Ug = 4.32 m·s-1 |
图 5表示了在床层底部区域(H = 200~500 mm)上行和下行聚团密度的径向分布,统计了2 000张图片在床层底部区域聚团密度(单位面积出现聚团的个数)。下行聚团密度在径向分布极不均匀,下行聚团主要集中在边壁区域(距壁面20~30 mm),超过80%的下行聚团位于此区域,这与CARLOS [19]采用离散颗粒模型计算获得的结果一致。上行聚团密度总体较小,在径向分布相对均匀。在边壁区域下行聚团数量远大于上行聚团数量,而在中心区域上行聚团略多于下行聚团。其原因在于循环流化床颗粒浓度的环核结构分布,在边壁区域颗粒浓度高,气体速度较小造成边壁区域大量颗粒返混下行,形成下行聚团的机会较多;而在中心区域,颗粒浓度低,气体速度大,颗粒被气体携带上行,因此形成较多的上行聚团。
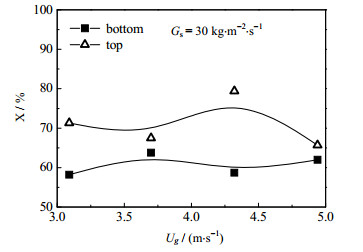
图 6显示了气速和下行聚团百分比的关系,图中每个点表示2 000张图片所含的下行聚团数量与总聚团数量之比,线是各数据点的光滑连接,用以观察下行聚团百分比随气速的变化趋势。从图中可以看出气速对下行聚团的数量没有明显的影响;不论是在提升管顶部还是在底部,向下运动的聚团数量都比向上运动的聚团数量要多,占聚团总数的60%~70%。在顶部向下运动的聚团所占百分比更高一些,在70%左右,而底部向下运动的聚团在60%左右。顶部占比较大是因为顶部聚团主要是由于颗粒受出口限制返流形成的,因此下行聚团更多。
|
图 6 下行聚团百分比与表观气速的关系 Fig.6 Relationship between downward cluster ratio and superficial gas velocity |
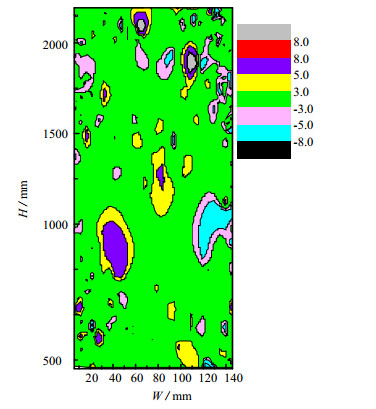
图 7显示聚团速度在提升管整个床层(200~2 400 mm)的分布,聚团速度分布很分散,图中可以看出绿色区域占床层面积大,说明大多数聚团速度在[-3, 3] m·s-1,与文献报告的结果一致[20]。下行速度大于8 m·s-1的聚团主要在床层边壁区域和底部区域,且比较分散,说明较大的聚团速度主要出现在提升管底部和床层边壁区域,这是由于边壁区域颗粒浓度大[21],形成较大的聚团,因而下行速度大;在提升管底部易形成较大聚团[22]且聚团密度较大[23],聚团下行速度较大。聚团速度大于8 m·s-1的上行聚团较少,在床层上部中心区域出现一小块,这是由于中心区域气体速度较大,而且上部区域形成的聚团密度较小[22],因此上行聚团速度较大。
|
图 7 聚团速度全床分布 Fig.7 Distribution of cluster velocity in the whole bed Ug= 4.32 m·s-1, Gs = 45 kg·m-2·s-1 |
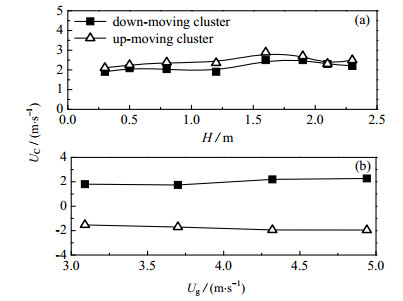
图 8(a)显示了聚团速度沿轴向的变化,上升聚团速度要略大于下降聚团的速度,这是由于下降的聚团与气体流动方向相反,气体对聚团的曳力阻碍聚团下行;与之相反,气体曳力对上升的聚团有拖曳作用。不论是上升聚团还是下降聚团,聚团总体速度沿轴向有轻微的增大,在顶部区域略有减小,这是由于顶部区域的颗粒返混受制于提升管出口结构,由于采用较强约束的T形出口结构,因而颗粒返混较大,造成聚团速度有所下降。图 8(b)显示聚团速度随气速的变化,随着床层表观气速的增加,无论是上行还是下行聚团的速度都增大,这与LI的研究结果相同。LI [24]采用光纤对提升管内聚团速度进行了研究,对提升管低部848个聚团以及顶部435个聚团进行研究发现聚团速度随气体速度的增加而增大。这是由于随着气速的增加,颗粒的速度也增大,因而颗粒聚团速度也随着增大。
|
图 8 聚团速度轴向分布以及表观气速的关系 Fig.8 Axial distribution of cluster velocity and relationship between cluster velocity and gas velocity Ug = 4.32m·s-1, Gs = 30 kg·m-2·s-1 |
聚团除了沿竖直方向的运动外,由于气体的湍动作用聚团在横向也移动,横向运动对于气固在径向的混合以及传热和传质都有重要影响。
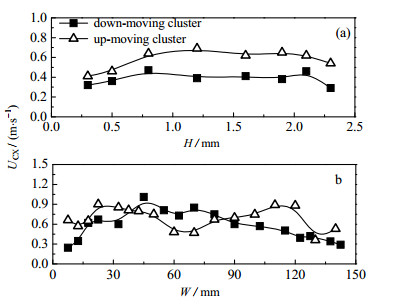
图 9(a)显示了聚团横向速度截面平均值沿床层高度的变化,从图中可以看出聚团横向速度在整个床层变化较小,在0.3~0.6 m·s-1,只是在床层底部略有增加而在顶部略有下降;上行聚团横向速度较下行聚团横向速度要大,这是由于上行聚团在中心区域较多,而中心区域气体速度较大,因而受气体湍动作用较强,造成聚团横向速度较大。图 9(b)显示了在提升管底部区域聚团横向速度的径向分布,不论是上行还是下行聚团,其横向速度在中心区域较大,而边壁区域较小,这是由于在边壁区域气体速度较小,对聚团的湍动作用就弱。在边壁区域上行聚团的横向速度要略大下行聚团的横向速度,这是由于在边壁区域下行聚团体积较大,向下运动的惯性较大,因此聚团侧向移动较小;而在中心区域下行聚团的横向速度大于上行聚团速度,这是由于中心区域气体速度较大,上行聚团与气体顺流,与气体作用较小;而下行的聚团与上行的气体逆流碰撞,产生较大的湍动作用促使聚团的横向移动速度增大。
|
图 9 聚团横向速度的轴径向分布
Fig.9 Distribution of the x- component of cluster velocity
(a) axial distribution (b) radial distribution Ug = 4.32 m·s-1, Gs = 30 kg·m-2·s-1 |
采用高速数字相机对提升管内气固流动进行摄像,在Matlab上编制了图像处理程序,通过对2 000张数字图片中上万个聚团进行统计分析,获得结论如下:
(1) 采用拉格朗日方法计算聚团速度,能获得较为准确的聚团速度;
(2) 下行聚团数量较多,占总聚团数量的60%~70%,边壁区域下行聚团密度远大于上行聚团,中心区域上行聚团密度略大于下行聚团;
(3) 聚团速度主要分布在[-3, 3] m·s-1且随表观气速增加而增加,上升聚团速度略大于下降聚团速度;
(4) 聚团横向速度截面平均值较小,聚团横向速度在靠近边壁区域较小,中心区域较大。
| 符号说明: | |||
| Gs | —颗粒截面循环流率,kg·m-2·s-1 | Ug | —表观气速,m·s-1 |
| H | —床层高度,m | W | —床层宽度,mm |
| N | —聚团密度,number·cm-2 | x1 | —聚团质心初始横坐标,mm |
| T | —阈值 | x2 | —聚团质心终点横坐标,mm |
| Uc | —聚团总体速度,m·s-1 | y1 | —聚团质心初始纵坐标,mm |
| Ucx | —聚团横向速度,m·s-1 | y2 | —聚团质心初始纵坐标,mm |
| Ucy | —聚团纵向速度,m·s-1 | Z | —灰度值 |
| [1] |
HOU B L, LI H Z. Relationship between flow structure and transfer coefficient in fast fluidized bed[J]. Chemical Engineering Journal, 2010, 157(2/3): 509-519. |
| [2] |
CHEN H Z, LI H Z, MOOSON K. Two-phase structure in a high-density downer[J]. Powder Technology, 2005, 158(1/2/3): 115-123. |
| [3] |
DONG W G, WANG W, LI J H. A multiscale mass transfer model for gas-solid riser flow: Part 1-Sub-grid and simple test[J]. Chemical Engineering Science, 2008, 63(10): 2798-2810. DOI:10.1016/j.ces.2008.01.038 |
| [4] |
LUBEN C G, RENATO C S, APARECIDO H A, et al. Cluster identification and characterization in the riser of a circulating fluidized bed from numerical simulation results[J]. Applied Mathematical Modelling, 2008, 32(3): 327-340. DOI:10.1016/j.apm.2006.12.005 |
| [5] |
SOONG C. TUZLA K. CHEN J. Identification of particle clusters in circulating fluidized beds[C]//Avidan A A. Fluidized Bed Technology Ⅳ Engineering Foundation. New York. 1993: 615-620.
|
| [6] |
DUVVURI S. A model for cluster size in risers[J]. Powder Technology, 2010, 199(1): 48-54. |
| [7] |
FIRUZIAN N, SOTUDEH-GHAREBAGH R, MOSTOUFI N. Experimental investigation of cluster properties in dense gas-solid fluidized beds of different diameters[J]. Particuology, 2014, 16: 69-74. DOI:10.1016/j.partic.2013.10.008 |
| [8] |
LIU H P, LU H L. Numerical study on the cluster flow behavior in the riser of circulating fluidized beds[J]. Chemical Engineering Journal, 2009, 150(2/3): 374-384. |
| [9] |
XU X, ZHU J. A new method for the determination of cluster velocity and size in a circulating fluidized bed[J]. Industrial Engineering Chemistry Research, 2012, 51(4): 2143-2151. DOI:10.1021/ie200849h |
| [10] |
陈恒志, 李洪钟. 高密度下行床反应器的流体力学特性[J]. 化工学报, 2005, 56(3): 455-461. CHEN H Z, LI H Z. Hydrodynamics in high-density downer reactor[J]. Journal of Chemical Industry and Engineering, 2005, 56(3): 455-461. DOI:10.3321/j.issn:0438-1157.2005.03.015 |
| [11] |
漆小波, 黄卫星, 祝京旭, 等. 循环流化床提升管中颗粒速度的径向分布及其沿轴向的发展[J]. 高校化学工程学报, 2002, 16(2): 168-173. QI X B, HUANG W X, ZHU J X, et al. Radial distribution and axial development of particle velocities in a long CFB riser[J]. Journal of Chemical Engineering of Chinese Universities, 2002, 16(2): 168-173. DOI:10.3321/j.issn:1003-9015.2002.02.010 |
| [12] |
YANG J S, ZHU J. A novel method based on image processing to visualize clusters in a rectangular circulating fluidized bed riser[J]. Powder Technology, 2014, 254: 407-415. DOI:10.1016/j.powtec.2014.01.015 |
| [13] |
ZOU R P, YU A B. The packing of spheres in a cylindrical container - the thickness effect[J]. Chemical Engineering Science, 1995, 50(9): 1504-1507. DOI:10.1016/0009-2509(94)00483-8 |
| [14] |
HELLIAND E, OCCELLI R, TADRIST L. Numerical study of cluster formation in a gas particle circulating fluidized bed[J]. Powder Technology, 2000, 110(3): 210-221. DOI:10.1016/S0032-5910(99)00260-0 |
| [15] |
TAKEUCHI H, PYATENKO A, TATANO H. Flowing behavior of particles in the riser of a circulating fluidized bed[C]//Kwauk M, Li J. Circulating Fluidized Bed Technology V. Beijing: Science Press, 1996: 164-169.
|
| [16] |
CHEN H Z, TIAN X X, GU S M, et al. Effect of mixing state of binary particles on bubble behavior in 2D fluidized bed[J]. Chemical Engineering Communications, 2018, 205(8): 1119-1128. DOI:10.1080/00986445.2018.1434160 |
| [17] |
BUSCIGLIO A, VELLA G, MICALE G. On the bubbling dynamics of binary mixtures of powders in 2D gas-solid fluidized beds[J]. Powder Technology, 2012, 231: 21-34. DOI:10.1016/j.powtec.2012.07.033 |
| [18] |
RHODES M, MINEO H, HIRAMA T. Particle motion at the wall of a circulating fluidized-bed[J]. Powder Technology, 1992, 70(3): 207-214. DOI:10.1016/0032-5910(92)80055-2 |
| [19] |
CARLOS A E, VARAS E A, PETERS J F, et al. CFD-DEM simulations and experimental validation of clustering phenomena and riser hydrodynamics[J]. Chemical Engineering Science, 2017, 169: 246-258. DOI:10.1016/j.ces.2016.08.030 |
| [20] |
XU J, LU X F, WANG Q H, et al. Visualization of gas-solid flow characteristics at the wall of a 60-meter-high transparent CFB riser[J]. Powder Technology, 2018, 336: 180-190. DOI:10.1016/j.powtec.2018.05.059 |
| [21] |
陈巨辉, 殷维杰, 孟诚, 等. 亚格子湍动能模型及循环流化床气固湍流特性分析[J]. 高校化学工程学报, 2016, 30(4): 800-805. CHEN J H, YIN W J, MENG C, et al. A SGS turbulent kinetic energy model and analysis of gas-solid turbulent flow in circulating fluidized beds[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(4): 800-805. |
| [22] |
WEI F, YANG G Q, JIN Y, et al. The characteristics of cluster in a high density circulating fluidized[J]. The Canadian Journal of Chemical Engineering, 1995, 73(5): 650-655. DOI:10.1002/cjce.5450730508 |
| [23] |
MODAL D N, KALLIO S, SAXEN H, et al. Experimental study of cluster properties in a two-dimensional fluidized bed of Geldart B particles[J]. Powder Technology, 2016, 291: 420-436. DOI:10.1016/j.powtec.2015.12.031 |
| [24] |
LI H Z, ZHU Q S, LIU H Z, et al. The cluster-size distribution and motion behavior in a fast fluidized-bed[J]. Powder Technology, 1995, 84(3): 241-246. DOI:10.1016/0032-5910(95)02985-B |




