2. 江南大学 轻工过程先进控制教育部重点实验室, 江苏 无锡 214122
2. Key Laboratory of Advanced Process Control for Light Industry Ministry of Education, Jiangnan University, Wuxi 214122, China
随着我国绿色发展战略的不断推进,各类污水治理和达标排放显得尤为重要。因此,近些年已有大量相关研究表明,对污水处理过程实施优化控制是提升污水处理厂治理效率的有效方法[1-3]。活性污泥法是一种广泛应用的污水生物处理工艺,该工艺利用活性污泥的生物凝聚、吸附和氧化作用[4-6],从而达到净水的效果。考虑到污水处理过程是一个极为复杂的非线性系统,污水处理厂需改善其设备和运行策略,使其在复杂工况下依然能达到严格的出水水质标准,并尽可能降低能源消耗。从生化反应机理来看[7],好氧区溶解氧质量浓度ρO和厌氧区硝态氮质量浓度ρNO是决定出水水质的2个关键因素,可以通过鼓风机和回流泵分别对两者进行调节,但其运行会消耗大量能源。因此,设计能耗和出水水质的多目标优化问题,对ρO和ρNO的设定值进行寻优能有效降低能耗、提升出水水质。
近十年来,在污水处理过程优化控制中,多目标优化控制渐渐取代单目标优化控制成为研究的主流。根本原因是单目标优化控制在问题考虑上较为单一,一般会侧重于降低污水处理过程中的能耗[8-11],导致出水水质提升较少。多目标优化控制能够弥补这一缺陷,在对ρO和ρNO设定值寻优的过程中,会综合考虑降低能耗和提升出水水质。
Hreiz等[12]采用精英多目标遗传算法能降低能耗和提升出水水质,从而获取第2生化反应单元硝态氮质量浓度ρNO2和第5生化反应单元溶解氧质量浓度ρO5的设定值。Vega等[13]将污水处理过程分成不同层次,分层控制,上层采用静态、动态优化算法,对ρO5、ρNO2设定值进行寻优,下层引入非线性模型预测控制技术对设定值进行跟踪。Han等[14]提出了一种非线性多目标模型预测控制策略,该策略利用自组织径向基函数神经网络建立溶解氧质量浓度和硝态氮质量浓度的预测模型,再构建多梯度优化控制器来调节ρO5和ρNO2。Qiao等[15]提出了一种动态多目标优化控制方法,利用模糊神经网络建立能耗和出水水质的预测模型,再通过非支配排序遗传算法寻取ρO5和ρNO2的最优设定值。周红标等[16]提出了一种基于pareto支配和分解的混合多目标骨干粒子群算法,能有效帮助粒子跳出局部最优,再利用自组织模糊神经网络对选取的ρO5、ρNO2设定值进行跟踪控制。乔俊飞等[17]提出一种基于知识的改进多目标粒子群算法,通过记忆算法优化过程中历史信息,引导种群搜索,获取优质的ρO5、ρNO2设定值,再采用模糊神经网络建立跟踪控制器。以上多目标优化控制方法在降低能耗、提升出水水质两方面均取得了较优的效果,但是出水氨氮质量浓度ρNh和出水总氮质量浓度ρNtot存在较长时间的峰值超标,如此处理后排出的污水不会对水生植物的生长及人类的健康造成影响[18]。
2016年Santín等[19]首次提出决策控制系统用于抑制ρNh和ρNtot超标,该方法利用入水氨氮质量浓度和入水流量对ρNh和ρNtot进行预测,然后通过控制外加碳源流量和内回流流量实现对ρNh和ρNtot的调节,以避免超标。栗三一等[20]在此基础上引入了ρO5、ρNO2作为ρNh和ρNtot预测模型的输入,并利用基于密度的局部搜索多目标算法对能耗和出水水质进行优化,使得控制策略在抑制超标和降低能耗方面同时得到了提升。两者虽然均能有效避免ρNh和ρNtot超标,但在实施超标抑制控制策略时无法兼顾多目标优化控制,并且控制策略仍可改进。
综上所述,本研究提出一种污水处理优化控制过程的超标抑制控制方法,以解决ρNh和ρNtot的峰值超标问题。利用AdaBoost-LSSVM对ρNh和ρNtot建立预测模型,并加入ρO3、ρO4、ρO5和ρNO2作为模型输入,可降低能耗、提升出水水质、提高ρNh和ρNtot的预测精度。在超标抑制控制中,增加对ρO3、ρO4和外回流的控制,以抑制ρNh超标,使得该控制策略在抑制超标的同时,仍能通过控制内回流对ρNO2设定值进行跟踪,保证出水水质。此外,改进外回流和外加碳源的控制策略,进而降低超标抑制过程中所产生的能耗。
2 污水处理优化控制过程描述 2.1 BSM1模型基准仿真模型1号(benchmark simulation model No.1, BSM1)是国际水质协会和欧盟科学技术合作组织合作开发的污水处理基准仿真平台 [21]。该模型共有5个生化反应单元[22]。第1个生化反应单元的物料平衡公式为
| $ \frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}t}} = \frac{1}{{{V_1}}}({q}_{V, {\text{a}}} \cdot {\rho _{\text{a}}} + {q}_{V, {\text{r}}} \cdot {\rho _{\text{r}}} + {q}_{V, {\text{0}}} \cdot {\rho _{\text{0}}} + {r_{\text{1}}} \cdot {V_1} - {q_V}_{_1} \cdot {\rho _1}) $ | (1) |
式中:ρ1为第1个生化反应单元中基础组分的质量浓度,mg·L−1;V1为第1个生化反应单元的体积,m3;
第2-5单元的生化反应如下:
| $ \frac{{{\rm{d}}{\rho _k}}}{{{\rm{d}}t}} = \frac{1}{{{V_k}}}({q_{V, k - 1}} \cdot {\rho _{k - 1}} + {r_k} \cdot {V_k} - {q}_{V, k} \cdot {\rho _k}){\text{ (}}k{\text{ = 2, 3, 4, 5)}} $ | (2) |
式中:ρk为第k个生化反应单元中基础组分的质量浓度,mg·L−1;Vk为第k个生化反应单元的体积,m3;rk为第k个生化反应单元中基础组分的反应速率;
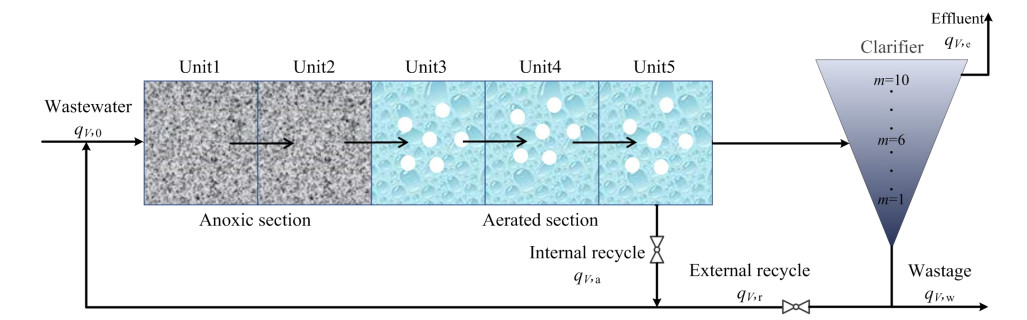
图 1为BSM1模型的总体结构,该模型的2个评价指标为总能耗(overall cost index,OCI)和出水水质(effluent quality index,EQI),OCI的定义如下:
| $ {\rm{OCI}} = \frac{1}{{T \times {1\;}000}}\int_{{t_0}}^{{t_{\text{f}}}} {[4{q_{V, {\text{a}}}}(t) + 8{q_{V, {\text{r}}}}(t) + 50{q_{V, {\text{w}}}}(t)} + \frac{8}{{1.8}}\sum\limits_{i = 1}^5 {{V_i}{K_{{\text{La}}i}}(t)]} {\rm{d}}t + \frac{{400}}{T}\int_{{t_0}}^{{t_f}} {\sum\limits_{i = 1}^5 {{q_{V, {{\text{EC}}i}}}} } {\rm{d}}t $ | (3) |
|
图 1 BSM1模型的总体结构 Fig.1 Overall framework of BSM1 model |
式中:t0为开始时间;tf为结束时间;T为采样周期;Vi为第i个生化反应单元的体积;KLai为第i个生化反应单元的曝气量;
EQI的定义如下:
| $ {\rm{EQI}} = \frac{1}{{T \times {1\;}000}}{\int_{{t_0}}^{{t_f}} {[{\rm{2TSS}}(t) + {\rm{COD}}(t) + 3{\rho _{{\text{NKj}}}}(t) + 10{\rho _{{\text{NO}}}}(t) + {\rm{2BO}}{{\rm{D}}_5}(t)]} \;}{q_{V, {\text{e}}}}(t){\rm{d}}t $ | (4) |
式中:TSS为固体悬浮物质量浓度,mg·L−1;COD为化学需氧量,mg·L−1;ρNKj为凯氏氮质量浓度,mg·L−1;ρNO为硝态氮质量浓度,mg·L−1;BOD5为5日生化需氧量;
BSM1模型下的污水处理过程共14 d,可分为112个周期进行优化控制。在该过程中,ρO3、ρO4、ρO5和ρNO2是决定OCI和EQI的4个关键因素,而这4个因素分别可以通过
污水处理过程多目标优化问题可描述如下:
| $ \begin{array}{l} {\text{mi}}{{\text{n}}\;}\;{f_{{\text{OCI}}}}(\mathit{\boldsymbol{x}}), {f_{{\text{EQI}}}}(\mathit{\boldsymbol{x}}) \\ {\text{s}}{\text{.t}}{\text{. }}\left\{ \begin{array}{l} {\rho _{{\text{Nh, e, avg}}}} < {4\;}{\text{mg}} \cdot {{\text{L}}^{ - 1}} \\ {\rho _{{\text{Ntot, e, avg}}}} < {18\;}{\text{mg}} \cdot {{\text{L}}^{ - 1}} \\ {\text{BO}}{{\text{D}}_{{\text{5, e, avg}}}} < {10\;}{\text{mg}} \cdot {{\text{L}}^{ - 1}} \\ {\text{CO}}{{\text{D}}_{{\text{e, avg}}}} < {100\;}{\text{mg}} \cdot {{\text{L}}^{ - 1}} \\ {\text{TS}}{{\text{S}}_{{\text{e, avg}}}} < {30\;}{\text{mg}} \cdot {{\text{L}}^{ - 1}} \\ {\mathit{\boldsymbol{l}}_i} \leqslant {\mathit{\boldsymbol{x}}_i} \leqslant {\mathit{\boldsymbol{u}}_i}, i{\text{ = 1, 2, 3, 4}} \end{array} \right. \end{array} $ | (5) |
式中:fOCI(x)和fEQI(x)分别为能耗和出水水质的优化目标函数;x=[ρO3, ρO4, ρO5, ρNO2]为决策向量;s.t.为约束条件,是污水处理的5个出水水质参数指标;ρNh, e, avg为出水氨氮质量浓度平均值;ρNtot, e, avg=ρNKj, e, avg+ρNO, e, avg为出水总氮质量浓度平均值(ρNKj, e, avg为出水凯氏氯质量浓度平均值,ρNO, e, avg为出水硝态氮质量浓度平均值);li和ui分别为各决策变量的上、下界。
各优化周期经多目标优化算法优化后,需从其获得的pareto解集A中选取一组偏好解作为ρO3、ρO4、ρO5和ρNO2控制器的设定值,具体的选取流程如下:
Step1 将pareto解集A中所有解分别作为当前优化周期控制器的设定值,并获取各解对应该优化周期的出水氨氮质量浓度平均值。
Step2 选取出水氨氮质量浓度平均值最小的一组解作为各PID控制器的设定值。
该选取方法能有效降低出水氨氮质量浓度平均值、提升出水水质,并且将选取的设定值应用于超标抑制控制其所需能耗也随之降低。
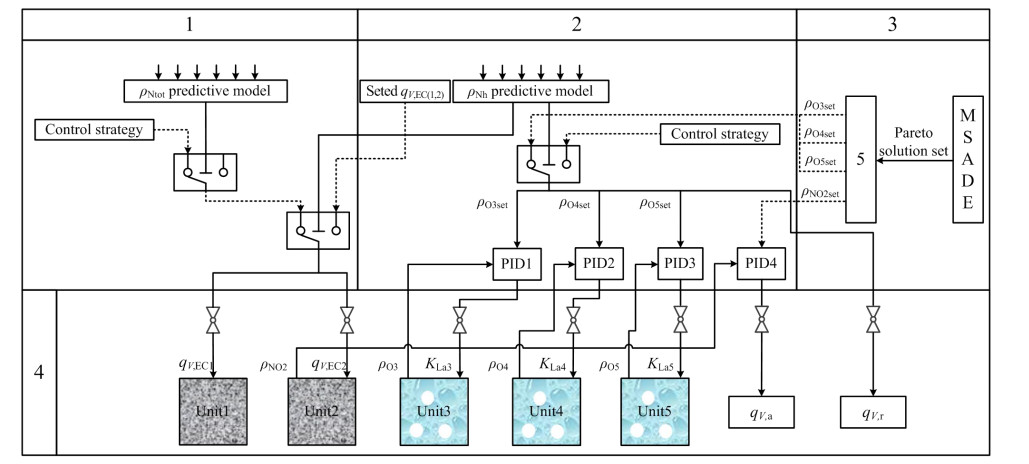
3 超标抑制控制策略为避免污水处理过程中出现ρNh和ρNtot超标,本研究设计的超标抑制控制方法利用AdaBoost-LSSVM方法建立ρNh和ρNtot的预测模型,对ρNh、ρNtot的实时预测。若未超标,则一直对当前优化周期的设定值进行跟踪控制;若超标,则引入抑制ρNh、ρNtot超标的抑制控制策略。具体控制结构如图 2所示。
|
图 2 超标抑制控制总体结构 Fig.2 Overall framework of over-standard suppression control 1. excessive total nitrogen concentration in effluent suppression module 2. excessive ammonia nitrogen concentration in effluent suppression module 3. multi-objective optimization module 4. controlled object 5. set value selection |
AdaBoost算法是Freund和Schapire于1997年提出的[24],打破了单一预测模型仅在预测误差较小样本上的优势[25],根据预测误差更新样本权值,使得误差较大的样本受到重视,权值更新后的样本将被用来训练下一个新的子预测模型,最终在子预测模型结果组合的过程中,整体预测误差较小的子预测模型将被赋予较大的加权值。本研究利用AdaBoost算法来整合最小二乘支持向量机(least squares support vector machines,LSSVM) [26]训练的多个子模型,在建模的过程中逐步优化各子模型的权重,然后根据权重将子模型融合起来,构成本研究的AdaBoost-LSSVM模型。
AdaBoost算法的具体实现步骤如下:
Step1 初始化样本权值w1k:
| $ {\mathit{\boldsymbol{w}}_{1k}} = \frac{1}{N}\;(k = 1, 2, \cdot \cdot \cdot , N) $ | (6) |
式中:N为训练样本的数量。
Step2 For m=1, 2, …, M, m为子预测模型的数量:
(1) 建立m个子预测模型,并利用各子预测模型获得训练集的预测结果Gm(xk),k=1, 2, …, N,其中,xk为训练集中的辅助变量。
(2) 计算各训练样本预测的相对误差emk:
| $ {\mathit{\boldsymbol{e}}_{mk}} = \frac{{|{\mathit{\boldsymbol{y}}_k} - {G_m}({\mathit{\boldsymbol{x}}_k})|}}{{{E_m}}} $ | (7) |
式中:yk为训练集中的主导变量,Em为第m个子预测模型对训练样本预测的最大误差。
(3) 计算第m个子预测模型的权重am:
| $ {\mathit{\boldsymbol{a}}_m} = \frac{{{\mathit{\boldsymbol{e}}_m}}}{{1 - {\mathit{\boldsymbol{e}}_m}}} $ | (8) |
式中:em为第m个子预测模型误差率。
(4) 更新样本权重wm+1, k:
| $ {\mathit{\boldsymbol{w}}_{m + 1, k}} = \frac{{{\mathit{\boldsymbol{w}}_{mk}}}}{{{\mathit{\boldsymbol{Z}}_m}}}\mathit{\boldsymbol{a}}_m^{1 - {\mathit{\boldsymbol{e}}_{mk}}} $ | (9) |
式中:Zm为归一化因子。
Step3 组合子预测模型的结果,得到模型的最终预测值G(xk):
| $ G({\mathit{\boldsymbol{x}}_k}) = \frac{{\sum\limits_{m = 1}^M {{{\ln }\;}(\frac{1}{{{\mathit{\boldsymbol{a}}_m}}}){G_m}({\mathit{\boldsymbol{x}}_k})} }}{{\sum\limits_{m = 1}^M {{{\ln }\;}(\frac{1}{{{\mathit{\boldsymbol{a}}_m}}})} }} $ | (10) |
AdaBoost-LSSVM模型中,LSSVM的核函数选取了高斯径向基核函数K(x, xk):
| $ K(\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_k}) = {\text{ex}}{{\text{p}}\;}{\text{(}} - \frac{{{\text{||}}\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_k}{\text{|}}{{\text{|}}^2}}}{{2{\sigma ^2}}}{\text{)}} $ | (11) |
式中:
LSSVM算法中,惩罚因子γ影响模型的预测精度。本研究为测试γ对氨氮和总氮预测模型的影响,子预测模型γ的取值范围定为3×102到3×109。从表 1可以看出,氨氮和总氮预测模型中子预测模型的数量过多,预测性能提升率明显下降;子预测模型的数量过少,该集成学习模型的预测性能相较于单一模型提升较小。最终,子预测模型的数量设定为4,γ分别定为3×103、3×104、3×105和3×106,可避免出现过拟合或者欠拟合,还能提升整个模型的泛化性能。表中RMSE为均方根误差。
|
|
表 1 各子预测模型数量下预测模型精度 Table 1 Prediction model accuracy under the number of sub-prediction models |
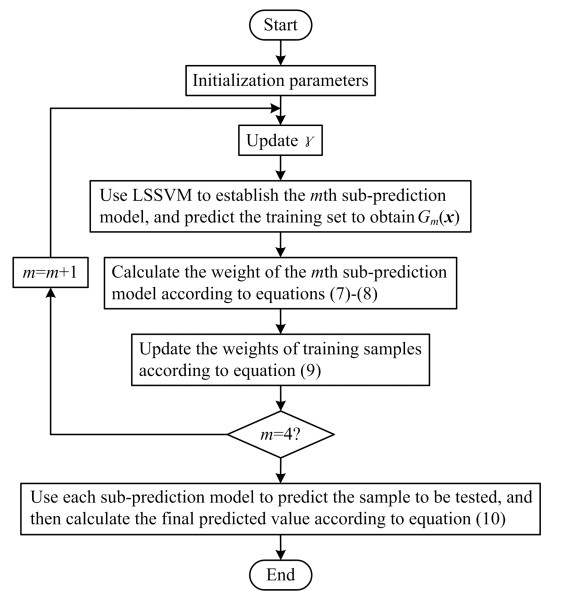
AdaBoost-LSSVM建模流程如图 3所示。
|
图 3 AdaBoost-LSSVM建模流程图 Fig.3 AdaBoost-LSSVM modeling flow chart |
由式(1)和(2)可以发现,ρNh和ρNtot除了与污水的入水流量及其自身入水质量浓度相关,还与生化反应池中13种基础组分质量浓度相关。在污水处理过程中,厌氧区的硝态氮主要包含硝酸盐氮和亚硝酸盐氮,经过反硝化反应会产生一部分氨氮,而好氧区将溶解氧质量浓度保持在3 mg·L−1以下能促进硝化反应去除氨氮,将氨氮转化成硝酸盐氮,两者比其他基础组分对氨氮浓度的影响大。此外,考虑到好氧区有3个单元,仅控制某一单元溶解氧质量浓度会出现氨氮去除不达标的情况,对好氧区溶解氧质量浓度实现全面控制可有效弥补该不足。因此,本研究选取入水流量、入水氨氮质量浓度、生化反应池中3、4、5分区溶解氧质量浓度和第2分区硝态氮质量浓度作为建立出水氨氮质量浓度预测模型的输入。
总氮中无机氮部分的主要成分为氨氮和硝态氮,氨氮质量浓度受溶解氧和硝态氮质量浓度的影响较大,而硝态氮又是总氮的主要成分。因此,本研究选取入水流量、入水总氮质量浓度、生化反应池中3、4、5分区溶解氧质量浓度和第2分区硝态氮质量浓度作为建立出水总氮质量浓度预测模型的输入。
3.2.2 数据采集及建模本研究考虑了污水处理过程中从入水到各生化反应单元及出水的延时因素[20],采集到各辅助变量的数据应与延时后采集到的ρNh和ρNtot相对应,建立的预测模型能对ρNh和ρNtot进行预测,相应的控制策略便能提前实施,以避免ρNh和ρNtot超标。
因为设定值ρO3set、ρO4set、ρO5set和ρNO2set的优化范围分别为0.7~1.7、1~2、2~3和0.5~2 mg·L−1,所以数据采集时,网格搜索法以步长0.2共获得875种设定值组合,并分别赋予各PID控制器,在BSM1模型上运行14 d,每30 min采样一次,共获得579 250组数据,526 590组作训练集,52 660组作测试集。
利用AdaBoost-LSSVM建模方法,建立ρNh和ρNtot的预测模型,具体的模型输入结构如图 4(a)~(b)所示。

|
图 4 出水氨氮和总氮质量浓度预测模型输入 Fig.4 Input of prediction model for effluent ammonia nitrogen and total nitrogen concentration 1. influent flow 2. influent ammonia nitrogen concentration 3. influent total nitrogen concentration 4. unit 3 dissolved oxygen concentration 5. unit 4 dissolved oxygen concentration 6. unit 5 dissolved oxygen concentration 7. unit 2 nitrate concentration |
此前,Santin等[19]选取入水氨氮质量浓度、入水流量和温度作为预测模型的输入,栗三一等[20]增加了第2单元硝态氮质量浓度和第5单元溶解氧质量浓度作为预测模型的输入,本研究去除了温度因素,增加了第3、4单元溶解氧质量浓度。表 2选取RMSE作为3种方法所建模型性能的评价标准,从中可以看出,本研究的预测模型精度较其他2种方法有较大的提升。
|
|
表 2 预测模型精度对比 Table 2 Accuracy comparison of prediction models |
当ρNh预测值超标且小于6 mg·L−1时,增加qV, r至120 000 m3·d−1,从而对流入第1个生化反应单元的氨氮质量浓度进行稀释,该稀释过程持续至入水氨氮峰值到达第3个生化反应单元,而后将ρO3set、ρO4set、ρO5set设为优化调节范围内的最大值,并根据第3个生化反应单元的氨氮质量浓度ρNh3来调节qV, r,考虑到qV, r过大会导致回流到生化反应池后氨氮和总氮质量浓度大幅上升,不利于超标抑制控制,因此,其可调节范围为0~100 000 m3·d−1。具体的调节原理为:若ρNh3过高,则减少qV, r,以增加水力停留时间,使硝化反应更充分,提升去除氨氮的效果;若ρNh3降低了,则可增加qV, r,从而稀释氨氮质量浓度。
根据仿真试验,经过多目标优化控制后的ρNh3不会超过14 mg·L−1,于是本研究设计了式(12)用于调节qV, r:
| $ {q}_{V, {\rm{r}}} = (14 - {\rho _{{\text{Nh3}}}}) \times {15\;}000 $ | (12) |
当ρNh预测值超标且大于6 mg·L−1时,反硝化过程的脱氮要求很高,需将第1、2生化反应单元的外加碳源流量qV, EC1和qV, EC2均设为5 m3·d−1,促进氨氮和硝酸盐的吸收,提升脱氮效果并降低总氮质量浓度,其他控制策略与小于6 mg·L−1时一致。
当ρNh预测值达标且第5生化反应单元氨氮质量浓度低于3 mg·L−1时,则结束出水氨氮超标抑制控制,恢复至多目标优化控制。
3.4 出水总氮质量浓度超标抑制控制当ρNtot预测值超标且ρNh预测值小于6 mg·L−1时,根据式(13)计算所需外加碳源总量qEC,其取值范围为0~7 m3·d−1,并将其分配给qV, EC1和qV, EC2,两者的上限值均为5。若qV, EC≤5,则qV, EC1= qV, EC;若qV, EC > 5,则qV, EC1=5,qV, EC2= qV, EC −5。
| $ {q}_{V, {{\text{EC}}}} = ({\rho _{{\text{Ntot}}}} - 18) \times 2 $ | (13) |
当ρNtot预测值达标且第5生化反应单元总氮浓度低于13.5 mg·L−1时,则结束出水总氮超标抑制控制,恢复至多目标优化控制。
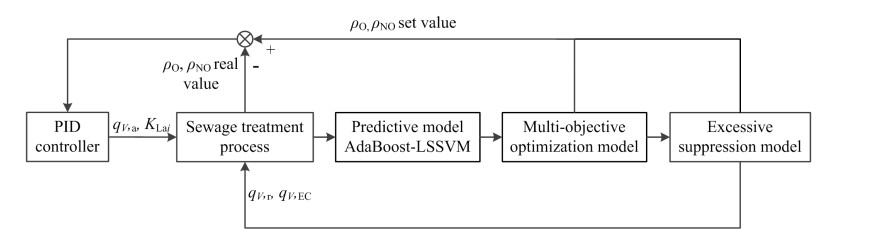
3.5 超标抑制优化控制过程整个超标抑制优化控制过程的框架结构如图 5所示,超标抑制控制策略的实施建立在污水处理优化控制的基础上,通过AdaBoost-LSSVM预测模型实时预测ρNh和ρNtot,并根据预测结果调整控制策略。未超标,则保持多目标优化控制,通过PID控制器调节KLai和qV, a,实现对ρO、ρNO设定值的跟踪控制,从而降低能耗、提升出水水质;超标,则加入超标抑制控制策略,根据ρNh、ρNtot的超标情况调整ρO、ρNO设定值、qV, r和qV, EC,避免两者超标。因此,该优化控制过程能够兼顾能耗、出水水质的优化和ρNh、ρNtot超标的抑制。
|
图 5 超标抑制优化控制结构图 Fig.5 Structure diagram of over-standard suppression optimization control |
本实验在污水处理多目标优化控制过程的基础上,加入了ρNh和ρNtot超标抑制控制方法,并与现有的超标抑制控制方法相比较,经验证本研究的控制方法既能兼顾能耗和出水水质,也能避免ρNh和ρNtot超标。所有实验均基于国际基准仿真平台BSM1。
4.1 污水处理多目标优化控制将多目标优化控制方法应用于BSM1模型下的污水处理过程,该过程选取的仿真数据是晴天条件下的污水数据。整个仿真过程为14 d,分为112个周期进行优化控制,每个优化周期是3 h。各优化周期内利用多目标优化算法对ρO3set、ρO4set、ρO5set和ρNO2set进行寻优,并通过PID控制器对其进行实时跟踪,以保证降低能耗、提升出水水质。
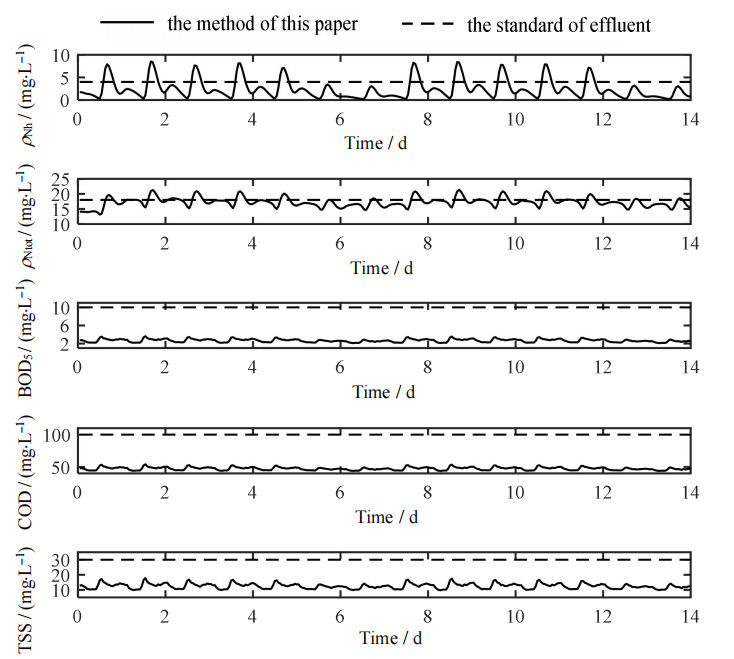
图 6为采用上述优化控制方法获得的5种出水水质参数变化情况,由式(5)中的出水水质参数可以看出,BOD5、COD和TSS不存在超标,并且远低于出水标准,而ρNh和ρNtot均存在较长时间的超标。因此,需设计策略抑制ρNh和ρNtot超标。
|
图 6 出水水质参数变化情况 Fig.6 Changes of effluent water quality parameters |
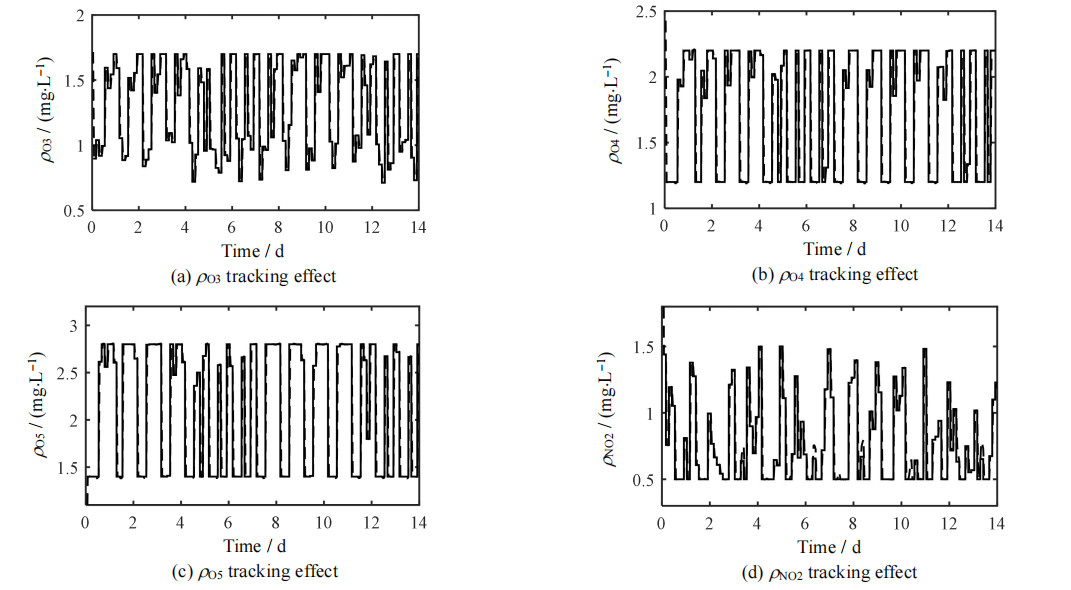
图 7(a)~(d)为4个PID控制器跟踪ρO3set、ρO4set、ρO5set和ρNO2set,ρO3set、ρO4set、ρO5set的跟踪效果良好,ρNO2set的跟踪过程中虽存在小部分的超调,但整体效果也较好。
|
图 7 控制器的跟踪效果
Fig.7 Tracking effect of controller
concentration:  real value real value  set value set value
|
表 3给出了本研究多目标优化控制方法与其他现有多目标优化控制方法应用于污水处理过程的效果对比。其中,Openloop为开环控制;ESN为文献[27]提出的基于状态回声网络的优化控制方法;dMOPSO为文献[17]提出的基于分解的多目标粒子群算法的优化控制方法;NSGA2-DLS为文献[20]提出的基于密度的局部搜索NSGA2算法与神经网络相结合的优化控制方法。从表中可以看出,本研究多目标优化控制方法的5项出水水质参数均达标;在OCI方面,本研究的多目标优化控制方法取得了最优的结果,比开环控制方法降低了3.41%;在EQI方面,本研究的多目标优化控制方法比开环控制方法降低了6.47%,虽没有取得最优的结果,但与最优的ESN方法仅差0.45%。综上分析,本研究多目标优化控制方法能有效降低能耗、提升出水水质。
|
|
表 3 各多目标优化控制方法的效果对比 Table 3 Effect comparison of various multi-objective optimization control methods |
在多目标优化控制方法中加入超标抑制控制方法,并将其应用于污水处理过程,以抑制ρNh和ρNtot超标。
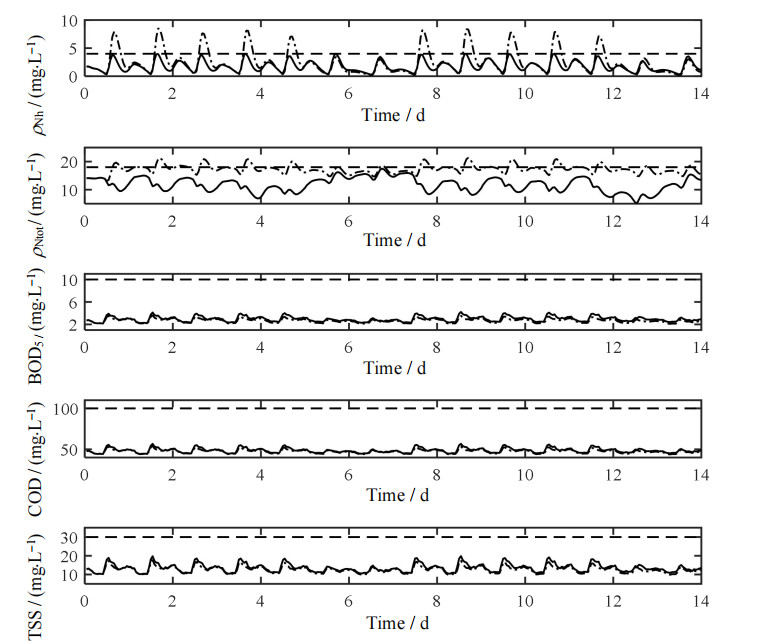
图 8为多目标优化控制中加入超标抑制控制前后5项出水水质参数的变化情况对比。从图中可以看出,加入超标抑制控制后,ρNh和ρNtot的超标峰值得到了有效的抑制,并且不存在超标情况,BOD5、COD和TSS变化较小,依然满足出水标准。
|
图 8 加入超标抑制控制前后出水水质参数的变化情况
Fig.8 Changes of effluent quality parameters before and after adding over-standard suppression control
 multi-objective optimal control multi-objective optimal control the standard of effluent the standard of effluent excessive suppression control excessive suppression control
|
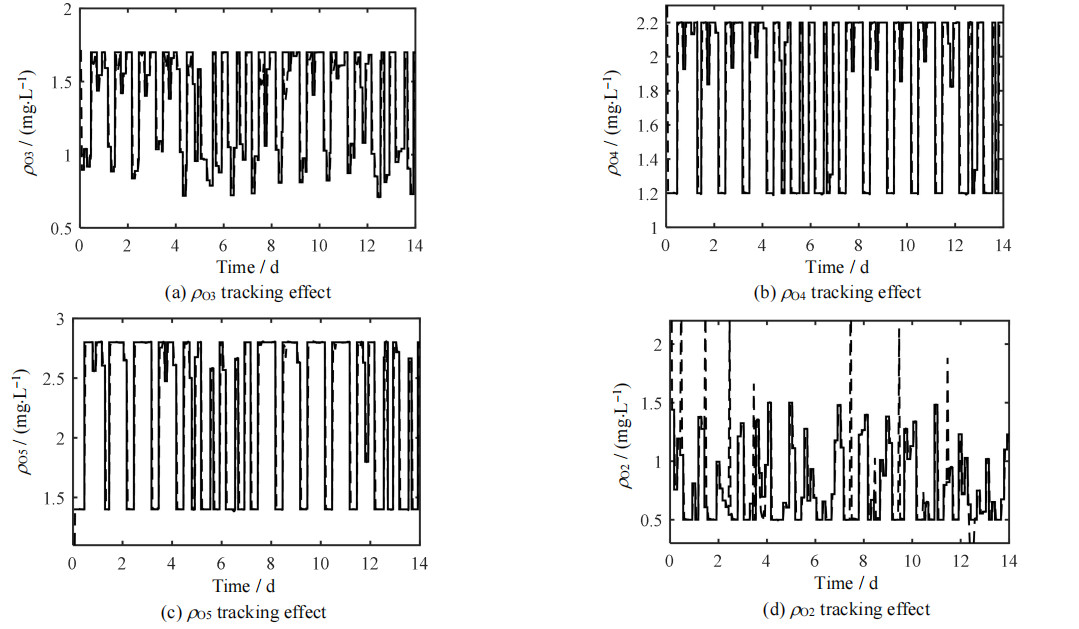
图 9(a)~(d)为加入超标抑制控制后设定值ρO3set、ρO4set、ρO5set和ρNO2set的跟踪效果,从图中可以看出,ρO3set、ρO4set、ρO5set依然能保持较好的跟踪效果,ρNO2set虽存在部分超标,但能很快地调节过来。文献[19]、[20],在切换至抑制ρNh超标的控制策略后,依然是选择qV, a作为操作变量,用以调节ρNh,却牺牲了对于ρNO2set的跟踪控制。本研究引入qV, r作为调节ρNh的操作变量,既能保证对各设定值的跟踪控制,又能有效抑制ρNh超标。
|
图 9 加入超标抑制控制后控制器的跟踪效果
Fig.9 Tracking effect of controller after adding over-standard suppression control
concentration:  real value real value  set value set value
|
为了进一步地验证本研究方法在抑制ρNh和ρNtot超标、降低能耗、提升出水水质3方面的有效性,表 4给出了本研究控制方法与Jeppsson[28]、Nopens[29]、Flores-Alsina[30]、Santin[19]、栗三一等[20]采用的控制方法的效果对比,其中,P为超标时长占整个污水处理过程时长的百分比。从表 4中可以看出,本研究的控制方法取得了最低的能耗和最优的出水水质,并且ρNh和ρNtot的超标抑制效果也为最佳。
|
|
表 4 各超标抑制控制方法的效果对比 Table 4 Comparison of the effects of various over-standard suppression control methods |
本研究提出的控制方法是在一种污水处理优化控制过程中融入超标抑制控制,既能高效地抑制出水氨氮和总氮浓度超标,又能降低能耗、提升出水水质。在预测模型方面,将AdaBoost算法与LSSVM相结合,并增加第3、4生化反应单元的溶解氧浓度作为模型输入,建立的能耗、出水水质、出水氨氮和总氮质量浓度预测模型精度取得了较大的提升;在抑制ρNh和ρNtot超标方面,设计的超标抑制控制方法有效避免ρNh和ρNtot超标。此外,该控制方法中引入了外回流替代内回流作为调节出水氨氮质量浓度的操作变量,使得内回流在超标抑制控制阶段能够继续对第2生化反应单元的硝态氮质量浓度设定值进行跟踪控制,为该阶段降低能耗、提升出水水质提供了保障。因此,本研究提出的超标抑制控制方法可为污水处理优化过程避免ρNh和ρNtot超标提供思路。
| [1] |
BAYRAM A, KANKAL M, TAYFUR G, et al. Prediction of suspended sediment concentration from water quality variables[J]. Neural Computing and Applications, 2014, 24(5): 1079-1087. DOI:10.1007/s00521-012-1333-3 |
| [2] |
PRASSE C, STALTER D, SCHULTE-OEHLMANN U, et al. Spoilt for choice: A critical review on the chemical and biological assessment of current wastewater treatment technologies[J]. Water Research, 2015, 87(15): 237-270. |
| [3] |
闵佳峰, 彭鑫, 李智, 等. 考虑微生物风险的城市污水处理多目标优化控制[J]. 高校化学工程学报, 2020, 34(6): 1482-1491. MIN J F, PENG X, LI Z, et al. Multi-objective optimal control of urban wastewater treatment considering microbiological risk[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(6): 1482-1491. DOI:10.3969/j.issn.1003-9015.2020.06.020 |
| [4] |
OTURAN M A, AARON J. Advanced oxidation processes in water/wastewater treatment: principles and applications. A review[J]. Critical Reviews in Environmental Science and Technology, 2014, 44(23): 2577-2641. DOI:10.1080/10643389.2013.829765 |
| [5] |
DAI H, CHEN W, LU X. The application of multi-objective optimization method for activated sludge process: a review[J]. Water Science & Technology, 2016, 73(2): 223-235. |
| [6] |
LU Q, WU H Y, LI H Y, et al. Enhanced biological nutrient removal in modified carbon source division anaerobic anoxic oxic process with return activated sludge pre-concentration[J]. Chinese Journal of Chemical Engineering, 2015, 23(6): 1027-1034. DOI:10.1016/j.cjche.2014.11.013 |
| [7] |
SWEETAPPLE C, FU G, BUTLER D. Multi- objective optimisation of wastewater treatment plant control to reduce greenhouse gas emissions[J]. Water Research, 2014, 55(15): 52-62. |
| [8] |
OSTACE G S, BAEZA J A, GUERRERO J, et al. Development and economic assessment of different WWTP control strategies for optimal simultaneous removal of carbon, nitrogen and phosphorus[J]. Computers & Chemical Engineering, 2013, 53(4): 164-177. |
| [9] |
BÉRAUD B, STEYER J P, LEMOINE C, et al. Towards a global multi objective optimization of wastewater treatment plant based on modeling and genetic algorithms[J]. Water Science & Technology, 2007, 56(9): 109-116. |
| [10] |
张平, 苑明哲, 王宏. 前置反硝化污水生化处理过程优化控制[J]. 信息与控制, 2008(1): 113-118, 128. ZHANG P, YUAN M Z, WANG H. Optimization control of pre-denitrification wastewater biochemical treatment process[J]. Information and Control, 2008(1): 113-118, 128. DOI:10.3969/j.issn.1002-0411.2008.01.019 |
| [11] |
韩广, 乔俊飞, 韩红桂, 等. 基于Hopfield神经网络的污水处理过程优化控制[J]. 控制与决策, 2014, 29(11): 2085-2088. HAN G, QIAO J F, HAN H G, et al. Optimal control of wastewater treatment process based on hopfield neural network[J]. Journal of Control and Decision, 2014, 29(11): 2085-2088. DOI:10.13195/j.kzyjc.2013.0944 |
| [12] |
HREIZ R, ROCHE N, BENYAHIA B, et al. Multi-objective optimal control of small-size wastewater treatment plants[J]. Chemical Engineering Research & Design, 2015, 102: 345-353. |
| [13] |
VEGA P, REVOLLAR S, FRANCISCO M, et al. Integration of set point optimization techniques into nonlinear MPC for improving the operation of WWTPs[J]. Computers & Chemical Engineering, 2014, 68: 78-95. |
| [14] |
HAN H G, QIAN H H, QIAO J F. Nonlinear multiobjective model-predictive control scheme for wastewater treatment process[J]. Journal of Process Control, 2014, 24(3): 47-59. DOI:10.1016/j.jprocont.2013.12.010 |
| [15] |
QIAO J F, ZHANG W. Dynamic multi-objective optimization control for wastewater treatment process[J]. Neural Computing and Applications, 2016, 29(11): 1261-1271. |
| [16] |
周红标, 乔俊飞. 混合多目标骨干粒子群优化算法在污水处理过程优化控制中的应用[J]. 化工学报, 2017, 68(9): 3511-3521. ZHOU H B, QIAO J F. Optimal control of wastewater treatment process using hybrid multi-objective barebones particle swarm optimization algorithm[J]. CIESC Journal, 2017, 68(9): 3511-3521. |
| [17] |
乔俊飞, 韩改堂, 周红标. 基于知识的污水生化处理过程智能优化方法[J]. 自动化学报, 2017, 43(6): 1038-1046. QIAO J F, HAN G T, ZHOU H B. Knowledge-based intelligent optimal control for wastewater biochemical treatment process[J]. Journal of Automatica Sinica, 2017, 43(6): 1038-1046. |
| [18] |
柯仲祥. 污水处理过程中出水水质预测及多目标优化控制[D]. 天津: 天津工业大学, 2021. KE Z X. Prediction of effluent quality and multi-objective optimal control in sewage treatment process [D]. Tianjin: Tianjin Polytechnic University, 2021. |
| [19] |
SANTÍN I, PEDRET C, VILANOVA R, et al. Advanced decision control system for effluent violations removal in wastewater treatment plants[J]. Control Engineering Practice, 2016, 49: 60-75. DOI:10.1016/j.conengprac.2016.01.005 |
| [20] |
栗三一, 乔俊飞, 李文静, 等. 污水处理决策优化控制[J]. 自动化学报, 2018, 44(12): 88-99. LI S Y, QIAO J F, LI W J, et al. Sewage treatment decision optimization control[J]. Journal of Automatica Sinica, 2018, 44(12): 88-99. |
| [21] |
CRISTEA V M, POP C, AGACHI P S, et al. Model predictive control of the waste water treatment plant based on the benchmark simulation model no. 1-bsm1[J]. Computer-Aided Chemical Engineering, 2008, 25(8): 441-446. |
| [22] |
JEPPSSON U, PONS M N. The COST benchmark simulation model-current state and future perspective[J]. Control Engineering Practice, 2004, 12(3): 299-304. DOI:10.1016/j.conengprac.2003.07.001 |
| [23] |
赵杨, 熊伟丽. 基于多策略自适应差分进化算法的污水处理过程多目标优化控制[J]. 化工学报, 2021, 72(4): 2167-2177. ZHAO Y, XIONG W L. Multi-objective optimization control of wastewater treatment process based on multi-strategy adaptive differential evolution algorithm[J]. CIESC Journal, 2021, 72(4): 2167-2177. |
| [24] |
FREUND Y, SCHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139. |
| [25] |
曹莹, 苗启广, 刘家辰, 等. AdaBoost算法研究进展与展望[J]. 自动化学报, 2013, 39(6): 745-758. CAO Y, MIAO Q G, LIU J C, et al. Research Progress and Prospects of AdaBoost Algorithm[J]. Journal of Automatica Sinica, 2013, 39(6): 745-758. |
| [26] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machines classifiers[J]. Neural Network Letters, 1999, 19(3): 293-300. |
| [27] |
乔俊飞, 王莉莉, 韩红桂. 基于ESN的污水处理过程优化控制[J]. 智能系统学报, 2015, 10(6): 831-837. QIAO J F, WANG L L, HAN H G. Optimal control for wastewater treatment process based on ESN neural network[J]. CAAI Transactions on Intelligent Systems, 2015, 10(6): 831-837. |
| [28] |
JEPPSSON U, PONS M N, NOPENS I, et al. Benchmark simulation model No 2: General protocol and exploratory case studies[J]. Water Science and Technology, 2007, 56(8): 67-78. |
| [29] |
NOPENS I, BENEDETTI L, JEPPSSON U, et al. Benchmark simulation model No 2: Finalisation of plant layout and default control strategy[J]. Water Science and Technology, 2010, 62(9): 1967-1974. |
| [30] |
FLORES-ALSINA X, COMAS J, RODRÍGUEZ R I, et al. Evaluation of plant-wide WWTP control strategies including the effects of filamentous bulking sludge[J]. Water Science and Technology, 2009, 60(8): 2093-2103. |




