动力学参数的高精度估计对于鲁棒、可控和安全的工艺设计以及从实验室小试到放大生产都是至关重要的。光谱的应用非常广泛,尤其是在化学分析领域[1-2]。光谱技术通常用于化学反应监测,特别是在紫外可见、拉曼、红外和近红外波长区域。这些数据提供了大量关于反应过程中各物质的瞬态浓度信息[3-4]。一种常用的方法是自建模曲线分辨技术[5-8],它能在不使用任何机理模型或反应系统先验信息的情况下,从光谱测量中得到独立的化学物质量以及相应的吸收光谱和浓度曲线。在得到浓度信息后,反应动力学参数可以通过使用非线性优化拟合进行估计。然而,这种后验动力学建模方法的主要问题是自建模曲线分辨方法存在旋转歧义和强度歧义等问题[9-11],因此会显著降低动力学参数估计的精度。此外,Gauss-Newton-Levenberg-Marquardt方法[12-16]也被广泛应用于反应动力学参数估计,且通常具有良好的性能。这种方法在给定反应动力学参数初值后,通过对描述模型的常微分方程组(ordinary differential equations,ODEs)积分得到相应组分的浓度曲线,然后通过估计预测光谱与测量光谱的误差平方和对动力学参数的灵敏度分析来计算动力学参数的扰动步长,以减小光谱数据的拟合误差。然而,这种方法是序贯的,不适用于不稳定的和病态的ODEs,主要是因为它会导致系统的状态无界以及算法收敛上的困难[17]。还有一种广泛应用的方法是多元曲线分辨交替最小二乘方法[18-19],该方法利用软建模约束和动力学模型约束获得原始测量中存在的所有吸光物质的浓度曲线和相应的纯光谱[20-21]。在估计过程中,用最小二乘法交替更新浓度矩阵和光谱矩阵;然后将模型与浓度数据进行拟合,得到动力学参数。这些交替迭代一直持续到预测光谱和测量光谱的残差平方和几乎没有变化为止。由于在计算过程中没有用到导数信息,这使得收敛过程变得十分缓慢,并且估计的动力学参数精度也不够高。陈伟锋等[22]提出一种反应动力学参数估计的联立求解方法。该方法假设测量过程中的噪声为高斯白噪声,并采用随机微分方程描述带有系统噪声的反应过程。在已知测量噪声方差和系统噪声方差的前提下,利用极大似然估计原理设计了反应动力学参数估计方法。同时提出了测量噪声方差和系统噪声方差的估计方法。以上所述方法针对的测量过程中的噪声均为零均值高斯白噪声,然而在高频率的测量过程中,相邻的测量噪声之间存在相关性,从而导致有色的测量噪声,此外,白色的外部干扰经反馈和积分环节也可以形成有色的测量噪声[23-24],因此需要设计一种针对有色噪声的参数估计方法。本研究针对含有有色噪声的光谱数据,通过测量数据差分,并基于配点法和极大似然估计原则设计了一种反应动力学参数的估计方法。
2 反应动力学参数估计的联立方法反应过程中每个采样时间测得的光谱可以按行排列,形成一个二维矩阵。如果没有测量误差,则比尔·朗伯定律预测了溶液在特定波长λ和给定时间t下的光谱为
| $ d(t, \lambda ) = {c_1}(t){s_1}(\lambda ) + {c_2}(t){s_2}(\lambda ) + ... + {c_{{n_{\text{c}}}}}(t){s_{{n_{\text{c}}}}}(\lambda ) $ | (1) |
式中:ck(t)为第k种吸光物质在t时刻的浓度,sk(λ)为第k种吸光物质在波长λ处的单位浓度的吸光度,nc为吸光物质的数量。假设ntp为时间上的采样点数,nwp为波长维度上的采样点数,比尔·朗伯定律可以用下式表示:
| $ {\mathit{\boldsymbol{D}}} = {\mathit{\boldsymbol{C}}}{{\mathit{\boldsymbol{S}}}^{\text{T}}} + {\mathit{\boldsymbol{E}}} $ | (2) |
式中:D为ntp×nwp的光谱矩阵(每个元素视为一个随机变量),C为ntp×nc的浓度矩阵,S为nwp×nc的吸光度矩阵,E为ntp×nwp的测量误差矩阵,T为转置符,假设每次测量都是相互独立的。
当测量噪声为高斯白噪声时,误差矩阵E的各个分量满足以下形式:
| $ {\zeta _{i, l}} \in N(0, {\delta ^2}) $ |
| $ i = 1, ..., {n_{{\text{tp}}}}, l = 1, ..., {n_{{\text{wp}}}} $ | (3) |
式中:ζi, l为第i个采样时刻第l个采样波长上的测量噪声,服从零均值正态分布N(0, δ2),δ2为正态分布的方差,通常被称为零均值高斯白噪声。
在实际过程中,反应系统可能存在噪声,但本研究不考虑系统噪声,即过程应该建模为如下微分方程和测量光谱模型:
| $ {\text{d}}{\mathit{\boldsymbol{c}}}(t) = f({\mathit{\boldsymbol{c}}}(t), {\mathit{\boldsymbol{\theta }}})dt $ | (4) |
| $ {d_{i, l}} = \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_i}){s_k}({\lambda _l})} + {\zeta _{i, l}}\\ i = 1, ..., {n_{{\text{tp}}}}, l = 1, ...{n_{{\text{wp}}}} $ | (5) |
式中:c(t)为状态变量向量,即各时刻各吸光物质的浓度;θ为反应动力学参数向量,即各步化学反应速率常数;
| $ p({\mathit{\boldsymbol{D}}} - {\mathit{\boldsymbol{C}}}{{\mathit{\boldsymbol{S}}}^{\text{T}}}) = \prod\limits_{i = 1}^{{n_{{\text{tp}}}}} {\prod\limits_{l = 1}^{{n_{{\text{wp}}}}} {p({\zeta _{i, l}})} } $ | (6) |
假设方差是已知的,根据极大似然估计原则,得到如下公式:
| $ \begin{array}{*{20}{c}} {\min \sum\limits_{i = 1}^{{n_{{\text{tp}}}}} {\sum\limits_{l = 1}^{{n_{{\text{wp}}}}} {{{\left( {{d_{i, l}} - \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_i}){s_k}({\lambda _l})} } \right)}^2}/{\delta ^2}} }}\\ {{\rm{s.t.}}\;\;\frac{{{\text{d}}{\mathit{\boldsymbol{c}}}(t)}}{{{\text{d}}t}} = f({\mathit{\boldsymbol{c}}}(t), {\mathit{\boldsymbol{\theta }}})}\\ {{\mathit{\boldsymbol{C}}} \geqslant 0, {\mathit{\boldsymbol{S}}} \geqslant 0} \end{array} $ | (7) |
为求解式(7),用正交配置法将上式中的常微分方程进行离散,选取数值稳定的Radau配置点[25-26]作为插值点,将有限元j上的状态变量表示为
| $ {c^K}(t) = \sum\limits_{m = 0}^K {{l_m}(\tau ){c_{jm}}} {, _{}}t = {t_{pj - 1}} + {h_j}\tau {, _{}}\tau \in [0, 1]\\ {l_m}(\tau ) = \prod\limits_{m' = 0, \ne m}^K {\frac{{(\tau - {\tau _{m'}})}}{{({\tau _m} - {\tau _{m'}})}}} $ | (8) |
式中:cK(t)为拉格朗日插值多项式,K为每个有限元上的插值点个数,lm(τ)为多项式基函数,cjm为有限元j上的第m个插值点。
将式(8)代入微分方程,得到以下配置方程:
| $ \sum\limits_{m = 0}^K {{{\mathop l\limits^ \cdot }_m}(\tau )} {c_{jm}} - {h_j} \cdot f({c_{jm}}, {\mathit{\boldsymbol{\theta }}}) = 0 $ | (9) |
式中:
利用式(8)可计算c(t)在采样时间ti时的值,最终式(7)可变成以下形式:
| $ \min \sum\limits_{i = 1}^{{n_{{\text{tp}}}}} {\sum\limits_{l = 1}^{{n_{{\text{wp}}}}} {{{\left( {{d_{i, l}} - \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_i}){s_k}({\lambda _l})} } \right)}^2}/{\delta ^2}} } $ |
| $ {\rm{s.t.}}\;\;\sum\limits_{m = 0}^K {{{\mathop l\limits^ \cdot }_m}(\tau )} {c_{jm}} - {h_j} \cdot f({c_{jm}}, {\mathit{\boldsymbol{\theta }}}) = 0 $ |
| $ {c^K}({t_i}) = \sum\limits_{m = 0}^K {{l_m}({\tau _i}){c_{jm}}} $ |
| $ {\tau _i} = \frac{{({t_i} - {t_{pj - 1}})}}{{({t_{_{pj}}} - {t_{pj - 1}})}} $ |
| $ {\mathit{\boldsymbol{C}}} \geqslant 0, {\mathit{\boldsymbol{S}}} \geqslant 0 $ |
| $ j = 1, ..., {n_{\text{e}}}, \;m = 1, ..., K $ | (10) |
式中:ne为有限元个数。本研究用基于内点法的IPOPT求解器[27]进行求解,当成功求解式(10)后,便获得了动力学参数、浓度和吸光物质的纯光谱的估计。然而这种方法针对的测量噪声为零均值高斯白噪声,是基于高斯白噪声假设的参数估计方法。
3 基于有色噪声的反应动力学参数估计方法在实际应用中,一阶自回归模型是描述有色噪声的常用模型[24]。其形式如式(11)所示:
| $ {\xi _{i + 1, l}} = \phi {\xi _{i, l}} + \varphi {\zeta _{i, l}} $ |
| $ i = 1, ..., {n_{{\text{tp}}}} - 1{, _{}}l = 1, ..., {n_{{\text{wp}}}} $ | (11) |
式中:ξi+1, l=ϕξi, l+φζi, l为一阶自回归过程;ξi, l为有色噪声;ϕ为自相关系数,描述有色噪声相邻点之间的相关程度;φ为互相关系数,描述有色噪声与高斯白噪声之间的相关程度。
将式(5)中的高斯白噪声ζi, l替换为式(11)所定义的有色噪声,并忽略系统噪声,式(5)转化为以下形式:
| $ {d_{i, l}} = \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_i}){s_k}({\lambda _l})} + {\xi _{i, l}} $ |
| $ {\xi _{i + 1, l}} = \phi {\xi _{i, l}} + \varphi {\zeta _{i, l}} $ |
| $ i = 1, ..., {n_{{\text{tp - 1}}}}{, _{}}l = 1, ..., {n_{{\text{wp}}}} $ | (12) |
通过对同类测量值差分的方法消除有色噪声,令d’i, l=di+1, l-ϕdi, l,将式(12)中的di, l替换为d’i, l,可得以下形式的测量模型:
| $ d{'_{i, l}} = \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_{i + 1}}){s_k}({\lambda _l}) - \phi {c_k}({t_i}){s_k}({\lambda _l})} + \varphi {\zeta _{i, l}} $ |
| $ i = 1, ..., {n_{{\text{tp}}}} - 1{, _{}}l = 1, ..., {n_{{\text{wp}}}} $ | (13) |
此时,模型中已不含有色噪声。
如果假设噪声方差是已知的,那么可以根据式(13)并运用极大似然估计方法,得到如下优化公式:
| $ \min \sum\limits_{i = 2}^{{n_{{\text{tp}}}}} {\sum\limits_{l = 1}^{{n_{{\text{wp}}}}} {{{\left( {{d_{i, l}} - \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_i}){s_k}({\lambda _l})} - \phi \left( {{d_{i - 1, l}} - \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_{i - 1}}){s_k}({\lambda _l})} } \right)} \right)}^2}/{\varphi ^2}{\delta ^2}} } $ |
| $ {\rm{s.t.}}\;\;\frac{{{\text{d}}{\mathit{\boldsymbol{c}}}(t)}}{{{\text{d}}t}} = f({\mathit{\boldsymbol{c}}}(t), {\mathit{\boldsymbol{\theta }}}) $ |
| $ {\mathit{\boldsymbol{C}}} \geqslant 0, {\mathit{\boldsymbol{S}}} \geqslant 0 $ | (14) |
为求解式(14),采用正交配置法将式(14)中的常微分方程进行离散,选取数值稳定的Radau配置点作为插值点。利用式(8)计算c(t)在采样时间ti时的值,式(14)可变成以下形式:
| $ \min \sum\limits_{i = 2}^{{n_{{\text{tp}}}}} {\sum\limits_{l = 1}^{{n_{{\text{wp}}}}} {{{\left( {{d_{i, l}} - \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_i}){s_k}({\lambda _l})} - \phi \left( {{d_{i - 1, l}} - \sum\limits_{k = 1}^{{n_{\text{c}}}} {{c_k}({t_{i - 1}}){s_k}({\lambda _l})} } \right)} \right)}^2}/{\varphi ^2}{\delta ^2}} } $ |
| $ {\rm{s.t.}}\;\;\sum\limits_{m = 0}^K {{{\mathop l\limits^ \cdot }_m}(\tau )} {c_{jm}} - {h_j} \cdot f({c_{jm}}, {\mathit{\boldsymbol{\theta }}}) = 0 $ |
| $ {c^K}({t_i}) = \sum\limits_{m = 0}^K {{l_m}({\tau _i}){c_{jm}}} $ |
| $ {\tau _i} = \frac{{({t_i} - {t_{pj - 1}})}}{{({t_{pj}} - {t_{pj - 1}})}} $ |
| $ {\mathit{\boldsymbol{C}}} \geqslant 0, {\mathit{\boldsymbol{S}}} \geqslant 0 $ |
| $ j = 1, ..., {n_{\text{e}}}{, _{}}m = 1, ..., K $ | (15) |
式(15)便是基于有色噪声假设的参数估计方法。当噪声自相关系数ϕ已知时,ϕ取为真实值;当噪声自相关系数ϕ未知时,ϕ作为未知参数与化学反应动力学参数一同估计。同样,式(15)通过基于内点法的IPOPT求解器成功求解后,便能获得动力学参数、浓度和吸光物质的纯光谱以及噪声自相关系数的估计。
4 仿真分析 4.1 仿真案例描述 4.1.1 仿真案例1考虑一个两步连续反应(A→B,B→C)[22],其中,物质A、B、C为案例1的吸光物质,物质A的初始浓度为1.0×10-3mol·L-1,物质B与物质C的初始浓度均为零。令k1、k2分别为反应A→B和B→C的化学反应速率常数,通过模拟速率为k1 = 2.0 s-1以及k2 = 0.2 s-1的反应机理获得浓度矩阵。将3个具有显著重叠的近红外光谱作为3个假定组分(A、B、C)的纯物质光谱。通过正态分布的随机数产生高斯白噪声,利用式(12)引入有色噪声测量误差。其光谱数据为一300×100的矩阵D1。
取自相关系数和互相关系数分别为ϕ = 0.5和φ = 1.5的有色噪声。有色噪声模型中的高斯白噪声的标准差δ分别取D1的均值(矩阵D1中所有元素的平均值)的1%、3%、5%、10%,由于纯光谱数据矩阵D1的均值约为0.1,则令δ分别等于0.001、0.003、0.005、0.010。纯光谱数据以及有色噪声影响下的光谱数据,如图 1所示。
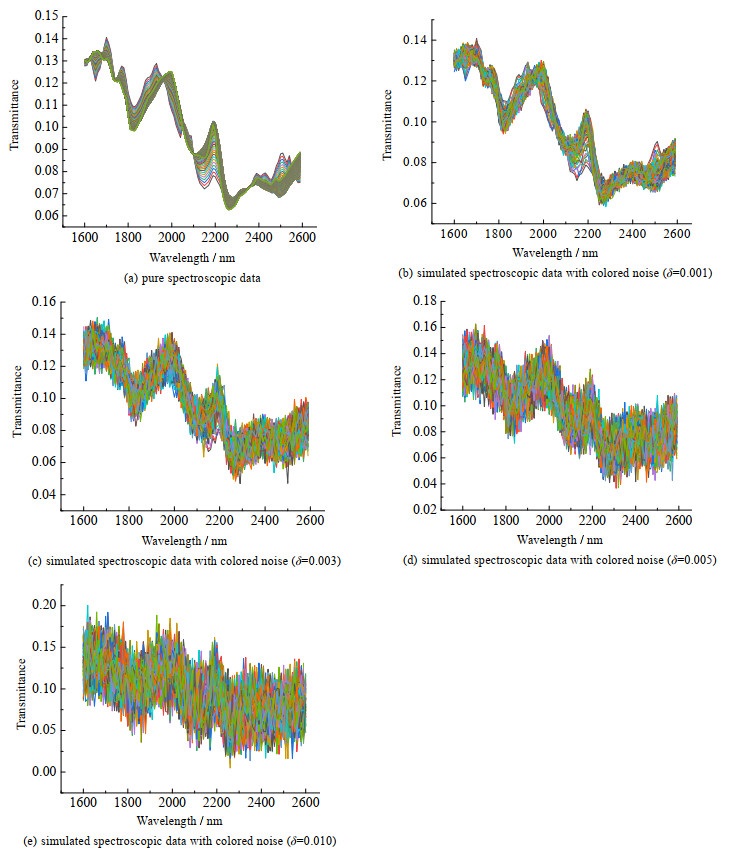
|
图 1 仿真案例1的纯光谱数据和含有色噪声的光谱数据 Fig.1 Spectroscopic data without and with colored noise for case 1 |
考虑一个两步连续反应(D+E→F, 2F→G) [22],其中,物质D、E、F为案例2的吸光物质,物质G为非吸光物质。物质D的初始浓度为1.0 mol·L-1,物质E的初始浓度为0.8 mol·L-1,物质F与物质G的初始浓度均为零。令k1′、k2′分别为反应D+E→F和2F→G的化学反应速率常数,通过模拟速率为k1′= 2.0 s-1以及k2′= 1.0 s-1的反应机理获得浓度矩阵。同样将3个具有显著重叠的近红外光谱作为3个假定组分(D、E、F)的纯物质光谱。其光谱数据为一400×100的矩阵D2。
取自相关系数和互相关系数分别为ϕ = 0.5和φ = 1.5的有色噪声。有色噪声模型中的高斯白噪声的标准差δ分别取D2的均值(矩阵D2中所有元素的平均值)的1%、3%、5%、10%,由于纯光谱数据矩阵D2的均值约为50,则令δ分别等于0.5、1.5、2.5、5.0。
4.2 有色噪声模型完全已知情况下的参数估计结果在有色噪声模型已知的情况下,式(15)中的自相关系数ϕ取真实值0.5。仿真案例1和仿真案例2针对不同强度的有色噪声采用基于高斯白噪声假设的参数估计方法和本研究提出的方法分别做了30组仿真实验,参数估计结果取平均值。仿真实验结果如表 1、2所示,表中White Gaussian noise指基于高斯白噪声假设的参数估计方法,Colored noise指本研究提出的基于有色噪声假设的参数估计方法。
|
|
表 1 有色噪声模型已知情况下仿真案例1参数估计结果 Table 1 Parameter estimation results of case 1 when the colored noise model is known |
|
|
表 2 有色噪声模型已知情况下仿真案例2参数估计结果 Table 2 Parameter estimation results of case 2 when the colored noise model is known |
对比表 1和2中的相对误差可以看到,噪声标准差较小时,基于高斯白噪声假设的参数估计方法得到的结果与本研究提出的基于有色噪声假设的参数估计方法得到的结果较为接近,同时基于有色噪声假设的参数估计方法略优于基于高斯白噪声假设的参数估计方法;当噪声标准差较大时,基于有色噪声假设的参数估计方法明显优于基于高斯白噪声假设的参数估计方法。
4.3 仅知道噪声模型结构的情况下的参数估计结果在仅知道有色噪声是一阶自回归过程的情况下,令式(15)中的自相关系数ϕ为待估参数。通过式(15)同时估计反应动力学参数以及有色噪声的自相关系数。同样,针对仿真案例1和案例2分别做了30组仿真实验,结果取平均值,仿真结果如表 3、4所示。
|
|
表 3 仅噪声模型结构已知时仿真案例1采用基于有色噪声的参数估计方法得到的参数估计结果 Table 3 Parameter estimation results of case 1 obtained by the parameter estimation method based on colored noise when only the noise model structure is known |
|
|
表 4 仅噪声模型结构已知时仿真案例2采用基于有色噪声的参数估计方法得到的参数估计结果 Table 4 Parameter estimation results of case 2 obtained by the parameter estimation method based on colored noise when only the noise model structure is known |
对比表 3和1以及对比表 4和2可知,在仅知道有色噪声是一阶自回归过程的情况下采用基于有色噪声假设的参数估计方法得到的反应动力学参数估计结果与有色噪声模型完全已知情况下的结果仍然是较为接近的,并且该方法估计所得的有色噪声自相关系数与真实值相比,2个仿真案例的相对误差都小于4%,效果较好。
4.4 噪声类型未知情况下的参数估计结果未知光谱中包含的噪声是高斯白噪声还是有色噪声(若是有色噪声,假设为一阶自回归结构)的情况下,采用所提出的方法对反应动力学参数进行估计。用于测试的光谱中包含的测量噪声为4.1节中用于构造有色噪声的高斯白噪声,即仿真案例1的测量噪声为δ等于0.001、0.003、0.005、0.010时的高斯白噪声,仿真案例2的测量噪声为δ分别等于0.5、1.5、2.5、5.0时的高斯白噪声。同样分别进行30次仿真实验,结果取平均值,仿真结果如表 5、6所示。
|
|
表 5 噪声类型未知情况下仿真案例1参数估计结果 Table 5 Parameter estimation results of case 1 when the noise type is unknown |
|
|
表 6 噪声类型未知情况下仿真案例2参数估计结果 Table 6 Parameter estimation results of case 2 when the noise type is unknown |
从表 5和6中可以看出,在测量噪声为高斯白噪声的情况下,基于有色噪声的参数估计方法表现仍非常出色,其参数估计结果与基于高斯白噪声的参数估计方法相比不相上下,且估计出的自相关系数均小于0.02,可由此得出噪声相关性很小、测量噪声为白噪声的结论,这与事实相符合。可见本研究所提出的基于有色噪声假设的参数估计方法能够较好地估计反应动力学参数和噪声自相关系数,并可由此判断出测量噪声的类型(白噪声/有色噪声)。
5 结论光谱技术通常用于化学反应监测,已经发展了几种利用光谱数据进行动力学参数估计的方法。本研究提出了极大似然和联立配置方法的动力学参数估计的统一框架。
目前绝大多数的参数估计方法是基于测量光谱数据中仅含有高斯白噪声的假设来设计的,然而实际测量数据中存在的噪声多为有色噪声,直接沿用基于高斯白噪声设计的方法进行参数估计是不合理的,并且得到的结果也是不可靠的。本研究针对含有有色噪声的光谱数据,通过测量数据差分,并基于配点法和极大似然估计原则设计了一种反应动力学参数的估计方法。在结合多次仿真模拟后得出:在测量噪声为有色噪声的情况下,当噪声标准差较小时,所提出的基于有色噪声假设的参数估计方法略优于基于高斯白噪声假设的参数估计方法;当噪声标准差较大时,基于有色噪声假设的参数估计方法明显优于基于高斯白噪声假设的参数估计方法。此外,本研究所提出的方法还能较好地估计出噪声自相关系数,并可通过估计出的噪声自相关系数准确判别噪声类型(白噪声/有色噪声)。
| [1] |
李雪, 王丽, 刘光宪, 等. 光谱技术分析对BSA糖基化反应的影响[J]. 光谱学与光谱分析, 2021, 41(2): 478-483. LI X, WANG L, LIU G X, et al. Spectroscopic analysis of the influence on BSA glycosylation reaction[J]. Spectroscopy and Spectral Analysis, 2021, 41(2): 478-483. |
| [2] |
李晓静, 王晓杰, 王爽, 等. 光谱分析在水质检测中的应用进展[J]. 盐科学与化工, 2019, 48(9): 12-16. LI X J, WANG X J, WANG S, et al. Application progress of spectral analysis in water quality detection[J]. Journal of Salt Science and Chemical Industry, 2019, 48(9): 12-16. DOI:10.3969/j.issn.2096-3408.2019.09.003 |
| [3] |
ROGGO Y, CHALUS P, MAURER L, et al. A review of near infrared spectroscopy and chemometrics in pharmaceutical technologies[J]. Journal of Pharmaceutical and Biomedical Analysis, 2007, 44(3): 683-700. DOI:10.1016/j.jpba.2007.03.023 |
| [4] |
QUINN A C, GEMPERLINE P J, BAKER B, et al. Fiber-optic UV/visible composition monitoring for process control of batch reactions[J]. Chemometrics and Intelligent Laboratory Systems, 1999, 45(1/2): 199-214. |
| [5] |
LAWTON W H, SYLVESTRE E A. Self modelling curve resolution[J]. Technometrics, 1971, 13(3): 617-633. DOI:10.1080/00401706.1971.10488823 |
| [6] |
LAWTON W H, SYLVESTRE E A, MAGGIO M S. Self modelling nonlinear regression[J]. Technometrics, 1972, 14(3): 513-532. DOI:10.1080/00401706.1972.10488942 |
| [7] |
KARIMVAND S K, PAHLEAHLEVAN A, JAFARI J M, et al. A simple self modelling curve resolution (SMCR) method for two-component systems[J]. Analytica Chimica Acta, 2021, 1154: 338320. DOI:10.1016/j.aca.2021.338320 |
| [8] |
ZADE S V, SAWALL M, NEYMEYR K, et al. Introducing the monotonicity constraint as an effective chemistry-based condition in self-modeling curve resolution[J]. Chemometrics and Intelligent Laboratory Systems, 2019, 190: 22-32. DOI:10.1016/j.chemolab.2019.04.002 |
| [9] |
TAULER R, SMILDE A, KOWALSKI B. Selectivity, local rank, three-way data analysis and ambiguity in multivariate curve resolution[J]. Journal of Chemometrics, 1995, 9(1): 31-58. DOI:10.1002/cem.1180090105 |
| [10] |
DE JUAN A, TAULER R. Multivariate curve resolution (MCR) from 2000:progress in concepts and applications[J]. Critical Reviews in Analytical Chemistry, 2006, 36(3/4): 163-176. |
| [11] |
ABDOLLAHI H, TAULER R. Uniqueness and rotation ambiguities in multivariate curve resolution methods[J]. Chemometrics and Intelligent Laboratory Systems, 2011, 108(2): 100-111. DOI:10.1016/j.chemolab.2011.05.009 |
| [12] |
LWVENBERG K. A method for the solution of certain problems in least squares[J]. Quarterly of Applied Mathematics, 1944, 2(2): 164-168. DOI:10.1090/qam/10666 |
| [13] |
MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. SIAM Journal on Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [14] |
YANG R, ZHANG Y. A method of low concentration methane measurement in tunable diode laser absorption spectroscopy and Levenberg-Marquardt algorithm[J]. Optik-International Journal for Light and Electron Optics, 2020, 224: 165657-165663. DOI:10.1016/j.ijleo.2020.165657 |
| [15] |
LV C Q, MA C F. A Levenberg-Marquardt method for solving semi-symmetric tensor equations[J]. Journal of Computational and Applied Mathematics, 2018, 332: 13-25. DOI:10.1016/j.cam.2017.10.005 |
| [16] |
SHIRANGI M G, EMERICK A A. An improved TSVD-based Levenberg-Marquardt algorithm for history matching and comparison with Gauss-Newton[J]. Journal of Petroleum Science and Engineering, 2016, 143: 258-271. DOI:10.1016/j.petrol.2016.02.026 |
| [17] |
BIEGLER L T. Nonlinear Programming: Concepts, algorithms, and applications to chemical processes[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2010.
|
| [18] |
ISHIHARA S, HATTORI Y, OTSUKA M. MCR-ALS analysis of IR spectroscopy and XRD for the investigation of ibuprofen-nicotinamide cocrystal formation[J]. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2019, 221: 117142-117146. DOI:10.1016/j.saa.2019.117142 |
| [19] |
CASTRO R C, RIBEIRO D S M, SANTOS J L M, et al. Near infrared spectroscopy coupled to MCR-ALS for the identification and quantification of saffron adulterants: Application to complex mixtures[J]. Food Control, 2021, 123: 107776-107783. DOI:10.1016/j.foodcont.2020.107776 |
| [20] |
JUAN A, MAEDER M, MARTINEZ M, et al. Combining hard- and soft- modelling to solve kinetic problems[J]. Chemometrics and Intelligent Laboratory Systems, 2000, 54(2): 123-141. DOI:10.1016/S0169-7439(00)00112-X |
| [21] |
JAUMOT J, JUAN A, TAULER R. MCR-ALS GUI 2.0:New features and applications[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 140(15): 1-12. |
| [22] |
CHEN W F, BIEGLER L T. SALVADOR G M. An approach for simultaneous estimation of reaction kinetics and curve resolution from process and spectral data[J]. Journal of Chemometrics, 2016, 30(9): 506-522. DOI:10.1002/cem.2808 |
| [23] |
黄玉龙, 张勇刚, 李宁, 等. 一种带有色量测噪声的非线性系统辨识方法[J]. 自动化学报, 2015, 41(11): 1877-1892. HUANG Y L, ZHANG Y G, LI N, et al. A nonlinear system identification method with colored measurement noise[J]. Acta Automatica Sinica, 2015, 41(11): 1877-1892. |
| [24] |
WANG X X, PAN Q. Nonlinear Gaussian filter with the colored measurement noise: Proceedings of the 17th International Conference on Information Fusion [C]. Salamanca, Spain: IEEE, 2014: 1-7.
|
| [25] |
BIEGLER L T, CERVANTES A M, WACHTER A. Advances in simultaneous strategies for dynamic process optimization[J]. Chemical Engineering Science, 2002, 57(4): 575-593. DOI:10.1016/S0009-2509(01)00376-1 |
| [26] |
KAMESWARAM S, BIEGLER L T. Convergence rates for direct transcription of optimal control problems using collocation at Radau points[J]. Computational Optimization & Applications, 2008, 41(1): 81-126. |
| [27] |
WACHTERA, BIEGLER LT. On the implementation of a primal-dual interior point filter line search algorithm for large-scale nonlinear programming[J]. Mathematical Programming, 2006, 106(1): 25-57. DOI:10.1007/s10107-004-0559-y |




