2. 中国石油天然气股份有限公司大连石化分公司, 辽宁 大连 116000;
3. 辽宁石油化工大学 机械工程学院, 辽宁 抚顺 113001;
4. 辽宁石油化工大学 环境与安全工程学院, 辽宁 抚顺 113001
2. Dalian Petrochemical Company, PetroChina Company Limited, Dalian 116000, China;
3. School of Mechanical Engineering, Liaoning Petrochemical University, Fushun 113001, China;
4. School of Environmental & Safety Engineering, Liaoning Petrochemical University, Fushun 113001, China
天然气(NG)作为具有高热值且产量丰富的清洁能源,正在逐渐取代煤、石油等化石燃料,成为能源市场中的主要能源之一[1]。将液化天然气(LNG)接收站的LNG气化,可获得能够提供给用户使用的天然气。在LNG的气化过程中,会产生830~860 kJ·kg−1的冷能[2]。回收LNG气化过程中产生的冷能可以提高能源利用率,减少对环境的破坏[3-4]。
Rao等[5]将太阳能驱动的单级有机朗肯循环(SORC)与LNG直接膨胀结合形成联合发电系统,但㶲效率仅为10.62%。Abdollahpour等[6]将太阳能作为热源,设计了以CO2为工质的跨临界有机朗肯循环(TORC)与LNG直接膨胀相结合的系统,而系统的㶲效率仅为8.53%。以上2篇文献说明SORC与LNG直接膨胀结合的系统㶲效率较低。主要原因是SORC的蒸发器中冷、热流股的温差较大,导致㶲损增加[7]。Bao等[8]对双级有机朗肯循环(DORC)进行了研究,系统的热效率和㶲效率分别提高了42.91% 和52.31%。Sun等[9]分别将SORC和DORC与LNG直接膨胀相结合,对2种系统进行比较和优化。优化结果表明DORC系统拥有更好的性能。Li等[10]将有机闪蒸循环(OFC)、有机三边循环(TLC)和SORC进行对比,证明OFC的性能更具优势。Ho等[11]对OFC、以CO2为工质的TORC、以氨水为工质的有机朗肯循环(ORC)和优化后的ORC进行对比。发现使用芳烃作为工质时,OFC能效提高了5%~20%。Lee等[12]将带有两相膨胀机的有机闪蒸循环(OFCT)与亚临界有机闪蒸循环(BOFC)和SORC进行对比,结果发现OFCT的㶲效率高于其余2种循环,文献证明使用两相膨胀机可明显改善单级OFC的性能。
从以上的研究发现DORC和OFC均可用于发电,但只利用其中一种循环,系统性能较低。此外,未见有将DORC和跨临界有机闪蒸循环(TOFC)相结合的冷热电联供系统的相关研究。因此,本研究以LNG为冷源,将2种循环相结合设计出新型冷热电联供系统(CCHP)。构建全新的数学模型,讨论重要参数对系统的影响。对系统进行多目标优化,获得系统的最优热力性能、经济性能以及环境性能。
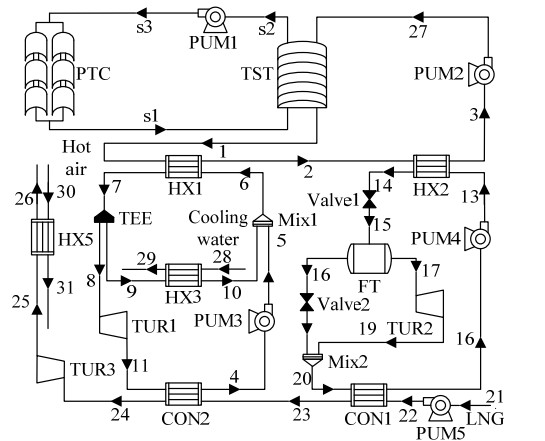
2 系统描述在沿海的LNG接收站周边建立太阳能集热系统,可实现太阳能与LNG冷能的有效结合。图 1为提出的CCHP系统流程图,系统包括太阳能集热子系统、DORC、TOFC和LNG膨胀系统。

|
图 1 CCHP系统流程图 Fig.1 Schematic diagram of CCHP system 1-35, s1-s3. stream |
太阳能集热子系统中therminol-66(流股s2)经过泵1(PUM1)增压后,在槽式太阳能集热器(PTC)中由太阳能加热,流经储热罐(TST)为CCHP系统提供能量。
在DORC中,高压状态的工质R134a(流股6)进入换热器1(HX1)吸收therminol-66的热量达到饱和蒸气状态。高压的蒸气(流股7)通过分流器(TEE)分成2个流股,其中一股(流股8)进入膨胀机1(TUR1)做功发电,之后低压工质为ORC-Ⅱ提供热量;另一股(流股9)用于制热,随后与增压后的工质在混合器1(Mix1)中混合。过冷状态CO2(流股12)通过泵4(PUM4)增压后,在换热器4(HX4)中吸收ORC-Ⅰ的余热(流股11)。而后,饱和蒸气状态的CO2(流股14)进入膨胀机2(TUR2)发电,最后,在冷凝器2(CON2)与LNG换热冷却为液态。
在TOFC中,液态工质R32(流股16)通过泵5(PUM5)增压后,在换热器2(HX2)中吸收therminol-66的热量,达到超临界蒸气状态。随后超临界状态的蒸气进入膨胀机3(TUR3)做功发电。气液混合的工质在闪蒸罐(FT)中进行闪蒸,其中闪蒸蒸气(流股20)进入膨胀机4(TUR4)发电,而分离出的液态工质(流股21)通过节流阀(Valve)降压后在混合器2(Mix2)中与排气(流股22)混合。低压的工质在冷凝器1(CON1)中与LNG换热冷却至液体状态。
在LNG膨胀系统中,液态LNG(流股25)通过泵6(PUM6)增压,进入冷凝器1(CON1)吸收低压气态的R32(流股24)的热量,再经过冷凝器2(CON2)被低压状态的CO2(流股15)加热。随后通过膨胀机5(TUR5)做功发电。最后在换热器5(HX5)中与热空气换热,达到环境温度,从而达到供冷的目的。
3 计算模型为了更好地研究作者设计的CCHP系统性能,需要做出如下假设[13-15]:
(1) 底部CCHP系统在稳定状态下运行。
(2) 底部CCHP系统中换热器及冷凝器为管壳式换热器,泵为潜液泵,膨胀机为向心透平膨胀机。
(3) 假定气液分离过程为理想过程;节流过程为等焓过程。
(4) 膨胀机和泵的等熵效率为恒定值,为85%。
3.1 热力学分析基于热力学第一定律和热力学第二定律,从能量和㶲2个方面分析CCHP系统的性能。
3.1.1 太阳能集热子系统能量分析输入PTC的总能量为
| $ {\mathit{\Phi} _{{\rm{in}}}} = {G_{\rm{B}}}{A_{{\text{ap}}}} $ | (1) |
式中:Φin为输入热流量,kW;GB为太阳直接辐射强度,kW·m−2;Aap为光圈面积,m2。
| $ {\mathit{\Phi} _{\text{u}}} = {F_{\text{R}}}\left[ {{G_{\text{B}}}{A_{{\text{ap}}}}{\eta _{\text{o}}} - {A_{\text{r}}}{U_{\text{L}}}\left( {{T_{{\rm{in}}}} - {T_{\text{0}}}} \right)} \right] $ | (2) |
式中:Φu为有用热流量,kW;FR为热迁移因子;ηo为光学效率;Ar为接收器面积,m2;UL为热损失系数,kW·(m2·K)−1;Tin为进口热力学温度,K;T0为环境热力学温度,K。
TST中能量公式为[18]
| $ \left[ {\left( {{\rho _{{\rm{HTF}}}}{V_{{\rm{HTF}}}}{c_p}_{{\rm{, HTF}}}} \right) + \left( {{\rho _{{\rm{TST}}}}{V_{{\rm{TST}}}}{c_p}_{, {\rm{TST}}}} \right)} \right]\frac{{{\rm{d}}{T_{{\rm{TST}}}}}}{{{\rm{d}}t}} = {\mathit{\Phi} _{\rm{u}}} + {\mathit{\Phi} _{{\rm{load}}}} + {\mathit{\Phi} _{\rm{L}}} $ | (3) |
式中:ρHTF、ρTST分别为热传导流体(HTF)和TST的密度,kg·m−3;VHTF、VTST分别为热传导流体和TST的体积,m3;cp, HTF、cp, TST分别为热传导流体和TST的比热容,kJ·(kg·K)−1;TTST为TST中的热力学温度,K;t为时间,s;Φload为底部联合循环所需热流量,kW;ΦL为TST与环境之间的热流量损失,kW。
| $ {\mathit{\Phi} _{{\rm{load}}}} = \left( {{q_{m, {\text{HTF}}}}{c_{p, {\text{HTF}}}}} \right)\left( {{T_{{\rm{TST}}}} - {T_{33}}} \right) $ | (4) |
| $ {\mathit{\Phi} _{\rm{L}}} = \left( {{U_{\rm{L}}}_{, {\rm{TST}}}{A_{{\rm{TST}}}}} \right)\left( {{T_{{\rm{TST}}}} - {T_0}} \right) $ | (5) |
式中:
PUM1的输入功为
| $ {P_{{\text{PUM1}}}} = {q_{m, {\rm{s2}}}}({h_{{\rm{s2}}}} - {h_{{\rm{s3}}}}) $ | (6) |
式中:PPUM1为PUM1的输入功率,kW;qm, s2为流量节点s2的质量流量,kg·s−1;hs2为流量节点s2的质量焓,kJ·kg−1;hs3为流量节点s3的质量焓,kJ·kg−1。
3.1.2 底部CCHP系统能量分析泵的输入功为
| $ {P_{{\text{PUM}}}} = {q_m}\left( {{h_{{\rm{out}}}} - {h_{{\rm{in}}}}} \right) $ | (7) |
式中:PPUM为底部CCHP系统泵的输入功率,kW;qm为质量流量,kg·s−1;hout为出口质量焓,kJ·kg−1;hin为进口的质量焓,kJ·kg−1。
膨胀机做功为
| $ {P_{{\text{TUR}}}} = {q_m}\left( {{h_{{\rm{in}}}} - {h_{{\rm{out}}}}} \right) $ | (8) |
式中:PTUR为底部CCHP系统膨胀机的输出功率,kW。
CCHP系统总净输出功为
| $ {P_{{\text{net}}}} = \sum {{P_{{\text{TUR}}, k}} - } \sum {{P_{{\text{PUM}}, k}}} $ | (9) |
式中:Pnet为CCHP系统净输出功率,kW;∑PTUR, k为k个膨胀机输出功率的总和,kW;∑PPUM, k为第k个泵输入功率的总和,kW。
CCHP系统产生的冷流量表示为
| $ {\mathit{\Phi} _{\text{C}}} = {q_{m, 31}}\left( {{h_{32}} - {h_{31}}} \right) $ | (10) |
式中:ΦC为CCHP系统的冷流量,kW;qm, 31为流量节点31的质量流量,kg·s−1;h32为流量节点32的质量焓,kJ·kg−1;h31为流量节点31的质量焓,kJ·kg−1。
CCHP系统产生的热流量表示为
| $ {\mathit{\Phi} _{\text{H}}} = {q_{m, 34}}\left( {{h_{34}} - {h_{35}}} \right) $ | (11) |
式中:ΦH为CCHP系统的热流量,kW;qm, 34为流量节点34质量流量,kg·s−1;h34为流量节点34的质量焓,kJ·kg−1;h35为流量节点35的质量焓,kJ·kg−1。
3.1.3 㶲分析工质的㶲值为[20]
| $ {E_i} = {q_{m, i}}\left[ {\left( {{h_i} - {h_0}} \right) - {T_0}\left( {{s_i} - {s_0}} \right)} \right] $ | (12) |
式中:Ei为工质的㶲值,kW;qm, i为流量节点i的质量流量,kg·s−1;hi为流量节点i的质量焓,kJ·kg−1;h0为环境温度的质量焓,kJ·kg−1。si为流量节点i的质量熵,kJ·(kg·K)−1;s0为环境温度的质量熵,kJ·(kg·K)−1。
太阳辐射的㶲值为[21]
| $ {E_{\text{s}}} = {G_{\text{B}}}{A_{{\text{ap}}}}\left[ {1 + \frac{1}{3}{{\left( {\frac{{{T_0}}}{{{T_{\text{s}}}}}} \right)}^4} - \frac{4}{3}\left( {\frac{{{T_0}}}{{{T_{\text{s}}}}}} \right)} \right] $ | (13) |
式中:Es为太阳能㶲值,kW;Ts为太阳能热力学温度,K。
LNG的㶲值为
| $ {E_{{\rm{LNG}}}} = {q_{m, 25}}\left[ {\left( {{h_{25}} - {h_0}} \right) - {T_0}\left( {{s_{25}} - {s_0}} \right)} \right] $ | (14) |
式中:ELNG为LNG㶲值,kW;qm, 25为流量节点25的质量流量,kg·s−1;h25为流量节点25的质量焓,kJ·kg−1;s25为流量节点25的质量熵,kJ·(kg·K)−1。
3.2 㶲经济和㶲环境分析 3.2.1 㶲经济㶲经济是将㶲分析和经济相结合,是评估热力系统能效的重要方式[22]。第k个组件㶲成本平衡方程可描述为[13]
| $ \sum {{{\dot C}_{{\rm{out}}, k}} + {{\dot C}_{P, k}} = \sum {{{\dot C}_{{\text{in}}, k}} + {{\dot C}_{\phi , k}} + {{\dot C}_{{\text{Z}}, k}}} } $ | (15) |
式中:
| $ \dot C = c{E_i} $ | (16) |
式中:
| $ {\dot C_{{\text{Z}}, k}} = \frac{{{C_{{\text{Z}}, k}} \cdot {i_{{\rm{CRF}}}} \cdot \varphi }}{\tau } $ | (17) |
| $ {i_{{\rm{CRF}}}} = \frac{{{i_{\rm{r}}}{{\left( {1 + {i_{\rm{r}}}} \right)}^n}}}{{{{\left( {1 + {i_{\rm{r}}}} \right)}^n} - 1}} $ | (18) |
式中:CZ, k为k组件投资成本,$;各组件投资成本公式详见文献[16]和[24]。τ为年工作时长,取8 000 h;φ为维持系数,取1.06。iCRF为资本回收因子;ir为利率,本文取10%;n为系统寿命,取20 a。
3.2.2 㶲环境㶲环境分析用来评估系统对环境的影响。环境影响平衡方程为[25-26]
| $ \sum {{{\dot B}_{{\rm{in}}, k}}} + {\dot B_{{\text{Z}}, k}} = \sum {{{\dot B}_{{\rm{out}}, k}}} $ | (19) |
| $ \dot B = b{E_i} $ | (20) |
式中:
| $ {\dot B_{{\text{Z}}, k}} = \frac{{{B_{{\text{Z}}, k}}}}{{\tau \times n}} $ | (21) |
| $ {B_{{\text{Z}}, k}} = \sum {\left( {{\omega _{j, k}} \times {m_{j, k}}} \right)} $ | (22) |
式中:
为了从热力学、经济和环境3个方面综合评估提出的CCHP系统的性能,选择㶲效率、总单位产品成本率和总单位产品环境影响率作为评价标准。
提出系统㶲效率公式为
| $ {\eta _{{\rm{ex}}}} = \frac{{{P_{{\rm{net}}}} + {\mathit{\Phi} _{\text{H}}} + {\mathit{\Phi} _{\text{C}}}}}{{{E_{\rm{s}}} + {E_{{\rm{LNG}}}}}} $ | (23) |
式中:ηex为㶲效率,%。
总单位产品成本率可表示为
| $ {c_{p, {\rm{tot}}}} = \frac{{\sum {{{\dot C}_{{\text{Z, }}k}}} + {{\dot C}_{{\text{LNG}}}} + {{\dot C}_{\text{s}}}}}{{{P_{{\text{net}}}} + {E_{32}} + {E_{35}}}} $ | (24) |
式中:cp, tot为总单位产品成本率,$·GJ−1;
总单位产品环境影响率可表示为
| $ {b_{{\rm{p, tot}}}} = \frac{{\sum {{{\dot B}_{{\text{Z}}, k}}} }}{{{P_{{\text{net}}}} + {E_{32}} + {E_{35}}}} $ | (25) |
式中:bp, tot为总单位产品环境影响率,mPts·GJ−1;∑
本研究设计的CCHP系统采用Matlab建立数学计算模型,系统模拟应用HYSYS。太阳能子系统的设计与计算参考文献[6]、[16]和[28]。提出的系统在基础工况运行时的输入参数如表 1所示。系统选用的LNG为混合物,组分详见参考文献[29]。
|
|
表 1 系统的输入参数 Table 1 Input parameters of the system |
图 2为TUR1进口热力学温度T8对净输出功、㶲效率、总单位产品成本率、总单位产品环境影响率的影响。从图 2(a)中可以看出,随着TUR1进口温度T8增加,系统净输出功增加且系统㶲效率增长。在TUR1、TUR3和PUM3的流量保持恒定的情况下,T8的升高使这3个设备的焓差增加,进而使得TUR1、TUR3的做功量增多,且PUM3的耗功量增加。T8的增加导致TUR4中的流量增加,TUR4的做功量增加。由于TUR1、TUR3和TUR4的做功量共增长26.04 kW,PUM3的耗功量增加5.28 kW,所以系统的净输出功增加。HX3中热源出口温度和流量不变,T9随T8的升高而增加,使得HX3中的焓差降低,系统的热量降低6.10 kW。在系统冷量保持不变的情况下,由于系统净输出功的增加量多于热量的改变量,所以系统的㶲效率呈现增长的趋势。从图 2(b)中可以看出,随TUR1进口热力学温度T8升高,总单位产品成本率和总单位产品环境影响率均降低。主要原因是LNG的成本率恒定且太阳能的成本率为0,随着T8的增加,TUR1、TUR3、TUR4以及PUM3的投资成本率增加量为0.58 $·h−1,整体大于HX3的投资成本率减少量0.20 $·h−1。净输出功的增加量为20.76 kW,多于流股32的㶲流量减少量0.61 kW,所以总单位产品成本率呈现下降趋势。从图中可以看出与总单位产品成本率的变化趋势相似,总单位产品环境影响率呈降低趋势。原因为T8增加,TUR1、TUR3、TUR4和PUM3的环境影响率的增长量为0.33 mPts·h−1,HX3的环境影响率的减少量为0.02 mPts·h−1,使得组件总环境影响率表现为增加。净输出功与流股32的㶲流量关系如前所述,所以总单位产品环境影响率表现为下降趋势。

|
图 2 T8对净输出功、㶲效率、总单位产品成本率以及总单位产品环境影响率的影响 Fig.2 Effects of T8 on Pnet, ηex, cp, tot and bp, tot |
图 3为HX3中R134a进口质量流量qm, 9对净输出功、㶲效率、总单位产品成本率、总单位产品环境影响率的影响。从图 3(a)中可以看出,净输出功随qm, 9的增加而减少。随着qm, 9的增加,TUR3中的流量减少,在TUR3的焓差不变的情况下,TUR3的做功量降低;TUR4和TUR5中的流量不变,焓差的降低使得TUR4和TUR5的做功量减少。TUR3-5做功量总体减少56.63 kW,所以系统净输出功呈下降趋势。在HX3中热源的焓差恒定的情况下,随qm, 9的增加,系统产生的热量升高,增加量为94.48 kW。系统的产热量的增加量高于净输出功的减少量,所以㶲效率升高。从图 3(b)中可以看出,总单位产品成本率和总单位产品环境影响率随qm, 9的增加而增加。主要原因为qm, 9增加使得HX3的投资成本率和环境影响率增加,TUR3-5的投资成本率和环境影响率减少,投资成本率和环境影响率总体分别减少0.65 $·h−1和0.46 mPts·h−1。流股32的㶲流量随qm, 9的增加而增加,增加量为4.00 kW,总体低于净输出功的减少量。投资成本率和环境影响率的变化速率低于净输出功的变化速率,所以总产品单位产品成本率和总单位产品环境影响率呈升高的趋势。

|
图 3 qm, 9对净输出功、㶲效率、总单位产品成本率以及总单位产品环境影响率的影响 Fig.3 Effects of qm, 9 on Pnet, ηex, cp, tot and bp, tot |
图 4为PUM6出口压力p26对净输出功、㶲效率、总单位产品成本率、总单位产品环境影响率的影响。从图 4(a)中可以看出,净输出功随PUM6出口压力p26的增加而增加。在TUR5和PUM6流量不变的情况下,p26的增加使得TUR5和PUM6的焓差增加,TUR5的做功量增加119.18 kW,PUM6的耗功量增加26.49 kW,所以净输出功为上升趋势。在HX5中冷源的流量不变,p26的增加使得HX5产出的冷量增加,为93.18 kW。所以在系统产热量为定值时,冷量和净输出功同时升高,所以㶲效率表现为增长的趋势。从图 4(b)中可以看出,随PUM6出口压力p26的增加,总单位产品成本率和总单位产品环境影响率均降低。原因为p26的增加,一方面使得组件PUM6、TUR5和HX5的投资成本率和环境影响率增加,分别增加1.69 $·h−1和1.35 mPts·h−1;另一方面促进系统净输出功的升高,流股35的㶲流量增加量为1.07 kW。净输出功和流股35的㶲流量的增长速度高于投资成本率和环境影响率,所以总单位产品成本率和总单位产品环境影响率逐渐减小。

|
图 4 p26对净输出功、㶲效率、总单位产品成本率以及总单位产品环境影响率的影响 Fig.4 Effects of p26 on Pnet, ηex, cp, tot and bp, tot |
图 5为FT进口压力p19对净输出功、㶲效率、总单位产品成本率、总单位产品环境影响率的影响。从图 5(a)中可以看出,净输出功和㶲效率随FT进口压力p19的增加而降低。原因为TUR3的流量不变,p19的增加使得TUR3中的焓差减小,进而TUR3的做功量减少,减少量为83.16 kW。TUR4的进口流量以及焓差随p19的升高而增加,使得TUR4的做功量增加72.44 kW,所以净输出功呈下降趋势。在系统热量和冷量恒定时,净输出功减少,导致系统㶲效率减少。从图 5(b)中可以看出,总单位产品成本率和总单位产品环境影响率随p19的增加而增加。原因为p19的增加使得TUR3的投资成本率和环境影响率分别减少1.02 $·h−1和0.60 mPts·h−1,TUR4的投资成本率和环境影响率分别增加0.97 $·h−1和0.56 mPts·h−1。流股32的㶲流值与流股35的㶲流值不变,系统净输出功降低,投资成本率和环境影响率的变化速率均小于净输出功的变化速率,所以总单位产品成本率和总单位产品环境影响率升高。

|
图 5 p19对净输出功、㶲效率、总单位产品成本率以及总单位产品环境影响率的影响 Fig.5 Effects of p19 on Pnet, ηex, cp, tot and bp, tot |
如图 6所示,为了检验DORC与TOFC组成的CCHP系统性能(定义为DORC-TOFC),建立了SORC与BOFC组成的CCHP系统(定义为SORC-BOFC),2个系统的输入参数均相同。
|
图 6 SORC-BOFC系统流程图 Fig.6 Schematic diagram of the SORC-BOFC CCHP system 1-31, s1-s3. stream |
表 2展示了2个CCHP系统的对比结果。从表中可以看出,2个系统的产热量相同,但是DORC-TOFC系统的净输出功、冷量和㶲效率均高于SORC-BOFC系统。
|
|
表 2 DORC-TOFC与SORC-BORC对比结果 Table 2 Comparison of simulation results between DORC-TOFC and SORC-BORC |
本研究选择系统㶲效率分析系统的热力性能;应用总单位产品成本率分析系统的㶲经济性能;采用总单位产品环境影响率分析系统的㶲环境性能。4个决策变量T8、qm, 9、p26以及p19的取值范围如表 3所示。
|
|
表 3 决策变量取值范围 Table 3 Values ranges of decision variables |
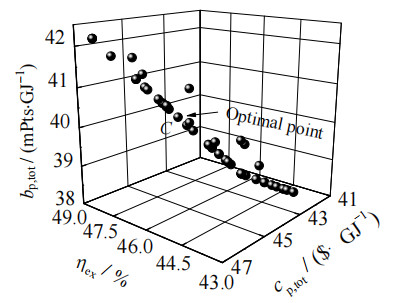
采用NSGA-II方法对CCHP系统进行3目标优化。图 7为㶲效率、总单位产品成本率和总单位产品环境影响率的帕累托前沿。图中点C为最优解,此时T8为372.80 K、qm, 9为0.32 kg·s−1、p26为6 991.91 kPa以及p19为302.33 kPa,得到的系统㶲效率、总单位产品成本率以及总单位产品环境影响率分别为47.23%、44.20 $·GJ−1和40.06 mPts·GJ−1。
|
图 7 系统3目标优化结果 Fig.7 Three-objective optimization results of the CCHP system |
本研究将DORC和TOFC相结合建立了以太阳能为热源、LNG冷能为冷源的新型CCHP系统。从系统的热力性能、㶲经济和㶲环境3个方面对系统进行了分析,建立了3目标优化模型。得出如下结论:
(1) 与SORC-BOFC系统相比,新型DORC-TOFC系统的性能更好。
(2) 可根据使用者对净输出功、热量和冷量的不同需求对系统进行调节。
(3) 总单位产品成本率和总单位产品环境影响率具有相同的变化趋势。可以通过适当降低HX3的进口流量和FT的进口压力,降低总单位产品成本率和总单位产品环境影响率;降低以上2个参数可减少成本并降低对环境的影响。
(4) 最佳运行工况时,系统㶲效率、总单位产品成本率和总单位产品环境影响率分别为47.23%,44.20 $·GJ−1,40.06 mPts·GJ−1。
| [1] |
吴小华, 蔡磊, 李庭宇, 等. LNG冷能利用技术的最新进展[J]. 油气储运, 2017, 36(6): 624-635. WU X H, CAI L, LI T Y, et al. Latest progress of LNG cold energy utilization technology[J]. Oil & Gas Storage and Transportation, 2017, 36(6): 624-635. |
| [2] |
潘本艺, 杨帆, 周莉, 等. 液化天然气冷能利用的联合动力循环[J]. 高校化学工程学报, 2021, 35(4): 702-710. PAN B Y, YANG F, ZHOU L, et al. Combined power cycle for cold energy utilization of liquefied natural gas[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(4): 702-710. DOI:10.3969/j.issn.1003-9015.2021.04.016 |
| [3] |
LI C H, LIU J W, ZHENG S Y, et al. Performance analysis of an improved power generation system utilizing the cold energy of LNG and solar energy[J]. Applied Thermal Engineering, 2019, 159: 113937. DOI:10.1016/j.applthermaleng.2019.113937 |
| [4] |
INVERNIZZI C M, IORA P. The exploitation of the physical exergy of liquid natural gas by closed power thermodynamic cycles. An overview[J]. Energy, 2016, 105: 2-15. DOI:10.1016/j.energy.2015.09.020 |
| [5] |
RAO W J, ZHAO L J, LIU C, et al. A combined cycle utilizing LNG and low-temperature solar energy[J]. Applied Thermal Engineering, 2013, 60(1/2): 51-60. |
| [6] |
ABDOLLAHPOUR A, GHASEMPOUR R, KASAEIAN A, et al. Exergoeconomic analysis and optimization of a transcritical CO2 power cycle driven by solar energy based on nanofluid with liquefied natural gas as its heat sink[J]. Journal of Thermal Analysis and Calorimetry, 2020, 139(1): 451-473. DOI:10.1007/s10973-019-08375-6 |
| [7] |
SADREDDINI A, ASHJARJ M A, FANI M, et al. Thermodynamic analysis of a new cascade ORC and transcritical CO2 cycle to recover energy from medium temperature heat source and liquefied natural gas[J]. Energy Conversion and Management, 2018, 167: 9-20. DOI:10.1016/j.enconman.2018.04.093 |
| [8] |
BAO J J, LIN Y, ZHANG R X, et al. Strengthening power generation efficiency utilizing liquefied natural gas cold energy by a novel two-stage condensation Rankine cycle (TCRC) system[J]. Energy Conversion and Management, 2017, 143: 312-325. DOI:10.1016/j.enconman.2017.04.018 |
| [9] |
SUN Z X, LAI J P, WANG S J, et al. Thermodynamic optimization and comparative study of different ORC configurations utilizing the exergies of LNG and low grade heat of different temperatures[J]. Energy, 2018, 147: 688-700. DOI:10.1016/j.energy.2018.01.085 |
| [10] |
LI Z, LU Y, HUANG Y Q, et al. Comparison study of trilateral Rankine cycle, organic flash cycle and basic organic Rankine cycle for low grade heat recovery[J]. Energy Procedia, 2017, 142: 1441-1447. DOI:10.1016/j.egypro.2017.12.532 |
| [11] |
HO T, MAO S S, GREIF R. Comparison of the organic flash cycle (OFC) to other advanced vapor cycles for intermediate and high temperature waste heat reclamation and solar thermal energy[J]. Energy, 2012, 42(1): 213-223. DOI:10.1016/j.energy.2012.03.067 |
| [12] |
LEE H Y, PARK S H, KIM K H. Comparative analysis of thermodynamic performance and optimization of organic flash cycle (OFC) and organic Rankine cycle (ORC)[J]. Applied Thermal Engineering, 2016, 100: 680-690. DOI:10.1016/j.applthermaleng.2016.01.158 |
| [13] |
SARABCHI N, MAHMOUDI S M S, YARI M, et al. Exergoeconomic analysis and optimization of a novel hybrid cogeneration system: High-temperature proton exchange membrane fuel cell/Kalina cycle, driven by solar energy[J]. Energy Conversion and Management, 2019, 190: 14-33. DOI:10.1016/j.enconman.2019.03.037 |
| [14] |
BOYAGHCHI F, CHAVOSHI M. Multi-criteria optimization of a micro solar-geothermal CCHP system applying water/ CuO nanofluidbased on exergy, exergoeconomic and exergoenvironmental concepts[J]. Applied Thermal Engineering, 2017, 112: 660-675. DOI:10.1016/j.applthermaleng.2016.10.139 |
| [15] |
王德鹏, 黄永, 魏林瑞. 利用液化天然气冷能发电新流程及模拟分析[J]. 化学工业, 2019, 37(2): 14-18. WANG D P, HUANG Y, WEI L R. New process and simulation analysis of power generation using LNG cold energy[J]. Chemical Industry, 2019, 37(2): 14-18. |
| [16] |
BOYAGHCHI F, SABAGHIAN M. Multi objective optimisation of a Kalina power cycle integrated with parabolic trough solar collectors based on exergy and exergoeconomic concept[J]. International Journal of Energy Technology and Policy, 2016, 12(2): 154-180. DOI:10.1504/IJETP.2016.075673 |
| [17] |
张鹤飞. 太阳能热利用原理与计算机模拟[M]. 2版. 西安: 西北工业大学出版社, 2004: 34-108. ZHANG H F. Solar thermal utilization principle and computer simulation[M]. 2nd ed. Xi'an: Northwestern Polytechnical University Press, 2004: 34-108. |
| [18] |
BOYAGHCHI F A, SOHBATLOO A. Assessment and optimization of a novel solar driven natural gas liquefaction based on cascade ORC integrated with linear fresnel collectors[J]. Energy Conversion and Management, 2018, 162: 77-89. DOI:10.1016/j.enconman.2018.02.013 |
| [19] |
WANG J F, YAN Z Q, WANG M, et al. Parametric analysis and optimization of a building cooling heating power system driven by solar energy based on organic working fluid[J]. International Journal of Energy Research, 2013, 37(12): 1465-1474. DOI:10.1002/er.2952 |
| [20] |
ZHANG L, PAN Z, YU J, et al. Multiobjective optimization for exergoeconomic analysis of an integrated cogeneration system[J]. International Journal of Energy Research, 2019, 43(5): 1868-1881. DOI:10.1002/er.4429 |
| [21] |
WANG J J, LU Z R, LI M, et al. Energy, exergy, exergoeconomic and environmental (4E) analysis of a distributed generation solar-assisted CHP (cooling, heating and power) gas turbine system[J]. Energy, 2019, 175: 1246-1258. DOI:10.1016/j.energy.2019.03.147 |
| [22] |
MANESH M H K, NAVID P, MARIGORTA A M B, et al. New procedure for optimal design and evaluation of cogeneration system based on advanced exergoeconomic and exergoenvironmental analyses[J]. Energy, 2013, 59: 314-333. DOI:10.1016/j.energy.2013.06.017 |
| [23] |
TALEBIZADEHSARDARI P, EHYAEI M A, AHMADI A, et al. Energy, exergy, economic, exergoeconomic, and exergoenvironmental(5E) analyses of a triple cycle with carbon capture[J]. Journal of CO2 Utilization, 2020, 41: 101258. DOI:10.1016/j.jcou.2020.101258 |
| [24] |
FANG Z, SHANG L, PAN Z, et al. Exergoeconomic analysis and optimization of a combined cooling, heating and power system based on organic Rankine and Kalina cycles using liquified natural gas cold energy[J]. Energy Conversion and Management, 2021, 238: 114148. DOI:10.1016/j.enconman.2021.114148 |
| [25] |
BOYAGHCHI F A, ASGARI S. A comparative study on exergetic, exergoeconomic and exergoenvironmental assessments of two internal auto-cascade refrigeration cycles[J]. Applied Thermal Engineering, 2017, 122: 723-737. DOI:10.1016/j.applthermaleng.2017.05.065 |
| [26] |
CAVALCANTI E J C. Exergoeconomic and exergoenvironmental analyses of an integrated solar combined cycle system[J]. Renewable and Sustainable Energy Reviews, 2017, 67: 507-519. DOI:10.1016/j.rser.2016.09.017 |
| [27] |
ZHANG C, LIU C, XU X X, et al. Energetic, exergetic, economic and environmental (4E) analysis and multi-factor evaluation method of low GWP fluids intrans-critical organic Rankine cycles[J]. Energy, 2018, 168: 332-345. |
| [28] |
DING Y, LIU C, ZHANG C, et al. Exergoenvironmental model of organic Rankine cycle system including the manufacture and leakage of working fluid[J]. Energy, 2017, 145: 52-64. |
| [29] |
YANG X Y, ZHAO H B. Thermodynamic performance study of the SOFC-STIG distributed energy system fueled by LNG with CO2 recovery[J]. Energy, 2019, 186: 115860. DOI:10.1016/j.energy.2019.115860 |




