2. 数字社区教育部工程研究中心,北京 100124;
3. 城市轨道交通北京实验室,北京 100124;
4. 计算智能与智能系统北京市重点实验室,北京 100124;
5. 内蒙古工业大学电力学院,内蒙古 呼和浩特 010051
2. Engineering Research Center of Digital Community, Ministry of Education, Beijing 100124, China;
3. Beijing Laboratory for Urban Mass Transit, Beijing 100124, China;
4. Beijing Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China;
5. School of Electric Power, Inner Mongolia University of Technology, Hohhot 010051, China
随着工业技术的发展和市场需求的快速变化,间歇过程已成为重要的生产方式,被广泛应用于化学、生物医药等方面。然而某些生产如发酵过程,其质量变量难以在线测量,离线测量导致结果严重滞后,不能及时指导生产。因此,为提高产品质量和工艺效率,在线质量预测相关技术的重要性日益突出[1-3]。
偏最小二乘(partial least square,PLS)[4-5]是质量预测建模方法的典型代表,其中多向偏最小二乘(multiway partial least square, MPLS)[6-7]作为PLS算法的拓展,通常被认为是质量预测的一个里程碑。但是传统的基于PLS的质量预测方法是根据历史数据建立单一的模型,忽略了间歇过程的多阶段特性以及局部过程的行为特征,显然对整个生产过程建立单一模型是不完善的,因此许多学者对阶段划分进行了研究[8-12]。CAMACHO等提出了一种线性局部模型逼近方法,实现阶段划分的目的[8],LU等提出了基于K-means的间歇过程子时段划分方法[9],但是以上方法属于硬分类算法,不能很好地反映过渡阶段的特性,可能会导致“误分类”的现象;GE等提出基于重复性因子的多阶段在线质量测量的方法[10],在过渡阶段建模时采用即时学习建模策略;邓晓刚等提出了一种基于多阶段多向核熵成分分析的故障检测方法,利用时序核熵主元关联矩阵的相似性实现阶段划分[11]。但是上述方法仅依据过程变量信息把整个生产过程划分为不同阶段并建立子模型进行质量预测或监测,没有考虑质量变量对阶段划分的影响。
针对上述问题,本文提出了一种基于扩展得分矩阵的多阶段间歇过程质量预测方法。该方法充分考虑质量变量对划分阶段的影响,将能表征质量变量的得分矩阵扩展到能表征过程变量的得分矩阵中,扩展后的得分矩阵同时包含了过程变量和质量变量的信息,利用CS (Cauchy-Schwarz)统计量沿时间方向依次计算相邻两个时间片扩展得分矩阵的相似度并进行阶段划分。然后对各个阶段分别建立MPLS预测模型,在一定程度上提高了质量预测精度。最后将本文所提方法应用于青霉素发酵仿真平台和大肠杆菌生产数据上进行验证,实验结果证明本文所提方法有更好的预测精度和更高的稳定性。
2 基本理论 2.1 偏最小二乘(PLS)偏最小二乘(partial least squares,PLS)方法由WOLD等提出[13],PLS是一种多个因变量对多个自变量的回归建模方法。给予一组从过程操作中收集到的数据,其中历史数据矩阵X表示在线可以直接测量到的变量(算法中被认为是自变量,这里简称测量变量),数据矩阵Y表示通过其它一些方法收集到的质量相关变量(算法中被认为是需要从X导出的因变量,这里简称质量变量)。在建立PLS模型时,算法试图最大化X与Y之间的相互关系,将它们分解成以下形式:
| $\boldsymbol{X}=\sum\limits_{r=1}^{A} t_{r} p_{r}^{\rm{T}}+\boldsymbol{E}=\boldsymbol{T} \boldsymbol{P}^{\rm{T}}+\boldsymbol{E}$ | (1) |
| $\boldsymbol{Y}=\sum\limits_{r=1}^{B} u_{r} q_{r}^{\rm{T}}+\boldsymbol{F}=\boldsymbol{U} \boldsymbol{Q}^{\rm{T}}+\boldsymbol{F}$ | (2) |
其中A和B分别代表X和Y提取的主成分个数(A、B不一定相等),用交叉验证法来确定其个数[14];T= {t1, t2, …tA}为对X的得分矩阵,U= {u1, u2, …uB}为对Y的得分矩阵,它们尽可能多地代表了X和Y的主要信息;P和Q分别为对X和Y的负荷向量;E和F分别为对X和Y的残差矩阵。
PLS是一种有偏回归方法,其自变量X与因变量Y的最终回归模型可表示为:
| $\boldsymbol{Y}=\boldsymbol{X} \boldsymbol{\beta}+\boldsymbol{E}_{\rm{Y}}$ | (3) |
其中β是回归系数向量,EY是预测误差。
2.2 相似性度量指标本文采用CS统计量来定义扩展得分矩阵的相似度[15-17],其定义如下:
| $V_{\rm{CS}}=\cos \angle(\boldsymbol{M}, \boldsymbol{N})=\sum\limits_{j}^{l} \frac{\boldsymbol{m}_{j}^{\rm{T}} \boldsymbol{n}_{j}}{\left\|\boldsymbol{m}_{j}\right\|\left\|\boldsymbol{n}_{j}\right\|}$ | (4) |
其中M,N是两个同行同列的矩阵,M= [m1, m2, …, ml], N= [n1, n2, …, nl]。CS统计量来计算两个矩阵的相似度时,Vcs值越大,表明两个矩阵的相似度越大,Vcs值越小,则两个矩阵的相似度越小。
3 基于得分扩展矩阵的多阶段间歇过程质量预测针对间歇过程具有的多阶段特性,提出一种基于扩展得分矩阵的多阶段间歇过程质量预测方法,该方法在划分阶段时不仅考虑到质量变量的影响,而且进一步考虑生产过程的时序性,避免一般聚类方法可能将一个阶段的时间片被划分到另一个阶段,阶段划分结果可读性欠缺的问题,使得模型准确性大大提高。
3.1 基于扩展得分矩阵相似度的阶段划分由于每个阶段对质量变量的影响程度不同,阶段划分时如果只考虑过程变量,忽略质量变量信息,并不能准确地将整个生产过程划分为多个子阶段。为解决此问题,本文将质量变量的得分矩阵Ui扩展到过程变量的得分矩阵Ti中,扩展后的矩阵有效包含了两个子矩阵的信息[18-19],扩展得分矩阵的相似度代表了两个时间片矩阵的相似性,可较为精确地表征生产过程的阶段变化,提高阶段划分精度。扩展得分矩阵如下式:
| ${\boldsymbol{\tilde T}_i} = \left[ {{\boldsymbol{T}_i} \ \ {\boldsymbol{U}_i}} \right]{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {{t_{11}}}& \cdots &{{t_{1A}}} \\ {{t_{21}}}& \ddots & \vdots \\ \vdots &{}&{} \\ {{t_{I1}}}&{}&{{t_{IA}}} \end{array}{\rm{ }}\begin{array}{*{20}{c}} {{u_{11}}}& \cdots &{{u_{1B}}} \\ {{u_{21}}}& \ddots & \vdots \\ \vdots &{}&{} \\ {{u_{I1}}}&{}&{{u_{IB}}} \end{array}} \right]_i}{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {{{\tilde t}_{11}}}&{{{\tilde t}_{12}}}& \cdots &{{{\tilde t}_{1(A + B)}}} \\ {{{\tilde t}_{21}}}&{{{\tilde t}_{22}}}&{}&{{{\tilde t}_{2(A + B)}}} \\ \vdots &{}& \ddots &{} \\ {{{\tilde t}_{I1}}}&{}&{}&{{{\tilde t}_{I(A + B)}}} \end{array}} \right]_i}$ | (5) |
其中Ti和Ui分别是X和Y的得分矩阵,为方便后续计算,令
| $ \boldsymbol{T}_{i}=\left[\boldsymbol{t}_{1}, \boldsymbol{t}_{2} \cdots \boldsymbol{t}_{\rm{A}}\right]_{i}{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {{t_{11}}}&{{t_{12}}}& \ldots &{{t_{1A}}} \\ {{t_{21}}}&{{t_{22}}}&{}&{{t_{2A}}} \\ \vdots &{}& \ddots &{} \\ {{t_{I1}}}&{}&{}&{{t_{IA}}} \end{array}} \right]_i} $ | (6) |
| $\boldsymbol{U}_{i}=\left[\boldsymbol{u}_{1}, \boldsymbol{u}_{2} \cdots \boldsymbol{u}_{B}\right]_i{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {{u_{11}}}&{{u_{12}}}& \ldots &{{u_{1B}}} \\ {{u_{21}}}&{{u_{22}}}&{}&{{u_{2B}}} \\ \vdots &{}& \ddots &{} \\ {{u_{I1}}}&{}&{}&{{u_{IB}}} \end{array}} \right]_i}$ | (7) |
使用CS统计量计算两个扩展得分矩阵的相似度,以此作为阶段划分的依据。为使实验和表述更加直观,将CS统计量做如式(8)调整。
| $V_{i \rm{CS}}=\cos \angle\left(\tilde{\boldsymbol{T}}_{i}, \tilde{\boldsymbol{T}}_{i+1}\right)=\frac{1}{l} \sum\limits_{j}^{l} \frac{\tilde{\boldsymbol{T}}_{i j}^{\rm{T}} \tilde{\boldsymbol{T}}_{i+1 j}}{\left\|\tilde{\boldsymbol{T}}_{i j}\right\|\left\|\tilde{\boldsymbol{T}}_{i+1 j}\right\|}$ | (8) |
其中
|
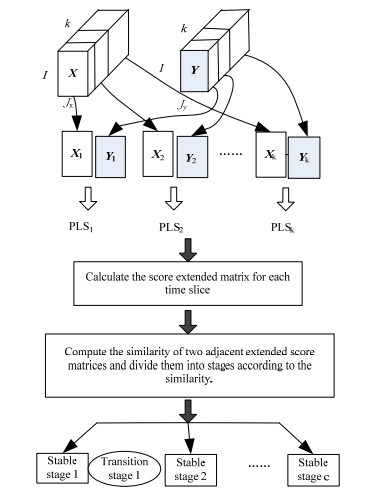
图 1 基于扩展得分矩阵的阶段划分 Fig.1 Stage separation processes based on extended score matrices |
间歇过程其历史过程数据是三维矩阵,由X(I×Jx×K)表示,其中,I为批次,Jx为过程数据变量,假设其可在线测量,K为每个批次采样数[20]。质量数据由Y(I×Jy×K)表示,其中Jy由离线测量得到。假设建立模型所采用的各批次操作时间都是等长的。
1) 将三维过程数据X(I×Jx×K)沿批次方向展开得到K个时间片数据子矩阵Xi(I×Jx),其中i = 1, 2, …, k,沿批次展开后,对数据进行标准化处理
| ${\tilde x_{k.j}} = \frac{{{x_{k, j}} - {{\bar x}_{k.j}}}}{{{S_{k, j}}}}$ | (9) |
其中,j = 1, 2, …J,k = 1, 2, …K,
2) 每个时间片数据对进行PLS回归分析,得到相应的X的得分向量Ti和Y的得分向量Ui,它们能很好地表征数据X和Y。将质量变量的得分向量Ui扩展到过程变量的得分矩阵Ti中,得到扩展得分矩阵
3) 从第一个时间片开始沿时间方向根据式(8)依次计算相邻两个得分扩展矩阵的相似度,Vics的大小可以表征两个扩展矩阵的相似度即时间片矩阵的相似度。当Vics值接近1时,两个相邻时间片矩阵的相似性较大,该时刻处于稳定阶段;当两个相邻时间片的相似度小于某个阈值时,而且之后的连续三对相邻时间片矩阵的相似度小于该阈值,说明生产过程正在发生改变,该时刻处于过渡阶段,此点就作为阶段的划分点。阈值是根据经验值选取,经过多次实验,当阈值大于0.6或者小于0.45时, 阶段划分结果明显不符合发酵过程机理特征。当阈值处于0.45~0.6时,阶段划分结果相同且比较符合发酵过程的机理特征,故在实验中取均值将阈值定为0.525。继续沿时间方向依次计算相邻两个时间片矩阵的相似度,直至最后一个时间片矩阵。
3.2 离线建模根据上述阶段划分方法可将整个生产过程划分为几个不同阶段,各个阶段内的数据特征高度相似。对每个阶段单独建立预测模型。
1) 将已划分好的各阶段的三维过程数据Xc(I×Jx×K)、质量数据Yc(I×Jy×K)分别按批次方向展开成二维过程数据矩阵Xc(I×KcJx)和质量数据矩阵Yc(I×KcJy),将二维过程数据矩阵和质量数据矩阵按式(9)进行标准化处理。其中I代表批次,Jx, Jy分别为过程变量数和质量变量数,Kc代表阶段C包含的采样时刻;
2) 对标准化后每个阶段的二维过程数据和质量数据进行PLS回归分析
| $\boldsymbol{X}_{\rm{c}}=\boldsymbol{T}_{\rm{c}} \boldsymbol{P}_{\rm{c}}^{\rm{T}}+\boldsymbol{E}_{\rm{c}}$ | (10) |
| $\boldsymbol{Y}_{\rm{c}}=\boldsymbol{U}_{\rm{c}} \boldsymbol{Q}_{\rm{c}}^{\rm{T}}+\boldsymbol{F}_{\rm{c}}$ | (11) |
写成回归形式则第c个阶段的回归模型为:
| $\boldsymbol{Y}_{\rm{c}}=\boldsymbol{X}_{\rm{c}} \boldsymbol{\beta}_{\rm{c}}+\boldsymbol{E}_{\rm{Y}}$ | (12) |
其中Tc、Uc分别为X和Y得分矩阵,PcT、QcT为负载矩阵,Ec与Fc为残差矩阵,βc为第c阶段预测模型的回归系数,EY为残差。
3.3 在线质量预测在线预测的具体步骤如下:
1) 在新的批次采集到的变量数据Xnew(1×J),采用离线建模时得到的均值和方差进行标准化处理;
2) 根据时刻选择相应的阶段模型,代入式(12):
Pensim仿真平台[21]是由伊利诺伊理工学院(Illinois Institute of Technology,IIT)以CINAR教授为学科带头研发的,专门为青霉素发酵过程而设计,已经成为国际上较有影响的青霉素仿真平台。Pensim 2.0可以对不同操作条件下青霉素生产过程的微生物浓度、青霉素浓度、CO2浓度、氧浓度、pH值以及产生的热量等进行仿真。
青霉素发酵过程每个批次的反应时间为400 h,每小时采样一次,选择10个过程变量如表 1所示和1个质量变量(产物浓度)进行监测。为使训练数据足够多,本实验共生产了80批正常数据,其中60批用作训练建模,20批数据作为测试数据。为了更接近实际生产情况,所有测量变量均加入了测量噪声。
|
|
表 1 青霉素发酵过程变量 Table 1 Process variables of penicillin fermentation |
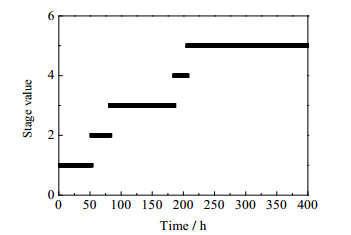
在训练建模阶段,过程变量矩阵和质量变量矩阵分别为X(60×10×400)和Y(60×1×400)。图 2为基于得分扩展矩阵的步进有序时段划分方法对青霉素发酵过程的阶段划分结果,横坐标表示采样时刻,纵坐标表示划分的阶段数量。从仿真结果图中可以看出,过程明显地被划分为3个稳定阶段和2个过渡阶段。时间区间分别为:稳定阶段1(1~52)、过渡阶段1(53~75)、稳定阶段2(76~187)、过渡阶段2(188~204)、稳定阶段3(205~400)。
|
图 2 阶段划分结果 Fig.2 Stage separation results |
为检验本文所提方法在质量预测方面的有效性,实验将本文方法(扩展得分矩阵法)、不考虑质量变量,只用X的得分矩阵求相似度进行阶段划分的方法(得分矩阵法)、传统的基于过程变量聚类进行阶段划分的方法(FCMx-MPLS法)以及基于过程变量和质量变量的扩展矩阵聚类进行阶段划分的方法(FCMxy-MPLS法)作对比。通常情况下,判断质量预测精度标准采用均方根误差(RMSE),当RMSE的值较小时,表明预测精度较大;当RMSE的值较大时,表明预测精度较小。评估整个批次的预测误差定义如下式:
| ${\rm{RMSE}}_{\rm { Batch }}= \sqrt {\frac{{\sum\limits_{kc = 1}^K {{{\left\| {{y^{kc}} - {{\hat y}^{kc}}} \right\|}^2}} }}{K}} $ | (13) |
ykc是一个批次中第kc时刻的质量实际值,
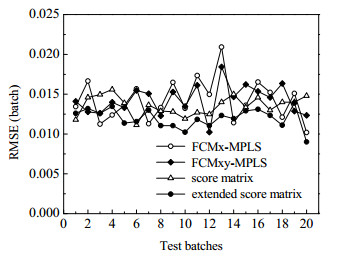
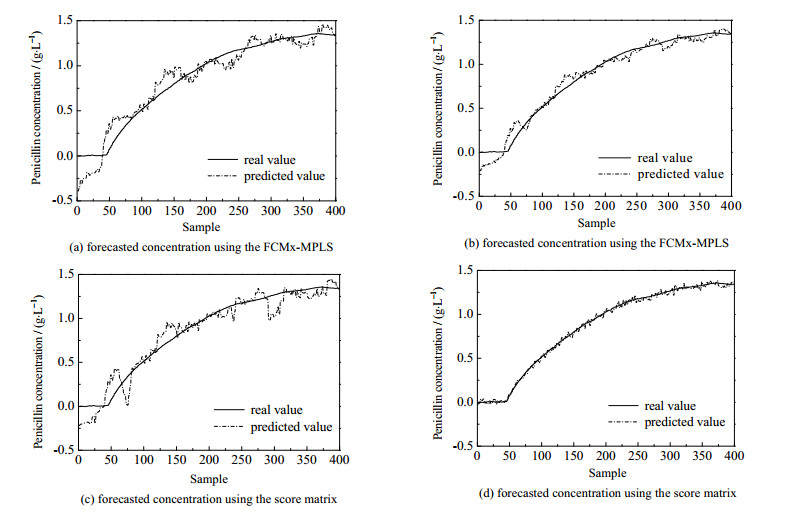
图 3为4种不同方法在质量预测时,不同批次的预测精度图。其中20批次中有16批次本文方法的质量预测精度优于FCMx-MPLS方法,有18批次的预测精度本文所提方法优于得分矩阵方法,FCMx-MPLS和FCMxy-MPLS方法批次间的预测误差变化较大。从图中可以看出在20测试批次中,本文所提方法的质量预测效果优于其他3种方法,而且传统的基于过程变量聚类进行阶段划分的方法的稳定性最差。为进一步说明结果,实验对单一批次的预测曲线进行分析,这里选择了第8测试批次。图 4为4种方法的产物浓度预测曲线,相比于图 4(d),图 4(a)、(b)和(c)的预测偏差较大,图 4(d)的预测曲线虽然仍有波动,但是波动幅度较小,预测精度明显比图 4(a)、(b)和(c)要高。相比于没有考虑质量变量的阶段划分方法,本文方法质量预测精度有所提高。
|
图 3 20测试批次的预测效果 Fig.3 Prediction results of 20 batches |
|
图 4 第8测试批次的质量预报 Fig.4 Quality prediction results of the 8th test batch |
工业生产中制备药用蛋白大多利用大肠杆菌发酵,常采用补料分批发酵方式,是比较复杂的生物发酵过程。实验依托北京市某生物制药厂进行,所生产的产品为白介素。该生产过程的持续时间约为6 h,过程中工作人员根据OD600值变化确定如何进行操作,而且OD600也是表征最终产物浓度的变量,药厂对OD600采用离线测量方法,有一定的时间滞后,不能及时反馈并指导生产。因此对OD600进行精确建模和预测有重要的实际意义。
选取的7个过程变量和1个质量变量如表 2所示。罐内发酵时间为6 h,采样间隔为5 min。共采集30批正常数据,其中20批次用于阶段划分和离线建模,得到三维过程数据矩阵X(20×7×72)和质量数据Y(20×1×72),剩余10批次作为测试组。为使实验结果更具有说服力,采用与上节仿真实验相同的4种阶段划分方法。
|
|
表 2 生产过程变量 Table 2 Variables of production processes |
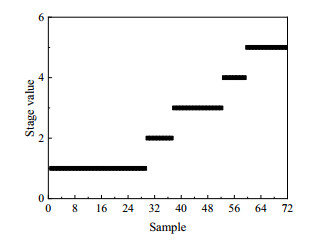
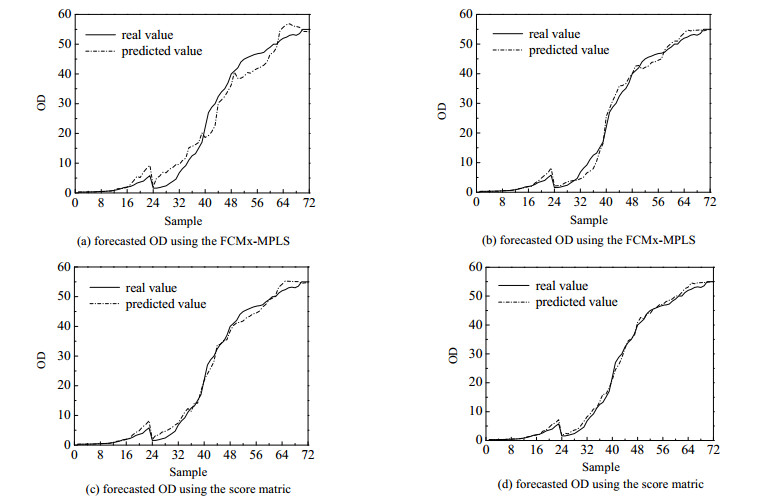
图 5是大肠杆菌发酵过程的阶段划分结果,从图中可以看出整个生产过程被分为3个稳定阶段和2个过渡阶段。图 6显示的是10个测试批次的大肠杆菌质量预测效果图,从图中可以明显看出本文所提方法的质量预测精度最高,为进一步分析,选择其中的一个测试批次数据绘制预测曲线。从图 7可以看出图 7(d)的预测曲线最接近于实际值,图 7(a)、(b)和(c)的预测曲线相对于实际值,都有不同程度的偏离,预测精度较低。
|
图 5 阶段划分结果 Fig.5 Stage separation results |

|
图 6 10测试批次的预测效果 Fig.6 Prediction results of 10 batches |
|
图 7 第5测试批次的质量预报 Fig.7 Quality prediction results of the 5th test batch |
根据以上两组实验结果可以看出,本文所提方法在阶段划分方面是有效的,能将整个生产过程较为准确地划分为不同阶段。在与不考虑质量变量信息的阶段划分方法的对比中可以看出,考虑质量变量后的阶段划分方法在质量预测的精度和稳定性方面都有所提高。在仿真实验中,由于所采集的数据较为理想,预测误差较小,大肠杆菌发酵过程受外界因素干扰,整体的质量预测精度远远低于青霉素仿真实验,但是对比的3种方法中,本文所提的基于得分扩展矩阵的阶段划分方法的质量预测精度依然最高。
6 结论本文提出了一种基于扩展得分矩阵的阶段划分方法。该方法考虑了质量变量对阶段划分存在的影响,将质量变量的得分矩阵扩展到过程变量的得分矩阵中,采用CS统计量的大小来衡量两个扩展得分矩阵的相似度,根据相似度的变化实现对生物发酵过程的阶段划分。最后利用青霉素发酵仿真平台和大肠杆菌实例验证,通过与FCMx-MPLS、FCMxy-MPLS、不考虑质量变量的得分矩阵相似性度量阶段划分方法相比较,实验结果证明了本文所提方法的有效性。
| [1] |
周东华, 李钢, 李元. 数据驱动的工业过程故障诊断技术[M]. 北京: 科学出版社, 2011. ZHOU D H, LI G, LI Y. Data-driven fault diagnosis technology for industrial processes[M]. Beijing: Science Press, 2011. |
| [2] |
仇力, 栾小丽, 刘飞. 基于主元相似度的间歇过程操作曲线多阶段融合优化[J]. 高校化学工程学报, 2018, 32(3): 628-635. QIU L, LUAN X L, LIU F. Fusion optimization of multi-stage batch process trajectories based on similarity of principal components[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 628-635. DOI:10.3969/j.issn.1003-9015.2018.03.018 |
| [3] |
刘毅, 陈坤, 王海清. 选择性递推LSSVR及其在过程建模中的应用[J]. 高校化学工程学报, 2008, 22(6): 1043-1048. LIU Y, CHEN K, WANG H Q. Selective recursive LSSVR and its applications in process modeling[J]. Journal of Chemical Engineering of Chinese Universities, 2008, 22(6): 1043-1048. DOI:10.3321/j.issn:1003-9015.2008.06.023 |
| [4] |
KOURTI T, MACGREGOR J F. Process analysis, monitoring and diagnosis, using multivariate projection methods[J]. Chemometrics & Intelligent Laboratory Systems, 1995, 28(1): 3-21. |
| [5] |
WANG X Z, MCGREAVY C. Data mining and knowledge discovery for process monitoring and control[M]. London: Springer, 1999.
|
| [6] |
NOMIKOS P, MACGREGOR J F. Multi-way partial least squares in monitoring batch processes[J]. Chemometrics & Intelligent Laboratory Systems, 1995, 30(1): 97-108. |
| [7] |
AWDUCHE D, RRKHTER Y. Multiprotocol lambda switching:Combining MPLS traffic engineering control with optical crossconnects[J]. Communications Magazine IEEE, 2001, 39(3): 111-116. DOI:10.1109/35.910598 |
| [8] |
CAMACHO J, PICO J. Multi-phase principal component analysis for batch processes modelling[J]. Chemometrics & Intelligent Laboratory Systems, 2006, 81(2): 127-136. |
| [9] |
LU N Y, GAO F, WANG F. Sub-PCA modeling and on-line monitoring strategy for batch processes[J]. AIChE Journal, 2004, 50(1): 255-259. DOI:10.1002/(ISSN)1547-5905 |
| [10] |
GE Z Q, ZHAO L P, YAO Y, et al. Utilizing transition information in online quality prediction of multiphase batch processes[J]. Journal of Process Control, 2012, 22(3): 599-611. DOI:10.1016/j.jprocont.2012.01.004 |
| [11] |
邓晓刚, 张琛琛, 王磊. 基于多阶段多向核熵成分分析的间歇过程故障检测方法[J]. 化工学报, 2017, 68(5): 1961-1968. DENG X G, ZHANG C C, WANG L. Fault detection in batch process by multistage multiway kernel entropy component analysis[J]. CIESC Journal, 2017, 68(5): 1961-1968. |
| [12] |
YING S, DING X S, HAO H, et al. Data-driven monitoring for stochastic systems and its application on batch process[J]. International Journal of Systems Science, 2013, 44(7): 1366-1376. DOI:10.1080/00207721.2012.659708 |
| [13] |
WOLD S, RUHE A, WOLD H, et al. The collinearity problem in linear regression. the partial least squares (PLS) approach to generalized inverses[J]. SIAM Journal on Scientific and Statistical Computing, 1984, 5(3): 735-743. DOI:10.1137/0905052 |
| [14] |
王惠文. 偏最小二乘回归的线性与非线性方法[M]. 北京: 国防工业出版社, 2006. WANG H W. Partial least squares regression - Linear and nonlinear methods[M]. Beijing: National Defense Industry Press, 2006. |
| [15] |
KOHAVI R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proceedings of the 14th international joint conference on artificial intelligence, Volume 2. San Francisco: Morgan Kaufmann Publishers Inc. 1995: 1137-1143.
|
| [16] |
齐咏生, 张海利, 高学金, 等. 基于KECA的化工过程故障监测新方法[J]. 化工学报, 2016, 67(3): 1063-1069. QI Y S, ZHANG H L, GAO X J, et al. Novel fault monitoring strategy for chemical process based on KECA[J]. CIESC Journal, 2016, 67(3): 1063-1069. |
| [17] |
JENSSEN R, PRINCIPE J C, ERDOGMUS D. The Cauchy-Schwarz divergence and Parzen windowing:Connections to graph theory and Mercer kernel[J]. Journal of the Franklin Institute, 2006, 343(6): 614-629. DOI:10.1016/j.jfranklin.2006.03.018 |
| [18] |
QIN Y, ZHAO C H, WANG X Z, et al. Subspace decomposition and critical phase selection based cumulative quality analysis for multiphase batch processes[J]. Chemical Engineering Science, 2017, 166: 130-143. DOI:10.1016/j.ces.2017.03.033 |
| [19] |
YANG Y Q, XU L, HU C Y. Extended adjacency matrix indexes and their applications[J]. Journal of Chemical Information & Computer Sciences, 1994, 34(5): 1140-1145. |
| [20] |
LI D L, ZHANG Z H. Configuration analysis of metamorphic mechanisms based on extended adjacency matrix operations[J]. Chinese Journal of Mechanical Engineering, 2011, 24(5): 767-773. DOI:10.3901/CJME.2011.05.767 |
| [21] |
常鹏, 王普, 高学金, 等. 基于多向核熵成分分析的微生物发酵过程多阶段划分及故障监测[J]. 高校化学工程学报, 2015, 29(3): 650-656. CHANG P, WANG P, GAO X J, et al. Multi-stage separation and fault monitoring of microbial fermentation processes based on multi-way kernel entropy component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(3): 650-656. DOI:10.3969/j.issn.1003-9015.2015.03.022 |




