2. 齐鲁工业大学(山东省科学院),山东省科学院海洋仪器仪表研究所,山东 青岛 266001
2. Institute of Oceanographic Instrumentation, Qilu University of Technology(Shandong Academy of Sciences), Qingdao 266001, China
喷射器是一种利用高速高压流体卷吸低速流体,将湍射流的湍动扩散作用用来传递能量和质量的流体机械及混合反应设备。由于喷射器具有无运动部件、结构简单、紧凑轻便、运行可靠、无泄漏、免维修等优点,特别适用于水下、高压、高温、真空、放射、腐蚀等环境,被广泛应用于化学、化工、生物、环境等行业中[1]。但由于喷射器内部涉及两股不同压力的流体的混合,导致内部流动很复杂,且传能与传质效率较低,提高喷射器性能成为了国内外越来越多学者关注的焦点。
20世纪70年代以来,国内外学者主要通过2种途径来提高喷射器的性能,一种是传统的改变喷射器结构尺寸[2-3],尤其是对于具有易于更换、灵活方便、生产成本低等优点的喷嘴的改进[4-5]。GUILLAUME等[6]采用了长宽比为3的椭圆形喷嘴的喷射器,与圆形喷嘴喷射器相比较发现,椭圆形喷嘴喷射器的卷吸能力和效率均更高。YANG等[7]研究了不同形状喷嘴的喷射器性能,结果表明不同形状的喷嘴对喷射器喷射系数和背压影响较大,以圆锥形喷嘴为参考标准,十字型喷嘴对喷射系数提升幅度最大。别海燕等[8]研究了喷嘴结构对液-液喷射器性能的影响,建立了喷嘴出口形状分别为圆形、标准椭圆形、三角形和方形4种结构的喷射器模型,通过数值模拟对比分析得出椭圆喷嘴喷射器的性能优于其他3种结构的喷射器。而另一种有效的途径就是在同一装置上采用非恒定射流来提高喷射器效率,如脉冲射流、振荡射流等[9]。CROW等[10]于1971年首先在射流泵装置上进行了脉冲射流的试验研究,结果表明对于同一喷射器脉冲射流的卷吸率比恒定射流提高了32%。王玲花等[11]通过试验探究了脉冲频率及面积比对液体喷射泵性能参数的影响,试验结果表明脉冲射流频率在一定范围内变化可以提高喷射泵的性能,频率越大、面积比越小,喷射泵性能提高越多,并且脉冲射流关阀时间对脉冲液体喷射泵性能也有影响。BIE等[12]研究了不同脉冲频率和振幅的脉冲射流对圆形喷嘴喷射器性能的影响,发现相比于恒定射流喷射器,脉冲频率和振幅越高的喷射器,其卷吸性能和效率提升更加显著。本文在此基础上,将上述2种提高喷射器性能的方法进行结合,对喷射器进行性能优化,并运用大涡模拟探究其内部流动特性。
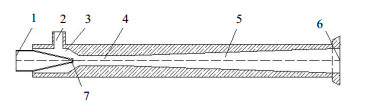
2 计算模型 2.1 物理模型喷射器的主要结构包括喷嘴、吸入室、主流入口、次流入口、混合段与扩散段,其结构示意图如图 1所示。由于在异形喷嘴中椭圆形喷嘴对喷射器性能的提升效果最好,本文选择了如图 2所示的2种喷嘴结构。圆形喷嘴的出口截面直径D=5×10-3 m,保证椭圆喷嘴出口截面面积与圆形喷嘴面积相等,可确定椭圆喷嘴相应的几何尺寸。喷射器其他的基本尺寸为主流入口直径为8D,次流入口直径为4D,混合段直径为2.4D,喉嘴距为3.2D,混合段长度为14.4D,扩散段扩散角度为5.5°。对于2种喷嘴结构的喷射器,分别采用恒定射流和脉冲射流作为工作流体,形成了4种类型的喷射器,其喷嘴和射流类型如表 1所示。
|
图 1 喷射器结构示意图 Fig.1 Schematic diagram of the ejector 1. primary flow inlet 2. secondary flow inlet 3. suction chamber 4. mixing chamber 5. diffuser 6. exit 7. nozzle |

|
图 2 2种喷嘴的结构示意图 Fig.2 Schematic diagram of two nozzle structures |
|
|
表 1 4种喷射器的类型 Table 1 Types of the four ejectors |
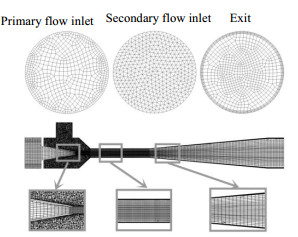
对建立的三维模型进行网格划分,由于大涡模拟对网格质量要求较高,对整个喷射器模型进行分区域划分网格,部分区域需要进行网格加密处理。混合段和扩散段靠近管壁处均加入较密的边界层网格。除吸入室外的区域形状规则,采用计算速度快的结构网格进行网格划分,并在射流剪切层进行局部加密。吸入室中喷嘴出口截面至混合段入口的区域也使用结构网格进行网格划分,而吸入室其余区域结构较复杂,采用非结构网格中适应性比较强的混合网格进行划分。
网格质量和数量对计算节点的生成影响很大,进而也会影响到离散化方法的确定。对建立的三维模型进行网格无关性检验,将椭圆喷嘴喷射器分别划分成网格数为630 090、864 151和1 256 826的模型,通过对比发现模拟结果与网格数量无关。为保证计算速度和计算精度,以网格数量为630 090的模型进行后续的模拟研究。网格划分示意图如图 3所示。
|
图 3 喷射器的网格划分 Fig.3 Grid mesh of the ejector |
大涡模拟是在流动区域内对基于Favre平均的小尺度脉冲过滤的N-S方程(纳维-斯托克斯,Navier-Stokes)进行网格过滤,从而得到较大尺度涡的基本方程组。
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}}}{{\partial {x_i}}} = 0 $ | (1) |
式中:ρ为流体密度,kg·m-3;t为时间,s;ui为坐标轴三个方向的速度分量,m·s-1;xi为坐标轴三个方向的长度,m。
动量方程组:
| $ \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}}}{{\partial t}} + \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{u}}_j}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}(\mu \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}}}{{\partial {x_j}}}) - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} $ | (2) |
式中:τij为亚格子紊动应力;p为微元体上受到的压力,Pa;μ为流体黏度,Pa·s。
本文采用的Smagorinsky在1963年提出的Smagorinsky亚格子模型,其雷诺应力模型[13]为
| $ {\tau _{ij}} - \frac{1}{3}{\delta _{ij}}{\tau _{kk}} = - 2{\nu _t}{\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{ij}}}} $ | (3) |
| $ {\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{ij}}}}{\rm{ = }}\frac{1}{2}(\frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}}}{{\partial {x_j}}} + \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{j}}}}}{{\partial {x_i}}}) $ | (4) |
| $ {\nu _t}{\rm{ = (}}{C_{\rm{s}}}L{)^2}\left| \mathit{\boldsymbol{S}} \right| = {{\rm{(}}{C_{\rm{s}}}L)^2}{(2{\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{ij}}}}{\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{ij}}}})^{1/2}} $ | (5) |
式中:δij为Kronecker常数;τkk为亚格子应力的同向部分;νt为亚格子涡黏系数;Sij为可解尺度的应变率张量;Cs为Smagorinsky系数,本文取0.1;L为过滤尺度,m;S为应变率张量的幅值。
将亚格子应力涡黏模型式(3)代入到滤波后的N-S方程(2)中,得到大涡模拟方程:
| $ \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}}}{{\partial t}} + \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{j}}}}}{{\partial {x_j}}} = - \frac{\partial }{{\partial {x_i}}}\left( {\frac{p}{\rho } + \frac{{{\tau _{kk}}}}{3}} \right) + \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + {\nu _t})\left( {\frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{i}}}}}{{\partial {x_j}}} + \frac{{\partial {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{j}}}}}{{\partial {x_i}}}} \right)} \right] $ | (6) |
喷射器的工作流体入口和引射流体入口均选用水作为流体介质,工作流体入口采用速度入口边界,其中恒定射流喷射器的速度入口为1.2 m·s-1,脉冲射流喷射器的速度入口使用UDF(用户自定义函数,user defined function)定义,其平衡值与恒定射流入口速度相同,脉冲振幅为0.2 m·s-1。引射流体入口采用压力入口边界,设为0.1 MPa(绝压,下同)。出口采用压力出口边界,设为0.2 MPa。壁面采用无滑移壁面边界条件。
3.3 求解设置采用有限体积法对瞬态控制方程进行离散,非耦合隐式方案进行求解,对流项离散采用二阶迎风格式。进行数值模拟时,对控制方程在空间上进行离散,在每个时间步上进行离散方程的求解。在时间域上采用二阶隐式格式。利用SIMPLE算法求解实现压力与速度的耦合,速度修正方程中压力项采用Standard方法,动量的求解采用有界中心差分格式,其余采用二阶迎风格式。
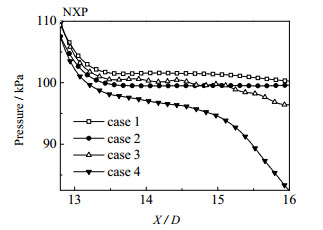
4 结果分析 4.1 内部流动特性 4.1.1 喷射器轴向与径向压力分布高压的工作流体在进入喷射器后,经过喷嘴加速,将其压力能转化为动能,在喷嘴出口平面(nozzle exit plain, NXP)高速射入吸入室,在混合段入口附近区域内形成了低压区,喷射器内部与次流入口产生了压差,使得引射流体可以被卷吸入喷射器[14]。低压区的值越小,压差越大,表明卷吸能力越强。如图 4所示为4种喷射器在射流中心线上的局部压力分布曲线。图中的横坐标X/D为喷射器中从主流入口到扩散段出口的无量纲长度,X为轴向长度。由图可知,工作流体从喷嘴射出后压力进一步降低,case 4的轴向压力以更快的下降速度形成了最小的低压值,说明在次流入口压力相同的条件下,case 4具有更大的压差,能够为卷吸引射流体提供更高的动力。
|
图 4 4种喷射器沿射流中心线的压力曲线 Fig.4 Pressure distribution along the center lines of the four ejectors |
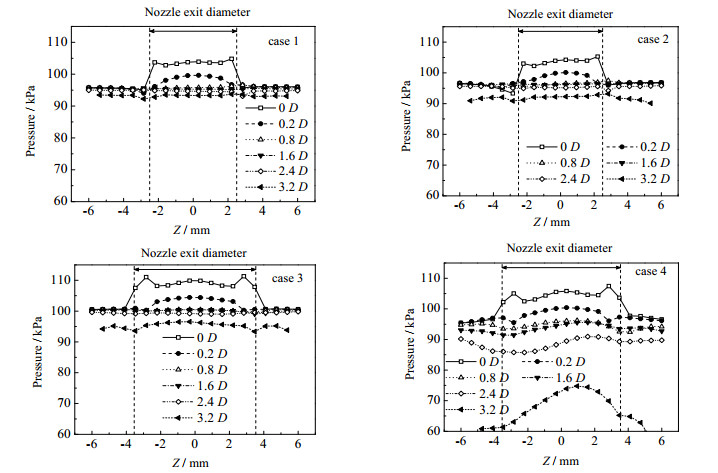
4种喷射器从喷嘴出口到混合段入口的区域内,在距离喷嘴出口平面0D, 0.2D, 0.8D, 1.6D, 2.4D, 3.2D处的截面径向压力分布如图 5所示。图中的横坐标Z为喉嘴段截面距离轴线的径向长度,正负代表相对位置。可以发现4种喷射器的径向压力基本都呈现出对称性分布的规律,这说明工作流体从喷嘴喷出后暂未产生流体偏移现象,左右对称的压力分布更有利于喷射器的卷吸及混合。而且在喷嘴出口平面上,喷嘴边界以内区域的压力高于其以外区域的压力,使得压力能转化为动能后的工作流体能够顺利地射入吸入室。随着两股流体的混合,径向压力呈现整体下降趋势,并且喷嘴边界内区域的压力下降得更快,径向压差逐渐减小,使得在进入混合段之前的压力在径向上逐渐趋于平衡。直到混合段入口平面,4种喷射器的压力均出现不同程度的波动和下降,其中case 4的径向压力下降幅度最大,更低的压力值能卷吸更多的引射流体,而且在混合段入口处的其轴向压力梯度最大,为两股流体的混合提供了更大的动力。
|
图 5 4种喷射器径向压力分布 Fig.5 Radial distribution of pressure in the four ejectors |
随着内层高速流体与外层低速流体的掺混,产生了对高速流体的阻力,使得高速流体边缘部分流速降低,难以维持初始速度。随着混合过程的进行,在喷嘴出口边界向内外扩展的掺混区逐渐形成剪切层。剪切层内的中速流体,将吸收到的更内层的高速流体的能量,传递给更外层的低速流体,促使了速度梯度的形成。而仍保持初始速度且未受掺混影响的射流核心区在经过一定距离后,掺混逐渐由边缘发展到射流中心,使得射流的全断面上都发展成湍流。
如图 6所示为4种喷射器混合段内不同位置的速度分布切片图,表征了混合段中各截面流体速度v的大小。由图可知,case 1在混合段内势流核心区变化最小,形成的中速流体区域也最小,该喷射器内两股流体的混合性能较差。由于喷嘴和射流类型的改变,加剧了两股流体的掺混,使得case 2和case 3的混合性能优于case 1。而case 4中最短的射流核心区和最大的中速流体区,证明该喷射器具有最优的混合性能。
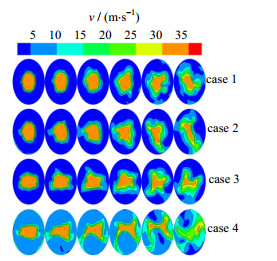
|
图 6 4种喷射器混合段内不同位置的速度分布 Fig.6 Velocity distribution at different positions in mixing sections of the four ejectors |
表征流体元旋转角速度的物理量称为涡量,而涡量高度聚集的流体区域就是涡,流体场就是由涡量不同的涡旋叠加而成的。当下发展了多种严格的、定量的、不依赖于坐标系的漩涡判别准则,在常用的4种逐点判别方法中,由HUNT等[15]提出的Q涡准则,定义流场中速度梯度张量▽V的第二矩阵不变量Q具有正值的区域为漩涡,另外漩涡区域的压强要低于周围压强。Q定义如下:
| $ Q = - \frac{1}{2}({\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{ij}}}}{\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{ij}}}} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\mathit{\boldsymbol{ij}}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\mathit{\boldsymbol{ij}}}}) $ | (7) |
式中:Ωij为速度梯度张量矩阵反对称部分。
当所得的Q值为正值时,代表已经克服了流体间的应变力与剪切力并主要产生旋转,因此该区域可以很好的代表湍流结构[16]。从喷嘴射出的高速工作流体与周围的低速引射流体间形成速度不连续的间断面,不稳定的速度间断面必然会产生波动,并发展成旋涡,从而引起湍动,这样就会把周围的低速流体卷吸到射流中心。采用Q涡准则得到4种喷射器基于速度的涡量等值面(Q=1×106)分布图,分别如图 7和8所示。
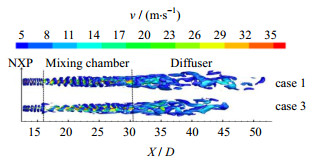
|
图 7 2种喷射器基于速度的Q涡等值面分布图 Fig.7 Velocity-based Q-criterion isosurface of the two ejectors |
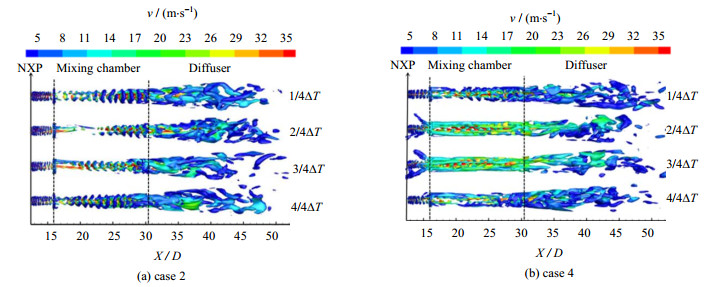
|
图 8 一个脉冲周期中2种喷射器基于速度的Q涡等值面分布图 Fig.8 Velocity-based Q-criterion isosurface of the two ejectors within one pulse cycle |
图 7为采用恒定射流的2种喷射器所形成的涡量等值面,可以看到在喷嘴出口到混合段入口的区域内,都出现了较密的环形柱状涡,这是由于从喷嘴高速射出的工作流体与被卷吸进入的低速引射流体之间较大的速度梯度产生的。在进入混合段后, 高速流体的能量通过涡结构传递给低速流体,使得涡结构因两股流体的剧烈混合而不断壮大。进入扩散段后,速度梯度进一步减小,随着能量传递趋于平衡,涡结构进一步扭曲变形,大尺度的涡由于能量的耗散最终破碎成小尺度的涡。对比2种喷射器可以发现,由于喷嘴形状的差异,case 3的椭圆形喷嘴周长更大,导致两股流体的接触面积更大,更易发生能量交换,同时在扩散段内大尺度的涡耗散得更快,说明两股流体在case 3中混合速度更快,混合效果更好。
对于脉冲射流喷射器,在一个脉冲周期中,由于工作流体入口流速的周期变化,导致在脉冲射流喷射器中两股流体的速度梯度时刻发生变化,涡量也随之改变。所以图 8选取了一个脉冲周期中4个时刻的涡量等值面(Q=1×106),以探究脉冲射流对2种喷射器内部流动特性的影响。图中,ΔT为一个脉冲周期,在脉冲周期的中间阶段(2/4ΔT),相比于case 2,case 4的柱状涡更为集中靠前,说明在工作流体入口流速达到最大值时,case 4内湍动程度更大,造成的湍动耗散更大,其混合性能更好。而case 4除了两股流体接触面上相互作用产生的环形柱状涡,在混合段的上、下2个壁面上还出现了层状涡。这是由于椭圆喷嘴长短轴长度的不同,从高速脉冲射流得到更多能量的低速流体更易从短轴侧进入混合段,上、下壁面边界层上的低速流体获得了更多的能量,速度提高的黏性流体流经固体就形成了较大涡量的层状涡,表明case 4的混合段内能量传递效率更高,掺混更剧烈。
4.2 性能分析工作流体与引射流体的流量比(
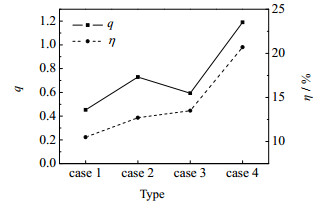
|
图 9 4种喷射器的性能参数对比图 Fig.9 Comparison of performance parameters of the four ejectors |
如图 10所示为4种喷射器沿射流中心线的引射流体质量分数分布曲线。由图可知,各曲线在进入混合段之前相互重合,此时引射流体还未与射流中心线上的工作流体发生混合。在此之后case 4最早呈现上升趋势,随后其余曲线也逐渐发生分离,最终各曲线在扩散段趋于恒定,即各喷射器基本完成了混合。说明各喷射器中两股流体的混合速度不同,case 4的混合速度最快,引射流体能更早与内层的工作流体发生混合,混合性能更好。而且在混合段出口和扩散段入口的区域内,由于流体由面积恒定的圆柱形混合段流入了面积逐渐增大的圆台形扩散段,流体的动能逐渐转化为压力能,中心的流体向四周扩散,各曲线也就出现了不同程度的波动情况。
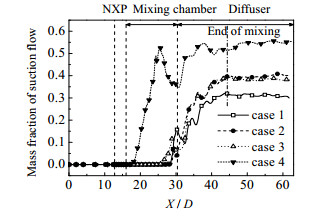
|
图 10 4种喷射器射流中心线上引射流体质量分数曲线 Fig.10 Mass fraction profiles of suction flow along the center lines of the four ejectors |
(1) 各喷射器在喷嘴出口到混合段入口区域内,压力沿轴线呈现对称性的下降趋势,形成的低压区为卷吸引射流体提供动力。在进入混合段后,两股流体进一步混合,势流核心区缩小,中速流体区域扩大,最终在扩散段中完成混合。
(2) 大涡模拟能够很好地模拟出喷射器内部旋涡的情况,尤其是对于脉冲喷射器,可以很好地观察一个脉冲周期中旋涡的变化过程,更有助于对喷射器内部流动特性进行分析。
(3) 在4种喷射器中,椭圆喷嘴脉冲射流喷射器的卷吸性能、混合性能、效率均最好。而对于性能最差的圆形喷嘴恒定射流喷射器,采用脉冲射流和椭圆喷嘴的方法均能不同程度地提升其性能。
| [1] |
WANG X D, DONG J L. Numerical study on the performances of steam-jet vacuum pump at different operating conditions[J]. Vacuum, 2010, 84(11): 1341-1346. DOI:10.1016/j.vacuum.2010.03.001 |
| [2] |
毕荣山, 谭心舜, 林柯利, 等. 结构尺寸对液-液喷射器湍流混合性能的影响[J]. 高校化学工程学报, 2010, 24(5): 752-757. BI R S, TAN X S, LIN K L, et al. The effect of configuration diminsion on turulent mixing in liquid-liquid ejectors[J]. Journal of Chemical Engineering of Chinese Universities, 2010, 24(5): 752-757. DOI:10.3969/j.issn.1003-9015.2010.05.005 |
| [3] |
耿利红, 马新灵, 魏新利, 等. 喷射器几何结构对压缩/喷射制冷循环性能的影响研究[J]. 高校化学工程学报, 2015, 29(5): 1073-1081. GENG L H, MA X L, WEI X L, et al. Effects of ejector geometry on performance of compression/ejection refrigeration cycle[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1073-1081. DOI:10.3969/j.issn.1003-9015.2015.05.008 |
| [4] |
DAOTONG CHONG Q Z F Y. Research on the steam jet length with different nozzle structures[J]. Experimental Thermal and Fluid Science, 2015, 64: 134-141. DOI:10.1016/j.expthermflusci.2015.02.015 |
| [5] |
CHANG Y J, CHEN Y M. Enhancement of a steam-jet refrigerator using a novel application of the petal nozzle[J]. Experimental Thermal & Fluid Science, 2000, 23(6): 677-686. |
| [6] |
GUILLAUME D W, JUDGE T A. Improving the efficiency of a jet pump using an elliptical nozzle[J]. Review of Scientific Instruments, 1999, 70(12): 4727-4729. DOI:10.1063/1.1150141 |
| [7] |
YANG X, LONG X, YAO X. Numerical investigation on the mixing process in a steam ejector with different nozzle structures[J]. International Journal of Thermal Sciences, 2012, 56: 95-106. DOI:10.1016/j.ijthermalsci.2012.01.021 |
| [8] |
别海燕, 李春红, 安维中, 等. 喷嘴结构对液-液喷射器性能影响的CFD模拟[J]. 计算机与应用化学, 2016, 33(10): 1068-1073. BIE H Y, LI C H, AN W Z, et al. CFD simulation of the influence of nozzle structure on the performance of liquid-liquid ejector[J]. Computers and Applied Chemistry, 2016, 33(10): 1068-1073. |
| [9] |
王玲花, 高传昌. 脉冲射流泵研究进展[J]. 水利电力机械, 2006, 28(6): 33-35. WANG L H, GAO C C. Study progress of pulse jet pump[J]. Water Conservancy & Electric Power Machinery, 2006, 28(6): 33-35. DOI:10.3969/j.issn.1674-1951.2006.06.013 |
| [10] |
CROW S C, CHAMPAGNE F H. Orderly structure in jet turbulence[J]. Fluid Mechanics, 1971, 48(3): 547-591. DOI:10.1017/S0022112071001745 |
| [11] |
王玲花, 高传昌, 王为术, 等. 脉冲频率对液体喷射泵性能影响的试验研究[J]. 水利学报, 2008, 39(3): 318-324. WANG L H, GAO C C, WANG W S, et al. Experimental study on effect of pulse frequency on performance of pulse liquid jet pump[J]. Journal of Hydraulic Engineering, 2008, 39(3): 318-324. DOI:10.3321/j.issn:0559-9350.2008.03.010 |
| [12] |
BIE H Y, LI C H, AN W Z, et al. CFD simulation of the effect of pulsed jet on the performance of liquid-liquid ejector[J]. Chemical engineering transactions, 2017, 61: 865-870. |
| [13] |
SMAGORINSKY J S. General circulation experiments with the primitive equations[J]. Monthly Weather Review, 1963, 91(1): 99-164. |
| [14] |
ALLOUCHE Y, BOUDEN C, VARGA S. A CFD analysis of the flow structure inside a steam ejector to identify the suitable experimental operating conditions for a solar-driven refrigeration system[J]. International Journal of Refrigeration, 2014, 39(1): 186-195. |
| [15] |
HUNT J C R, WRAY A A, Moin P. Eddies, streams, and convergence zones in turbulent flows[C]// Studying Turbulence Using Numerical Simulation Databases. California: Center for Turbulence Research, 1988: 193-208.
|
| [16] |
FU W S, LAI Y C, LI C G. Estimation of turbulent natural convection in horizontal parallel plates by the Q criterion[J]. International Communications in Heat & Mass Transfer, 2013, 45(7): 41-46. |




