相变蓄热技术因蓄热密度高、蓄/放热过程温度恒定等优点而在太阳能利用、工业余/废热回收及电子器件热管理等领域广受关注[1~3]。但是,由于相变材料的低导热系数(≤ 0.2 W·m-1·K-1),使得该技术的应用及推广受到极大限制。解决上述问题的有效方法之一是通过合理设计传(蓄)热系统以达到增强传热的目的。
在相变蓄热装置中添加肋片的方法因其经济及高效性而成为最具发展前景的强化传热措施之一[4]。大量学者针对肋片的形状、尺寸、间距、位置等因素的作用展开系统性研究。除采用空气等传热系数极小的物质作为传热流体外,通常情况下肋片添加在传热热阻较大的相变材料侧。Liu等[5]对添加肋片的套管式相变蓄热器的热性能进行实验研究,发现宽度小的薄肋片的强化传热效果优于宽度大的厚肋片。Hosseini等[6]研究了肋片数量、肋片厚度及高度等参数对新型针肋式电子元件冷却器热性能的影响,结果表明,增加肋片数量、厚度及高度可大大降低芯片的表面温度并延长其使用寿命。Agyenim等[7]对比了水平套管式蓄热器中赤藓糖醇(erythritol)融化及凝固过程中环肋和直肋的强化传热效果,得出直肋具有更好的效果。Wang等[8]建立了不同肋片尺寸及肋片分布的蓄热器模型,并将其与光管模型进行对比,分析了肋片几何参数对套管式相变蓄热器热性能的影响。Lacroix等[9]发现肋片的强化传热效果与传热流体的进口流量有关,对进口流体温度低、流量适中的工况,可取得最优的强化传热效果;而对进口温度高、流量大的工况,即使增加肋片数量也很难达到显著增强传热的目的。
添加肋片会起到增大传热面积和削弱自然对流强度的双重作用。Gharebaghi等[10]对矩形腔中竖直壁面上水平向肋片数量的作用进行研究,发现装置的传热效果并非完全与肋片数量正相关。较多的肋片数量会减小浮生力驱动流的作用范围,从而使蓄热过程的主导传热机制转化为热传导。类似研究也证实肋片会在一定程度上限制蓄热过程中自然对流作用的产生及发展。而且,添加肋片会降低装置的蓄热密度。因此,对肋片数量、肋片分布及肋片构造的优化研究十分必要。
数值计算方法的出现,为求解导热、对流共同作用的相变过程及其强化传热带来极大便利。考虑到现阶段强化传热的肋片大多为均匀分布的等高直肋,而自然对流作用下的蓄热过程具有材料融化的竖向不均匀性[11, 12]。为此,本文针对传统等高直肋实施优化,得到变高度的阶梯形肋片,并以套管式蓄热器为例验证其作用效果,这对深入理解及设计、优化套管式相变蓄热器具有指导意义。
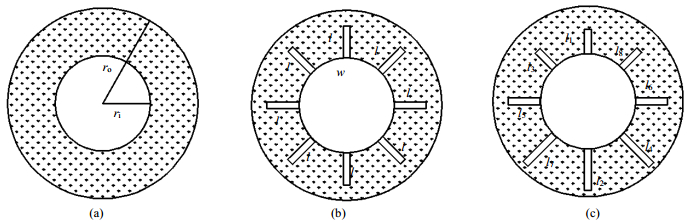
2 数学物理模型 2.1 物理模型图 1所示为本文计算的水平套管式相变蓄热器的结构示意图。其中,内管半径ri = 15 mm,外壳半径ro = 30 mm。肋片个数包括n = 0 (光管)和n = 8 (带肋片)两种,肋片宽度w = 2 mm。除光管蓄热器(a)外,其余各带肋片装置的传热面积及相变材料体积均相等。等高直肋装置(b)的肋片高度均为l,阶梯形肋片装置(c)的肋片高度l1~7随肋片偏移距离s的变化而改变,具体关系为s = l2 - l = l - l1。同一方向的两肋片高度之和为定值,且各肋片的高度满足l1 = l3 = l8 < l = l5 = l6 < l2 = l4 = l7。本文的具体工况设置见表 1。
|
图 1 水平套管式相变蓄热器的结构示意图 Fig.1 Schematic diagram of the horizontal sleeve-tube LHES units (a) no fin (b) rectangular fins of equal height (c) stepped-fins |
|
|
表 1 计算工况汇总表 Table 1 Conditions of four LTES unit groups |
铜肋片的导热系数λ = 387.6 W·m-1·K-1,密度为ρ = 8978 kg·m-3,比热为cp = 381 J·(kg·K)-1。相变材料月硅酸(lauric acid,PCM)的热物性参数见表 2。由于系统结构的对称性,选择模型的一半作为计算区域,同时忽略轴向传热,将PCM的传热进一步简化为二维轴对称问题。经网格无关性验证,各蓄热器模型的最小网格尺寸为0.3 mm,利用边界层网格对靠近热源的区域实施局部加密。非稳态计算的时间步长为0.05 s。
2.2 数学模型本文采用焓法模型计算套管内月硅酸的融化过程,通过建立整体的能量方程,确定焓的分布,进而确定温度场及相变面的位置。将发生相变的物质看作多孔介质,并认为各单元的孔隙率等于液相率,纯固相区域内,孔隙率为0,对应区域的速率为0;固液两相区由孔隙率减少导致的动量损失可表示为:
| $ S = {A_{{\rm{mush}}}}\frac{{{{\left( {1 - \beta } \right)}^2}}}{{{\beta ^3} + \varepsilon }}\overrightarrow v $ | (1) |
式中,模糊区常数Amush = 108,为防止分母为零引起的震荡,ε为一个极小的常数,本文取ε = 0.001[14]。计算过程同时考虑蓄热阶段导热、自然对流两种传热机制的作用,且PCM密度满足Boussinesq假设。融化后的PCM流体为不可压缩牛顿流体,流动为层流,忽略黏性耗散,具体数学模型见文献[8]。
本文计算中设置相变材料熔点为参考温度,利用SIMPLE算法对压力-速度的耦合进行离散,PRESTO算法对压力项进行离散[15]。非稳态计算中,每个时间步长的最大迭代次数设为200,质量、动量方程的残差为10-3,能量方程的为10-6。压力、动量、能量及液相率的松弛因子分别为0.3,0.7,1和0.9。
2.3 初始及边界条件初始时刻,整个计算区域的温度Tini均匀分布且低于相变材料的熔点,即相变材料具有一定的过冷度。
蓄热过程开始,蓄热器内管温度维持Tw不变,相变材料与内管的接触面设为耦合传热(coupled-wall)边界,蓄热器的外管壁面设为绝热。考虑到计算模型的对称性,将套管式蓄热器的竖向对称轴设为对称边界,包括相变材料与肋片所在区域。
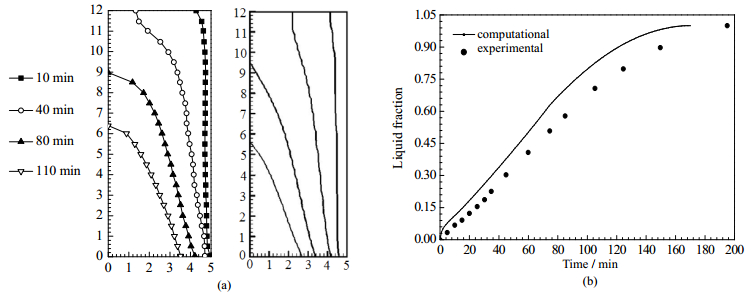
2.4 模型验证图 2所示为本文计算的月桂酸在竖向矩形腔的融化过程与文献实验数据[16]的对比结果。如图所示,各时刻的相界面分布呈现较好的一致性,即采用该模型可较好地反映相变材料的融化特性。计算所得液相率较实验结果略高,是由于模型中设定除热源外的其余竖面均绝热,而实验过程存在装置壁面向环境的散热量所致。
|
图 2 数值计算与实验结果[16]的对比 Fig.2 Comparison of numerical and experimental results (a) solid-liquid interface (b) liquid fraction of experimental results[16] |
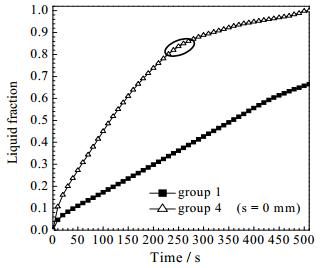
图 3对比了第1组工况和第4组工况(s = 0)的液相率曲线。由于不同热源温度下等高直肋的作用类似,故选择某一温度为例进行分析。如图所示,Tw = 363.15 K时,带有8个等高直肋装置的液相率变化明显快于无肋片装置(光管)的。这是由于在低导热性相变材料中添加高导热系数的铜肋片后,加快并扩展了内部热源向套管内低温固相材料的热传递速率,进而增加了对应装置内固相材料的融化速率。
|
图 3 第1组工况和第4组工况的液相率对比 Fig.3 Comparison of liquid fractions of group1 and group4 |
但如图 3所示,虽然8等高直肋装置的液相率变化加快,该装置的液相率曲线存在拐点,从蓄热前期的液相率线性增长到中后期的变化平缓,对应了固相材料的融化速率从前期的快速融化到中后期的逐渐衰减。这表明常用的等高直肋虽较光管式装置实现了强化传热,但蓄热后期装置内的传热及材料的融化速率仍存在较大提升空间。为此,本文在此基础上进一步分析了阶梯形肋片的强化传热效果。
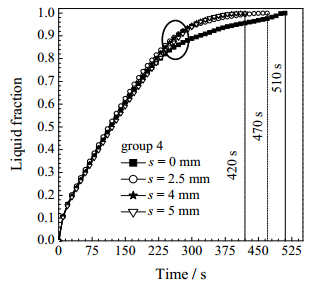
3.2 肋高不均匀性的影响为加快蓄热后期固相材料的融化速率,本文在传热面积相等的条件下对前述等高直肋实施偏移,获得非等高的阶梯形肋片以期改善装置底部材料的融化状况,进而实现装置热性能的进一步提升。以肋片个数n = 8,热源温度Tw = 363.15 K为例,图 4给出了不同肋片偏移距离s = 0,2.5,4和5 mm (即第4组工况)的对比结果。
|
图 4 第4组工况的液相率变化曲线 Fig.4 Profiles of liquid fraction of group 4. |
如图 4所示,蓄热前期各装置的液相率曲线基本重合,在s = 0 mm即等高直肋装置的液相率曲线出现拐点的时刻,出现s > 0即阶梯形肋片装置与等高直肋装置液相率曲线的分离。而且,s > 0装置的蓄热时间均较s = 0的有所减少,表明利用非等高的阶梯形肋片可实现装置蓄热速率的进一步加快。
当肋片偏移距离从s = 0增大至2.5,4和5 mm时,对应装置的蓄热时间分别减少40,90和90 s。即随s的增加,阶梯形肋片的强化传热效果先逐渐增加而后趋于稳定,具体原因可由图 5所示的相界面及温度分布得到解释。
|
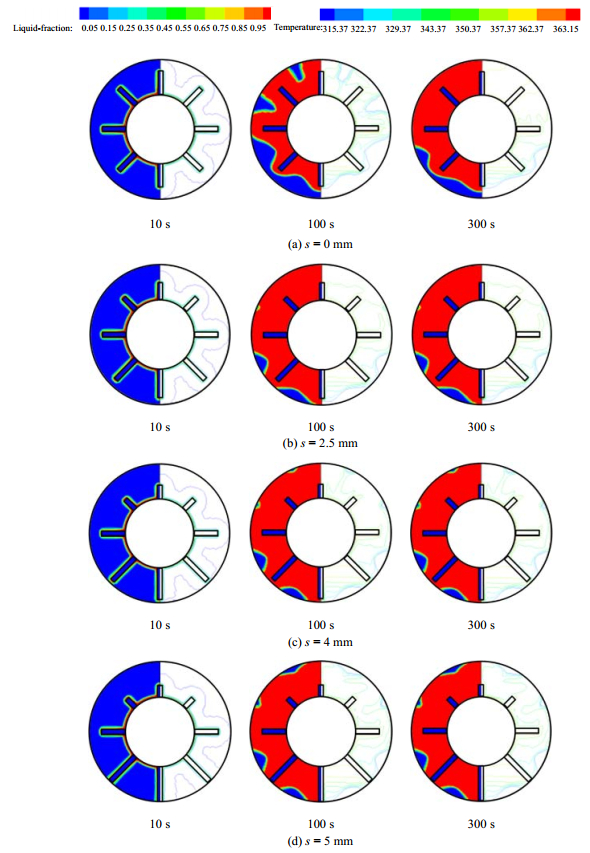
图 5 不同时刻下第4组工况的相界面(左侧)及温度场(右侧)分布 Fig.5 Liquid fractions (left) and temperature fields (right) at selected time intervals during melting of group 4 |
t = 10 s的初始蓄热阶段,热传导作用下各装置内均是靠近热源及肋片的少量固相材料完成融化,形成沿内管及肋片均匀分布的薄液相层。随融化过程的进行,液相材料逐渐增多并出现自然对流的作用,使得装置上部材料的融化速率较快而下部的偏慢,表现为装置内相界面的竖向不均匀分布。s越小的装置,这一现象也越明显。非等高阶梯形肋片的出现,一定程度上改善了装置内材料融化及温度分布的竖向不均匀性。t = 300 s的中后期阶段,s = 0及2.5 mm装置内上部的材料已完全融化,而s = 4及5 mm装置的上部、下部区域均存在未融化的固相材料。
s从0增大到2.5及4 mm的过程,蓄热时间明显缩短,但s继续增大至5 mm时,蓄热时间基本不变。这是因为相对较小的肋片偏移(s = 2.5及4 mm)有效改善了后期阶段装置底部固相材料的融化状况。但是,当s由4 mm进一步增大到5 mm时,虽然蓄热后期装置下部仍维持较高强度的热传导作用,但装置下部较大的肋片高度限制了前期阶段自然对流作用的产生及发展,从而导致该装置的蓄热时间不再有显著变化。
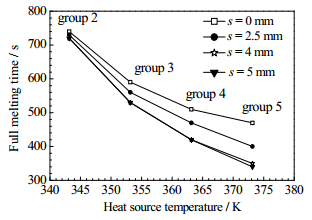
3.3 热源温度的影响为进一步分析阶梯形类肋片在不同热源温度下的强化传热效果,图 6对比了第2、3、4及5组工况的蓄热时间。如图所示,第2组工况的蓄热时间无明显差异,即较低的热源温度下非等高的阶梯形肋片的强化传热效果并不明显。随热源温度的增加,阶梯形肋片的强化传热效果逐渐增强。热源温度对装置蓄热时间影响的具体结果见表 3。其中,蓄热时间的缩短百分比γ定义为:
| $ \gamma = \frac{{{t_{{\rm{full,s}}}} - {t_{{\rm{full}}}}}}{{{t_{{\rm{full}}}}}} $ | (2) |
|
图 6 第2、3、4、5组工况的蓄热时间 Fig.6 Completed melting time of group 2, 3, 4 and 5 |
|
|
表 3 装置的蓄热时间缩短百分比(γ)与热源温度的关系 Table 3 Percentages of thermal storage time reduction (γ) for various heat source temperatures |
可以看出,热源温度Tw = 373.15 K,肋片偏移距离s = 5 mm时,蓄热时间缩短百分比出现最大值27.7%。而且,不同的热源温度作用下,s = 4及5 mm两种肋片偏移距离的蓄热时间无明显差异。
4 结论(1) 在水平套管式蓄热器的内管外布置等高直肋虽实现强化传热,但蓄热后期阶段装置底部固相材料的融化速率仍然较低。
(2) 导热-对流共同作用的相变蓄热过程,采用上低下高的不均匀阶梯形肋片可有效改善套管内固相材料融化的竖向不均匀性,随阶梯形肋片高度不均匀性的增加,其强化传热效果先增强而后趋于稳定。
(3) 热源温度越高,不均匀阶梯形肋片的强化传热效果越显著。
符号说明:
| Amush | — 模糊区常数 | t | — 时间,s |
| cp | — 比热容,J·kg-1·K-1 | Ti,Tw | — 分别为热源、相变材料的初始温,K |
| dmax, dmin | — 分别为肋片的最大、最小高度,mm | — 速度矢量,m·s-1 | |
| g | — 重力加速度,m·s-2 | w | — 肋片宽度,mm |
| h | — 显热焓,J·kg-1·K-1 | β | — 热膨胀系数,K-1,液相率 |
| H | — 焓,J | γ | — 装置的蓄热时间缩短百分比 |
| l | — 肋片高度,mm | λ | — 导热系数,W·m-1·K-1 |
| L | — 相变潜热,J·kg-1 | μ | — 运动黏度,m2·s-1 |
| n | — 肋片个数,个 | ρ | — 密度,kg·m-3 |
| P | — 压力,Pa | 下标 | |
| ri,ro | — 分别为内管、外壳半径,mm | full | — 均匀肋片装置的蓄热时间 |
| s | — 肋片的偏移距离,mm | full,s | — 不均匀肋片装置的蓄热时间 |
| Sh | — 与相相关的源项 | Ini | — 初始值 |
| Si | — 动量方程源项 | Ref | — 参考值 |
| Sb | — 反映浮生力作用的源项 | s, l | — 分别为固相和液相 |
| [1] | Zhang Y, Chen C, Qi D W. Review on phase change material storage in solar energy application[J]. Applied Mechanics & Materials, 2014, 587(587-589): 309-314. |
| [2] | Nomura T, Akiyama T. High-temperature latent heat storage technology to utilize energy of solar heat and industrial exhaust heat[J]. International Journal of Energy Research, 2017, 41(2): 240-251. DOI:10.1002/er.v41.2. |
| [3] | YIN Hui-bin(尹辉斌), GAO Xue-nong(高学农), ZHANG Zheng-guo(张正国). Application of phase-change thermal control in heat shock resistance of electronic devices(相变温控应用于电子设备的抗热冲击性能研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2017, 31(3): 554-560. DOI:10.3969/j.issn.1003-9015.2017.00.023. |
| [4] | Jegadheeswaran S, Pohekar S D. Performance enhancement in latent heat thermal storage system:a review[J]. Renewable & Sustainable Energy Reviews, 2009, 13(9): 2225-2244. |
| [5] | Liu Z, Sun X, Ma C. Experimental investigations on the characteristics of melting processes of stearic acid in an annulus and its thermal conductivity enhancement by fins[J]. Energy Conversion & Management, 2005, 46(6): 959-969. |
| [6] | Hosseini S M J. A parametric investigation of a PCM-based pin fin heat sink[J]. Mechanical Sciences, 2015, 6(1): 65-73. DOI:10.5194/ms-6-65-2015. |
| [7] | Agyenim F, Eames P, Smyth M. A comparison of heat transfer enhancement in a medium temperature thermal energy storage heat exchanger using fins[J]. Solar Energy, 2009, 83(9): 1509-1520. DOI:10.1016/j.solener.2009.04.007. |
| [8] | Wang P, Yao H, Lan Z, et al. Numerical investigation of PCM melting process in sleeve tube with internal fins[J]. Energy Conversion & Management, 2016, 110(FEB): 428-435. |
| [9] | Lacroix M. Study of the heat transfer behavior of a latent heat thermal energy storage unit with a finned tube[J]. International Journal of Heat & Mass Transfer, 1993, 36(8): 2083-2092. |
| [10] | Maryam G, Sezai I. Enhancement of heat transfer in latent heat storage nodules with internal fins[J]. Numerical Heat Transfer Part A Applications, 2007, 53(7): 749-765. DOI:10.1080/10407780701715786. |
| [11] | Li Z, Wu Z G. Analysis of HTFs, PCMs and fins effects on the thermal performance of shell-tube thermal energy storage units[J]. Solar Energy, 2015, 122(2): 382-395. |
| [12] | YANG Xiu(杨秀), CHEN Zhen-qian(陈振乾). Numerical simulation on melting phase change heat transfer in ice storage ball filled with aluminum foam(蓄冰球中填充泡沫铝的融化相变传热过程的数值模拟)[J]. Journal of Chemical Industry and Engineering (China)(化工学报), 2008, 59(s2): 139-142. |
| [13] | Cao X, Yuan Y, Xiang B, et al. Numerical investigation on optimal number of longitudinal fins in horizontal annular phase change unit at different wall temperatures[J]. Energy & Buildings, 2018, 158: 348-392. |
| [14] | Hu Z, Li A, Gao R, et al. Effect of the length ratio on thermal energy storage in wedge-shaped enclosures[J]. Journal of Thermal Analysis & Calorimetry, 2014, 117(2): 807-816. |
| [15] | Hosseini M J, Ranjbar A A, Rahimi M, et al. Experimental and numerical evaluation of longitudinally finned latent heat thermal storage systems[J]. Energy & Buildings, 2015, 99: 263-272. |
| [16] | Shokouhmand H, Kamkari B. Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit[J]. Experimental Thermal and Fluid Science, 2013, 50: 201-212. DOI:10.1016/j.expthermflusci.2013.06.010. |




