2. 武汉大学 水射流理论与新技术湖北省重点实验室,湖北 武汉 430072
2. Key Laboratory of Hubei Province for Water Jet Theory & New Technology, Wuhan University, Wuhan 430072, China
气力提升系统(airlift system)以压缩空气为工作介质,在管内通过动量交换以及浮力作用实现液体或浆体的输送,为一种典型的特殊用途泵。由于该系统内部未含运动部件,结构简单,已逐渐成为举升矿浆、淤泥、石油及输送危险性液体的有效可靠工具[1-3]。
对于气力提升理论模型的研究,早期以YOON等[4],KAJISHIMA等[5]和ANIL等[6]的研究为最为突出。他们基于动量定理建立了管内混合流体流动模型,并利用迭代方法对模型进行求解,得到了管内各相流速变化特征。由于在模型中未考虑管内流型转变,因而理论值与实验值相差较大。在此基础上,CACHARD等[7]和裴江红等[8]分别在环状流和弹状流状态下构建了混合流体模型,其预测精度较前者有较大幅度提高。不过由于该模型局限于单一流型工况,而实际中管内一般涉及多种流型,因而其适用性受限。鉴于此,胡东与唐川林等[9-10]综合分析流型转变因素,在模型建立中引入压力及相含率控制方程,大大提高了模型的预测精度。
综合分析国内外学者对于气力提升理论模型的分析可发现,多数学者在分析及计算模型时主要以获得管内气、液、固各相流速为目的,鲜有涉及反映气力提升性能的效率模型。KHALIL等[11]和PENG[12]和NIZ等[13]虽以颗粒质量流速与气体质量流速的比值作为效率模型,然其过于简单,不能精确评价气力提升系统的优劣。随后,MAHROUS[14]与PUMPS等[15]则利用颗粒能量(重力势能与动能)与气体能量的比值定义效率,该方案显著提高了效率模型精度。不过由于该模型未考虑颗粒所受浮力之作用,其精确性仍有待提高。值得指出的是,在计算上述效率模型时均需代入气、液、固各相流速的实测值,因此其实际上仍为经验模型。针对上述不足,本文基于能量守恒原理,拟构建一种精度高、通用性强的效率模型,并融合动量方程以期获得浆料气力提升效率特性曲线。
2 浆料气力提升原理目前,多数学者认为气力提升系统之所以能实现浆料输送是因管内混合流体的密度差所致[16-17]。此观点能很好解释进气口之上的气-液-固三相段稳定运移过程,但不能分析进气口之下的液-固提升原理。而且气力提升由气体喷射伊始至稳定输送存在一瞬态过程,难以利用上述观点给予解释。鉴于此,部分研究者利用气塞效应分析浆料提升原理,较好克服了第一种学说的弊端[18-19]。然而,这一观点在分析高浸入深度工况浆料输送时受阻。因为在数千米的深海及深井时,提升管底部段气泡因高围压存在难以聚集、结合形成泰勒泡,也就不能利用气塞效应进行分析。由上可知,浆料气力提升内部流动过程较为复杂,单一观点或学说难以支撑,因此需考虑多工况、多阶段对浆料提升原理加以分析,有助于丰富浆料气力提升原理。
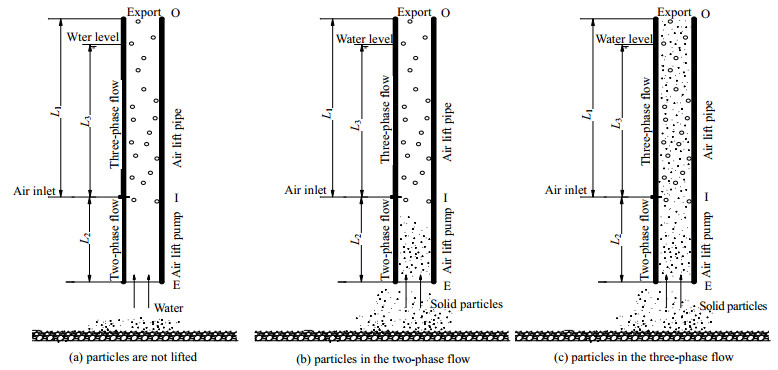
图 1为浆料气力提升原理示意图,其中E、I和O分别指气力泵底部、进气口与排料口,L1、L2和L3分别为进气口至管排料口长度,进气口与气力泵底部距离以及进气口至水平面长度。气体首先经空压机增压,在气力泵出口与其内部水流发生较为强烈的动量交换。因环境围压与相间摩擦作用,气体被剪切为大量小气泡,大量气泡聚集在管内进气口附近,使得进气口之上原有液柱上下端压力平衡被破坏,液柱被迫上升。因输入气力泵内气体不断增加,管内液体便持续上升,直至由排料口输出,而气力泵底部外围流体则不断补充进入泵内,使得水底颗粒表层附近形成一向上的绕流场,导致颗粒受流体拖曳力作用。若输入气量较低,管内流型为泡状流,气-液间滑移较大,气力泵底部流体速度也较小,颗粒所受拖曳力不足以克服其重力,从而造成浆料气力提升失效(图 1a)。当气量升高,气泵内小气泡集结数量大幅增加,气泡聚结成体积近乎为管径的泰勒泡,从而推动前端液柱上升。显然,该工况下气、液间滑移现象较前者减弱,从而使得管内液体流速大幅增加。若流体流速的增加使得颗粒所受拖曳力大于其重力,颗粒便离开槽底进入泵内,在进气口之下形成液-固两相段(图 1b)。但当颗粒越过进气口之后因其旋转、冲击及其对气泡的挤压使得小气泡难以聚合形成泰勒泡,气塞动力因此消失,此后管内大量小气泡似网状结构托举固体颗粒快速上升。显然,在三相流形成后,管内泡状流结构对增强气力携固性能尤为重要,而在气-液两相流中,该流态反而不利于气力提升,这也说明气力提升系统的扬水与携固原理存在很大差异。值得指出的是,在气-液-固三相中,大量小气泡因体积小受到浮力及围压作用会沿管加速上升,导致其轨迹线上颗粒受到附加力作用进一步快速上移。由上述分析可知,在气-液-固三相段中,颗粒的上升主要受管内流型结构影响,气泡越小、密集程度越高,则气力携固性能越佳。同时气泡的加速作用也对颗粒上升的影响尤为重要。在液-固两相段内,颗粒的提升基本取决于其所受拖曳力。可见,气力携固原理较为复杂,在管内需分成三相段和两相段进行分析,而在提升过程中具有瞬态和稳态过程。
|
图 1 浆料气力提升示意图 Fig.1 Schematic diagrams of typical slurry air-lift processes |
气力提升效率是衡量其提升系统性能优劣的关键指标,可定义为排料口(O)固体所持有能量与进气口输入气体能量的比值,如式(1):
| $ \eta = {N_{\rm{S}}}/{N_{\rm{G}}} $ | (1) |
式中NS为提升管O处排出颗粒的能量,W;NG为进气口I处输入气体的能量,W。
| $ {N_{\rm{G}}} = \int_{{P_{\rm{O}}}}^{{P_{\rm{E}}}} {{Q_{{\rm{GX}}}}} {\rm d}p = {P_0}{Q_{\rm{G}}}\ln (\frac{{{P_{\rm{E}}}}}{{{P_0}}}) $ | (2) |
其中
| $ {P_{\rm{E}}} = {\rho _{\rm{L}}}g({L_2} + {L_3}) + {P_0} - 0.5{\rho _{\rm{L}}}J_{\rm{L}}^2 $ | (3) |
式中:QGX为提升管内气体体积流量,m3·s-1;QG为排料口O处气体体积流量m3·s-1;PE和P0分别为气力泵底部E处压力以及大气压,Pa;ρL为液体密度,kg·m-3;g为重力加速度,m·s-2;JL为液体表观流速,m·s-1。
因颗粒在水平面下
| $ \eta = \frac{{{N_{\rm{S}}} - {E_{\rm{B}}}}}{{{N_{\rm{G}}}}} = \frac{{{E_{{\rm{V}}2}} + {E_2} - {E_{\rm{B}}}}}{{{N_{\rm{G}}}}} $ | (4) |
式中:EV2为浮力对颗粒做功,W;E2为颗粒重力势能,W;EB为颗粒平均动能,W。
上式各项计算如下:
| $ {E_2} = {\rho _{\rm{S}}}g({L_1} + {L_2}){Q_{\rm{S}}} = A{\rho _{\rm{S}}}g({L_1} + {L_2}){J_{\rm{S}}} $ | (5) |
| $ {E_{{\rm{V}}2}} = \frac{1}{2}{\rho _{\rm{S}}}{Q_{\rm{S}}}{(\frac{{{Q_{\rm{S}}}}}{A})^2} \approx \frac{{{\rho _{\rm{S}}}{Q_{\rm{S}}}^3}}{{2{A^2}}} = \frac{1}{2}A{\rho _{\rm{S}}}J_{\rm{S}}^3 $ | (6) |
| $ {E_{\rm{B}}} = {\rho _{\rm{L}}}g({L_2} + {L_3}){Q_{\rm{S}}} = A{\rho _{\rm{L}}}g({L_2} + {L_3}){J_{\rm{S}}} $ | (7) |
其中ρS为颗粒密度,kg·m-3;QS为颗粒的体积流量,m3·s-1;JS为固相表观流速,m·s-1;A为管截面积,m2。
整理式(1)至(7),可得气力提升系统的扬固效率:
| $ \eta = \frac{{{\rho _{\rm{S}}}g({L_1} + {L_2}){J_{\rm{S}}} + 0.5{\rho _{\rm{S}}}J_{\rm{S}}^3 - {\rho _{\rm{L}}}g({L_2} + {L_3}){J_{\rm{S}}}}}{{{P_0}{J_{\rm{G}}}\ln (\frac{{{\rho _{\rm{L}}}g({L_2} + {L_3}) + {P_0} - 0.5{\rho _{\rm{L}}}J_{\rm{L}}^2}}{{{P_0}}})}} $ | (8) |
基于KASSAB等[20]提出的动量模型(式9),将效率模型(式8)与动量模型联立,继而利用迭代方法在Matlab中求解,即可计算得出效率特性曲线,其中所需参数如表 1所示。
|
|
表 1 求解模型所需参数 Table 1 Parameters used in the model |
| $ \begin{array}{l} A[{\rho _{\rm{L}}}g({L_2} + {L_3})] - A\int_{\rm{E}}^{\rm{I}} {[{\rho _{\rm{L}}}{\beta _{{\rm{L, LS}}}} + {\rho _{\rm{S}}}{\beta _{{\rm{S, LS}}}}]gdZ} - A\int_{\rm{I}}^{\rm{o}} {[{\rho _{\rm{G}}}{\beta _{{\rm{G, 3}}}} + {\rho _{\rm{L}}}{\beta _{{\rm{L, 3}}}} + {\rho _{\rm{S}}}{\beta _{{\rm{S, 3}}}}]gdZ} \\ - \pi D\int_{\rm{E}}^{\rm{I}} {{\tau _{{\rm{LS}}}}dZ - } \pi D\int_{\rm{I}}^{\rm{o}} {{\tau _3}dZ} - A({J_{{\rm{G, O}}}}{\rho _{{\rm{G, O}}}}{u_{{\rm{G, O}}}} + {J_{\rm{L}}}{\rho _{\rm{L}}}{u_{{\rm{L, O}}}} + {J_{\rm{S}}}{\rho _{\rm{S}}}{u_{{\rm{S, O}}}})\\ {\rm{ + }}A({J_{\rm{L}}}{\rho _{\rm{L}}}{u_{{\rm{L, E}}}} + {J_{\rm{S}}}{\rho _{\rm{S}}}{u_{{\rm{S, E}}}}) = 0{\rm{ }} \end{array} $ | (9) |
式中A为管内截面积,m2;D为管内径,m;ρ为密度,kg·m-3;J为表观流速,m·s-1;u为速度,m·s-1;τ为剪切应力,N·m-2;β为体积份数;g为重力加速度,m·s-1;L1,L2和L3分别指吸入段(两相)、提升段(三相)及浸入段长度,m;下标G, L, S, LS和3分别表示气体,液体,固体,固-液两相以及气-液-固三相。
以获得η-JG特征曲线为例,首先联立效率模型与动量模型消除JS,再利用迭代方法,具体计算过程如下:
1) 参考Mahrous的计算[14],选择n= 2 000,这既可保证计算精度,又能节约计算时间;
2) 给定JG与JL;
3) 因管内压力变化为连续,且气-液-固三相段中相邻节点间距离极短,可设两两节点压力变化为线性,且初步设置P(1)为I点管外水压,计算P(k)/P(k+1)和△Z(k),其中0<k <n;
4) 计算I、O以及节点处的JG;
5) 假设η为某个值;
6) 计算I、O以及节点处βG, 3,βL, 3和βS, 3;
7) 分别计算∆Pf, LS/∆Z,∆Pf, 3(k)/∆Z,∆PE和∆PI;
8) 计算式(9)左边项;
9) 重复步骤(5)~(8),直至式(9)左项趋近于0;
10) 更新P(k);
11) 重复步骤(4)~(10),直到P(1)趋于恒定值,然后输出η。
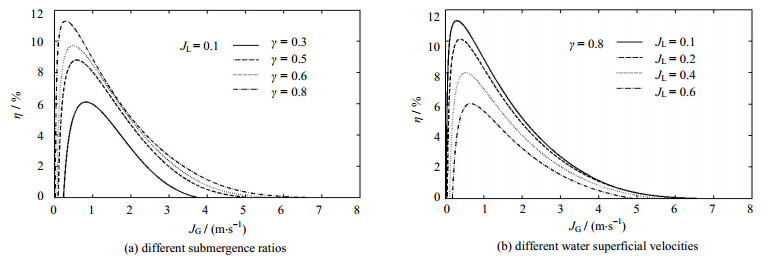
图 2为系统效率随气体表观流速的变化规律。由图可得,效率随气体表观流速先急剧上升,待越过峰值点后其下降趋势变缓。结果说明,在追求高效率时仅需较小气量即可。结合笔者之前的研究[10]可认为,最佳效率与最高固相表观流速所处位置相差甚远,即系统的最优工况难以重合。
|
图 2 效率与气体表观流速的变化关系 Fig.2 Profiles of lifting efficiency as a function of superficial velocity of injected air |
分析图 2(a)还可得,对应每条特性曲线,气体表观流速均存在一“启动”值JG, min (η= 0对应的气体左极限值),且仅当气量越过该“启动”值才能保证气力携固的顺利实施。此外,还存在一最大气体表观流速JG, max (η = 0对应的气体右极限值)。这说明气量值过低或过高均不利于颗粒的提升,该结论与气力输送液体的结论基本一致。此外,随着浸入率升高,JG, min逐渐减小,而JG, max却随之加大。此结论说明增大浸入率能扩大气力携固时对应的有效气量值范围(JG, min,JG, max)。从图 2(b)还可知,液体表观流速加大会降低气力提升效率,也使得有效气量值范围变窄,削弱了系统的携固性能。究其原因可认为是气体能量中用于增加液体输送的能量扩大,而举升固体的能量减弱所致。
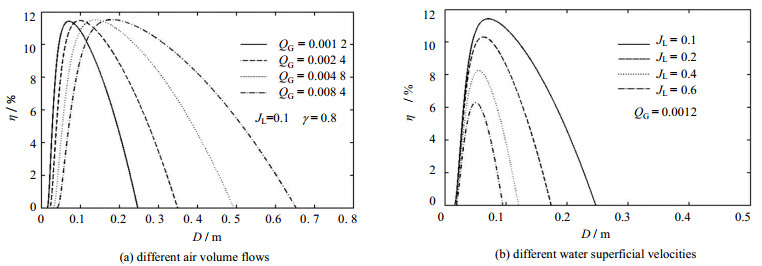
图 3体现了管径对效率的影响规律。由图可见,该变化特征与图 2大致相同,即效率随管径的增加首先快速增至峰值,尔后开始下降,不过其下降趋势因气体体积流量不同而存在较大差异,气量值越小,曲线下降幅度越大。此外,与图 2类似,效率峰值处对应的管径很小,这说明在考虑高效率时,应以小管径为宜。对这一特征可做如下解释,若管径过大,会造成气动力不足,且管内流型与小管径相较发生显著改变,导致气力携固性能减弱。而当气量值极小时,又会因阻力损失加剧而导致系统性能由优转劣,同样不利于颗粒提升。
|
图 3 效率随管径的变化规律 Fig.3 Profiles of lifting efficiency as a function of pipe diameter |
由上图还可得,同样存在临界管径Dmin与Dmax两种情况(η = 0对应的最小管径与最大管径)。分析其原因可知,若管径很小,则所消耗于阻力损失的能量比重就大,导致颗粒提升未能实现。而当管径很大时,混合流体截面积增加,致使原有气动力不足,同样造成颗粒举升失效。此外,分析图还可发现,随气体流量的增加,曲线峰值大致相同,然其所处位置以及Dmin和Dmax均呈增加趋势,且Dmax的增幅要显著高于前两者,这使得有效管径范围更宽。研究图 3(b)还可发现,除效率峰值随JL增加而减小外,其它变化规律与图 3(a)基本类似。由此可总结得出,较小的管径与气量就可达到理想的提升效率,该结论与前述结论大致相同,也体现了气力提升系统在携固方面的优势。
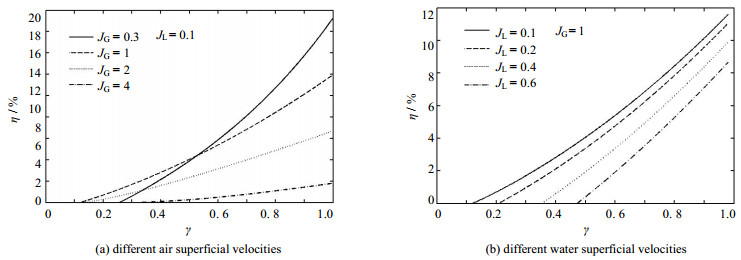
图 4体现了浸入率对效率的影响规律。由此可见,随浸入率增加,效率呈递增趋势,这与气-液两相的垂直提升规律基本相同。从图 4(a)可发现,任一工况均存在一临界浸入率γmin,仅当系统超过该值才能保证气力携固的完成。分析γmin的诱变因素可发现,无论气量值过低还是过高,均造成气力携固性能的减弱。其主要原因可解释如下,当系统处于低浸入率时,若气量值太小,系统动力源不足,导致液体流速较低,从而使得颗粒所受拖曳力不足以克服其自身重力。而当气量值过高,则又易导致气流来不及与液体混合而直接冲溢出水平面,导致能量耗散。因此,在低浸入率下无论前述何种情况均不利于颗粒的提升。当浸入率很高,水平面与排料口接近平齐,系统能量基本勿需克服液体的重力势能,因此仅需很小的气量即可实现管内流型的优化,使系统达到极佳的提升效果,过高的气量反而会造成管内流型恶化。另外,由图 4(b)还可发现,在既定气量下,随液体表观流速加大,临界浸入率γmin呈递增趋势。
|
图 4 效率随浸入率的变化规律 Fig.4 Profiles of lifting efficiency as a function of submergence ratio |
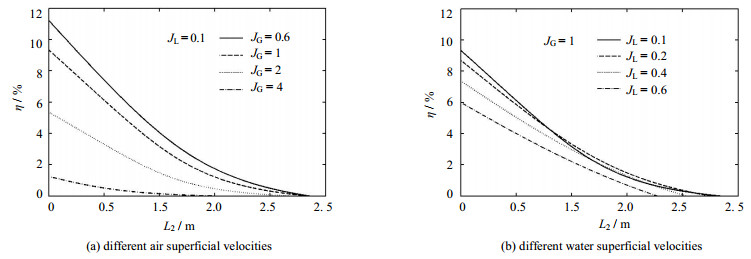
图 5给出了效率随进气口位置的变化规律。由图可见,系统效率随L2加大而呈递减变化规律,即进气口位置上移会导致系统扬固性能减弱。此外,对任一特性曲线,L2出现一极限值L2, max (η = 0对应的液-固两相长度)。对此现象可做如下解释,若L2过长,则进气口靠近水平面,致使气-液混合不充分,使得传质特性变差,导致气力提升性能减弱。
|
图 5 效率随进气口位置的变化规律 Fig.5 Profiles of lifting efficiency as a function of air inlet |
分析图 5(a)还可发现,降低气量值会导致系统进气口位置的有效范围(0,L2, max)缩小。对其特征可做如下解释,高气量值下对应的进气口位置较低气量值时应更低于水平面,否则易因混合段过短造成气流直接冲出水面,甚至还引发啸叫,严重制约气力提升系统的携固性能。此外,进气口位置较低时还可视系统输送段为扬程,液-固两相段长度较小,气-液-固三相段起主导作用,而在三相段中固体颗粒无论是处于瞬态临界提升还是处于稳态输送其阻力损失均优于液固两相段,这使得此时气力携固性能较佳。但随着液-固段L2加大,气力提升系统逐渐由扬程转变为吸程,系统携固性能便因临界提升变难和阻力损失加大开始衰减。
对图 5(b)分析可得,液体表观流速越高,L2, max愈小。同时还发现,液体表观流速越小,曲线下凹程度也越明显,导致曲线出现交叉。结果表明,当进气口位置过低与过高时,需降低液体表观流速,若进气口位置介于之间(0.62 m ≤ L2 ≤ 1.98 m),则需提高液体表观流速以增强效率。对此规律可做如下解释,L2较小时,系统主要为扬程工作,气体能量主要消耗于液固体输送,此时液体表观流速加大会导致固体输送减弱,因而效率减小。而随进气口位置上移,系统吸程段长度增加,不同JL下系统提升颗粒的能力均减弱,但由于在高JL下固体排量衰减较慢,管中能量损失相对较小,导致此时其对应的固体表观流速相对低JL下的较大,因此提升效率转而上升。但随着进气口位置逐渐接近L2, max,系统以吸程工作为主,能量损失加大,原有高JL下举升颗粒的气体能量被削弱,导致效率降低。
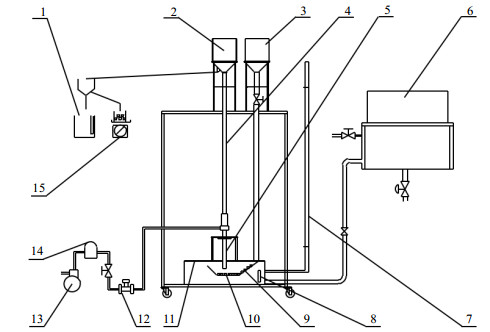
5 模型验证为验证模型精确性,搭建如下实验台(图 6)。压缩气体由空压机经流量计,进入气力泵内,实现气-液固三相混合流体输送。为便于测试,以球形麦饭石陶瓷为工作介质(密度:1 967 kg·m-3,直径2 mm)。本实验中气体流量由控制阀调节,并由智能涡街流量计(型号:EL1-50,范围:0~50 m3·h-1)测定,并换算成表观流速。水和颗粒被导出后分别由计量缸和天平称量而得,再由设定的取样时间(t = 8 s)即可求得液体表观流速与固体表观流速。值得指出的是,由于颗粒具有一定的含水性,因此每次采样完毕后需将其吹干,之后再进行测量。实验中对水与颗粒分别测量5次,并取平均值。
|
图 6 实验系统 Fig.6 Schematic diagram of the experimental setup 1. measuring cylinder 2. splitter 3. conveyor 4. lifting pipe 5. air lift pump 6. adjustable water tank 7.level gauge 8. baffle 9. solid particles 10. cone bucket 11. fixed water tank 12. flow meter 13. air compressor 14. filter 15. blance |
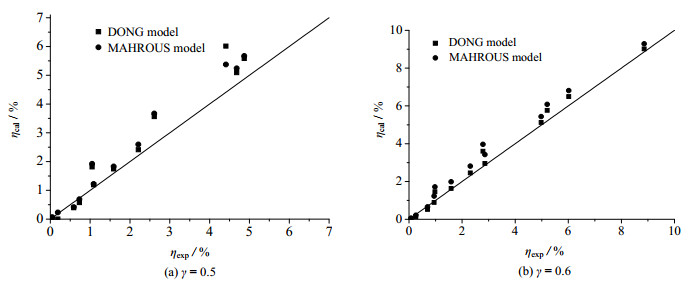
由图 7可知,效率的计算值与实验值在低浸入率下存在很大偏差,而在较高浸入率时吻合较好。这是由于低浸入率工况对应的管内混合流体掺混极强烈所致。当γ= 0.5时,实验过程中就观测到管内存在明显的非规则振荡,且伴有“气吼”声。该现象导致混合流体阻力损失加剧,并使得模型计算中相关参数(如阻力系数、进气口系数等)不再为常值,从而造成模型预测失效。当浸入率升高后,混合流体运动因围压升高而变得较为平稳,且“气吼”声消失,取而代之的是轻微的“啸叫”声。本文所建模型在浸入率超过0.65时可认为其具有较佳的预测精度。另外,气量值过低和过高也会导致模型预测精度降低。而在较高浸入率及中等气量范围内,本文所建模型预测精度较佳,将本模型与MAHROUS[21]的效率模型进行比较可知,前者的预测精度整体优于后者。分析其原因可知,MAHROUS在效率模型计算中未考虑颗粒所受浮力的情况,且他们视进气口压力为围压,未考虑此处混合流体流速及管内摩阻损失引起的压降,因此其模型预测精度不高。以图 7(b)为例,当0.6 m·s-1 ≤ JG ≤ 3 m·s-1时,本模型效率计算值偏离实验值最大仅为7.8%,远低于MAHROUS模型的16.7%。
|
图 7 效率实验值与计算值的比较 Fig.7 Comparison of numerical results with experimental data (dS = 0.002 m) |
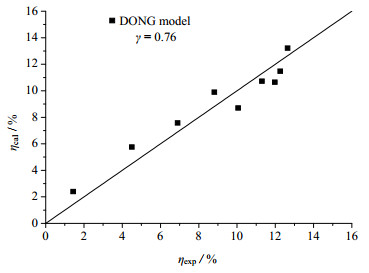
为检验前述理论模型在实际工程应用中的预测精度,将试采结果(湖南省道县后江桥铁锰矿区浆料气力提升试验)与理论值进行比较,结果如图 8所示,其中矿石密度约为2 900 kg·m-3,管内径及开采深度分别为284 mm和300 m。由此可知,本文所建理论模型的预测值与实测值平均误差接近15%,虽高于室内模拟实验情况,但对工程仍具有较强的指导作用,也说明该模型应用在数百米深井及深海时仍具有较高的可靠性。事实上,由于实际开采中受复杂环境影响,井底温度变化、矿浆供给不匀、流固耦合以及各相间作用复杂性增强等都会造成模型精度减弱。
|
图 8 扬固试验结果与理论模型的比较 Fig.8 Comparison of proposed model and experimental results for lifting solid particles |
(1) 以能量守恒为基础,建立了浆料气力提升系统的效率模型,并通过其与气-液-固三相流体的动量方程耦合求解,计算得出了不同工况下的效率曲线。
(2) 效率随气体表观流速的增加呈现先增加后减小的趋势,且峰值位置均靠近坐标原点,说明在追求系统的高效率时输入较小的气量即可。
(3) 当浸入率超过γmin后才能保证系统正常携固,之后效率随此呈递增规律。
(4) 在有效管径范围内(Dmin,Dmax),效率随管径的变化表现出先升后降的规律,且峰值对应的最佳管径很小。此外,在既定液体表观流速下,气体流量的加大使得最佳管径变大,但未改变效率的峰值。而当气体流量恒定时,液体表观流速的变化对效率峰值及其所处位置均影响较大。
(5) 进气口位置上移有碍于气力携固性能的增强,且存在极大值L2, max。当进气口位置靠近气力泵底部或接近水平面,应降低JL以保证系统具有较高的提升效率。而当进气口介于管中间位置则需适度增加JL以维持系统的高效工作。此外,在既定工况下,气体流量的增加可有效拓宽进气口位置的变动范围(0,L2, max)。
(6) 实验值在中等气量范围内与理论值吻合较好,而气量值过低或过高均导致模型失准。此外,浸入率越高,两者吻合程度愈高。
| [1] |
CLARK N N, DABOLT R J. A general design equation for air lift pumps operating in slug flow[J]. AIChE Journal, 1986, 32(1): 56-64. DOI:10.1002/aic.690320107 |
| [2] |
ABOU-TALEB F S, AL-JARRAH J A. Experimental study of an air lift pump[J]. Engineering, Technology & Applied Science Research, 2017, 7(3): 1670-1680. |
| [3] |
YANG J, ZHANG D, CHEN Y, et al. Feasibility analysis and trial of air-lift artificial upwelling powered by hybrid energy system[J]. Ocean Engineering, 2017, 129(1): 520-528. |
| [4] |
YOON C H, PARK Y C. Numerical analysis of solid-liquid-air three-fluid transient flow for air lift system[C]//Proceedings of the Fourteenth International Offshore and Polar Engineering Conference, Toulon: 2004, 23-28.
|
| [5] |
KAJISHIMA T, SAITO T. Numerical simulation of unsteady flow in air-lift pump[J]. JSME International Journal, Series B, 1996, 39(3): 525-532. DOI:10.1299/jsmeb.39.525 |
| [6] |
ANIL M, AGARWAL V K, ALAM M S, et al. CFD modeling of three-phase bubble column:1. Study of flow pattern[J]. Chemical and Biochemical Engineering, 2007, 21(3): 197-205. |
| [7] |
CACHARD F D, DELHAYE J M. A slugh-churn flow model for small-diameter airlift pumps[J]. International Journal of Multiphase Flow, 1996, 22(4): 627-649. DOI:10.1016/0301-9322(96)00003-1 |
| [8] |
裴江红, 唐川林. 影响气举装置临界提升气体表观速度因素的研究[J]. 矿冶工程, 2015, 35(1): 14-16. PEI J H, TANG C L. Affecting factors for apparent air velocity of critical lift in air lift[J]. Mining and Metallurgical Engineering, 2015, 35(1): 14-16. DOI:10.3969/j.issn.0253-6099.2015.01.004 |
| [9] |
胡东, 王晓川, 唐川林, 等. 气力提升理论模型建立及验证[J]. 高校化学工程学报, 2016, 30(5): 1074-1081. HU D, WANG X C, TANG C L, et al. Modeling and validation of an airlift lifting system[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(5): 1074-1081. |
| [10] |
HU D, KANG Y, TANG C L, et al. Modeling and analysis of airlift system operating in three-phase flow[J]. China Ocean Engineering, 2015, 29(1): 121-132. DOI:10.1007/s13344-015-0009-z |
| [11] |
KHALIL M F, ELSHORBAGY K A, KASSAB S Z, et al. Effect of air injection method on the performance of an air lift pump[J]. International Journal of Heat and Fluid Flow, 1999, 20(6): 598-604. DOI:10.1016/S0142-727X(99)00051-X |
| [12] |
PENG H K. Experimental and theoretical study of air-lift artificial upwelling[D]. Taiwan: Taiwan University, 1999.
|
| [13] |
NIZ V E, VAN F K, MOORE R G, et al. An experimental study on three-phase flow in high pressure air injection (HPAI)[J]. Journal of Canadian Petroleum Technology, 2009, 48(9): 47-53. DOI:10.2118/09-09-47 |
| [14] |
MAHROUS A F. Numerical study of solid particles-based airlift pump performance[J]. WSEAS Transactions on Applied and Theoretical Mechanics, 2012, 7(3): 221-230. |
| [15] |
PUMPS T A. Rectangular airlift pump design outperforms cylindrical units[J]. Global Aquaculture Advocate, 2012, 15(6): 77-79. |
| [16] |
SESHADRI A, MAHADEVAN S, MUNIYANDI V. Measurement of liquid film thickness in air-water two phase flows in conventional and mini channels using image processing[J]. Korean Journal of Chemical Engineering, 2015, 32(5): 826-836. DOI:10.1007/s11814-014-0246-5 |
| [17] |
WANG Z N, KANG Y, DENG L I, et al. Investigating the hydrodynamics of airlift pumps by wavelet packet transform and the recurrence plot[J]. Experimental Thermal & Fluid Science, 2018, 92(3): 56-68. |
| [18] |
HATTA N, FUJIMOTO H, ISOBE M, et al. Theoretical analysid of flow characteristics of multiphase mixtures in a vertical pipe[J]. International Journal of Multiphase Flow, 1998, 24(4): 539-561. DOI:10.1016/S0301-9322(97)00074-8 |
| [19] |
AWARI G K, ARDHAPURKAR P M, WAKDE D G. Performance analysis of air-lift pump design[J]. Journal of Mechanical Engineering Science, 2004, 218(10): 1155-1161. DOI:10.1243/0954406042369099 |
| [20] |
KASSAB S Z, KANDIL H A, WARDA H A. Air-lift pumps characteristics under two-phase flow conditions[J]. International Journal of Heat and Fluid Flow, 2007, 30(1): 88-98. |
| [21] |
Mahrous A F. Numerical study of solid particles-based airlift pump performance[J]. WSEAS Transactions on Applied and Theoretical Mechanics, 2012, 7(3): 221-230. |




