换热网络综合是确定化工生产过程中各物流间换热匹配的结构和相应的换热负荷匹配问题,对其进行合理的优化设计,可以取得明显的节能效益或经济收益[1]。换热网络最优化方法可分为热力学方法和数学规划法两大类。以夹点技术[2~5]为代表的热力学方法具有物理概念清晰和操作简单的特点,但这类方法属于分步综合的范畴,不能同时兼顾换热单元数、换热面积及能量回收之间的权衡关系,通常只能得到接近最优的换热网络设计方案。数学规划法将所研究的问题描述为由目标函数和约束条件表示的数学模型,并根据数学模型的类型选择合适的优化方法进行求解,得到满足条件并使目标函数最小(或最大)的解。
数学规划法可分为确定性优化方法和启发式优化方法两类。相比之下,启发式优化方法具有对问题目标函数的要求更为宽松、可操作性强以及计算效率高等优点,因此在化工过程系统优化领域得到越来越多的应用。自1989年Dolan等将模拟退火算法(Simulated Annealing,SA)[6, 7]应用到换热网络的结构优化后,遗传算法(Genetic Algorithm,GA)[8, 9]、差分进化算法(Differential Evolution,DE)[10, 11]和粒子群算法(Particle Swarm Optimization,PSO)[12, 13]等启发式优化方法相继被应用于换热网络最优化问题。
萤火虫算法(Fire-fly Algorithm,FA)是一种新的启发式优化方法,由剑桥学者Yang Xin-she[14]于2008年根据萤火虫个体的发光特性和相互吸引行为提出。FA具有概念简单,控制参数少,易于应用等优点,在众多领域得到了广泛的应用[15~18]。本文将该算法引入换热网络最优化,并进行改进研究。建立了光吸收系数自适应策略和最优个体随机摄动策略,在增强算法全局搜索能力的同时保证收敛精度,并通过算例对算法及改进策略进行验证。
2 换热网络优化数学模型换热网络优化问题可描述为:一组需要冷却的热流体和一组需要加热的冷流体,已知每股物流的热容流率,热流体从初始温度冷却到目标温度,冷流体从初始温度加热到目标温度。通过确定冷热流体间的匹配关系和换热负荷,同时配合冷热公用工程作为补充,使所有的流体均达到目标温度,并使换热设备费用和冷热公用工程费用尽可能小。
2.1 换热网络分级超结构模型采用1990年Yee和Grossmann[19]提出的无分流分级超结构模型,以2股热流体,3股冷流体为例,如图 1所示,图中每条水平线代表一股流体,箭头代表流体的流动方向。热流体用
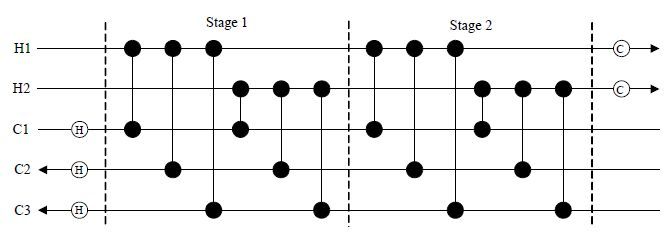
|
图 1 换热网络无分流分级超结构 Fig.1 Superstructure of heat exchanger networks with no stream splits |
以满足工艺条件下换热网络年综合费用(Total Annual Cost,TAC )最小为目标函数:
| $\begin{align} & \min \sum\limits_{i=1}^{NH}{({{C}_{\text{CU}}}{{Q}_{\text{CU},i}}+{{C}_{\text{F,CU}}}{{z}_{\text{CU},i}}+{{C}_{\text{CU}}}A_{_{\text{CU},i}}^{{{B}_{\text{CU}}}})}+ \\ & \ \ \ \ \ \sum\limits_{j=1}^{NC}{({{C}_{\text{HU}}}{{Q}_{\text{HU},j}}+{{C}_{\text{F,HU}}}{{z}_{\text{HU},j}}+{{C}_{\text{HU}}}A_{_{\text{HU},j}}^{{{B}_{\text{HU}}}})+} \\ & \ \ \ \ \ \sum\limits_{i}^{NH}{\sum\limits_{j}^{NC}{\sum\limits_{k}^{NS}{({{C}_{\text{F,EX}}}{{z}_{i,j,k}}+{{C}_{\text{EX}}}A_{_{i,j,k}}^{{{B}_{\text{EX}}}}}}})\ \ \\ \end{align}$ | (1) |
其中Q为换热负荷;A为换热单元面积;z为判断换热单元有无的整型变量;C为费用计算系数;B为面积费用计算指数;下标CU、HU分别表示冷、热公用工程,F表示固定投资,EX表示存在于冷热流体之间的换热单元,i、j和k分别表示热流体、冷流体和级数的编号。
约束条件主要包括:单股流体热平衡、冷热流体出口温度热力学约束和公用工程热平衡约束。
1) 单股流体热平衡约束:
| $\left( T_{i}^{\text{in}}-T_{i}^{\text{out}} \right)F{{h}_{cp,i}}=\sum\limits_{k=1}^{NS}{\sum\limits_{j=1}^{NC}{{{Q}_{i,j,k}}+}{{Q}_{\text{CU},i}}}\ \ \ \ \ i=1,\cdots ,NH$ | (2) |
| $\left( T_{j}^{\text{in}}-T_{j}^{\text{out}} \right)F{{c}_{cp,j}}=\sum\limits_{k=1}^{NS}{\sum\limits_{i=1}^{NH}{{{Q}_{i,j,k}}+}{{Q}_{\text{HU},j}}}\ \ \ \ j=1,\cdots ,NC$ | (3) |
其中
2) 冷热流股出口温度热力学约束:
| ${{T}_{i,k}}\ge \ {{T}_{i,k+1}}\ \ \ \ \ \ i=1,\cdots ,NH\ \ k=1,\cdots ,NS$ | (4) |
| ${{T}_{j,k}}\ge \ {{T}_{j,k+1}}j=1,\cdots ,NC;\ k=1,\cdots ,NS$ | (5) |
| $T_{i,NS}^{\text{out}}\ge T_{i}^{\text{out}}\ \ \ i=1,\cdots ,NH$ | (6) |
| $T_{j}^{\text{out}}\ge T_{j,1}^{\text{out}}\ \ \ j=1,\cdots ,NC$ | (7) |
3) 冷热公用工程热平衡约束:
| $\left( T_{i,NS}^{\text{out}}-T_{i}^{\text{out}} \right)F{{h}_{cp,i}}={{Q}_{\text{CU},i}}\ \ \ \ \ i=1,\cdots ,NH$ | (8) |
| $\left( T_{j}^{\text{out}}-T_{j,1}^{\text{out}} \right)F{{c}_{cp,j}}={{Q}_{\text{HU},j}}\ \ \ \ \ j=1,\cdots ,NC$ | (9) |
4) 最小换热温差约束:
为了防止出现计算中出现温度交叉和换热面积无限大的情况,定义相应的最小换热温差约束:
| $T_{i}^{\text{in}}-T_{j}^{\text{out}}\ge \Delta {{T}_{\min }}$ | (10) |
| $T_{i}^{\text{out}}-T_{j}^{\text{in}}\ge \Delta {{T}_{\min }}$ | (11) |
其中$\Delta {{T}_{\min }}$为设定的最小传热温差。
3 萤火虫算法原理萤火虫算法的基本思想是:每个萤火虫的位置代表待求解问题的一个解,萤火虫的发光亮度取决于求解问题的目标函数值,目标函数值越好,萤火虫的发光亮度越强。亮度强的萤火虫吸引亮度弱的萤火虫,使亮度弱的萤火虫向亮度强的萤火虫移动。随着迭代过程的进行,种群中亮度弱的萤火虫不断向比自己更亮的萤火虫靠近,最终大多数萤火虫会聚集在最亮的萤火虫附近,最亮的萤火虫位置就是问题的最优解。
首先建立萤火虫
假设萤火虫的绝对亮度比萤火虫
| ${{\beta }_{ij}}={{\beta }_{0}}\exp (-\gamma r_{ij}^{2})$ | (12) |
其中
| ${{r}_{ij}}=\left\| {{X}_{i}}-{{X}_{j}} \right\|=\sqrt{\sum\limits_{k=1}^{d}{{{({{x}_{i,k}}-{{x}_{j,k}})}^{2}}}}$ | (13) |
其中
萤火虫
| ${{X}_{j}}(t+1)={{X}_{j}}(t)+{{\beta }_{ij}}({{X}_{i}}(t)-{{X}_{j}}(t))+\alpha \cdot \left\{ rand(0,1) \right\}$ | (14) |
其中
换热网络综合中不同物流的匹配属于典型的组合优化问题,随着流股数量的增加,呈现组合爆炸的态势,增加了问题的求解难度。FA算法求解换热网络综合问题时存在进化后期搜索效率低的问题。为了提高算法性能,结合问题特征进行如下改进。
4.1 整型变量的连续化FA算法应用于换热网络综合问题时,每个萤火虫的位置代表问题的一个可行解,包含如下变量:
(1) 表示冷热流股之间是否存在换热单元的整型变量Z
| $Z=\left\{ {{z}_{i,j,k}} \right\}\ \ \ i=1,\cdots ,NH;\ j=1,\cdots ,NC;\ \ k=1,\cdots ,NS$ | (15) |
其值为1表示存在换热单元,其值为0表示不存在换热单元。
(2) 表示每个换热单元换热负荷的连续变量Q
| $Q=\left\{ {{q}_{i,j,k}} \right\}\ \ \ i=1,\cdots ,NH;\ j=1,\cdots ,NC;\ \ k=1,\cdots ,NS$ | (16) |
整型变量的存在造成了换热网络目标函数的不连续,为了避免这种不连续给优化带来困难,对整型变量做如下连续化处理:在初始状态将所有整型变量约束为1,表示所有换热单元在初始状态均存在,当优化中换热负荷或公用工程为0时,对应的整型变量为0。即对目标函数增加整型变量等式约束条件:
| $s.t.\ \ Z=\ \left\{ {{z}_{i,j,k}} \right\}\ =1\ \ \ \ \ i=1,\cdots ,NH\rm{;}\ \ j=1,\cdots ,NC\ ;\ \ k=1,\cdots ,NS$ | (17) |
整型变量的连续化处理简化了换热网络综合问题模型,能够提升计算效率,更好发挥FA算法强大的连续变量搜索能力。
4.2 光吸收系数自适应策略从萤火虫位置更新公式(14) 可以看出,个体向解空间内亮度更高的个体移动,忽略了全局最优解的作用。为了增强FA运用于换热网络的全局搜索能力,建立了光吸收系数
由式(12) 可知,最大吸引力
从图 2可以看出,当
标准FA中,
| ${{\beta }_{\min }}={{\beta }_{0}}\exp (-\gamma r_{\max }^{2})$ | (18) |
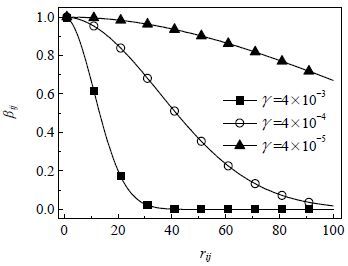
|
图 2 γ 取值对rij-βij 曲线的影响 Fig.2 Effects of γ values on the profile of rij-βij curves |
对上式变形,得第(t+1) 代值随第t代
| $\gamma (t+1)=\frac{1}{r_{\max }^{2}(t)}\ln (\frac{{{\beta }_{0}}}{{{\beta }_{\min }}})$ | (19) |
优化过程中,种群的离散程度是不断变化的,总体趋势是前期分布较为离散,后期逐渐聚拢,最优个体与其他个体空间距离逐渐缩小,式(19) 的作用是保证种群聚拢程度发生变化时最优个体对其他个体的相对吸引力
标准FA中,个体向解空间内亮度高于自身的其他个体移动,忽略了全局最优个体的寻优,本文建立了萤火虫最优个体的随机摄动策略,允许最优个体在确定的邻域范围内随机摄动,最优个体记为
| ${{V}_{best}}(t+1)={{X}_{best}}(t)+step\cdot \left\{ rand(0,1) \right\}$ | (20) |
其中step为摄动步长,
随机摄动如引起适应度值增加,则接受随机摄动操作,否则以变异概率CR接受随机摄动操作。
| ${{X}_{best}}(t+1)=\left\{ \begin{align} & {{V}_{best}}(t+1)\ \ \text{if}\ f({{V}_{best}})<f({{X}_{best}})\ \ \text{or }\ rand(0,1) <CR \\ & {{X}_{best}}(t)\ \ \ \ \ \text{otherwise} \\ \end{align} \right.$ | (21) |
将结合上述策略的改进萤火虫算法(Modified Firefly Algorithm,MFA)应用于换热网络优化,步骤如下:
Step1 计算参数设置。计算参数包括最大迭代次数Iterations;种群规模NP,换热网络级数NS;算法控制参数
Step 2 种群初始化。每个换热单元的热负荷通过如下方式随机生成:
| ${{q}_{i,j,k}}=rand(0,\ 1)\times {{q}_{i,j,\max }}$ | (22) |
其中
Step 3 个体亮度评价。对所有初始化后的萤火虫依次进行亮度比较。为简单起见,将问题的目标函数值直接作为MFA的适应度,即萤火虫的绝对亮度。
Step 4 执行光吸收系数自适应策略。求得当前最优个体与其他个体的最大距离,按公式(19) 更新光吸收系数。
Step 5 个体位置更新。每个萤火虫依次与其他个体进行亮度比较,若萤火虫具有比更高的亮度,则
Step 6 执行最优个体随机摄动策略。最优个体按公式(20) 、(21) 执行随机摄动策略。
Step 7 迭代终止判断。对移动后的种群进行迭代终止判断,若满足条件则宗旨,否则转Step3继续执行。
5 算例验证与分析为了验证改进萤火虫算法的有效性,将其应用于两个换热网络综合实例,采用Fortran77语言编程,计算机配置为:CPU Intel(R)Xeon(R) E5-2670,主频2.3GHz,4 GB RAM。
5.1 算例1算例1为换热网络综合优化的10股流算例,在Ahmad等[21]1985年首次提出,其物流参数见表 1,优化所得年综合费用为7074000 $·yr-1。Yerramsetty等 [10]于2008年首次使用DE优化算例1,方大俊等[23, 24](2013、2015年)、陈上等[25](2015年)对DE进行改进并优化了该算例,取得了优于Yerramsetty的结果。
| 表 1 算例1流体参数表 Table 1 Flow parameters of case 1 |
使用标准FA和改进后的MFA对算例1进行优化,FA最终结果为5610735$·yr-1,MFA最终结果为5594562$·yr-1,比FA算法减少16173$·yr-1,比Ahmad所得结果减少1479438$·yr-1,所得结果与前述研究结果对比见表 2。改进算法得到了比所列文献中其他群体智能算法(如GA、DE、PSO和SA等)更优的结果。FA和MFA优化所得换热网络结构如图 3所示。
| 表 2 算例1 优化结果对比 Table 2 Comparison on optimized results of case 1 |
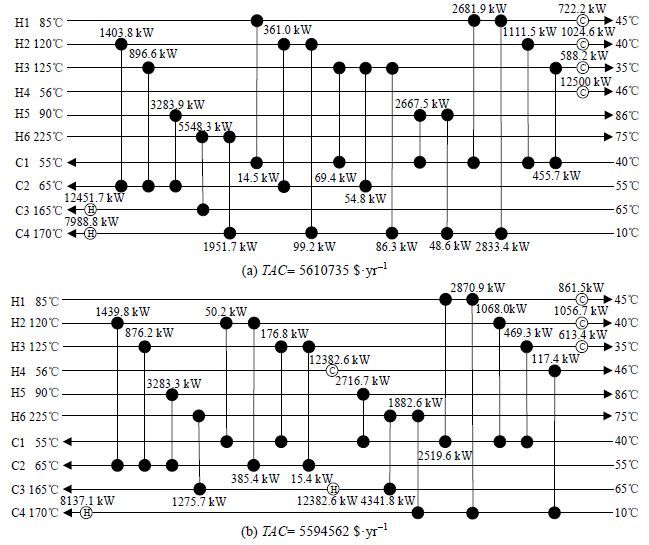
|
图 3 算例1优化结果 Fig.3 Optimal structure results of case 1 (a) FA (b) MFA |
从表 3可以看出,换热网络综合优化是运行费用(冷热公用工程费用)和固定投资费用(换热器面积费用)的权衡。以文献[25]为例进行对比,MFA所得冷、热公用工程较文献[25]各高出214 kW(公用工程费用UC高24610 $·yr-1),但MFA所得换热器面积比文献[25]所得结果低650 m2(费用低39000 $·yr-1),故MFA所得年综合费用比文献[25]方法所得结果低14390 $·yr-1。
5.2 算例2算例2是换热网络最优化中经典的10SP1算例,该算例源于Pho和Lapidus[28]1973年在AIChE杂志发表的文章,由5股热流体和5股冷流体组成,其物流参数见表 3。
| 表 3 算例2 流体参数表 Table 3 Flow parameters of case 2 |
许多学者对10SP1进行了研究,随着研究的深入和优化技术的发展,10SP1算例不断被研究学者引用以检验其方法的有效性。根据已发表文献显示,该算例存在较多局部极值点。目前该算例最优结果为43392 $·yr-1,由Linnhoff在文献[4]获得。
使用FA和MFA对算例2进行优化,MFA优化结果为43689 $·yr-1,比FA优化结果44027 $·yr-1减少338 $·yr-1,比Pho和Lapidus优化结果减小471 $·y-1,FA和MFA优化所得换热网络结构如图 4(a) 和(b)所示。从图 4可以看出,MFA和FA所得换热网络结构较为接近,再次验证该算例存在较多局部极值点。表 4列出了优化算例2与其他文献的优化结果对比,从该表可以看出,MFA取得了仅次于文献[4]、[32]、[33]和[35]的结果,其中[32]和[33]为有分流模型。
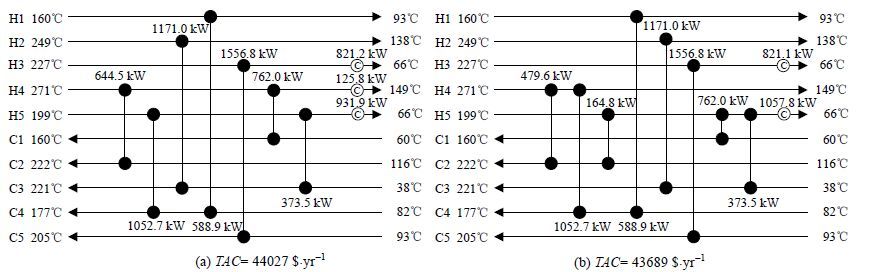
|
图 4 算例2优化结果 Fig.4 Optimal structure results of case 2 (a) FA (b) MFA |
从两个算例看出,MFA均取得了优于FA和其他多数文献方法的结果,证明了改进策略的有效性。FA采用了一种全局的种群拓扑结构,单个个体和其他所有个体互通信息,这种模式信息传递速度较快,但是也存在容易陷入局部极小点的不足,MFA在FA的基础上建立的光吸收系数自适应策略和最优个体的随机摄动策略,更好地权衡了算法的全局搜索能力和局部收敛精度。
6 结论将萤火虫算法运用于换热网络最优化并进行改进研究。采用Grossmann无分流分级超结构同步优化模型,并允许公用工程灵活布置在流股任何位置。
(1) 对表示换热网络结构的整型变量作连续化处理,避免了整型变量造成的结构不连续给优化带来的困难,简化换热网络综合问题模型,提升了计算效率;
(2) 建立的光吸收系数随最优个体与其他个体空间距离变化的自适应公式,保证种群聚拢程度发生变化时最优个体对其他个体的相对吸引力大于设定的下限值,能够提升算法全局搜索能力;
(3) 建立的最优个体随机摄动策略,使最优个体在确定的邻域范围内随机摄动,随机摄动后如引起适应度值增加,则接受随机摄动操作,否则以变异概率接受随机摄动操作,提高了求解效率;
(4) 将引入光吸收系数和最优个体随机策略的改进萤火虫算法(MFA)应用于公开发表文献的相关算例,并与GA、DE、SA和PSO等算法所得结果进行比较,MFA取得优于多数文献方法的结果,验证了MFA应用于换热网络最优化的有效性。
符号说明:
| C | ——面积费用计算系数 | z | ——表示换热单元有无的整型变量 |
| CR | ——最优个体随机摄动变异概率 | α | ——萤火虫位置更新公式中的随机扰动步长 |
| d | ——变量维数 | βij | ——萤火虫i对j的相对吸引力 |
| Fcp | ——流体热容流率,kW×℃-1 | ||
| Fccp | ——冷流体热容流率,kW×℃-1 | β0 | ——绝对吸引力 |
| Fhcp | ——热流体热容流率,kW×℃-1 | γ | ——光吸收系数 |
| I | ——萤火虫绝对亮度 | 上标 | |
| NC | ——冷流体数 | in | ——表示流体进口 |
| NH | ——热流体数 | out | ——表示流体出口 |
| NS | ——分级超结构级数 | 下标 | |
| Q | ——换热量,kW | best | ——表示最优个体 |
| rij | ——萤火虫i对j的笛卡尔距离 | CU | ——表示冷公用工程 |
| step | ——最优个体的随机摄动步长 | EX | ——表示冷热流体之间的换热单元 |
| T | ——温度,℃ | F | ——表示固定投资 |
| t | ——迭代次数 | HU | ——表示热公用工程 |
| DTmin | ——最小传热温差设定值,℃ | i,j | ——表示冷热流体或萤火虫编号 |
| TA | ——换热单元总面积,m2 | k | ——表示分级超结构级编号 |
| [1] | DAI You-yuan(戴猷元), et al. Introduction to chemical(化工概论)[M].Beijing (北京): Chemical Industry Press(化学工业出版社), 2012. |
| [2] | Linnhoff B, Flower J R. Synthesis of heat exchanger networks:I. Systematic generation of energy optimal networks[J]. AIChE Journal , 1978, 24(4): 633-642. DOI:10.1002/(ISSN)1547-5905. |
| [3] | Linnhoff B, Flower J R. Synthesis of heat exchanger networks:Ⅱ. Evolutionary generation of networks with various criteria of optimality[J]. AIChE Journal , 1978, 24(4): 642-654. DOI:10.1002/(ISSN)1547-5905. |
| [4] | Linnhoff B, Mason D R, Wardle I. Understanding heat exchanger networks[J]. Computers & Chemical Engineering , 1979, 3(1-4): 295-302. |
| [5] | Linnhoff B, Hindmarsh E. The pinch design method for heat exchanger networks[J]. Chemical Engineering Science , 1983, 38(5): 745-763. DOI:10.1016/0009-2509(83)80185-7. |
| [6] | Dolan W, Cummings P, LeVan M. Process optimization via simulated annealing:application to network design[J]. AIChE Journal , 1989, 35(5): 725-736. DOI:10.1002/(ISSN)1547-5905. |
| [7] | Dolan W, Cummings P, LeVan M. Algorithmic efficiency of simulated annealing for heat exchanger network design[J]. Computers & Chemical Engineering , 1990, 14(10): 1039-1050. |
| [8] | Lewin D R, Wang H, Shalev O. A generalized method for HEN synthesis using stochastic optimization-I. General framework and MER optimal synthesis[J]. Computers & Chemical Engineering , 1998, 22(10): 1503-1513. |
| [9] | Lewin D R. A generalized method for HEN synthesis using stochastic optimization-Ⅱ. The synthesis of cost-optimal networks[J]. Computers & Chemical Engineering , 1998, 22(10): 1387-1405. |
| [10] | Yerramsetty K. Murty C. Synthesis of cost-optimal heat exchanger networks using differential evolution[J]. Computers & Chemical Engineering , 2008, 32(8): 1861-1876. |
| [11] | Thuy N, Pendyala R, Marneni N. Heat exchanger network optimization using differential evolution with stream splitting[J]. Applied Mechanics and Materials , 2014, 625: 373-377. DOI:10.4028/www.scientific.net/AMM.625. |
| [12] | Silva A P, Ravagnani M A S S, Biscaia E C, et al. Optimal heat exchanger network synthesis using particle swarm optimization[J]. Optimization and Engineering , 2010, 11(3): 459-470. DOI:10.1007/s11081-009-9089-z. |
| [13] | Huo Z Y, Zhao L, Yin H C. Sloving large-scale heat exchanger network synthesis problems using particle swarm optimization[J]. Applied Mechanics and Masterials , 2011, 148-149: 636-640. DOI:10.4028/www.scientific.net/AMM.148-149. |
| [14] | Yang X S, et al. Nature-inspired metaheuristic algorithms[M].Beckingtion: Luniver Press, 2008: 83-96. |
| [15] | Wang H, Cui Z, Sun H, et al. Randomly attracted firefly algorithm with neighborhood search and dynamic parameter adjustment mechanism[J]. Soft Computing , 2016: 1-15. |
| [16] | Basu B, Mahanti G K. Thinning of concentric two-ring circular array antenna using firefly algorithm[J]. Scientia Iranica , 2012, 19(6): 1802-1809. DOI:10.1016/j.scient.2012.06.030. |
| [17] | Kazerm A, Ebrahim S, Hussainb F K, et al. Firefly algorithm with chaos-based fire algorithm for stock market price forecasting[J]. Communications in Nonlinear Science and Numerical Simulation , 2013, 18(1): 89-98. DOI:10.1016/j.cnsns.2012.06.009. |
| [18] | Maheshwar , Kaushik K, Arora V. A Hybrid data clustering using firefly algorithm based improved genetic algorithm[J]. Procedia Computer Science , 2015, 58: 249-256. DOI:10.1016/j.procs.2015.08.018. |
| [19] | Yee T F, Grossmann I E. Simultaneous optimization models for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & Chemical Engineering , 1990, 14(10): 1165-1184. |
| [20] | Pariyani A, Gupta A, Ghosh P. Design of heat exchanger networks using randomized algorithm[J]. Computers & Chemical Engineering , 2006, 30(6-7): 1046-1053. |
| [21] | Ahmad, S. Heat exchanger networks:Cost trade-offs in energy and capital[D]. Manchester:University of Manchester Institute of Science and Technology, 1985. |
| [22] | Ravagnani M, Silva A P, Arroyo P A, et al. Heat exchanger network synthesis and optimization using genetic algorithm[J]. Applied Thermal Engineering , 2005, 25(7): 1003-1017. DOI:10.1016/j.applthermaleng.2004.06.024. |
| [23] | FANG Da-jun(方大俊), CUI Guo-min(崔国民), WAN Yi-qun(万义群), et al. Performance analysis of heat exchanger networks synthesis by differential evolution algorithm(微分进化算法优化换热网络的性能)[J]. Chemical Industry and Engineering Progess(化工进展) , 2013, 32(10): 2288-2291. |
| [24] | FANG Da-jun(方大俊), CUI Guo-min(崔国民), XU Hai-zhu(许海珠), et al. Optimization of heat exchanger networks with cooperation differential evolution algorithm based on penalty factors(基于罚因子协进化微分算法优化换热网络)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29(2): 407-412. |
| [25] | CHEN Shang(陈上), CUI Guo-min(崔国民), PENG Fu-yu(彭富裕), et al. Optimization of the heat exchanger network by differential evolution algorithm based on dynamic update strategy(采用动态更新策略的微分进化算法优化换热网络)[J]. Journal of Engineering for Thermal Energy & Power(热能动力工程) , 2015, 30(4): 509-514. |
| [26] | PENG Fu-yu(彭富裕), CUI Guo-min(崔国民), CHEN Jia-xing(陈家星). Bilevel optimization method for heat exchanger network synthesis based on simulated annealing algorithm(基于模拟退火算法的换热网络双层优化方法)[J]. PetroChemical Technology(石油化工) , 2014, 43(5): 536-544. |
| [27] | XIAO Yuan(肖媛), CUI Guo-min(崔国民), PENG Fu-yu(彭富裕), et al. An improved particle swarm optimization for precocious phenomenon in nonlinear system engineering(粒子群算法在非线性系统应用中的早熟现象及其改进)[J]. Chinese Journal of Computational Physics(计算物理) , 2015, 32(6): 693-700. |
| [28] | Pho T K, Lapidus L. Topics in computer-aided design Ⅱ. Synthesis of optimal heat exchanger network by tree searching algorithm[J]. AIChE Journal , 1973, 19(6): 1181-1189. |
| [29] | Nishida N, Liu Y A, Lapidus L. Topics in computer-aided design Ⅲ. A simple and practical approach to the optimal synthesis[J]. AIChE Journal , 1977, 23(1): 77-93. DOI:10.1002/(ISSN)1547-5905. |
| [30] | Floudas C A, Ciric A R. Strategies for overcoming uncertainties in heat exchanger network synthesis[J]. Computers & Chemical Engineering , 1989, 13(10): 1133-1152. |
| [31] | WEI Guan-feng(魏关锋), YAO Ping-jing(姚平经), LUO Xin(罗行), et al. Multi-stream heat exchanger networks synthesis with genetic algorithm(用遗传算法进行多流股换热器的换热网络综合)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2003, 17(4): 425-430. |
| [32] | Lin B, Miller D C. Solving heat exchanger network synthesis problems with Tabu search[J]. Computers & Chemical Engineering , 2004, 28(8): 1451-1464. |
| [33] | Pariyani A, Gupta A, Ghosh P. Design of heat exchanger networks using randomized algorithm[J]. Computers & Chemcical Engineering , 2006, 30(6-7): 1046-1053. |
| [34] | Gupta A, Ghosh P. A randomized algorithm for the efficient synthesis of heat exchanger networks[J]. Computers & Chemical Engineering , 2010, 34(10): 1632-1639. |
| [35] | Peng F Y, Cui G M. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm[J]. Applied Thermal Engineering , 2015, 78(12): 136-149. |




