结晶作为一种纯化和分离工艺,广泛应用于化工和制药过程。混合和传热是冷却结晶过程的关键工艺参数,它们决定了过饱和度的空间分布,从而影响晶体产品的质量和性质[1-3]。传统搅拌方式由于局部混合较差,传热速率低和剪切速率不均,容易产生较宽的停留时间分布,导致较宽的产品尺寸分布[4-6],结晶过程及晶体产品质量控制有一定的局限。
研究表明,对于含有周期性间隔孔板的管道,当流体受到叠加在净流量上的振荡时,可以表现出有效流体混合和类似活塞流停留时间分布[7-8]。同时,停留时间独立于进料量,可以由振幅和频率控制[9]。这种管式结晶器可以用于连续操作,由于具有良好的混合和传热性能,能够严格控制局部过饱和度,可以抑制爆发成核并实现晶体的均匀生长[10-12]。
此外,在常见的振荡流反应器中,当流动振荡和挡板同时存在时具有明显的传热增强效应[13-14]。例如MACKLEY和STONESTREET[13]测试了内径为12 mm并带有挡板的振荡流反应器传热性能,发现当叠加振荡时,努塞尔数Nu可达稳态流动的30倍。SOLANO等[15]对内插螺旋线管振荡流反应器进行了计算流体力学CFD数值模拟,发现传热速率强烈依赖于振荡雷诺数Reo,与斯特劳哈尔数St关系并不明显。ONYEMELUKWE等[16]研究了内径为5 mm光滑周期收缩孔SPC管的传热性能,发现传热主要由Ren决定,St比Reo影响要大。
尽管上述研究结果表明振荡流具有一定的混合和传热强化效应,但对于其应用在结晶过程中流动和传热的控制,以至于局部过饱和度的控制是否能实现、如何实现、以及实现程度等问题,还不十分明确,对SPC结晶器振荡流传递特性和机制的了解也尚不清晰,特别是瞬时传热系数的时变规律鲜见报道。本文使用Fluent软件对层流状态下的振荡流结晶器进行了三维非稳态数值模拟,基于SPC结晶器考察振荡流强化的水力学特性,并重点讨论了振荡参数对传热特性的影响。
2 模型与数值模拟方法 2.1 物理模型振荡流结晶器模型的具体结构和参数如图 1所示,操作时竖直放置,流体由底部流入,通过振荡流和光滑挡板的叠加产生周期性变化的涡旋流场。使用网格化软件Gambit构建了结构化的非均匀网格,在主流区范围内设置了粗网格,在边界层附近进行了网格加密。

|
图 1 振荡流结晶器结构 Fig.1 Structure of an oscillatory flow crystallizer |
利用Fluent软件,采用不可压缩非稳态层流模型,以313.15 K饱和(NH4)2SO4溶液为工质。采用压力求解器,压力场和速度场由SIMPLE算法求解。动量和能量方程的离散采用二阶迎风格式,非稳态项采用二阶隐式离散格式。质量、动量和能量控制方程如式(1)~(3)所示。
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \vec v} \right) = 0$ | (1) |
| $\frac{{\partial \left( {\rho \vec v} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho \vec v\vec v} \right) = - \nabla p + \nabla \cdot \left[ {\mu \left( {\nabla \vec v + \nabla {{\vec v}^T}} \right)} \right] + \rho \vec g$ | (2) |
| $\frac{{\partial \left( {\rho T} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho \vec vT} \right) = \nabla \cdot \left( {\frac{k}{{{c_{\rm{p}}}}}\nabla T} \right) + {S_{\rm{T}}}$ | (3) |
具有净流速度和叠加振荡的入口速度和质量流量定义如下:
| $v(t) = {v_{{\rm{net}}}} + 2\pi f{x_0}{\sin _{}}(2{\rm{ \mathsf{ π}}} ft)$ | (4) |
| $\dot m(t) = \rho Av(t)$ | (5) |
管入口温度为313.15 K,管出口条件为压力出口,壁面为恒壁温边界条件,温度为308.15 K;同时壁面采用无滑移边界条件。为保证流动和传热随时间充分发展,模拟采用9个腔室,结晶器总长300 mm。每次模拟均大于10个振荡周期,以保证流动和传热随时间成周期发展。
周向瞬时努塞尔数、周向瞬时平均热流密度和流体温度分别定义如下:
| $Nu(t) = \frac{{q(t)}}{{{T_{{\rm{wall}}}}(t) - {T_{{\rm{bulk}}}}(t)}}\frac{d}{k}$ | (6) |
| $ q(t) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2\pi } {q(\theta , t)} \;{\rm{d}}\theta $ | (7) |
| $ {T_{{\rm{bulk}}}}(t) = \frac{{\int_A {T(x, z, t)\rho \left| {{v_y}} \right|{\rm{d}}A} }}{{\int_A {\rho \left| {{v_y}} \right|{\rm{d}}A} }} $ | (8) |
上述提到的3个无量纲参数定义如下:
| $R{e_{\rm{o}}} = \frac{{2{\rm{ \mathsf{ π}}} f{x_0}d\rho }}{\mu }$ | (9) |
| $R{e_{\rm{n}}} = \frac{{{v_{{\rm{net}}}}d\rho }}{\mu }$ | (10) |
| $St = \frac{d}{{4{\rm{ \mathsf{ π}}} {x_0}}}$ | (11) |
式中:Reo表示振荡流结晶器内流体的混合强度,Ren表征净流量对振荡流结晶器内流体的影响,St反映涡旋的传播程度。
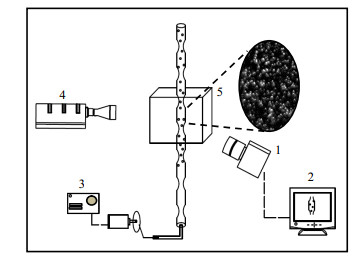
2.3 模型验证 2.3.1 实验验证方法为了验证模拟结果,使用粒子图像测速(particle image velocimetry, PIV)技术进行可视化实验。结晶器底部装有振动装置,偏心轮带动连接杆产生正弦波形运动,并通过改变转速来控制频率。为避免光线折射和玻璃管曲率影响,在玻璃管外加装方形有机玻璃盒,实验时注入去离子水,以抵消折射影响。实验工质为去离子水, 荧光粒子为Rhodamine B。激光光源为LWGL532-12W,可输出波长532 nm,厚度为1 mm的片光。荧光粒子受激光激发后可发射580 nm左右的发射光。发射光使用Photron高速相机进行拍摄成像,该相机前装有Nikon镜头(50 mm,1.4D),并在镜头前加装滤波片。使用MicroVec V3 PIV处理软件,对结晶器的实验图像进行处理,实验流程如图 2所示。
|
图 2 PIV实验流程图 Fig.2 Schematic diagram of the PIV setup 1. photron fastcam mini ux100 2. pc 3. oscillatory device 4. lwgl532-12w 5. rhodamine b particles |
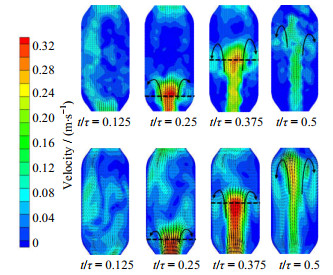
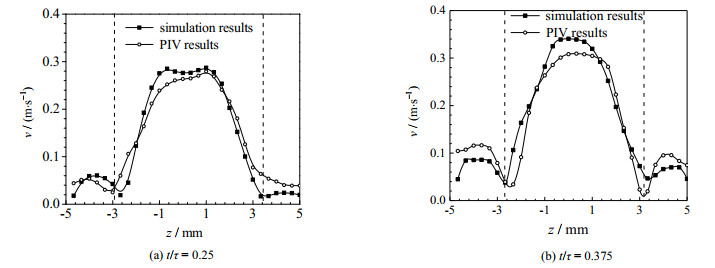
通过PIV可视化实验,考查了振荡条件下的流场图,并与模拟结果进行比较。图 3为前半周期4个相位点的实验和模拟结果流场图。从图中可以看出,在不同相位时刻整体流动速度和流动形态实验与模拟结果基本一致,PIV实验和模拟结果都显示了涡旋结构,涡旋出现的时刻、位置十分相近。t/τ = 0.25时,涡旋由腔室底部边缘生成,流体存在明显径向发展;t/τ = 0.375时,涡旋不断向上转移,同时使流体达到充分混合。图中虚线处沿径向的速度分布在图 4给出。可以看出,实验和模拟得到的速度分布非常接近,在腔室中部主流区速度最大,涡旋中心处速度较低,涡旋在径向上生成的位置一致;结果表明,数值模拟结果与实验结果吻合良好,认为该模型准确可靠。
|
图 3 不同时刻的PIV速度场(上排)和数值模拟结果(下排)对比 Fig.3 PIV velocity field (top row) and numerical simulation results (bottom row) at different times Ren = 0, Reo = 379.2, St = 0.25 |
|
图 4 沿径向方向的PIV实验和数值模拟速度分布对比 Fig.4 Velocity distribution obtained by PIV and numerical simulation at radial direction |
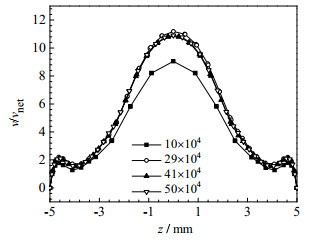
为了证明计算结果与网格数目无关,考察了网格细化程度对流动力学以及传热特性的影响。共划分了4种网格数目,分别为50万、41万、29万和10万,为了保证结果更加准确,每种网格均对边界层进行了加密。图 5为t/τ = 0.5,y = 150 mm,Ren = 52,Reo = 163.2,St = 0.4时不同网格数目下,腔室轴向方向速度大小的样本结果。通过计算得到网格数为29万与50万的最大误差结果为2.57%。为了既能准确描述流动过程,同时也较节约计算资源,网格数目选取为29万。
|
图 5 不同网格数目下的速度大小 Fig.5 Velocity profiles under different grid numbers |
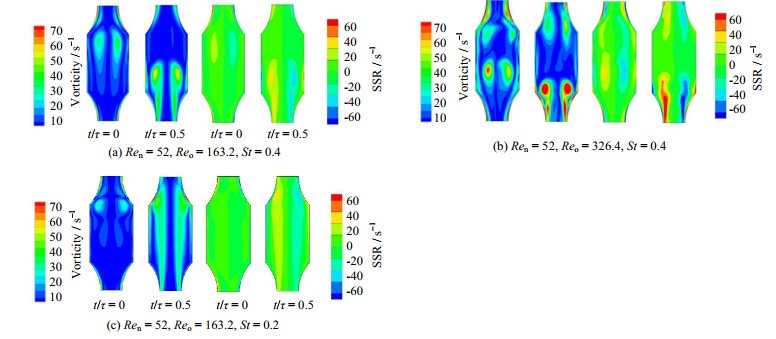
前述模型验证中已知振荡条件下的流场状态,为了进一步表征涡旋强度,探究不同操作条件对流动状态的影响,图 6为中部腔室不同Reo和St条件下的涡量场和剪切应变率场云图。结果表明涡量和剪切应变率强的区域与流场中的涡旋区是高度匹配的。从图 6(b)中可以看出,当Reo增加时,相较于图 6(a)涡旋强度和剪切应变率明显增加,涡旋中心处强度最大,并且在腔室上部出现了一对新的涡旋区。随着流体湍动增强,流动状态由对称开始趋于非对称,这与NI等[8]的结论一致。从图 6(c)可以看出,当St减小,即振幅变大时,流场剪切应变率强度相较于图 6(a)基本不变,但是涡旋在t/τ = 0.5时已经运动至腔室上部,同时区域存在明显增加。此外,由于叠加振荡,上述这些现象具有周期性规律。
|
图 6 不同振荡条件下结晶器内一个周期不同时刻的涡量场(左)和剪切应变率场(右) Fig.6 Contours of vorticity magnitude (left) and shear strain rate field (right) at different times in a crystallizer under different oscillation conditions |
在传统搅拌系统中的晶核大部分由晶体和螺旋桨之间的接触成核提供[17]。在振荡流成核机制中很大程度减少了这一成核方式的发生,同时流体剪切对成核起重要作用。从上述分析表明,可以通过调节振荡参数来改变剪切力分布,从而达到控制剪切成核速率的目的。此外,在振荡流结晶器中Reo的增加可以较强地促进流场混合,涡旋的生成使过饱和度空间分布更加均匀,创造了更加有利于晶体生长的条件。
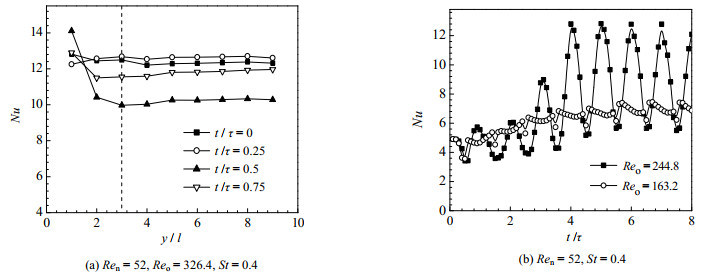
3.3 振荡流条件下的传热特性分析 3.3.1 验证传热随时间和空间充分发展将振荡参数Ren = 52,Reo = 0作为振荡流的初始条件,此时为稳态操作,只有净流量没有叠加振荡,该条件下的Nu为5.08。当叠加振荡时,在管进口处传热并不能充分发展,Nu沿着管轴向位置发生变化。在每个腔室中间位置取横截面的周向平均传热系数,取一个周期内4个时刻,得到Nu随轴向距离变化的情况如图 7(a)所示。从图中可以看出,当l=0.09 m,Nu在第3个腔室之后每个时刻都基本趋于平稳,表明传热在空间上达到充分发展。在稳态传热充分发展阶段,传热系数不随时间发生变化。当振荡存在时,流场由稳态转变为非稳态,传热系数即随时间发生波动,从图 7(b)中看出,当振荡达到4个周期时,Nu开始随时间发生周期性变化,即传热随时间达到充分发展。
|
图 7 传热特性在空间和时间上的演化趋势 Fig.7 Evolution of heat transfer characteristics in space and time |
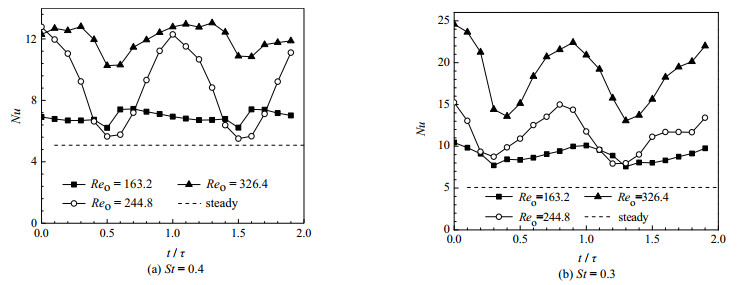
图 8为分别在St = 0.4和St = 0.3时不同Reo对应的管周向瞬时Nu。从图中可以看出Nu存在周期性波动,当Reo增加时,Nu显著增加。由上述分析可知,由于振荡极大增加了径向混合,涡旋的生成和传播破坏了流动边界层;当St一定时,随着流体振荡频率加快,涡旋单位时间内往复频次变高使流体扰动增强,同时流场瞬时速度增加,涡量和剪切应变率明显变强,导致叠加振荡条件下的传热系数均大于只有净流条件下稳态流动时的传热系数。同时,传热会受到流体温度振荡变化的影响,在前半循环较热的流体向上移动,在后半循环较冷的流体向下移动,涡旋的存在增强了冷热流体的混合,促进了传热过程。
|
图 8 不同振荡雷诺数时Nu周期变化规律 Fig.8 Time-periodic Nu evolution at several oscillatory Reynolds numbers |
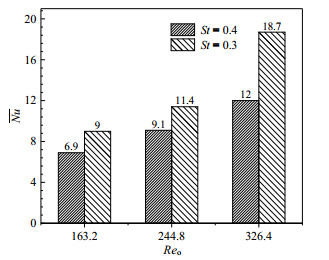
图 9为在St = 0.4和St = 0.3时,不同Reo对应的一个周期内平均Nu,随Reo增加而增加。当Reo = 326.4,St = 0.3时,Nu为18.7,为稳态流动时的3.7倍。对于同一振荡雷诺数下,St = 0.3时的Nu均比St= 0.4时要高,可见St对传热过程也有较大影响。
|
图 9 不同振荡雷诺数时Nu均值 Fig.9 Nu average values at different oscillatory Reynolds numbers |
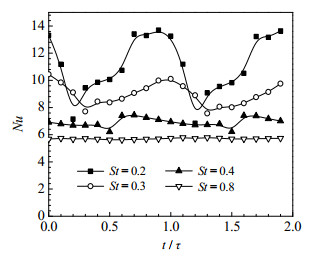
为了进一步明晰St对振荡流结晶器传热过程的影响,图 10为Reo = 163.2时,不同St时的Nu周期变化规律。可以看出,当St减小,即振幅增大时,此时传热性能较高。从图 6所示的流场结构可以看出,由于振幅增加时,涡旋在腔室内传播程度更大且涡旋区域增加,增强了冷热流体混合,促进了传热过程。同时,在低振幅时,Nu较为平稳,随着St的减小,Nu振荡幅度变大。
|
图 10 不同斯特劳哈尔数时Nu周期变化规律 Fig.10 Periodic Nu evolution under different Strouhal numbers |
对于结晶过程,传热特性与溶液过饱度的分布密切相关,最终决定成核和生长速率;上述的研究结果表明,传热特性有明显的演化规律且可以通过振荡参数(Reo和St)进行有效的控制。因此,采用SPC结晶器耦合振荡流动方式可以对结晶传热过程进行调控。
4 结论针对SPC结晶器,基于流场和传热特性的分析,利用数值模拟方法描述了振荡流的流动特性及其传热演变规律,具体结论如下:
(1) 当叠加振荡时结晶器内的流动存在明显的涡旋结构,涡旋的存在优化了流场混合特征。
(2) 涡量和剪切应变率强度随Reo增加而增强,当St减小时,剪切应变率强度基本不变,但是涡旋区域增加,为振荡流结晶过程剪切成核速率的调控提供了分析基础。
(3) 在传热完全发展阶段,本文强调了对传热特性的调控过程,传热系数由冷热流体的运动和流场结构驱动,随时间成周期性变化,并且由Reo和St决定。在本模型参数范围内,当Reo增加时,传热性能明显增强,当St减小时,有效促进传热,Nu可达稳态流动的3.7倍;这为结晶场中过饱和度的控制提供了依据。
符号说明:
|
|
| [1] |
ZHAO L, RAVAL V, BRIGGS N E B, et al. From discovery to scale-up:α-lipoic acid nicotinamide cocrystals in a continuous oscillatory baffled crystalliser[J]. CrystEngComm, 2014, 16: 5769-5780. DOI:10.1039/C4CE00154K |
| [2] |
张建华, 曹付明, 张宏建, 等. 初始过饱和度对谷氨酸结晶的影响研究[J]. 高校化学工程学报, 2013, 27(1): 43-49. ZHANG J H, CAO F M, ZHANG H J, et al. Effects of initial super-saturation on the polymorphism and size distribution of glutamic acid[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(1): 43-49. |
| [3] |
关国强, 唐凯, 李红, 等. 基于ATR-UV实时浓度检测的扑热息痛冷却结晶过程研究[J]. 化工学报, 2015, 66(9): 3580-3587. GUAN G Q, TANG K, LI H, et al. Cooling crystallization of paracetamol in ethanol solution based on real-time ATR-UV measurement[J]. CIESC Journal, 2015, 66(9): 3580-3587. |
| [4] |
FERGUSON S, ORTNER F, QUON J, et al. Use of Continuous MSMPR crystallization with integrated nanofiltration membrane Recycle for enhanced yield and purity in API crystallization[J]. Crystal Growth & Design, 2014, 14(2): 617-627. |
| [5] |
POWER G, HOU G, KAMARAJU V K, et al. Design and optimization of a multistage continuous cooling mixed suspension, mixed product removal crystallizer[J]. Chemical Engineering Science, 2015, 133: 125-139. DOI:10.1016/j.ces.2015.02.014 |
| [6] |
KWON S I, NAYHOUSE M, CHRISTOFIDES P D, et al. Modeling and control of crystal shape in continuous protein crystallization[J]. Chemical Engineering Science, 2014, 107: 47-57. DOI:10.1016/j.ces.2013.12.005 |
| [7] |
OLIVA J A, KANJAKHA P, ALASTAIR B, et al. Experimental investigation of the effect of scale-up on mixing efficiency in oscillatory flow baffled reactors (OFBR) using principal component based image analysis as a novel noninvasive residence time distribution measurement approach[J]. Chemical Engineering Journal, 2018, 351: 498-505. DOI:10.1016/j.cej.2018.06.029 |
| [8] |
NI X, JIAN H, FITCH A W. Computational fluid dynamic modelling of flow patterns in an oscillatory baffled column[J]. Chemical Engineering Science, 2002, 57(14): 2849-2862. DOI:10.1016/S0009-2509(02)00081-7 |
| [9] |
PHAN A N, HARVEY A P. Characterisation of mesoscale oscillatory helical baffled reactor-Experimental approach[J]. Chemical Engineering Journal, 2012, 180: 229-236. DOI:10.1016/j.cej.2011.11.018 |
| [10] |
ALVAREZ A J, MYERSON A S. Continuous plug flow crystallization of pharmaceutical compounds[J]. Crystal Growth & Design, 2010, 10(5): 2219-2228. |
| [11] |
NI X, LIAO A. Effects of mixing, seeding, material of baffles and final temperature on solution crystallization of L-glutamic acid in an oscillatory baffled crystallizer[J]. Chemical Engineering Journal, 2010, 156: 226-233. DOI:10.1016/j.cej.2009.10.045 |
| [12] |
CRUZ P, ROCHA F, FERREIRA A. Determination of the critical mixing intensity for secondary nucleation of paracetamol in an oscillatory flow crystallizer[J]. CrystEngComm, 2018, 20: 829-836. DOI:10.1039/C7CE01940H |
| [13] |
MACKLEY M R, STONESTREET P. Heat transfer and associated energy dissipation for oscillatory flow in baffled tubes[J]. Chemical Engineering Science, 1995, 50(14): 2211-2224. DOI:10.1016/0009-2509(95)00088-M |
| [14] |
STEPHENS G G, MACKLEY M R. Heat transfer performance for batch oscillatory flow mixing[J]. Experimental Thermal & Fluid Science, 2002, 25(8): 583-594. |
| [15] |
SOLANO J P, HERRERO R, ESPÍN S, et al. Numerical study of the flow pattern and heat transfer enhancement in oscillatory baffled reactors with helical coil inserts[J]. Chemical Engineering Research & Design, 2012, 90(6): 732-742. |
| [16] |
ONYEMELUKWE L L, BENYAHIA B, REIS N M, et al. The heat transfer characteristics of a mesoscale continuous oscillatory flow crystalliser with smooth periodic constrictions[J]. International Journal of Heat and Mass Transfer, 2018, 123: 1109-1119. DOI:10.1016/j.ijheatmasstransfer.2018.03.015 |
| [17] |
丁绪淮, 谈遒. 工业结晶[M]. 北京: 化学工业出版社, 1985. DING X H, TAN Q. Industrial crystallization[M]. Beijing: Chemical Industry Press, 1985. |




