乙烯和丙烯是基础有机化工原料,在现代石油化学工业中有十分重要的作用[1]。生产工艺分为2大类:一类是石油路线;另一类是非石油路线[2]。我国富煤、贫油、少气的能源特点决定了以煤为原料,经甲醇生产低碳烯烃(MTO)具有重要的战略意义[3]。该工艺乙烯和丙烯的收率较高,但副产物中有相对较多的C4、C5烯烃。因此,MTO装置通常配有烯烃催化裂解装置,将C4、C5烯烃裂解,提高乙烯和丙烯的收率。截至“十三·五”末,我国已建成32套甲醇制烯烃装置,烯烃催化裂解装置的加工能力也快速提升。
反应系统是烯烃裂解制乙烯/丙烯的核心,高效催化剂是提高反应速率和低碳烯烃选择性的关键[4],工业上多选用ZSM-5分子筛[5]。性质活泼的烯烃在高温下易在催化剂表面结焦,致使催化剂失活,反应速率、装置产能和产品质量、反应器出料温度和组成均相应地发生变化[6]。烯烃裂解反应器的产物是换热网络的热源,其温度和组成影响换热网络目标能耗和夹点位置。因此,反应单元和换热网络高度集成与耦合,催化剂活性变化对反应与换热网络目标能耗的影响复杂且非线性。烯烃催化裂解反应的催化剂失活速度快,当催化剂活性降低至一定程度,需对催化剂进行再生(更换)以维持稳定高效的生产运行。不同的再生周期影响单位产品的平均能耗,建立反应器与换热网络耦合模型,研究催化剂失活对系统参数的影响,优化催化剂再生周期对于稳定生产、提高乙烯/丙烯产率和产品经济效益具有重要意义。
近年来,许多学者依据夹点技术、数学规划法、模拟仿真或实验验证等方法对反应-换热网络集成进行了研究,主要集中于探究进/出口物流温度、热负荷、反应转化率和选择性等关键参数的控制及其与换热网络的关系,以期实现反应参数优化和降低系统能耗[7-13]。但这些研究主要针对稳态生产工艺,未考虑生产周期内催化剂活性变化引起的系统波动。Tian等[11]研究表明,从催化剂的使用初期至末期,换热网络的加热和冷却公用工程消耗量明显变化,甚至可从夹点问题变为阈值问题,但未考虑催化剂再生周期的优化。刘俊涛等[14]针对C4烯烃催化裂解增产丙烯,从热力学、反应机理等方面分析了其特点,介绍了该技术的研究进展。反应网络与集总动力学模型的建立,反应动力学参数(动力学常数、反应活化能、指前因子等)的确定及产品分布或动力学行为的预测是该技术的研究热点[15-18]。此外,学者们对催化剂失活机理、失活动力学、结焦失活特点和原因以及催化剂再生性能等方面也进行了大量的研究[19-25]。根据文献调研,关于烯烃催化裂解反应机理和催化剂活性已有较深入的研究,对于催化剂的研究主要集中在提高反应速率、选择性和使用寿命,但对于催化剂失活对烯烃催化裂解反应和换热网络能耗的影响、催化剂再生周期的优化还鲜有报道。
本研究拟基于反应动力学、催化剂失活动力学和换热网络的集成原理,构建考虑催化剂失活的通用反应器-换热网络耦合集成模型,以单位产品的平均能耗为评价指标分析整个生产周期内反应器参数和能耗的变化,优化催化剂再生周期。据此对C4+烯烃催化裂解装置反应单元及换热网络进行集成优化,探究产品组成、双烯总收率、反应器出口温度、换热网络最小加热和冷却公用工程用量及单位产品的平均能耗随催化剂失活的变化情况,确定催化剂的最佳再生周期。
2 考虑催化剂失活的通用反应器-换热网络耦合模型 2.1 催化剂失活对反应单元的影响反应器内所发生的反应复杂多样。对于包含n种组分的复杂催化反应过程,第j个反应可由式(1)描述。
| $ \sum\limits_{i = 1}^n {{v_{i, j}}} {A_i} = 0 $ | (1) |
式中若组分Ai为反应物,νi, j为负值;若
对于给定催化剂类型和反应条件的固定床反应器,Ai的反应速率ri可由式(2)表示。设计方程见式(3)。当反应在气相中发生时,可用组分分压pi代替浓度。
| $ {r_i} = \sum\limits_{j = 1}^f {{v_{i, j}}} {r_j} $ | (2) |
| $ \mathrm{d} F_i=r_i \mathrm{d} m $ | (3) |
| $ r_j=k_j \prod\limits_{i=1}^n c_i^{\alpha_{i, j}}=k_j^* \exp \left[-\frac{E_j}{R}\left(\frac{1}{T}-\frac{1}{T^*}\right)\right] \prod\limits_{i=1}^n c_i^{\alpha_{i, j}} $ | (4) |
对于固定床反应器,催化剂失活可视为催化剂有效组分的减少。催化剂活性降低至0 < φ < 1时,反应器内催化剂有效装填量将由初始时刻的mini变为φ·mini。根据这一特性和式(2)~(4),可推导出反应温度及产物组成与催化剂活性的关系,如式(5)所示。由该式可见,催化剂失活不仅影响反应器出口物料组成,还会影响反应器温度。若该反应器为绝热反应器,其出口物料组成及温度之间的关系可由式(6)所示的热量平衡方程确定。基于反应速率方程及动力学参数,使用Matlab软件联立求解式(5)和(6),可得不同催化剂活性对应的反应器出口温度T及组成Fi。
| $ \frac{\mathrm{d} F_i}{\mathrm{~d} \varphi}=m^{\mathrm{ini}} \sum\limits_{j=1}^f\left\{v_{i, j} k_j^* \exp \left[-\frac{E_j}{R}\left(\frac{1}{T}-\frac{1}{T^*}\right)\right]\left(\prod\limits_{i=1}^n c_i^{\alpha_{i, j}}\right)\right\} $ | (5) |
| $ \sum\limits_{i=1}^n F_i C_{p, i} \mathrm{~d} T=-\sum\limits_{i=1}^n\left[\Delta_{\mathrm{f}} H_{\mathrm{m}}^{\Theta}\left(A_i\right)\right] \mathrm{d} F_i $ | (6) |
反应器的进料、出料及相关流股通常是换热网络的热阱/源。在进料组成和温度不变的情况下,催化剂失活导致反应器出料温度和组成不断变化,进而影响复合曲线、公用工程用量和夹点位置。
根据源阱位置规则[10]可以确定反应器出口流股在温-焓图中的位置,进而确定其温度和组成变化对夹点位置和系统目标能耗的影响。本研究将根据图 1所示换热网络的复合曲线进行分析。ABCDEF为热复合曲线,GHIJKL为冷复合曲线,Pinch表示夹点,QH和QC分别为最小加热和冷却公用工程用量。反应器通常在较高温度下操作,其出口物流是位于夹点上方的热源。图 1中,C点对应反应器出口温度,D点对应出口流股的目标换热温度。
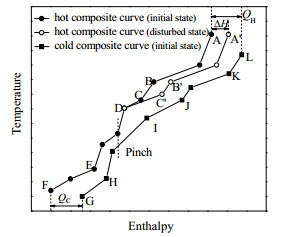
|
图 1 温-焓图 Fig.1 Temperature-enthalpy diagram |
受催化剂失活影响,反应器出口流股的温度和热容流率同时变化。当出口温度由Tini变化至T′、组分Ai的摩尔流率由
| $ \Delta H=q_C^{\mathrm{ini}}\left(T^{\prime}-T^{\mathrm{ini}}\right)+\Delta q_C\left(T^{\prime}-T^T\right) $ | (7) |
| $ q_C^{\mathrm{ini}}=\sum\limits_{i=1}^n F_i^{\mathrm{ini}} C_{p, i} $ | (8) |
| $ \Delta q_C=\sum\limits_{i=1}^n\left(F_i^{\prime}-F_i^{\mathrm{ini}}\right) C_{p, i} $ | (9) |
分析图 1可知,该情况下夹点位置不变,QH和QC的变化量分别如式(10)和(11)所示。
| $ \Delta Q_{\mathrm{H}}=-\Delta H=-q_C^{\mathrm{ini}}\left(T^{\prime}-T^{\mathrm{ini}}\right)-\left(T^{\prime}-T^T\right) \sum\limits_{i=1}^n\left(F_i^{\prime}-F_i^{\mathrm{ini}}\right) C_{p, i} $ | (10) |
| $ \Delta Q_{\mathrm{C}}=0 $ | (11) |
不同的化工过程,反应器出口物流属性及其在温焓图中的位置不同。催化剂失活导致的冷热公用工程变化量不同,但都遵循相同的变化规律。假定夹点位置不变,按上述方法分析可得不同情况下最小加热和冷却公用工程变化量的通用计算式,结果汇总见表 1[26]。当出口流股跨夹点时,分为夹点上和夹点下,分别由式(12)和(13)计算焓值变化。
|
|
表 1 夹点位置不变时最小公用工程用量随反应器参数变化情况[26] Table 1 Variations of minimum utility consumptions with reactor parameters (the pinch position remains unchanged) |
| $ \Delta H_1=q_C^{\mathrm{ini}}\left(T^{\prime}-T^{\mathrm{ini}}\right)+\left(T^{\prime}-T_{\mathrm{P}}\right) \Delta q_C $ | (12) |
| $\Delta H_2=\left(T_{\mathrm{P}}-T^T\right) \Delta q_C $ | (13) |
当物流的温度或热容流率变化导致冷热复合曲线靠近时,最小传热温差可能会小于10 K。这种情况下,需将复合曲线平移一定距离ΔHS以满足最小传热温差要求。夹点位置可能会相应改变;换热网络中冷、热公用工程用量也会改变,其值为ΔHS与表 1所示值之和。
若反应产物分布随催化剂活性的变化影响后续多个流股的参数,则需要分别确定各变化参数流股的属性及其在温焓图中的位置,依照上述分析方法分别确定其参数波动对冷热复合曲线的影响,叠加各参数的影响即可确定多流股参数变化对换热网络能耗的影响[26]。
2.3 反应与换热网络集成催化剂失活不仅影响反应单元参数,还会影响换热网络能耗。准确评价催化剂失活的影响需综合考虑目标产品产量与换热网络能耗。在一个催化剂再生周期内,由于产品的产量和能耗均随催化剂的活性改变,当催化剂的再生成本及系统投资费用较低时,可以建立单位产品的平均能耗Eav作为评价指标。考虑到单位加热和冷却公用工程品质不同,在计算中将不同类型的能源按各自对应的能耗折算成标准煤,其计算见式(14)。单位产品的平均能耗越低,能量利用效率越高。
| $ E_{\mathrm{av}}=\int_1^{\varphi}\left(h\left|Q_{\mathrm{H}}^{\mathrm{ini}}+\Delta Q_{\mathrm{H}}\right|+c\left|Q_{\mathrm{C}}^{\mathrm{ini}}+\Delta Q_{\mathrm{C}}\right|\right) \mathrm{d} \varphi /\left(\int_1^{\varphi} F_{\text {target }} \mathrm{d} \varphi\right) $ | (14) |
根据式(5)~(14)可建立考虑催化剂失活的通用反应-换热网络耦合模型。在设计阶段,可依据该模型确定反应和换热网络参数以及单位产品能耗随催化剂失活的变化,以Eav为关键评价指标确定催化剂最佳再生节点。该模型可拓展应用于比较不同类型催化剂对应的最优再生周期、选择适宜催化剂并确定其对应的再生活性、设计具有足够操作灵活性和高经济效益的系统。对于催化剂和反应器类型已知的实际生产系统,该模型可用于确定反应器出口温度、产品组成、换热网络目标能耗及催化剂活性之间的关系,推断产物组成及系统目标能耗变化,结合自动监测和控制系统指导系统操作参数的调整。在分析中,可根据催化剂的失活动力学—式(15)进一步考虑催化剂活性与反应温度、组分浓度、运行时间等因素的关系。
| $ -\mathrm{d} \varphi / \mathrm{d} t=A_{\mathrm{d}} \exp \left(-E_{\mathrm{d}} /(R T)\right) c_{\mathrm{d}}^s \varphi^d $ | (15) |
某C4+烯烃催化裂解装置包含3个操作单元:反应单元、压缩单元和分离单元。反应单元包括气化、反应器进出物料换热、反应器进料预热、烯烃催化裂解反应、产物冷却及催化剂再生系统等;压缩单元包括反应产物压缩和凝液分离;分离单元包括脱丙烷塔和脱丁烷塔。该装置采用连续切换再生流程;反应器(R101)采用一开一备(A线和B线)的操作方式,通过切换A线和B线对催化剂进行烧焦再生;现行催化剂再生周期为7 d。该装置的生产流程简图如图 2所示。
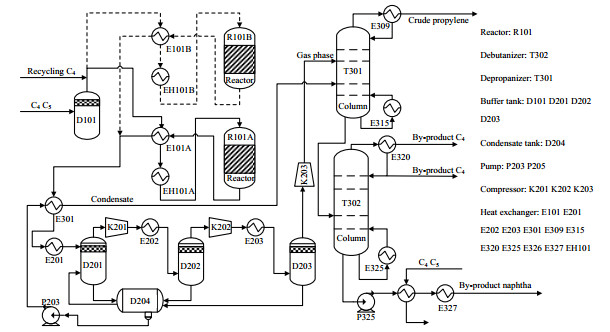
|
图 2 C4+烯烃催化裂解装置流程图 Fig.2 Flowsheet of C4+ olefin catalytic cracking unit |
C4+烯烃裂解制乙烯/丙烯是多个串联和平行反应耦合在一起的复杂反应体系。丁烯、戊烯首先通过双分子反应路径经齐聚生成中间产物,然后裂解生成低碳烯烃。在烯烃发生裂解反应的同时,也不可避免地伴随着聚合反应、异构化反应、氢转移反应、芳构化反应及生焦反应等,生成各种异构化产物、C5~C10烯烃或芳烃、各种烷烃及焦炭、少量氢气及甲烷等。主要反应构成的反应网络如图 3(a)所示。
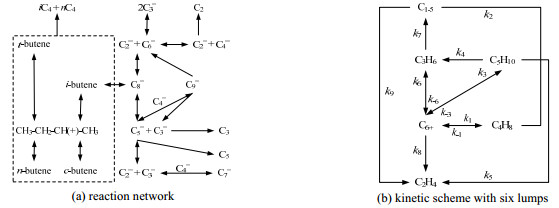
|
图 3 烯烃催化裂解反应网络 Fig.3 Reaction network of olefin catalytic cracking |
考虑到反应产物组成的复杂多样,文献大多采用集总分析法研究其动力学。图 3(b)所示的六集总(C1-5、C2H4、C3H6、C4H8、C5H10、C6+)反应网络模型,包含了烯烃裂解中的主要反应:齐聚(反应−1、−3、−6)、裂解(反应1、3、4、5、6、8、9)和氢转移(反应2、7)反应,可用于描述C4+烯烃裂解制乙烯/丙烯的反应系统。各集总反应速率见式(16)~(21),对应的动力学参数见表 2[17]。
| $ {r_{{{\text{C}}_{{\text{1 - 5}}}}}} = {k_2}{p_{{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}}} - {k_7}{p_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}} + {k_9}{p_{{{\text{C}}_{{\text{1 - 5}}}}}} $ | (16) |
| $ {r_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}}} = {k_5}{p_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}} + {k_8}{p_{{{\text{C}}_{{\text{6 + }}}}}} + {k_9}{p_{{{\text{C}}_{{\text{1 - 5}}}}}} $ | (17) |
| $ {r_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}} = {k_4}{p_{{\text{C}}{}_{\text{5}}{{\text{H}}_{{\text{10}}}}}} - {k_{ - 6}}{p_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}}^{\text{2}} + {k_6}{p_{{{\text{C}}_{{\text{6 + }}}}}} - {k_7}{p_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}} $ | (18) |
| $ {r_{{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}}} = - {k_{ - 1}}{p_{{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}}}^{1.5} + {k_1}{p_{{{\text{C}}_{{\text{6 + }}}}}} - {k_2}{p_{{{\text{C}}_{\text{4}}}{\text{H}}{}_{\text{8}}}} $ | (19) |
| $ {r_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}} = - {k_{ - 3}}{p_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}}^2 + {k_3}{p_{{{\text{C}}_{{\text{6 + }}}}}} - {k_4}{p_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}} - {k_5}{p_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}} $ | (20) |
| $ {r_{{{\text{C}}_{{\text{6 + }}}}}} = {k_{ - 1}}{p_{{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}}}^{1.5} - {k_1}{p_{{{\text{C}}_{{\text{6 + }}}}}} + {k_{ - 3}}{p_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}}^2 - {k_3}{p_{{{\text{C}}_{{\text{6 + }}}}}} + {k_{ - 6}}{p_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}}^2 - {k_6}{p_{{{\text{C}}_{{\text{6 + }}}}}} - {k_8}{p_{{{\text{C}}_{{\text{6 + }}}}}} $ | (21) |
|
|
表 2 反应动力学参数 Table 2 Kinetic parameters of the reactions |
将式(16)~(21)代入式(5)和(6)可得式(22)~(28),据此可分析C4+烯烃催化裂解过程中各集总组分含量xi (集总组分Ci在反应体系中以CH2为基本单位算得的摩尔分数[17])及反应器出口温度随催化剂活性的变化。
| $ F_{\mathrm{c} \text {, total }}^0 \mathrm{~d} x_{\mathrm{C}_{1-5}}=m^{\text {ini }}\left(k_2 p_{\mathrm{C}_4 \mathrm{H}_8}-k_7 p_{\mathrm{C}_3 \mathrm{H}_6}+k_9 p_{\mathrm{C}_{1-5}}\right) \mathrm{d} \varphi $ | (22) |
| $ F_{\mathrm{c}, \text { total }}^0 \mathrm{~d} x_{\mathrm{C}_2 \mathrm{H}_4}=m^{\text {ini }}\left(k_5 p_{\mathrm{C}_5 \mathrm{H}_{10}}+k_8 p_{\mathrm{C}_{6+}}+k_9 p_{\mathrm{C}_{1-5}}\right) \mathrm{d} \varphi $ | (23) |
| $ F_{\mathrm{c}, \text { total }}^0 \mathrm{~d} x_{\mathrm{C}_3 \mathrm{H}_6}=m^{\text {ini }}\left(k_4 p_{\mathrm{C}_5 \mathrm{H}_{10}}-k_{-6} p_{\mathrm{C}_3 \mathrm{H}_6}{ }^2+k_6 p_{\mathrm{C}_{6+}}-k_7 p_{\mathrm{C}_3 \mathrm{H}_6}\right) \mathrm{d} \varphi $ | (24) |
| $ F_{\mathrm{c} \text {, total }}^0 \mathrm{~d} x_{\mathrm{C}_4 \mathrm{H}_8}=m^{\text {ini }}\left(-k_{-1} p_{\mathrm{C}_4 \mathrm{H}_8}^{1.5}+k_1 p_{\mathrm{C}_{6+}}-k_2 p_{\mathrm{C}_4 \mathrm{H}_8}\right) \mathrm{d} \varphi $ | (25) |
| $ F_{\mathrm{c}, \text { total }}^0 \mathrm{~d} x_{\mathrm{C}_5 \mathrm{H}_{10}}=m^{\mathrm{ini}}\left(-k_{-3} p_{\mathrm{C}_5 \mathrm{H}_{10}}{ }^2+k_3 p_{\mathrm{C}_{6+}}-k_4 p_{\mathrm{C}_5 \mathrm{H}_{10}}-k_5 p_{\mathrm{C}_5 \mathrm{H}_{10}}\right) \mathrm{d} \varphi $ | (26) |
| $ F_{\mathrm{c}, \text { total }}^0 \mathrm{~d} x_{\mathrm{C}_{6+}}=m^{\mathrm{ini}}\left(k_{-1} p_{\mathrm{C}_4 \mathrm{H}_8}{ }^{1.5}-k_1 p_{\mathrm{C}_{6+}}+k_{-3} p_{\mathrm{C}_5 \mathrm{H}_{10}}{ }^2-k_3 p_{\mathrm{C}_{6+}}+k_{-6} p_{\mathrm{C}_3 \mathrm{H}_6}{ }^2-k_6 p_{\mathrm{C}_{6+}}-k_8 p_{\mathrm{C}_{6+}}\right) \mathrm{d} \varphi $ | (27) |
| $ \sum\limits_{i=1}^n F_i C_{p, i} \mathrm{~d} T=F_{\text {total }} \cdot \bar{C}_p \cdot \mathrm{d} T=-F_{\mathrm{c}, \text { total }}^0 \sum\limits_{i=1}^n\left[\Delta_{\mathrm{f}} H_{\mathrm{m}}^{\Theta}\left(A_i\right) / n_{c, i}\right] \mathrm{d} x_i $ | (28) |
当反应压力较低且反应压降可以忽略时,各组分分压pi与其摩尔分数呈正比,如式(29)所示。根据物料衡算,可知系统中碳含量不变。因此,任意时刻反应器中CH2总摩尔流量可近似恒定,等于反应器进料中CH2的总摩尔流量,如式(30)所示。
| $ p_i=p \cdot y_i=p \cdot\left(x_i / n_{c, i}\right) /\left(\sum x_i / n_{c, i}\right) $ | (29) |
| $ F_{\mathrm{c}, \text { total }}=F_{\mathrm{c}, \text { total }}^0=2079.83\; \mathrm{kmol} \cdot \mathrm{h}^{-1} $ | (30) |
C4+烯烃催化裂解反应器为绝热固定床反应器,初始运行时刻反应器进、出口温度分别为823和803.35 K,催化剂装填量mini为2 940 kg,反应压力为100 kPa。反应器进料数据见表 3;各集总组分的标准摩尔生成焓和定压热容与温度的关系见表 4[27]。
|
|
表 3 反应器进料数据 Table 3 Reactor feed data |
|
|
表 4 各集总组分热力学性质及热化学数据[27] Table 4 Thermodynamic property and thermochemical data of each lumped component |
根据式(22)~(30)可构建C4+烯烃催化裂解装置反应模型。在Matlab中对该模型进行数值积分可得φ=1时反应器出口处各集总组分摩尔分数及出口温度,并与实际数据对比,如表 5所示。
|
|
表 5 φ=1时反应器出口数据 Table 5 Reactor effluent data when φ=1 |
由表 5可见,该反应器模型可准确预测反应产物组成和温度,计算结果与实际数据的相对误差小于4%。依据该模型,采用四阶龙格库塔法计算可得反应器出口处各集总组分的xi及T随φ的变化关系。此外,工业上常采用双烯总收率(即乙烯和丙烯的总收率)Y作为装置生产能力评价指标(Y≥43%),依据式(31)和(32)即可确定Y与φ的关系。
| $ Y = \left( {{x_{{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}}} + {x_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}}} \right)/\left( {x_{{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}}^{\text{0}} + x_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}^{\text{0}}} \right)/\text{MBR} \times 100\% $ | (31) |
| $ \text{MBR} = \left( {{x_{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}}} + {x_{{\text{C1 - 5}}}} + {x_{{\text{C6 + }}}}} \right)/\left( {x_{{\text{C1 - 5}}}^{\text{0}} + x_{{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}}^{\text{0}} + x_{{{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{10}}}}}^{\text{0}}} \right) \times 100\% $ | (32) |
现行烯烃催化裂解装置共有5股冷物流(C1~C5)和6股热物流(H1~H6)。初始时刻,各流股数据如表 6所示。其中,H3为反应器出口物流。取最小传热温差ΔTmin为10 K,绘制冷热复合曲线见图 4(a)。由该图可得,换热网络的最小加热和冷却公用工程用量分别为3 870.2和6 303.9 kW;平均夹点温度为340.5 K,冷夹点对应P点。
|
|
表 6 初始换热网络物流数据 Table 6 Initial hot and cold stream data |

|
图 4 催化剂失活前后温-焓图 Fig.4 Temperature-enthalpy diagram before and after catalyst deactivation |
图 4(a)中,反应器出口物流H3跨夹点:点A对应H3初始温度,位于夹点之上;B点为H3目标温度,位于夹点之下。假设夹点位置不变,根据表 1,ΔQH和ΔQC可分别由式(33)和(34)计算。根据不同催化剂活性下反应器出口组成、温度、式(33)和(34)可得不同催化剂活性下系统最小加热和冷却公用工程。
图 4(b)为催化剂活性由1降低为0.3时换热网络冷热复合曲线变化情况。由该图可得,φ=0.3时,换热网络平均夹点温度为340.5 K,最小加热和冷却公用工程用量分别为4 781.4和6 234.4 kW,与式(33)、(34)的计算结果吻合。因此夹点不变假设成立,依据式(33)和(34)可确定系统的公用工程变化量。
| $ \Delta Q_{\mathrm{H}}=-q_{C, \mathrm{H} 3}^{\mathrm{ini}}\left(T^{\prime}-803.3\right)-\left(T^{\prime}-315\right) \cdot F_{\mathrm{c}, \text { total }}^0 \sum\left(x_i-x_i^{\mathrm{ini}}\right) \cdot C_{p, i} / n_{c, i} $ | (33) |
| $ \Delta Q_{\mathrm{C}}=(345.5-315) \cdot F_{\mathrm{c}, \text { total }}^0 \sum\left(x_i-x_i^{\mathrm{ini}}\right) \cdot C_{p, i} / n_{c, i} $ | (34) |
将式(33)和(34)代入式(14),可得式(35)。该式可用于计算催化剂活性由1降为0 < φ < 1的过程中生产单位产品(C2H4、C3H6)的平均能耗。
| $ E_{\mathrm{av}}=\frac{\int_1^{\varphi}\left\{24854.1 h+9813.5 c+\left[1098 c-36 h\left(T^{\prime}-315\right)\right]\left[1+100 \sum\left(x_i-x_i^{\mathrm{ini}}\right) C_{p, i} / n_{c, i}\right]\right\} \mathrm{d} \varphi}{\int_1^{\varphi}\left(x_{\mathrm{C}_2 \mathrm{H}_4} / n_{c, \mathrm{C}_2 \mathrm{H}_4}+x_{\mathrm{C}_3 \mathrm{H}_6} / n_{c, \mathrm{C}_3 \mathrm{H}_6}\right) \mathrm{d} \varphi} $ | (35) |
该系统所用加热和冷却公用工程分别为蒸汽和冷却水,其转换因子h和c分别为3.41×10−5和3.42×10−6 kg·kJ−1(以标准煤计)[28]。依据式(22)~(30)、式(33)和(34)所示反应参数及换热网络能耗随催化剂失活变化情况,计算可得催化剂活性由1降为不同值时整个周期内生产单位产品的平均能耗,并绘制Eav-φ曲线。此外,依据反应器集总组分组成、出口温度及双烯总收率随催化剂活性变化关系可分别绘制xi-φ曲线、T-φ曲线和Y-φ曲线;根据换热网络最小加热和冷却公用工程用量与催化剂活性间的关系式,绘制QH-φ曲线和QC-φ曲线。综合以上所有曲线构建的xi-T-Y-QH-QC-Eav-φ图如图 5所示。根据该图可确定任意催化剂活性对应的产物组成、反应器出口温度、目标产物总收率、加热和冷却公用工程用量及生产单位产品的平均能耗。
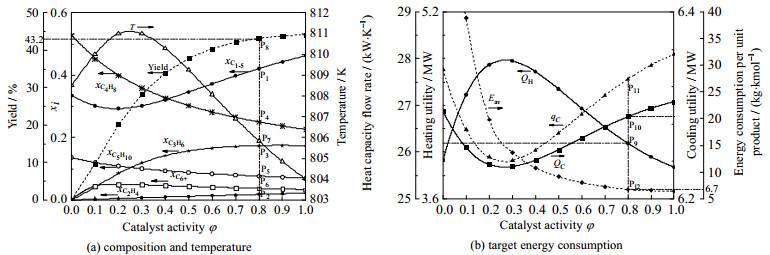
|
图 5 不同催化剂活性下系统参数变化 Fig.5 Variations of system parameters under different catalyst activities |
(1) 图 5(a)中xi-φ曲线表明,随着催化剂不断失活,反应物C4H8和C5H10的转化率不断降低,产品中C4H8和C5H10集总组分摩尔分数升高,目标产品C2H4和C3H6产量不断降低。
(2) 由xC1-5-φ和xC6+-φ曲线可得,催化剂失活前期和中期C1-5烃类摩尔分数随催化剂失活不断降低,末期摩尔分数增加,C6+烃类变化趋势相反。原因为:反应过程中丁烯和戊烯主要通过齐聚反应生成C6+烃类,继而裂解生成乙烯和丙烯。受催化剂失活影响,齐聚反应和裂解反应速率均不断下降。催化剂失活中前期,裂解反应受催化剂活性影响较大,C1-5烃类摩尔分数有明显降低,齐聚反应速率大于裂解反应速率,C6+集总组分摩尔分数稍有增加;催化剂失活末期,齐聚反应受催化剂失活影响较大,齐聚反应速率低于裂解反应,且此时双烯选择性降低至下限值,大分子烃类物质不断裂解生成C1-5烃类,C6+烃类摩尔分数降低,C1-5集总组分摩尔分数增加。
(3) T-φ曲线表明反应器出口温度随催化剂失活先增加后降低。这是因为,齐聚反应放热,裂解反应吸热;当齐聚反应速率高于其他类型反应时,反应器出口温度升高;反之,温度下降。
(4) 图 5(a)中Y-φ曲线表明,随着反应器运行时间的不断延长,催化剂不断失活,装置生产能力评价指标—双烯总收率不断降低。当催化剂活性降低至0.8时,Y≈43.2%,接近下限值43%,应及时切换反应器,对催化剂进行烧焦再生。
(5) 图 5(b)中Q-φ曲线表明,加热公用工程用量随催化剂失活先增加后减少,冷却公用工程变化趋势相反,且加热公用工程变化量约为冷却公用工程变化量的12~13倍。原因在于:1) 反应器出口流股H3为跨夹点的热源,由式(12)、(13)及表 1可知,H3热容流率降低时,加热公用工程用量增加,冷却公用工程用量减少。H3热容流率受组成和温度影响,变化趋势如图 5(b) qC-φ曲线所示:反应前期,qC, H3随催化剂失活不断降低,催化剂活性降低至[0.2, 0.3]时,出口温度、C1-5及C6+集总组分摩尔分数呈现相反的变化趋势,继而导致qC, H3升高。2) H3目标温度恒定,供给温度变化主要影响加热公用工程用量。供给温度升高,加热公用工程用量减小。因此,在H3热容流率和供给温度变化的共同作用下,系统加热公用工程用量随催化剂失活先增加后减少,冷却公用工程用量先减少后增加,且加热公用工程变化量大于冷却公用工程变化量。
(6) 随着催化剂不断失活,目标产品产率降低,能量利用效率不断下降,生产单位产品所需能量不断增加。Eav-φ曲线表明,单位产品生产能耗在催化剂活性区间[0.8, 1]内近似平稳,在[0.4, 0.8]区间内随活性降低缓慢增加,在[0, 0.4]区间内随活性降低迅速增加。
结合Y-φ曲线和Eav-φ曲线分析可得,为保证产品品质和较高的经济效益,当催化剂活性降低为0.8时,应及时切换反应器,对催化剂进行再生。催化剂活性由1降至0.8时,单位产品生产能耗由5.96增加至6.71 kg·kmol−1(以标准煤计,下同),增加约13%。该催化剂活性对应的C1-5、C2H4、C3H6、C4H8、C5H10、C6+集总组分摩尔分数分别为0.43、0.02、0.18、0.25、0.08、0.04,反应器出口温度为805.8 K,双烯总收率为43.2%,最小加热和冷却公用工程用量分别为4 074.9和6 287.7 kW,如点P1~P10所示。
烯烃催化裂解过程中,相比温度项和运行时间项,浓度项对失活动力学方程影响较小,可以忽略。此外,反应温度随运行时间不断变化,即T=f(t)。这种情况下,催化剂活性仅为系统运行时间的函数,式(15)可以简化为φ=g(t),即可以由系统运行时间估计催化剂活性。根据工厂实际生产数据绘制产物组成及出口温度随系统运行时间变化关系曲线,见图 6。由该图可得,系统运行107.5 h时,C1-5、C2H4、C3H6、C4H8、C5H10、C6+集总组分摩尔分数分别为0.439、0.018、0.195、0.238、0.074、0.036,反应器出口温度为805.7 K,与计算所得φ=0.8时相应数据对比,误差不超过8%。因此催化剂最佳再生周期约为107.5 h (4.5 d)。实际生产操作中反应线路切换周期约7 d,结合图 5和6可得系统运行7 d后对应催化剂活性约为0.4,单位产品能耗为10.75 kg·kmol−1。当催化剂再生周期调整为4.5 d,单位产品生产能耗可降至6.71 kg·kmol−1,节省41.5%。
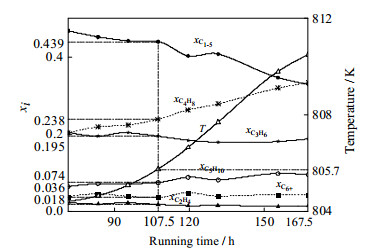
|
图 6 工厂实际生产数据 Fig.6 Actual production data |
本研究基于反应动力学、催化剂失活动力学和换热网络的公用工程迁移规律,构建了考虑催化剂活性的反应-换热网络耦合集成模型,并据此对C4+烯烃催化裂解装置进行了分析,结论如下:
(1) 本研究所建立的反应-换热网络耦合模型可用于探究催化剂失活对反应物转化率、目标产品产率及换热网络能耗的影响,确定催化剂的最佳再生活性,指导催化剂的选择和反应器设计。
(2) 对于现有装置,可根据xi-T-Y-QH-QC-Eav-φ关系曲线,预测产物组成、催化剂活性、双烯总收率及系统目标能耗值,并可进一步结合自动控制系统实现对系统操作参数的实时调整。
(3) 对C4+烯烃催化裂解装置的分析表明,受催化剂失活影响,反应温度、产品组成及系统目标能耗不断变化。综合考虑双烯总收率及单位产品能耗优化所得催化剂的最佳再生活性为0.8,最佳催化剂再生周期为107.5 h。再生周期优化后,单位产品平均生产能耗可降低41.5%。
4.2 展望(1) 本研究提出的模型建立在反应器进料温度恒定的基础上,实际生产过程中,通常采用提高进料温度的方法补偿催化剂失活,以延长催化剂再生周期。如何建立同时考虑催化剂失活和反应器进料温度变化的反应-换热网络集成模型仍有待进一步深入研究。
(2) 对于催化反应过程,催化剂再生、购买及换装导致投资费用增加,此外,催化剂再生周期的优化可能增加系统开停车次数,造成整体生产成本的增加。后续研究将综合考虑多方面因素,引入单位产品成本作为优化指标,完善本研究所构建的模型。
符号说明:
Ai —组分 QC —最小冷却公用工程用量,kW
Ad —催化剂失活速率指前因子 QH —最小加热公用工程用量,kW
c —冷却公用工程转换因子,kg·kJ−1(以标准煤计) qC —热容流率,kW·K−1
ci —组分Ai的浓度,kmol·m−3 rC1-5~rC6+
cd —与失活有关的组分浓度,kmol·m−3 —各集总组分的反应速率,kmol·g−1·h−1
Cp, i —组分Ai摩尔定压热容,kJ·kmol−1·K−1 ri —组分Ai的反应速率,kmol·g−1·h−1
Eav —单位产品平均能耗,kg·kmol−1(以标准煤计) R —通用气体常数,8.314 J·mol−1·K−1
Ed —催化剂失活活化能,kJ·mol−1 t —系统运行时间,h
Ej —反应j的活化能,kJ·mol−1 T —反应器出口温度,K
Fc, total —以CH2为当量的烯烃摩尔流量,kmol·h−1 Tin —换热器进口温度,K
Fi —组分Ai的摩尔流量,kmol·h−1 Tout —换热器出口温度,K
Ftarget —出料中目标产品的产量,kmol·h−1 TP —夹点温度,K
Ftotal —流股总摩尔流量,kmol·h−1 TT —流股目标温度,K
f —反应器内发生的反应数 T* —参考温度,K
h —加热公用工程转换因子,kg·kJ−1(以标准煤计) ΔTmin —最小传热温差,K
ΔH —流股焓值变化量,kW xi —集总组分Ci以CH2为基本单位算得的摩尔分数
ΔH1 —夹点上流股焓值变化量,kW yi —组分Ai的摩尔分数
ΔH2 —夹点下流股焓值变化量,kW Y —双烯总收率,%
ΔHS —复合曲线在温焓图中的平移距离 vi, j —组分Ai在第j个反应中的化学计量系数
kj —反应j的速率常数,j=1~9,−1,−3,−6 φ —催化剂活性
kj* —参考温度T*下反应j的速率常数 ΔfHmΘ(Ai)
m —反应器内催化剂装填量,kg —组分Ai标准摩尔生成焓,kJ·mol−1
MBR —物料平衡率 上标
n —系统组分数 d, s —级数
nc, i —集总组分Ci平均碳数 ini —初始参数
p —反应压力,Pa 0 —进料参数
pi —组分Ai的分压,Pa,Ai= C1-5、C2H4、C3H6、C4H8、αi, j —组分Ai在第j个反应中的反应级数
C5H10、C6+ ' —变化后的参数
| [1] |
李志, 孙启文, 刘继森, 等. 甲醇制烯烃催化剂失活模型[J]. 应用化学, 2014, 31(4): 394-399. LI Z, SUN Q W, LIU J S, et al. Deactivation model of the catalyst used in methanol to olefin process[J]. Chinese Journal of Applied Chemistry, 2014, 31(4): 394-399. |
| [2] |
应卫勇, 曹发海, 房鼎业. 碳一化工主要产品生产技术[M]. 北京: 化学工业出版社, 2004. YING W Y, CAO F H, FANG D Y. Main product production technology of C1 chemistry[M]. Beijing: Chemical Industry Press, 2004. |
| [3] |
应磊. SAPO-34及ZSM-5催化剂上甲醇与烯烃转化动力学研究[D]. 杭州: 浙江大学, 2015. YING L. Kinetics of methanol and olefins transformation over SAPO-34 and ZSM-5 catalyst [D] Hangzhou: Zhejiang University, 2015. |
| [4] |
FOGLER H S. Elements of chemical reaction engineering[M]. 4th ed. Upper Saddle River, New Jersey: Pearson Education, 2006.
|
| [5] |
潘红艳, 田敏, 何志艳, 等. 甲醇制烯烃用ZSM-5分子筛的研究进展[J]. 化工进展, 2014, 33(10): 2625-2633. PAN H Y, TIAN M, HE Z Y, et al. Advances in research on modified ZSM-5 molecular sieves for conversion of methanol to olefins[J]. Chemical Industry and Engineering Progress, 2014, 33(10): 2625-2633. |
| [6] |
李建文. MTO反应产物中C4、C5烯烃催化裂解的研究[D]. 上海: 华东理工大学, 2016. LI J W. Study on catalytic cracking of C4 C5 olefins from MTO [D]. Shanghai: East China University of Science and Technology, 2016. |
| [7] |
GLAVIC P, KRAVANJA Z, HOMSAK M. Modeling of reactors for process heat integration[J]. Computers & Chemical Engineering, 1988, 12(2/3): 189-194. |
| [8] |
JOGWAR S S, BALDEA M, DAOUTIDIS P. Dynamics and control of reactor - feed effluent heat exchanger networks: 2008 American Control Conference [C]. Seattle, Washington: The American Automatic Control Council., 2008.
|
| [9] |
TANGE M, MAEDA T, NAKANO A, et al. Experimental study of hydrogen storage with reaction heat recovery using metal hydride in a totalized hydrogen energy utilization system[J]. International Journal of Hydrogen Energy, 2011, 36(18): 11767-11776. DOI:10.1016/j.ijhydene.2011.06.023 |
| [10] |
ZHANG D, LIU G L, LI Y F. Graphical optimization method for coupled heat exchanger network and reactor[J]. Energy, 2018, 156: 635-646. DOI:10.1016/j.energy.2018.05.089 |
| [11] |
TIAN X, YIN C F, LV D H, et al. Effect of catalyst deactivation on the energy consumption of gasoline–diesel hydrotreating process[J]. Energy & Fuels, 2018, 32(10): 10879-10890. |
| [12] |
吕东晖, 李伟, 王鹏, 等. 催化裂化装置反应器及其能量系统的优化[J]. 石油化工, 2018, 47(4): 350-355. LYU D H, LI W, WANG P, et al. Optimization of fluid catalytic cracking unit reactor and energy system[J]. Petrochemical Technology, 2018, 47(4): 350-355. DOI:10.3969/j.issn.1000-8144.2018.04.008 |
| [13] |
ZHANG D, LV D H, YIN C F, et al. Combined pinch and mathematical programming method for coupling integration of reactor and threshold heat exchanger network[J]. Energy, 2020, 205: 118070. DOI:10.1016/j.energy.2020.118070 |
| [14] |
刘俊涛, 谢在库, 徐春明, 等. C4烯烃催化裂解增产丙烯技术进展[J]. 化工进展, 2005, 24(12): 1347-1351. LIU J T, XIE Z K, XU C M, et al. Advances in catalytic cracking of C4 olefin to propylene[J]. Chemical Industry and Engineering Progress, 2005, 24(12): 1347-1351. DOI:10.3321/j.issn:1000-6613.2005.12.006 |
| [15] |
李博, 龙军, 侯栓弟. 烯烃催化裂解反应动力学的研究[J]. 计算机与应用化学, 2009, 26(2): 129-132. LI B, LONG J, HOU S D. Kinetic modeling of olefins cracking performance on zeolite catalyst[J]. Computers and Applied Chemistry, 2009, 26(2): 129-132. |
| [16] |
EPELDE E, AGUAYO A T, OLAZAR M, et al. Kinetic model for the transformation of 1-butene on a K-modified HZSM-5 catalyst[J]. Industrial & Engineering Chemistry Research, 2014, 53(26): 10599-10607. |
| [17] |
LI J W, LI T, MA H F, et al. Kinetics of coupling cracking of butene and pentene on modified HZSM-5 catalyst[J]. Chemical Engineering Journal, 2018, 346: 397-405. DOI:10.1016/j.cej.2018.04.061 |
| [18] |
BERTA A H, HWANG H D, ASFHA H B, et al. Reaction mechanism and kinetic modeling of olefin conversion over phosphorus modified ZSM-5 catalyst[J]. Korean Journal of Chemical Engineering, 2022, 39(6): 1460-1471. DOI:10.1007/s11814-021-1016-9 |
| [19] |
郑仁垟, 谢在库. 多相催化时空演变的全生命周期表征策略[J]. 催化学报, 2021, 42(12): 2141-2148. ZHENG R Y, XIE Z K. Full life cycle characterization strategies for spatiotemporal evolution of heterogeneous catalysts[J]. Chinese Journal of Catalysis, 2021, 42(12): 2141-2148. |
| [20] |
MOULIJN J A, VAN DIEPEN A E, KAPTEIJN F. Catalyst deactivation: Is it predictable? What to do?[J]. Applied Catalysis A: General, 2001, 212(1/2): 3-16. |
| [21] |
陆铭, 孙洪敏, 郭燏, 等. ZSM-5沸石催化剂的失活历程和活性稳定性[J]. 石油学报(石油加工), 2001, 17(4): 59-63. LU M, SUN H M, GUO J, et al. Study on deactivation process and activity stability of ZSM-5 zeolite[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2001, 17(4): 59-63. |
| [22] |
邓任生, 魏飞, 邓欣, 等. 超短接触催化裂解过程中的焦炭沉积规律Ⅱ结焦过程的动力学模型[J]. 石油与天然气化工, 2000, 29(5): 237-239. DENG R S, WEI F, DENG X, et al. Study of coke formation on catalyst in hydrocarbon catalytic pyrolysis process II. Kinetic model for coke formation[J]. Chemical Engineering of Oil & Gas, 2000, 29(5): 237-239. |
| [23] |
戴立顺, 胡云剑, 李建华. 工业运转中渣油加氢催化剂的活性评估及寿命预测[J]. 石油炼制与化工, 2000, 31(12): 13-16. DAI L S, HU Y J, LI J H. Activity evaluation of residue hydrotreating catalyst during commercial running and its remaining life prediction[J]. Petroleum Processing and Petrochemicals, 2000, 31(12): 13-16. |
| [24] |
张海娟, 王振宇, 李江红, 等. 反应条件对丙烷脱氢催化剂积炭行为的影响[J]. 天然气化工(C1化学与化工), 2014, 39(2): 38-42. ZHANG H J, WANG Z Y, LI J H, et al. Effect of reaction conditions on coke formation over the catalyst for propane dehydrogenation[J]. Natural Gas Chemical Industry, 2014, 39(2): 38-42. |
| [25] |
黄捷, 宁春利, 尚勤杰, 等. SAPO-34催化剂在甲醇制低碳烯烃(MTO)反应中的积炭性质及再生性能[J]. 复旦学报(自然科学版), 2012, 51(5): 566-573. HUANG J, NING C L, SHANG Q J, et al. Research on coking and regeneration behavior of SAPO-34 catalyst in methanol-to-olefin (MTO) reaction[J]. Journal of Fudan University (Natural Science), 2012, 51(5): 566-573. |
| [26] |
ZHANG D, WANG P, LIU G L. A novel sensitivity analysis method for the energy consumption of coupled reactor and heat exchanger network system[J]. Energy & Fuels, 2018, 32(6): 7210-7219. |
| [27] |
王子宗. 石油化工设计手册[M]. 北京: 化学工业出版社, 2015. WANG Z Z. Petrochemical design manual[M]. Beijing: Chemical Industry Press, 2015. |
| [28] |
国家市场监督管理总局, 国家标准化管理委员会. 综合能耗计算通则: GB/T 2589-2020 [S]. 北京: 中国标准出版社, 2020. State Administration for Market Regulation, Standardization Administration of the People's Republic of China. General rules for calculation of the comprehensive energy consumption: GB/T 2589-2020 [S]. Beijing: Standards Press of China, 2020. |




