2. 西安交通大学 能源与动力工程学院,陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
造粒塔是尿素生产过程中关键设备,其顶部排放的气体中会夹带大量尿素粉尘,粉尘不仅对环境与人体造成严重危害,同时降低了企业的效益[1, 2]。造粒塔中每吨尿素所需空气量在6000~10000 m3·h-1,采用电除尘、过滤式除尘等方法设备投资大,经济效益低。因此,国内外均采用喷淋洗涤的方式处理。
喷淋洗涤过程中气液固三相流动特性研究是除尘研究的基础。近年来国内外学者对喷淋洗涤过程中的多相流动进行了详细的研究。Luca等对喷淋塔内的气液两相流场进行模拟研究,得出的模拟结果与实验数据吻合的较好,提出可运用数值模拟技术来优化结构设计[3]。孟宪禹对喷淋脱硫塔内流场的均匀性进行了研究,结果发现,喷淋液滴对流场的影响很大,不能忽略[4]。丁志江等对喷淋塔内部流场进行了三维数值模拟,分析了喷淋压力、进口气速、液滴分布等对气液流场的影响[5]。刘嘉宇则主要从液滴运动的角度探讨了如何增强液滴利用率,减少液滴夹带等问题[6]。
对于喷淋除尘性能的研究多数为实验研究,而数值模拟方面的研究较少。赵增慧结合喷淋塔应用实例,给出了喷淋覆盖率的选择、喷淋层与喷嘴布置的设计方法,对除尘效率的改善有明显效果[7]。宦宣州以典型湿法脱硫工艺中的吸收塔为研究对象,搭建了试验台,研究了塔内烟气流速、入口粉尘质量浓度等及吸收塔内主要部件布置形式对粉尘颗粒物脱除效果[8]。张立栋通过搭建多层喷雾洗涤塔实验台,研究了液气体积比、塔内气体平均流速、粉尘浓度、喷雾压力等操作参数对除尘效率的影响规律[9]。Amitava等利用两相流雾化喷嘴对高速喷雾下除尘器对粉尘颗粒的脱除效率进行实验研究,提出了粉尘浓度与除尘器效率的简易方程[10]。
目前造粒塔尾气粉尘脱除的相关研究鲜见报道,工业过程中仅根据运行经验和工程分析对相关参数做出调整。针对喷淋液滴捕集尿素等亲水性粉尘问题,研究采用欧拉-拉格朗日方法进行模拟,将气相视为连续相,液相视为离散相,固相体积分数极小,视为气相的一部分,随气相运动。在此过程中,为了实现液滴捕集灰尘的计算,还需要自定义粉尘捕集模型。本文研究喷淋洗涤过程中多相流动的流体力学特性以及除尘效率变化规律,为造粒塔粉尘洗涤回收设备的设计与优化提供依据。
2 数学模型本文采用欧拉方法求解气相与粉尘流动,采用拉格朗日方法对液滴进行追踪计算。
2.1 气相流场模型气相流场模型主要包括连续性方程、动量方程及能量方程,湍流模型采用标准k-ε模型。流体的连续性方程、动量方程、能量方程可用以下通用形式:
| $ \frac{{\partial \left( {\rho u\varphi } \right)}}{{\partial x}} + \frac{{\partial \left( {\rho \nu \varphi } \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w\varphi } \right)}}{{\partial z}} = \frac{\partial }{{\partial x}}\left( {{\Gamma _{\varphi ,t}}\frac{{\partial \varphi }}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{\Gamma _{\varphi ,t}}\frac{{\partial \varphi }}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{\Gamma _{\varphi ,t}}\frac{{\partial \varphi }}{{\partial z}}} \right) + {S_\varphi } $ | (1) |
式中:ρ是流体密度,t是时间,ϕ是通用变量,u、v、w分别是流体沿x、y、z方向的流速,Γϕ是广义扩散系数,Sϕ是广义源项。
标准k-ε方程:
| $ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{{x_j}}}} \right] + {G_k} - \rho \varepsilon $ | (2) |
| $ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{{x_j}}}} \right] + \frac{{{C_{1\varepsilon }}}}{K}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} $ | (3) |
式中,k是湍流脉动能,m2·s-2;ε是湍流脉动动能耗散率,kg·m-1·s-1。
2.2 液滴运动模型液滴的运动满足牛顿第二定律,因此,通过受力分析可以求解液滴的运动轨迹,液滴的平衡方程如下:
| $ \frac{{{\rm{d}}\overrightarrow {{v_{\rm{d}}}} }}{{{\rm{d}}t}} = \frac{{({\rho _{\rm{d}}} - {\rho _{\rm{g}}})\overrightarrow {\rm{g}} }}{{{\rho _{\rm{d}}}}} + \frac{{\overrightarrow {{v_{\rm{g}}}} - \overrightarrow {{v_{\rm{d}}}} }}{{{\tau _{\rm{r}}}}} $ | (4) |
式中,
| $ {\tau _r} = \frac{{{\rho _{\rm{d}}}d_{\rm{d}}^{\rm{2}}}}{{18{\mu _{\rm{g}}}}}\frac{{24}}{{{C_{\rm{d}}}Re}} $ | (5) |
| $ Re = \frac{{{{\rm{ \mathsf{ ρ} }}_{\text{g}}}{d_{_{\rm{d}}}}\left| {\overrightarrow {{v_{_{\rm{d}}}}} - \overrightarrow {{v_{\rm{g}}}} } \right|}}{{{{\rm{ \mathsf{ μ} }}_{\text{g}}}}} $ | (6) |
多数研究中液滴假设为球形,其曳力系数Cd, sphere如下[11]:
| $ {C_{{\rm{d,sphere}}}} = \left\{ {\begin{array}{*{20}{l}} \quad {\text{0}}{\text{.424}}& Re {\text{ > 1000}} \hfill \\ \frac{{{\text{24}}}}{{Re}}{\text{(1}} + \frac{{\text{1}}}{{\text{6}}}& R{e^{{\text{2/3}}}}{\text{)}} Re{\text{ < 1000}} \hfill \\ \end{array}} \right. $ | (7) |
实际中液滴在运动过程中会发生形变,形变程度y=0时液滴为球形,y=1时液滴为盘状。形变的大小对曳力系数的影响很大,为了更加精确地模拟液滴运动,本文进行如下改进[12]:
| $ {C_{\rm{d,sphere}}} = {C_{{\rm{d,sphere}}}}(1 + 2.632y) $ | (8) |
式中,液滴的形变程度在0~1之间变化,由下式计算得到[12]:
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} = \frac{{{C_{\rm{F}}}}}{{{C_{\rm{b}}}}}\frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{d}}}}}\frac{{{v_{{\rm{rel}}}}^2}}{{{r^2}}} - \frac{{{C_{\rm{k}}}\sigma }}{{{\rho _{\rm{d}}}{r^3}}}y - \frac{{{C_{\rm{l}}}{\mu _{\rm{d}}}}}{{{\rho _{\rm{d}}}{r^2}}}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} $ | (9) |
式中,CF、Cb、Ck、Cl均为常数,本文中分别取1/3、1/2、8、5。
液滴的碰撞在喷淋过程中不可避免,为了更加准确地模拟液滴的运动过程,目前计算液滴碰撞的算法可以分为确定性算法与随机性算法两类。本文采用O’Rourke碰撞随机性算法,通过计算碰撞概率与取随机数的方法判断液滴碰撞行为是否发生,克服了确定性算法计算量大的困难[13]。
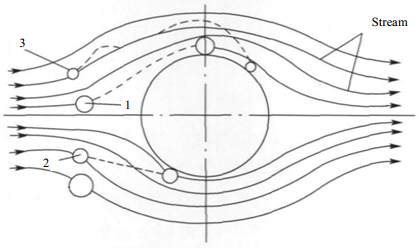
2.3 粉尘捕集模型当气流携带着固体颗粒(相对液滴的大小,颗粒的尺寸要小得多)接近液滴时,捕集分离涉及的机理包括:惯性碰撞、截留、布朗扩散等,如图 1所示。
|
图 1 除尘机理 Fig.1 Mechanism of particle removal processes studied 1. inertial impaction 2. direct interception 3. Brownian motion |
一般将捕集的颗粒数与掠过气体体积中最初的颗粒数之比定义为捕集效率E。理论上可以认为若固体颗粒最初位于液滴中心轴的某一距离y0内,则该固体颗粒可以碰到液滴上[14]。因此,单个液滴的捕集效率可以定义为以半径为y0的圆面积与液滴投影面积之比:
| $ E{\rm{ = }}\frac{{4\zeta y_0^2}}{{d_{\rm{d}}^{\rm{2}}}} $ | (10) |
式中,ζ为附着系数,根据相关文献取值为1。
单个球形液滴对固体颗粒的惯性捕集效率[15]:
| $ {\eta _{\rm{I}}}{\rm{ = }}{\left( {\frac{{{K_{\rm{I}}}}}{{{K_{\rm{I}}} + 0.35}}} \right)^2} $ | (11) |
式中,KI为惯性参数,由下式计算可得:
| $ {K_{\rm{I}}}{\rm{ = }}\frac{{{C_{\rm{c}}}{v_{{\rm{rel}}}}d_{\rm{p}}^{\rm{2}}{\rho _{\rm{p}}}}}{{18{\mu _{\rm{g}}}{d_{\rm{d}}}}} $ | (12) |
式中,Cc为肯宁汉滑移修正系数。
单个球形液滴对固体颗粒的拦截捕集效率:
| $ {\eta _{\rm{R}}}{\rm{ = }}{(1 + {K_{\rm{R}}})^2} - \frac{3}{2}(1 + {K_{\rm{R}}}) + \frac{1}{{2(1 + {K_{\rm{R}}})}} $ | (13) |
式中,KR为拦截参数,
单个球形液滴对固体颗粒的扩散捕集效率:
| $ {\eta _{\rm{D}}}{\rm{ = }}2\sqrt {\frac{2}{{Pe{\rm{ }}{d_{\rm{d}}}}}} $ | (14) |
式中,Pe为Peclet数。
将惯性捕集、拦截捕集、布朗扩散三种捕集机理结合起来,单个液滴的总捕集效率E的表达式为:
| $ E{\rm{ = }}1 - \left( {1 - {\eta _{\rm{I}}}} \right)\left( {1 - {\eta _{\rm{R}}}} \right)\left( {1 - {\eta _{\rm{D}}}} \right) $ | (15) |
结合单个液滴的捕集效率与液滴运动方程,可以精确计算液滴运动过程中的粉尘捕集情况,从而得到喷淋洗涤过程的除尘效率。
3 求解策略及模型验证(1) 计算条件 根据工业实际情况,气相采用密度为1.1 kg·m-3,动力黏度为1.79×10-5 Pa·s的空气,其中尿素粉尘密度为1335 kg·m-3。数值模拟时,气体入口速度设置为平均速度,即气体垂直于进口截面,且均匀分布。出口压力设置为表压0 Pa。壁面绝热,无滑移。
液相采用实心圆锥喷淋,液滴的密度为1000 kg·m-3,初始粒径满足Rosin-Rammler分布,粒径范围为0.6~1.4 mm,中位粒径为1 mm,均匀度指数为7.45,液滴的初始速度v0由液滴体积流量Q与喷嘴开孔面积S决定,喷淋密度P由液滴体积流量Q与塔体横截面积A决定。
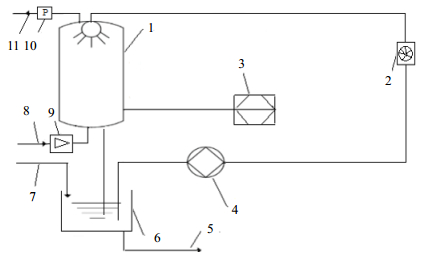
(2) 模型验证 图 2给出了喷淋洗涤实验装置图。整个装置由机玻璃塔、水箱、水泵、数据采集系统等组成。清水经水泵从水箱抽出,通过涡轮流量计计量,由喷头喷出后回流至水箱。
|
图 2 实验装置图 Fig.2 Schematic diagram of the experimental setup 1. plexiglass column 2. turbine flowmeter 3.PIV 4.water pump 5. water outlet 6. water tank 7. water inlet 8. gas inlet 9. vortex street flowmeter 10. pressure gage 11. gas outlet |
按照实验装置喷淋区域大小建立物理模型并划分网格。图 3显示了本次计算中所划分的网格,模拟对象为直径1 m,高2 m的圆筒状喷淋洗涤装置,喷嘴位于塔高1.5 m处。为使计算更加精确,对壁面与喷头附近网格进行了适当加密。在本文模拟工况下,网格在3.0×104以上时,流场情况与除尘效率基本不再发生变化。

|
图 3 网格示意图 Fig.3 Scheme of grids designed in the study |
以实验中的液滴流量、气体气速等作为模拟参数进行数值模拟。表 1为液滴喷淋时某一平面上实验所测液滴平均粒径与模拟值的对比,平均误差在10%以内,验证了空气与液滴运动模型的正确性。
|
|
表 1 喷头下游600 mm处液滴直径对比 Table 1 Comparison of droplet sizes at 600 mm below the nozzle |
在单个液滴的捕集效率确定之后,通过粉尘质量守恒方程可以估算喷淋区域液滴群的总体除尘效率[16, 17]。以dz高度的微元体为对象:
| $ - {Q_{\rm{g}}}{\rm{d}}c = (\frac{{{Q_{\rm{l}}}}}{{\pi d_{\rm{d}}^{\rm{3}}/6}}\frac{{{\rm{d}}z}}{{{v_{\rm{d}}}}})\frac{\pi }{4}d_{\rm{d}}^2{v_{{\rm{rel}}}}cE $ | (16) |
上式在有效喷淋区域积分即可得到总体除尘效率:
| $ \eta = 1 - \exp ( - \frac{{3{Q_{\rm{l}}}H{v_{{\rm{rel}}}}E}}{{2{Q_{\rm{g}}}{d_{\rm{d}}}{v_{\rm{d}}}}}) $ | (17) |
Lim等以该方法计算了反向喷射洗涤器中的除尘效率,Cheng利用该理论计算了水平管道内喷淋除尘效率,与实验值对比,发现理论值能较好地预测除尘效率[18]。因此本文对比了空塔气速为1 m·s-1、粉尘粒径为40 μm时,不同喷淋密度下除尘效率的理论值与模拟值。结果表明相对误差均不超过10%,验证了除尘模型的正确性,具体如表 2所示。
|
|
表 2 理论与数值模拟除尘效率对比 Table 2 Comparison of removal efficiency between theory and simulation |
本文首先对塔内气相流场与液滴运动情况进行分析,在此基础上利用液滴捕集粉尘机理,计算得到洗涤塔内尿素粉尘分布情况,进而探讨了空塔气速、喷淋密度、粉尘粒径等因素对除尘效率的影响。
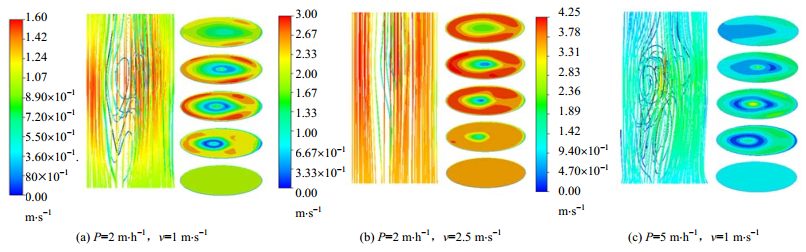
4.1 流体力学特性 4.1.1 气相流场图 4分别给出了不同工况下的气相流场。由图可知,由于喷嘴附近液滴浓度高、速度大,喷嘴周围空气受液滴影响而改变速度方向,从而在喷嘴附近形成漩涡。喷淋密度增大,空气的湍动强度越强烈。在一定程度上,湍动强度的增强将有利于粉尘的碰撞与捕集。此外,空塔气速v为1 m·s-1时,喷淋密度P从2 m·h-1增大到5 m·h-1,壁面速度从1.6 m·s-1增大到2.8 m·s-1左右,增大了近75%。这是由于空气在喷嘴附近受到较大阻力,导致其从壁面附近绕流,产生较为严重的壁流现象。
|
图 4 气体速度分布 Fig.4 Distribution of gas velocities |
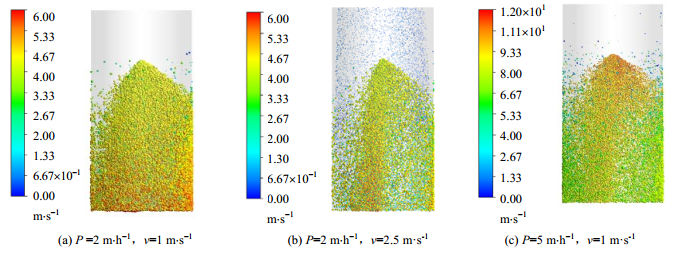
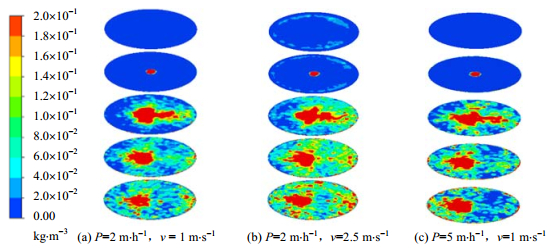
图 5、图 6为不同工况下液滴的速度分布和液滴浓度分布。由图可知,喷淋密度为2 m·h-1时,空塔气速v从1 m·s-1增加到2.5 m·s-1,液滴在入口截面的平均速度从4.60 m·s-1减小到3.81 m·s-1,出口截面液滴的夹带速率从0 g·s-1增加到1.07 g·s-1。由此可见,气速的提高一方面减小了粉尘在塔内停留的时间,另一方面降低了液滴的平均速度,使得液滴在横截面上的分布更加均匀,浓度增大。但是气速不宜过大,否则将使雾滴夹带现象更加严重,增加雾滴脱除系统负荷。空塔气速为1 m·s-1时,喷淋密度从2 m·h-1增大到5 m·h-1,液滴流量变为原来的2.5倍,液滴浓度与均匀程度有所增加。但同时液滴速度也随之增大,降低了液滴的停留时间,抑制了液滴浓度的进一步提升。
|
图 5 液滴速度分布 Fig.5 Distribution of droplet velocities |
|
图 6 液滴浓度分布 Fig.6 Distribution of droplets mass concentrations |
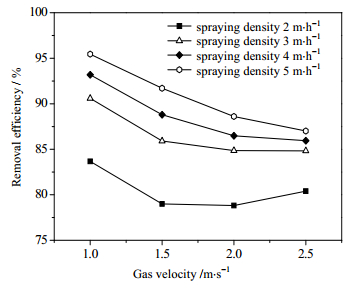
空塔气速对40 μm粉尘除尘效率的影响规律如图 7所示。由图可知,除尘效率随空塔气速的变化并不仅仅是单调递减的。喷淋密度为2 m·h-1时,气速超过2 m·s-1时除尘效率开始增加。喷淋密度增加,曲线拐点发生在气速2.5 m·s-1以后。分析原因,气速增加,空气中粉尘在塔内停留时间变短,粉尘与液滴接触不充分,除尘效果变差。但与此同时,当气速增大到一定程度时,液滴速度减小、浓度增大,除尘效率又有所上升。
|
图 7 除尘效率随空塔气速变化曲线 Fig.7 Particle removal efficiency as a function of gas velocity |
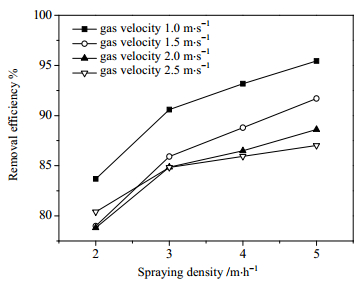
喷淋密度对40 μm粉尘除尘效率的影响规律如图 8所示。由图可知,在喷淋密度从2 m·h-1增大到5 m·h-1,除尘效率平均增加了13.05%。由此可见,喷淋密度增大,液滴流量提高,液滴与空气的接触面积增大,除尘效率增大。但同时液滴速度增大使液滴在塔内停留时间减少,除尘不够充分,导致除尘效率的增长速度有所减缓。
|
图 8 除尘效率随喷淋密度变化曲线 Fig.8 Particle removal efficiency as a function of spraying density |
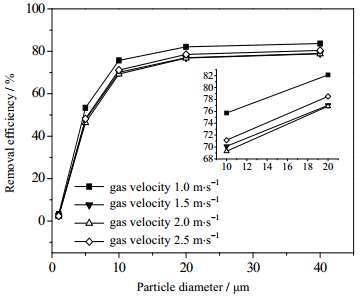
图 9是喷淋密度为2 m·h-1,空塔气速为1~2.5 m·h-1时,各粒径粉尘的除尘效率。由图可知,随气速增加,1 μm以内的粉尘去除效率在1%以内波动,最大为3.34%,基本不受气速的影响,5 μm以上的粉尘受气速影响较大,去除效率在7%以内波动。5 μm粉尘最大去除效率为53.36%,10 μm粉尘最大去除效率为75.71%,20 μm以上粉尘去除效率基本稳定,最大除尘效率在83.68%以上。
|
图 9 气速对各粒径粉尘去除效率影响 Fig.9 Effects of gas velocity on the removal of different size particles |
由此可见,无论气速如何改变,1 μm左右的粉尘脱除效率基本不变。当粉尘粒径小于10 μm时,除尘效率迅速恶化。粉尘粒径大于10 μm时,除尘效率受粒径的影响逐渐减小,在10%以内波动。分析原因,10 μm以下的粉尘所受惯性较小,在湍流的作用下随机运动,被液滴捕集的概率减小。大于10 μm的粉尘,由于惯性的作用,易撞击液滴而被脱除。
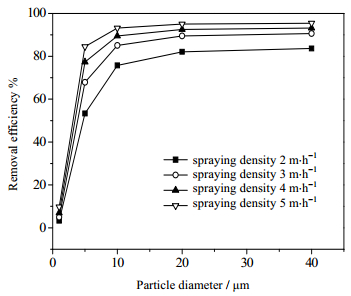
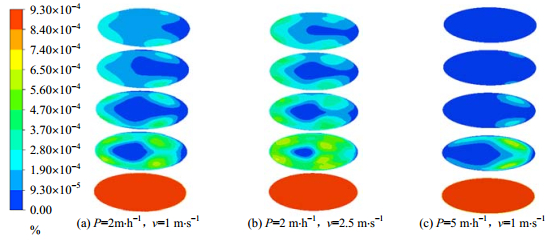
图 10是空塔气速为1 m·s-1,喷淋密度为2~5 m·h-1时,各粒径粉尘的除尘效率。由图可知,随喷淋密度的增大,1 μm粉尘的去除效率从3.34%增大到9.76%。10 μm粉尘在喷淋密度为4 m·h-1时,除尘效率达到了90%,20 μm粉尘在喷淋密度超过3 m·h-1时,除尘效率已经达到了90%,随喷淋密度进一步增大最终将达到100%。由此可见,喷淋密度对不同粒径粉尘去除效率的影响大于空塔气速的影响。结合图 11中40 μm粉尘分布云图分析原因,可以发现喷淋密度为2 m·h-1、空塔气速在1~2.5 m·s-1时,粉尘壁面逃逸现象始终存在,因此改变空塔气速不能有效提高除尘性能,而增大喷淋密度,液滴的速度、浓度增加,则有效地减少了粉尘逃逸。
|
图 10 喷淋密度对各粒径粉尘去除效率影响 Fig.10 Effects of spraying density on the removal of different size particles |
|
图 11 粉尘分布云图 Fig.11 Distribution of dust mass fractions |
本文采用实验与数值模拟相结合的方法对尿素粉尘的喷淋洗涤过程进行了研究,分析了流动特性与除尘性能,主要结论如下:
(1) 建立气液固三相流动模型,结合液滴捕集粉尘的理论研究,实现了液滴捕集粉尘过程的模拟,并且验证了模型的正确性。
(2) 通过数值模拟得出各相的速度分布、质量分布等,模拟结果显示,粉尘会随空气沿壁面附近逃逸,增大喷淋密度,改善效果明显。针对粒径10 μm以上的粉尘,喷淋洗涤方式除尘效率能达到95%以上。
符号说明:
| Cd | — 曳力系数 | ε | — 湍流脉动动能耗散率,kg·m-1·s-1 |
| E | — 单液滴的总捕集效率,% | ϕ | — 通用变量 |
| k | — 湍流脉动动能,m2·s-2 | ηI | — 惯性捕集效率,% |
| KI | — 惯性参数 | ηR | — 拦截捕集效率,% |
| KR | — 拦截参数 | ηD | — 扩散捕集效率,% |
| P | — 单位横截面上的体积流量m3·(h·m2)-1=m·h-1 | ρ | — 流体密度,kg·m-3 |
| Pe | — Peclet数 | Γϕ | — 广义扩散系数 |
| Sϕ | — 广义源项 | ζ | — 附着系数 |
| u | — 流体沿x方向流速,m·s-1 | 下标 | |
| v | — 流体沿y方向流速,m·s-1 | g | — 气体 |
| vrel | — 相对速度,m·s-1 | d | — 液滴 |
| w | — 流体沿z方向流速,m·s-1 |
| [1] | LI Si-yuan(李嗣源), HAN Liang(韩亮). Recovery process of dust from urea prilling tower(尿素造粒塔粉尘回收工艺)[J]. Chemical Industry and Engineering Progress(化工进展), 2009, 28(51): 243-244. |
| [2] | TANG Hai (唐海). Numerical studies of falling droplet (液滴降落过程的数值研究)[D]. Chengdu (成都): Sichuan University (四川大学), 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1212551 |
| [3] | Luca Inzoli F. Multiphase euler-lagrange CFD simulation applied to wet flue gas desulphurization technology[J]. International Journal of Multiphase Flow, 2009, 35(2): 185-194. DOI:10.1016/j.ijmultiphaseflow.2008.09.005. |
| [4] | MENG Xian-yu (孟宪禹). Numerical studies of falling droplet (湿法烟气脱硫系统喷淋塔流场均匀性研究)[D]. Beijing (北京): Beijing Jiaotong University (北京交通大学), 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2917322 |
| [5] | DING Zhi-jiang(丁志江), LIU Bi-tao(刘碧涛), XIAO Li-chun(肖立春). Numerical simulation on gas-liquid phase flow of flue gas purification spray scrubber for boron ferroalloy(硼铁合金烟气净化喷淋塔气液两相流数值模拟)[J]. Environmental Engineering(环境工程), 2015, 33(3): 82-87. |
| [6] | LIU Jia-yu (刘嘉宇). Numerical simulation on gas-liquid phase flow of flue gas purification spray scrubber for boron ferroalloy (WFGD过程中脱硫浆液液滴夹带特性的数值模拟研究)[D]. Nanjing (南京): Southeast University (东南大学), 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2921732 |
| [7] | ZHAO Zeng-hui(赵增慧), YU Li(于力), LIANG Cun-zhen(梁存珍). A study on improving the efficiency of wet flue gas desulphurization and dust removal.(提高湿法烟气脱硫喷淋塔脱硫和除尘效率的探讨)[J]. Journal of Beijing Institute of Petro-chemical Technology(北京石油化工学院学报), 2014, 22(3): 18-21. DOI:10.3969/j.issn.1008-2565.2014.03.005. |
| [8] | HUAN Xuan-zhou(宦宣州), HE Yu-dong(何育东), WANG Shao-liang(王少亮). Experiments about synergistic dust removal by WFGD system(湿法脱硫吸收塔协同除尘试验)[J]. Thermal Power Generation(热力发电), 2017, 46(7): 97-102. |
| [9] | ZHANG Li-dong(张立栋), LI Xiao-bo(李晓博), WANG Qing(王擎). Performance of dust removal in a multi-layer spray column scrubber(多层喷雾洗涤塔对粉尘颗粒的脱除特性)[J]. Chemical Industry and Engineering Progress(化工进展), 2017, 36(7): 2375-2380. |
| [10] | Amitava B, Manindra N B. Particulate scrubbing in high-velocity water sprays[J]. Journal of Chemical Engineering of Japan, 2004, 33(3): 514-518. |
| [11] | Buzzard J L, Nedderman R M. The drag coefficients of liquid droplets accelerating through air[J]. Chemical Engineering Science, 1967, 22(12): 1577-1586. DOI:10.1016/0009-2509(67)80196-9. |
| [12] | Liu A B, Mather D, Reitz R D. Modeling the effects of drop drag and breakup on fuel sprays[R]. Detroit: International Congress and Exposition, 1993. |
| [13] | O'Rourke PJ. Collective drop effects on vaporizing liquid sprays[R]. Los Alamos: Los Alamos National Lab, 1981. |
| [14] | LIU Xiao-yan (刘晓燕). Effect of droplets on aerosol particle collection efficiency in wet dust removal processes (湿式除尘中液滴对气溶胶粒子捕集效率的影响)[D]. Shanghai (上海): Donghua University (东华大学), 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2279445 |
| [15] | FAN Feng-xian(凡凤仙), YANG Lin-jun(杨林军), YUAN Zhu-lin(袁竹林). Removal and condensation growth of inhalable particles in spray scrubber(喷淋塔内可吸入颗粒物的脱除与凝结增长特性)[J]. CIESC Journal(化工学报), 2010, 61(10): 2708-2713. |
| [16] | Erank O E. Collection of Aerosols in a Venturi Scrubber[J]. Industrial & Engineering Chemistry, 1951, 43(6): 1358-1363. |
| [17] | Lim K S, Lee S H, Park H S. Prediction for particle removal efficiency of a reverse jet scrubber[J]. Journal of Aerosol Science, 2006, 37(12): 1826-1839. DOI:10.1016/j.jaerosci.2006.06.010. |
| [18] | Cheng L. Collection of Airborne Dust by Water Sprays[J]. Industrial & Engineering Chemistry Process Design & Development, 2002, 12(3): 221-225. |




