2. 西安交通大学 能源与动力工程学院, 陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
换热器作为在不同温度的流体间传递热能的装置,在石油、化工、能源等方面得到广泛应用,且随着工业的不断发展,对能源利用、开发、节约的要求也不断提高。因此对换热器结构、换热性能的研究和改善具有重要意义。近年来,根据热力学第二定律来评价传热过程的方法日趋广泛,但是基于熵产最小理论在换热器的设计中仍然存在很多的悖论[1]。过增元从热电类比出发,引入了一种表征热量“势能”的物理量“火积”和“火积耗散极值原理”,火积代表一种热量的传递能力[2, 3]。传热过程中热量是守恒的,而火积是不守恒的,不可逆的传热过程引起了火积的耗散,火积耗散值越大,则不可逆性越高[4]。目前火积理论已经在体点散热、航天器热控流体并联回路、平板太阳能集热器、区域供热网络和换热器的优化设计等领域得到了广泛的应用[5~8]。郭江峰等人基于总火积耗散数最小原理对板翅式换热器进行了优化设计,从而得出传热火积耗散数和阻力火积耗散数均减小的优化结构,提高了换热器的效能[9]。李梦寻等人以火积耗散最小为目标函数对管壳式换热器的结构进行了优化设计,采用遗传算法得出最优结构,提高了换热器性能[10]。郭春生等提出了一种新的换热器评价标准-火积耗散均匀性系数,并对不同结构的板式换热器的数值模拟结果进行了分析,得出性能最优的结构[11]。但是目前火积理论应用于螺旋折流板换热器性能分析的文章仍未见诸报端,且火积理论较少应用于实验结果的分析和对比中。
本文首次基于螺旋折流板的优化结构螺旋折面折流板换热器,采用PEC准则和火积耗散理论对改进后的折面螺旋折流板换热器与平面螺旋折流板换热器的实验数据进行了对比分析,得出火积耗散数的变化规律。这对火积理论应用于螺旋折流板换热器的进展具有重要意义。
2 火积耗散理论过增元等基于热电比拟的方法对比发现,在热力学系统中缺乏与电能对应的物理量,从而针对这一点,定义了火积概念,用以表征热量的势能[12]。对于一个稳态等容系统,假定其内能为U,温度为T。当其内能变化为dU时,火积的微分定义式为
| $dG\text{ }=\text{ }TdU$ | (1) |
对于该物体,假定温度和内能之间的关系是
| $U={{C}_{v}}MT$ | (2) |
Cv为定容比热,M为质量。从0 K到温度T积分,即可得火积为
| $G=\int_{0}^{T}{{{C}_{v}}MTdT=\frac{1}{2}UT}$ | (3) |
此状态量代表了热量的势能,表示物体传递热量的能力。
根据火积耗散理论,换热器中的火积耗散主要包括传热引起的火积耗散ET和黏性阻力引起的火积耗散。
有限温差传热引起的火积耗散(ET)即为换热器入口的火积减去出口的火积。
| $\begin{align} & {{E}_{T}}={{E}_{inlet}}-{{E}_{outlet}}=\left( \frac{1}{2}{{C}_{h}}T_{hi}^{2}+\frac{1}{2}{{C}_{c}}T_{ci}^{2} \right)-\left( \frac{1}{2}{{C}_{h}}T_{ho}^{2}+\frac{1}{2}{{C}_{c}}T_{co}^{2} \right)= \\ & \int{q\left( x \right)}\left( {{T}_{h}}\left( x \right)-{{T}_{c}}\left( x \right) \right)dx \\ \end{align}$ | (4) |
式中C表示热容流量,下标h和c分别表示热流体和冷流体。下标i和o分别表示进口和出口。q(x)为x处的热流量。Th(x)表示x处的热流体温度,Tc(x)为x处的冷流体温度。由克服黏性阻力引起的火积耗散为
| ${{E}_{\Delta P}}=\frac{{{m}_{h}}\Delta {{P}_{h}}}{{{\rho }_{h}}}\times \frac{{{T}_{ho}}-{{T}_{hi}}}{\ln \left( {{{T}_{ho}}}/{{{T}_{hi}}}\; \right)}+\frac{{{m}_{c}}\Delta {{P}_{c}}}{{{\rho }_{c}}}\times \frac{{{T}_{co}}-{{T}_{ci}}}{\ln \left( {{{T}_{co}}}/{{{T}_{ci}}}\; \right)}$ | (5) |
m为质量流量,为流体密度,为阻力压降。
总火积耗散为二者之和
| $E={{E}_{T}}+{{E}_{\Delta P}}$ | (6) |
应用文献[13] 中的火积耗散数对以上火积耗散进行无量纲化,被称为火积耗散数,Q为实际换热量。
| ${{E}^{*}}=\frac{E}{Q\left( {{T}_{hi}}-{{T}_{ci}} \right)}$ | (7) |
在稳态传热且无内热源的情况下,微元介质的火积不随时间而变化,等效温差即为按照边界热流占流过系统的总热流的份额进行加权平均的温度差。
| $\Delta T=\sum\nolimits_{in}{{{\left( \frac{Aq}{Q}T \right)}_{in}}-}\sum\nolimits_{out}{{{\left( \frac{Aq}{Q}T \right)}_{out}}}$ | (8) |
| $Q\Delta T={{\int_{V}{K\left( \nabla T \right)}}^{2}}dV$ | (9) |
式(9) 左侧是换热量和当量温差的乘积,右侧是火积耗散,由此分析火积耗散极值原理,即当换热量恒定, 火积耗散极小值对应最小当量传热温差,而当传热温差恒定时,火积耗散的极大值与最大传热量对应。
本文中由于传热温差的变化范围不超过总传热温差的2%,因此可认为是等传热温差的情况,符合火积耗散极大值原理。
3 螺旋折面折流板结构传统的螺旋平面折流板换热器是将折流板布置成近似的螺旋面,使换热器中的壳侧流体实现连续的柱塞状螺旋流动,有效地改善了传统弓形折流板壳侧压降大、容易形成流动死区的特点,与弓形折流板相比,螺旋折流板换热器具有提高单位压降下的传热系数、减少压降等显著优点。因此随着近年来螺旋折流板的广泛应用,改善螺旋折流板换热器的结构和性能具有重要意义[14~17]。王斯民等针对螺旋折流板换热器壳侧折流板间存在三角漏流区,首次提出了折面螺旋折流板的结构,用以改善该换热器的性能[18],图 1显示了螺旋平面折流板换热器和螺旋折面折流板换热器的管束结构。

|
图 1 管束结构示意图 Fig.1 Configurations of different tube bundles |
由图中可以看出,折面折流板使相邻两块平面折流板在搭接时形成的夹角被合拢,即快速通道三角区被有效的封闭。有效改善了螺旋平面折流板换热器在搭接处的三角漏流,使壳程的流动更加接近于标准的螺旋流,同时使流体向管束中心靠拢,增大了壳侧流体的流速和Re,且靠近管束中心区域的流体流速也相应增大,即有利于传热性能的提高,很好地改善了螺旋折流板换热器的性能。
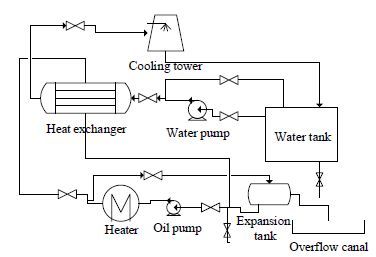
4 实验装置图 2为螺旋折流板换热器的实验流程示意图,实验系统主要包括油路循环、水路循环和测试系统。壳程介质为昆仑L-QC310导热油,管程介质为水,壳体材料使用20号钢,布管方式为正方形排列。循环用的水贮存于水箱中,通过水泵进入系统循环使用,经换热器加热后的水通过冷却塔进行冷却。导热油则通过电加热器加热到所需的温度后经油泵进入换热器。实验过程中保持管程和壳程流体进口温度和管程流量基本不变,改变壳程导热油的流量进行分组实验。实验试件包括50% 搭接的18°、27° 平面折流板与折面折流板换热器共四种结构。在对换热器试件的传热与阻力研究下,探索螺旋折流板的换热规律[19]。
|
图 2 换热实验流程图 Fig.2 Schematic diagram of the experimental setup |
螺旋折流板换热器的实验模型参数如表 1,改进结构与原始结构的实验模型除了折流板形式外,其他几何参数均相同。本实验管程水流量使用LWGY系列涡轮流量计测量水的体积流量,壳程导热油流量采用耐高温的DLWGY系列涡轮流量计测量体积流量。实验中,使用四线制Pt100铂电阻温度计来测量管程流体导热油和壳程流体水的进、出口的温度,采用压差变送器测量纯管束区压降,以及壳程流体带进出口区压降的总压降。试验数据采集系统采用多通道数据采集仪,实时监控测量数据及变化[20]。
| 表 1 实验装置的尺寸参数 Table 1 Size parameters of the experimental setup |
本文分别采用换热器综合评价因子PEC准则和火积耗散理论分析了螺旋折流板换热器的实验结果,验证火积理论应用于螺旋折流板换热器的适用性,同时对比螺旋平面折流板换热器和螺旋折面折流板换热器的综合性能。
换热器的有效度代表实际换热量与最大可能换热量之间的比值,有效反映了换热器的性能。
| $\varepsilon =\left\{ \begin{align} & \frac{{{T}_{hi}}-{{T}_{ho}}}{{{T}_{hi}}-{{T}_{co}}},{{\left( M{{C}_{p}} \right)}_{h}}<{{\left( M{{C}_{p}} \right)}_{c}} \\ & \frac{{{T}_{ci}}-{{T}_{co}}}{{{T}_{hi}}-{{T}_{cc}}},{{\left( M{{C}_{p}} \right)}_{h}}>{{\left( M{{C}_{p}} \right)}_{c}} \\ \end{align} \right.$ | (10) |
传热单元数
| $NTU=\frac{KA}{{{\left( M{{C}_{p}} \right)}_{min}}}$ | (11) |
换热系数的计算如下
| $K=\frac{Q}{A\Delta {{t}_{min}}}$ | (12) |
| $Nu=\frac{K{{D}_{e}}}{\lambda }$ | (13) |
阻力因子f
| $f=\frac{2\Delta P}{{{\rho }_{s}}{{u}^{2}}}\cdot \frac{B}{L}$ | (14) |
式中,Cp为定压比容,K为换热器综合换热系数,A为换热面积,De为导热管外径,l 为热导率,ΔP为壳程压降,B为螺旋折流板换热器螺距,u为壳层最小流通截面的流速,ρs为导热油密度,L为换热管管长。
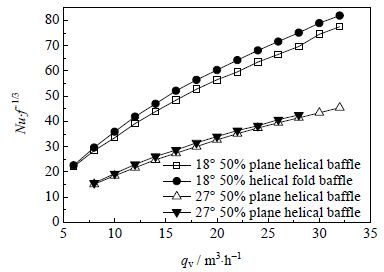
图 4为换热器综合评价指标PEC准则数Nu/f1/3随着壳程导热油流量变化的趋势,从图中可以看出,在保持管程流量和管壳程进出口温度基本不变的情况下,在相同的螺旋角和搭接度下,螺旋折面折流板换热器的综合性能和均要优于螺旋平面折流板换热器,说明折面螺旋折流板换热器有效阻挡了三角快速通道,壳侧流通面积减小,使壳侧的流体速度增大且向中心聚拢,导致壳侧流体的Re增大,同时靠近管束中心处的流速也增大,有效地提高了换热器的壳侧换热性能。且从图中可知,流量不变时,18° 螺旋角50% 搭接的螺旋折面折流板换热器的性能最佳,且明显优于27° 螺旋角的情况。这是由于在换热器壳体总长保持不变的情况下,螺旋角较小时,换热器内螺旋周期个数较多,流道变窄而流体流过的路径更长,流体在换热器中的湍动也会更加强烈,换热更充分,所以螺旋角较小时的综合评价性能更高。
|
图 4 PEC准则数随壳程流量的变化曲线 Fig.4 PEC criterion as a function of shell side flux |
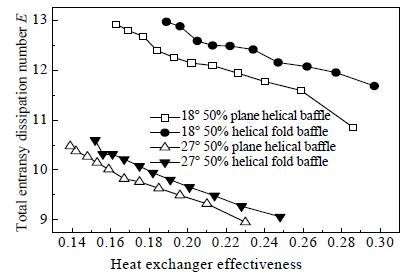
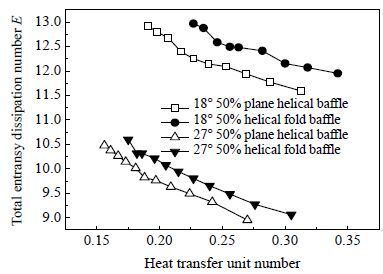
图 5和图 6是总火积耗散数和换热器有效度、传热单元数之间的关系,从图中可以看出,换热器的总火积耗散数均随着有效度和传热单元数的增加而逐渐减小,这说明火积耗散数的大小和换热器的传热能力是有关的。在有效度或传热单元数相同的情况下,18° 螺旋折流板换热器的总火积耗散数明显大于27° 螺旋折流板换热器,这是由于18° 螺旋角下螺旋周期长和流道长、湍动程度大引起的。实验试件的折流板数量根据螺旋角不同而不同。其中壳体长度均为2500 mm下,27° 螺旋角的折流板数量为42片,18° 螺旋角的折流板数量增加到了66片。且螺旋折面折流板换热器的性能也均优于螺旋平面折流板换热器,规律与图 4 PEC准则的结果相符,这是由于折面螺旋折流板有效封堵了搭接三角区的快速流道,使流体向壳体中心聚拢,同时由于壳侧流体的流通面积减小,流体流速增加,增强了换热。这与图 4的规律相符,证明了火积耗散理论的可靠性和对于螺旋折流板换热器的适用性。
|
图 5 总火积耗散数E随换热器有效度的变化曲线 Fig.5 Total entransy dissipation number as a function of heat exchanger effectiveness |
|
图 6 总火积耗散数E随换热器传热单元数的变化曲线 Fig.6 Total entransy dissipation number as a function of heat transfer unit number |
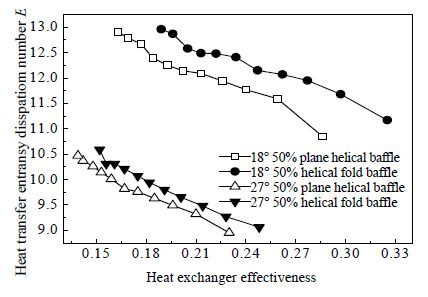
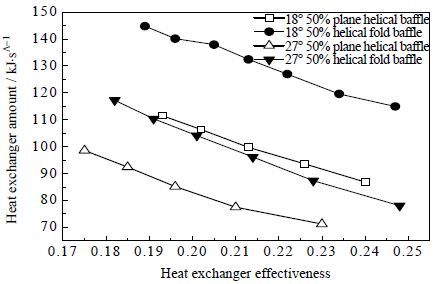
图 7和图 8分别为传热火积耗散数ET和实际换热量随换热器有效度的变化关系图,由图中可知,传热火积耗散和换热量均随着有效度的增加而减小,由实验数据可知,壳侧流速越大,有效度越小。传热火积耗散是由流体的不可逆换热过程引起的,即随着流速增大,湍动更加剧烈,换热量增大,同时传热火积耗散数也增大,符合火积耗散极大值理论。且有效度相同的情况下,依然是18° 螺旋折面折流板换热器的性能最优。与图 5对比可得,总火积耗散数E随有效度的变化趋势与传热火积耗散数ET随有效度的变化趋势基本相同。表 2为三组有效度不同情况下的各火积耗散数分布,由分析可知,总火积耗散数的值主要取决于传热火积耗散数的大小。传热火积耗散数的值约为阻力火积耗散数的千余倍。
|
图 7 传热火积耗散数ET随换热器有效度的变化曲线 Fig.7 Heat transfer entransy dissipation number as a function of heat exchanger effectiveness |
|
图 8 换热量随有效度的变化曲线 Fig.8 Heat exchanger amount as a function of heat exchanger effectiveness |
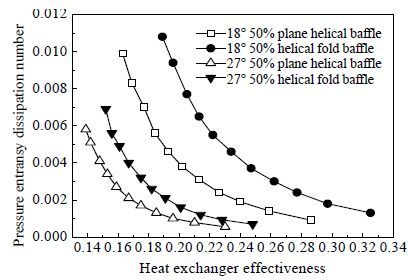
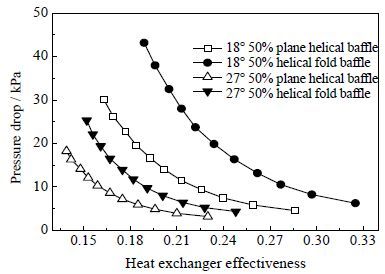
从图 9和图 10可以看出,阻力火积耗散数和总压降均随着换热器有效度的增加而逐渐减小,且随着有效度的增大,压力降的变化逐渐变缓,这是因为流量越大,即有效度较小时,压力降和阻力火积耗散数的增加越明显。有效度相同时,18° 50% 螺旋折面折流板换热器的压降和阻力火积耗散最大。这是由于螺旋折面折流板换热器的三角漏流被有效封堵,且螺旋角较小时,螺旋折流板换热器的板片数较多,螺距减小,壳侧流体流道变窄,同时流体的轴向速度减小,流体流动更接近于横向流,流体流经的管子数目增加,增加了流动的阻力,因此导致压降和阻力火积耗散同时增大。
|
图 9 压力火积耗散数随换热器有效度的变化曲线 Fig.9 Pressure entransy dissipation number as a function of heat exchanger effectiveness |
|
图 10 压力降随换热器有效度的变化曲线 Fig.10 Pressure drop as a function of heat exchanger effectiveness |
且由表 2可知,压力火积耗散数的大小远远小于传热火积耗散数的值,传热火积耗散数的值约为阻力火积耗散数的上千倍,说明由黏性阻力的不可逆性引起的阻力火积耗散火积耗散对于总火积耗散的影响是较小的。对于总火积耗散数的计算,阻力火积耗散数可以忽略不计。
| 表 2 有效度不同时火积耗散数的值 Table 2 Entransy dissipation number values under different effective degrees |
(1) 本文首次将火积理论应用于螺旋折流板换热器的性能分析中,且结果与综合评价标准PEC准则结果相符,说明运用火积耗散理论来进行换热器实验数据分析的适用性。
(2) 运用PEC准则和火积耗散极值原理分析螺旋平面折流板换热器和螺旋折面折流板换热器,结果表明螺旋折面折流板换热器的综合性能优于螺旋平面折流板换热器,即螺旋折面折流板换热器有效的改善了三角区漏流,提高了换热器的性能。同时在搭接度相同的情况下,18° 螺旋折流板换热器性能明显优于27° 螺旋角的情况,这是由于18° 螺旋折流板换热器内螺旋周期个数较多,流道变窄而流体流过的路径更长,流体在换热器中的湍动也会更加强烈。
(3) 传热火积耗散数的值要远远大于阻力火积耗散数,约为阻力火积耗散数的千余倍,在总火积耗散中占重要位置,说明传热损失在换热器的不可逆损失中是主要因素。
符号说明:
| A | — 换热面积,m2 | Q | — 换热量,J |
| B | — 螺旋折流板换热器螺距,m | q(x) | — x处的热流量,J×s |
| Cv | — 比定容热容,J×kg-1×K-1 | T | — 温度,K |
| De | — 换热管外径,m | u | — 壳侧最小流通截面的流速,m⋅s-1 |
| ET | — 传热火积耗散 | — 有效度 | |
| — 阻力火积耗散 | — 热导率,W⋅m-1×K-1 | ||
| E* | — 火积耗散数 | r | — 密度,kg⋅m-3 |
| G | — 火积,J×K | 下标 | |
| K | — 总换热系数,J×kg-1×K-1 | c | — 冷流体 |
| L | — 换热管管长,m | h | — 热流体 |
| M | — 动量,kg×m⋅s-1 | i, inlet | — 入口 |
| m | — 质量,kg | o, outlet | — 出口 |
| — 壳侧压降,kPa |
| [1] | Bejan A . Second Law analysis in heat transfer[J]. Energy , 1980, 5 (8/9) : 720-732 |
| [2] | LIU Xiong-bin(柳雄斌), GUO Zeng-yuan(过增元), MENG Ji-an(孟继安) . The entransy dissipation thermal resistance analysis in the heat exchanger(换热器中的火积耗散与热阻分析)[J]. Progress in Natural Science(自然科学进展) , 2008, 18 (10) : 1186-1190 |
| [3] | GUO Zeng-yuan(过增元) . The new thermal physical quantities(热学中的新物理量)[J]. Journal of Engineering Thermal Physics(工程热物理学报) , 2008, 29 (1) : 112-114 |
| [4] | HAN Guang-ze(韩光泽), GUO Zeng-yuan(过增元) . Thermal capacity loss mechanism and mathematical expression(导热能力损耗的机理及数学表述)[J]. Proceedings of the CSEE(中国电机工程学报) , 2007, 27 (17) : 98-102 |
| [5] | Chen Q, Liang X G, Guo Z Y . Entransy theory for the optimization of heat transfer-a review and update[J]. International Journal of Heat and Mass Transfer , 2013, 63 : 65-81 DOI:10.1016/j.ijheatmasstransfer.2013.03.019 |
| [6] | Andresen B, Gordon J M . Optimal paths for minimizing entropy generation in a common class of finite time heating and cooling processes[J]. Heat Fluid Flow , 1992, 13 (3) : 294-299 DOI:10.1016/0142-727X(92)90043-9 |
| [7] | LIU Xiao-hua(刘晓华), JIANG Yi(江亿), ZHANG Tao(张涛) . Match properties of heat exchange network in thermal-hygro environment building(建筑热湿环境营造过程中换热网络的匹配特性分析)[J]. HVAC(暖通空调) , 2011, 43 (3) : 29-37 |
| [8] | SONG Wei-ming(宋伟明), MENG Ji-an(孟继安), LIANG Xin-gang(梁新刚) . The principle of temperature field uniformity in one-dimensional heat exchanger(一维换热器中温差场均匀性原则的证明)[J]. CIESC Journal(化工学报) , 2008, 59 (10) : 2460-2464 |
| [9] | GUO J F, CHENG L, XU M T . Entransy dissipation number and its application to heat exchanger performance evaluation[J]. Chinese Scieuce Bulletin , 2009, 54 (15) : 2708-2713 |
| [10] | LI Meng-xun(李梦寻), GUO Jiang-feng(郭江峰), XU Ming-tian(许明田) . The application of the entransy dissipation theory in optimum design of the shell-and-tube heat exchanger(火积耗散理论在管壳式换热器优化设计中的应用)[J]. Journal of Engineering Thermal Physics(工程热物理学报) , 2010, 31 (7) : 1189-1192 |
| [11] | GUO Chun-sheng(郭春生), CHENG Lin(程林), DU Wen-jing(杜文静) . New heat exchanger evaluation standard-entransy dissipative uniformity coefficient(换热器新评价标准——火积耗散均匀性系数)[J]. Journal of Harbin Institute of Technology University(哈尔滨工业大学学报) , 2012, 44 (3) : 144-148 |
| [12] | GUO Zeng-yuan(过增元), LI Zhi-xin(李志信), ZHOU Sen-quan(周森泉) . The principle of uniformity of the temperature difference of heat exchanger(换热器中的温差场均匀性原则)[J]. China's Scientific E:Science and Technology(中国科学E辑:技术科学) , 1996, 26 (1) : 25-31 |
| [13] | GUO J F, XU M T, CHENG L . Principle of equipartition of entransy dissipation for heat exchanger design[J]. Science China Technological Sciences , 2010, 53 (5) : 1309-1314 DOI:10.1007/s11431-010-0128-y |
| [14] | DENG Bin(邓斌), WU Yang(吴扬), TAO Wen-quan(陶文铨) . The numerical simulation of the shell side flow of helical baffle heat exchanger(螺旋折流板换热器壳侧流动的数值模拟)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报, 11) , 2004, 38 : 1106-1109 |
| [15] | WEN Jian(文键), YANG Hui-zhu(杨辉著), DU Dong-dong(杜冬冬) . The numerical studies on the heat transfer reinforcement of the helical baffle heat exchanger(螺旋折流板换热器换热强化的数值研究)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报) , 2014, 48 (9) : 43-48 |
| [16] | WANG Qiu-wang(王秋旺) . The shell side heat transfer strengthen research progress of the helical baffle heat exchanger(螺旋折流板管壳式换热器壳程传热强化研究进展)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报) , 2004, 38 (9) : 882-886 |
| [17] | GAO Xiao-dong(高晓东), FENG Xiao(冯霄) . Experimental study of helical baffled heat exchanger with double helical structure(双螺旋结构螺旋折流板换热器试验研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2007, 21 (4) : 547-549 |
| [18] | WANG Si-min(王斯民), WEN Jian(文键) . Experiment on heat transfer performance of helical baffled heat exchanger without short circuit flow(无短路区新型螺旋折流板换热器换热性能的实验研究)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报) , 2012, 46 (9) : 12-15 |
| [19] | WEN Jian(文键), YANG Hui-zhu(杨辉著), XUE Yu-lan(薛玉兰) . Experimental investigation on heat transfer performance of heat exchanger with ladder-type fold baffles(旋梯式螺旋折流板换热器换热性能的实验研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29 (4) : 795-801 |
| [20] | CAO Chun-nuan (曹春暖). The numerical simulation research on the high efficiency helical folding baffle heat exchanger (高效螺旋折面板换热器数值模拟研究)[D]. Xi'an (西安):Xi'an Jiaotong University (西安交通大学), 2013. |




