2. 浙江大学 化学工程与生物工程学院, 浙江 杭州 310058
2. College of Chemical Engineering and Biological Engineering, Zhejiang University, Hangzhou 310058, China
沼气主要成分为CH4和CO2,其中CO2体积分数为15%~35%[1-2]。现有沼气主要用作民用炊事、生活照明、发电等。当沼气作为燃料直接燃烧时,将产生CO2。化学链技术是一种极具经济价值和发展前景的新型绿色清洁低碳燃烧技术,该技术通过使用某种化学介质,将一个特定的化学反应分解为若干次级化学反应,从而达到优化流程、便于分离的目的[3-5]。
对化学链反应系统开发的基础研究可分为3个层次,一是基本物理化学研究,包括载氧体种类、制备、理化性质及表征等;二是化学热力学的研究,主要包括过程方向和平衡;三是过程动力学的研究,包括反应动力学和传递过程动力学。
当前研究者们[6-7]所采用的载氧体主要分为金属氧化物和新型硫酸盐,其中最主要的是金属氧化物NiO和Fe2O3,而Fe2O3载氧体环境兼容性好,价格低廉,选用Fe2O3取代NiO载氧体已成为当前研究的热点。目前金属氧化物载氧体主要制备方法有[8]:机械混合法、冷冻成粒法、浸渍法、分散法、溶胶-凝胶法等,其中冷冻成粒法和浸渍法是制备载氧体最常用的方法。
化学链燃烧系统热力学平衡研究主要基于Aspen Plus软件进行,如沈来宏等[9]、诸林等[10]、Li等[11];李康等[12]基于吉布斯最小自由能原理,对铜基载氧体前驱体燃烧合成过程进行了平衡模拟计算。但应用热力学原理对化学链燃烧系统中发生的反应方向的判断进而获得有实际意义的操作条件则未见报道。
对化学链燃烧系统动力学的研究,主要基于三类物理模型[13-17];整体反应模型、收缩未反应芯模型和晶核成长模型,晶核成长模型是基于对载氧体颗粒的X射线衍射(X-ray diffraction,XRD)及扫描电子显微(scanning electron microscopy,SEM)等微观分析,认为在载氧体颗粒不同截面处,金属元素由于氧化或还原程度不同,存在不同的价态,提出相应的物理模型,并据此建立数学方程,但这类方程中含有晶粒成长模型参数,而该参数的取得目前仍基于经验,故该模型虽更接近真实情况,但相比于缩芯模型,其求解也更为复杂,而精度并无太大的提高,故当前仍以缩芯模型为主。
本研究采取固定床反应器进行载氧体燃烧反应的动力学研究,并对传统的缩芯模型进行了改进,分别推导获得动力学方程的微分式和积分式,测定了方程中各分过程模型参数,方程能较好地拟合实验数据,从而为工业反应器的设计提供理论基础。
2 实验原理及方法 2.1 实验药品本文所用药品如表 1所示:
|
|
表 1 各种实验所用原料一览表 Table 1 List of raw materials used in various experiments |
当前,对动力学方程测定大多采用热重分析仪(TGA)进行的。在TGA装置中,通过改变反应温度,分析载氧体的失重与反应时间的关系,进而获得反应活化能与指前因子。但由于装置的局限性,实验测定的动力学参数通常是表观反应速率参数,包含了扩散过程的影响。载氧体上氧化还原过程极为复杂,对于各分过程性质则无法获得。本工作采用固定床反应器进行铁基载氧体燃烧还原反应动力学的研究。
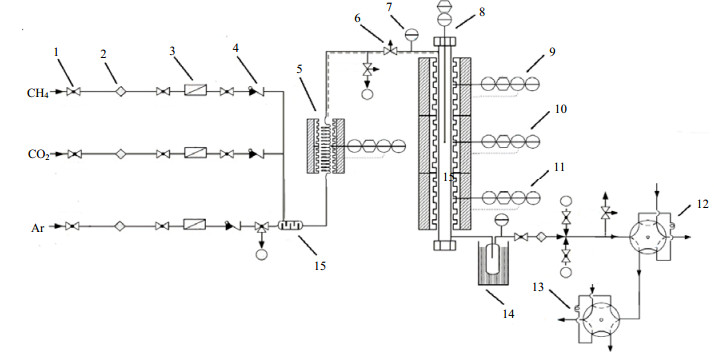
2.2.1 反应动力学实验测定工艺流程实验流程如图 1所示。
|
图 1 气固相非催化反应动力学研究工艺流程图 Fig.1 Flow chart of gas-solid non-catalytic reaction kinetics experiment 1. two-way valve 2. filtrator 3. mass flowmeter 4. non-return valve 5. preheater 6. switch valve 7. pressure meter 8. thermocouple 9, 10, 11. reactor temperature control instrument 13. six-way valve 14. ice-water bath 12, 15. mixer |
称取一定量、一定粒径的载氧体,装填进反应管中,反应管安装完毕,通Ar一定时间,置换管路中空气,置换完毕,关闭反应器进口、出口阀门。切换成CH4+CO2混合模拟沼气,同时打开旁路系统,至规定时间后,在系统出口处通过皂膜流量计测定气体流量及用色谱测定气体组成。
将预热器及反应器加热到指定温度,关闭旁路系统,同时打开反应器进口、出口阀门,至一定时间,测定出口流量及气体组成。原料气与产物气成分可通过色谱在线分析。
2.2.2 宏观反应速率RCH4的获得
|
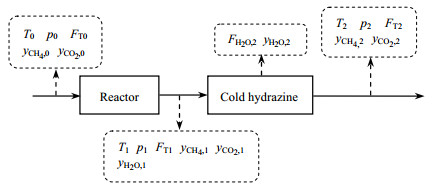
图 2 工艺流程简化示意图 Fig.2 Simplified schematic diagram of process parameters |
图 2中各符号含义为:下标0、1、2分别为反应器入口、反应器出口、冷肼即反应系统出口位置,T为温度,K;p为压力,Pa;F为摩尔流量,mol⋅s−1;y表示摩尔分数。物料衡算所需的独立变量包括反应器进口端的组成yCH4, 0、yCO2, 0,反应系统出口端的组成yCH4, 2、yCO2, 2,以及反应器进口端气体体积流量qV, T0。反应器进口端的摩尔流量FT0、出口端的组成yCH4, 1、反应系统出口的摩尔流量FT2可由所选独立变量推导求得。
| $ {F_{{\text{T0}}}}{\text{ = }}\frac{{{p_0}{q_V}{{_, }_{{\text{T0}}}}}}{{R{T_0}}} $ | (1) |
| $ {F_{{\text{T2}}}}{\text{ = }}{F_{{\text{T0}}}} $ | (2) |
| $ {y_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, 1}}}}{\text{ = }}\frac{{{y_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, 2}}}}}}{{{\text{2}}{y_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, 0}}}}{\text{ + }}{y_{{\text{C}}{{\text{O}}_{\text{2}}}{\text{, 2}}}} - {y_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, 2}}}}}} $ | (3) |
反应器中平均反应速率可由下式计算:
| $ {R}_{{\text{CH}}_{\text{4}}\text{, s}}=\frac{{F}_{\text{T0}}{y}_{{\text{CH}}_{\text{4}}\text{, }0}-{F}_{\text{T2}}{y}_{{\text{CH}}_{\text{4}}{,}\text{2}}}{{S}_{\text{T}}}\text{=}\frac{{F}_{\text{T0}}\left({y}_{{\text{CH}}_{\text{4}}\text{, }0}-{y}_{{\text{CH}}_{\text{4}}{,}\text{2}}\right)}{{S}_{\text{T}}} $ | (4) |
| $ {R_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, s}}}} = {{{R_{{\text{C}}{{\text{H}}_{\text{4}}}}}} / a} $ | (5) |
式中:a为载氧体颗粒的比表面积,m2⋅m−3;RCH4, s为单位时间单位载氧体外表面积CH4反应掉的物质的量,mol⋅m−2⋅s−1;宏观反应速率RCH4定义为单位时间单位载氧体体积CH4反应掉的物质的量,mol⋅m−3⋅s−1;ST为整个床层全部载氧体颗粒外表面积,m2。
此时的RCH4, s值相当于在平均摩尔分率(yCH4, 0+yCH4, 1)/2时的表观反应速率。
ST的计算:
| $ {S_{\text{T}}} = \pi d_{\text{p}}^2\frac{{{m_{\text{T}}}}}{{{\rho _{\text{P}}}{V_{\text{P}}}}}{\text{ = }}\frac{{6{m_{\text{T}}}}}{{{\rho _{\text{P}}}{d_{\text{p}}}}} $ | (6) |
式中:dp为单个载氧体平均粒径,m;VP为单个载氧体平均体积,m3;mT为反应器中一次装载载氧体总质量,kg;ρP为载氧体颗粒密度,kg⋅m−3。
载氧体密度ρp的确定:随机取粒径为0.3~0.9 mm的一定数目载氧体称重,根据密度定义即可得到密度值,重复3次,取平均值得载氧体颗粒密度ρP为1 355.764 3 kg⋅m−3。
2.3 载氧体的沼气化学链燃烧还原反应动力学模型的建立沼气化学链燃烧反应为气固相非催化反应,为更好地拟合实验数据,分别采用了2种物理模型,一是整体反应模型,二是未反应收缩芯模型。整体反应模型中反应总级数分别设定为一级和二级,考虑到载氧体中有γ-Al2O3存在,同时反应产物中有固体生成,可以认为载氧体颗粒在反应前后粒径不变。
以下各动力学方程的推导建立在下列反应的基础上。
| $ {\text{C}}{{\text{H}}_{\text{4}}}\left( {\text{g}} \right){\text{ + }}\frac{4}{3}{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( {\text{s}} \right){\text{ = }}\frac{8}{3}{\text{Fe}}\left( {\text{s}} \right){\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O}}\left( {\text{g}} \right) + {\text{CO}}{_2}\left( {\text{g}} \right) $ | (r1) |
式中:g为气体;s为固体。
2.3.1 颗粒粒径不变时缩芯模型的宏观反应速率方程(1) 各分过程速率方程
CH4通过气膜的扩散(外扩散过程):
| $ - \frac{1}{{{S_{\text{p}}}}}\frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}t}}{\text{ = }}{k_{\text{g}}}\left( {{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{g}}}} - {c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{s}}}}} \right) $ | (7) |
式中:cCH4, g、cCH4, s分别为CH4在气相主体中、载氧体外表面上的浓度,mol⋅m−3;kg为传质分系数,m⋅s−1;nCH4为气体中CH4的物质的量,mol;Sp为颗粒外表面积,m2;t为时间,s。等式左边是扩散通量,为单位时间、单位颗粒外表面CH4的扩散的物质的量。
通过灰层CH4的扩散(内扩散过程):
| $ - \frac{1}{{{S_r}}}\frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}t}}{\text{ = }}{D_{\text{e}}}{\left( {\frac{{{\text{d}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}r}}} \right)_r} $ | (8) |
式中:cCH4为灰层中CH4的浓度,mol⋅m−3;De为灰层有效扩散系数,m2⋅s−1;Sr为半径为r(rc < r < rP)处灰层的外表面积,是个变数,m2;r、rc、rP分别为灰层、未反应芯、颗粒半径,m。
表面反应速率:假设反应主要在未反应芯外表面处进行,反应为一级,则:
| $ - \frac{1}{{{S_{\text{c}}}}}\frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_4}}}}}{{{\text{d}}t}}{\text{ = }}{k_{\text{s}}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{c}}}} $ | (9) |
式中:Sc为未反应核(核芯处的表面积,反应过程不断地变化着)表面积,m2;ks为以颗粒未反应芯外表面积计的反应速率常数,m⋅s−1;cCH4, c为CH4在未反应芯表面处浓度,mol⋅m−3。式(9)的左边为单位时间、单位颗粒未反应芯外表面反应量。
(2) 宏观反应速率方程的微分表达式
cCH4, s、cCH4, c是未知量,难以直接测量,应消去。
式(7)可写成:
| $ - \frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}t}}{\text{ = 4}}\pi r_{\text{P}}^2{k_{\text{g}}}\left( {{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}} - {c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, s}}}}} \right) $ | (10) |
式(8)可变通如下:对灰层内扩散的CH4作物料衡算,由于灰层中无化学反应,故
| $ {\text{4}}\pi {\left( {r{\text{ + d}}r} \right)^{\text{2}}}{D_{\text{e}}}{\left( {\frac{{{\text{d}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}r}}} \right)_{{\text{r + dr}}}}{\text{ = 4}}\pi {r^{\text{2}}}{D_{\text{e}}}{\left( {\frac{{{\text{d}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}r}}} \right)_r} $ | (11) |
化简:
| $ \frac{{{{\text{d}}^{\text{2}}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}{r^{\text{2}}}}}{\text{ + }}\frac{2}{r}\frac{{{\text{d}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}r}}{\text{ = 0}} $ | (12) |
边界条件:
| $ \left\{ \begin{gathered} r{\text{ = }}{r_{\text{P}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }}{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{s}}}} \\ r{\text{ = }}{r_{\text{c}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_{{\text{C}}{{\text{H}}_4}}}{\text{ = }}{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{c}}}} \\ \end{gathered} \right. $ | (13) |
最后:
| $ - \frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_4}}}}}{{{\text{d}}t}}{\text{ = 4}}\pi r_{\text{P}}^2\frac{{{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{s}}}} - {c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{c}}}}}}{{\left( {{r_{\text{P}}} - {r_{\text{c}}}} \right)\frac{{{r_{\text{P}}}}}{{{D_{\text{e}}}{r_{\text{c}}}}}}} $ | (14) |
式(9)可变通为
| $ - \frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{{\text{d}}t}}{\text{ = 4}}\pi r_{\text{P}}^2\frac{{{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{c}}}}}}{{{{r_{\text{P}}^2} / {\left( {r_{\text{c}}^2{k_{\text{s}}}} \right)}}}} $ | (15) |
结合式(10)、(14)和(15),得
| $ - \frac{{{\text{d}}{n_{{\text{C}}{{\text{H}}_4}}}}}{{{\text{d}}t}}{\text{ = }} - \frac{3}{4}\frac{{{\text{d}}{n_{{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}}}}}}{{{\text{d}}t}}{\text{ = 4}}\pi r_{\text{P}}^2\frac{{{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{g}}}}}}{{{{{1 / {{k_{\text{g}}}}}{\text{ + }}{{\left( {{r_{\text{P}}} - {r_{\text{c}}}} \right){r_{\text{P}}}} / {\left( {{D_{\text{e}}}{r_{\text{c}}}} \right)}}{\text{ + }}r_{\text{P}}^2} / {\left( {r_{\text{c}}^2{k_{\text{s}}}} \right)}}}} $ | (16) |
式中:nFe2O3为载氧体Fe2O3的物质的量,mol。式(16)即为宏观反应速率方程的微分表达式。
(3) 宏观反应速率方程的积分表达式
rc与反应时间t的关系:
| $ {\text{d}}{n_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}{\text{ = }}4\pi {\rho _{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}r_{\text{c}}^2{\text{d}}{r_{\text{c}}} $ | (17) |
式中:ρFe2O3为Fe2O3的单位体积物质的量,mol⋅m−3。
代入式(7)得:
| $ -\frac{\text{d}{r}_{\text{c}}}{\text{d}t}\text{=}\frac{4}{3{\rho }_{{\text{Fe}}_{2}{\text{O}}_{3}}}\frac{{c}_{{\text{CH}}_{\text{4}}{,}\text{g}}}{{r}_{\text{c}}^{2}/\left({r}_{\text{P}}^{2}{k}_{\text{g}}\right)\text{+}\left({r}_{\text{P}}-{r}_{\text{c}}\right){r}_{\text{c}}/\left({D}_{\text{e}}{r}_{\text{P}}\right)\text{+1}/{k}_{\text{s}}} $ | (18) |
载氧体中Fe2O3转化率xFe2O3与rC的关系为
| $ {x_{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}{\text{ = 1}} - {\left( {\frac{{{r_{\text{c}}}}}{{{r_{\text{P}}}}}} \right)^3} $ | (19) |
积分式(18),最后得
| $ t{\text{ = }}\frac{{3{\rho _{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}}{{{\text{4}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{g}}}}}}\left\{ {\frac{{{r_{\text{P}}}}}{{3{k_{\text{g}}}}}{x_{_{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}{\text{ + }}\frac{{r_{\text{P}}^2}}{{6{D_{\text{e}}}}}\left[ {1 - 3{{\left( {1 - {x_{_{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}} \right)}^{{2 / 3}}}{\text{ + }}2\left( {1 - {x_{_{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}} \right)} \right]{\text{ + }}\frac{{{r_{\text{P}}}}}{{{k_{\text{s}}}}}\left[ {1 - {{\left( {1 - {x_{_{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}} \right)}^{{1 / 3}}}} \right]} \right\} $ | (20) |
式(20)为宏观反应速率方程的积分表达式。由上式可知,CH4分子总反应时间t由3部分组成,一是经过气膜传递时间tG,二是通过灰层扩散所需时间tD,三是反应时间tR。
2.3.2 颗粒粒径不变时整体反应模型的宏观反应速率方程外扩散过程与载氧体反应过程是串联进行的,随着反应的进行,载氧体中Fe2O3的含量不断减少,颗粒反应速率不断减小,现设整个过程为拟稳定过程,即认为在任一时刻,CH4分子的扩散速率NCH4等于载氧体颗粒反应速率−rCH4等于表观反应速率RCH4。分2种情况讨论:
(1) 设反应为二级
扩散速率:
| $ {N_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }}{k_{\text{g}}}\left( {{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{g}}}} - {c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{s}}}}} \right) $ | (21) |
反应速率:
| $ -{r}_{{\text{CH}}_{\text{4}}}\text{=}{k}_{\text{2}}{c}_{{\text{CH}}_{\text{4}}\text{, s}}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\text{=}{k}_{\text{2}}{c}_{{\text{CH}}_{\text{4}}, \text{s}}{c}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}}\left(1-{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\right) $ | (22) |
式中:NCH4为单位时间通过载氧体外表面积的CH4扩散的物质的量,mol⋅m−2⋅s−1;−rCH4为单位时间单位载氧体体积反应的物质的量,mol⋅m−3⋅s−1;cFe2O3、cFe2O3, 0分别为单位体积载氧体所含的Fe2O3和初始Fe2O3的物质的量浓度,mol⋅m−3;k2为二级反应速率常数,m3⋅mol−1⋅s−1。
根据拟稳定假设,则
| $ {R_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }}{N_{{\text{C}}{{\text{H}}_{\text{4}}}}}a{\text{ = }} - {r_{{\text{C}}{{\text{H}}_{\text{4}}}}} $ | (23) |
最后:
| $ {R}_{{\text{CH}}_{\text{4}}}\text{=}-{r}_{{\text{CH}}_{\text{4}}}\text{=}\frac{{c}_{{\text{CH}}_{\text{4}}, \text{g}}}{\frac{1}{{k}_{\text{g}}a}\text{+}\frac{1}{{k}_{2}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}\left(1-{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\right)}} $ | (24) |
该式为微分式。
| $ -{r}_{{\text{CH}}_{\text{4}}}\text{=}\frac{3}{4}\left(-{r}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\right)\text{=}-\frac{3}{4}\frac{\text{d}{n}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{{V}_{\text{p}}\text{d}t}\text{=}\frac{3}{4}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}\frac{\text{d}{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{\text{d}t} $ | (25) |
式中:-rFe2O3为载氧体中Fe2O3的反应速率,mol⋅m−3⋅s−1。
则
| $ \frac{\text{3}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{4}\frac{\text{d}{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{\text{d}t}\text{=}\frac{{c}_{{\text{CH}}_{\text{4}}, \text{g}}}{\frac{1}{{k}_{\text{g}}a}\text{+}\frac{1}{{k}_{2}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}\left(1-{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\right)}} $ | (26) |
积分,最后得积分式:
| $ t\text{=}\frac{\text{3}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{\text{4}{c}_{{\text{CH}}_{\text{4}}{,}\text{g}}}\left(\frac{1}{{k}_{\text{g}}a}{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\text{+}\frac{1}{{k}_{2}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{\mathrm{ln}}\;\frac{1}{1-{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}\right) $ | (27) |
(2) 设反应为一级
反应速率:
| $ - {r_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }}{k_{\text{v}}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{s}}}} $ | (28) |
式中:kv为以单位载氧体体积计的反应速率常数,s−1。
根据拟稳定假设,则
| $ {R_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }} - {r_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }}\frac{{{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{g}}}}}}{{{1 / {\left( {{k_{\text{g}}}a} \right)}}{\text{ + }}{1 / {{k_{\text{v}}}}}}} $ | (29) |
则
| $ \frac{\text{3}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{4}\frac{\text{d}{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{\text{d}t}\text{=}\frac{{c}_{{\text{CH}}_{\text{4}}, \text{g}}}{1/\left({k}_{\text{g}}a\right)\text{+}1/{k}_{\text{v}}} $ | (30) |
最后,得积分式:
| $ t\text{=}\frac{\text{3}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{\text{4}{c}_{{\text{CH}}_{\text{4}}{}_{{,}}{\text{g}}}}\left(\frac{1}{{k}_{\text{g}}a}\text{+}\frac{1}{{k}_{\text{v}}}\right){x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}} $ | (31) |
Fe2O3与CH4之间的反应,其固体产物除了可能为Fe外,更有可能是FeO、Fe3O4或两者的复合物[19],当固体产物不同,反应计量系数值也不同,为此引入虚拟固体产物概念,该虚拟固体产物以分子式Fe2O3⋅nFeO表示,Fe2O3与CH4之间的反应可写成如下集总虚拟式:
| $ {\text{C}}{{\text{H}}_{\text{4}}}\left( {\text{g}} \right){\text{ + }}\frac{{4\left( {n{\text{ + }}2} \right)}}{n}{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( {\text{s}} \right){\text{ = }}\frac{8}{n}{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}} \cdot n{\text{FeO}}\left( {\text{s}} \right){\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O}}\left( {\text{g}} \right){\text{ + C}}{{\text{O}}_{\text{2}}}\left( {\text{g}} \right) $ | (r2) |
则上述动力学方程(20)、(27)、(31)分别修正为
| $ t{\text{ = }}\frac{n}{{4\left( {n{\text{ + 2}}} \right)}}\frac{{{\rho _{{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}}}}}}{{{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}}}\left\{ {\frac{{{r_{\text{P}}}}}{{3{k_{\text{g}}}}}{x_{{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}}}}{\text{ + }}\frac{{r_{\text{P}}^2}}{{6{D_{\text{e}}}}}\left[ {1 - 3{{\left( {1 - {x_{{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}}}}} \right)}^{{2 / 3}}}{\text{ + }}2\left( {1 - {x_{{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}}}}} \right)} \right]{\text{ + }}\frac{{{r_{\text{P}}}}}{{{k_{\text{s}}}}}\left[ {1 - {{\left( {1 - {x_{{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}}}}} \right)}^{{1 / 3}}}} \right]} \right\} $ | (32) |
| $ t\text{=}\frac{n}{4\left(n\text{+2}\right)}\frac{{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{{c}_{{\text{CH}}_{\text{4}}\text{, g}}}\left(\frac{1}{{k}_{\text{g}}a}{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\text{+}\frac{1}{{k}_{2}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{\mathrm{ln}}\;\frac{1}{1-{x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}\right) $ | (33) |
| $ t\text{=}\frac{n}{4\left(n\text{+2}\right)}\frac{{c}_{{\text{Fe}}_{2}{\text{O}}_{3}{,}0}}{{c}_{{\text{CH}}_{\text{4}}\text{, g}}}\left(\frac{1}{{k}_{\text{g}}a}\text{+}\frac{1}{{k}_{\text{v}}}\right){x}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}} $ | (34) |
式中:n为虚拟组成比,需要根据实验数据进行计算获得。
3 结果与讨论 3.1 铁基载氧体制备配制一定量的硫酸亚铁饱和溶液,将研磨好的0.3~0.9 mm的三氧化二铝倒入硫酸亚铁饱和溶液中浸渍1 h,过滤,将浸渍完的样品放入120 ℃的烘箱中干燥,再将干燥后的样品转移到坩埚中,在马弗炉中进行程序升温至800 ℃煅烧至无烟,反复浸渍5次,Fe2O3质量分数可以达到48.14%,最后再将煅烧好的样品过筛(0.3~0.9mm)获得最终载氧体,以进行动力学表征。Fe2O3含量分析采取国标GB/T 2463-2008。
3.2 沼气化学链燃烧热力学计算及反应温度选择参与化学链燃烧反应的各组分标准生成焓ΔHfθ与标准熵Sθ如表 2所示。
|
|
表 2 各组分生成热与生成熵数据一览表 Table 2 Data for formation heat and entropy of each component |
以Fe2O3为载氧体,进行沼气的化学链燃烧反应,可能的反应有:
| $ 12{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + C}}{{\text{H}}_{\text{4}}}{\text{ = }}8{\text{F}}{{\text{e}}_{\text{3}}}{{\text{O}}_{\text{4}}}{\text{ + C}}{{\text{O}}_{\text{2}}}{\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O }} $ | (r3) |
| $ {\text{4F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + C}}{{\text{H}}_{\text{4}}}{\text{ = }}8{\text{FeO + C}}{{\text{O}}_{\text{2}}}{\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O}} $ | (r4) |
| $ {\text{4F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + 3C}}{{\text{H}}_{\text{4}}}{\text{ = }}8{\text{Fe + 3C}}{{\text{O}}_{\text{2}}}{\text{ + 6}}{{\text{H}}_{\text{2}}}{\text{O}} $ | (r5) |
以反应(r3)为例,温度为298 K,标准反应焓变和标准反应熵变分别为
| $ \Delta H_{298}^\theta {\text{ = }}8 \times \left( { - {1\;}118} \right){\text{ + }}\left( { - 393} \right){\text{ + }}2 \times \left( { - 242} \right){\text{ + }}74.8 - 12 \times \left( { - 824} \right){\text{ = }}{141.8\;}\;{\rm{kJ}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}} $ | (35) |
| $ \Delta S_{298}^\theta {\text{ = }}8 \times \left( {{\text{146}}} \right){\text{ + 214 + }}2 \times 189 - 186.2 - 12 \times 87.4{\text{ = 52}}{{\text{5}}_{}}\;{\rm{J}} \cdot {{\rm{k}}^{ - 1}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}} $ | (36) |
当反应温度为T时,标准反应的焓变ΔHTθ和熵变ΔSTθ随温度变化很小,可用ΔH298θ和ΔS298θ代替ΔHTθ和ΔSTθ,故反应自由能ΔGTθ:
| $ \Delta G_T^\theta {\text{ = }}\Delta H_{298}^\theta - T\Delta S_{298}^\theta \leqslant 0 $ | (37) |
对反应(r3),反应温度记为Tr3,则:
| $ {T_{{\text{r3}}}} \geqslant \frac{{\Delta H_{298}^\theta }}{{\Delta S_{298}^\theta }}{\text{ = }}\frac{{141.8 \times {{10}^3}}}{{525}}{\text{ = }}{270.1_{}}\;{\text{K}}_{ } $ | (38) |
由上述数据可知,该反应为吸热反应;同时由反应温度数值可知,该反应在室温下即可发生。同理可分别计算按反应(r4)、反应(r5)进行时所需要的温度Tr4、Tr5:
| $ {T_{{\text{r4}}}} \geqslant \frac{{\Delta H_{298}^\theta }}{{\Delta S_{298}^\theta }}{\text{ = 586}}{\text{.}}{{\text{1}}_{}}\;{\text{K}} $ | (39) |
| $ {T_{{\text{r5}}}} \geqslant \frac{{\Delta H_{298}^\theta }}{{\Delta S_{298}^\theta }}{\text{ = 818}}{\text{.8}}{{\text{2}}_{}}\;{\text{K}} $ | (40) |
由热力学数据计算可知,Fe2O3与CH4在270.1 K下即可进行反应生成Fe3O4,但由实验知,实际反应须在600 ℃以上才能观测到具体反应的发生,这体现了反应热力学与动力学之间的差异性。热力学计算温度仅仅预测了反应必须达到该温度时才有可能发生,但由于其反应动力学速率极其缓慢,实际反应温度要远远超过热力学计算温度,综合热力学、动力学以及能量有效利用等多方面因素,本实验将载氧体还原反应温度选择在660~740 ℃。
3.3 外扩散消除实验研究由外扩散规律可知,若以反应速率RCH4为目标函数,在保证反应温度、反应物初始浓度以及接触时间相同的前提下,同时要求载氧体转化率xFe2O3不大于20%,改变CH4、CO2混合气体流速qV, T0以观察其对反应过程速率的影响,当气体流量qV, T0的增加不再改变反应速率RCH4时,便可判断外扩散的影响已经消除。
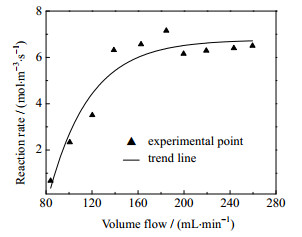
实验条件:反应温度为680 ℃,样品粒径为0.3~0.9 mm,qV, T0: mT=55 min⋅mL−1⋅g−1,yCH4, 0: yCO2, 0=3:1,反应30 s时取样分析,同时切断CH4气体,停止实验。以反应速率RCH4为纵坐标,体积流量为横坐标,结果如图 3所示。
|
图 3 气体体积流量与表观反应速率之间的关系 Fig.3 Relationship between gas volume flow and apparent reaction rate |
由图 3可知,在流量小于180 mL⋅min−1时,反应速率随流速增大而不断增加,当流量达到180 mL⋅min−1后,反应速率趋于平稳,由此判断出此时外扩散过程对反应过程的影响已消除。后续实验测定表面反应本征动力学时,气体流量定为220 mL⋅min−1,载氧体质量约4 g。
3.4 本征反应动力学研究当外扩散消除,同时保持转化率xFe2O3小于20% 时,灰层扩散可忽略不计,整个过程由反应过程控制,此时无论是缩芯模型,还是整体反应模型,反应无论是一级还是二级,动力学模型都可简化为:
| $ {R_{{\text{C}}{{\text{H}}_{\text{4}}}}} \approx - {r_{{\text{C}}{{\text{H}}_{\text{4}}}}}{\text{ = }}{k_{\text{v}}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, s}}}} $ | (41) |
则:
| $ {k_v}{\text{ = }}{{{R_{{\text{C}}{{\text{H}}_{\text{4}}}}}} / {{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, s}}}}}} $ | (42) |
由于外扩散消除:
| ${c_{{\rm{C}}{{\rm{H}}_{\rm{4}}},{\rm{s}}}} = {c_{{\rm{C}}{{\rm{H}}_{\rm{4}}}{\rm{,g}}}} $ | (43) |
| $ {c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}{\text{ = }}\frac{{p{y_{{\text{C}}{{\text{H}}_{\text{4}}}}}}}{{RT}} $ | (44) |
其中:
| $ p{\text{ = }}{{\left( {{p_0}{\text{ + }}{p_1}} \right)} / 2} $ | (45) |
| $ {y_{{\text{C}}{{\text{H}}_4}}}{\text{ = }}{{\left( {{y_{{\text{C}}{{\text{H}}_4}, 0}}{\text{ + }}{y_{{\text{C}}{{\text{H}}_4}, 1}}} \right)} / 2} $ | (46) |
式中:yCH4为反应器中CH4的平均摩尔分数;R为摩尔气体常数,8.314 J⋅mol−1⋅K−1。
实验条件为:混合气体流速为220 mL⋅min−1,外扩散影响消除,载氧体质量为4 g左右,yCH4: yCO2=3:1,改变反应温度,同时通过物料衡算求取反应速率RCH4,数据如表 3所示。
|
|
表 3 不同反应温度下反应速率RCH4和反应速率常数kV Table 3 Reaction rate RCH4 and reaction rate constant kV at different temperatures |
根据阿伦尼乌斯方程:
| $ {k_{\text{v}}} = {k_0}\exp {}_{}\left( { - \frac{E}{{RT}}} \right) $ | (47) |
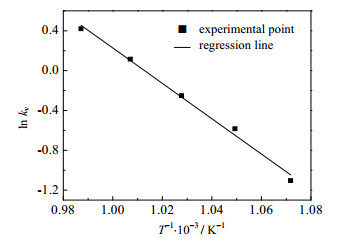
将kv的对数ln kv对1/T作图结果如图 4所示。
|
图 4 反应速率常数kv对温度T的关系图 Fig.4 Reaction rate constant kv versus temperature T |
由此可得:反应活化能E=147.574 kJ⋅mol−1,指前因子k0=6.399 5×107 s−1。
对kv数据进行误差分析,数据如表 4所示,误差Err定义为
| $ {\rm{Err}} = \frac{{{k_{{\rm{v}},\exp }} - {k_{{\rm{v}},{\rm{cal}}}}}}{{{k_{{\rm{v}},{\rm{cal}}}}}} \times 100\% $ | (48) |
|
|
表 4 反应速率常数kv和误差分析 Table 4 Error analysis of reaction rate constant kv |
式中:kv, exp、kv, cal分别为实验测定值和模型计算值,s−1。
由表 4中数据知,kv相对误差最大为6.62%,说明数据可信,kv与温度T之间的关系式:
| $ {k_{\rm{v}}} = {6.399_{}}\;5 \times {10^7} \times \exp (\frac{{ - {{147}\;}{{573.835}\;}6}}{{RT}}) $ | (49) |
Fe2O3与CH4之间的反应,其固体产物除了可能为Fe外,更有可能是FeO和Fe3O4,当固体产物不同,反应计量系数值也不同,到底是哪一种固体产物或是复合物,需要根据实验数据来进行判断。
实验在如下条件下进行,反应温度680 ℃,混合气流量220.0 mL⋅min−1,yCH4, 0: yCO2, 0=3:1,载氧体质量约4.0 g,改变反应时间t,反应结束,准确测量载氧体失重质量,数据列于表 5。
|
|
表 5 不同反应时间t时载氧体失重实验相关数据 Table 5 Relevant data of oxygen carrier weight loss experiment at different reaction times t |
从表 5中数据可以看出,反应在70 s以后就不再继续进行了,失重不再加大,反应器出口处CH4含量不再变化,反应速率趋近于零,说明CH4与Fe2O3之间反应结束,Fe2O3不再变化。为获得该温度下反应不再进行时Fe2O3准确的失重值,将反应时间延长至3 600 s,待反应结束,将反应器中固体产物取出,称重、重复4次、平均失重值为0.154 0 g。现根据以上数据判断反应固体产物可能的存在形式。
假设反应按(r6)进行
| $ {\text{ 4F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + 3C}}{{\text{H}}_{\text{4}}}{\text{ = 8Fe + 6}}{{\text{H}}_{\text{2}}}{\text{O + 3C}}{{\text{O}}_{\text{2}}} $ | (r6) |
因反应时间70 s以后反应便不再进行,现反应时间为1 h,可认为Fe2O3全部反应完毕,此时载氧体中纯Fe2O3不再存在。根据物料衡算,得:
| $ \frac{{m}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}/{M}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{{m}_{\text{Fe}}/{M}_{\text{Fe}}}\text{=}\frac{4}{8} $ | (50) |
| $ \Delta m\text{=}{m}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}\text{+}{m}_{\text{Fe}}-{m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}}\text{=}{m}_{\text{Fe}}-{m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}} $ | (51) |
式中:mFe2O3, 0为Fe2O3初始质量,g;mFe为固体产物Fe质量,g;MFe2O3、MFe分别为Fe2O3、Fe的相对分子质量,Δm为反应完毕载氧体失重,g。
则
| $ \Delta m\text{=}\frac{2{M}_{\text{Fe}}-{M}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{{M}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}} $ | (52) |
根据载氧体制备实验:
| $ {m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}}\text{=}{0.481}\;4{m}_{\text{T}} $ | (53) |
代入上式,则
| $ \Delta m{\text{ = }}\frac{{2 \times {\text{56}} - {\text{160}}}}{{160}} \times {\text{0}}{\text{.48}}{{\text{1}}\;}{\text{4}} \times {\text{4 = }} - {\text{0}}{\text{.57}}{{\text{7}}\;}{\text{7}} $ | (54) |
该失重值(绝对值)比实验值0.154 0 g要大,因此可以推定反应产物不是以纯Fe的形式存在。
假设反应按(r7)进行:
| $ {\text{ 4F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + C}}{{\text{H}}_{\text{4}}}{\text{ = 8FeO + 2}}{{\text{H}}_{\text{2}}}{\text{O + C}}{{\text{O}}_{\text{2}}} $ | (r7) |
同样可推导获得
| $ \Delta m\text{=}\frac{2{M}_{\text{FeO}}-{M}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}}}{{M}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}}}{m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}}\text{=}\frac{2\times 72-\text{160}}{160}\times \text{0}{\text{.481}}\;\text{4}\times \text{4=}-\text{0}{\text{.192}}\;\text{6} $ | (55) |
式中:MFeO表示FeO的相对分子质量。该失重值(绝对值)比实验值0.154 0 g要大,因此可以推定反应产物也不是以纯FeO的形式存在。
假设反应按(r8)进行
| $ {\text{ 12F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + C}}{{\text{H}}_{\text{4}}}{\text{ = 8F}}{{\text{e}}_{\text{3}}}{{\text{O}}_{\text{4}}}{\text{ + 2}}{{\text{H}}_{\text{2}}}{\text{O + C}}{{\text{O}}_{\text{2}}} $ | (r8) |
同样可推导获得
| $ \Delta m\text{=}\frac{2{M}_{{\text{Fe}}_{3}{\text{O}}_{\text{4}}}-{M}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{{M}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}{m}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}\text{0}}\text{=}\frac{8/12\times 232-\text{160}}{160}\times \text{0}{\text{.481}}\;\text{4}\times \text{4=}-\text{0}{\text{.064}}\;\text{2} $ | (56) |
式中:MFe3O4表示Fe3O4的相对分子质量。该失重值(绝对值)比实验值0.154 0 g要小,因此可以合理推定反应固体产物应以Fe2O3与FeO的某种虚拟复合形式存在,现设其虚拟组成为Fe2O3⋅nFeO,则反应式可写成如下集总形式:
| $ {\text{ F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ + }}\frac{1}{4}\frac{n}{{n{\text{ + }}2}}{\text{C}}{{\text{H}}_{\text{4}}}{\text{ = }}\frac{2}{{n{\text{ + }}2}}{\text{F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}} \cdot n{\text{FeO + }}\frac{1}{2}\frac{n}{{n{\text{ + }}2}}{{\text{H}}_{\text{2}}}{\text{O + }}\frac{1}{4}\frac{n}{{n + 2}}{\text{C}}{{\text{O}}_{\text{2}}} $ | (r9) |
根据物料衡算:
| $ \Delta m\text{=}\left(\frac{2}{n\text{+}2}\times \frac{{M}_{{\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}.n{\rm{FeO}}}}{{M}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}}}-1\right){m}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0} $ | (57) |
则:
| $ n\text{=}-\frac{2\Delta m}{\left(\Delta m/{m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}}\text{+}0.1\right){m}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}{,}\text{0}}}\text{=}{7.987}\;6\approx 8 $ | (58) |
式中:MFe2O3⋅nFeO表示Fe2O3⋅nFeO的相对分子质量。
最终固体生成物可写成虚拟形式:Fe2O3⋅8FeO,即n=8,化学方程式可写成如下的集总形式:
| $ {\text{C}}{{\text{H}}_{\text{4}}}{\text{ + }}5{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ = F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}} \cdot 8{\text{FeO + 2}}{{\text{H}}_{\text{2}}}{\text{O + C}}{{\text{O}}_{\text{2}}} $ | (r10) |
(1) 表面反应动力学控制
由于气速为220 mL⋅min−1,外扩散影响已经消除,对缩芯模型也不考虑灰层扩散的影响,则整个过程表现为反应动力学控制,载氧体Fe2O3转化率仅仅是反应时间t的函数,此时反应动力学模型可以选用如下3种形式:
缩芯模型:
| $ t{\text{ = }}\frac{{{\rho _{\text{B}}}}}{{{\text{5}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}}}\frac{{{r_{\text{P}}}}}{{{k_{\text{S}}}}}\left[ {1 - {{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{1 / 3}}}} \right] $ | (59) |
整体反应模型(二级):
| $ t{\text{ = }}\frac{{\text{1}}}{{{\text{5}}{k_2}{c_{{\text{C}}{{\text{H}}_{\text{4}}}, {\text{g}}}}}}{\ln \;}\frac{1}{{1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}}} $ | (60) |
整体反应模型(一级):
| $ t\text{=}\frac{{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}0}}{\text{5}{c}_{{\text{CH}}_{\text{4}}, \text{g}}}\frac{1}{{k}_{\text{v}}}{x}_{{\text{Fe}}_{\text{2}}{\text{O}}_{\text{3}}} $ | (61) |
其中
| $ {k}_{\text{v}}\text{=}{k}_{\text{s}}a\text{=}{k}_{2}{c}_{{\text{Fe}}_{2}{\text{O}}_{\text{3}}{,}\text{0}} $ | (62) |
实验条件:反应温度为680 ℃,混合气流量220.0 mL⋅min−1,yCH4, 0: yCO2, 0=3:1,载氧体质量约4.0 g,kv=0.557 6 s−1,cCH4, g=11.287 6 mol⋅m−3,改变反应时间texp(实验测量值),待反应结束,准确测量载氧体失重质量,同时根据上述3个模型分别计算反应时间tcal,数据如表 6所示。
|
|
表 6 不同模型不同转化率时的反应时间计算值tcal Table 6 Calculated reaction time tcal at different conversion rates for different models |
由表 6中数据可见,3种模型反应时间计算值tcal与实验测定值texp之间相差较大,说明整个表观过程由反应动力学控制的假设不准确,整体反应模型存在缺陷,不考虑灰层扩散的缩芯模型也不能反映实际情况。
(2) 考虑灰层扩散影响的缩芯模型
现对缩芯模型作出改进,考虑灰层扩散的影响,在消除外扩散影响的情况下,表观动力学方程为
| $ t{\text{ = }}\frac{{{\rho _{\text{B}}}}}{{{\text{5}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}}}\left\{ {\frac{{r_{\text{P}}^2}}{{6{D_{\text{e}}}}}\left[ {1 - 3{{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{2 / 3}}}{\text{ + }}2\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)} \right]{\text{ + }}\frac{{{r_{\text{P}}}}}{{{k_{\text{s}}}}}\left[ {1 - {{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{1 / 3}}}} \right]} \right\} $ | (63) |
令:
| $ {t_{\text{D}}}{\text{ = }}\frac{{{\rho _{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}}}{{{\text{5}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}}}\frac{{r_{\text{P}}^2}}{{6{D_{\text{e}}}}}\left[ {1 - 3{{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{2 / 3}}}{\text{ + }}2\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)} \right] $ | (64) |
| $ {t_{\text{R}}}{\text{ = }}\frac{{{\rho _{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}}}{{{\text{5}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}}}\frac{{{r_{\text{P}}}}}{{{k_{\text{s}}}}}\left[ {1 - {{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{1 / 3}}}} \right] $ | (65) |
则:
| $ t{\text{ = }}{t_{\text{D}}}{\text{ + }}{t_{\text{R}}} $ | (66) |
上式表明,总反应时间由两部分组成,一是CH4在灰层中的扩散时间tD,另一是表面反应时间tR。由式(63)可以计算出不同反应时间texp时灰层扩散系数De,对De取平均值后,再代入式(63),可获得反应时间模型计算值tcal,相关数据如表 7所示。
|
|
表 7 不同反应时间时的CH4灰层扩散系数De Table 7 Diffusion coefficient De of CH4 in ash layer at different reaction times |
表中误差Err定义为
| $ {\text{Err = }}\frac{{{t_{\exp }} - {t_{{\text{cal}}}}}}{{{t_{{\text{cal}}}}}} \times 100{{\% }} $ | (67) |
讨论:1) 灰层扩散系数De的求取:当载氧体颗粒结构一定,在恒温条件下De应为常数,但由于气固相非催化反应数据测量误差一般较大,尤其是在反应开始一段时间,因反应速率快,测量误差更为明显,所以表中反应时间小于40 s时,De值存在一定偏差, 随着反应进行,De测定值波动越来越小,所以本实验对De取后4个值平均,即De=1.084 1×10−9 m2⋅s−1;
2) 反应时间tcal及模型的选择:以De值代入模型式(63)中,可以获得反应时间模型计算值tcal,见上表。由表中误差数据可见,反应时间为30 s时,误差最大,达到12.97%,其余各点误差值都小于10%,说明该模型能较好地拟合实际反应过程;
3) 灰层扩散的影响:由表中tR、tD数据大小变化可知,随着反应时间延长,tD所占比例越来越大,当texp=70 s时,tD/tR=81.35%,CH4分子在灰层中扩散所需时间占反应时间的81.35%,说明随着反应的进行,灰层越来越厚,CH4通过灰层所需时间也越来越多,灰层扩散对反应过程的影响也越来越严重。
3.5.3 模型验证实验条件:改变反应温度为700 ℃,反应器进口处yCH4,0: yCO2,0=3:2,混合气流量仍为220.0 mL⋅min−1,载氧体质量约4.0 g,kv=0.777 7 s−1,cCH4, g=8.844 8 mol⋅m−3,De=1.084 1×10−9 m2⋅s−1,改变texp,结果如表 8所示:
|
|
表 8 模型验证 Table 8 Model validation |
由表可见,当改变反应温度、CH4浓度以及反应时间时,模型计算结果能较好地拟合实际值, 误差在10% 范围内,说明模型可靠。
4 结论通过实验及相关理论分析,获得如下结论:
1) 通过理论推导获得了关于铁基载氧体CH4还原反应动力学模型,各模型中含有一定的模型参数;由热力学数据计算可知,Fe2O3与CH4之间反应生成固体产物Fe3O4、FeO、Fe的可能热力学温度分别为270.1、586.1和818.82 K,热力学计算为后续的反应操作温度的选择提供了理论基础。
2) 通过改变混合气流量实验,可知当流量在180 mL⋅min−1以后,反应速率不再增加,表明外扩散影响消除,该流量点为临界点,测定表面反应本征动力学时流量必须保持大于该临界值,实际实验时气体流量取值为220 mL⋅min−1。
3) 在消除外扩散及灰尘扩散影响的前提下进行了表面反应动力学测定,回归获得了反应活化能和指前因子,活化能E=147.574 kJ⋅mol−1,指前因子k0=6.399 5×107 s−1,动力学方程如下:
| $ - {r_{{\text{C}}{{\text{H}}_{\text{4}}}}} = {6.399\;}5 \times {10^7} \times \exp (\frac{{ - {{147}\;}{{573.835}\;}6}}{{8.314T}}){c_{{\text{C}}{{\text{H}}_{\text{4}}}}} $ |
4) 引入了虚拟固体产物组成概念, 并通过实验获得了集总虚拟反应式:
| $ {\text{C}}{{\text{H}}_{\text{4}}}{\text{ + }}5{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{ = F}}{{\text{e}}_2}{{\text{O}}_{\text{3}}} \cdot 8{\text{FeO + 2}}{{\text{H}}_{\text{2}}}{\text{O + C}}{{\text{O}}_{\text{2}}} $ |
由该式可知,虚拟固体产物组成比n=8,该参数的确定改进了传统的缩芯模型对实验数据的拟合精度,进而获得灰尘扩散系数De,对反应模型进行了筛选,最优动力学模型积分式如下:
| $ t{\text{ = }}\frac{{{\rho _{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}}}{{{\text{5}}{c_{{\text{C}}{{\text{H}}_{\text{4}}}{\text{, g}}}}}}\left\{ {\frac{{r_{\text{P}}^2}}{{6{D_{\text{e}}}}}\left[ {1 - 3{{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{2 / 3}}}{\text{ + }}2\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)} \right]{\text{ + }}\frac{{{r_{\text{P}}}}}{{{k_{\text{s}}}}}\left[ {1 - {{\left( {1 - {x_{{\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}}}} \right)}^{{1 / 3}}}} \right]} \right\} $ |
其中模型参数:灰层扩散系数De=1.084 1×10−9 m2⋅s−1,表面反应速率常数(680 ℃) ks=5.576×103 m.s−1,当忽略温度对De的影响时,上式可适应于变温情况。
| [1] |
张良佺, 欧阳书情, 毛琰昊, 等. 热钾碱溶液脱除沼气中CO2的反应动力学[J]. 农业机械学报, 2019, 50(5): 362-369. ZHANG L Q, OUYANG S Q, MAO Y H, et al. Fundamental study on CO2 removal from biogas using hot potassium carbonate solvent- reaction kinetics of CO2 absorption[J]. Transactions of the Chinese Society for Agricultural, 2019, 50(5): 362-369. |
| [2] |
张良佺, 郑猫英, 毛琰昊, 等. 热钾碱溶液脱除沼气中CO2的反应机制及相际传质过程[J]. 农业机械学报, 2019, 50(4): 283-289. ZHANG L Q, ZHENG M Y, MAO Y H, et al. Reaction mechanism and interphase mass transfer of CO2 from biogas by hot potassium carbonate solvent[J]. Transactions of the Chinese Society for Agricultural, 2019, 50(4): 283-289. |
| [3] |
魏泽华, 刘道诚, 荆洁颖, 等. 化学链燃烧中铁基载氧体研究进展[J]. 洁净煤技术, 2019, 25(3): 19-27. WEI Z H, LIU D H, JING J Y, et al. Research progress on fe-based oxygen carrier in chemical looping combustion[J]. Clean Coal Technology, 2019, 25(3): 19-27. DOI:10.13226/j.issn.1006-6772.19032902 |
| [4] |
汪根宝, 胡骏, 陈时熠, 等. 铁基载氧体化学链CH4/CO2转化研究进展[J]. 中南大学学报(自然科学版), 2021, 52(1): 70-85. WANG G B, HU J, CHEN S Y, et al. Advances in Fe-based chemical looping technology for CH4/CO2 conversion[J]. Journal of Central South University (Science and Technology), 2021, 52(1): 70-85. |
| [5] |
CORMOS A M, PETRESCU L, CORMOS C C. Techno-economic implications of time-flexible operation for iron-based chemical looping combustion cycle with energy storage capability[J]. Energy, 2023, 278: 127746. DOI:10.1016/j.energy.2023.127746 |
| [6] |
崔东旭, 曾德望, 肖睿. 一种铜铁铝复合载氧体化学链燃烧性能[J]. 石油学报, 2020, 36(6): 1200-1205. CUI D X, ZENG D W, XIAO R. Performance of a Cu-Fe-Al-O oxygen carrier in chemical looping combustion[J]. Acta Petrolei Sinica, 2020, 36(6): 1200-1205. DOI:10.3969/j.issn.1001-8719.2020.06.010 |
| [7] |
刘玉楼, 郑敏, 蒲思旭. Fe2O3/MgO载氧体反应性能的研究[J]. 动力工程学报, 2020, 40(9): 757-764. LIU Y L, ZHENG M, PU S X. Study on reaction properties of Fe2O3/MgO oxygen carrier[J]. Journal of Chinese Society of Power Engineering, 2020, 40(9): 757-764. |
| [8] |
韩丹华, 郭雪岩, 王志远. 化学链重整制氢NiO-CeO2/γ-Al2O3复合载氧体的性能[J]. 化工进展, 2022, 41(1): 192-200. HAN D H, GUO X Y, WANG Z Y. Performance of NiO-CeO2/γ-Al2O3 composite oxygen carriers for hydrogen generation with chemical looping reforming[J]. Chemical Industry and Engineering Progress, 2022, 41(1): 192-200. |
| [9] |
沈来宏, 肖军, 肖睿, 等. 基于CaSO4载氧体的煤化学链燃烧分离CO2研究[J]. 中国电机工程学报, 27(2): 69-74. SHEN L H, XIAO J, XIAO R, et al. Chemical looping combustion of coal in interconnected fluidized beds of CaSO4 oxygen carrier[J]. Proceedings of Chinese Society for Electrical Engineering, 27(2): 69-74. |
| [10] |
诸林, 蒋鹏, 范峻铭. 化学链重整联合CO2捕集制氢系统热力学分析[J]. 太阳能学报, 2015, 36(8): 1978-1984. ZHU L, JIANG P, FAN J M. Thermodynamics analysis of hydrogen production system by chemical-looping reforming coupled with CO2 Capture[J]. Acta Energiae Solaris Sinica, 2015, 36(8): 1978-1984. |
| [11] |
LI G, LIU F, LIU T et al. Life cycle assessment of coal direct chemical looping hydrogen generation with Fe2O3 oxygen carrier[J]. Journal of Cleaner Production, 2019, 239: 118118. DOI:10.1016/j.jclepro.2019.118118 |
| [12] |
李康, 郑敏, 范宝山, 等. 化学链燃烧铜基载氧体前驱体煅烧反应热力学研究[J]. 新能源进展, 2021, 9(6): 519-523. LI K, ZHENG M, FAN B S, et al. Thermodynamic study of calcination reaction of copper-based oxygen carrier precursor in chemical looping combustion[J]. Advances in New and Renewable Energy, 2021, 9(6): 519-523. |
| [13] |
ANCA O, YU-YEN C, ROBERT P, et al. Kinetic model development and bayesian uncertainty quantification for the complete reduction of Fe-based oxygen carriers with CH4, CO, and H2 for chemical looping combustion[J]. Chemical Engineering Science, 2022, 252: 117512. DOI:10.1016/j.ces.2022.117512 |
| [14] |
CHEN Y Y, NADGOUDA S, SHAH V, et al. Oxidation kinetic modelling of Fe-based oxygen carriers for chemical looping applications: Impact of the topochemical effect[J]. Applied Energy, 2020, 279: 115701. DOI:10.1016/j.apenergy.2020.115701 |
| [15] |
JARRETT R, RANJANI S, HANJING T, et al. Experimental and kinetic analysis for particle scale modeling of a CuO-Fe2O3-Al2O3 oxygen carrier during reduction with H2 in chemical looping combustion applications[J]. Applied Energy, 2018, 228(5): 1515-1530. |
| [16] |
NIELS N M, CHIANG M H. KU Y, et al. Kinetics for chemical looping process with fabricated Fe2O3-CuO/Al2O3 oxygen carriers[J]. Chemical Engineering Science, 2022, 258: 117730. DOI:10.1016/j.ces.2022.117730 |
| [17] |
ALBERTO A, JUAN A, ANA C, et al. Kinetics of redox reactions of ilmenite for chemical-looping combustion[J]. Chemical Engineering Science, 2011, 66(5): 689-702. |




