2. 浙江大学衢州研究院, 浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
水溶性聚合物溶液黏度的模型预测对于其实际工业生产及应用十分重要。从理论角度出发,探究聚合物共混溶液黏度的影响因素可以引导人们更好地理解黏度在聚合物共混溶液中遵循的基本行为,对指导生产起到了重要的推动作用[1-3]。Flory等[4-6]在统计热力学和晶格假设等基础上提出了半理论半经验的黏度模型。而在聚合物的研究中,黏度与相对分子质量之间已经建立了有效的经验公式,但是尚无可靠的理论方法。针对聚合物的共混水溶液体系,黏度显然还与其溶质结构有关,如链长、支化程度、官能团等。丙烯酰胺类水溶性聚合物共混水溶液常用于胶黏剂、采油压裂液增稠剂等领域,对其黏度的预测具有重要的应用价值。
经典热力学理论没有为黏度提供与溶液性质互联的推导方法。为了将热力学扩展到液体的黏流行为,Kincaid等[7]建立了黏度和热力学性质之间的关系,为预测液体黏度提供了清晰的技术路线。可从热力学中选择多种不同的模型求解共混体系的吉布斯自由能[8-12],为流体黏度理想的微观相互作用提供了理论解释。另外,分子间的摩擦与近邻的数量、性质息息相关,可使用局部组成模型对超额项进行建模,为非理想性的短程相互作用提供理论支持。常用的局部组成模型有NRTL[13]、Wilson[14]、UNIQUAC[15]和基团贡献模型(GCM)[16]。遗传算法是一种受自然进化启发而建立的数值优化算法,通过不断考察数值对目标函数的适应度,拥有高效的变量响应能力[17]。因此常使用遗传算法求解模型的未知参数。本研究基于局部组成模型和Eyring模型机理,结合基团贡献和静电作用模型,利用遗传算法模拟,提出了一种半理论半经验模型,用于预测丙烯酰胺类水溶性聚合物共混水溶的黏度。
2 实验部分 2.1 仪器与试剂TA仪器公司ARES-G2旋转流变仪。窄分布聚丙烯酰胺(PAM)、窄分布聚甲基丙烯酰氧乙基三甲基氯化铵(PDMC)、窄分布聚甲基丙烯酰氧乙基二甲基苄基氯化铵(PAODBAC)均为实验室自制[18]。
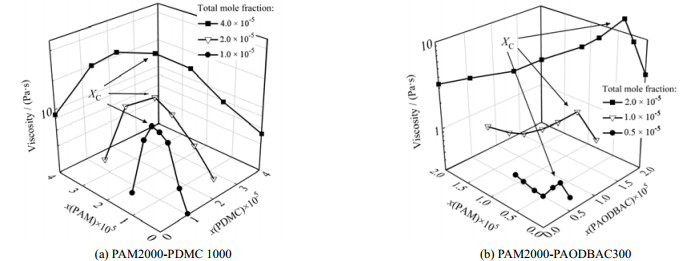
2.2 共混水溶液的黏度表征使用聚合度(DP)为2 000的PAM与聚合度为1 000的PDMC配制相同总摩尔分数的水溶液,将二者以特定体积比例混合,得到一系列相同总摩尔分数、不同组成的PAM2000-PDMC1000共混体系,使用流变仪在25 ℃条件下测得其黏度。为了避免在超低剪切速率下测量值波动带来的实验误差,使用1 s−1剪切速率,即本聚合物共混水溶液体系在第一牛顿区与假塑性区分界处的流变仪结果作为黏度测量值,结果如图 1(a)所示。以PDMC、PAODBAC在溶液总物质的量中的摩尔分数表示组成,在不同的总聚合物摩尔分数下,都出现了一个黏度由增长转为降低的临界溶质组成XC。对于PAM2000-PAODBAC300共混水溶液体系,在25 ℃条件下使用流变仪测得其黏度,如图 1(b)所示,该体系黏度与聚合物组成的关系同样存在临界溶质组成现象。
|
图 1 不同摩尔分数下共混水溶液体系黏度受溶质组成的影响 Fig.1 Effects of polymer composition on viscosity of blend aqueous solutions under different mole fractions |
采用Eyring的绝对速率方程构建模型理论基础,将黏度与热力学函数联系起来。具体方程如下:
| $ \eta V_{\mathrm{m}}=N_{\mathrm{A}} h \exp \left(\frac{\Delta g^{*}}{R T}\right)$ | (1) |
真实的黏度体系具有非理想性,其∆g*是理想项与超额项的贡献总和:
| $\Delta g^{*}=\Delta g_{\mathrm{id}}^{*}+\Delta g_{\mathrm{E}}^{*}$ | (2) |
Eyring方程被广泛应用于电解质和聚合物溶液,可表示理想和非理想混合物体系的黏度[1-5]。对于理想溶液,该式可写成:
| $ \eta_{\mathrm{id}} V_{\mathrm{id}}=N_{\mathrm{A}} h \exp \left(\frac{\Delta g_{\mathrm{id}}^{*}}{R T}\right)$ | (3) |
由于∆gid*是理想溶液的共混结果,故可采用理想条件下的混合模型求解,具体表达式如下:
| $ \ln \left(\eta_{\mathrm{id}} V_{\mathrm{id}}\right)=\sum\limits_{i} x_{i} \ln \left(\eta_{i} V_{i}\right)$ | (4) |
∆gE*反映了共混水溶液由于复杂局部组成与相互作用引起的非理想性。共混水溶液属于混合模型,其混合熵必须满足普适的变化规律,即Flory-Huggins方程[6]:
| $\frac{{\Delta g_{\rm{E}}^{*, {\rm{FH}}}}}{{RT}} = \sum\limits_i {{x_i}} \ln \left( {\frac{{{\varphi _i}}}{{{x_i}}}} \right)$ | (5) |
| $\varphi_{i}=\frac{r_{i} n_{i}}{\sum_{j} r_{j} n_{j}} $ | (6) |
共混聚合物水溶液中存在大量的有机基团,因此应从基团贡献模型的角度出发考虑微观相互作用。这种微观相互作用对溶液黏度的影响是非理想性的,可以将共混水溶液中溶质的超额吉布斯自由能与对称归一化的活度系数相联系,因此基团贡献引起的超额吉布斯自由能∆gE*, GCM可由式(7)得到:
| $ \frac{\Delta g_{\mathrm{E}}^{*, \mathrm{GCM}}}{R T}=\sum_{i} x_{i} \ln \gamma_{i}$ | (7) |
γi是分子i在共混水溶液中的活度系数,可分解为组合和残余2部分:
| $ \ln \gamma_{i}=\ln \gamma_{i}^{\mathrm{C}}+\ln \gamma_{i}^{\mathrm{R}} $ | (8) |
分子i的组合活度系数,本研究采用UNIFAC模型的计算方法:
| $\ln \gamma _i^{\rm{C}} = \ln \frac{{{\mathit{\Phi }_i}}}{{{x_i}}} + \frac{z}{2}{q_i}\ln \frac{{{\theta _i}}}{{{\mathit{\Phi }_i}}} + {l_i} - \frac{{{\mathit{\Phi }_i}}}{{{x_i}}}\sum\limits_i {{x_i}} {l_i}$ | (9) |
式中:
分子i的残余活度系数,本研究采用基团贡献法并进行改进,得到式(10):
| $ \ln \gamma _i^{\rm{R}} = \sum_k {v_k^{(i)}} \left[ {\ln {\mathit{\Gamma }_k} - \ln \mathit{\Gamma }_k^{(i)}} \right] $ | (10) |
式中:
由于PDMC、PAODBAC都是带正电的聚电解质,共混水溶液中存在较强的静电相互作用,其对共混水溶液中的黏度也产生了一定的影响。但与一般的聚电解质水溶液不同,在体系中与同样为高分子的PAM以相近比例混合,静电作用将在一定程度上受到干扰。当聚电解质浓度较低时,PAM将对聚电解质间的静电相互作用产生屏蔽作用,使其对共混水溶液黏度的影响减弱。因此,本模型在Pitzer-Debye-Hüchel模型(PDH)的基础上[19-20],提出一种适用于静电屏蔽条件下的改进模型——mPDH,如式(11)所示。静电屏蔽因子J与聚电解质浓度呈正比,与PAM的浓度呈反比,并通过选择合适的经验参数K进一步降低预测结果与实验值之间的误差。
| $\frac{\Delta g_{\mathrm{E}}^{*, \mathrm{mPDH}}}{R T}=-\left(\sum\limits_{i} x_{i}\right) \frac{4 A_{\varphi} I_{\mathrm{x}}}{M_{m}^{0.5} \rho} \ln \left(1+\rho I_{\mathrm{x}}^{0.5}\right)$ | (11) |
式中:
因此,在综合考虑Flory-Huggins理论、基团贡献模型和mPDH的基础上,本研究模型中超额吉布斯自由能∆gE*由下式计算:
| $ \Delta g_{\mathrm{E}}^{*}=\Delta g_{\mathrm{E}}^{*, \mathrm{FH}}+\Delta g_{\mathrm{E}}^{*, \mathrm{GCM}}+\Delta g_{\mathrm{E}}^{*, \mathrm{mPDH}} $ | (12) |
对于共混水溶液黏度的预测,假设所有成分在整个模拟温度和组成范围内均保持完全溶解,呈均一稳定的溶液状态。首先需要了解该条件下各溶质在其纯水溶液中的黏度,可使用流变仪对一系列纯组分的溶液进行测量,从而得到半经验性的纯组分黏度函数。在本研究黏度模型中使用Abriz等[21]给出的经验模型估算水的纯组分黏度。
以PAM2000-PDMC1000体系为例。对于γiC的计算,从基团贡献模型的角度分析,PAM分子可被拆解为─CH2─、> CH─、> C═O和─NH2,查文献可知上述基团的Rk、Qk值[22],从而计算其ri和qi值,并以此作为本模型计算的基础参数,如表 1所示。对于γiR的计算,由于传统的基团贡献模型主要用于小分子有机溶剂的混合黏度和液−液相分离预测,而常见有机溶质中不涉及的基团往往缺少文献报道,如 > C═O和─NH2、─COO─和─NH2、> N(CH3)─和─COO─共3对6个参数。因此,文献[22]中给出的基团相互作用参数数据并不全面,缺乏常见溶剂所含基团以外的相互作用参数,并且无从推导,因而阻碍了基团贡献模型对聚合物水溶液的应用。
|
|
表 1 窄分布聚合物分子体积参数ri和分子表面积参数qi计算结果 Table 1 Calculation result of volume parameter ri and area parameter qi of narrow polymers |
为了建立针对窄分布PAM水溶液共混体系的预测模型,必须得到上述参数的有效估算值。针对一定条件下的体系,可通过赋予未知参数合理初值的方式,使用模型对黏度进行预测。不断对比体系黏度测量值与预测值的误差,优化未知参数,从而得到适应本体系的最佳赋值,将其作为该参数的有效估算值补全参数表。最后使用以该参数表建立的模型预测其他条件下共混体系的黏度,从而验证参数估算值的合理性。遵循该思路,研究使用Matlab软件建立遗传算法,将聚合物总摩尔分数为2.0×10−5的条件下PAM2000-PDMC1000共混水溶液体系作为模型预测对象,以式(13)为最小化目标函数,求解得到了未知相互作用参数的有效估算值,如表 2所示,即得到体系黏度预测所需的完整相互作用参数。
| $ F=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left[1-\frac{\eta_{i}^{\mathrm{cal}}}{\eta_{i}^{\exp }}\right]^{2}} $ | (13) |
|
|
表 2 未知相互作用参数的拟合求解结果 Table 2 Fitting results of unknown interaction parameters |
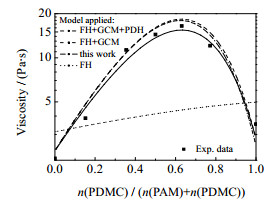
以总摩尔分数为1.0×10−5的PAM2000-PDMC1000为例,使用不同模型进行黏度预测,结果如图 2所示。图 2中FH线是以Flory-Huggins方程计算混合过程中的超额吉布斯自由能时,体系黏度的预测结果。该预测线近似于直线,这是由于Flory-Huggins方程仅考虑混合熵对超额吉布斯自由能的贡献,其在焓变较少的小分子有机物或电解质共混水溶液中的适用性尚可,但由于聚电解质水溶液的共混体系中存在不可忽视的焓变现象,因此需要进一步引入合适的模型以模拟焓变对共混体系黏度的影响。
|
图 2 不同预测模型中PAM2000-PDMC1000共混黏度测量值与预测值的对比 Fig.2 Comparison of experimental viscosity values and predicted values from different models for PAM2000-PDMC1000 blend aqueous solutions |
图 2中FH+GCM线是在Flory-Huggins方程的基础上,继续引入基团贡献模型后的黏度预测结果,体现了局部基团之间短程相互作用力对共混体系黏度的影响。该预测线随PDMC摩尔分数的变化趋势与实验测量值的变化趋势保持一致,说明基团贡献模型的引入大大提高了模型在聚电解质水溶液中预测的准确性。但预测值明显大于实验值,这说明存在其他未被考虑的影响因素。
图 2中FH+GCM+PDH线是FH+GCM模型继续引入PDH模型后的黏度预测结果。作为聚电解质,PDMC的分子内、分子之间不同带电链段之间存在作用范围为长程的静电相互作用。PDH模型可表现该现象对共混水溶液黏度的影响,但显然其影响甚微。事实上,经典PDH方程更适用于修正带电能力弱的小分子电解质水溶液中静电作用对超额吉布斯自由能的影响,而高聚合度的聚电解质还须考虑链段的带电规律和静电作用距离等因素。
由于聚电解质中每个聚合单体单元都带正电荷,静电排斥作用占主导,在微观上分子链段之间难以缠结,在宏观上共混体系的黏度降低,该现象随着PDMC摩尔分数的增加而增强。同时,静电排斥作用也受到PAM摩尔分数的影响,PAM摩尔分数的提高增大了PDMC分子之间的距离,在一定程度上减轻了静电排斥作用,因此PAM摩尔分数的增加将有效促进黏度的增长效应。为了提高PDH方程对本体系中预测静电相互作用的准确性,模型引入静电屏蔽因子J,通过反复调试经验参数K的大小,可将预测误差进一步缩小。在25 ℃条件下,K取10时,预测结果如图 2中本研究模型线所示。与上述2种预测模型相比,本模型综合考虑了该共混水溶液体系的各影响因素,可将共混水溶液黏度的预测值控制在合理的范围内,展现出了极大的优势,因此可作为本体系的综合模型使用。
为了分析本模型的适用性,使用式(13)表征模型的预测误差,对主要参数进行单变量分析以获取其有效的应用范围。
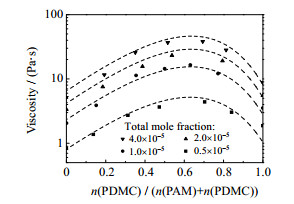
4.2.1 聚合物总摩尔分数通过改变模型计算过程中共混水溶液总摩尔分数参数的赋值,可明确该模型在各体系中的总摩尔分数适用范围。分别预测总摩尔分数为0.5×10−5、1.0×10−5、2.0×10−5和4.0×10−5的PAM2000-PDMC1000共混体系黏度,与实验值对比结果如图 3所示。
|
图 3 不同总摩尔分数下PAM2000-PDMC1000共混体系黏度的测量值与预测值的对比 Fig.3 Comparison of experimental viscosity values and predicted values of PAM2000-PDMC1000 blend aqueous solutions under different total mole fractions |
各总摩尔分数下的预测值与实验值基本吻合,对其误差的分析见表 3。除总摩尔分数为4.0×10−5条件下误差值稍大以外,在更低总摩尔分数下的预测误差皆在0.1以内,说明该模型适用于较宽总摩尔分数范围内的聚电解质共混水溶液黏度预测。
|
|
表 3 不同总摩尔分数下PAM2000-PDMC1000共混黏度的预测误差 Table 3 Predictive errors of PAM2000-PDMC1000 blend aqueous solution under different total mole fractions |
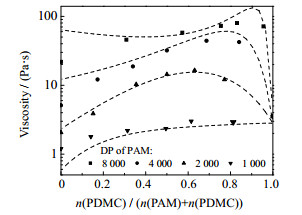
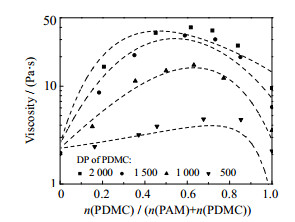
通过改变模型计算过程中聚合物聚合度参数的赋值,可明确该模型在各体系中聚合物相对分子质量的适用范围。对于总摩尔分数为1.0×10−5的PAM-PDMC共混体系,分别改变PAM和PDMC聚合度后预测体系黏度,其与实验值的对比结果分别如图 4和5所示。
|
图 4 不同PAM聚合度下PAM-PDMC1000共混体系黏度测量值与预测值的对比 Fig.4 Comparison of experimental viscosity values and predicted values of PAM-PDMC1000 blend aqueous solutions under different degree of polymerization of PAM |
|
图 5 不同PDMC聚合度下PAM2000-PDMC共混体系黏度测量值与预测值的对比 Fig.5 Comparison of experimental viscosity values and predicted values of PAM2000-PDMC blend aqueous solutions under different degree of polymerization of PDMC |
如图 4所示,当PAM的聚合度为1 000和2 000时,预测值与实验值误差较小;当PAM聚合度为4 000时,预测线与实验值随PDMC摩尔分数的变化趋势基本相同,但各预测值均偏大;当PAM聚合度为8 000时,预测线变化趋势开始与实验测量值偏离,且预测的黏度最大值高于实验值。综上可知,对PAM水溶液使用本模型进行黏度预测时,PAM的聚合度不宜过高,当聚合度小于4 000时预测结果较合理。
如图 5所示,当PDMC聚合度达到2 000时,预测值与实验值的偏离明显增大,误差F较大。聚合度低于1 500时,误差F均小于0.05。综上可知,本模型适用于PDMC聚合度低于1 500的水溶液体系。
图 4中,在低PDMC摩尔分数时,除PAM聚合度为2 000的预测线外,其余PAM聚合度条件下模型预测值都存在误差:当聚合度更大时,预测值偏高;当聚合度更小时,预测值偏小。当PDMC摩尔分数为0时,溶液退化为纯PAM水溶液,可见误差随着PAM摩尔分数的增高而增大。推测该误差来源于模型对不同聚合度PAM水溶液黏度预测的不准确性,基团贡献模型对未知相互作用参数的估算误差是该条件下预测值偏离的主要原因。由于对未知相互作用参数的估算是针对PAM聚合度为2 000时的实验测量值进行的,为了最小化该条件下的PAM纯水溶液黏度预测值误差,所得的相互作用参数集高估了聚合度PAM纯水溶液中分子间相互作用的影响。对于PAM纯水溶液,─NH2与 > C═O未知相互作用参数的估算值对预测误差起主导作用,导致当聚合度更高时,分子间相互作用被放大,预测值偏高,反之亦然。
而在图 5中,当PDMC摩尔分数接近100% 时,同样出现了与纯PAM水溶液类似的预测误差。对于PDMC纯水溶液,> N(CH3)─与─COO─未知相互作用参数的估算值对预测误差起主导作用。可见,该误差在本质上来自遗传算法对未知相互作用参数的拟合偏差。
4.2.3 聚合物种类通过改变模型所应用的聚合物种类对黏度进行预测,拓展模型的应用范围。为了验证本模型对相似结构聚合物水溶液体系的适用性,采用与PDMC结构类似的PAODBAC与PAM形成共混水溶液。使用本模型预测25 ℃下的PAM2000-PAODBAC共混水溶液体系黏度。当更换共混水溶液体系中聚合物溶质的种类后,可方便地更改模型中的相互作用参数,使之更好地模拟新体系中溶质之间的真实微观相互作用力。分别改变总摩尔分数和PAODBAC聚合度,预测结果如图 6、7所示。其中,以总摩尔分数为1.0×10−5的PAM2000-PAODBAC300体系黏度预测值为优化目标,得到该体系的经验参数K为275。
|
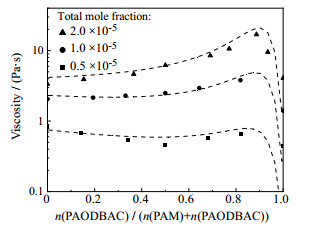
图 6 不同总摩尔分数下PAM2000-PAODBAC300共混体系黏度的测量值与预测值的对比 Fig.6 Comparison of experimental viscosity values and predicted values of PAM2000-PAODBAC300 blend aqueous solutions under different total mole fractions |
|
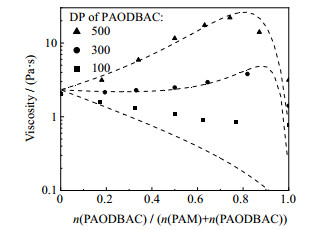
图 7 不同PAODBAC聚合度下PAM2000-PAODBAC共混体系黏度测量值与预测值的对比 Fig.7 Comparison of experimental viscosity values and predicted values of PAM2000-PAODBAC blend aqueous solutions under different degree of polymerization of PAODBAC |
图 6显示,更改聚合物种类后,本模型对不同总摩尔分数条件下的预测值与实验测量值的变化趋势仍保持一致,且数值基本吻合。该预测结果与PAM2000-PDMC1000体系结果类似,在0.5×10−5~2.0×10−5总摩尔分数下的误差F皆小于0.1,表明本模型可在较宽的总摩尔分数范围内准确预测PAM2000-PAODBAC300共混水溶液体系黏度,对于类似结构聚合物水溶液体系对总摩尔分数依赖性的预测有较好的可拓展性。
图 7显示了本模型在不同PAODBAC聚合度条件下,对PAM2000-PAODBAC体系的预测情况。当聚合度为300和500时,误差F较小,模型具有较高的预测水平。而当其聚合度为100时,模型预测的变化趋势基本一致,但其预测值存在较大误差。与PAM-PDMC体系预测偏离的原因类似,该误差是模型引入大量相互作用参数时的误差造成的。尤其是在PAM-PAODBAC体系中,本模型还需充分考虑苯环疏水作用对体系黏度产生的影响。另外,本模型通过分析基团贡献模型中聚合度对摩尔表面积和体积的影响,对相对分子质量较大的聚合物水溶液黏度预测进行了优化,因此在聚合度较高时,预测结果误差较小。
当体系中的PAODBAC聚合度降低时,由于强疏水性苯环的存在,低聚合度PAODBAC仍对共混体系提供了不可忽视的超额吉布斯自由能,使真实溶液的黏度保持在较大值。而本模型中相互作用参数均以基团为最小单元进行拟合,在低聚物体系中更倾向于突出疏水作用。因此在低PAODBAC聚合度条件下,本模型所预测的超额吉布斯自由能变化值也随之大大降低,使黏度预测结果逐渐偏小。
综上可知,本模型对相似结构聚电解质共混水溶液体系的黏度预测具有较好的适用性,预测结果比较可靠。
5 结论通过表征丙烯酰胺类水溶性聚合物水溶液的黏度,发现其共混水溶液存在黏度极大值。以Eyring黏度-热力学关联理论为基础,结合FH理论、基团贡献模型和静电相互作用模型,首次建立了一种适用于聚丙烯酰胺类水溶性聚合物的黏度预测模型,并得到以下结论:
(1) 使用遗传算法估算了6个基团贡献模型中所需的未知相互作用参数,并以此为基础成功预测了PAM-PDMC和PAM-PAODBAC共混水溶液的黏度,模型在较宽的总摩尔分数和溶质聚合度范围内可取得令人满意的适用性。
(2) 预测结果表明,与单独使用FH、基团贡献或者静电相互作用模型相比,本模型在丙烯酰胺类水溶性聚合物共混水溶液黏度的模拟中具有更好的预测能力。
符号说明:
|
|
| [1] |
MA D, LIU Q, ZHU C Y, et al. Volumetric and viscometric properties of ternary solution of (N-methyldiethanolamine + monoethanolamine + ethanol)[J]. The Journal of Chemical Thermodynamics, 2019, 134(1): 5-19. |
| [2] |
GUO H, HUI L, SHEN S F. Monoethanolamine+2-methoxyethanol mixtures for CO2 capture: Density, viscosity and CO2 solubility[J]. The Journal of Chemical Thermodynamics, 2019, 132(2): 155-163. |
| [3] |
FU K, ZHANG P, FU D. Experiment and model for the viscosity of carbonated 3-(dimethylamino) propan-1-ol and 2-(ethylamino) ethanol blended aqueous solutions[J]. The Journal of Chemical Thermodynamics, 2019, 134(2): 61-68. |
| [4] |
FLORY P J. Thermodynamics of high polymer solutions[J]. Journal of Chemical Physics, 1941, 9(8): 660-661. |
| [5] |
HUGGINS M L. Solutions of long chain compounds[J]. Journal of Chemical Physics, 1941, 9(5): 440-441. |
| [6] |
MCALLISTER R A. The viscosity of liquid mixtures[J]. AIChE Journal, 1960, 6(3): 427-431. DOI:10.1002/aic.690060316 |
| [7] |
KINCAID J F, EYRING H, STEARN A E. The theory of absolute reaction rates and its application to viscosity and diffusion in the liquid state[J]. Chemical Reviews, 1941, 28(2): 301-365. DOI:10.1021/cr60090a005 |
| [8] |
CAO W H, FREDENSLUND A, RASMUSSEN P. Statistical thermodynamic model for viscosity of pure liquids and liquid-mixtures[J]. Industrial & Engineering Chemistry Research, 1992, 31(11): 2603-2619. |
| [9] |
SADEGHI R. Segment-based Eyring-Wilson viscosity model for polymer solutions[J]. The Journal of Chemical Thermodynamics, 2005, 37(5): 445-448. DOI:10.1016/j.jct.2004.10.009 |
| [10] |
FANG S, HE C H. A new one parameter viscosity model for binary mixtures[J]. AIChE Journal, 2011, 57(2): 517-524. DOI:10.1002/aic.12272 |
| [11] |
NOVAK L T. Modeling the viscosity of liquid mixtures: polymer-solvent systems[J]. Industrial & Engineering Chemistry Research, 2003, 42(8): 1824-1826. |
| [12] |
CHEN C Y, ZENG H D, DENG Y F, et al. A novel viscosity-temperature model of glass-forming liquids by modifying the Eyring viscosity equation[J]. Applied Sciences-Basel, 2020, 10(2): 11-18. |
| [13] |
ZAFARANI M T, MAJDAN C R. New excess Gibbs energy equation for modeling the thermodynamic and transport properties of polymer solutions and nanofluids at different temperatures[J]. Industrial & Engineering Chemistry Research, 2011, 50(13): 8245-8262. |
| [14] |
SADEGHI R. Extension of the electrolyte NTRL and Wilson models for correlation of viscosity of strong electrolyte solutions at different temperatures[J]. Fluid Phase Equilibria, 2007, 259(2): 157-164. DOI:10.1016/j.fluid.2007.07.008 |
| [15] |
BOSSE D, BART H J. Viscosity calculations on the basis of Eyring's absolute reaction rate theory and COSMOSPACE[J]. Industrial & Engineering Chemistry Research, 2005, 44(22): 8428-8435. |
| [16] |
TOCHIGI K, YOSHINO K, RATTAN V K. Prediction of kinematic viscosities for binary and ternary liquid mixtures with an ASOG-VISCO group contribution method[J]. International Journal of Thermophysics, 2005, 26(2): 413-419. DOI:10.1007/s10765-005-4505-x |
| [17] |
ROSTAMI A, KALANTARI M M, KARIMI M, et al. Efficient estimation of hydrolyzed polyacrylamide (HPAM) solution viscosity for enhanced oil recovery process by polymer flooding[J]. Oil & Gas Science and Technology-Revue d IFP Energies Nouvelles, 2018, 73(3): 528-538. |
| [18] |
LIANG J, SHAN G R, PAN P J. Aqueous RAFT polymerization of acrylamide: A convenient method for polyacrylamide with narrow molecular weight distribution[J]. Chinese Journal of Polymer Science, 2017, 35(1): 123-129. DOI:10.1007/s10118-017-1874-0 |
| [19] |
PITZER K S, MAYORGA G. Thermodynamics of electrolytes.Ⅱ. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent[J]. Journal of Physical Chemistry, 1973, 77(19): 2300-2308. DOI:10.1021/j100638a009 |
| [20] |
PITZER K S. Thermodynamics of electrolytes. Ⅰ. Theoretical basis and general equations[J]. Journal of Physical Chemistry, 1973, 77(2): 268-277. DOI:10.1021/j100621a026 |
| [21] |
ABRIZ A M, CEGINCARA R M. Modeling the transport and volumetric properties of solutions containing polymer and electrolyte with new model[J]. Iranian Journal of Chemistry & Chemical Engineering-International English Edition, 2018, 37(4): 235-252. |
| [22] |
HANSEN H K, RASMUSSEN P, FREDENSLUND A, et al. Vapor-liquid-equilibria by UNIFAC group contribution.5. Revision and extension[J]. Industrial & Engineering Chemistry Research, 1991, 30(10): 2352-2355. |