盐水层CO<sub>2</sub>埋存时岩石流体综合作用及对选址影响

引用本文

崔国栋, 潘众, 杨昌华, 许艳梅, 张亮, 汪毅, 任韶然. 盐水层CO₂埋存时岩石流体综合作用及对选址影响[J]. 高校化学工程学报, 2018, 32(3): 696-707. DOI: 10.3969/j.issn.1003-9015.2018.03.027.

CUI Guo-dong, PAN Zhong, YANG Chang-hua, XU Yan-mei, ZHANG Liang, WANG Yi, REN Shao-ran. Rock-Fluid Interactions and their Effects on Site Selection of CO₂ Storage in Saline Aquifer[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 696-707. DOI: 10.3969/j.issn.1003-9015.2018.03.027.

基金项目

国家自然科学基金（51674282）；中央高校基本科研业务费专项资金资助（17CX06006，18CX05009A）；中国石油大学（华东）研究生创新工程资助项目（YCX2017022）；十三五国家油气重大专项（2016ZX05056004-003）；长江学者和创新团队发展计划（IRT1294及1086/14R58）。

通讯联系人

任韶然, E-mail: rensr@upc.edu.cn

作者简介

崔国栋(1990-), 男, 河北沧州人, 中国石油大学(华东)博士生。

文章历史

收稿日期：2017-08-28;
修订日期：2017-12-11。

Contents Abstract Full text Figures/Tables PDF

盐水层CO₂埋存时岩石流体综合作用及对选址影响

崔国栋 ¹, 潘众 ², 杨昌华 ³, 许艳梅 ², 张亮 ¹, 汪毅 ¹, 任韶然 ¹

1. 中国石油大学(华东) 石油工程学院，山东青岛 266580;
2. 中石油华北油田，河北任丘 062552;
3. 西安石油大学石油工程学院，陕西西安 710065

收稿日期：2017-08-28；修订日期：2017-12-11。

基金项目：国家自然科学基金（51674282）；中央高校基本科研业务费专项资金资助（17CX06006，18CX05009A）；中国石油大学（华东）研究生创新工程资助项目（YCX2017022）；十三五国家油气重大专项（2016ZX05056004-003）；长江学者和创新团队发展计划（IRT1294及1086/14R58）。

作者简介：崔国栋(1990-), 男, 河北沧州人, 中国石油大学(华东)博士生。

通讯联系人：任韶然, E-mail: rensr@upc.edu.cn

摘要：为研究盐水层CO₂埋存过程中，CO₂注入导致的岩石流体作用对储层物性和CO₂注入性的影响，将地层水蒸发盐析与地化反应进行耦合，建立了盐水层CO₂埋存反应流动综合模型。利用该模型，分析了流体流动规律、矿物溶解/沉淀和盐析，并对储层物性进行了敏感性研究。模拟结果表明，沿CO₂运移方向，储层分为干涸区（纯CO₂渗流区）、气液两相渗流区和CO₂溶解区三个区域。盐析主要发生在干涸区域，地化反应导致的矿物溶解/沉淀反应则主要发生在气液两相渗流区和CO₂溶解区。地化反应导致的矿物溶解/沉淀分布范围大，但其变化量较小，施工阶段可忽略其对注入性的影响。而受地层水回流影响，大量NaCl被地层水携带至干涸区域前缘处析出，造成储层孔隙度和渗透率严重下降，使得盐析对CO₂注入性影响远大于矿物溶解/沉淀的影响。注入速率、地层水盐度和初始渗透率对岩盐析分布影响较大，CO₂埋存选址时，应选择合适的盐水层降低岩石流体作用对注入性的影响。

关键词：盐水层 CO₂埋存蒸发盐析地化反应 CO₂注入性

Rock-Fluid Interactions and their Effects on Site Selection of CO₂ Storage in Saline Aquifer

CUI Guo-dong¹, PAN Zhong², YANG Chang-hua³, XU Yan-mei², ZHANG Liang¹, WANG Yi¹, REN Shao-ran¹

1. School of Petroleum Engineering, China University of Petroleum(East China), Qingdao 266580, China;
2. PetroChina Huabei Oilfield Company, Renqiu 062552;
3. College of Petroleum Engineering, Xi'an Shiyou University, Xian 710065

Abstract: In order to study rock-fluid interactions and their effects on reservoir physical properties and injectivity during CO₂ geological storage, a comprehensive reaction transport model was established by coupling salt precipitation and geochemical reactions. Effects of fluid flow, mineral dissolution/precipitation and salt precipitation on reservoir physical properties were studied by sensitivity analysis. Simulation results show that the reservoir can be divided into three zones along with CO₂ migration, which are dry-out zone (i.e. CO₂ only), gas-liquid two-phase seepage zone and single aqueous phase zone with dissolved CO₂. Salt precipitation mainly occurs in the dry-out zone, and mineral dissolution/precipitation caused by geochemical reactions mainly occurs in the gas-liquid two-phase seepage zone and single aqueous phase zone. Mineral dissolution/precipitation happens in large areas but with little variation during CO₂ injection. Therefore, its effect on reservoir physical properties can be neglected during injection. Back flow of formation water results in large amount of NaCl moving towards the edge of the drying zone, which precipitates in that zone and seriously damages reservoir porosity and permeability. Therefore, salt precipitation has significant effects on the reservoir physical properties and CO₂ injectivity. Factors including injection rate, salinity, and permeability show great effects on salt precipitation, and saline aquifer with moderate injection rate, salinity, and permeability should be considered for CO₂ geological storage.

Key words: saline aquifer CO₂ geological storage evaporation and salt precipitation geochemical reactions CO₂ injectivity

1 前言

CO₂作为主要的温室气体，是导致温度上升的主要原因^[1]。自工业革命以来，随着CO₂的持续排放，大气中CO₂浓度已经逐渐上升了45%，达到400 ppm^[2]。因此，必须采取一定的手段，降低CO₂向大气中的人工排放。而在化石能源依旧大比例占据能源市场情况下，CO₂捕获埋存被认为是现有阶段最可行有效的CO₂减排手段^{[1, 3, 4]}。相对于废弃油气藏等其他埋存方式，盐水层埋存由于具有分布广、埋存体积大及距离CO₂排放源近等优势，被认为是最具有前景的CO₂埋存方式^{[1, 2, 5]}。

盐水层的注入性、存储性以及安全性是影响CO₂盐水层埋存成功实施的三大主要因素，地质选址时必须得以保证^{[6, 7]}。但是，CO₂注入过程中，其会与地层水及储层岩石发生复杂的岩石流体作用，影响到CO₂注入性和存储性^[8~15]。一方面，注入的CO₂会与地层水发生酸化反应^[8]，打破已有的地层水-岩石地化平衡，导致储层部分矿物溶解和沉淀，影响到储层物性和CO₂注入性^[9~12]。另一方面，干燥CO₂的持续注入会不断蒸发地层水，导致地层水中NaCl不断升高并从地层水中析出，堵塞储层孔隙，最终降低储层可注性^[13~16]。前期CO₂埋存研究表明，CO₂-地层水-岩石地化反应会影响储层孔隙度和渗透率，但缺乏对注入性影响的定量分析^{[11, 12]}。而相关蒸发盐析研究表明，CO₂的持续注入会导致水中NaCl析出，更会在一定条件下导致NaCl在注入井附近大量堆积，加剧对储层的伤害^{[15, 16]}。

但是，相应研究均未将地化反应和盐析一起综合分析。实际CO₂注入时，地层水蒸发不仅会导致水中NaCl的析出，更会影响矿物离子浓度从而影响地化反应。同时，NaCl析出会影响CO₂流动特征，进而影响到CO₂-地层水-岩石间的地化反应。因此，必须将地化反应和地层水蒸发盐析放在一起共同研究，从而为盐水层CO₂埋存安全高效的实施提供指导。为此，本文利用热力学平衡方程和化学动力学方法建立了考虑地层水蒸发、CO₂-地层水-岩石地化反应和水中NaCl析出的综合反应流动模型，分析了CO₂注入过程中发生的岩石流体作用，及其对储层物性和注入压力的影响。同时，对影响岩石流体作用的主要因素进行了敏感性分析，旨在从机理及现场应用角度对CO₂高效埋存和选址提供帮助。

2 埋存相关数学模型 2.1 质量守恒方程

在常规气水两相质量守恒方程的基础上，考虑水相中组分的扩散及化学反应引起的质量变化，建立了新的质量守恒方程，如下所示：

$ \frac{\partial }{{\partial t}}\left[ {\phi \left( {{c_{i{\rm{g}}}}{\rho _{\rm{g}}}{S_{\rm{g}}} + {c_{i{\rm{w}}}}{\rho _{\rm{w}}}{S_{\rm{w}}}} \right)} \right] = \nabla \cdot \left[ {\frac{{{c_{i{\rm{g}}}}{\rho _{\rm{g}}}k{k_{{\rm{rg}}}}}}{{{\rm{1}}{{\rm{0}}^{\rm{6}}}{\mu _{\rm{g}}}}}\left( {\nabla p - {\rho _{\rm{g}}}g\nabla D} \right) + \frac{{{c_{i{\rm{w}}}}{\rho _{\rm{w}}}k{k_{{\rm{rw}}}}}}{{{\rm{1}}{{\rm{0}}^{\rm{6}}}{\mu _{\rm{w}}}}}\left( {\nabla p - {\rho _{\rm{w}}}g\nabla D} \right)} \right]{\rm{ + }}{q_i} + {F_{i{\rm{w}}}} + {R_{i{\rm{w}}}} $

(1)

2.2 水中CO₂扩散模型

水中组分的扩散会增加影响到CO₂-地层水-岩石地化反应。本文结合Fick第二定律，求得方程(1)中扩散变化量F_iw为：

$ {F_{i{\rm{w}}}} = \nabla \cdot ({M_i}{S_{\rm{W}}}\varphi {D_{i{\rm{w}}}}\nabla {C_{i{\rm{w}}}}) $

(2)

对于水中CO₂扩散速率D_CO₂，可采用Wilke-Chang分子扩散模型计算^{[17, 18]}：

$ {D_{CO{}_2}} = \frac{{7.4 \times {{10}^{ - 15}}{{\left( {a{M_{{{\rm{H}}_2}{\rm{O}}}}} \right)}^{0.5}}T}}{{{\mu _{\rm{w}}}v_{{\rm{C}}{{\rm{O}}_2}}^{ - 0.6}}} $

(3)

图 1为采用Wilke and Change方程计算出的CO₂扩散系数与实验数据对比图^[19~21]。可以看出，270~350 K时，两者具有较好的吻合度，说明Wilke-Change方程在270~350 K内可较为准确计算出CO₂在地层水中的扩散系数。

图 1 不同温度下地层水中CO₂扩散系数 Fig.1 Diffusion coefficients of CO₂ in formation water at different temperatures

2.3 地化-盐析反应模型

为准确分析地化反应和盐析规律及两者对储层的综合影响，模拟时将反应分为水相反应和矿物反应。其中水相反应无固体矿物参与，反应过程符合热力学过程，可认为在瞬间达到平衡^{[9, 22]}。矿物溶解/析出由于速率较慢，必须考虑其动力学过程^{[9, 22]}。同时大量实验表明，NaCl析出是一个复杂的反应动力学过程，需要一定的时间过程^{[10, 23]}。而目前盐析模拟方法主要采用热力学方法，忽略了其反应动力学过程^{[13, 24, 25]}。为此，尝试采用反应动力学方法模拟NaCl析出过程，同时得以将盐析现象与CO₂-地层水-岩石地化反应耦合。反应方程式如下所示：

$ {r_\beta } = {k_\beta }\hat A\left( {1 - \frac{{{Q_\beta }}}{{{K_{{\rm{eq}}, \beta }}}}} \right){\kern 1pt} $

(4)

$ {k_\beta } = {k_{0\beta }}\exp \left[ { - \frac{{{E_\beta }}}{R}\left( {\frac{1}{T} - \frac{1}{{{T_0}}}} \right)} \right], {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat A = {\hat A^0} \cdot \frac{{{N_\beta }}}{{N_\beta ^0}} $

(5)

由于不考虑埋存过程中储层温度的变化，故直接将储层温度(本文为50℃)下各反应化学的平衡常数输入模型中。同时结合反应速率(式(4))，可求得地化-盐析反应引起的变化量R_iw为：

$ {R_{i{\rm{w}}}} = = \sum\limits_{\beta = 1}^{{R_{{\rm{mn}}}}} {{r_\beta }{M_\beta }} $

(6)

2.4 蒸发溶解模型

干燥CO₂注入储层过程中，地层水会不断蒸发溶解至CO₂中，最终在储层压力和温度条件下达到平衡。本文采用热力学平衡方法计算水和CO₂在气相和水相中的分布^[26~30]，即在气水两相中的逸度相同：

$ {f_{i, {\rm{g}}}} = {f_{i, {\rm{w}}}};{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = {{\rm{H}}_2}{\rm{O}}, {\rm{C}}{{\rm{O}}_2} $

(7)

其中，H₂O在气相中的逸度f_{H₂O, g}由状态方程^[26]计算，在水中的逸度由以下公式求出^{[27, 28]}：

$ {f_{{{\rm{H}}_2}{\rm{O}}, {\rm{w}}}} = {y_{{{\rm{H}}_2}{\rm{O}}, {\rm{w}}}} \cdot {f_{{{\rm{H}}_2}{\rm{O}}}} $

(8)

$ {f_{{{\rm{H}}_2}{\rm{O}}}} = f_{{{\rm{H}}_2}{\rm{o}}}^{\rm{s}}\;\exp \left( {\int_{p_{{{\rm{H}}_2}{\rm{O}}}^{\rm{s}}}^p {\frac{{{v_{{{\rm{H}}_2}{\rm{O}}}}}}{{RT}}{\rm{d}}p} } \right) $

(9)

$ \frac{{f_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}^{\rm{s}}}}{{P_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}^{\rm{s}}}} = \left\{ \begin{array}{l} 0.95958 + 9.66833 \times {10^{ - 5}}T' - 6.175' \times {10^{ - 7}}{{T'}^2} - 3.08333 \times {10^{ - 10}}{{T'}^3}{,_{}}T' > 90^\circ {\rm{F}}\\ 1,{\rm{otherwise}} \end{array} \right. $

(10)

CO₂在气相中的逸度f_{CO₂, g}亦由状态方程计算，在水相中的逸度由以下公式^{[29, 30]}求出：

$ {f_{{\rm{C}}{{\rm{O}}_{{\rm{2, }}}}{\rm{w}}}} = {y_{{\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{, w}}}} \cdot {H_{{\rm{salt, C}}{{\rm{O}}_{\rm{2}}}}} $

(11)

$ {\rm{ln}}\left( {\frac{{{H_{{\rm{salt, C}}{{\rm{O}}_{\rm{2}}}}}}}{{{H_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}}}} \right) = {k_{{\rm{salt, C}}{{\rm{O}}_{\rm{2}}}}}{m_{{\rm{salt}}}} $

(12)

$ \ln {H_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = \ln H_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}^{\rm{s}} + \frac{1}{{RT}}\int_{p_{{{\rm{H}}_{\rm{2}}}{\rm{0}}}^{\rm{s}}}^p {{{\overline v }_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{\rm{d}}p} $

(13)

$ {k_{{\rm{salt, C}}{{\rm{O}}_{\rm{2}}}}} = 0.11572 - 6.0293 \times {10^{ - 4}}{T^{\rm{c}}} + 3.5817 \times {10^{ - 6}}{T^{\rm{c}}}^2 - 3.7772 \times {10^{ - 9}}{T^{\rm{c}}}^3 $

(14)

$ \begin{array}{l} \ln H_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}^{\rm{s}} = \ln p_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}^{\rm{s}} - 9.4234{\left( {T/{T_{{\rm{c, }}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}} \right)^{ - 1}} + 4.0087{\left( {1 - T/{T_{{\rm{c, }}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}} \right)^{0.355}}{\left( {T/{T_{{\rm{c, }}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}} \right)^{ - 1}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; + 10.3199\left[ {\exp \left( {1 - T/{T_{{\rm{c, }}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}} \right)} \right]{\left( {T/{T_{{\rm{c, }}{{\rm{H}}_{\rm{2}}}{\rm{O}}}}} \right)^{ - 0.41}} \end{array} $

(15)

$ {v_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = 37.51 - 9.585 \times {10^{ - 2}}{T^{\rm{c}}} + 8.74 \times {10^{ - 4}}{T^{\rm{c}}}^2 - 5.044 \times {10^{ - 7}}{T^{\rm{c}}}^3 $

(16)

3 CO₂埋存综合模型

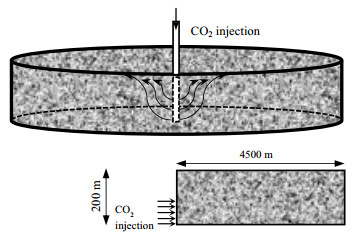
依据上述岩石-流体相关数学模型，结合油藏数值模拟软件GEM，建立耦合地层水蒸发、CO₂-地层水-岩石地化反应、NaCl析出和孔渗变化的CO₂埋存反应流动综合模型。GEM为油藏多相多组分软件，具有良好的地化反应计算功能，已广泛应用于CO₂地质埋存领域^{[9, 10, 31]}。模拟时，由于没有考虑温度变化，仅将水动力学和地化反应进行耦合求解。地化-盐析与流体流动间的影响，则通过孔隙度-渗透率关系式^[16]来实现。先将连续的数学偏微分方程组转换成离散的有限差分方程组，采用隐式压力显式饱和度法求解。考虑实际CO₂盐水层埋存，取以注入井为中心的圆柱形区域为研究对象，如图 2所示。目标盐水层顶部埋深1.2 km，厚200 m，半径为4500 m。储层压力按静水压力计算，顶部压力12 MPa，储层温度为50℃。储层孔隙度为0.18，水平渗透率为300 md，垂直渗透率率为100 md。模型上下层为封闭边界，模拟时仅有能量传递。储层径向网格299个，轴向1个，纵向20个。注入井在储层下部10层射孔，注入速率为15 kg·s^-1，其他参数见表 1。

图 2 CO₂盐水层埋存基础模型示意图 Fig.2 Schematic diagram of CO₂ geological storage in a saline aquifer

表 1 数值模拟基本模型主要参数设置 Table 1 Key parameters in the basic simulation model

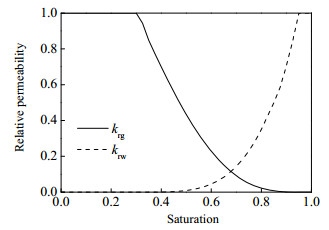
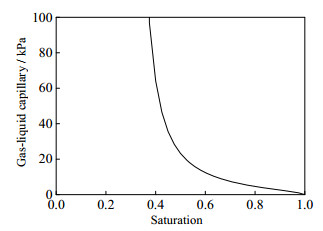
模型中气液相对渗透率采用Cory相渗模型计算^[32]，计算公式如式(17)所示，其中束缚水饱和度为0.3，残余气饱和度为0.05，得到相渗曲线如图 3所示。毛管力采用van Genuchten模型计算^[33]，计算公式如式(18)所示，其中毛管力系数p_cap⁰取值4×10^-3 MPa，van Genuchten毛管力参数γ取值0.412，毛管力曲线如图 4所示。

$ {k_{{\rm{rw}}}} = S_{{\rm{wn}}}^4;\;\;{k_{{\rm{rg}}}} = {\left( {1 - {S_{{\rm{wn}}}}} \right)^2}\left( {1 - S_{{\rm{wn}}}^2} \right) $

(17)

$ {p_{{\rm{cap}}}} = p_{_{{\rm{cap}}}}^0{\left( {S_{{\rm{wn}}}^{ - 1/\gamma } - 1} \right)^{1 - \gamma }} $

(18)

$ {S_{{\rm{wn}}}} = \frac{{{S_{\rm{w}}} - {S_{{\rm{wir}}}}}}{{1 - {S_{{\rm{wir}}}} - {S_{{\rm{gres}}}}}} $

(19)

图 3 气液相对渗透率曲线 Fig.3 Profiles of gas-liquid relative permeability

图 4 气液毛管力曲线 Fig.4 Profile of gas-liquid capillary force

由于储层矿物组成和地层水离子组成会严重影响CO₂-地层水-岩石地化反应，不同盐水层注入CO₂后会发生不同的地化反应，从而使得地化反应的研究不具有普遍性。为此，选取具有代表性的三种矿物进行分析，从机理上分析矿物溶解/沉淀对储层物性的影响。地层水和矿物初始组成参考相关文献如表 2所示，由于盐水层中NaCl含量最高，基础模型中设为2.5 mol·L^-1。文中所有反应热力学参数^{[16, 22, 31]}见表 3，矿物反应动力学参数^{[22, 23, 31]}见表 4。

表 2 地层水及岩石矿物组成 Table 2 Compositions of formation water and rock minerals

表 3 化学反应式及其反应平衡系数 Table 3 Chemical reaction equations and reaction equilibrium coefficients

表 4 矿物反应动力学参数取值 Table 4 The kinetic parameters of mineral reactions

4 岩石流体作用分析

在基础模型基础上，只改变网格尺寸大小，验证模型的准确性及精确性。建立了三个对比模型，分别为：将径向网格尺寸减小一半，建立网格数目为598×1×20的Case-2X径向对比模型；将垂向网格尺寸减小一半，建立了网格数目为299×1×40的Case-2Z垂向对比模型；同时将径向和垂向网格尺寸减小一半，建立了网格数目为598×1×40的Case-2X+2Z整体对比模型。不同尺寸模型结果如图 5所示，可以看出，虽然网格尺寸对干涸区域分布和储层物性有所影响，但影响不大。故可认为网格尺寸在一定的范围内对储层流体渗流和岩石流体组作用的影响不大，可采用基础模型对CO₂埋存中的岩石流体作用进行分析。

图 5 不同网格尺寸时储层孔隙度变化分布 Fig.5 Porosity variation distributions under different grid sizes (positive value means decrease of porosity, negative value means increase of porosity)

4.1 地化-盐析耦合现象分析

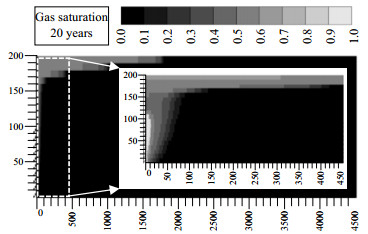
图 6为注入20年后储层中CO₂饱和度分布。可以看出，由于注入的CO₂与地层水存在密度差，导致注入的CO₂在浮力的作用下向储层顶部运移，形成漏斗状分布。在CO₂的运移过程中，注入井附近区域地层水首先被完全蒸发，形成干涸区(纯CO₂渗流区)。后续注入的CO₂沿着漏斗状渗流通道运移至储层顶部，并沿着储层顶部向储层内部运移，形成气液两相渗流区。纯CO₂渗流区随着CO₂持续注入不断扩展，20年后发展成短轴长约20 m的半椭圆形。

图 6 注入20年后CO₂饱和度分布 Fig.6 CO₂ saturation distribution after 20 years of injection

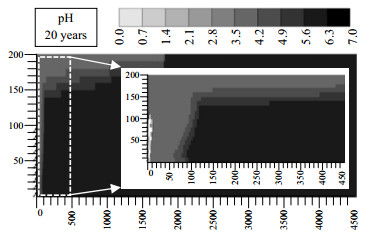
注入的CO₂溶解至地层水中，与地层水反应生成H⁺，导致地层水pH值下降。由pH值分布图 7可以看出，CO₂在地层水中的溶解使得地层水pH值由7降为4左右，导致地层水呈酸性。对比图 6与图 7可以发现，pH值变化区域随CO₂运移而运移，但其分布区域明显大于CO₂分布区域，并在CO₂溶解区(CO₂地层水接触边界附近)呈现出较大的pH值。这主要是因为溶解的CO₂在浓度差作用下会逐渐扩散到地层水中，从而使得相邻区域地层水呈现弱酸性。而注入区域附近由于地层水完全蒸发，无法显示溶液pH值。

图 7 注入20年后pH分布 Fig.7 pH distribution after 20 years of injection

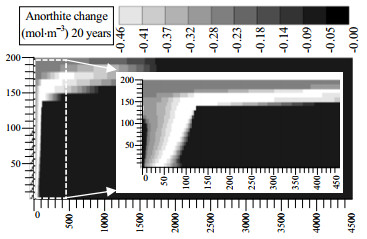
图 8为注入20年后储层中钙长石变化量分布，其中正值表明矿物沉淀，负值表明矿物溶解。可以看出随着CO₂在储层中的运移，钙长石发生溶解反应，20年后单位体积溶解量最高可达0.46 mol·m^-3。这是因为CO₂与地层水反应生成H⁺，打破了表 3中钙长石反应平衡常数，反应向右进行，导致钙长石溶解并生成Ca²⁺、Al³⁺和SiO_2(aq)离子。同时由图可以看出，储层中钙长石变化最剧烈处为CO₂溶解区域。这是因为相较于CO₂-地层水两相层中的钙长石可以与H⁺反应从而较多的溶解于地层水中。

图 8 注入20年后钙长石变化量分布 Fig.8 Anorthite variation distribution after 20 years of injection

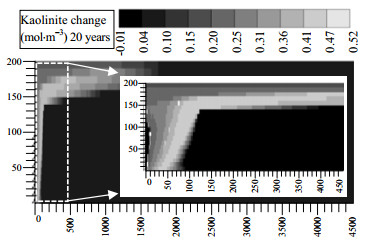
图 9为20年后储层中高岭石变化量分布，不同于钙长石，储层中CO₂的注入导致高岭石发生沉淀反应。这是因为钙长石反应速率较高于高岭石，导致高岭石与地层水中H⁺反应速率较慢。钙长石的溶解反应已消耗了部分H⁺，并且生成了大量的Al³⁺和SiO₂(aq)离子，从而导致表 3中高岭石反应向左进行，发生沉淀反应。同时也可以看出，储层中高岭石变化最剧烈处亦为CO₂溶解区域。

图 9 注入20年后高岭石变化量分布 Fig.9 Kaolinite variation distribution after 20 years of injection

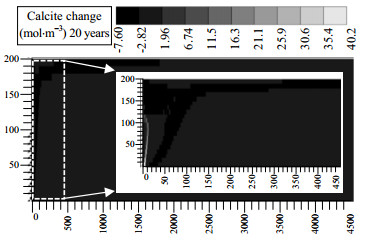
图 10为20年后储层中方解石变化量分布。可以看出，方解石在CO₂-地层水渗流区域发生溶解反应，且与钙长石和高岭石变化规律相同，20年后最大溶解量为7.6 mol·m^-3。但是，与钙长石和高岭石明显不同，方解石在干涸区域发生沉淀反应，并在干涸区域前缘发生大量沉淀。这是因为受CO₂持续蒸发作用，注入井区域地层水快速蒸发，从而在干涸区域前缘与储层内部地层水形成了较大的地层水饱和度梯度。随着地层水饱和度梯度的增加，干涸区域前缘处气液毛管力随之增加，当气液毛管力高于驱替压力时，储层内部地层水向注入井方向流动^{[15, 16]}。储层内部地层水回流至干涸前缘处时，受到持续注入的CO₂蒸发，导致水中离子浓度升高。由方解石反应时可知，地层水离子浓度升高，导致方解石反应向左发生，从而产生方解石沉淀。由于储层内部地层水不能补充注入井区域地层水的蒸发减少量，干涸区域前缘不断地向储层深部推进，从而导致方解石沉淀区域不断扩大。虽然蒸发导致离子浓度升高亦会导致钙长石和高岭石向左反应，但其反应速率较小，在地层水完全蒸发前无法快速的发生的沉淀。

图 10 注入20年后方解石变化量分布 Fig.10 Calcite variation distribution after 20 years of injection

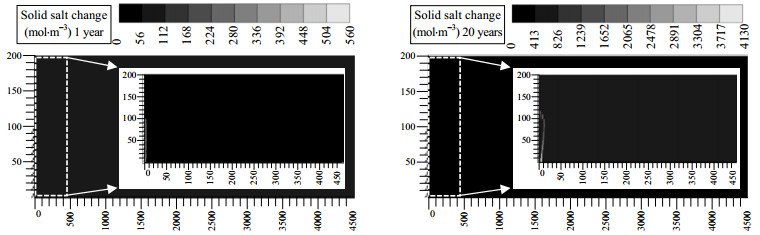
图 11为不同时间下储层中NaCl沉淀分布。可以看出，CO₂的注入会导致地层水中NaCl的析出，且NaCl沉淀区域随着储层干涸区域发展而发展，并在干涸区域前缘析出量最大。CO₂注入1年后，干涸区域前缘处NaCl析出量为560 mol·m^-3左右，而20年后，干涸区前缘处NaCl析出量便达2000~4000 mol·m^-3。这是因为在地层水回流作用下，水中NaCl不断被携带至干涸区域处，并在蒸发作用下持续析出所致。同时，地层水在重力影响亦会向下流动，导致干涸区域底部NaCl析出量最大。随着干涸区域不断增加，干涸区域前缘与储层内部地层水的接触面积越来越大，导致地层水补充量越多，从而使得干涸前缘NaCl析出量随干涸区域增加而增加。但是值得注意的是，当干涸区域增加到一定范围时，CO₂导致的地层水蒸发量和储层内部地层水的供应量达到平衡，干涸区域变不再扩展。此时储层内部NaCl会被地层水源源不断的携带至干涸区域前缘析出，从而完全堵塞储层。故盐水层注CO₂埋存时，须采取一定措施，降低盐析对储层和注入性的影响。

图 11 不同时间下析出NaCl分布 Fig.11 Precipitated salt distributions at different times

4.2 储层物性及注入性分析

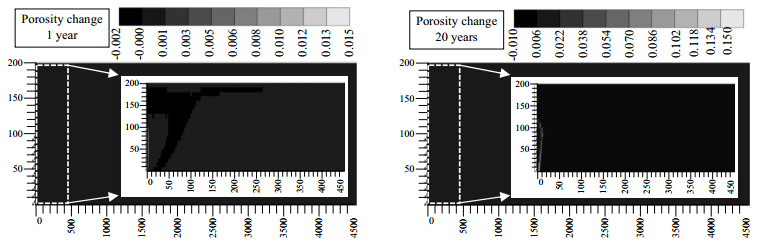
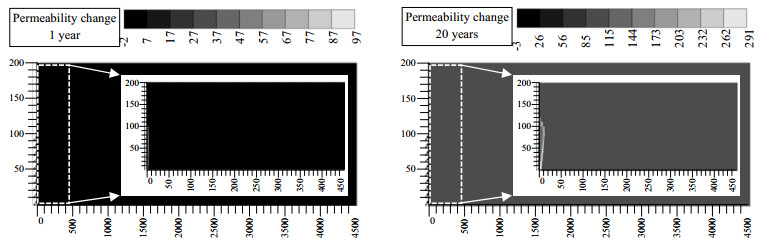
储层中矿物的沉淀和溶解势必会影响到储层孔隙度和渗透率。由上文分析可知，储层中CO₂-地层水两相渗流区域内矿物溶解量远大于矿物的沉淀量，故相应区域孔隙度及渗透率变低。由图 12可以看出，注入1年及20年后，两相渗流区域内孔隙度分别降低了0.002和0.01，变化量较小。而在注入井区域，由于大量NaCl在干涸区域前缘析出，导致孔隙度和渗透率大幅度下降。由图 12和图 13可以看出，1年后干涸区域前缘处孔隙度和渗透率分别降低了约0.01和50 md，20年后孔隙度和渗透率分别降低了约0.05和100 md，部分区域渗透率更是降低了290 md，几乎完全堵塞该处储层。图 14为注入井底端射孔处注入压力随时间的变化。可以看出，当考虑地化反应和盐析时，20年后注入压力由14 MPa升高到18.2 MPa；而当不考虑地化反应和盐析时，20年后注入压力才升至17.7 MPa。可见，岩石流体间作用，特别是盐析作用，导致CO₂埋存施工期限内注入压力生高了0.5 MPa

图 12 不同时间下储层孔隙度变化分布图 Fig.12 Porosity variation distribution at different times

图 13 不同时间下储层渗透率变化分布图（单位为md = 10^-15m²） Fig.13 Permeability variation distribution at different times (md = 10^-15m²)

图 14 注入井底部射孔处注入压力随时间的变化 Fig.14 Injection pressures at the bottom perforation at different times

5 敏感性及对选址影响

储层物性会影响流体流动特征，从而影响岩石流体作用。但实际储层物性复杂，且各物性相互影响，将其放在一起很难定量分析。为此，本文仅分析各个单一储层物性变化对岩石流体作用的影响，旨在从机理上给CO₂埋存选址及操作提供一定帮助。储层间各个物性的相互影响及其对岩石流体作用的影响，会在本文研究的基础上在下一步工作中进行。

5.1 注入速率分析

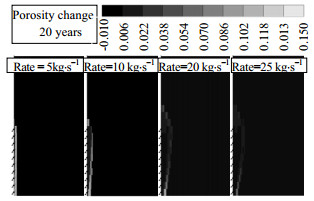
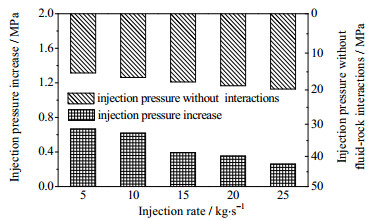
20年后不同注入速率下注入井区域储层孔隙度变化如图 15所示。随着CO₂注入速率增加，干涸区域变大，导致注入井附近更多区域孔隙度受到影响。但孔隙度受岩石流体作用影响随着注入速率的增加而降低。注入速率为5 kg·s^-1时，孔隙度约降低了0.12；而当注入速率为25 kg·s^-1时，孔隙度仅降低了0.03左右。这是因为孔隙度变化主要受盐析影响，随着注入速率的增加，减弱了地层水回流作用，使得NaCl无法被大量携带至干涸区域前缘处沉淀，降低了盐析对储层孔隙度的伤害。由图 16可见，注入速率为5 kg·s^-1时，岩石流体作用导致20年后注入压力升高了0.6 MPa；而当注入速率升高至25 kg·s^-1时，注入压力仅升高了0.25 MPa。可见，盐水层CO₂埋存时，可适当提高CO₂注入速率，降低盐析对注入性影响。

图 15 不同注入速率时储层孔隙度变化分布 Fig.15 Porosity variation distribution under different injection rates

图 16 不同注入速率时岩石流体对底端射孔处注入压力影响 Fig.16 Effects of rock-fluid interactions on injection pressure at the bottom perforation under different injection rates

5.2 地层水盐度分析

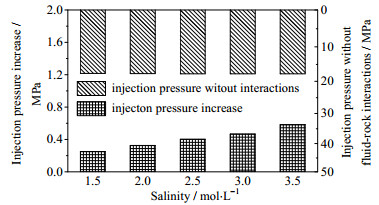
20年后不同地层水盐度下注入井区域孔隙度变化如图 17所示。地层水盐度改变对干涸区域分布没有影响，但盐析量随地层水盐度增加而增加，导致干涸区域孔隙度变化增大。可见，地层水盐度增加会加剧盐析对注入井区域储层物性的伤害，降低了注入井附近区域孔隙度和渗透率。由图 18可以看出，地层水盐度为1.5 mol·L^-1时，岩石流体作用(主要为盐析作用)导致20年后注入压力增加0.2 MPa；而当地层水盐度升至3.5 mol·L^-1时，则会导致20年后注入压力增加0.6 MPa。可见，地层水盐度增加会影响CO₂注入性。故盐水层CO₂埋存选址时，应尽量选取盐度较低的储层，降低盐析对储层和注入性的影响。

图 17 不同地层水盐度时储层孔隙度变化分布 Fig.17 Porosity variation distributions under different salinities

图 18 不同地层水盐度时岩石流体对底端射孔处注入压力影响 Fig.18 Effects of rock-fluid interactions on injection pressure at the bottom perforation under different salinities

5.3 初始孔隙度分析

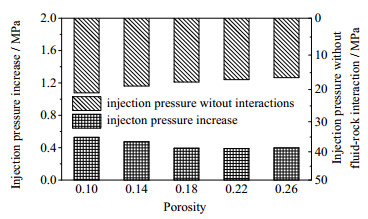
20年后不同孔隙度下注入井区域孔隙度变化如图 19所示。虽然不同初始孔隙度下储层孔隙度变化幅度差别不大，但由于初始孔隙度赋值不同，相同孔隙度变化幅度对应着不同程度的储层伤害。初始孔隙度越小，对应的孔隙度变化程度越大，岩石流体作用对储层的伤害越大。由图 20可以看出，初始孔隙度为0.1时，岩石流体作用导致注入压力增加0.5 MPa；初始孔隙度为0.26时，岩石流体作用仅导致注入压力增加0.4 MPa。同样说明，初始孔隙度的增加会降低盐析对储层物性的伤害，有利于CO₂注入性。故盐水层CO₂埋存选址时，应尽量选取孔隙度较大的储层，不仅可增加CO₂注入性，还可增加CO₂埋存体积。

图 19 不同初始孔隙度时储层孔隙度变化分布 Fig.19 Porosity variation distributions under different initial porosities

图 20 不同孔隙度时岩石流体对底端射孔处注入压力影响 Fig.20 Effects of rock-fluid interactions on injection pressure at bottom perforation under different initial porosities

5.4 初始渗透率分析

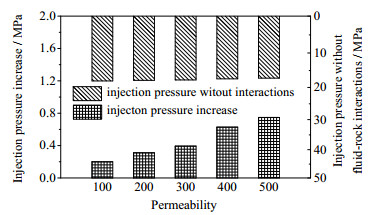
20年后不同渗透率下注入井区域孔隙度变化如图 21所示。随着初始渗透率增加，虽然干涸区域减小，但孔隙度变化幅度增加。初始渗透率为100 md时，岩石流体作用对储层孔隙度影响不大，仅导致干涸区域底部孔隙度下降0.03左右。初始渗透率为500 md时，岩石流体作用则导致孔隙度降低0.1左右，干涸区域上部孔隙度降幅更是达到0.15。这是因为随着初始渗透率的增加，驱替压差降低，地层水回流作用增加，从而加剧了盐析对储层孔隙度的伤害。由图 22可以看出，初始渗透率为100 md时，岩石流体作用仅导致注入压力升高0.15 MPa；而当初始渗透率为500 md时，岩石流体作用导致注入压力升高了0.75 MPa。可见，初始渗透率的增加会加剧盐析对储层的伤害，故在CO₂埋存时，不易选取渗透率较大的储层。

图 21 不同初始渗透率时储层孔隙度变化分布 Fig.21 Porosityvariation distributions under different initial permeabilities

图 22 不同渗透率时岩石流体对底端射孔处注入压力影响 Fig.22 Effects of rock-fluid interactions on injection pressure at bottom perforation under different permeabilities

6 结论

基于化学热力学平衡原理和动力学过程，成功将地层水蒸发盐析过程和CO₂-地层水-岩石地化反应过程耦合，建立了盐水层CO₂埋存反应流动综合模型，对CO₂注入过程中岩石流体反应及其对注入性的影响进行了分析。主要得到以下结论：

(1) 注入的CO₂在驱替压力和浮力作用下，呈漏斗状不断向储层深部运移。在地层水蒸发作用下，沿CO₂运移方向逐渐形成干涸区(纯CO₂渗流区)、气液两相渗流区和CO₂溶解区域。三个区域随CO₂持续注入不断形成及发展。

(2) CO₂的注入会打破储层中原有的矿物-地层水化学平衡，导致部分矿物溶解或沉淀。受地层水分布影响，矿物溶解/沉淀主要发生在气液两相渗流区和CO₂溶解区域；而CO₂溶解区地层水较多，溶解/沉淀导致的矿物变化量最大。

(3) 干涸区域前缘地层水饱和度梯度大，储层内部地层水在毛管力作用下会不断回流至干涸区域前缘，在地层水蒸发作用下，造成水中NaCl大量析出。模拟结果表明，受盐析影响，干涸区域前缘孔隙度平均下降0.05左右，渗透率平均下降100 md，部分储层更是完全堵塞。盐析现象对CO₂注入性影响远大于矿物溶解/沉淀的影响。

(4) 敏感性分析表明，注入速率、地层水盐度、初始渗透率对盐析影响较大，初始孔隙度影响较小。盐水层CO₂埋存选址时，地层水盐度和渗透率不易过高，从而降低岩石流体作用特别是盐析对储层和注入性的影响。

符号说明：

a	—水的无量纲关联系数，本文取2.6	N_β⁰	—初始时刻单位体积岩石中矿物β的摩尔量，mol·m^-3
$ \hat A $	—单位体积岩石内矿物β的反应表面积，m²·m^-3	N_β	—当前时刻单位体积岩石中矿物β的摩尔量，mol·m^-3
$ {\hat A^0} $	—初始时刻的反应表面积，m²·m^-3	p_cap	—气水毛管力，MPa
c_ig	—气相中组分i的质量分数，无量纲	p_cap⁰	—毛管力系数，MPa
c_iw	—水相中组分i的质量分数，无量纲	p_H₂O^s	—纯水的饱和压力，MPa
C_iw	—水相中组分i的浓度，mol·L^-1	p	—储层压力，MPa
D	—深度，m	Q_β	—矿物反应β的离子活度积，无量纲
D_CO₂	—水相中CO₂的扩散系数，m²·s^-1	q_i	—组分i的注入/采出量，kg·(m³·s)^-1
D_iw	—水相中组分i的扩散系数，m²·s^-1	r_β	—矿物β的溶解/沉淀反应速率，mol·m^-3·s^-1
E_β	—矿物反应β的活化能，J·mol^-1	R_mn	—矿物反应的个数
f_{CO₂, g}	—气相中CO₂的逸度，MPa	R_iw	—化学反应致组分i变化量，kg·(m³·s)^-1
f_{CO₂, w}	—液相中CO₂的逸度，MPa	S_wn	—归一化后的含水饱和度，无量纲
f_H₂O	—任何温度压力下纯水的逸度，MPa	S_wir	—为束缚水饱和度，无量纲
f_{H₂O, g}	—气相中水的逸度，MPa	S_gres	—为残余气饱和度，无量纲
f_{H₂O, w}	—液相中水的逸度，MPa	S_g	—气相饱和度，无量纲
f_H₂O^s	—纯水在饱和压力下的逸度，MPa	S_w	—水相饱和度，无量纲
F_iw	—水相中组分i的扩散变化量，kg·(m³·s)^-1	T'	—储层温度，°F
g	—重力加速度，m·s^-2；	T	—储层温度，K
H_{salt, CO₂}	—液相中CO₂的亨利常数，MPa	T_{c, H₂O}	— CO₂的临界温度，K
H_CO₂	—纯水中CO₂的亨利常数，MPa	T^c	—储层温度，℃
H_CO₂^s	—饱和压力下纯水中CO₂的亨利常数，MPa	v_H₂O	—水的摩尔体积，m³·mol^-1
k	—岩石绝对渗透率，md = 10^-15m²	v_CO₂	— CO₂的偏摩尔体积，m³·mol^-1
k_rg	—气相相对渗透率，无量纲	y_{H₂O, w}	—水相中H₂O摩尔分数，无量纲
k_rw	—水相相对渗透率，无量纲	y_{CO₂, w}	—液相中CO₂摩尔分数，无量纲
k_{salt, CO₂}	—盐度对CO₂溶解的影响系数，kg·mol^-1	γ	— van Genuchten毛管力参数，无量纲
k_β	—矿物反应β的反应速率常数，mol·m^-2·s^-1	▽	—微分算子
K_{0, β}	—参考温度T₀下的速率常数，mol·m^-2·s^-1	μ_g	—气相的黏度，m×Pa×s
K_{eq, β}	—矿物反应β的化学平衡常数，无量纲	μ_w	—水相的黏度，m·Pa·s
m_salt	—溶解盐的质量摩尔浓度，mol·kg^-1	ρ_g	—气相密度，kg·m^-3
M_i	—组分i的摩尔质量，g·mol^-1	ρ_w	—水相密度，kg·m^-3
M_H₂O	—水的摩尔质量，g·mol^-1	φ	—岩石孔隙度，无量纲
M_β	—组分β的摩尔质量，g·mol^-1

参考文献

[1]	De Silva G P D, Ranjith P G, Perera M S A. Geochemical aspects of CO₂ sequestration in deep saline aquifers:a review[J]. Fuel , 2015, 155: 128-143. DOI:10.1016/j.fuel.2015.03.045.
[2]	Celia M A, Bachu S, Nordbotten J M, et al. Status of CO₂ storage in deep saline aquifers with emphasis on modeling approaches and practical simulations[J]. Water Resources Research , 2015, 51(9): 6846-6892. DOI:10.1002/2015WR017609.
[3]	Baines S J, Worden R H. Geological storage of carbon dioxide[J]. Geological Society, London, Special Publications , 2004, 233(1): 1-6. DOI:10.1144/GSL.SP.2004.233.01.01.
[4]	Herzog H, Eliasson B, Kaarstad O. Capturing greenhouse gases[J]. Scientific American , 2000, 282(2): 72-79. DOI:10.1038/scientificamerican0200-72.
[5]	Chadwick A, Arts R, Bernstone C, et al. Best practice for the storage of CO₂ in saline aquifers-observations and guidelines from the SACS and CO₂store projects[M].Swindon: Halstan & Co Ltd, 2008.
[6]	Oldenburg C M. Screening and ranking framework for geologic CO₂ storage site selection on the basis of health, safety, and environmental risk[J]. Environmental Geology , 2008, 54(8): 1687-1694. DOI:10.1007/s00254-007-0947-8.
[7]	Rutqvist J. The geomechanics of CO₂ storage in deep sedimentary formations[J]. Geotechnical and Geological Engineering , 2012, 30(3): 525-551. DOI:10.1007/s10706-011-9491-0.
[8]	HU Shan(胡珊), WU Xiao-min(吴晓敏), SONG Yang(宋阳), et al. Numerical investigation on mass transfer of CO₂ storing in deep saline aquifers(二氧化碳深盐水层埋存传质数值模拟)[J]. CIESC Journal(化工学报) , 2012, 63(S1): 59-63.
[9]	Nghiem L, Sammon P, Grabenstetter J, et al. Modeling CO₂ storage in aquifers with a fully-coupled geochemical EOS compositional simulator[C]//Proceedings in SPE/DOE symposium on improved oil recovery. Tulsa: Society of Petroleum Engineers, 2004.
[10]	Jin M, Ribeiro A, Mackay E, et al. Geochemical modelling of formation damage risk during CO₂ injection in saline aquifers[J]. Journal of Natural Gas Science and Engineering , 2016, 35: 703-719. DOI:10.1016/j.jngse.2016.08.030.
[11]	André L, Audigane P, Azaroual M, et al. Numerical modeling of fluid-rock chemical interactions at the supercritical CO₂-liquid interface during CO₂ injection into a carbonate reservoir, the Dogger aquifer (Paris Basin, France)[J]. Energy Conversion & Management , 2007, 48(6): 1782-1797.
[12]	Cui G, Zhang L, Tan C, et al. Injection of supercritical CO₂ for geothermal exploitation from sandstone and carbonate reservoirs:CO₂-water-rock interactions and their effects[J]. Journal of CO₂ Utilization , 2017, 20: 113-128. DOI:10.1016/j.jcou.2017.05.006.
[13]	Andre L, Peysson Y, Azaroual M. Well injectivity during CO₂ storage operations in deep saline aquifers-Part 2:Numerical simulations of drying, salt deposit mechanisms and role of capillary forces[J]. International Journal of Greenhouse Gas Control , 2014, 22: 301-312. DOI:10.1016/j.ijggc.2013.10.030.
[14]	Miri R, Hellevang H. Salt precipitation during CO₂ storage-a review[J]. International Journal of Greenhouse Gas Control , 2016, 51: 136-147. DOI:10.1016/j.ijggc.2016.05.015.
[15]	Ott H, Roels S M, De Kloe K. Salt precipitation due to supercritical gas injection:Ⅰ. Capillary-driven flow in unimodal sandstone[J]. International Journal of Greenhouse Gas Control , 2015, 43: 247-255. DOI:10.1016/j.ijggc.2015.01.005.
[16]	Cui G, Zhang L, Ren B, et al. Geothermal exploitation from depleted high temperature gas reservoirs via recycling supercritical CO₂:heat mining rate and salt precipitation effects[J]. Applied Energy , 2016, 183: 837-852. DOI:10.1016/j.apenergy.2016.09.029.
[17]	Wilke C R, Chang P. Correlation of diffusion coefficients in dilute solutions[J]. AIChE Journal , 1955, 1(2): 264-270. DOI:10.1002/(ISSN)1547-5905.
[18]	Reid R C, Prausnitz J M, Sherwood T K. The properties of gases and liquids[M].New York: McGraw-Hill, 1977.
[19]	LI Lan-lan (李兰兰). Determination of diffusion coefficients of CO₂ and CH₄ in NaCl aqueous solutions under wide temperature-pressure conditions by in situ micro-Raman spectroscopy (显微激光拉曼光谱原位测定广阔温压条件下CO₂、CH₄在盐水溶液中的扩散系数) [D]. Wuhan (武汉): China University of Geosciences (中国地质大学), 2013.
[20]	Tamimi A, Rinker E B, Sandall O C. Diffusion coefficients for hydrogen sulfide, carbon dioxide, and nitrous oxide in water over the temperature range 293~368 K[J]. Journal of Chemical and Engineering Data , 1994, 39(2): 330-332. DOI:10.1021/je00014a031.
[21]	GUO Biao(郭彪), HOU Ji-rui(侯吉瑞), YU Chun-lei(于春磊), et al. Determination of diffusion coefficient for carbon dioxide in the porous media(CO₂在多孔介质中扩散系数的测定)[J]. Journal of Petrochemical Universities(石油化工高等学校学报) , 2009, 22(4): 38-40.
[22]	CUI Guo-dong(崔国栋), REN Shao-ran(任韶然), ZHANG Liang(张亮), et al. Effects of rock-fluid interaction and water back flow on heat mining efficiency of geothermal development via carbon dioxide injection(二氧化碳羽流地热系统中地层水回流和岩石-流体作用对采热能力的影响)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2016, 30(5): 1043-1052.
[23]	Alkattan M, Oelkers E H, Dandurand J L, et al. Experimental studies of halite dissolution kinetics, 1. The effect of saturation state and the presence of trace metals[J]. Chemical Geology , 1997, 137(3-4): 201-219. DOI:10.1016/S0009-2541(96)00164-7.
[24]	Borgia A, Pruess K, Kneafsey T J, et al. Numerical simulation of salt precipitation in the fractures of a CO₂-enhanced geothermal system[J]. Geothermics , 2012, 44: 13-22. DOI:10.1016/j.geothermics.2012.06.002.
[25]	Kim K Y, Han W S, Oh J, et al. Characteristics of salt-precipitation and the associated pressure build-up during CO₂ storage in saline aquifers[J]. Transport in Porous Media , 2012, 92(2): 397-418. DOI:10.1007/s11242-011-9909-4.
[26]	Peng D Y, Robinson D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals , 1976, 15(1): 59-64.
[27]	Saul A, Wagner W. International equations for the saturation properties of ordinary water substance[J]. Journal of Physical and Chemical Reference Data , 1987, 16(4): 893-901. DOI:10.1063/1.555787.
[28]	Rowe Jr A M, Chou J C S. Pressure-volume-temperature-concentration relation of aqueous sodium chloride solutions[J]. Journal of Chemical and Engineering Data , 1970, 15(1): 61-66. DOI:10.1021/je60044a016.
[29]	Li Y K, Nghiem L X. Phase equilibria of oil, gas and water/brine mixtures from a cubic equation of state and Henry's law[J]. The Canadian Journal of Chemical Engineering , 1986, 64(3): 486-496. DOI:10.1002/cjce.v64:3.
[30]	Harvey A H. Semiempirical correlation for Henry's constants over large temperature ranges[J]. AIChE Journal , 1996, 42(5): 1491-1494. DOI:10.1002/(ISSN)1547-5905.
[31]	Kumar A, Datta-Gupta A, Shekhar R, et al. Modeling time lapse seismic monitoring of CO₂ sequestration in hydrocarbon reservoirs including compositional and geochemical effects[J]. Petroleum Science and Technology , 2008, 26(7-8): 887-911. DOI:10.1080/10916460701825505.
[32]	Corey A T. The interrelation between gas and oil relative permeabilities[J]. Producers Monthly , 1954, 19(1): 38-41.
[33]	Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal , 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x.