高温高压气液两相流体输运,是许多工业装置中必不可少的工艺过程[1-3]。如在超临界流体微细晶体成核技术中[4-5],流体要通过加压设备向成核设备输送并利用快速降压来促进化合物的成核晶化最终制备粒度分布均匀的微细晶体,该过程的压力可达30 MPa;再如亚/超临界水氧化工艺中产物的输送、降压和分离等过程[6-7],该工艺的压力和温度分别为20 MPa和300 ℃以上。这些工艺的特点决定了输运流体往往处于临界或近临界状态,此时压力的少许改变将引起工质物性剧烈波动,并引发相变使得两相流动过程极为复杂。因此涉及高温高压下输运管路结构的设计与优化,精确预测管内压降与阻力特性,是相关工业技术中急需解决的关键问题。
近年来,针对管内气液两相流动过程,国内外学者进行了大量的实验与模拟研究。如Carraretto等[8]的研究表明压降随管路长度增加呈线性降低;Banafi等[9]通过对管内空气-水流动过程研究发现压力梯度随流速增加逐渐增大;Garcia等[10]对水平管内压降的影响因素进行了评估,表明压力梯度随质量流量的增加、管径的减小、饱和温度的降低而增大;赵月[11]模拟了层流和湍流状态下突扩管内流体的流动特性,发现局部阻力与管径的突扩比以及雷诺数具有很高的关联性。尽管对于两相流动的研究较多,但实验条件一般为常温、常压,且在利用数值模拟进行研究时通常假设工质物性和温度恒定。而在实际的工业应用中,一些特殊工艺流程决定了管路输运过程通常处于高温高压状态,此时气液两相物理性质强烈依赖于温度和压力的变化,同时过程还涉及压力降低导致的剧烈相变,这使得压降、温度和流速等参数波动较大,难以测量,而实际上这些参数的精确计算对于输运管路的设计与优化至关重要[12]。
鉴于上述现状,本研究针对典型管路单元,选取亚/超临界水氧化处理有机废水工艺中的典型工况,通过对高温高压下多组分气液两相流模型的合理构建,结合流体仿真技术探究管内气液两相流动特性并对实验中难以测量的参数进行预测,为设计与优化管路结构以实现经济高效的输运过程提供一定指导。
2 模型与数值模拟方法 2.1 物理模型管路模型的结构如图 1所示,总长度均为1 m。采用细网格进行非结构化网格划分,并在主流区设置均匀网格,在边界层附近对网格进行加密操作,同时对网格无关性进行检验。

|
图 1 管路结构及网格划分 Fig.1 Pipeline structure and grid |
基于CFD软件,采用压力基求解器进行非稳态计算,湍流模型选择Realizable k-ε模型,边界条件采用质量流量入口、压力出口以及无滑移绝热壁面。管壁粗糙度根据材质特性取0.05 mm,近壁面处采用标准壁面函数进行处理,由于流动工质为多组分气液两相构成且过程涉及减压相变,气液相间存在一定的滑移速度,因此多相流模型采用内置的耦合漂移通量滑移的混合(Mixture)模型,动量方程和能量方程的离散采用二阶迎风格式,非稳态相采用二阶隐式离散,时间步长取0.001 s。质量、动量和能量的控制方程如(1) ~ (3)所示。
| $ \frac{\partial }{{\partial t}}\left( {\rho m} \right) + \nabla \cdot \left( {{\rho _{\text{m}}}{\upsilon _{\text{m}}}} \right) = \mathop m\limits^ \cdot $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {{\rho _{\text{m}}}{\upsilon _{\text{m}}}} \right) + \nabla \cdot \left( {{\rho _{\text{m}}}{\upsilon _{\text{m}}}} \right) = - \nabla p + \nabla \cdot \left[ {{\mu _{\text{m}}}\left( {\nabla {\upsilon _{\text{m}}} + \nabla \upsilon _{\text{m}}^{\text{T}}} \right)} \right] + {\rho _{\text{m}}}g + F + \nabla \cdot \left( {\sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}} {{\boldsymbol{\upsilon}} _{{\text{dr, }}k}}} \right) $ | (2) |
| $ \frac{\partial }{{\partial t}}\sum\limits_{k = 1}^n {\left( {{\alpha _k}{\rho _k}{E_k}} \right)} + \nabla \cdot \sum\limits_{k = 1}^n {\left( {{\alpha _k}{\upsilon _k}\left( {{\rho _k}{E_k} + p} \right)} \right)} = \nabla \cdot \left( {{k_{{\text{eff}}}}\nabla T} \right) + {S_{\text{E}}} $ | (3) |
选取亚/超临界水氧化处理有机废水工艺中的典型工况,工质构成包括气态水、液态水、氮气、二氧化碳和氧气等;入口处总质量流量为0.80 kg·s−1,气体占72.5%。采用Aspen Plus软件中的ENRTL-RK模型对压力在5~25 MPa的混合物物性进行计算,入口条件设置为组分的质量流量,计算得到气液相对应的物性参数平均值,根据Fluent软件中物性为温度响应耦合的特点,将结果拟合为物性随温度的变化方程,如式(4)~(11)所示。
| $ {\rho _{\text{g}}} = - 4.39 \times {10^{ - 1}} + 7.49 \times {10^{ - 4}}{{\rm{e}}^{\left( {T/47.17} \right)}} $ | (4) |
| $ {\mu _{\text{g}}} = - 1.84 \times {10^{ - 6}} + 5.19 \times {10^{ - 8}}T - 4.00 \times {10^{ - 12}}{T^2} $ | (5) |
| $ {k_{\text{g}}} = - 5.90 \times {10^{ - 3}} + 8.66 \times {10^{ - 5}}T - 3.59 \times {10^{ - 10}}{T^2} $ | (6) |
| $ {c_{{\text{p, g}}}} = 4.33 \times {10^3} - 1.42 \times 10T + 1.76 \times {10^{ - 2}}{T^2} $ | (7) |
| $ {\rho _{\rm{L}}} = 1.21 \times {10^3} - 1.22 \times {10^{ - 1}}T - 1.20 \times {10^{ - 3}}{T^2} $ | (8) |
| $ {\mu _{\rm{L}}} = 7.41 \times {10^{ - 5}} + 3.57 \times {10^{ - 2}}{{\rm{e}}^{\left( { - T/74.16} \right)}} $ | (9) |
| $ {k_{\rm{L}}} = - 4.39 \times {10^{ - 1}} + 5.80 \times {10^{ - 3}}T - 7.56 \times {10^{ - 6}}{T^2} $ | (10) |
| $ {c_{{\rm{p, L}}}} = 1.13 \times {10^4} - 3.83 \times 10T + 4.96 \times {10^{ - 2}}{T^2} $ | (11) |
采用自定义函数(user-defined function,UDF)定义了相变的发生条件、质量和能量传递量,分别以源项的形式并入质量和能量方程[13],源项如式(12)~(16),这里的γ为时间松弛因子[14],它在一定程度上反映了控制体内相间的传质速率,在模拟过程中需要对其值的选取进行微调以匹配实验数据。本研究将流动减压闪蒸过程类比于流动沸腾相变过程对该因子的取值进行了验证。通过对亚/超临界水氧化工艺中典型工况下(入口雷诺数在4 011~16 042)水平直管内的模拟结果分析后发现,当γ=1 000 s−1时,传热系数为2.6 W·cm−2·K−1,一般的流动沸腾相变传热过程中铜表面的传热系数在2~3 W·cm−2·K−1 [15],两者数量级相当,说明时间松弛因子的取值合理。
| $ {m_{{\text{Lg}}}} = \frac{{ - \gamma {\rho _{\rm{L}}}\alpha \left( {{T_{\rm{L}}} - {T_{{\text{sat}}}}} \right)}}{{{T_{{\text{sat}}}}}} $ | (12) |
| $ \frac{{\partial {m_{\rm{Lg}}}}}{{\partial \alpha }} = \frac{{ - \gamma {\rho _{\rm{L}}}\left( {{T_{\rm{L}}} - {T_{{\text{sat}}}}} \right)}}{{{T_{{\text{sat}}}}}} $ | (13) |
| $ {m_{{\text{gL}}}} = \frac{{\gamma {\rho _{\text{L}}}\alpha \left( {{T_{\rm{L}}} - {T_{{\text{sat}}}}} \right)}}{{{T_{{\text{sat}}}}}} $ | (14) |
| $ \frac{{\partial {m_{{\text{gL}}}}}}{{\partial \alpha }} = 0 $ | (15) |
| $ {S_{\text{E}}} = {m_{\rm{Lg}}} \cdot {h_{{\text{sat}}}} = \frac{{ - {h_{{\text{sat}}}}\gamma {\rho _{\rm{L}}}\alpha \left( {{T_{\rm{L}}} - {T_{{\text{sat}}}}} \right)}}{{{T_{{\text{sat}}}}}} $ | (16) |
为了证明模拟结果与网格数目无关,考察了网格细化程度对管内压力的影响,划分了4种不同数目的网格,分别为15万、23万、35万和47万。表 1为D0=0.008 m、L0=1 m时,不同网格数目下,管内压力的分布特点。通过计算发现,当网格数目为15万与47万时,压降的误差仅为0.1%。因此,从既能准确描述气液两相流动特性又不会过多占用计算资源2个方面考虑,最终选取的网格数目为15万。
|
|
表 1 不同网格数目下管路内气液两相流动压降 Table 1 Pressure drop of gas-liquid two-phase flow in the pipeline under different grid numbers |
管内气液两相流动压降一般包括摩擦压降、动量压降、重位压降以及局部阻力压降,如式(17)所示。验证过程采用的模型为水平等径直管,重位压降和局部阻力压降不予考虑。目前针对高温高压下多组分气液两相流动过程模拟鲜有报道,因此本研究选取了文献[16-18]中高温高压下纯水的气液两相流动过程进行对比,结果如表 2所示。2种计算方法的相对误差在20% 以内,表明采用本研究建立的模型对管内高温高压下多组分气液两相流动特性的模拟方法准确可行。
| $ \Delta p = \Delta {p_{\text{f}}} + \Delta {p_{\text{g}}} + \Delta {p_{\text{a}}} + \Delta {p_{\text{b}}} $ | (17) |
| $ \Delta {p_{\text{f}}} = \psi \lambda \frac{L}{D}\frac{{{{\left( {{\rho _{\text{m}}}{\upsilon _{\text{m}}}} \right)}^2}}}{{2{\rho _{\text{L}}}}}\left[ {1 + x\left( {\frac{{{\rho _{\text{L}}}}}{{{\rho _{\text{g}}}}} - 1} \right)} \right] $ | (18) |
|
|
表 2 管内纯水气液两相流动压降的数值模拟值与经验公式计算值 Table 2 Simulated and empirically calculated pressure drop of gas-liquid two-phase flow of pure water in the pipe |
当
| $ \psi {\text{ = 1 + }}\frac{{x\left( {1 - x} \right)\left( {\frac{{{1_{}}000}}{{\rho \upsilon }} - 1} \right)\frac{{{\rho _{\text{L}}}}}{{{\rho _{\text{g}}}}}}}{{1 + x\left( {\frac{{{\rho _L}}}{{{\rho _{\text{g}}} - 1}}} \right)}} $ | (19) |
当
| $ \psi = 1 + \frac{{x\left( {1 - x} \right)\left( {\frac{{{1_{}}000}}{{\rho \upsilon }} - 1} \right)\frac{{{\rho _{\text{L}}}}}{{{\rho _{\text{g}}}}}}}{{1 + \left( {1 - x} \right)\left( {\frac{{{\rho _{\text{L}}}}}{{{\rho _{\text{g}}} - 1}}} \right)}} $ | (20) |
| $ \lambda = \frac{1}{{4{{\left( {\lg 3.7\frac{D}{\varepsilon }} \right)}^{\text{2}}}}} $ | (21) |
| $ \Delta {p_{\text{a}}} = {\left( {\rho \upsilon } \right)^2}\left( {{x_{{\text{out}}}} - {x_{{\text{in}}}}} \right)\left( {\frac{1}{{{\rho _{\text{g}}}}} - \frac{1}{{{\rho _{\text{L}}}}}} \right) $ | (22) |
图 2为管内压力分布,当管径一定时,由于流动阻力的存在,压力沿流动方向逐渐降低;针对不同直径管内流动过程研究发现,当D0=0.008 m时,Δp=4.7 MPa,随着管径的增大,压降逐渐降低,当D0=0.016 m时,Δp=0.2 MPa,表明当管径增大至一定范围时,压降变化不再显著。此外,经典两相流中关于压降的计算通常忽略加速压降的贡献(仅占总压降的2%),将总压降近似等价为摩擦压降,而在亚/超临界流动中,加速压降占比达到15% 以上,因此计算总压降时要将其考虑在内。同时,根据经验公式,加速压降的计算还要对干度、密度以及流速进行精确预测,而亚/超临界流动过程中的高温高压条件给实验测量带来一定的难度,数值模拟可以很好地弥补这一缺点。图 3描述了气含率的变化,当压力低于饱和压力时,组分中的水发生相变,气含率增加,当D0=0.008 m,管路出口处φ=96.2%,随着管径的增大,气含率逐渐升高,当D0=0.016 m时,出口处φ=97.8%,产生这种现象的原因主要是在管路长度和质量流量恒定的条件下,管径越小,流体流速越大,流体在管内的停留时间相对较短,由于流动过程并不能瞬间达到相平衡,因此流体快速通过管路时相变率较低,从而导致整体气含率相对较少。

|
图 2 水平直管内压力变化 Fig.2 Pressure variation in the horizontal |

|
图 3 水平直管内气含率变化 Fig.3 Gas holdup variation in the horizontal straight pipe |
流速的变化规律如图 4所示,由于相变的发生使得气体增加,整体比容上升,且质量流量恒定时,流速随管径的增大逐渐减小。关于温度变化情况如图 5所示,管内相变过程吸收热量(管路视为绝热),因此温度沿流动方向逐渐降低但变化曲线并不是呈简单的线性分布,除了相变的影响外,与工质物性的剧烈变化也存在一定关系。

|
图 4 水平直管内流速变化 Fig.4 Velocity variation in the straight horizontal pipe |

|
图 5 水平直管内温度变化 Fig.5 Temperature variation in the straight horizontal pipe |
进一步对管内的阻力损失进行分析,结果如图 6所示。管内阻力损失随管径增大逐渐降低,但当管径增大到0.016 m时,管内阻力变化趋于平缓。说明在管路的设计与优化过程中,流量恒定的条件下存在一个临界管径。针对亚/超临界水氧化处理有机废水工艺中的输运问题,如果从降低阻力损失,提高输运效率方面考虑应选择较大直径的管路,但管径的增大也将增加设计成本。此外,产物的输运过程中还要求一定的压降以实现气液相分离,基于这一方面的考虑应选择较小管径,但如果管径过小,流体的高流速易加重管路的磨蚀,缩短管路的使用寿命[19]。因此如果采用水平直管输运,管径范围应控制在0.010~0.014 m较为适宜,此时管内流速远低于声速,对管路造成的磨蚀效应相对较小。

|
图 6 水平直管内阻力损失 Fig.6 Resistance loss in the horizontal straight pipe |
本节探究了相同扩张比(E=D2/D1=1.5)下渐扩管内流体的流动特性,其中渐扩段管路长度分别为L1=0、0.1、0.2、0.3和0.4 m。
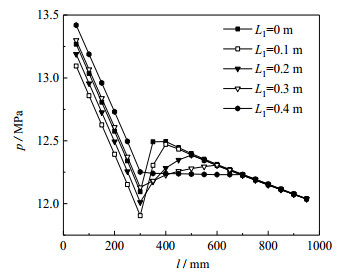
图 7为水平渐扩管内压力分布。等径段内流体由于只受摩擦阻力的影响,压降与管路长度呈线性关系;而在渐扩段内压力随渐扩管路长度的增加呈现不同的变化趋势,当L1 < 0.3 m时,管内压力升高;当L1 > 0.3 m时,压力则沿流动方向逐渐降低。主要原因是渐扩段内流体同时受摩擦阻力与局部阻力的共同影响。关于流速的变化如图 8所示,从图中可以发现,管路出入口段流速的变化规律与等径直管相同,均呈逐渐增大的趋势,但在渐扩段内,管内流速除了受相变的影响,还与管径的变化存在一定关系,当流经各截面的质量流量恒定时,流体流速随管径的增大而减小,且后者的影响要远大于前者,因此流速沿流动方向迅速降低。此外,从图 9所示的温度变化可以发现,管内温度沿流动方向逐渐降低,这与水平等径直管内变化趋势相同,但当L1=0 m时,温度在突扩截面处突然降低。而突扩截面处气含率呈现突然升高的特征,如图 10所示。
|
图 7 水平渐扩管内压力变化 Fig.7 Pressure variation in the horizontal diffuser pipe |

|
图 8 水平渐扩管内速度变化 Fig.8 Velocity variation in the horizontal diffuser pipe |

|
图 9 水平渐扩管内温度变化 Fig.9 Temperature variation in the horizontal diffuser pipe |

|
图 10 水平渐扩管内气含率变化 Fig.10 Gas holdup variation in the horizontal diffuser pipe |
针对突扩截面处温度以及气含率的反常现象,对管内速度和气体分布特点进行了分析,结果如图 11和12所示。首先,从速度分布云图中可以发现,当L1=0 m时,即突扩管路,流体流经突扩截面在上下拐角处分别形成一个带有涡旋的回流区,涡旋的产生增大能量的消耗,导致突扩截面拐角处温度降低幅度增大;同时,回流现象导致流体在截面上下拐角处聚集,与液相相比,气相惯性较小更易于在此回流区聚集,其结果使得拐角处气含率较高,出现2个对称的高气含率区,如图 10所示,导致截面处的平均气含率异常升高。

|
图 11 水平渐扩段管内速度分布 Fig.11 Velocity distribution in the horizontal diffuser pipe |

|
图 12 水平渐扩管内气含率分布 Fig.12 Gas holdup distribution in the horizontal diffuser pipe |
水平渐扩管内压降和阻力损失变化如图 13所示。从图中可以看出,两者均随着渐扩段管路长度的增加呈现先降低后升高的趋势,即当L1=0.1 m时,压降和阻力损失达到最低值,分别为0.9和1.4 MPa,此时输运效率较高。结合图 8可以发现,渐扩管内流速降低,这有利于削弱流体对管路的磨蚀,延长管路的使用寿命。因此如果选择渐扩管,渐扩段的适宜长度为0.1 m。

|
图 13 水平渐扩管内压降和阻力损失 Fig.13 Pressure drop and resistance loss in the horizontal diffuser pipeline |
本节考察了相同收缩比(K=D2 /D1=2/3)水平渐缩管内流体的流动特性,其中渐缩段管路长度分别为L1=0、0.1、0.2、0.3和0.4 m。
水平渐缩管内压力始终沿流动方向降低,且在等径段流体由于只受摩擦阻力的影响,压力变化与水平等径直管类似,但不同管径下压力的变化率不同,主要是因为在质量流量恒定的条件下,不同管径内流体的平均流速不同,大管径内流速低、压力减小缓慢,小管径内流速相对较高、压力降低较快,在渐缩段内,管内压降的变化率随渐缩段管路长度的增加而降低,当L1=0.1 m时,∆p=7.89 MPa,而当L1=0.4 m时,∆p=4.45 MPa,如图 14所示。图 15描述了管内流速的变化,从图中可以发现,流速沿流动方向逐渐增大且渐缩段内的变化率较高,这是因为渐缩段内流体除了受气体增加导致整体比容上升的影响外,管径的减小也使得部分压力能转化为速度能。与水平渐扩管路相比,水平渐缩管内温度始终沿流动方向呈非线性降低,当L1=0 m时,突缩截面处的温度并没有出现反常,如图 16所示。同时从图 17描述的水平渐缩管内气含率的变化情况也可看出,随着相变的进行,管内气含率逐渐升高,且在突缩截面处并没有表现出陡然升高的特点。

|
图 14 水平渐缩管内压力变化 Fig.14 Pressure variation in the horizontal tapered pipe |

|
图 15 水平渐缩管内速度变化 Fig.15 Velocity variation in the horizontal tapered pipe |

|
图 16 水平渐缩管内温度变化 Fig.16 Temperature variation in the horizontal tapered pipe |

|
图 17 水平渐缩管内气含率变化 Fig.17 Gas holdup variation in the horizontal tapered pipe |
进一步对图 18中管内速度分布分析后发现,与水平渐扩管路相比,水平渐缩管内流体流经突变截面时,在拐角处并未发生回流现象[20],因此温度及气含率的变化与水平等径直管类似,并没有出现反常。

|
图 18 水平渐缩段管内速度分布 Fig.18 Velocity distribution in the horizontal tapered pipe |
渐缩管内压降与阻力损失随渐缩段管路长度的增加先降低后升高再降低,且数值高于相同条件下(工质组成、初始边界条件相同)渐扩管内对应的压降值,如图 19所示。因此针对工艺流程中如需快速降压,可考虑采用渐缩管路。但值得注意的是,当L1=0 m时管路内的压降虽然达到最大值,但由于管路突变使得速度在变径处急剧升高,因此对管路的安全控制有更高要求,同时压降瞬间剧烈变化还可能导致水合物的形成进而堵塞管路。因此,在亚/超临界水氧化工艺流程中,如考虑快速降压,宜采用水平渐缩管路,其中渐缩段管路长度应控制在0.2~0.3 m,此范围内的流体流速在40~140 m·s−1,低于声速。

|
图 19 水平渐缩管内压降和阻力损失 Fig.19 Pressure drop and resistance loss in the horizontal tapered pipe |
综上所述,不同管路构型中压降、温度以及流速等参数存在很大差别,通过数值模拟方法明晰了管内流动特性,获得两相流相关参数,进而指导管路的设计与优化。本研究是基于特定工艺流程下的模拟结果,而在实际的管路设计过程中,不同工艺流程中的组分构成、物性参数和相变传递量等均存在一定差异,在这种情况下,必须对物性和相变方程进行重新拟合。
4 结论针对高温高压气液两相流体输运问题,选取亚/超临界水氧化处理有机废水工艺中的典型工况,采用Fluent软件对等径直管、渐扩管以及渐缩管内流动特性进行了三维非稳态模拟,得到如下结论:
(1) 管内温度沿流动方向呈非线性降低,气含率逐渐升高;等径直管和渐缩管内流速均沿流动方向逐渐增大,但渐缩管内流速波动较大;而渐扩管内流体流速则先缓慢增大,再迅速降低,后又小幅增大。
(2) 不同结构管路内压降及阻力损失具有不同的变化特点。其中等径直管内压降及阻力损失随管径增大而减小,且存在一个临界直径,超过该直径压降及阻力损失几乎不再变化;渐扩管内压降和阻力损失随渐扩段管路长度的增加呈先降低后升高的变化趋势,即存在一个压降和阻力损失最低点,此时输运效率最高;水平渐缩管内压降及阻力损失随渐缩段管路长度的增加先降低后升高再降低,且数值高于相同条件下的渐扩管路。因此,该管型有利于实现压力的快速降低。
(3) 综合全文分析,针对本研究所选取的亚/超临界水氧化处理有机废水工艺中的典型工况,若采用等径直管输运,管径应控制在0.01~0.014 m;若采用渐扩管路输运,渐扩段长度应控制在0.1 m左右;若考虑快速降压时,则宜采用渐缩管路,此时渐缩段长度应控制在0.2~0.3 m。
符号说明:
|
|
| [1] |
WANG Y, LIU Z, CHANG Y, et al. Experimental study of gas-liquid two-phase wavy stratified flow in horizontal pipe at high pressure[J]. International Journal of Heat and Mass Transfer, 2019, 143(11): 118537. |
| [2] |
JOHNSON G W, BERTELSEN A F, NOSSEN J. An experimental investigation of roll waves in high pressure two-phase inclined pipe flows[J]. International Journal of Multiphase Flow, 2009, 35(10): 924-932. DOI:10.1016/j.ijmultiphaseflow.2009.06.003 |
| [3] |
WANG Y, CHANG Y, LIU Z, et al. Experimental and theoretical study of interface characteristics of gas–liquid stratified flow in horizontal pipe at high pressure[J]. Applied Scientific Research, 2020, 105(3): 1249-1275. |
| [4] |
SHETH P, SANDHU H, SINGHAL D, et al. Nanoparticles in the pharmaceutical industry and the use of supercritical fluid technologies for nanoparticle production[J]. Current Drug Delivery, 2012, 9(3): 269-284. DOI:10.2174/156720112800389052 |
| [5] |
MCHUGH M A, KRUKONIS V J. Supercritical fluid extraction. Principles and practices[J]. Solvent Extraction, 1994, 32(1): 20-25. |
| [6] |
BERMEJO M D, MARTÍN A, QUEIROZ J P S, et al. Computational fluid dynamics simulation of a transpiring wall reactor for supercritical water oxidation[J]. Chemical Engineering Journal, 2010, 158(3): 431-440. DOI:10.1016/j.cej.2010.01.013 |
| [7] |
JIN H, ZHAO X, GUO L J, et al. Experimental investigation on methanation reaction based on coal gasification in supercritical water[J]. International Journal of Hydrogen Energy, 2017, 42(7): 4636-4641. DOI:10.1016/j.ijhydene.2016.06.216 |
| [8] |
CARRARETTO I M, COLOMBO L, FASANI D, et al. Pressure drop and void fraction in horizontal air–water stratified flows with smooth interface at atmospheric pressure/[J/OL]. Fluids, 2020, 5(3)[2021-03-27]. https://doi.org/10.3390/fluids5030101.
|
| [9] |
BANAFI A, TALAEI M R, GHAFOORI M J. A comprehensive comparison of the performance of several popular models to predict pressure drop in stratified gas–liquid flow with low liquid loading[J]. Journal of Natural Gas Science & Engineering, 2014, 21: 433-441. |
| [10] |
GARCIA J J, KHOSRAVI A, NUNES R O, et al. Experimental investigation of pressure drop during two-phase flow of R1234yf in smooth horizontal tubes with internal diameters of 3.2 mm to 8.0 mm[J]. International Journal of Refrigeration, 2019, 104: 426-436. DOI:10.1016/j.ijrefrig.2019.05.019 |
| [11] |
赵月. 基于CFD的管道局部阻力的数值模拟[D]. 大庆: 东北石油大学, 2011. ZHAO Y. Numerical simulation of pipeline local resistance based on CFD[D]. Daqing: Northeast Petroleum University, 2011. |
| [12] |
OKEREKE N U, EDET P E, BABA Y D, et al. An assessment of hydrates inhibition in deepwater production systems using low- dosage hydrate inhibitor and monoethylene glycol[J]. Journal of Petroleum Exploration and Production Technology, 2019, 10(3): 1169-1182. |
| [13] |
KUMAR S P, PRASAD B, VENKATARATHNAM G, et al. Influence of surface evaporation on stratification in liquid hydrogen tanks of different aspect ratios[J]. International Journal of Hydrogen Energy, 2007, 32(12): 1954-1960. DOI:10.1016/j.ijhydene.2006.08.052 |
| [14] |
NIE Y G, MAO Y, WANG J Y, et al. CFD simulation of flash boiling of supercritical pentane during asphalt granulation[J]. Chemistry and Technology of Fuels and Oils, 2014, 49(6): 482-488. DOI:10.1007/s10553-014-0473-9 |
| [15] |
WEN R, LI Q, WANG W, et al. Enhanced bubble nucleation and liquid rewetting for highly efficient boiling heat transfer on two-level hierarchical surfaces with patterned copper nanowire arrays[J]. Nano Energy, 2017, 38: 59-65. DOI:10.1016/j.nanoen.2017.05.028 |
| [16] |
林宗虎, 王树众, 王栋. 气液两相流和沸腾传热[M]. 西安: 西安交通大学出版社, 2003. LIN Z H, WANG S Z, WANG D. Gas-liquid two-phase flow and boiling heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2003. |
| [17] |
陈学俊, 周芳德. 管内汽液两相流动摩擦阻力的试验研究[J]. 动力工程, 1986, 9(1): 1-6. CHEN X J, ZHOU F D. Experimental study on frictional resistance of vapor-liquid two-phase flow in pipe[J]. Power Engineering, 1986, 9(1): 1-6. |
| [18] |
林宗虎. 管内汽-水两相流摩擦阻力及真实容积含气量计算(制定锅炉水力计算标准专题报告)[R]. 西安: 西安交通大学, 1976. LIN Z H. Calculation of frictional resistance and real volume gas content of steam water two phase flow in tube(Special report on formulating boiler hydraulic calculation standard)[R]. Xi'an: Xi'an Jiaotong University, 1976. |
| [19] |
AROMADA S A, KVAMME B. Impacts of CO2 and H2S on the risk of hydrate formation during pipeline transport of natural gas[J]. Frontiers of Chemical Science and Engineering, 2019, 13(3): 616-627. DOI:10.1007/s11705-019-1795-2 |
| [20] |
ROUL M K, DASH S K. Two-phase pressure drop caused by sudden flow area contraction/expansion in small circular pipes[J]. International Journal for Numerical Methods in Fluids, 2011, 66(11): 1420-1446. DOI:10.1002/fld.2322 |




