2. 三一重工股份有限公司, 湖南 长沙 430100;
3. 清华大学 核能与新能源技术研究院, 北京 100084;
4. 中国海洋工程研究院(青岛), 山东 青岛 266555
2. SANY Heavy Industry Co. Ltd., Changsha 430100, China;
3. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China;
4. China Institute of Ocean Engineering (TsingTao), Qingdao 266555, China
质子交换膜燃料电池(PEMFC)是一种将氢气的化学能直接转化为电能的能源装置,同时它具有零污染、体积功率密度高和无噪音等优点,被称为最具潜力的动力装置之一[1-2]。PEMFC运行期间,未反应的氢气被直接排放到大气中,这将导致氢气的浪费及一定的安全隐患。为了克服这个问题,对PEMFC系统进行优化,提出了阳极闭口模式,这种方法是通过电磁阀关闭阳极出口[3-9],能够实现100% 燃料利用率。但是闭口模式也会引发一系列问题,出口的封闭导致从阴极渗透过来的氮气在流道内积聚,氢气摩尔分数下降。在闭口模式运行期间,通过可视化手段观察到阳极流道中有液态水积聚,这是因为阴极产生的水在膜两侧形成了浓度梯度,导致反向扩散,将水传输到阳极[10]。Siegel等[11]利用中子成像方法观察到,在闭口模式运行期间,液态水被气体推向阳极出口,并积聚在出口区域,尽管阳极发生了一定程度的水淹,但是这可能并不是导致PEMFC性能下降的主要因素,相反,更多的研究表明从阴极侧渗透过来的氮气在阳极积累才是导致电池性能下降的主要因素[12]。Manokaran等[13]在阳极闭口模式下使用不同氧化剂测试,表明纯氧用作氧化剂时,PEMFC的电流密度没有明显下降,但空气作为氧化剂时,初始电流密度为0.6 A⋅cm−2和0.3 A⋅cm−2时,性能稳定12 min左右即开始下降,下降幅度达到50% 左右。闭口模式下的氮气渗透导致氢气摩尔分数降低,引发催化剂中碳载体的腐蚀[14],这将直接影响PEMFC性能。Ahluwalia等[15]研究发现阳极通道中氮气摩尔分数达到25%~60% 时,电压将降低10~18 mV。为了克服阳极闭口模式下的这些问题,提出从理论角度更加准确地寻找吹扫策略,建立多参数耦合下阳极闭口模式的数学模型,并在实验结果上对模型内参数进行标定,深入探究了电流密度、化学计量比以及温度对阳极闭口模式下电压下降速率的影响,得到了电压较低时传输到阳极的氮气含量,通过实验与计算结果发现阳极闭口模式下氮气会从阴极向阳极渗透,当氢气摩尔分数为0.75时,电压不断下降,为缓解电压持续下降,使PEMFC电压恢复到工作区间,提出了有效的吹扫策略,为PEMFC系统优化奠定了理论基础。
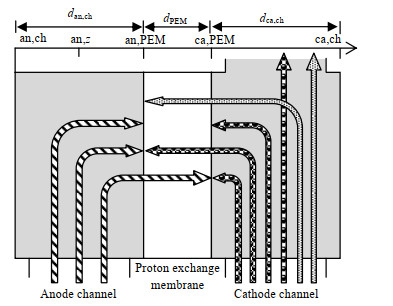
2 数学模型气体在PEMFC中的传输模型如图 1所示,气体在z方向上传输,阴极侧是含有氧气和氮气的混合气体,在通道内是流通状态,dan,ch、dPEM、dan,ca分别代表阳极流道深度、质子交换膜厚度和阴极流道深度,mm;an, ch代表阳极流道外侧位置;an, z代表垂直于传递方向上流道与质子交换膜(PEM)之间的任意位置;an, PEM和ca, PEM分别代表阳极和阴极侧PEM位置;ca, ch代表阴极流道外侧位置。模型由流道模型、气体传输模型和电池电压模型3个子模型构成。
|
图 1 气体传输模型及z轴的不同位置 Fig.1 Schematic diagram of the gas transport model and z-axis position |
在该模型中,阴极和阳极的摩尔流量计算如下:
| $ {N_{{{\text{O}}_{\text{2}}}{\text{, ca}}}} = \frac{{I \cdot {S_{\text{f}}}}}{{4F}}{\xi _{{\text{ca}}}} $ | (1) |
| $ {N_{{{\text{H}}_{\text{2}}}{\text{, an}}}} = \frac{{I \cdot {S_{\text{f}}}}}{{2F}}{\xi _{{\text{an}}}} $ | (2) |
式中:NO2,ca、NH2,an分别为阴极氧气和阳极氢气的摩尔流量,mol⋅s−1;Sf为电化学反应的有效面积,cm2;I为电流密度,A⋅cm−2;F为法拉第常数,C⋅mol−1;ξca与ξan为阴极和阳极的化学计量比。由于向阴极供应的气体为空气,氮气摩尔流量计算如下:
| $ {N_{{{\text{N}}_{\text{2}}}{\text{, ca}}}}{\text{ = }}\frac{{{\text{1}} - {\varphi _{\text{O}}}_{_{\text{2}}}}}{{{\varphi _{\text{O}}}_{_{\text{2}}}}}{N_{{{\text{O}}_{\text{2}}}{\text{, ca}}}} $ | (3) |
式中:
| $ {x_{{\text{v, ca}}}}{\text{ = }}\frac{{{\rm{R}}{{\rm{H}}_{{\text{ca}}}}{p_{{\text{v,} \text{sat} }}}{{}}}}{{{p_{{\rm{ca}}}}}} $ | (4) |
式中:RHca为空气相对湿度;
| $ {N_{{\text{v, ca}}}}{\text{ = }}\frac{{{x_{{\text{v, ca}}}}}}{{{\text{1}} - {x_{{\text{v, ca}}}}}}{\text{(}}{N_{{{\text{O}}_{\text{2}}}{\text{, ca}}}}{\text{ + }}{N_{{{\text{N}}_{\text{2}}}{\text{, ca}}}}{\text{)}} $ | (5) |
式中:
| $ \int {{N_{{{\rm{N}}_2}, {\rm{an}}, {\rm{ch}}}}} {\rm{d}}t = {S_{\text{f}}}\int {{n_{{{\rm{N}}_2}, {\rm{diff}}}}{\rm{d}}t} $ | (6) |
式中:NN2,an,ch为阳极流道内积聚的氮气摩尔量,mol⋅m−2;nN2,diff为单位面积下氮气从阴极到阳极渗透通量,mol⋅m−2⋅s−1;通过理想气体方程,计算阳极流道中氮气的摩尔分数:
| $ {x_{{{\rm{N}}_2}, {\rm{an}}, {\rm{ch}}}} = \frac{{RT\int {{N_{{{\rm{N}}_2}, {\rm{an}}, {\rm{ch}}}}{\rm{d}}t} }}{{{p_{{\text{an}}}}{V_{{\rm{an}}, {\rm{ch}}}}}} $ | (7) |
式中:xN2,an,ch为阳极流道中氮气的摩尔分数;R为理想气体常数,J⋅(mol⋅K)−1;T为温度,K;pan为阳极入口压力,Pa;Van,ch为阳极流道的体积,m3;阴极氮气的摩尔分数大于阳极,因此阴极的氮气可以沿着z方向向阳极渗透,如图 2所示,当氮气渗透到阳极后,阳极流道中是氢气和氮气的混合气体。根据对流扩散理论,浓度梯度会引起扩散,混合气体整体运动时也会因对流作用对质量传递产生一定的影响,因此z轴上an, z位置处(见图 1)氮气渗透通量用对流-扩散方程描述:
| $ {n_{{{\rm{N}}_2}, {\rm{an}}, z}} = - \frac{{p{D_{{{\text{H}}_{\text{2}}}{\text{, }}{{\text{N}}_{\text{2}}}}}}}{{RT}}\frac{{{\rm{d}}{x_{{{\rm{N}}_2}, {\rm{an}}, z}}}}{{{\rm{d}}z}} + {x_{{{\rm{N}}_2}, {\rm{an}}, z}}({n_{{{\rm{H}}_2}, {\rm{an}}, z}} + {n_{{{\rm{N}}_2}, {\rm{an}}, z}}) $ | (8) |

|
图 2 阳极闭口模式下测试系统 Fig.2 Schematic diagram of the test system in dead-end of anode 1. electronic load 2. computer 3. air pump 4. relief valve 5. filter 6. mass flow controller 7. humidity 8. temperature sensor 9. pressure sensor 10. liquid gas separator 11. back valve 12. stack 13. solenoid valve 14. controller 15. hydrogen cylinder 16. radiator 17. cooling water 18. water pump |
式中:下标an, z代表图 1中z轴方向上流道与PEM之间的任意位置;DH2,N2为氢气和氮气的相互渗透率;mol⋅(m⋅s⋅Pa)−1;p为该位置处压力,Pa;nN2,an,z和nH2,an,z分别为阳极通道中流向膜的氮气和氢气摩尔通量,mol⋅(m2⋅s)−1。方程右侧的第一项是扩散效应,第二项是流体的整体运动,对方程左右积分,变为
| $ \int_{{\text{an, ch}}}^{{\text{an, PEM}}} {{\rm{d}}{x_{{{\rm{N}}_2}, {\rm{an}}, z}}} = \int_0^{{d_{{\text{ch, an}}}}} {\frac{{RT}}{{p{D_{{{\text{H}}_{\text{2}}}{\text{, N}}}}_{{\text{2}}}}}} x{}_{{{\rm{N}}_2}, {\rm{an}}, z}({n_{{{\rm{H}}_2}, {\rm{an}}, z}} + {n_{{{\rm{N}}_2}, {\rm{an}}, z}}){\rm{d}}z - \int_0^{{d_{{\text{ch, an}}}}} {\frac{{RT}}{{p{D_{{{\text{H}}_{\text{2}}}{\text{, }}{{\text{N}}_{\text{2}}}}}}}{n_{{{\rm{N}}_2}, {\rm{an}}, z}}{\rm{d}}z} $ | (9) |
方程左边积分的下限为流道距离膜最远位置,上限为膜的位置,方程右边的积分自变量为z,因此积分为流道顶部与膜之间的距离,如图 1所示。重新整理方程(9)得到PEM阳极侧的氮摩尔分数:
| $ {x_{{{\rm{N}}_2}, {\rm{an}}, {\rm{PEM}}}} = \left[ {{n_{{{\rm{H}}_2}, {\rm{an}}, {\rm{consumed}}}}\frac{{RT}}{{p{D_{{{\text{H}}_{\text{2}}}{\text{, N}}}}_{{\text{2}}}}}\int_0^{{d_{{\text{ch}}}}} {x{}_{{{\rm{N}}_2}, {\rm{an}}, z}{\rm{d}}z} } \right] + \left[ {{x_{{{\rm{N}}_2}, {\rm{an}}, {\rm{ch}}}} - \frac{{RT}}{{p{D_{{{\text{H}}_{\text{2}}}{\text{, N}}}}_{{\text{2}}}}}\int_0^{{d_{{\text{ch}}}}} {(1 - } x{}_{{{\rm{N}}_2}, {\rm{an}}, z}){n_{{{\rm{N}}_2}, {\rm{an}}, z}}{\rm{d}}z} \right] $ | (10) |
式中:nH2,an,consumed为阳极氢气消耗速率,mol−1(s⋅m2)−1;xN2,an,z为阳极z位置处氮气摩尔分数;xN2,an,ch为阳极流道内氮气摩尔分数;在方程(10)中,等号右边第一个括号中的积分表示阳极通道中的总氮摩尔分数,第2个括号表示阳极膜处氮气的摩尔分数受阳极流道中氮气摩尔分数的影响,将第2个括号简化为xN2,an,ch的线性近似值,相应的,方程(10)变为
| $ {x_{{{\rm{N}}_2}, {\rm{an}}, {\rm{PEM}}}} = ({a_{11}}{n_{{{\rm{H}}_2}, {\rm{an}}, {\rm{consumed}}}} + {a_{12}}){x_{{{\rm{N}}_2}, {\rm{an}}, {\rm{ch}}}} $ | (11) |
方程(11)中的a11和a12是根据实验数据标定的参数。
2.2 气体输运模型氢气的消耗采用如下公式进行计算:
| $ {n_{{{\rm{H}}_2}, {\rm{an}}, {\rm{consumed}}}} = \frac{I}{{{\text{2}}F}} + 2{D_{{{\text{O}}_{\text{2}}}{\text{, PEM}}}}\frac{{{p_{{O_2}, {\rm{ca}}, {\rm{PEM}}}}}}{{{d_{{\text{PEM}}}}}} + {D_{{{\text{H}}_{\text{2}}}{\text{, PEM}}}}\frac{{{p_{{{\rm{H}}_2}, {\rm{an}}, {\rm{PEM}}}}}}{{{d_{{\text{PEM}}}}}} $ | (12) |
式中:pO2,ca,PEM为阴极膜的氧气压力(图 1中ca, PEM位置处),Pa;pH2,an,PEM为阳极膜的氢气压力(图 1中an, PEM位置处),Pa;DH2,PEM与DO2,PEM分别为氢气和氧气在膜内的渗透率,与氢气相似,氧气消耗的计算式如下:
| $ {n_{{{\rm{O}}_2}, {\rm{an}}, {\rm{consumed}}}} = \frac{I}{{{\text{4}}F}}{\text{ + }}\frac{{{D_{{{\text{H}}_{\text{2}}}{\text{, PEM}}}}}}{2}\frac{{{p_{{{\rm{H}}_2}, {\rm{an}}, {\rm{PEM}}}}}}{{{d_{{\text{PEM}}}}}} + {D_{{{\text{O}}_{\text{2}}}{\text{, PEM}}}}\frac{{{p_{{{\rm{O}}_2}, {\rm{ca}}, {\rm{PEM}}}}}}{{{d_{{\text{PEM}}}}}} $ | (13) |
氮气的渗透通量通过膜两侧的氮气压力梯度计算:
| $ {n_{{{\rm{N}}_2}, {\rm{diff}}}} = {D_{{{\text{N}}_{\text{2}}}{\text{, PEM}}}}\frac{{{p_{{{\rm{N}}_2}, {\rm{ca}},{\rm{PEM}} }}{} - {p_{{{\rm{N}}_2}, {\rm{an}}, {{\rm{PEM}}} }}}}{{{d_{{\text{PEM}}}}}} $ | (14) |
式中:DN2,PEM为氮气在膜内的渗透率;pN2,ca,PEM和pN2,an,PEM分别为阴极侧和阳极侧膜氮气压力,Pa;在该模型中假设膜完全水合,因此忽略膜含水量对渗透率的影响,采用以下方程进行计算:
| $ {D_{{{\text{H}}_{\text{2}}}{\text{, PEM}}}}{\text{ = 1}}{\text{.8}} \times {\text{1}}{{\text{0}}^{ - {\text{14}}}}{\text{ex}}{{\text{p}}_{}}\left[ {\frac{{{E_{{{\text{H}}_{\text{2}}}}}}}{R}{\text{(}}\frac{{\text{1}}}{{{T_{{\text{ref}}}}}} - \frac{{\text{1}}}{T}{\text{)}}} \right] $ | (15) |
| $ {D_{{{\text{O}}_{\text{2}}}{\text{, PEM}}}}{\text{ = 1}}{\text{.8}} \times {\text{1}}{{\text{0}}^{ - {\text{14}}}}{\text{ex}}{{\text{p}}_{}}\left[ {\frac{{{E_{{{\text{O}}_{\text{2}}}}}}}{R}{\text{(}}\frac{{\text{1}}}{{{T_{{\text{ref}}}}}} - \frac{{\text{1}}}{T}{\text{)}}} \right] $ | (16) |
Baik等[16]对膜中的氮气渗透性进行了实验研究,在完全水合状态下,氮气在膜内的渗透率表示为
| $ {D_{{{\text{N}}_{\text{2}}}{\text{, PEM}}}}{\text{ = 5}}{\text{.14}} \times {\text{1}}{{\text{0}}^{ - {\text{13}}}}{\text{ex}}{{\text{p}}_{}}\left[ { - \frac{{{E_{{{\text{N}}_{\text{2}}}}}}}{{RT}}} \right] $ | (17) |
式中:Tref为参考温度,K;EH2、EO2、EN2分别为氢气、氧气、氮气渗透系数。具体数值见表 1。
|
|
表 1 模型中基本参数 Table 1 Basic parameters used in the mode |
根据操作条件和阳极中的氮积累,计算PEMFC的电压变化,可以表示为
| $ {U_{{\rm{cell}}}} = {U_{{\rm{rev}}}} - {U_{{\rm{act}}}} - {U_{{\rm{ohm}}}} - {U_{{\rm{con}}}} $ | (18) |
式中:Urev、Uact、Uohm和Ucon分别为可逆电压、活化极化过电位、欧姆极化过电位和浓差极化过电位,V。可逆电压的计算式如下:
| $ {U_{{\rm{rev}}}} = \frac{{ - {{\Delta }}{G^{\text{0}}}}}{{{\text{2}}F}} - \frac{{RT}}{{{\text{2}}F}}{\ln _{}}(\frac{{{p_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}{{{p_{{{\rm{H}}_2}, {\rm{an}}, {\rm{PEM}}}}p_{{{\rm{O}}_2}, {\rm{ca}}, {\rm{PEM}}}^{0.5}}}) $ | (19) |
式中:−∆G0为吉布斯自由能,J⋅mol−1;pH2O为水蒸气压力,pH2O近似为1,膜阳极和阴极侧的氢气和氧气分压可通过下式进行计算:
| $ {p_{{{\rm{H}}_2}, {\rm{an}}, {\rm{PEM}}}} = (1 - {x_{{\rm{v}}, {\rm{an}}}} - {x_{{{\rm{N}}_2}, {\rm{PEM}}, {\rm{an}}}}){p_{{\text{an}}}} $ | (20) |
| $ {p_{{{\rm{O}}_2}, {\rm{ca}}, {\rm{PEM}}}} = {w_{{{\text{O}}_{\text{2}}}}}(1 - {x_{{\rm{v}}, {\rm{ca}}}}){p_{{\text{ca}}}} $ | (21) |
| $ {\rm{活化极化过电位表示为}}\;\;\;\;\;\;\;\;\;\;{U_{{\rm{act}}}} = {a_{21}}{\ln _{}}(\frac{I}{{{\text{0}}{\text{.4}}}}) $ | (22) |
欧姆极化过电位是由PEMFC的内阻引起的,通过以下公式确定:
| $ {U_{{\rm{ohm}}}} = I{S_{\text{f}}}r $ | (23) |
式中:r为PEMFC的内阻,Ω,由实验数据确定。通常,浓差极化过电位是由阴极电极周围较低的氧分压引起的,在该模型中,氮气在阳极中的积累对浓差极化过电位的影响更为显著,因此,以指数形式表示:
| $ {U_{{\rm{con}}}} = {a_{31}}{\exp _{}}[{a_{32}}(1 - {x_{{{\rm{H}}_2}, {\rm{an}}, {\rm{PEM}}}})] $ | (24) |
式(24)表示浓差极化过电位随着氢气摩尔分数的降低而增加,方程(22)~(24)中的a21、r、a31和a32通过实际测得的电压变化进行标定。根据流道模型、气体运输模型和电压模型,通过Matlab中的Simulink建立计算模型,主要物性参数见表 1。
3 阳极闭口模式的测试系统搭建了一套完整的PEMFC电池测试系统,如图 2所示,氢气和空气在减压阀的作用下进入流量控制器,随后进入加湿器进行加湿处理,加湿后的气体进入电堆阴阳极,入口处的压力传感器用来观测入口压力。氢气供应系统中在出口端加一个常闭电磁阀,由可编程继电器控制,当PEMFC不进行闭口模式测试时,电磁阀打开,当加载电流时,通过控制器将电磁阀关闭,同时监控电压的变化。实验使用的是三片串联的小型电堆,活性面积为106.2 cm2 (15 cm×7.08 cm),质子交换膜采用Gore膜(Gore Inc,USA),气体扩散层采用德国西格里碳纸(SGL 29BC),阴阳极铂负载分别为0.4 mg⋅cm−2和0.2 mg⋅cm−2。电压采集系统主要由日本菊水公司生产的2台电子负载(KFM2150)和交流阻抗仪器(PLZ664WA)组成。
4 操作条件对电压及氮气渗透的影响 4.1 电流密度对电压及氮气渗透的影响电流密度的大小对PEMFC阳极闭口模式下电压的影响如图 3所示,研究结果表明,仿真与实验结果拟合较好。当关闭电磁阀后,电压稳定一段时间后下降,电压的降低一方面是由于在闭口模式下阳极处的水无法排出引发更严重的水淹,另一方面阴极的氮气会渗透到阳极积聚导致氢气浓度降低。电流密度分别为0.3、0.5和0.7 A⋅cm−2下的初始稳定电压分别为2.15、2.05和1.9 V,电压下降0.1 V时对应的时间分别为836、572和316 s。随着电流密度的增大,电压下降相同量所消耗的时间缩短,这是因为较大的电流密度下阴极需提供较大流量的空气,因此氮气含量越大,渗透到阳极的氮气就越多,电压下降速率就越快。电压低于1.4 V时,每个电池的电压低于0.45 V,对于电池的损伤很大,同时PEMFC的性能也已经很差,因此可以选择该节点进行吹扫处理。电流密度为0.7 A⋅cm−2时,电压下降到1.4 V所需时间为608 s,当电流密度减小到0.5 A⋅cm−2时,电压下降到1.4 V时的时间延长到812 s,随着电流密度的减小,电压下降到吹扫点的时间越长,这是因为初始电压的不同以及渗透速率的影响所产生的结果。

|
图 3 阳极闭口模式下电流密度对电压的影响 Fig.3 Effects of current density on voltage under anode dead-end mode |
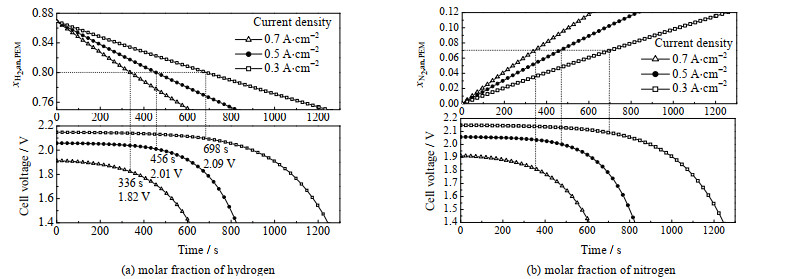
根据拟合好的模型,计算了不同电流密度下膜阳极侧氢气摩尔分数随时间的变化,同时与电压进行了对比。如图 4所示,当电磁阀关闭,氢气摩尔分数从0.869开始下降,考虑阳极流道完全饱和,因此另一部分0.131为饱和水蒸气的摩尔分数。氢气摩尔分数随时间线性下降,这是因为氮气在阳极与阴极之间存在较大的压力梯度,氮气在膜中的扩散通量在最初是最大的,因此导致氢气摩尔分数迅速降低,氢气摩尔分数的下降速率随电流密度的增大而增大,当PEMFC的电压下降到1.4 V时,氢气摩尔分数为0.75(氮气摩尔分数为0.119),该值接近Boillot的研究[17],在该研究中,当供应的氢摩尔分数低于0.8时,电池性能会显著下降。使用该模型确定氢气摩尔分数降低至0.8所需时间,如电流密度分别为0.3、0.5和0.7 A⋅cm−2时,氢气摩尔分数下降到0.8(氮气摩尔分数为0.069)时所需时间分别为698、456和336 s,对应的电压分别为2.09、2.01和1.82 V,该阶段内电压下降接近0.1 V。
|
图 4 电流密度对膜阳极侧氢气摩尔分数的影响 Fig.4 Effects of current density on hydrogen molar fraction at membrane anode side |
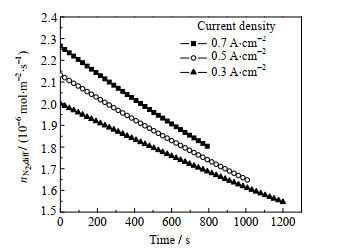
氮气渗透通量随时间的变化如图 5所示。研究结果表明,氮气的渗透导致电压下降,渗透通量呈现线性下降,这是因为在初期,阴极和阳极两侧氮气摩尔分数差很大,随着氮气渗透到阳极,两侧的摩尔分数差减小,渗透速率开始下降。从图中可知,电流密度为0.7 A⋅cm−2时,到电压为1.4 V这段时间内,渗透通量从2.27×10−6 mol⋅m−2⋅s−1下降到2.1×10−6 mol⋅m−2⋅s−1;电流密度降低到0.5 A⋅cm−2时,初始渗透通量为2.1×10−6 mol⋅m−2⋅s−1;电压下降到1.4 V时,渗透通量为1.87×10−6 mol⋅m−2⋅s−1。电流密度越大,渗透越大,这也就解释了之前的现象:电流密度越大,氢气摩尔分数下降通量越快,电压下降越快。在高电流密度下需要供应较多的空气,这就导致膜两侧氮气摩尔分数差越大,渗透通量也越大,渗透到阳极的氮气也越多。
|
图 5 电流密度对氮气渗透通量的影响 Fig.5 Effects of current density on nitrogen permeability |
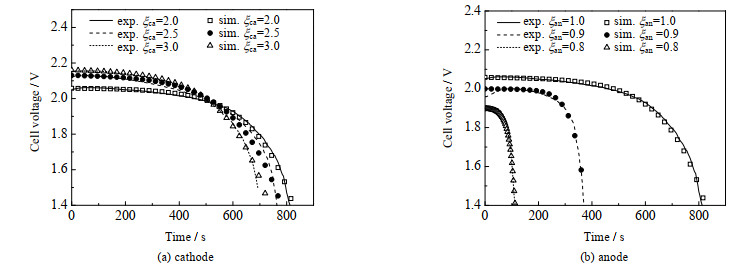
研究了闭口模式下阴极化学计量比对电压的影响,如图 6所示,关闭电磁阀时,阴极化学计量比为2、2.5和3时的初始电压分别为2.05、2.12和2.15 V。初始电压随化学计量比的增加而增大,这是因为较大的化学计量比一方面能够供应更多的反应气体,同时能够将阴极的水有效去除。化学计量比为2、2.5和3时,电压下降0.1 V所需时间分别为408、456和572 s;电压下降到1.4 V所需时间分别为812、764和720 s。虽然较大的化学计量比能增大初始电压,但电压的下降速率也越大。图 6(b)为氢气的化学计量比对电压的影响,因采用阳极闭口模式,若增大阳极化学计量比至1以上会导致阳极流道内气体聚集,压力增大,容易对膜造成不可逆的损害,因此研究化学计量比为0.9和0.8下电压的变化。研究结果表明,化学计量比为0.9和0.8时的初始电压分别为1.9 V和2.0 V,此时PEMFC处于缺气状态,当电压下降到1.4 V时,经历的时间分别为368 s和112 s。
|
图 6 阴阳极化学计量比对电压的影响 Fig.6 Effects of anode-cathode stoichiometric ratio on voltage |
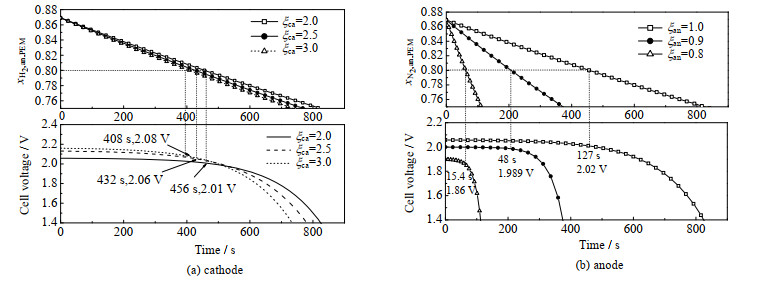
图 7为阴极和阳极化学计量比对氢气摩尔分数的影响。实验结果表明,阴极化学计量比为2.0、2.5和3时,阳极氢气摩尔分数降低至0.8所需时间分别为456、432和408 s,对应电压分别为2.01、2.06和2.08 V。随着化学计量比的增大,氢气下降速率加快,电压降低至1.4 V所经历的时间也越短。相比之下,阳极化学计量比对电压以及氢气摩尔分数的影响较大,降低阳极化学计量比至0.9时,氢气摩尔分数降低至0.8需216 s;当化学计量比降低至0.8时,氢气摩尔分数降低至0.8需61.6 s,这是因为阳极过低的化学计量比会增加氮气在阳极的摩尔分数,使氢气摩尔分数下降速率增大。
|
图 7 阴阳极化学计量比对膜阳极侧氢气摩尔分数的影响 Fig.7 Effects of anode-cathode stoichiometric ratio on hydrogen molar fraction at membrane anode side |
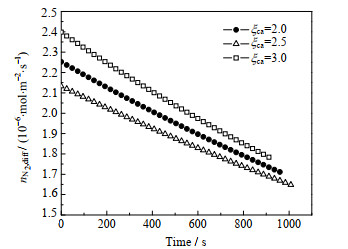
由研究可知,阳极化学计量比的变化不会影响氮气的渗透通量,这是因为在不同的阳极化学计量比下,阴极和阳极氮气摩尔分数差值一致,因此只展示阴极化学计量比对氮气渗透的影响。如图 8所示,随着阴极化学计量比的增大,氮气渗透通量增大,该结果与不同电流密度下的变化规律一致。
|
图 8 阴极化学计量比对氮气渗透通量的影响 Fig.8 Effects of cathode stoichiometric ratio on nitrogen permeability |
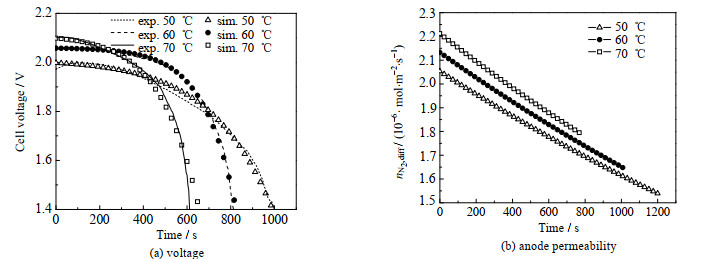
阳极闭口模式下温度对电压的影响如图 9所示,温度为50、60和70 ℃时,初始电压分别为1.988、2.05和2.106 V。随着温度的升高,电压大,这是因为温度越高,质子交换膜吸收的水越多,电导率越大,传输的质子就越多,PEMFC性能越高。但是,温度过高也会导致膜过于干燥,质子传输阻力增大,甚至对膜产生不可逆的损伤,一般工作温度在50~70 ℃。当电压下降到1.4 V时,温度为50、60和70 ℃所需时间分别为1 000、812和616 s。虽然温度越高初始电压越大,但电压下降速率也越大,这是因为温度越大,膜内氮气传输速率也越大。如图 9(b)所示,在任何时刻下温度为70 ℃的氮气传输速率都最大,因此电压下降到1.4 V所经历的时间越短。
|
图 9 温度对电压和氮气渗透通量的影响 Fig.9 Effects of temperature on voltage and nitrogen permeability |
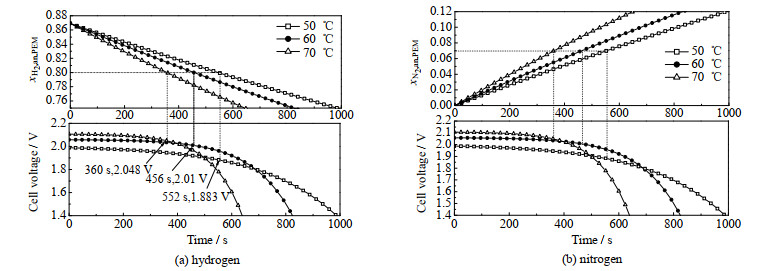
不同温度下阳极氢气摩尔质量和渗透的氮气摩尔质量随时间的变化如图 10所示。研究结果表明,氢气摩尔质量下降到0.75时对应的电压为1.4 V,当氢气摩尔质量下降到0.8时,温度为50、60和70 ℃时所需时间分别为552、456和360 s,此时对应的电压分别为1.883、2.01和2.048 V,氮气摩尔分数为0.07。随着温度的升高,氢气摩尔分数下降越快。
|
图 10 温度对膜阳极侧氢气和氮气摩尔分数的影响 Fig.10 Effects of temperature on hydrogen and nitrogen molar fractions at membrane anode side |
(1) 阳极闭口模式下,电压先稳定一段时间,然后逐渐降低,质子交换膜阳极侧氢气的含量随着时间延长呈现线性降低的趋势。氢气摩尔分数为0.75时,电压下降到1.4 V,此时PEMFC性能明显下降。
(2) PEMFC电压下降到1.4 V时所需的时间随着电流密度的增大而缩短;阴极和阳极的化学计量比越大,电压下降速率越小;温度越高,初始稳定电压越大,但稳定时间越短,电压保持在1.4 V以上的时间也越短。
(3) 为防止电压持续下降而导致PEMFC无法正常运行,可对其进行吹扫处理,吹扫间隔时间应随着电流密度、化学计量比和温度的增加而缩短。
(4) 通过计算得出氢气摩尔分数在0.8时吹扫最为有效。
| [1] |
XIE M, CHU T K, WANG X L, et al. Study on durability of proton exchange membrane fuel cell stack based on mesoporous carbon supported platinum catalysts under dynamic cycles conditions[J]. Journal of Power Sources, 2023, 553: 232277. DOI:10.1016/j.jpowsour.2022.232277 |
| [2] |
ALTARAWNEH R M, PICKUP P G. Pt and PtRu catalyst bilayers increase efficiencies for ethanol oxidation in proton exchange membrane electrolysis and fuel cells[J]. Journal of Power Sources, 2017, 366: 27-32. DOI:10.1016/j.jpowsour.2017.09.014 |
| [3] |
HWANG J J. Effect of hydrogen delivery schemes on fuel cell efficiency[J]. Journal of Power Sources, 2013, 239: 54-63. DOI:10.1016/j.jpowsour.2013.03.090 |
| [4] |
PROMISLOW K, ST-PIERRE J, WETTON B. A simple, analytic model of polymer electrolyte membrane fuel cell anode recirculation at operating power including nitrogen crossover[J]. Journal of Power Sources, 2011, 196(23): 10050-10056. DOI:10.1016/j.jpowsour.2011.08.070 |
| [5] |
BAO C, OUYANG M G, YI B L. Modeling and control of air stream and hydrogen flow with recirculation in a PEM fuel cell system—Ⅰ. Control-oriented modeling[J]. International Journal of Hydrogen Energy, 2006, 31(13): 1879-1896. DOI:10.1016/j.ijhydene.2006.02.031 |
| [6] |
BAO C, OUYANG M G, YI B L. Modeling and control of air stream and hydrogen flow with recirculation in a PEM fuel cell system—Ⅱ. Linear and adaptive nonlinear control[J]. International Journal of Hydrogen Energy, 2006, 31(13): 1897-1913. DOI:10.1016/j.ijhydene.2006.02.030 |
| [7] |
PÉREZ L C, IHONEN J, SOUSA J M, et al. Use of segmented cell operated in hydrogen recirculation mode to detect water accumulation in PEMFC[J]. Fuel Cells, 2013, 13(2): 203-216. DOI:10.1002/fuce.201200109 |
| [8] |
MEYER Q, ASHTON S, CURNICK O, et al. Dead-ended anode polymer electrolyte fuel cell stack operation investigated using electrochemical impedance spectroscopy, off-gas analysis and thermal imaging[J]. Journal of Power Sources, 2014, 254: 1-9. DOI:10.1016/j.jpowsour.2013.11.125 |
| [9] |
RAHIMI-ESBO M, RAMIAR A, RANJBAR A A, et al. Design, manufacturing, assembling and testing of a transparent PEM fuel cell for investigation of water management and contact resistance at dead-end mode[J]. International Journal of Hydrogen Energy, 2017, 42(16): 11673-11688. DOI:10.1016/j.ijhydene.2017.02.030 |
| [10] |
COZ E, THÉRY J, BOILLAT P, et al. Water management in a planar air-breathing fuel cell array using operando neutron imaging[J]. Journal of Power Sources, 2016, 331: 535-543. DOI:10.1016/j.jpowsour.2016.09.041 |
| [11] |
SIEGEL J B, MCKAY D A, STEFANOPOULOU A G, et al. Measurement of liquid water accumulation in a PEMFC with dead-ended anode[J]. Journal of the Electrochemical Society, 2008, 155(11): B1168. DOI:10.1149/1.2976356 |
| [12] |
LEE Y, KIM B, KIM Y. An experimental study on water transport through the membrane of a PEFC operating in the dead-end mode[J]. International Journal of Hydrogen Energy, 2009, 34(18): 7768-7779. DOI:10.1016/j.ijhydene.2009.07.010 |
| [13] |
MANOKARAN A, PUSHPAVANAM S, SRIDHAR P, et al. Experimental analysis of spatio-temporal behavior of anodic dead-end mode operated polymer electrolyte fuel cell[J]. Journal of Power Sources, 2011, 196(23): 9931-9938. |
| [14] |
BAUMGARTNER W R, PARZ P, FRASER S D, et al. Polarization study of a PEMFC with four reference electrodes at hydrogen starvation conditions[J]. Journal of Power Sources, 2008, 182(2): 413-421. DOI:10.1016/j.jpowsour.2008.01.001 |
| [15] |
AHLUWALIA R K, WANG X. Buildup of nitrogen in direct hydrogen polymer-electrolyte fuel cell stacks[J]. Journal of Power Sources, 2007, 171(1): 63-71. DOI:10.1016/j.jpowsour.2007.01.032 |
| [16] |
BAIK K D, KIM M S. Characterization of nitrogen gas crossover through the membrane in proton-exchange membrane fuel cells[J]. International Journal of Hydrogen Energy, 2011, 36(1): 732-739. DOI:10.1016/j.ijhydene.2010.09.046 |
| [17] |
BOILLOT M, BONNET C, JATROUDAKIS N, et al. Effect of gas dilution on PEM fuel cell performance and impedance response[J]. Fuel Cells, 2006, 6(1): 31-37. DOI:10.1002/fuce.200500101 |




