1 引言

间歇过程与连续过程相比，其操作过程更加注重多品种、多批次等灵活经济地操作模式，被广泛应用于发酵、药品、油漆和特种化学品等精细化工领域^[1]。大多数间歇过程属于非稳态生产操作, 控制参数操作轨迹随着时间变化，间歇过程的动态特性大范围内的非线性、多时段特性使传统PID控制很难实现全周期的高精度控制。香港科技大学高福荣团队研究表明，由于间歇过程的非线性和时变特性，参数不变的PID控制器不适用于直接控制间歇过程的关键过程变量^[2-3]。因此实现间歇动态特性大范围变化下的高精度控制成为当前的研究热点。葛志强等将机器学习中的数据挖掘引入到过程工业中，为间歇过程的控制与分析提供了一个新方向^[4]。

近年来，结合间歇过程的批次重复特性，迭代学习控制(ILC)被广泛应用，尤其将批间的迭代学习控制与批内的反馈控制相结合可有效抑制重复扰动^[5-6]。文献[7]围绕批次过程的多重时变特性，从建模、控制、监测与质量优化四个方面系统性地研究批次过程的高性能控制问题，同时针对批次过程建立二维等效模型，提出了二维模型预测迭代学习控制。在此基础上，文献[8]将基于迭代学习模型的多相批次过程应用模型预测控制。文献[9]针对具有状态时滞和时变不确定性的批次过程提出了基于二维模型的迭代学习控制。文献[10-11]针对时变不确定批次过程，提出基于迭代学习的PI控制器设计思路，进一步推导出闭环系统的鲁棒渐近稳定的充分条件，证明了批次方向闭环系统的单调收敛。文献[12]针对间歇过程非线性、时变性等特征，采用T-S模糊模型对间歇过程进行描述，在二维系统框架下实现间歇过程的迭代学习容错控制。

本文依据二维迭代学习控制理论，针对一类间歇反应过程的温度控制系统，在文献[10]迭代学习控制的PI控制器设计理论分析基础上，设计其二维迭代学习PI控制器(ILC_PI)，实现动态特性全周期大范围变化下的反应温度高精度控制，通过引入多种不同类型的扰动，测试系统性能，并与变参数PID控制器进行性能对比分析，验证上述控制方法的有效性。

2 二维ILC_PI控制算法

从二维系统的角度分析间歇过程，时间轴上的特性主要由过程动态特性决定，批次轴的特性主要由过程的重复性决定，间歇过程时间轴与批次轴上的二维动态性能指标可在模型建立和控制器的设计过程同步考虑。

2.1 二维系统Rosser模型

二维系统描述的是系统两个独立方向的动态行为。这里采用一种常用的二维系统状态空间模型：Rosser模型。二维Rosser模型的常见形式如下^[13]：

$ \left\{ {\begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{x}}}^{\rm{h}}}\left( {i + 1, j} \right)}\\ {{{\mathit{\boldsymbol{x}}}^v}\left( {i, j + 1} \right)} \end{array}} \right]}_{}}{ = _{}}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{A}}}_{11}}}&{{{\mathit{\boldsymbol{A}}}_{12}}}\\ {{{\mathit{\boldsymbol{A}}}_{21}}}&{{{\mathit{\boldsymbol{A}}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{x}}}^{\rm{h}}}\left( {i, j} \right)}\\ {{{\mathit{\boldsymbol{x}}}^v}\left( {i, j + 1} \right)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{B}}}_1}}\\ {{{\mathit{\boldsymbol{B}}}_2}} \end{array}} \right]{\mathit{\boldsymbol{u}}}\left( {i, j} \right), }\\ {{\mathit{\boldsymbol{y}}}{{\left( {i, j} \right)}_{}} = _{}^{}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{C}}}_1}}&{{{\mathit{\boldsymbol{C}}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x^{\rm{h}}}\left( {i, j} \right)}\\ {{x^{\rm{v}}}\left( {i, j} \right)} \end{array}} \right], } \end{array}} \right.i, j \ge 0 $

(1)

其中，i表示横坐标，j表示纵坐标；$ {x^{\rm{h}}}\left( {i, j} \right) \in {R^{{{\rm{n}}_{\rm{1}}}}}$表示横坐标状态量，$ {x^{\rm{v}}}\left( {i, j} \right) \in {R^{{{\rm{n}}_{\rm{2}}}}}$表示纵坐标状态量；$ u\left( {i, j} \right) \in {R^{\rm{m}}}$表示输入变量；$y\left( {i, j} \right) \in {R^{\rm{l}}} $表示输出变量；A₁₁, A₁₂, A₂₁, A₂₂, B₁, B₂, C₁ C₂表示适当维数的实数矩阵。系统的边界条件可以表示为：

$ {x^{\rm{h}}}\left( {0, j} \right), {x^v}\left( {i, 0} \right), \begin{array}{*{20}{c}} {}&{i, j = 0, 1, 2, \cdots } \end{array} $

(2)

本文将基于二维Rosser模型，进行PI控制与ILC相结合的控制方法研究。

2.2 间歇过程系统描述

一个多输入多输出(multi input multi output, MIMO)间歇过程系统描述如下：

$ {\Sigma _{\rm{p}}}:\left\{ {\begin{array}{*{20}{c}} {x\left( {t + 1, k} \right) = \left( {{\mathit{\boldsymbol{A}}} + \Delta {\mathit{\boldsymbol{A}}}} \right)x\left( {t, k} \right) + \left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)u\left( {t, k} \right) + w\left( {t, k} \right)}\\ {y\left( {t, k} \right) = {\mathit{\boldsymbol{C}}}x\left( {t, k} \right) + {\mathit{\boldsymbol{v}}}\left( {t, k} \right)} \end{array}} \right. $

(3)

其中，k表示批次，t表示时间；$x\left( {t, k} \right) \in {\mathbb{R}^{\text{n}}}, $$ u\left( {t, k} \right) \in {\mathbb{R}^{\text{n}}}, $$y\left( {t, k} \right) \in {\mathbb{R}^{\text{n}}} $分别表示系统在批次k时间t的状态，输入和输出量；$w\left( {t, k} \right) \in {\mathbb{R}^{\text{n}}} $表示非重复负载扰动；$v\left( {t, k} \right) \in {\mathbb{R}^{\text{m}}} $表示非重复测量扰动；A，B，C分别表示系统矩阵；x₀表示每个批次的初始条件，

$x\left( {0, k} \right) = {x_0}{;_{}}t{ = _{}}0, 1, \ldots N, T - 1;k = 1, 2, \ldots N $；$\Delta {\mathit{\boldsymbol{A}}}, \Delta {\mathit{\boldsymbol{B}}} $分别表示矩阵A和B的不确定扰动，如下式所示：

$ \Delta {\mathit{\boldsymbol{A}}} = {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}_{\text{A}}}{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}_{\text{A}}}{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}}_{\text{A}}}{, _{}}\Delta {\mathit{\boldsymbol{B}}} = {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}_{\text{B}}}{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}_{\text{B}}}{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}}_{\text{B}}} $

(4)

其中，$ \left\{ {{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}_{\text{A}}}, {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}}_{\text{A}}}} \right\}{, _{}}\left\{ {{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}_{\text{B}}}, {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}}_{\text{B}}}} \right\}$是描述结构不确定性的已知实常数矩阵，而${\Delta _{\text{A}}}{, _{}}{\Delta _{\text{B}}} $是不确定的，满足如下条件：

$ {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}_{\text{A}}}^{\text{T}}{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}_{\text{A}}} < I, {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}_{\text{B}}}^T{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}_{\text{B}}} < {\mathit{\boldsymbol{I}}} $

(5)

控制目标决定了控制律，在存在不确定性、扰动和噪声的情况下，输出都应尽可能准确地跟踪给定目标$ {y_R}\left( t \right)$。跟踪误差定义如下式：

$ e\left( {t, k} \right) \overset{\wedge}{=}{y_{\rm R}}\left( t \right) - y\left( {t, k} \right) $

(6)

2.3 二维ILC_PI控制器的设计

为了确保系统的稳定性，引入传统的PI控制器：

$ \bar e\left( {t, k} \right) = {u_0} + {K_1}\bar e\left( {t, k} \right) + {K_2}{\bar I_e}\left( {t, k} \right) $

(7)

u₀表示控制信号初值，其他值定义如下：

$ \bar e\left( {t, k} \right) = {y_{\rm r}}\left( {t, k} \right) - y\left( {t, k} \right) $

(8)

$ {\bar I_{\text{e}}}\left( {t, k} \right) = {\bar I_{\text{e}}}\left( {t - 1, k} \right) + \bar e\left( {t, k} \right) $

(9)

$ {\bar I_{\text{e}}}\left( {0, k} \right) = 0 $

(10)

其中，$ {y_{\text{r}}}\left( {t, k} \right)$为由迭代学习控制进行优化的设定值轨迹，$ \bar e\left( {t, k} \right)$则表示该设定值与输出之间的差值，$ {\bar I_{\text{e}}}\left( {t, k} \right)$表示其积分。这里与传统PI控制的不同之处在于设定值轨迹${y_{\text{r}}}\left( {t, k} \right) $会在批次过程中变化，由迭代学习控制更新其值，如式(11)：

$ {y_{\text{r}}}\left( {t, k} \right) = {y_{\text{r}}}\left( {t, k - 1} \right) + {L_{\text{1}}}\left[ {{{\bar I}_{\text{e}}}\left( {t - 1, k} \right) - {{\bar I}_{\text{e}}}\left( {t - 1, k - 1} \right)} \right] + {L_2}e\left( {t + 1, k - 1} \right) $

(11)

其中，L₁和L₂是学习增益矩阵，根据文献[10]提出的定理，可以选择合适的学习增益矩阵保证系统的稳定性。

上述分析表明：该方法核心仍然是PI控制，在此基础上通过上一批次的跟踪误差和批次方向余差的积分变化来优化下一批次控制器设定值。方便起见，对批次方向变化量进行如下定义：

$ \delta \vartheta \left( {t, k} \right) = \vartheta \left( {t, k} \right) - \vartheta \left( {t, k - 1} \right), \begin{array}{*{20}{c}} {}&{\vartheta { = _{}}x, y, u, \ldots } \end{array} $

(12)

因此式(13)可以写成如下形式：

$ {y_{\text{r}}}\left( {t, k} \right) = {y_{\text{r}}}\left( {t, k - 1} \right) + {L_{\text{1}}}\delta {\bar I_{\text{e}}}\left( {t - 1, k} \right) + {L_2}e\left( {t + 1, k - 1} \right) $

(13)

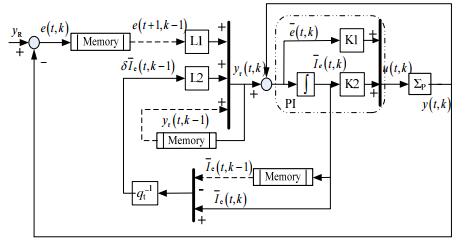
式(7)~(10)及式(12)构成了基于二维系统的迭代学习控制PI控制方法，其结构如图 1所示。从二维角度分析，该系统是由一个对象${\mathit{\Sigma }_{\text{p}}} $和二维控制器组成，虚线部分表示存储器中的上一批次信息，而实线部分表示系统实时信息。

2.4 间歇过程控制模型二维化

根据(7)、(13)，可以将系统(3)转化为如下形式：

$ \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\delta {\mathit{\boldsymbol{x}}}\left( {t + 1, k} \right)} \\ {\delta {{\bar I}_{\text{e}}}\left( {t, k} \right)} \\ {e\left( {t + 1, k} \right)} \end{array}} \right] = {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}}\left[ {\begin{array}{*{20}{c}} {\delta x\left( {t, k} \right)} \\ {\delta {{\bar I}_{\text{e}}}\left( {t - 1, k} \right)} \\ {e\left( {t + 1, k - 1} \right)} \end{array}} \right] + {\mathit{\boldsymbol{W}}}\delta \eta \left( {t, k} \right)} \\ {{\mathit{\boldsymbol{z}}}\left( {t, k} \right) = {\mathit{\boldsymbol{G}}}\left[ {\begin{array}{*{20}{c}} {\delta x\left( {t, k} \right)} \\ {\delta {{\bar I}_{\text{e}}}\left( {t - 1, k} \right)} \\ {e\left( {t + 1, k - 1} \right)} \end{array}} \right]} \end{array}} \right. $

(14)

$ \begin{gathered} \begin{array}{*{20}{c}} {}&{} \end{array}{{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}}_{}}{ = _{}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}} + \Delta {\mathit{\boldsymbol{A}}} - \left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)\left( {{K_1} + {K_2}} \right){\mathit{\boldsymbol{C}}}} \\ { - {\mathit{\boldsymbol{C}}}} \\ { - {\mathit{\boldsymbol{C}}}\left[ {{\mathit{\boldsymbol{A}}} + \Delta {\mathit{\boldsymbol{A}}} - \left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)\left( {{K_1} + {K_2}} \right){\mathit{\boldsymbol{C}}}} \right]} \end{array}} \right. \hfill \\ \left. {\begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)\left[ {{K_2} + \left( {{K_1} + {K_2}} \right){{\mathit{\boldsymbol{L}}}_1}} \right]}&{\left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)\left( {{K_1} + {K_2}} \right){{\mathit{\boldsymbol{L}}}_2}} \\ {{\mathit{\boldsymbol{I}}} + {{\mathit{\boldsymbol{L}}}_1}}&{{{\mathit{\boldsymbol{L}}}_2}} \\ { - {\mathit{\boldsymbol{C}}}\left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)\left[ {{K_2} + \left( {{K_1} + {K_2}} \right){{\mathit{\boldsymbol{L}}}_1}} \right]}&{{\mathit{\boldsymbol{I}}} - {\mathit{\boldsymbol{C}}}\left( {{\mathit{\boldsymbol{B}}} + \Delta {\mathit{\boldsymbol{B}}}} \right)\left( {{K_1} + {K_2}} \right){{\mathit{\boldsymbol{L}}}_2}} \end{array}} \right] \hfill \\ \end{gathered} $

(15)

$ {\mathit{\boldsymbol{W}}}{{\mathit{\boldsymbol{ = }}}_{}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{I}}}&{ - \left( {{\mathit{\boldsymbol{B + \boldsymbol{\varDelta} B}}}} \right)\left( {{K_1}{\mathit{\boldsymbol{ + }}}{K_2}} \right)} \\ \mathit{\pmb{0}}&{ - {\mathit{\boldsymbol{I}}}} \\ { - {\mathit{\boldsymbol{C}}}}&{{\mathit{\boldsymbol{C}}}\left( {{\mathit{\boldsymbol{B + \boldsymbol{\varDelta} B}}}} \right)\left( {{K_1}{\mathit{\boldsymbol{ + }}}{K_2}} \right) - {\mathit{\boldsymbol{I}}}} \end{array}} \right] $

(16)

$ {\rm{\delta }}\eta \left( {t, k} \right) = \left[ {\begin{array}{*{20}{c}} {{\rm{\delta }}w\left( {t, k} \right)} \\ {{\rm{\delta }}v\left( {t, k} \right)} \end{array}} \right]{, _{}}{\mathit{\boldsymbol{G}}} = \left[ {\begin{array}{*{20}{c}} \mathit{\pmb{0}}&\mathit{\pmb{0}}&{\mathit{\boldsymbol{I}}} \end{array}} \right] $

(17)

式中，I为适维单位矩阵。

定义：

$ {x^{\text{v}}}\left( {t, k} \right) = e\left( {t + 1, k - 1} \right) $

(18)

可知二维系统(3)是一个典型的Rosser系统。因此，ILC-PI控制器控制的鲁棒性分析等价于Rosser系统。根据文献[14]中提出的定理可以对该系统进行稳定性分析。

3 多批次间歇补料反应过程控制

本节选择一类平行反应进行研究，该反应过程同时存在主副两种反应，对温度的控制要求更高。这两种反应有不同的反应速率和活化能，分别定义如下^[15]。

第一个反应：

$ {\text{A + }}{{\text{B}}_{}}{\xrightarrow{{{k_1}}}_{}}{\text{C}} $

(19)

第二个反应：

$ {\text{2B}}\xrightarrow{{{k_2}}}{\text{D}} $

(20)

这里，k₁，k₂分别表示两个反应过程的反应速率。

由于第二个反应的活化能比第一个更大，所以低温条件有利于得到有用产物C，但是温度降低会降低固定时间下A的转化率，因此整个反应过程对温度的控制精度提出严格要求。

3.1 过程机理模型

间歇补料反应过程机理模型包含了一个总的质量平衡，三个反应物平衡反应器液体的能量平衡和夹套冷却水的能量平衡。其动态机理方程分别如下：

全质量平衡(假设密度恒定；m³·min^-1)：

$ \frac{{{\text{d}}{V_{\text{R}}}}}{{{\text{d}}t}} = F $

(21)

反应物A的平衡(kmol·min^-1)：

$ \frac{{{\text{d}}({V_{\text{R}}}{C_{\text{A}}})}}{{{\text{d}}t}} = - {V_{\text{R}}}k_{10}^{}{e^{ - {E_1}/RT}}{C_{\text{A}}}{C_{\text{B}}} $

(22)

反应物B的平衡(kmol·min^-1)：

$ \frac{{{\text{d}}({V_{\text{R}}}{C_{\text{B}}})}}{{{\text{d}}t}} = F{C_{{\text{B0}}}} - {V_R}k_{10}^{}{e^{ - {E_1}/RT}}{C_{\text{A}}}{C_{\text{B}}} - 2{V_{\text{R}}}k_{20}^{}{e^{ - {E_2}/RT}}{({C_{\text{B}}})^2} $

(23)

反应物D的平衡(kmol·min^-1)：

$ \frac{{{\text{d}}({V_{\text{R}}}{C_{\text{D}}})}}{{{\text{d}}t}} = {V_{\text{R}}}k_{20}^{}{e^{ - {E_2}/RT}}{({C_{\text{B}}})^2} $

(24)

反应器能量平衡(kJ·min^-1)：

$ \frac{{{\text{d}}({V_{\text{R}}}{T_{\text{R}}})}}{{{\text{d}}t}} = F{T_{{\text{F, in}}}} - \frac{{{\lambda _1}{V_{\text{R}}}{k_{10}}{e^{ - {E_1}/RT}}{C_{\text{A}}}{C_{\text{B}}}}}{{\rho {c_p}}} - \frac{{{\lambda _2}{V_{\text{R}}}{k_{20}}{e^{ - {E_2}/RT}}{{({C_{\text{B}}})}^2}}}{{\rho {c_{\text{p}}}}} - \frac{{U{A_{{\text{hx}}}}({T_{\text{R}}} - {T_{\text{J}}})}}{{\rho {c_{\text{p}}}}} $

(25)

夹套冷却水能量平衡(kJ·min^-1)：

$ \frac{{{\text{d}}{T_{\text{J}}}}}{{{\text{d}}t}} = \frac{{{F_{{\text{CW}}}}({F_{{\text{c, in}}}} - {T_{\text{J}}})}}{{{V_{\text{J}}}}} + \frac{{U{A_{{\text{hx}}}}({T_{\text{R}}} - {T_{\text{J}}})}}{{{V_{\text{J}}}{\rho _{\text{J}}}{c_{\text{J}}}}} $

(26)

换热面积(Ahx)随着时间变化，因为反应器中的液体体积随着加料而增加。瞬时传热面积由瞬时体积与总体积之比计算得到。表 1给出了动力学参数和过程参数值。

3.2 温度最佳操作轨迹设定

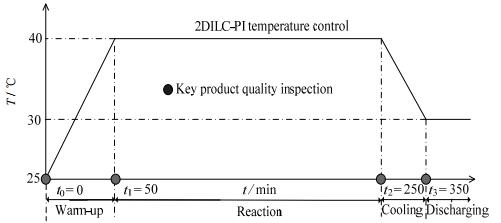
整个反应间歇过程包含预热、反应、冷却、出料等四个操作阶段，且在每个操作阶段温度控制要求都不同^[16]，例如在预热阶段，反应物A在初始时刻t₀常温下一次性加入反应器中，开始预加热直到温度到达设定值(40 ℃)；在反应阶段，以恒定进料流率F流加入反应物B直至反应结束，期间反应温度需控制维持在理想设定值，并将产物C最终质量维持在期望值，持续至反应物A完全耗尽，在冷却和出料阶段温度逐渐下降。本文根据间歇反应过程阶段操作特性，设计了间歇反应器的温度操作设定轨迹，如图 2所示。

3.3 2DILC_PI控制方案的设计

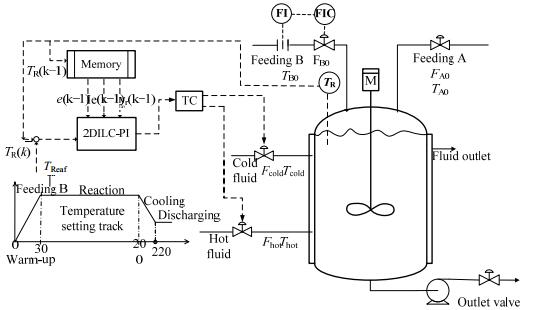
在上述两种反应组成的平行反应体系中，控制系统设计的重要目标是实现产品转化率和最终产品质量的一致性。产品质量控制可间接通过控制反应器温度跟踪预设轨迹来实现，在间歇补料反应操作过程中，考虑两个操作变量：冷流体和热流体流速。具体的控制结构如图 3所示。二维ILC-PI控制系统将冷热流体流速作为操作变量控制反应器内部温度，其他回路操作变量的控制采用传统PID来实现。

3.4 仿真结果分析

基于上述严格机理模型采用MATLAB软件建立间歇反应仿真平台，并通过程序编程实现二维ILC-PI控制。

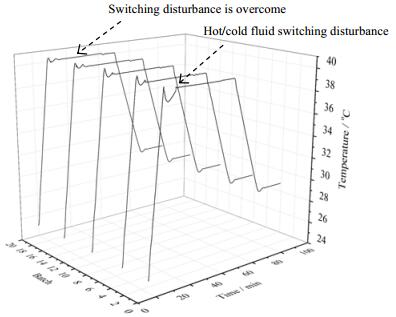
3.4.1 无外加扰动状态下动态响应性能测试

对于第一批次，因没有前批次信息，其实质就是传统PID控制，从第二批次加入ILC_PI控制，仿真结果如图 4所示。在反应过程中，因在50 s处进行了冷热流体切换操作，切换过程会对系统产生扰动。仿真结果图 4表明：在第一批次(即常规PI控制)中，闭环系统能够跟踪参考轨迹，但是在冷热流体切换过程中会造成较大超调，而随着批次间的迭代学习，切换操作造成的超调逐步减小，在第20批次的时候，超调已经基本被克服。

进一步引入流体流量、进料浓度、测量噪声扰动来进行跟踪性能和鲁棒性的分析。从第5批次开始，对每批次分别加入这三种扰动进行性能分析。

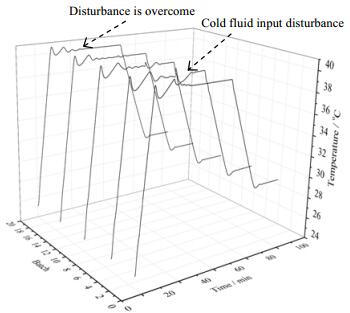
3.4.2 冷流体流量扰动下动态性能分析

针对冷流体输入，从第五批次开始每批次在2000 s处加入冷流体流量的扰动，大小为0.05 kmol·min^-1。经仿真运行，结果如图 5所示。

仿真运行结果表明，在第5批次内，冷流体输入扰动会在PI控制器作用下对闭环系统输出造成一定超调，但很快被抑制，同时通过批次间的迭代学习，后续批次的输入扰动造成的超调影响将逐批次减小。

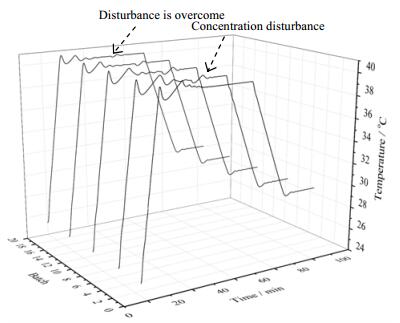
3.4.3 反应物B浓度扰动下动态性能分析

该机理模型中，进料B的浓度也是影响温度响应的一个重要因素，同样，从第5批次开始，在每批次2000 s处对进料B的浓度加入1 kmol·L^-1的扰动进行仿真运行，结果如图 6所示。

结果表明，进料B浓度对温度响应造成的扰动，会随着批次的迭代学习被很快克服，并且后续批次的浓度扰动造成的影响会随着批次间的迭代学习减小，至20批次时扰动的影响完全被消除。

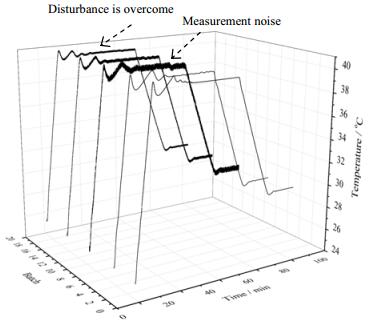
3.4.4 噪声扰动下动态响应性能测试

测试带有测量噪声的控制系统响应情况，从第10批次开始，对每批次加入v(t)=[-0.3 0.3]的测量噪声。仿真结果如图 7所示：在测量噪声的作用下，控制系统的输出虽然发生波动，依然能较好地跟踪参考轨迹，并且随着批次的增加，测量噪声对输出造成的波动已经大大减小。

对仿真结果分析可得，相对于传统PID控制而言，二维ILC_PI控制方法在跟踪性能上有着极大的优势，虽然初始收敛状态与传统PID类似，但经过若干批次迭代学习后，能够较好地满足跟踪性能，对于非重复扰动、输入扰动、测量噪声，该控制系统能快速克服其影响，对于重复扰动，该控制系统能够随着批次间的学习逐渐减小重复扰动对温度响应的影响；此外对于不同的参考轨迹，该方案也能在若干批次的学习后实现较好地跟踪。表 2分别针对无外加扰动、冷流体输入扰动、进料浓度扰动等三种情况，比较批次间迭代学习对跟踪性能与抗扰动性能的改进。

3.4.5 与变参数PID控制的性能对比分析

当前，由于被控对象的非线性、非稳态等特性，传统PID控制难以达到很好的控制效果，文献[17]中提出通过引入非线性函数根据偏差的大小在线调节PID参数来提高控制性能的变参数PID控制方法(VAPID)，本文针对3.1节中给出的机理模型，分别采用2D ILC_PI控制方法与变参数PID控制方法进行控制性能对比分析。

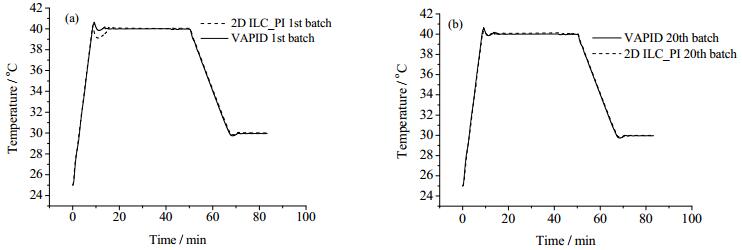
无扰动情况下，由于变参数PID控制方法批次间不存在迭代学习，各批次的仿真输出结果一致，这里仅采用变参数PID控制方法的第1批次输出与二维ILC_PI控制方法的第1批次、第20批次输出进行对比分析，仿真结果如图 8所示。

仿真结果表明：初始批次中，变参数PID控制性能要优于2DILC_PI，尤其是在冷热水切换过程中造成的扰动部分，但随着批次间的学习，在第20批次时，2D ILC_PI的控制性能已经得到很大改善。

在扰动分析方面，以反应物B浓度扰动为例，比较两种控制方法对扰动的克服情况从第5批次开始，在每批次2000 s处对进料B的浓度加入1 kmol·L^-1的扰动。结果表明，对于重复扰动，从初始批次起，二维ILC_PI控制方法的控制效果明显优于变参数PID控制方法，而且由于批次间的学习，在二维ILC_PI控制方法作用下，扰动作用会不断改善，而变参数PID控制方法缺少利用批次间信息，每批次的扰动作用一致，整体控制效果并不能得到改善。表 3给出了具体的性能指标的数值对比。

4 结论

本文多批次间歇过程的重复特性和二维动态特性，采用二维系统理论将时间方向的PI控制与批次方向的ILC结合，将工业中使用成熟的PI控制器作为内环结构，使用迭代学习控制器优化参考轨迹，得到基于二维系统的ILC-PI控制方法，并通过稳定性分析确定控制器参数选择方式。将该控制器应用于一类间歇补料平行反应过程中，在与传统PI控制方案的对比中，可以发现虽然初始批次性能与传统PI控制方案一致，但是在运行足够的批次后，最终控制系统的跟踪性能较好，并且在干扰和噪声的作用下能够具备鲁棒性；尤其对于重复扰动有更好改善作用，表明该控制方法在批次方向上对控制性能的优化作用。