2. 陕西省能源化工过程强化重点实验室,陕西 西安 710049;
3. 热流科学与工程教育部重点实验室,陕西 西安 710049
2. Shaanxi Key Laboratory of Energy Chemical Process Intensification, Xi'an 710049, China;
3. Key Laboratory of Thermo-Fluid Science and Engineering, Xi'an 710049, China
在供电系统中设置储能电池系统在一定程度上能缓解供电系统供电端和负载端的不匹配性,提高供电系统的稳定性[1-2]。目前市场上有钠流电池、铅酸电池、锂离子电池等多种流行的储能电池,电池类型不一样,其经济性和性能也就大不相同[3]。为了合理调度电池储能系统的功率,有必要将多种储能电池组合起来以降低系统的总费用。
目前,针对储能电池在混合供电系统中的功率调度问题展开了大量的研究。LUO等[1]指出集成多种不同的电池储能技术可有效利用各种储能技术优势以满足特定场景需求。KHALIPOUR等[4]在给定多种不同电池类型的情况下研究了光伏-电池系统费用最低的电池种类和相应的容量配置和功率调度。在光-风-柴-储混合供电系统中,MEREI等[5]研究了可由锂离子电池、铅酸电池和全钒液流电池3种电池组成的混合电池储能系统的容量配置和功率调度。然而,以上研究都偏向于关注系统的容量配置,调度只是容量配置的附带结果,而未关注到多种类电池的功率调度优化对系统经济性的影响。
此外,多种类电池储能系统中,各类电池的容量衰退特性存在差异,其对储能系统的功率调度和经济性也会产生影响。BORDIN等[6]将电池循环容量衰退添加到优化模型中,研究了在孤网系统中电池容量循环衰退对系统经济效益的影响。MEREI等[5]构建了含电池日历衰退和循环衰退的电池容量衰退模型。而WANKM LLER等[7]分析了在利用电池储能系统并网套利的情景下,两种不同锂离子电池的循环衰退对电池储能系统操作的影响。然而,电池的容量衰退体现在日历衰退和循环衰退两个方面,而目前的大部分研究仅关注电池的循环衰退,而忽略了日历衰退对储能系统功率调度和经济性的影响。
目前,量化储能电池日历衰退和循环衰退的容量衰退模型主要有机理模型[8]、半经验模型[9]和经验模型[10]。机理模型是采用电极电化学理论描述电池行为的方法。虽然该模型能精确地描述电池特性,但因涉及大量的非线性方程,求解过程困难;相比于机理模型,半经验模型形式较为简单,但仍然需要较多的非线性方程来描述电池特性;经验模型则是一类以实验数据为基础的、不考虑电池内部物理化学机制的数学模型。该模型虽没有前2种模型精确,较为简单,但也能较好地描述电池的容量衰退过程。因此,研究中采用经验模型来描述电池的容量衰退特性。
为此,在综合考虑储能电池日历衰退和循环衰退特性和多种类储能电池的功率调度对各类电池容量衰退及混合供电系统总费用影响的基础上,本文提出了一种基于电池容量衰退特性的多种类电池储能单元的功率调度方法,以期获得混合供电系统总费用最低时电池储能单元的功率调度方案。
2 问题描述混合供电系统由发电侧、负载侧和电池储能系统3部分组成。发电侧包括电网供电和可再生能源发电,如风电和光伏发电。电池储能单元可由N种不同的电池组成。负载侧所需的电量优先由可再生能源发电供给,不足时可由电池储能单元放电供给或电网供给;可再生能源的供电量有剩余时可向储能电池充电或直接废弃。
本文针对混合供电系统操作优化问题可描述为:已知(1)发电侧和负载侧的功率曲线;(2)外购电价;(3)电池储能系统的构成和初始容量。目标是在综合考虑多种类电池容量衰退特性的基础上,通过构建多种类电池功率调度模型,确定多种类电池储能系统的最优功率调度策略,使得混合供电系统的总费用最低。
3 基于容量衰退特性的多种类电池储能单元的功率调度模型 3.1 目标函数混合供电系统的总费用
| $ \min \;\;{C^{{\rm{tot}}}} = {C^{{\rm{inv}}}} + {C^{{\rm{oper}}}} $ | (1) |
本文,认为发电侧和负载侧是固定的,所以该混合供电系统的投资成本只计及电池储能系统购置费用。电池的购置成本与其自身的额定容量相关。本文将电池的购置费用平摊至其全生命长度中[11-15],故投资成本可表示为
| $ {C^{{\rm{inv}}}} = \sum\limits_{n \in {\bf{N}}} {{\alpha _{{\rm{NOK}}, n}}C_n^{{\rm{bat}}}E_n^{{\rm{bat}}, {\rm{nom}}}} $ | (2) |
式中:
混合供电系统的操作费用由电池储能系统的运行维护费用和混合供电系统所需要的电费两部分组成,可表示为
| $ {C^{{\rm{oper}}}} = \sum\limits_{n \in {\bf{N}}} {\sum\limits_{k \in {\bf{K}}} {{f_n} \cdot P_n^{{\rm{bat}}, {\rm{nom}}} \cdot {t_k}} } + \sum\limits_{k \in {\bf{K}}} {{\rho _k} \cdot E_k^{{\rm{imp}}}} $ | (3) |
式中:fn为电池n的单位功率的运行维护成本,
对于任一时间间隔k,发电侧的发电量、外界电网的供电量和电池的放电量之和等于负载侧的需求电量、电池的充电电量与弃电量之和,于是供电系统的在时间间隔k上的电量平衡可表示为
| $ P_k^{\rm{s}} \cdot {t_k} + E_k^{{\rm{imp}}} + \sum\limits_{n \in {\bf{N}}} {P_{k, n}^{\rm{d}} \cdot {t_k}} = P_k^{\rm{l}} \cdot {t_k} + \sum\limits_{n \in {\bf{N}}} {P_{k, n}^{\rm{c}} \cdot {t_k}} + E_k^{{\rm{out}}};k \in {\bf{K}} $ | (4) |
式中:
(1) 电池储能单元的电量平衡
任一类型电池经过时间间隔k后的电量等于电池经过时间间隔k-1后的电量,加上在时间间隔k上电池的充电电量,减去在时间间隔k上电池的放电电量。于是电池在时间间隔k上电量平衡可表示为
| $ {B_{k, n}} = {B_{k - 1, n}} + \eta _n^{\rm{c}} \cdot \left( {P_{k, n}^{\rm{c}} \cdot {t_k}} \right) - \left( {P_{k, n}^{\rm{d}} \cdot {t_{\rm{k}}}} \right)/\eta _n^{\rm{d}};\;\;k \in {\bf{K}}, n \in {\bf{N}} $ | (5) |
式中:
(2) 电池储能单元的电量约束
任一电池的荷电状态可表示为
| $ SO{C_{k, n}} \cdot E_{k, n}^{{\rm{bat}}} = {B_{k, n}};\;k \in {\bf{K}}, n \in {\bf{N}} $ | (6) |
式中:
任一电池荷电状态上下限约束可表示为
| $ SOC_n^{\min } \le SO{C_{k, n}} \le SOC_n^{\max };\;k \in {\bf{K}}, n \in {\bf{N}} $ | (7) |
式中:
(3) 电池储能单元的功率和充放电约束
任一电池类型的充电功率约束可表达为
| $ {\Gamma ^{\min }} \cdot z_{k, n}^c \le P_{k, n}^{\rm{c}} \le {\Gamma ^{\max }} \cdot z_{k, n}^{\rm{c}};\;\;k \in {\bf{K}}, n \in {\bf{N}} $ | (8) |
式中:
任一电池类型的放电功率约束可表达为
| $ {\Gamma ^{\min }} \cdot z_{k, n}^{\rm{d}} \le P_{k, n}^{\rm{d}} \le {\Gamma ^{\max }} \cdot z_{k, n}^{\rm{d}};\;k \in {\bf{K}}, n \in {\bf{N}} $ | (9) |
式中:
任一电池类型的充放电状态约束可表示为
| $ z_{k, n}^{\rm{c}} + z_{k, n}^{\rm{d}} \le 1;\;k \in {\bf{K}}, \;n \in {\bf{N}} $ | (10) |
式(10)表示任一电池类型在同一时间间隔上的状态不能同时为充电状态和放电状态。
在本文中,认为电池储能单元是一个整体,所以在电池储能单元中,各电池的充放电状态应保持一致,即当有电池为充电状态时,其它电池的状态不应为放电状态;反之亦然。这一约束可表示为
| $ z_{k, n}^{\rm{c}} + z_{k, n'}^{\rm{d}} \le 1;\;k \in {\bf{K}}, n' \in {\bf{N}}, n' \ne n $ | (11) |
电池的容量衰退特性表现为电池的循环衰退和日历衰退。其中,循环衰退是指电池在进行充放电时其额定容量的衰退过程;日历衰退则是指电池在静置时电池本身的容量衰退过程[5]。为综合考虑电池容量衰退过程对混合供电系统功率调度的影响,并区分循环衰退和日历衰退对电池调度的影响,根据文献[13],本文分别采用2个线性方程式表示电池的日历衰退和循环衰退过程。假定电池的日历衰退与时间正相关,而电池的循环衰退则采用等效循环数来计算。因而,电池的日历和循环容量衰退可分别表示为
| $ \alpha _{k, n}^{{\rm{cal}}} = \alpha _{k - 1, n}^{{\rm{cal}}} + \frac{{{t_{\rm{k}}}}}{{L_n^{{\rm{cal}}, 80\% }}} \cdot \left( {1 - z_{k, n}^{\rm{c}}} \right) \cdot \left( {1 - z_{k, n}^{\rm{d}}} \right);k \in {\bf{K}}, n \in {\bf{N}} $ | (12) |
式中:
| $ \alpha _{k, n}^{{\rm{cyc}}} = \alpha _{k - 1, n}^{{\rm{cyc}}}\frac{{\left( {P_{k, n}^{\rm{c}} + P_{k, n}^{\rm{d}}} \right) \times {t_k}}}{{2 \times E_n^{{\rm{bat}}, {\rm{nom}}}}} \times \frac{1}{{L_n^{{\rm{cyc}}, 80\% }}};\;k \in {\bf{K}}, n \in {\bf{N}} $ | (13) |
式中:
电池的容量衰退是由日历和循环容量衰退两部分组成的,于是任一电池类型的容量衰退量可表示为
| $ {\alpha _{k, n}} = \alpha _{k, n}^{{\rm{cal}}} + \alpha _{k, n}^{{\rm{cyc}}};k \in {\bf{K}}, n \in {\bf{N}} $ | (14) |
式中:
则任一电池类型经过任一时间间隔后的可用容量可表示为
| $ E_{k, n}^{{\rm{bat}}} = E_n^{{\rm{bat}}, {\rm{nom}}} \cdot \left( {1 - 0.2 \cdot {\alpha _{k, n}}} \right);k \in {\bf{K}}, n \in {\bf{N}} $ | (15) |
式中系数0.2表示储能电池总共的可衰退的容量占容量的20 %,即储能电池的容量衰退至额定容量的80%即为报废。
4 案例分析 4.1 基础数据本案例混合供电系统供电侧和负载侧的基础数据来源于文献[16]。其中该混合供电系统发电侧的发电曲线由风能发电、光伏发电和生物质发电曲线合成,负载侧的用电曲线由5个用电设备的用电曲线合成,如图 1所示。电池储能单元由Lead-acid、Li-ion和NaS 3种不同类型的电池组成,各电池的相关参数可见表 1。在本文中,电价取值为0.16 $·kW·h-1。

|
图 1 混合供电系统供电侧和负载侧的功率曲线 Fig.1 Power supply and demand curves of the hybrid power system |
由图 1可见,一天的时间间隔数为24,采用本文方法在以上优化条件下无法获得系统的最优功率调度方案。为简化计算,根据发电侧和负载侧的功率变化曲线,以下将图 1中的24 h划分为5个时间间隔,每个时间间隔的持续时间为6,2,4,6和6 h。在本案例中,研究该混合供电系统运行一年的功率调度和各电池的运行情况。
为描述方便,本文定义了单位日历容量衰退费用和单位循环容量衰退费用两个指标。其中,单位日历容量衰退表示储能电池静置1 h损耗储能电池所引起的费用,单位循环容量衰退费用则表示储能电池在放出1 kW·h电量损耗电池所引起的费用。由表 1 3种电池的基础参数可计算,Lead-acid、Li-ion和NaS电池单位日历容量衰退费用分别为1.19,1.71和0.31 $·h-1,单位循环容量衰退费用分别0.55,0.25和0.15 $·kW·h-1。
本文所有计算均在GAMS平台上实现,CPU为Intel(R) Xeon(R) X5670@2.93 GHz。该MINLP模型采用求解器SCIP作为全局求解器进行求解。其中MILP子问题采用CPLEX求解器求解,NLP子问题采用CONOPT求解器进行求解。本文所允许的计算相对误差为5 %。
当该混合供电系统只考虑循环衰退时,该模型有78 462个约束条件和47 463个变量;当同时考虑循环衰退和日历衰退时,该模型有94 910个约束条件和52 941个变量。
4.2 结果分析与讨论 4.2.1 调度结果分析表 2给出了该混合供电系统在总费用最低时的优化结果,S1表示只考虑电池循环衰退的情景,S2表示综合考虑电池日历衰退和循环衰退的情景。
|
|
表 2 混合供电系统在总费用最低时的优化结果 Table 2 The optimal results of the hybrid power system with minimum total costs |
由表 2可知,对比混合供电系统在2种不同情景下的情况,可以得知只考虑电池循环衰退时,混合供电系统的总费用是低于考虑电池日历衰退和循环衰退时系统的总费用的,并且这2种情景所对应的投资费用和操作费用的占比大小基本是相反的。在以供电系统总费用最低为目标的情况下,当只考虑电池循环衰退时,混合供电系统只选择NaS电池;综合考虑电池的日历衰退和循环衰退时,混合供电系统则会选择Lead-acid、Li-ion和NaS 3种电池。这是因为在单独考虑电池的循环容量衰退时,只有NaS电池的单位循环容量衰退费用是低于电网供电电价的,所以供电系统只选择了电池NaS,其他功率需求由电网供给;当综合考虑日历和循环容量衰退时,供电系统对电网和3种电池的选择则取决于3种电池单位循环容量衰退费用、单位日历容量衰退费用和电网电价,所以在这2种情景下系统对功率的调度是不一样的。
图 2给出了第一个月混合供电系统的功率调度情况。图中“Ps-Pd”表示供电量与用电量之差;为方便描述,将储能电池的充电量表示为负值,放电量标记为正值。
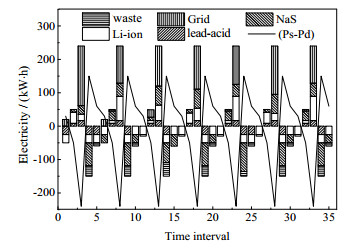
|
图 2 混合供电系统的功率调度曲线 Fig.2 Power dispatch of the hybrid power system |
由图 2可知,该混合供电系统在供电侧供电量大于或小于负荷侧用电量时,电池储能系统中各电池都得到了有效利用。例如,在时间间隔3,该混合供电系统供电侧供电量小于负载侧用电量,此时储能电池放电,电网为负载侧供电;在时间间隔4,该混合供电系统供电侧供电量大于负载侧用电量,储能电池充电,且有一部分废弃电量。与未设置电池储能系统的混合供电系统相比,该混合供电系统通过配置电池储能系统实现了供电侧供电量的有效利用,减少了外购电量和废弃电量。对比图 2中Lead-acid、Li-ion和NaS 3种电池的充放电量变化,3种电池的充放电电量比约为1:2.43:2.71,可以得知3种电池的被利用程度为NaS> Li-ion> Lead-acid。这是由于在Lead-acid、Li-ion和NaS这3种储能电池中,NaS电池的单位循环容量衰退费用是最低的,混合供电系统在进行功率配置时会优先选择NaS电池。
图 3给出了混合供电系统总费用最低时Lead-acid、Li-ion和NaS 3种储能电池的日历容量衰退和循环容量衰退变化。

|
图 3 3种电池的容量衰退变化曲线 Fig.3 Capacity degradation curves of three batteries |
由图 3可知,3种电池的容量衰退的顺序为Lead-acid > NaS > Li-ion;Lead-acid和NaS电池的容量衰退由日历和循环衰退两部分组成,而Li-ion电池的容量衰退只包含循环衰退。这是因为在电池储能系统中,Lead-acid电池的单位日历衰退费用和单位循环衰退费用在3种电池中都是比较高的且同时承担了该系统部分日历和循环衰退,所以Lead-acid电池的容量衰退最为严重且含有2种衰退;Li-ion电池的单位日历衰退费用最高,而单位循环衰退费用较低,为使得混合供电系统的总费用最低故Li-ion电池只有循环衰退而未出现日历衰退;与Li-ion和Lead-acid电池相比,NaS电池的单位日历衰退和循环衰退费用都是最低的,所以在系统中NaS电池出现2种容量衰退且NaS电池的容量衰退量也是比较高的。
4.2.2 多种类电池储能系统功率调度对混合供电系统总费用的影响图 4对比由Lead-acid、Li-ion和NaS 3种电池在不同组合下对应的混合供电系统的总费用。
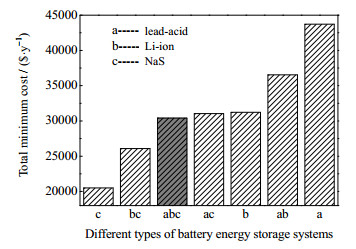
|
图 4 不同电池组成电池储能单元的经济性 Fig.4 Economics of the hybrid power system composed of different battery types |
由图 4可知,单种电池组成的电池储能系统的混合供电系统总费用由低到高依次为NaS < Li-ion < Lead-acid;对比含有2种电池组成的电池储能系统时混合供电系统的总费用,随着Li-ion和NaS电池组成比例的增加,混合供电系统的总费用是逐渐降低的。这主要是由Lead-acid、Li-ion和NaS 3种电池的单位日历容量衰退费用和单位循环容量衰退费用所决定的。值得注意的是由Lead-acid、Li-ion和NaS 3种电池组成的电池储能系统的混合供电系统的总费用是低于由Lead-acid和NaS 2种电池组成的电池储能系统的混合供电系统的总费用的。这说明了采用本文的模型可对混合供电系统功率进行有效的调度,使该混合供电系统的供电效率得到提升,提高了混合供电系统经济性。
5 结论为了降低储电费用和提高供电系统的稳定性,可组合多种类电池构建电池储能系统。本文构建了多电池单元储能系统功率调度优化模型,模型中综合考虑了多种类电池的日历和循环容量衰退特性对储能电池系统功率配置的影响,并通过一个风-光-生物质-储混合供电系统的案例验证了本文方法的有效性。结果表明,采用本文方法可实现混合供电系统容量的最优配置和功率的最优调度,有效提升混合供电系统的经济性和供电效率。虽然本文仅对Lead-acid、NaS和Li-ion电池3种电池组成的储能电池系统进行了案例研究,但本文模型和方法可拓展至更多的不同种类电池和相同种类、不同性能的电池所构成的储能电池系统容量配置和功率调度优化。
符号说明:
| B | —电量,kW·h | η | —效率 |
| Ctot | —系统总费用,$ | ρ | —电网的电价,$·kW·h-1 |
| Cinv | —投资费用,$ | 上标、下标 | |
| Coper | —操作费用,$ | bat | —电池 |
| Cbat | —电池的单位容量费用,$·kW·h-1 | c | —充电过程 |
| E | —容量,kW·h | cal | —日历过程 |
| f | —电池的运行维护费用,$·kW-1·y-1 | cyc | —循环过程 |
| K | —时间间隔集合 | d | —放电过程 |
| L | —电池寿命 | imp | —输入 |
| N | —电池种类集合 | k | —时间间隔 |
| NOK | —总的时间间隔数 | l | —负载侧 |
| P | —功率,kW | max | —上限 |
| SOC | —电池的荷电状态 | min | —下限 |
| t | —持续时间,h | n | —电池种类 |
| z | —二元变量 | nom | —额定 |
| α | —电池的容量衰退量,% | s | —发电侧 |
| Γ | —电池功率P的上下限 | ||
| [1] |
LUO X, WANG J, DOONER M, et al. Overview of current development in electrical energy storage technologies and the application potential in power system operation[J]. Applied Energy, 2015, 137: 511-536. DOI:10.1016/j.apenergy.2014.09.081 |
| [2] |
徐冬清, 范永生, 刘平, 等. 全钒液流电池复合材料双极板研究[J]. 高校化学工程学报, 2011, 25(2): 308-313. XU D Q, FAN Y S, LIU P, et al. Research of composite bipolar plate used for vanadium redox flow battery[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(2): 308-313. DOI:10.3969/j.issn.1003-9015.2011.02.022 |
| [3] |
叶季蕾, 陶琼, 薛金花, 等. 风电并网集成应用中的储能经济性进展分析[J]. 化工进展, 2016, 35(S2): 137-143. YE J L, TAO Q, XUE J H, et al. Economic progress analysis of energy storage in the application of wind power integration[J]. Chemical Industry and Engineering Progress, 2016, 35(S2): 137-143. |
| [4] |
KHALILPOUR R, VASSALLO A. Planning and operation scheduling of PV-battery systems:A novel methodology[J]. Renewable and Sustainable Energy Reviews, 2016, 53: 194-208. DOI:10.1016/j.rser.2015.08.015 |
| [5] |
MEREI G, BERGER C, SAUER D U. Optimization of an off-grid hybrid PV-Wind-Diesel system with different battery technologies using genetic algorithm[J]. Solar Energy, 2013, 97: 460-473. DOI:10.1016/j.solener.2013.08.016 |
| [6] |
BORDIN C, ANUTA H O, CROSSLAND A, et al. A linear programming approach for battery degradation analysis and optimization in offgrid power systems with solar energy integration[J]. Renewable Energy, 2017, 101: 417-430. DOI:10.1016/j.renene.2016.08.066 |
| [7] |
WANKMULLER F, THIMMAPURAM P R, GALLAGHER K G, et al. Impact of battery degradation on energy arbitrage revenue of grid-level energy storage[J]. Journal of Energy Storage, 2017, 10: 56-66. DOI:10.1016/j.est.2016.12.004 |
| [8] |
SANTHANAGOPALAN S, GUO Q, RAMADASS P, et al. Review of models for predicting the cycling performance of lithium ion batteries[J]. Journal of Power Sources, 2006, 156(2): 620-628. DOI:10.1016/j.jpowsour.2005.05.070 |
| [9] |
PARK J, APPIAH W A, BYUN S, et al. Semi-empirical long-term cycle life model coupled with an electrolyte depletion function for large-format graphite/LiFePO4 lithium-ion batteries[J]. Journal of Power Sources, 2017, 365: 257-265. DOI:10.1016/j.jpowsour.2017.08.094 |
| [10] |
CUI Y, DU C, YIN G, et al. Multi-stress factor model for cycle lifetime prediction of lithium ion batteries with shallow-depth discharge[J]. Journal of Power Sources, 2015, 279: 123-132. DOI:10.1016/j.jpowsour.2015.01.003 |
| [11] |
RIFFONNEAU Y, BACHA S, BARRUEL F, et al. Optimal power flow management for grid connected PV systems with batteries[J]. IEEE Transactions on Sustainable Energy, 2011, 2(3): 309-320. DOI:10.1109/TSTE.2011.2114901 |
| [12] |
DUGGAL I, VENKATESH B. Short-term scheduling of thermal generators and battery storage with depth of discharge-based cost model[J]. IEEE Transactions on Power Systems, 2015, 30(4): 2110-2118. |
| [13] |
HESSE H C, MARTINS R, MUSILEK P, et al. Economic optimization of component sizing for residential battery storage systems[J]. Energies, 2017, 10(7): 835. DOI:10.3390/en10070835 |
| [14] |
FENG X, GOOI H B, CHEN S. Capacity fade-based energy management for lithium-ion batteries used in PV systems[J]. Electric Power Systems Research, 2015, 129: 150-159. DOI:10.1016/j.epsr.2015.08.011 |
| [15] |
RANAWEERA I, MIDTGARD O M. Optimization of operational cost for a grid-supporting PV system with battery storage[J]. Renewable Energy, 2016, 88: 262-272. DOI:10.1016/j.renene.2015.11.044 |
| [16] |
ALWI S R W, TIN O S, ROZALI N E M, et al. New graphical tools for process changes via load shifting for hybrid power systems based on Power Pinch Analysis[J]. Clean Technologies and Environmental Policy, 2013, 15(3): 459-472. DOI:10.1007/s10098-013-0605-7 |
| [17] |
MARIAUD A, ACHA S, EKINS-DAUKES N, et al. Integrated optimisation of photovoltaic and battery storage systems for UK commercial buildings[J]. Applied Energy, 2017, 199: 466-478. DOI:10.1016/j.apenergy.2017.04.067 |
| [18] |
GALLO A B, SIMOES-MOREIRA J R, COSTA H K M, et al. Energy storage in the energy transition context:A technology review[J]. Renewable and Sustainable Energy Reviews, 2016, 65: 800-822. DOI:10.1016/j.rser.2016.07.028 |




