2. 中山大学 化学工程与技术学院, 广东 珠海 519082;
3. 广东省石化过程节能工程技术研究中心, 广东 广州 510275
2. School of Chemical Engineering and Technology, Sun Yat-Sen University, Zhuhai 519082, China;
3. Guangdong Engineering Centre for Petrochemical Energy Conservation, Guangzhou 510275, China
蒸发器作为常用制冷设备,其流体流动沸腾传热系数(FBHTC)一直是研究热点[1]。沸腾换热是一种典型的气液两相流相变换热类型,换热强度较高,广泛应用于石化、制冷、电力及核工业,尤其在核反应堆系统中因其传热温差较小,从而保证了反应堆系统的热效率[2]。由于沸腾传热机理较为复杂,正确预测其传热性能尤为重要,近些年各研究者针对管内饱和流动沸腾传热系数进行了大量实验和理论研究[3-4],提出了基于实验数据和传热机理的经验或半经验模型[5-10]。但是由于实验条件限制,仅局限于各自实验数据范围,很少有经验关联式适用于多种制冷剂,且与其他文献实验数据相比仍有较大误差;此外,文献报道的经验函数形式不同,缺乏足够理论支持,当考虑两相流沸腾时,这种简单关联式难以充分反映大范围工况下变量间复杂的非线性关系。近年来,人工神经网络(ANN)强大的学习算法已用于许多工程应用描述复杂问题,目前也在流动沸腾传热预测中得到快速发展,例如多层感知器网络(MLPN)[11],径向基函数网络(RBFN)[12]及广义回归神经网络(GRNN)[13],其中RBFN和GRNN较MLPN需要更多权重才能获得相同精度。为了避免直接使用物理变量作为神经网络输入导致的神经网络高维数和低泛化,Wang等[14]选取物理量相关的无量纲参数作为神经网络输入参数,Nusselt数作为输出,建立R22及替代制冷剂R134A、R407C和R410A(1307组数据集)在水平光滑管内沸腾换热系数的GRNN模型,但涵盖的制冷剂单一,范围有限,缺乏通用性。因此,Zhang等[15]和李斐[16]采用ANN和遗传神经网络(GNN)预测从常规通道到微通道尺度范围多种制冷剂的FBHTC,但由于数据样本量较少,两者均方根误差高达17.16% 和21.63%。另外,关于强化管换热器,Zhu等[17]研究了带分离翅片的微型通道流动沸腾和冷凝现象,并开发基于机器学习性能预测模型,预测效果较好;对于板式换热器,Amalfi等[18]提出将几何形状和流动条件同时作为输入参数,建立新型板式换热器流体流动沸腾局部传热系数和摩擦压力梯度的预测方法,其预测精度高于非线性回归方法。因在两相流过程中,由于气液相界面变形和运动等原因,形成了动态传递现象和流动机制,使之具有混沌运动的规律性,即为多变量相关的强烈复杂非线性系统,导致数学建模求解和预测较为困难,偏差较大。虽然液相对流传热区和泡核沸腾区占整个换热流程的较大比例,但数学建模时也需考虑分区和流型复杂的传热特性,无法直接采用简单的理论公式准确描述。
准确预测两相流FBHTC可以降低设备成本,避免蒸发器设计不足或过度。由于人工神经网络具有良好的预测潜力,本研究在分析经验关联式预测性能及预测误差的基础上,综合考虑影响FBHTC的关键输入参数,涉及参数范围广,流体种类多,基于实验数据驱动用机器学习中人工神经网络代替传统经验函数,采用PSO优化神经网络权重和偏置,从而建立PSO-MLPN模型预测蒸发器中水平光滑管内12种流体的流动沸腾传热性能,并对网络结构配置进行灵敏度分析。
2 数学模型 2.1 流体流动沸腾传热模型现有研究中提出几十种经验公式描述沸腾传热过程,主要分为光滑管和翅片管两类。具体模型主要有常见的增强模型、核态沸腾模型和叠加模型,基于低温工质模型和流型模型以及其他渐进模型和择大模型等,每个模型都涉及多种经验或半经验关联式。目前光滑管内流动沸腾传热常用广义关联式见表 1,关联式中所涉及的各个参数和变量的计算过程详见原始文献,可看出其传热系数大多表示为核沸腾和对流沸腾传热系数之和,都具有表征不同流体的代表系数和操作范围。
|
|
表 1 光滑管内沸腾传热系数常用广义关联式 Table 1 Popular generalized correlations for boiling heat transfer coefficient htp inside smooth tubes |
神经网络在不提供预定函数情况下,通过分析大量实验数据,学习气液两相在流体流动沸腾过程中的复杂规律,通过特征提取自动识别和选择最相关的特征,从而减少数据维度和提高预测准确性。因此建立MLNP时,连接权重的随机设置会导致预测误差,训练过程梯度下降速度慢,容易出现局部极小值,难以实现全局最优。因此,拟利用粒子群算法(PSO)优化神经网络的权重和偏置,减少实验次数并提高预测精度和泛化能力。首先对数据归一化,建立MLNP,通过权衡计算速度和精度的灵敏度分析确定网络拓扑超参数结构并初始化网络的权重和偏置;其次初始化PSO参数:最大迭代次数、种群大小、个体学习因子、社会学习因子、惯性权重等参数;然后初始化种群位置,根据神经网络结构,计算出需要优化的变量个数;最后适应度函数为网络预测的均方根误差,循环优化过程,不断更新最优位置。优化后的最优权重wijk和偏置参数bijk再赋给MLNP神经网络,即输出最优的粒子群算法优化的神经网络(PSO-MLNP)模型。损失函数fobj及性能评价指标—平均绝对误差(MAE)、均方根误差(RMSE)和决定系数(R2),计算公式为
| $ {f_{{\rm{obj}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {\left( {{h_{i, \exp }} - {h_{i, {\rm{pre}}}}} \right)/{h_{i, \exp }}} \right]}^2}} } $ | (7) |
| $ {\rm{MAE}} = \frac{1}{N}\sum\nolimits_{i = 1}^N {\left| {\left( {\left( {{h_{i, \exp }} - {h_{i, {\rm{pre}}}}} \right)/{h_{i, \exp }}} \right)} \right|} $ | (8) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {\left( {{h_{i, \exp }} - {h_{i, {\rm{pre}}}}} \right)/{h_{i, \exp }}} \right]}^2}} } $ | (9) |
| $ {R^2} = 1 - \sum\nolimits_{i = 1}^N {{{\left( {{h_{i, \exp }} - {h_{i, {\rm{pre}}}}} \right)}^2}} /{\sum\nolimits_{i = 1}^N {\left( {{h_{i, \exp }} - {{\overline h }_{i, \exp }}} \right)} ^2} $ | (10) |
式中:N为数据样本数,hi, exp、hi, pre和hi, exp分别为i数据点下的实验值、预测值和平均实验值。
3 蒸发器中流体流动沸腾性能数据库神经网络模型开发需要足够的实验数据样本,本研究从文献[4, 6, 12-14, 19-32]中收集12种常见流体(包括单一和混合制冷剂)的5 232组实验数据作为传热性能预测实验数据库,其中实验数据参数范围详见表 2。表 1中经验关联式显示了几种模型中相关变量参数对目标值的影响程度,为后续参数特征提取提供参考。Gungor-Winterton和Liu-Winterton关联式都包含了饱和核态池沸腾,除了与饱和性质和临界性质有关外,还和流体摩尔质量呈反比;另外,对流沸腾换热系数是核沸腾与液体对流相互作用的结果,根据液相强制对流关联式的Dittus-Boelter模型,对流传热系数的贡献受蒸气密度影响较大,同时与计算液相对流传热系数中的液体物性参数组合Φ(Φ=(cp, l/μl)0.4λl0.6)呈正比[32]。
|
|
表 2 训练神经网络所用实验数据参数范围 Table 2 Experimental data ranges for trained neural network |
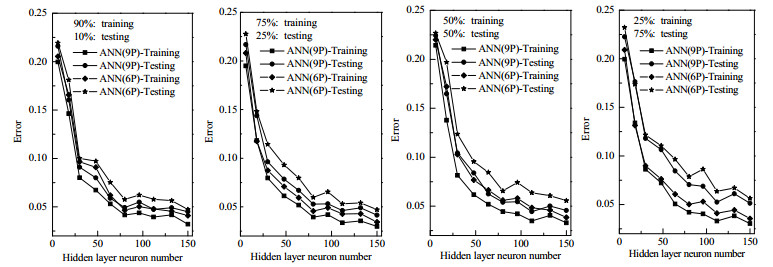
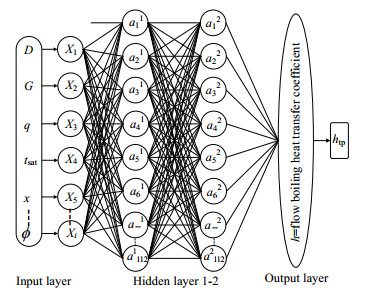
建模过程中,影响管内流动沸腾传热的输入参数可分为4大类:各个流体的热物理性质如密度、热容、黏度、导热系数、表面张力、汽化潜热以及摩尔质量;换热设备的几何参数如管内径,材料性质如管材导热系数;流体流动条件如温度、压力、质量流率和气相质量分数,热流密度。利用这些因素又可以组成各种综合无量纲因素,如物性参数组合Φ,MARTINELLI参数,沸腾数,对流数,弗劳德数等,得到更多参数组合,并广泛用于发展传热经验关联式。首先,对网络的超参数配置以及输入参数组合进行灵敏度分析。其中网络结构配置主要包括训练及测试数据集的比例权衡和神经元数的确定,均可采用试错法获得。而输入参数组合有2种,一种是传统六参数输入(D,G,q,tsat,x,Φ),称为ANN (6P);另一种是九参数输入(D,G,q,tsat,x,Φ,Xtt,Mr,Δhlg),称为ANN (9P),即将Xtt、Mr和影响Bo的Δhlg加入训练模型。图 1的灵敏度分析结果表明90% 数据用于训练时,虽然训练集和测试集的距离很小,但单独误差普遍大于75% 训练集;当整个数据库少于50% 的数据用于训练时,测试误差出现,并且训练集和测试集的距离越来越大,表明过拟合风险增加。同时,ANN (6P)的训练结果的MAE和RMSE都稍高于ANN (9P)。图 1和表 3可看出预测误差随神经元数的增加逐渐减少,之后趋于平缓,随隐藏层数的增加先减少后缓慢增大,直到隐藏层数为2,神经元数为112时,其MAE和RMSE值相对较低,综合考虑过度增加神经元数和隐藏层数会相应延长计算时间,也有可能导致过拟合,因此MLPN网络模型架构如图 2所示,包含2个隐藏层,112个神经元,9个输入参数,1个输出参数,75% 训练集,25% 测试集,学习率为0.01,ReLU激活函数,最大迭代次数为3 000,Batch_Size为256。该模型是在PC Intel (R) Core (TM) i5-9400CPU @ 2.90 GHz, 16.0-GB RAM的Windows 10-Python V3.9平台上搭建,流体气液相热物理性质均采用National Institute of Standards and Technology开发的REFPROP V9.0[33]进行计算,依据实验数据对管内沸腾传热性能进行预测。
|
图 1 不同训练数据规模下隐藏层神经元数对神经网络预测绝对误差的敏感性分析 Fig.1 Sensitivity analysis of hidden layer neuron with different training data on prediction absolute errors of neural network |
|
|
表 3 不同超参数下的目标误差值 Table 3 Target error values for different hyperparameters |
|
图 2 粒子群多层感知器网络模型的结构配置 Fig.2 Architecture configuration of PSO-MLPN |
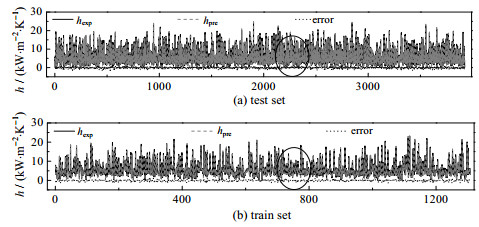
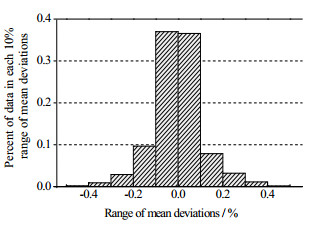
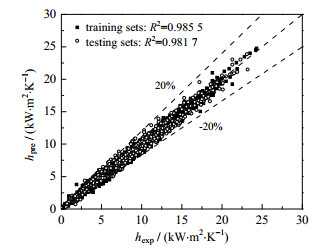
确定网络超参数结构配置后,神经网络预测值与实验值对比图及误差如图 3所示。横轴为实验数据点数量,纵轴为FBHTC的实验值和预测值,从拟合曲线局部放大图可以看出两者变化趋势几乎一致,网络输出值与实验结果非常吻合,并且图 4显示约90% 数据的偏差在±20% 以内。
|
图 3 神经网络预测值与实验值误差对比图 Fig.3 Comparison of errors from predicted and experimental neural network results |
|
图 4 预测的所有数据的平均偏差直方图 Fig.4 Mean deviation histogram for all predicted data |
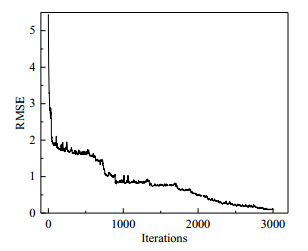
图 5表明训练集、测试集的R2均在0.98以上,误差分布较为均匀,但在目标值较小范围内,偏差较大的数据偏多,可能的原因是数据库中数据样本较少的流体(比如R507,R125和R417A)造成的偏差较大,并且其数量级也普遍较小,进而影响整体预测性能。另外,表 4为相同超参数配置下采用不同优化器如遗传算法(GA)、基于梯度下降的Adam和SGD的训练结果和时间对比,可看出PSO-MLPN在一定时间允许范围内比其他方法的预测精度高20%~53%,在此配置下,训练模型平均绝对误差、均方根偏差和决定系数分别为3.74%、10.09% 和0.984,其均方根偏差随着迭代次数的变化曲线如图 6所示。综上所述,训练后的网络具有相对较高的准确率和泛化能力,但个别数据预测结果与实验数据差异很大,主要由于网络没有足够训练或者可用的实验数据分布不均匀等原因。比如数据库中某些数据范围跨度较大(管径从小于1 mm的微通道到较大的常规通道25 mm、饱和温度从零下到零上等),某些小范围内数据样本缺失或样本不足。可通过增加更多训练数据,进一步优化网络配置,实现网络的更高精确度。
|
图 5 预测值与沸腾换热性能实验值的比较 Fig.5 Comparison of predicted and experimental values of boiling heat transfer performance |
|
|
表 4 相同配置下各优化器的训练结果和时间 Table 4 Training results and times of each optimizers under same configuration |
|
图 6 RMSE随迭代次数的收敛曲线 Fig.6 Convergence curve of RMSE with iterations |
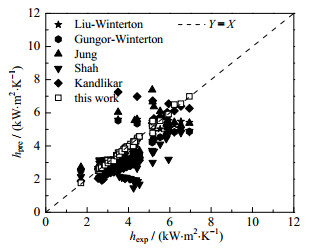
选取应用较为广泛的传统经验关联式,基于本研究数据集的单流体和多流体组分预测偏差计算结果见表 5,由于某些函数较早开发,并且采用的数据集也不包含本研究中所有制冷剂和数据样本,因此无论是单流体还是多流体组分都存在预测结果较差,有的误差甚至高达118.7%。对于单流体组分,Fang等[10]提出了新的关联式,其预测误差相对较小,比如R22、R407C和R12345yf,其他流体则误差偏大,而本研究预测模型对于单流体的预测结果普遍低于传统经验关联式,误差低至1.8%;对于多流体组分,Fang等[10]的关联式与本研究预测模型的误差都相对较低,分别为4.5% 和3.74%。图 7是以表 5中5个常用传统经验关联式包含在内的流体R22和R407C为例,分别与实验值和预测值对比,结果表明本研究预测结果优于其他传统经验关联式,因其流体的沸腾传热性能直接会影响蒸发器的整体总传热系数,进而在总换热量一定的情况下影响蒸发器的总换热面积和设备投资费用,从而可有效避免蒸发器设计不足或设计过度。
|
|
表 5 传统经验关联式的预测误差 Table 5 MAE of traditional empirical correlation |
|
图 7 6种预测模型与沸腾换热性能实验值的比较 Fig.7 Comparison of six prediction models and experimental values of boiling heat transfer performance |
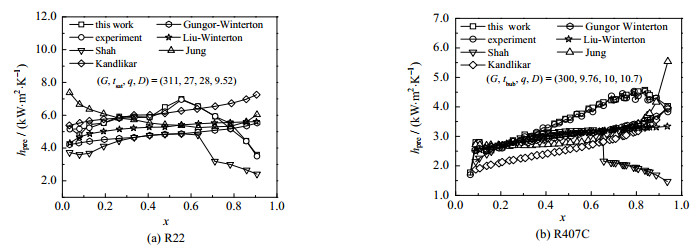
图 8分别为R22和R407C的预测沸腾换热系数与气相质量分数x的关系,以及实验数据和其他5个模型的对比结果。图 8(a)表明,制冷剂R22在操作工况为G = 311 kg⋅m−2⋅s−1,tsat = 27 ℃,q = 28 kW⋅m−2,D = 9.52 mm条件下,传热系数随着x的升高而增大,当x接近于0.6时,传热系数增加至最大值,然后急剧下降,相当于图 1所示的“烧干点”区域的特征。图 8(b)表明,R407C在操作工况G = 300 kg⋅m−2⋅s−1,tbub = 9.76 ℃,q = 10 kW⋅m−2,D= 10.70 mm条件下,实验值和PSO-MLPN预测值随蒸气质量的变化趋势相对平缓,直到x达到0.8左右开始下降。很明显,预测结果相较于常用的传统经验关联式,与实验结果具有更好的趋势和一致性。
|
图 8 R22与R407C的传热系数与气相质量分数的关系 Fig.8 Relationship between heat transfer coefficient and vapor quality of R22 and R407C |
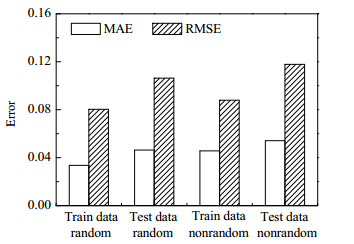
其次为了保证严谨性,取消随机取样,按照数据点顺序严格将其分为训练组和测试组,用于测试的数据均未包含在训练数据样本中,即可检验所提出网络模型的泛化能力,预测结果如图 9所示,其训练集和测试集的RMSE分别为8.79% 和11.78%,两者误差无明显差别,并且和随机抽样预测结果(8.04%和10.63%)偏差不大,故该网络模型的泛化能力较好,但由于涉及流体种类较多并且数据样本来自多种实验平台,导致误差仍在10% 左右。因此,后续研究仍需在流体数据样本质量和展现形式上进一步提高神经网络对复杂管内流体流动沸腾传热性能的预测能力。
|
图 9 两种类型的预测精度 Fig.9 Prediction accuracy of two predictions |
基于流体流动沸腾传热性能实验数据驱动,借助于REFPROP V9.0获取制冷剂热物性参数,建立PSO-MLPN预测模型,该模型采用机器学习中多层感知器作为通用逼近器,粒子群算法用于优化网络权重和偏置,并由灵敏度分析性能和模型精度决定网络结构超参数配置。结果表明,预测结果与实验数据的平均绝对误差、均方根偏差和决定系数分别为3.74%、10.09% 和0.984,其中约90% 数据的偏差在±20%以内;与传统经验函数相比,预测结果的优越性更为明显,与实验值具有更一致的变化趋势,且传热性能随气相质量分数的变化趋势更为一致。因此,研究提出的模型可用于预测复杂相变热交换器传热性能,为流体流动沸腾传热计算及实验数据提供对比值,在含相变过程的蒸发器设计优化和热系统工程应用中具有重要价值。
符号说明:
a11~a1121
—第1隐藏层的神经元
Re
—雷诺数 a12~a1122
—第2隐藏层的神经元
S
—抑制因子 b
—偏置
t
—温度,℃ Bd
—邦德数
w
—权重值 Bo
—沸腾数
X
—输入的变量 C1~C5
—两相沸腾传热相关参数
Xtt
—MARTINELLI参数 Co
—对流数
x
—气相质量分数 cp
—热容,J⋅(kg⋅K)−1
Y
—对比压力相关参数 D
—管径
ρ
—密度,kg⋅m−3 F
—对流强化因子
λ
—导热系数,W⋅(m2⋅℃)−1 Ff
—工质流体参数
μ
—黏度,Pa⋅s Fr
—弗劳德数
Φ
—物性参数组合 fobj
—损失函数
上、下标
G
—质量通量,kg⋅(m2⋅s)−1
bub
—泡点 h
—传热系数
exp
—实验值 hCo
—核态沸腾传热系数
g
—气相 Δhlg
—汽化潜热,kJ⋅kg−1
i, j
—数据点个数;神经元个数 L
—隐藏层数
k
—隐藏层数 Mr
—摩尔量,kg⋅kmol−1
—液相 N
—数据样本数
nb
—核态沸腾 Pr
—普兰特准数
pre
—预测值 q
—热通量,W⋅m−2
sat
—饱和状态 Rp
—表面粗糙度,m
W
—管壁 R2
—决定系数
| [1] |
刘延斌, 王学生, 王浩, 等. 单根C型管外过冷沸腾传热特性实验及分析[J]. 高校化学工程学报, 2022, 36(3): 346-353. LIU Y B, WANG X S, WANG H, et al. Experimental analysis of heat transfer characteristics out of single C-shaped tube under subcooled boiling conditions[J]. Journal of Chemical Engineering of Chinese Universities, 2022, 36(3): 346-353. |
| [2] |
SU G H, FUKUDA K, JIA D N, et al. Application of an artificial neural network in reactor thermohydraulic problem: Prediction of critical heat flux[J]. Journal of Nuclear Science and Technology, 2002, 39(5): 564-571. DOI:10.1080/18811248.2002.9715235 |
| [3] |
徐立, 李玉秀, 徐进良, 等. 微通道中纳米流体流动沸腾换热性能研究[J]. 高校化学工程学报, 2011, 25(4): 559-564. XU L, LI Y X, XU J L, et al. Flow boiling heat transfer performance of nanofluids in a microchannel[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(4): 559-564. DOI:10.3969/j.issn.1003-9015.2011.04.003 |
| [4] |
LALLEMAND M, BRANESCU C, HABERSCHILL P. Local heat transfer coefficients during boiling of R22 and R407C in horizontal smooth and microfin tubes[J]. International Journal of Refrigeration, 2001, 24(1): 57-72. DOI:10.1016/S0140-7007(00)00064-5 |
| [5] |
SHAH M M. Chart correlation for saturated boiling heat transfer: Equations and further study[J]. ASHRAE Transactions, 1982, 88(1): 185-196. |
| [6] |
GUNGOR K E, WINTERTON R H S. Simplified general correlation for saturated flow boiling and comparisons of correlations with data[J]. Chemical Engineering Research & Design, 1987, 65(2): 148-156. |
| [7] |
KANDLIKAR S G. A general correlation for saturated two-phase flow boiling heat transfer inside horizontal and vertical tubes[J]. ASME Journal of Heat and Mass Transfer, 1990, 112(1): 219-228. DOI:10.1115/1.2910348 |
| [8] |
LIU Z, WINTERTON R H S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation[J]. International Journal of Heat and Mass Transfer, 1991, 34(11): 2759-2766. DOI:10.1016/0017-9310(91)90234-6 |
| [9] |
JUNG D, RADERMACHER R. Transport properties and surface tension of pure and mixed refrigerants[J]. ASHRAE Transactions, 1991, 97(1): 90-99. |
| [10] |
FANG X D, WU Q, YUAN Y L. A general correlation for saturated flow boiling heat transfer in channels of various sizes and flow directions[J]. International Journal of Heat and Mass Transfer, 2017, 107: 972-981. DOI:10.1016/j.ijheatmasstransfer.2016.10.125 |
| [11] |
SCALABRIN G, CONDOSTA M, MARCHI P. Mixtures flow boiling: Modeling heat transfer through artificial neural networks[J]. International Journal of Thermal Sciences, 2006, 45(7): 664-680. DOI:10.1016/j.ijthermalsci.2005.09.011 |
| [12] |
WEN X L, WANG H T, WANG H. Prediction model of flow boiling heat transfer for R407C inside horizontal smooth tubes based on RBF neural network[J]. Procedia Engineering, 2012, 31: 233-239. DOI:10.1016/j.proeng.2012.01.1017 |
| [13] |
LIANG M L, ZHANG X H, ZHAO R, et al. Optimization of R245fa flow boiling heat transfer prediction inside horizontal smooth tubes based on the GRNN neural network[J]. Complexity, 2018, 2018: 9318048. DOI:10.1155/2018/9318048 |
| [14] |
WANG W J, ZHAO L X, ZHANG C L. Generalized neural network correlation for flow boiling heat transfer of R22 and its alternative refrigerants inside horizontal smooth tubes[J]. International Journal of Heat and Mass Transfer, 2006, 49(15/16): 2458-2465. |
| [15] |
ZHANG J, MA Y C, WANG M J, et al. Prediction of flow boiling heat transfer coefficient in horizontal channels varying from conventional to small-diameter scales by genetic neural network[J]. Nuclear Engineering and Technology, 2019, 51(8): 1897-1904. DOI:10.1016/j.net.2019.06.009 |
| [16] |
李斐. 人工神经网络及遗传算法预测流动沸腾传热系数[D]. 兰州: 兰州大学, 2019. LI F. Prediction of flow boiling heat transfer coefficient by artificial neural networks and genetic algorithms [D]. Lanzhou: Lanzhou University, 2019. |
| [17] |
ZHU G Y, WEN T, ZHANG D L. Machine learning based approach for the prediction of flow boiling/condensation heat transfer performance in mini channels with serrated fins[J]. International Journal of Heat and Mass Transfer, 2021, 166: 120783. DOI:10.1016/j.ijheatmasstransfer.2020.120783 |
| [18] |
AMALFI R L, KIM J. Machine learning-based prediction methods for flow boiling in plate heat exchangers: 20th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems [C]. San Diego: IEEE, 2021: 1131-1139. .
|
| [19] |
GRECO A, VANOLI G P. Flow-boiling of R22, R134a, R507, R404A and R410A inside a smooth horizontal tube[J]. International Journal of Refrigeration, 2005, 28(6): 872-880. DOI:10.1016/j.ijrefrig.2005.01.008 |
| [20] |
CHOI K I, CHIEN N B, OH J T. Heat transfer coefficient during evaporation of R-1234yf, R-134a, and R-22 in horizontal circular small tubes[J]. Advances in Mechanical Engineering, 2013. DOI:10.1155/2013/132397 |
| [21] |
ANWAR Z, PALM B, KHODABANDEH R. Flow boiling heat transfer, pressure drop and dryout characteristics of R1234yf: Experimental results and predictions[J]. Experimental Thermal and Fluid Science, 2015, 66: 137-149. DOI:10.1016/j.expthermflusci.2015.03.021 |
| [22] |
LU M C, TONG J R, WANG C C. Investigation of the two-phase convective boiling of HFO-1234yf in a 3.9 mm diameter tube[J]. International Journal of Heat and Mass Transfer, 2013, 65: 545-551. DOI:10.1016/j.ijheatmasstransfer.2013.06.004 |
| [23] |
LI M X, DANG C B, HIHARA E. Flow boili ng heat transfer of HFO1234yf and HFC32 refrigerant mixtures in a smooth horizontal tube: Part Ⅱ. Prediction method[J]. International Journal of Heat and Mass Transfer, 2013, 64: 591-608. DOI:10.1016/j.ijheatmasstransfer.2013.04.047 |
| [24] |
LONGO G A, MANCIN S, RIGHETTI G, et al. HFC32 and HFC410A flow boiling inside a 4 mm horizontal smooth tube[J]. International Journal of Refrigeration, 2016, 61: 12-22. DOI:10.1016/j.ijrefrig.2015.09.002 |
| [25] |
LILLO G, MASTRULLO R, MAURO A W, et al. Flow boiling of R32 in a horizontal stainless steel tube with 6.00 mm ID. Experiments, assessment of correlations and comparison with refrigerant R410A[J]. International Journal of Refrigeration, 2019, 97: 143-156. DOI:10.1016/j.ijrefrig.2018.09.024 |
| [26] |
GRECO A, VANOLI G P. Evaporation of refrigerants in a smooth horizontal tube: Prediction of R22 and R507 heat transfer coefficients and pressure drop[J]. Applied Thermal Engineering, 2004, 24(14/15): 2189-2206. |
| [27] |
WANG C C, CHIANG C S. Two-phase heat transfer characteristics for R-22/R-407C in a 6.5 mm smooth tube[J]. International Journal of Heat and Fluid Flow, 1997, 18(6): 550-558. DOI:10.1016/S0142-727X(97)00017-9 |
| [28] |
KIM Y, SEO K, CHUNG J T. Evaporation heat transfer characteristics of R-410A in 7 and 9.52 mm smooth/micro-fin tubes[J]. International Journal of Refrigeration, 2002, 25(6): 716-730. DOI:10.1016/S0140-7007(01)00070-6 |
| [29] |
SEO K, KIM Y. Evaporation heat transfer and pressure drop of R-22 in 7 and 9.52 mm smooth/micro-fin tubes[J]. International Journal of Heat and Mass Transfer, 2000, 43(16): 2869-2882. DOI:10.1016/S0017-9310(99)00338-5 |
| [30] |
SAITOH S, DANG C B, NAKAMURA Y, et al. Boiling heat transfer of HFO-1234yf flowing in a smooth small-diameter horizontal tube[J]. International Journal of Refrigeration, 2011, 34(8): 1846-1853. DOI:10.1016/j.ijrefrig.2011.05.018 |
| [31] |
DEL COL D, BORTOLIN S, TORRESIN D, et al. Flow boiling of R1234yf in a 1 mm diameter channel[J]. International Journal of Refrigeration, 2013, 36(2): 353-362. DOI:10.1016/j.ijrefrig.2012.10.026 |
| [32] |
GRECO A. Convective boiling of pure and mixed refrigerants: An experimental study of the major parameters affecting heat transfer[J]. International Journal of Heat and Mass Transfer, 2008, 51(3/4): 896-909. |
| [33] |
LEMMON E W, HUBER M L, MCLINDEN M O. NIST standard reference database 23, Reference fluid thermodynamic and transport properties-REFPROP, version 9.1 [DB/OL]. Gaithersburg: National Institute of Standards and Technology, 2013 [2023-08-17]. https://www.nist.gov/publications/nist-standard-reference-database-23-reference-fluid-thermodynamic-and-transport
|




