1 引言

高分子共混物是将两种或两种以上具有不同结构及性质的高分子材料进行共混所获得的高分子复合材料，具有单个高分子材料所不具备的优异性能，因而被广泛应用于生物医学、能量存储、电子信息等众多领域^[1-3]。对于二元高分子体系，当温度发生变化时，体系可由单相区进入两相区，进而发生相分离，其机制包括形核生长和调幅分解，此过程被称为热诱导相分离。当体系的初始成分、反应温度、时效时间、冷却(升温)速率等参数发生变化时，能够获得具有不同微观组织结构及物理化学性能的高分子复合材料^[4-6]。此外，热诱导相分离法具有简单、高效、易控制等特点，因而经常被用来合成各类高分子复合材料^[7-9]。

材料的物理化学性质与其微观组织结构密切相关，因而在材料学研究中，对材料微观组织的精确控制，以及对其与材料性能之间关系的研究极其重要。当将一外场施加于材料时，材料的微观组织结构发生变化，导致材料的性能也随之变化。常用来调控材料微观组织结构的外场有力场、温度场、电场、磁场等，相关研究也表明当对材料体系施加一外场时，材料的组织会呈现拉伸、取向、梯度等特征，从而形成具有独特组织结构及优异性能的材料^[10-14]。尽管电场的取向作用没有力场显著，但是电场的施加更为方便有效，尤其在薄膜或小尺寸器件的控制方面更具优势。

相场法是一种基于扩散界面模型模拟材料微观组织演化的数值方法，它的主要优点是避免了传统尖锐界面模型带来的界面追踪问题^[15-17]。采用相场法进行微观组织模拟最初源自对金属凝固中枝晶组织的模拟，随后，因其强大的能力被广泛应用于固态相变^[18-19]、晶粒生长和粗化^[20]、马氏体相变^[21-22]、铁电相变^[23]、铁磁相变^[24]等众多领域，所研究的空间尺度为介观尺度(即纳米到微米尺度)。

本研究采用相场模拟，探究了不同的初始成分以及不同的电场强度作用下，二元高分子共混体系的微观组织演化及动力学过程，采用高精度的半隐式傅里叶谱法^[25-26]对修改的Cahn-Hilliard-Cook (CHC)动力学方程进行求解，最终得到了不同参数条件下体系微观组织随时间的演化过程。此外，通过动力学研究，本研究揭示了电场对体系微观组织的取向过程。结果表明，通过相分离动力学和电场取向动力学的调控，有助于设计并指导合成具有独特微观组织结构及优异性能的高分子复合材料。

2 理论模型和数值方法

本研究考虑了一个二元不可压缩的高分子体系，由组元A和组元B组成。根据梯度热力学理论，体系的自由能泛函可表示如式(1)^[27-28]：

$ F\{ \varphi ({\boldsymbol{r}})\} = \int_V {[f\left( \varphi \right) + \kappa {{(\nabla \varphi )}^2}]} {\text{d}}V $

(1)

式中：$ {\boldsymbol{r}} $为位置矢量，m；φ为组元A的体积分数($1 - \varphi $为组元B的体积分数)；V为所研究体系的体积，m³；κ为梯度能系数(依赖于φ的正系数)，本研究中假定为常数；$f(\varphi )$为体系的局部自由能密度，J·m⁻³。$f(\varphi )$可根据Flory-Huggins (FH)格子理论表示如式(2)^[29-30]：

$ f(\varphi ) = \frac{\varphi }{{{N_{\text{A}}}}}\ln \varphi + \frac{{1 - \varphi }}{{{N_{\text{B}}}}}\ln (1 - \varphi ) + \chi \varphi (1 - \varphi ) $

(2)

式中：χ是与温度有关的FH相互作用参数；N_A和N_B分别为组元A和B的聚合度(本研究聚合度设定为N_A = N_B = N)。本研究中热力学参数来源于质子化和过氘化的聚丁二烯二元混合物，x=0.326/T−2.3×10⁻⁴，N=4 000^[31] (T为绝对温度，K)。

当对体系施加一电场作用时，体系总的自由能可表示为^[32-33]：

$ F = F\{ \varphi ({\boldsymbol{r}})\} - \frac{1}{2}\int_V {\varepsilon ({\boldsymbol{r}}{\text{)}}{{\left| {{\boldsymbol{E}}{\text{(}}{\boldsymbol{r}}{\text{)}}} \right|}^{\text{2}}}{\text{d}}{\boldsymbol{r}}} $

(3)

式中：F为加入电场作用后的总自由能，J；$\varepsilon ({\boldsymbol{r}})$是与位置相关的介电常数，F·m⁻¹；${\boldsymbol{{E}}}({\boldsymbol{r}})$是体系的电场强度矢量，V·m⁻¹。

当体系进行相分离时，其动力学过程可由经典的非线性扩散方程，即CHC方程进行描述^[34]：

$ \frac{{\partial \varphi }}{{\partial t}} = \nabla M\left( \varphi \right)\nabla \frac{{\delta F}}{{\delta \varphi }} + \xi ({\boldsymbol{r}}, t) $

(4)

式中：$M(\varphi )$是动力学系数(与原子的扩散率相关，本研究中设为常量)，m²·s⁻¹；$\xi ({\boldsymbol{r}}, t)$是热噪声项，其符合涨落-耗散定律^[35]：

$ \left\langle {\xi ({\boldsymbol{r}}, t)} \right\rangle = 0 $

(5)

$ \left\langle {\xi ({\boldsymbol{r}}, t)\xi ({\boldsymbol{r'}}, t')} \right\rangle = - 2{k_B}TM{\nabla ^2}\delta ({\boldsymbol{r}} - {\boldsymbol{r'}})\delta (t - t') $

(6)

式中：k_B为玻尔兹曼常数，J·K⁻¹；t为时间，s；$ \xi ({\boldsymbol{r'}}, t') $为不同位置下的热噪声项。

为方便研究电场作用下高分子共混体系的相分离过程，考虑了一个强度为E₀均匀的电场分布，沿y轴方向，并且假定介电常数ε是体积分数φ的二次函数，因此非线性的CHC方程可改写为：

$ \frac{{\partial \varphi ({\boldsymbol{r}}, t)}}{{\partial t}} = M{\nabla ^2}[\frac{1}{N}\ln \frac{\varphi }{{(1 - \varphi )}} + \chi (1 - 2\varphi ) - 2\kappa {\nabla ^2}\varphi ] + MBE_0^2\nabla _y^2\varphi + \xi ({\boldsymbol{r}}, t) $

(7)

式中：B为一参数，与所研究体系相关。

进一步，对动力学方程(7)进行无量纲处理，定义如下无量纲参数：x^*= x/L，y^*= y/L，t^*= Mt/NL²，B^*= NBE₀²，κ^*= κN/L²，ξ^*= NL²ξ/M，其中L为模拟中划分网格的长度单元，则无量纲的动力学方程可表示如式(8)：

$ \frac{{\partial \varphi ({{\boldsymbol{r}}^*}, {t^*})}}{{\partial {t^*}}} = {\nabla ^*}^2[\ln \frac{\varphi }{{(1 - \varphi )}} + \chi N(1 - 2\varphi ) - 2{\kappa ^*}{\nabla ^{*2}}\varphi ] + {B^*}\nabla _y^{*2}\varphi ({{\boldsymbol{r}}^*}, {t^*}) + {\xi ^{\text{*}}}({{\boldsymbol{r}}^*}, {t^*}) $

(8)

式中：B^*是与电场强度平方成正比的参量，可以通过改变B^*来调节电场强度。

采用高精度的半隐式傅里叶谱法对无量纲方程式(8)进行数值求解，所模拟区域为二维方形区域，其尺寸为256×256，在每个方向上均采用周期边界条件。在进行模拟时，采用的初始条件为$\varphi ({\boldsymbol{r}}, t = 0) = {\varphi _0} + \delta \varphi ({\boldsymbol{r}}, t = 0)$，其中${\varphi _0}$为平均的初始成分，$\delta \varphi $是一个无穷小的随机涨落，可通过随机数产生器得到。模拟采用的空间步长和时间步长分别为dx = dy = 1.0和dt = 0.01。通过求解式(8)可以得到浓度分布随时间的变化，即体系微观组织的演化过程。

3 结果与讨论

本工作主要研究了临界成分和非临界成分在不同电场强度下体系的微观组织演化及动力学过程。所采用的参数为$\chi N = 2.7$，${\kappa ^*} = 0.5$，此时T = 360 K。关于电场强度的影响，分别设置了低场强(B^* = 0.1)、中场强(B^* = 1.0)、高场强(B^* = 10) 3种强度。为了清楚阐明初始成分和电场强度对体系相分离过程的影响，研究了体系的微观组织演化和电场取向动力学。

3.1 临界成分下电场对体系相分离过程的影响

本部分研究了临界成分，即φ₀ = 0.5时，电场对体系微观组织演化的影响，其结果呈现于图 1中，所选取的电场强度为B^*=0.1、1.0、10。三组共混体系的微观组织演化过程分别展示于图 1(a)、(b)、(c)中，通过观察体系微观组织随时间的演化，再通过对比不同场强下的最终形貌，可以得出体系微观组织结构在电场和相分离二者作用竞争下的主要特征。

图 1(a)展示了弱电场(B^* = 0.1)作用下，体系微观组织随时间的演化过程。当无量纲时间t^* = 10时相分离开始，富A(黑色区域)和富B(白色区域)的两相开始析出，但体系的形貌并无显著的取向结构，表明此时电场的取向作用不明显。当t^* = 40~200时，体系相分离完成进入粗化阶段，两相开始粗化并同时受到电场的取向作用。当t^* = 400时，最终的形貌呈现出不规则的交联状，并沿y轴方向进行取向。图 1(b)展示了中电场(B^* = 1.0)作用下体系微观组织随时间的演化。当t^* = 10时，能够观察到两相组成的相分离结构，并且呈现出沿电场方向(y轴方向)的取向。此外，在两相界面处，能明显观察到众多模糊区域，这是由于较大的电应力作用所产生的缺陷。当t^* = 40时，相分离的结构已经稳定，界面处的缺陷也逐渐减少，体系的微观组织沿y轴方向呈现出树杈状结构。当t^* = 400时，粗化过程发生，缺陷逐渐消失，体系最终形成粗化的树杈状结构。可以看到，当电场强度增大时，取向过程变得显著，最终的形貌也展示出了显著的取向结构。图 1(c)展示了强电场(B^* = 10)作用下体系微观组织随时间的演化。当t^* = 10时，微观组织迅速被电场取向，呈现出树杈状结构。此外可以发现，与中场强相比，高场强产生的缺陷区域更大，这是因为高场强造成了更大的电应力。当t^* = 40时，微观组织取向的程度更加显著，并且界面处的电应力作用得到一定的释放，微观组织继续被拉伸，但体系仍存在少量的缺陷。当t^* = 200~400时，缺陷完全消失，且获得完美的取向结构。

为了进一步阐明在临界成分下，电场强度对体系微观组织结构的影响，模拟了当B^*从0到10逐渐变化时体系最终的微观组织结构，其结果呈现于图 2中。在无外加电场作用时(B^* = 0)，体系的微观组织呈现出各向同性的交联状结构，其取向也是完全随机的。随着电场强度逐渐增加，微观组织沿y轴方向的取向越来越显著，交联的结构也逐渐减少。当电场强度较小时(B^* = 0.1~0.2)，最终形貌呈现出具有一定取向的交联结构。当电场强度进一步增加时(B^* = 0.5~2.0)，最终的形貌转变为沿y轴方向取向的树杈状结构，通过延长时效时间，仍不能使其转变为完全规则的取向结构。当电场再进一步加强时(B^* = 5.0~10.0)，最终的形貌具有沿电场方向(y轴方向)的规则结构，即完美的取向结构。因此可以得到如下结论：电场强度的改变能够显著改变体系相分离的结构，使其从具有一定取向结构的交联状到树杈状，再到完美的取向结构。

3.2 非临界成分下电场对体系相分离过程的影响

本节研究了非临界成分下，电场辅助高分子体系相分离的组织演化过程。为便于研究，取一非临界成分(即φ₀ = 0.35)进行研究。与3.1小节相似，考虑了低场强(B^* = 0.1)、中场强(B^* = 1.0)、高场强(B^* = 10)的影响。

图 3展示了非临界成分下，体系微观组织随时间的演化过程。如图 3(a)所示，当电场强度较小(B^* = 0.1)，演化时间t^* = 10时，相分离开始。富A相呈现液滴状结构且随机分布，此时电场的作用比较弱。随着时间的增加(t^* = 40~200)，相分离结构逐渐形成，同时电场取向作用开始显现，但程度不明显。最终，当t^* = 400时，体系的微观组织呈现出沿电场方向取向的液滴状结构。通过对比图 1(a)和图 3(a)，可以发现，对于相同的电场强度，临界成分下的体系受到的取向作用更大。在图 3(b)中，中电场(B^* = 1.0)作用下，随着时间的推移，相分离结构逐渐形成并沿y轴方向取向，缺陷区域逐渐减小，最终消失，形成了共存的液滴状和纤维状结构。在图 3(c)中，强电场(B^* = 10)作用下，相分离结构形成后迅速被拉伸为具有取向结构的组织，且缺陷区域逐渐减少。最终(t^* = 400)，呈现出完美的取向结构。此结构与图 1(c)最终的组织结构非常相似，但是可以发现，在非临界成分的情况下，由于A相的体积分数较小，取向结构的分布较稀疏，其分布的平均周期较大。

为了进一步澄清电场强度对体系最终形貌的影响，图 4展示了非临界成分下，二元高分子体系最终形貌随电场强度的变化，其中B^*从0到10变化。可以看到，当B^*为0，体系呈现出各向同性的液滴状结构。随着电场强度逐渐增加(B^* = 0.1~0.2)，微观组织沿y轴方向取向，但取向程度较小，因此形成了拉伸状的液滴结构。随着电场进一步增强(B^* = 0.5~2.0)，微观组织从形变的液滴状结构转变为纤维状结构，且富A相为分散相。最终，当电场强度更大时(B^* = 5~10)，微观组织逐渐呈现出完美的取向分布，其结构类似于临界成分下的组织结构，但非临界成分下的富A相体积分数较小。

3.3 初始成分对电场取向动力学的影响

为了定量研究电场作用下，体系微观组织的取向动力学，定义各向异性参数D，表达如式(9)：

$ D = \frac{{\sum {[({\boldsymbol{k}}_y^2 - {\boldsymbol{k}}_x^2)/{{\boldsymbol{k}}^2}]S({{\boldsymbol{k}}_x}, {{\boldsymbol{k}}_y})} }}{{\sum {S({{\boldsymbol{k}}_x}, {{\boldsymbol{k}}_y})} }} $

(9)

式中：k为倒空间矢量(k_x、k_y为k的分量)，m⁻¹；S(k_x，k_y)为结构因子。当共混体系微观组织的取向完全平行于外加电场时，D为1；当共混体系微观组织的取向完全随机，即呈现完全的各向同性时，D为0。

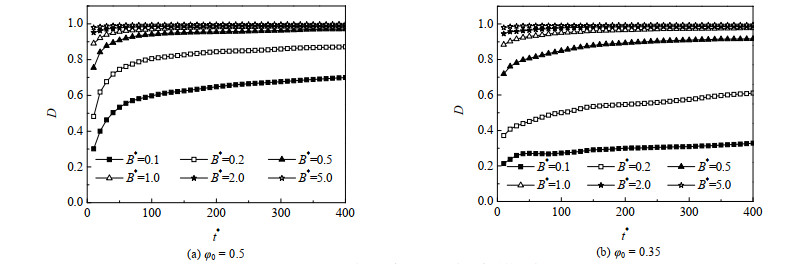
电场的施加造成了体系微观组织结构的变化，使其从完全的各向同性转变为各向异性结构，图 5展示了临界成分和非临界成分下，不同电场强度对应的取向动力学曲线。从图 5中可以观察到，随着时间发展，各向异性参数的值增加并达到平衡，这与实验结果相吻合^[36]。同时，随着B^*的增加，D也在逐渐增加。当B^* = 5.0时，D均快速达到1.0，这表明体系的微观组织快速被取向，且最终完美地沿电场方向取向。

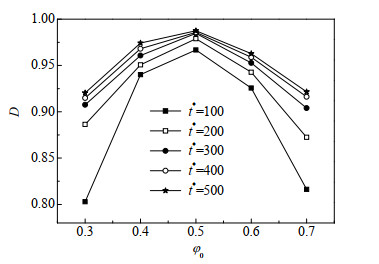
此外，本研究考察了初始成分对电场取向动力学的影响。首先，在临界(图 5(a))和非临界条件(图 5(b))下，观察到临界成分对电场的响应更强，取向速率更大。进一步，探索了其他初始成分对D的影响，结果呈现在图 6中。可以发现，对任意时刻，当初始成分远离临界成分时，电场的取向程度更小，这是因为电场的取向动力学需要与相分离动力学进行竞争。当相分离的驱动力比较大时，微观组织易形成交联状结构，从而易于被电场取向。反之，当初始成分远离临界成分时，相分离驱动力较小，形成了液滴状结构，其不易被电场取向。因此，通过调控相分离动力学和电场取向作用，有助于获得具有独特微观组织结构及优异性能的高分子复合材料。

4 结论

本研究采用相场模拟，考察了电场对二元高分子共混物相分离过程的影响。通过对体系微观组织结构和各向异性参数分析，揭示了电场对体系微观组织演化及动力学过程的作用机理。结果表明，电场的施加对高分子体系相分离的形貌发展及动力学过程有着显著的影响，具体如下：

(1) 在临界成分下，随着电场强度的增加，体系的微观组织从取向的交联状结构到具有取向的树杈状结构，再转变到完美的取向结构。此外，随着电场的增强，初期的形貌中呈现了越来越多的缺陷，并随时间逐渐减少，最终湮灭。

(2) 在非临界成分下，随着电场强度的增大，体系的微观组织由最初取向的液滴状到分散的纤维状结构，最终再转变到完美的取向结构。尽管最终的取向结构与临界成分下的相似，但二者的平均尺寸和体积分数不同。

(3) 通过取向动力学研究，本研究发现随着电场强度的增加，各向异性参数逐渐增大，并最终趋于稳定。对于具有临界成分的体系，由于较大的相分离驱动力以及交联状的组织结构，相分离结构对电场作用的响应更加显著。