2. 蓝星 (北京) 化工机械有限公司,北京 100176;
3. 蓝星沈阳轻工机械设计研究所,辽宁 沈阳 110015
2. Bluestar (Beijing) Chemical Machinery Corporation Limited, Beijing 100176, China;
3. Bluestar Shenyang Research Institute of Light Industry Machinery, Shenyang 110015, China
氯碱工业中离子膜电解技术因其能耗低、产量高、污染少等优点,已成为氯碱生产的最主要方法。离子膜电解槽是电解技术中的关键设备,随着电解槽新技术的发展[1],槽电压逐渐降低,电流密度不断提高。高电流密度运行加快了气体生成速率,所产生的气体在电解槽顶部滞留,极易发生“膜针孔效应”,缩短离子膜的使用寿命[2, 3];同时,随着电流密度增大,气升作用引起的电解液流动加快,将导致离子膜振动加强,从而会对膜的寿命产生不良影响。另外,气体体积分数增大还将对电解槽内电解液的导电性、电流密度分布以及槽内的热量传递和质量传递特性产生影响,这些因素也都将对离子膜的使用寿命产生影响。因此,研究高电流密度下电解槽内气液两相流动规律,对于开发和设计高电流密度电解槽具有重要意义。
关于氯碱电解槽的研究主要集中在电极上产生的气泡对槽电压、电解液的传递系数和电导率[4~-8]、电流密度分布以及操作条件对电流效率的影响等[9, 10]。这些研究结果为电解工艺条件优化提供了理论支持。然而,迄今为止,对离子膜电解槽内流体传递特性规律方面的研究报道较少。
Dahlkild[11, 12]基于Zuber[13]的漂移通量模型,建立了单流体混合模型,对垂直的电化学槽流场和电场进行分析,发现沿电极方向不均匀分布的气泡导致了不均匀分布的电流密度;气泡对电解槽内形成均匀浓度分布的作用远大于分子扩散作用。Dahlkild研究结果表明电解槽内气相运动和分布对槽电压及电解过程有重要影响。Hua[14]采用两相流双流体模型,通过求解每一相的质量和动量控制方程分析了气泡驱动作用下的流体流动,认为气相分布是由于对流传质和气泡的非均匀扩散造成的,气相质量方程中应当包括扩散项,动量方程中应当包括粘性力,并采用k-ε模型对气泡驱动的湍流流动进行了模拟。Aldas[15]、Mat[16]、Farshad[17]等结合Hua的两相流模型和Dahlkild的单流体混合模型对电解槽内两相流动模型进一步完善,分别对Na2SO4溶液、KOH溶液、NaCl溶液的电解过程进行模拟,得到了电解槽内气体体积分率、电流密度及速度分布等相关数据。在这些研究工作中,气体边界条件均设置为由底部进入电解槽,这样的简化与电解槽中气体是由侧壁的电极网上产生的实际工况存在较大差异,这使得其模拟结果的利用受到了一定的局限。岳雯婷等[18]利用流体力学计算软件,采用欧拉两相流耦合有限速率表面化学反应模型对电解槽阳极室单个格栅内流体传递特性进行了稳态数值模拟。气体由在电解槽侧面的电极网上设定的电极反应生成,得到了阳极室单个格栅内流体的速度、温度和浓度分布。考察了电流密度对液体循环量、膜面温度及膜面附近处最大速度的影响,其研究结果对新型高电流密度电解槽的开发具有重要指导意义。岳雯婷等研究发现,电解槽内液体循环量及顶部气体积累情况是影响电解槽内温度和浓度分布的最重要因素。
为验证数值模拟方法的正确性,本文建立了冷模实验装置,对液相速度、气含率等参数进行了测量。实验得到了高电流密度下电解槽内气含率、气体体积分数分布及循环板上开口处压力波动情况。研究结果可为设计高电流密度电解槽提供依据。
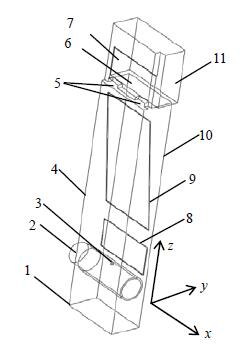
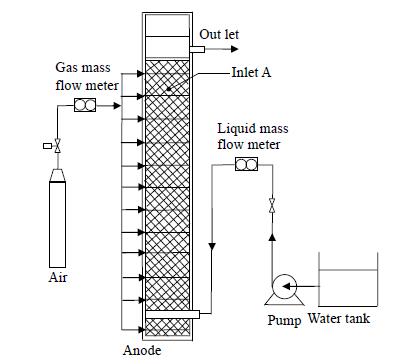
2 实验 2.1 实验装置实验电解槽由阳极室单个格栅和上部分离室构成,其具体结构如图 1所示。阳极室单个格栅的长宽高分别为92、33、1156 mm。格栅内安装有带盐水喷射孔的进口管、上部循环板和下部循环板;分离室内安装有溢流板。本文所采用的气液两相流动实验装置如图 2所示。在实验过程中,水箱里的盐水由泵经质量流量计控制流量后从电解槽底部进口管上的进口孔喷入电解槽阳极室格栅内;空气由空气压缩机经质量流量计控制流量后从侧面布满针孔的分布管进入阳极室 (如图 3所示),以此模拟电解槽内电极上生成的气体,因此该侧面称为膜侧。气体质量流量计的生产厂家为北京七星华创电子股份有限公司,型号为D07-19B,量程为0~10 slm,精度为±1%;液体质量流量计的生产厂家为北京首科实华自动化设备有限公司,型号为DMF-1-1-A,量程为0~25 kg×h-1,精度为±0.2%。由膜侧分布管通入阳极室的气体带动盐水向上流动,部分气液混合物由槽板上的出口孔进入分离室,经分离室溢流板溢流后流出电解槽,一部分液体由循环板背侧向下流动,形成自然循环。
|
图 1 电解槽结构图 Fig.1 Structural diagram of the electrolysis cell 1. coordinate origin 2. inlet 3. jet hole 4. membrane 5. outlet hole 6. channel plate 7. overflow plate 8. lower circular plate 9. circular plate 10. back plate 11. outlet |
|
图 2 实验装置示意图 Fig.2 Schematic diagram of the experimental setup |

|
图 3 气体进入方式 Fig.3 Pattern of gas inlet |
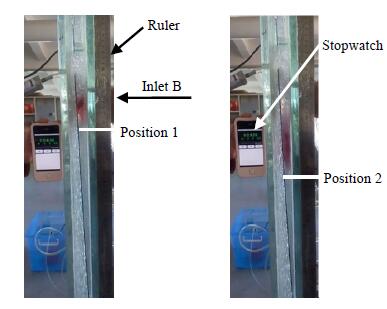
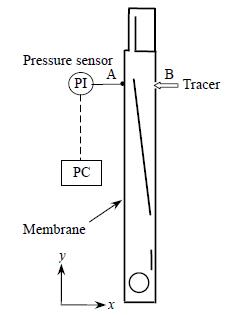
实验电解槽由玻璃制成,为测量循环板背侧液体下降速度及其上开口处压力波动情况,在循环板上开口处,电解槽背板上分别开有染料注射口 (图 4、图 5中的B点) 和压力测孔 (图 5中A点和B点)。压力传感器生产厂家为成都泰斯特电子信息有限责任公司,型号为cy301,精度为0.1%,量程为0~30 kPa,采样间隔为5 ms。
|
图 4 不同时刻染料位置 Fig.4 Position of dye at different times |
|
图 5 阳极室侧面示意图 Fig.5 Side view of the anode chamber A: z=1120 mm B: z=1100 mm |
实验盐水浓度为200 g×L-1,气液流量范围分别为Qg=0~8.26 L×min-1和QL=3.38~17 L×h-1。
2.2 速度测量方法采用示踪法测量循环板背侧下降液体的速度。以密度与盐水密度接近的铬黑T (1.109 g×cm-3) 指示剂为示踪染料。如图 4所示,电解槽背板上开孔B为示踪剂入口,当实验装置内气液流动连续稳定后,在某一时刻由开孔B向电解槽内注入一定剂量的示踪剂。注入的示踪染料会随液体向下流动,在此过程中,利用佳能1DX相机和100~400/F4.5~5.6 L IS USM镜头对染料下行过程进行拍照;利用秒表记录时间,直尺记录染料核心区下降的位置。由时间和位移计算液体的平均速度。
2.3 气含率测量方法采用突然停气法测定电解槽内气含率。待实验装置内气液流动连续稳定后,同时关闭气液两相进口阀,由于槽内气泡逸散,液面下降,记下液面到槽槽板的高度,由此可计算电解槽内的气含率。改变流量,考察不同气液流量下电解槽内气含率。
2.4 压力波动测量方法在循环板上开口处膜侧 (图 5中A点) 和背板侧 (图 4和图 5中B点) 设置了测压孔,将压力传感器由该孔伸入电解槽,由此测量该处的压力信号。实验数据由计算机采集,采样时间为180 s。改变流量,考察不同气液流量下的压力波动特性。
3 数值模拟方法 3.1 研究对象和基本假设以上述实验电解槽为模拟对象,采用欧拉-欧拉双流体两相流模型、标准k-ε湍流模型及有限速率表面化学反应模型对电解槽阳极室单个格栅内气液流动进行稳态数值模拟。
模拟电解槽尺寸与实验电解槽尺寸相同。在数值模拟过程中,假设电极网为光滑平面,气体生成速率恒定。假设气泡尺寸均匀,为实验测取的气泡直径的平均值,为1 mm[18]。采用上述简化假设建立了电解槽三维模型,如图 1所示。
3.2 网格划分采用四面体非结构化网格进行网格划分。基于前期工作结果,确定计算网格节点间距为2.6 mm[18]。
3.3 数学模型 3.3.1 基本方程采用欧拉-欧拉双流体两相流模型对气液两相流动进行模拟,每一相都被看作是充满整个流场的介质,流体按各自规律运动。由于两相共存于同一空间,因此存在相互作用。采用空间平均法,有下式:
| ${{\alpha }_{\text{L}}}+{{\alpha }_{\text{g}}}=1$ | (1) |
式中,αL和αg分别是液相和气相的体积分数。根据质量和动量守恒原理,可以得到稳态下各相连续性方程和动量方程。在直角坐标系中,连续性方程为:
气相连续性方程:
| $\nabla \cdot ({{\rho }_{\text{g}}}{{\alpha }_{\text{g}}}{{\vec{v}}_{\text{g}}})=0$ | (2) |
液相连续性方程
| $\nabla \cdot ({{\rho }_{\text{L}}}{{\alpha }_{L}}{{\vec{v}}_{\text{L}}})=0$ | (3) |
气相动量方程:
| $\nabla \cdot ({{\alpha }_{\text{g}}}{{\rho }_{\text{g}}}{{\vec{v}}_{\text{g}}}{{\vec{v}}_{\text{g}}})=-{{\alpha }_{\text{g}}}\nabla P+\nabla \cdot {{\tau }_{\text{g}}}+{{\alpha }_{\text{g}}}{{\rho }_{\text{g}}}\vec{g}+{{K}_{\text{Lg}}}({{\vec{v}}_{\text{L}}}-{{\vec{v}}_{\text{g}}})$ | (4) |
液相动量方程:
| $\nabla \cdot ({{\alpha }_{\text{L}}}{{\rho }_{\text{L}}}{{\vec{v}}_{\text{L}}}{{\vec{v}}_{\text{L}}})=-{{\alpha }_{\text{L}}}\nabla P+\nabla \cdot \tau {}_{\text{L}}+{{\alpha }_{\text{L}}}{{\rho }_{\text{L}}}\vec{g}+{{K}_{\text{gL}}}({{\vec{v}}_{\text{g}}}-{{\vec{v}}_{\text{L}}})$ | (5) |
其中KLg=KgL,为气相与液相动量交换系数,
即:
| ${{K}_{Lg}}={{K}_{\text{gL}}}=\frac{3}{4}{{C}_{\text{D}}}{{\alpha }_{\text{g}}}{{\alpha }_{\text{L}}}\frac{{{\mu }_{l}}}{D_{\text{b}}^{2}}{{\operatorname{Re}}_{\text{b}}}({{\vec{v}}_{\text{L}}}-{{\vec{v}}_{\text{g}}})$ | (6) |
其中Reb为相对雷诺数,
| $R{{e}_{\text{b}}}=\frac{{{\rho }_{\text{l}}}\left| {{{\vec{v}}}_{\text{L}}}-{{{\vec{v}}}_{\text{g}}} \right|{{D}_{\text{b}}}}{{{\mu }_{\text{l}}}}$ | (7) |
| ${{C}_{\text{D}}}=\frac{24}{R{{e}_{\text{b}}}}(1+0.15Re_{\text{b}}^{0.687})\left( R{{e}_{\text{b}}}>1000 \right)$ | (8) |
| ${{C}_{\text{D}}}=(24/R{{e}_{\text{b}}})+2\left( R{{e}_{\text{b}}}<1000 \right)$ | (9) |
以上方程中,vL、vg分别为液相和气相速度,τ为应力张量,P为各项共享的相同压力,µ为动力黏度,Db为气泡直径。
3.2.2 湍流模型k-ε两方程湍流模型被广泛用来计算液相湍流流动,如前已述及Hua[14]采用此模型对两相流进行了模拟。液相湍动能k和湍流耗散率ε的控制方程为:
| $\nabla \cdot ({{\alpha }_{\text{L}}}{{\rho }_{\text{L}}}{{\vec{v}}_{\text{L}}}\varphi )=\nabla \cdot ({{\alpha }_{\text{L}}}\frac{{{\mu }_{\text{l}}}}{{{\sigma }_{\text{ }\!\!\varphi\!\!\text{ }}}}\nabla \varphi )+H\varphi $ | (10) |
其中φ分别代表k和ε,H为广义源项,其中:
| ${{H}_{\text{k}}}={{\alpha }_{\text{L}}}({{G}_{\text{k}}}-{{\rho }_{\text{L}}}\varepsilon )$ | (11) |
| ${{H}_{\text{ }\!\!\varepsilon\!\!\text{ }}}={{\alpha }_{\text{L}}}\frac{\varepsilon }{k}({{C}_{1}}{{G}_{\text{k}}}-{{C}_{2}}{{\rho }_{\text{L}}}\varepsilon )$ | (12) |
| ${{G}_{\text{k}}}=\rho {{C}_{\text{ }\!\!\mu\!\!\text{ }}}\frac{{{k}^{2}}}{\varepsilon }\cdot {{T}^{2}}$ | (13) |
其中模型常数取值为C1=1.44,C2=1.92,Cμ=0.09,σk=1.0,σε=1.3。T为表面张力系数。
3.3.3 组分输运模型采用有限速率表面化学反应模型对电解反应进行计算,其基本方程表示为:
| $\nabla \cdot (\rho {{\vec{v}}_{i}}{{Y}_{i}})=-\nabla {{\vec{J}}_{i}}+{{R}_{i}}+{{S}_{i}}$ | (14) |
其中,Yi为i组分的分率,Ji为扩散项,Ri为反应速率,Si是源项。
3.3.4 边界条件为求解上述控制方程,给定盐水进口速度和气体生成速率,操作压力为标准大气压,出口采用自由流,考虑重力作用,相间相互作用,包括曳力、升力、阻力等,考虑湍流耗散率。
电流密度为4.5 kA×m-2下的液体流量按照工厂正常生产时盐水进口流量来确定,即146个单元槽,每个单元槽有24个格栅,液体进料量为26.9 m3×h-1。其他电流密度下的液体流量由此推算得到;气体生成速率则根据不同电流密度由法拉第第二定律计算得到,具体数值见表 1。控制方程采用一阶迎风格式进行离散,壁面采用标准壁面函数,速度与压力耦合采用SIMPLE算法,收敛条件为方程残差小于10-4。
| 表 1 不同电流密度下气液流量 Table 1 Volume flow rates at different current densities |
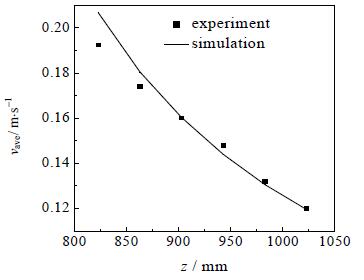
在染料示踪法中,由于速度分布而导致的染料分散给实验中速度的测量带来困难。实验中以染料核心区中心点为基准进行速度求取,并与截面平均速度的模拟值进行比较。当QL=7.67 L×h-1,Qg=3.71 L×min-1时 (相当于电流密度为4.5 kA×m-2),电解槽内循环板背侧不同位置处液体速度的实验值与模拟值的对比如图 6所示。由于本文实验测试距离仅为200 mm,因此尽管染料在下行的过程中有分布,但还是可以很清晰地看出染料的核心区。文中截面速度实验值与模拟值的平均偏差为2.60%,说明本文实验方法可靠。
|
图 6 液体速度实验值与模拟值对比 Fig.6 Comparison on liquid velocities between experimental and simulated data |
从图中可以看出实验测定值与模拟值平均偏差为2.60%,两者吻合良好。液体速度随着z坐标减小而增大,这是由于倾斜的循环板设计使循环板背侧液体流动截面越来越小,因而速度越来越大。
4.2 气含率及气体体积分数分布 4.2.1 气含率利用突然停止向设备内供应气体和液体的方法测定设备内的总体气含率,误差主要来源于实验操作和高度测量两方面。
在实验过程中,当电解槽内气液流动达到稳态后,尽量保证同时停止气体和液体进料,以避免停止气液进料不同步而产生的液面位置误差;实验中采用最小刻度为1 mm的直尺测量液面到槽板的高度,这样,高度的最大测量误差为1 mm,实验电解槽阳极室高度为1156 mm,因此由测量产生的气含率实验值最大误差为1/1156=0.08%,实验中测取的最小气含率数值为1.17%,因此本文中气含率实验值的最大相对误差为0.08 / 1.17=6.8%,一般实验误差在10%以内即满足工程应用,因此可认为本文实验所取得的总体气含率结果可靠。
不同气液流量下电解槽内气含率数据如表 2所示。由表 2可见,当QL=7.67 L×h-1,Qg=3.71 L×m in-1时 (I=4.5 kA×m-2),阳极室内气含率达到3.11%,而当QL=17.10 L×h-1,Qg=8.26 L×min-1时 (I=10 kA×m-2),气含率达到9.08%。这说明当电流密度提高到10 kA×m-2时,槽内气含率将达到4.5 kA×m-2时的近3倍。气含率越高,槽电压越大,电解液的电导率越低,从而将降低电解过程的电流效率[6]。
| 表 2 不同气液流量下的气含率 Table 2 Gas holdup under different gas and liquid flow rates |
表 3和表 4为分别仅改变气体和仅液体流量时的气含率。表 3中仅改变气体流量相当于实际运行中的电解槽增大电流密度而不增加盐水进料流量。表 4中仅改变液体流量相当于不增大电流密度而增大盐水进料流量。从表 3中可以看出气体流量 (或生成量) 越大,槽内气含率越大;从表 4中仅改变液体流量对气含率影响很小。这说明当增大电流密度时,不能依靠增大进液量的方法降低槽内气含率,而是需要从结构上改进电解槽设计。表 2~4中气含率的实验值和模拟值的平均误差为4.09%,两者吻合较好。
| 表 3 不同气体流量下的气含率 Table 3 Gas holdup under different gas flow rates |
| 表 4 不同液体流量下的气含率 Table 4 Gas holdup under different liquid flow rates |
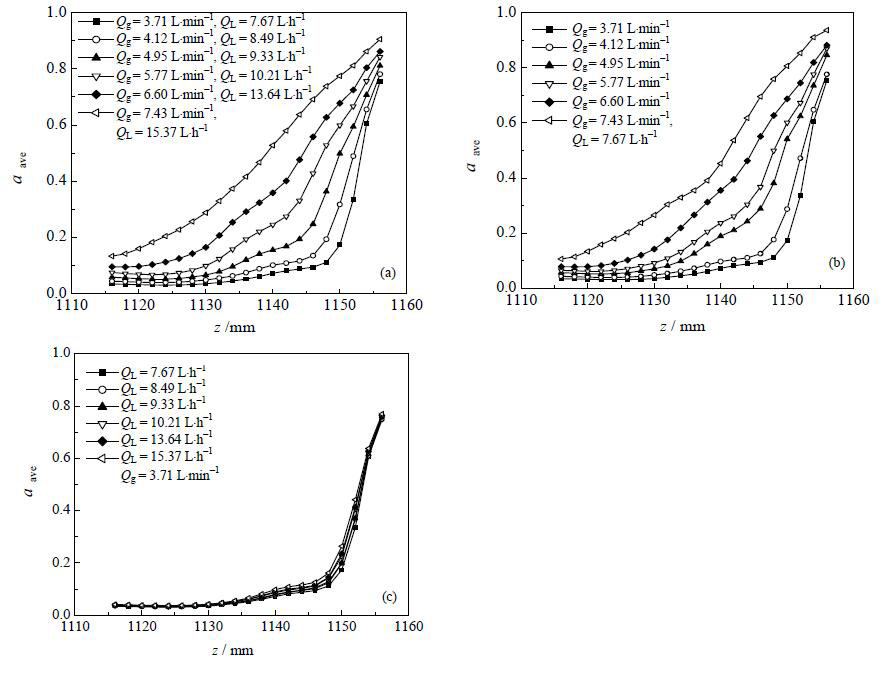
选取z=1116~1156 mm (即从循环板顶部到槽板之间) 区间的不同截面,计算各截面内的气体体积分数 (气含率) 平均值,不同气液流量下的模拟结果如图 7所示。
|
图 7 不同气液流量下循环板上部气体分布 Fig.7 Gas distribution above the circular plate at different flow rates |
由图 7(a)可见,越接近槽顶,气体体积分数平均值越大,并且随着气液流量增加,滞留在电解槽顶部的气体滞留量增加。在z=1116~1130 mm,气体体积分数增长较缓,而在z=1130~1146 mm开始逐渐加快,主要原因可能是因为气液两相从循环板顶部喷射而出所产生的射流所导致,此时液体在顶部形成旋涡,由于浮力和离心力的共同作用,气体会向旋涡边界移动,气体体积分数有所增加。而在z=1146~1156 mm气体体积分数平均值开始迅速加快,在顶部气体体积分数甚至达到90%以上。在实验中观察到的气体流量越大,电解槽顶部气体滞留层越厚,特别是在膜与槽板夹角处存在气体流动的死角,这主要是由于电解槽顶部出口通道狭窄,导致气体流通不畅,从而引起气体聚集,使得距电解槽顶部10 mm空间内气体滞留情况明显。
图 7(b)、(c)分别为改变气体和液体进口流量时格栅顶部气体体积分数分布。通过对比发现,仅改变气体流量时 (图 7(b)),气体体积分数增长情况同图 7(a)相似;仅改变液体的进口流量 (图 7(c)),对顶部气体积累情况几乎没有影响。这说明不能依靠增大盐水进口流量来降低上部气体积累程度。因此对于高电流密度电解槽,应改变气液分离结构来疏导气体,避免其积累而影响电解槽运行。
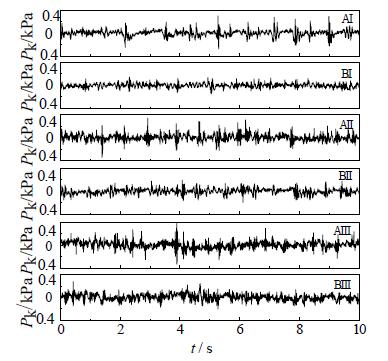
4.3 压力波动特性不同气液流量下循环板上开口处膜侧 (图 5中的A点) 和背板侧 (图 5中的B点) 压力信号的时间序列如图 8所示。从图 8可以看出,A、B处压力值随时间不断变化,说明两处压力随时间均有明显的波动现象。由湍流的N-S方程可知,压力的脉动势必引起速度的脉动,高频的压力和速度脉动是湍流的基本特征,这说明A、B处流体均有明显的湍动现象。
|
图 8 A、B处的压力信号的时间序列
Fig.8 Time series of the pressure signals at A and B positions
I.Qg=1.65 L·min-1, QL=3.38 L·h-1; II.Qg=3.71 L·min-1, QL=7.67 L·h-1; III.Qg=6.60 L·min-1, QL=13.64 L·h-1; |
对比图中AI、BI,AII、BII和AIII、BIII可以看出,相同气液流量下,A处压力随时间波动的幅值比B处大。经计算,AI、BI,AII、BII、AIII、BIII情况下压力信号的标准偏差分别为0.0525、0.0351、0.0574、0.0474、0.0632、0.0557。由这些数据可以看出,在相同流量下,A处比B处压力波动更剧烈,流体湍动更显著。这是因为A处气含率较大,气液两相在A处喷出产生了射流流动的结果。
随着流量增加,A、B处压力波动幅值均增大,压力在均值上下波动更明显。因此可以得出,流量越大,压力波动越明显,流动越不稳定。
生产实践中更关心膜侧的压力波动情况[19, 20],特别是A处,该处是离子膜容易受损的地方。本文对A处压力信号进行了傅里叶变换,得到了该处压力信号的频谱图。从频谱图可以看出压力波动的特征频率及压力信号功率在频域的分布情况。在变换之前,对压力信号进行去除稀疏的野点和去均值预处理。野点的去除是基于拉依达准则对数据中偏差较大的点进行剔除;去均值是将去除野点后的数据减去总体平均值。
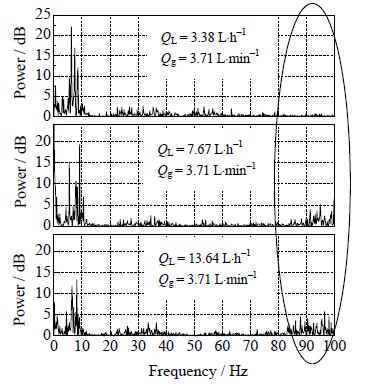
图 9为气体流量一定、不同液体流量时A处压力信号的频谱图。从图 9可以看出,当液体流量较小 (Ql=3.38 L×h-1) 时,信号的特征频率均出现在0~10 Hz,为低频成分;当液体流量为7.67和13.64 L×h-1时,信号的特征频率仍然主要在0~10 Hz,但特征频率对应的信号功率逐渐减小。从图中还可以看出,在这两个流量下,谱图里出现了明显的高频成分。当液体流量为7.67 L×h-1时,高频成分集中在90~100 Hz;当液体流量为13.64 L×h-1时,高频分布变宽,在80~100 Hz。与低频成分的能量相比,高频成分的能量较小。这说明液体流量增大会引起压力信号高频、低振幅脉动。
|
图 9 不同液体流量下A处压力信号频谱图 Fig.9 Frequency spectrograms of pressure signals (position A) under different liquid flow rates |
图 10为液体流量一定、不同气体流量时A处压力信号频谱图。从图 10可以看出,随着气体流量增加,图中10~20 Hz的频率成分逐渐减少。相应的,能量更加集中在0~10 Hz。这说明气体流量增大会引起压力信号低频、高振幅脉动。
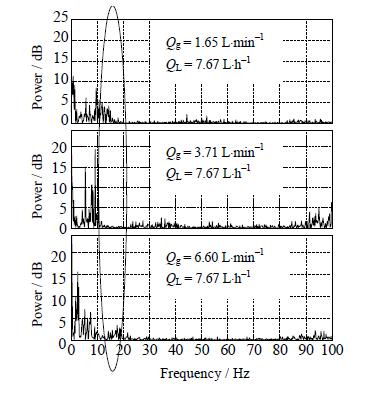
|
图 10 不同气体流量下A处压力信号频谱图 Fig.10 Frequency spectrograms of pressure signals (position A) under different gas flow rates |
对于电流密度为4.5 kA×m-2的工况 (Qg=3.71 L×min-1,Ql=7.67 L×h-1),电解槽内的压力波动主要是由气体流动引起的0~10 Hz的低频、高振幅脉动;高频脉动频率为90~100 Hz,但此区间分布的能量较小。
图 11为气体和液体流量均变化下A处压力信号频谱图,即电流密度变化时的压力信号频谱图。从图中可以看出,随着气体和液体流量同时增大 (或电流密度增大),压力频谱图有两个明显的变化:一个是90~100 Hz频率的能量逐渐增加。根据图 9的分析可知,这是由于液体流量增大引起的;另一个明显的变化是频率为10~20 Hz的能量逐渐减少,低频能量更加集中在0~10 Hz。根据图 10的分析可知,这是由于气体流量增大引起的。
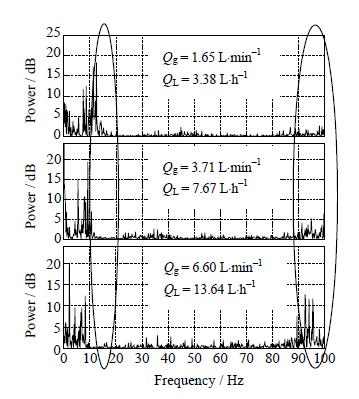
|
图 11 不同气液流量下A处压力信号频谱图 Fig.11 Frequency spectrograms of pressure signals (position A) under different gas and liquid flow rates |
从图 11可以看出,当电流密度增大时,电解槽内气体引起的低频脉动和液体引起的高频脉动都会增强。这表明,当电流密度增大时,压力波动对离子膜的损坏效应会更严重。因此,对于高电流密度的电解槽来说,通过结构改进及时移除顶部积累的气体固然很重要,而降低电解槽内气液流动产生的压力波动,或者开发强度更好的离子膜也是值得重视和研究的问题。
5 结论本文建立了氯碱工业离子膜电解槽阳极室单个格栅内气液两相流动特性研究的实验装置,测定了阳极室单个格栅内液体速度和气含率。实验结果较好的验证了模拟结果的正确性。对循环板上开口处膜侧瞬时压力信号的频谱图进行了分析,得到了该处压力波动特性。本文主要得出以下结论:
(1) 随着气液流量增大,电解槽内气含率增大,顶部气体滞留层增厚。当电流密度为10 kA×m-2时,槽内气含率为4.5 kA×m-2时的近3倍。
(2) 气体体积分数沿电解槽竖直方向逐渐增大,在距槽板10 mm区间内急剧增大,在膜与槽板夹角处最大。
(3) 循环板上开口处膜侧压力波动明显,高频低振幅脉动主要由液体流动引起,低频高振幅脉动主要由气体流动引起。
| 符号说明: | |||
| C | — 常数 | y | — 宽度方向坐标,mm |
| CD | — 曳力系数 | Y | — 组分的分率 |
| D | — 直径,m | z | — 高度方向坐标,mm |
| G | — 湍动能生产项,m2·s-2 | α | — 体积分数 |
| H | — 广义源项 | ε | — 湍流耗散率,m2·s-3 |
| I | — 电流密度,kA·m-2 | φ | — 通用变量 |
| J | — 扩散项,mol·m-2·s-1 | μ | — 动力黏度,kg·m-1·s-1 |
| k | — 湍动能,m2·s-2 | ρ | — 物理密度,kg·m-3 |
| K | — 动量交换系数 | τ | — 应力张量,Pa |
| P | — 压力,kPa | σ | — 常数 |
| Q | — 体积流量,L·min-1、L·h-1 | 下标 | |
| Re | — 雷诺数 | ave | — 平均值 |
| r | — 生成速率,mol·m-2·s-1 | b | — 气泡 |
| R | — 反应速率,mol·m-2·s-1 | g | — 气相 |
| S | — 源项,mol·m-2·s-1 | i | — 组分 |
| T | — 表面张力系数 | k | — 瞬时的 |
| v | — 速度,m·s-1 | L | — 液相 |
| x | — 长度方向坐标,mm |
| [1] | YI Bao-lian(衣宝廉), QU Tian-xi(曲天锡), ZHANG En-jun(张恩浚), et al. Plate filter press type chlor alkali cell with oxygen cathode(采用氧阴极的压滤机式氯碱电解槽)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 1996, 10(3): 258-263. |
| [2] | LI Su-gai(李素改). Energy consumption status and application progress of energy saving technology of chlor alkali industry(氯碱行业能源消耗现状及节能技术应用进展)[J]. China Chlor-Alkali(中国氯碱) , 2014, 5(3): 1-3. |
| [3] | ZHOU Qiang(周强), WANG Qi(王奇), JIANG Yong(江泳). Research on operation technologies of Asahi Kasei NCZ zero-polar distance electrolyzers(旭化成NCZ零极距电解槽应用技术研究)[J]. Chlor-Alkali Industry(氯碱工业) , 2012, 48(10): 13-16. |
| [4] | Janssen L J J, Hoogland J G. The effect of electrolytically evolved gas bubbles on the thickness of the diffusion layer[J]. Electrochimica Acta , 1970, 15(6): 1013-1023. DOI:10.1016/0013-4686(70)80041-X. |
| [5] | Gijsbers H F M, Janssen L J J. Distribution of mass transfer over a 0.5-m-tall hydrogen-evolving electrode[J]. Journal of Applied Electrochemistry , 1989, 195(5): 637-648. |
| [6] | Vogt H. The incremental ohmic resistance caused by bubbles adhering to an electrode[J]. Journal of Applied Electrochemistry , 1983, 13(1): 87-88. DOI:10.1007/BF00615891. |
| [7] | Xiong Y, Jialing L, Hong S. Bubble effects on ion exchange membranes-an electrochemical study[J]. Journal of Applied Electrochemistry , 1992, 22(5): 486-490. DOI:10.1007/BF01077554. |
| [8] | Bergner D. Membrane cells for chlor-alkali electrolysis[J]. Journal of Applied Electrochemistry , 1982, 12(6): 631-644. DOI:10.1007/BF00617483. |
| [9] | Chandran R R, Chin D T. Reactor analysis of a chlor-alkali membrane cell[J]. Electrochimica Acta , 1986, 31(1): 39-50. DOI:10.1016/0013-4686(86)80058-5. |
| [10] | Jalali A A, Mohannadi F, Ashrafizadeh S N. Effects of process conditions on cell voltage, current efficiency and voltage balance of a chlor-alkali membrane cell[J]. Desalination , 2009, 237(1): 126-139. |
| [11] | Dahlkild A A. Modeling the two-phase flow and current distribution along a vertical gas-evolving electrode[J]. Journal of Fluid Mechanics , 2001, 428(2): 249-272. |
| [12] | Wedin R, Dahlkild A A. Numerical and analytical hydrodynamic two-phase study of an industrial gas-lift chlorate reactor[J]. American Society of Mechanical Engineers, Pressure Vessels and Piping Division , 1999, 397(1): 125-136. |
| [13] | Zuber N, Findlay J A. Average volumetric concentration in two-phase flow systems[J]. Journal of Heat Transfer , 1965, 87(4): 453-462. DOI:10.1115/1.3689137. |
| [14] | Hua J S, Wang C H. Numerical simulation of bubble-driven liquid flows[J]. Chemical Engineering Science , 2000, 55(19): 4159-4173. DOI:10.1016/S0009-2509(00)00075-0. |
| [15] | Aldas K. Application of a two-phase flow model for hydrogen evolution in an electrochemical cell[J]. Applied Mathematics and Computation , 2004, 154(2): 507-519. DOI:10.1016/S0096-3003(03)00731-8. |
| [16] | Mat M D, Aldas K. Application of a two-phase flow model for natural convection in an electrochemical cell[J]. International Journal of Hydrogen Energy , 2005, 30(4): 411-420. DOI:10.1016/j.ijhydene.2004.04.002. |
| [17] | Farshad A, Hasan R. Applying a modified two-fluid model to numerical simulation of two-phase flow in the membrane chlor-alkali cells[J]. Iranian Journal of Chemistry and Chemical Engineering , 2008, 27(3): 51-61. |
| [18] | YUE Wen-ting(岳雯婷), ZHANG Li(张丽), LIU Xiu-ming(刘秀明), et al. Influence of current density on transfer characteristics in electrolysis cell of chlor-alkali industry(电流密度对氯碱工业离子膜电解槽传递特性影响)[J]. Journal of Chemical Industry and Engineering (China)(化工学报) , 2015, 66(3): 915-923. |
| [19] | Asahi Kasei Corporation. Used for alkali metal chloride aqueous solution of electrolyzer unit slots:Japan, JP 242002/99[P]. 1999-08-27. |
| [20] | Asahi Kasei Corporation. Bipolar press filter type electrolytic cell (双极压滤器型电解池): China, CN 92102754.0 [P]. 1992-12-09. |




