2. 浙江大学 控制科学与工程学院, 浙江 杭州 310027
2. College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, China
随着能源问题日益突出,能源消耗从2016年起至2030年将会有30%的可预见式增长[1, 2],离心泵作为在各个流程行业中都应用广泛的通用设备,有着迫切的节能需求。国际能源组调查显示,电机耗电量占世界消耗电量的46%,占工业耗电量的近70%[3]。在美国工业电机系统中,整个泵系统消耗的电量占工业总耗电量的25%[4]。中国第三次工业普查资料显示,水泵设备装机总功率已达到1.1亿千瓦,年总耗电量2200亿千瓦时,约占全国电力消耗总量的20%,约占工业用电量的30%[5],可见泵类设备的节能空间很大,因此高效泵机研究很有必要[6, 7]。当然单个泵机的设计效率越来越高并趋于极限,目前国内泵设备效率比发达国家仅低2%~5%,而多个泵以串并联方式构成的泵网络运行效率却要比国外低将近20%[8],主要原因在于设计和操作造成的工作点不合理。
泵网络耗能占比较高的行业包括供水和水处理[9, 10]、工业冷却水系统[11, 12]和采暖通风空调系统[13, 14]。Goldstein和Smith等[15, 16]调查了水处理过程,其用电量占美国国内总量4%,占全球电量7%[17],其中泵网络占80%。工业冷却水系统中泵网络能耗占比也很高[18]。美国的采暖通风和空调系统约占建筑总能耗的50%,占全美总能源消费的20%[19]。因此,如何通过设计和操作优化帮助泵类设备实现最佳性能将是研究者亟待解决的重点问题。
2001年12月,中国电机系统节能项目正式启动,主要针对电机、水泵、风机和压缩机等电机系统的节能[20]。2005年,美国水力协会在美国发起泵网络节能教育计划[21]。通过设计优化和操作控制来提高整个泵网络的运行性能,达到节能的目的。通常,对泵网络进行节能改造可以平均节约能耗20%,有的可以节约30%~50%[22]。本文将通过对比讨论当前研究者们对泵网络的寿命周期、面向泵网络设计与操作优化问题的建模以及求解算法等各方向的工作,对泵网络的节能设计和操作优化进行综述与展望。
2 泵网络设计与操作优化命题解析和研究内容离心泵网络节能是一个典型的化工过程优化问题,对象是多个单泵以串/并联构成的复杂网络结构,约束为达到指定流量和扬程、物料能量衡算和基本性能方程,目标为总成本最低。设计优化类命题通过调整泵网络结构来最小化对象成本,而解决操作优化命题则通过调整设备开停和变频等方式最小化对象成本。无论是设计或是操作优化命题都可以写成如下通用形式[23]:
| $\begin{gathered} {\rm{min}}\quad \;f\left( x \right) \hfill \\ {\rm{s}}{\rm{.t}}{\rm{.}}\quad \;g\left( x \right) \geqslant 0 \hfill \\ \quad \;\quad h\left( x \right) = 0 \hfill \\ \end{gathered} $ | (1) |
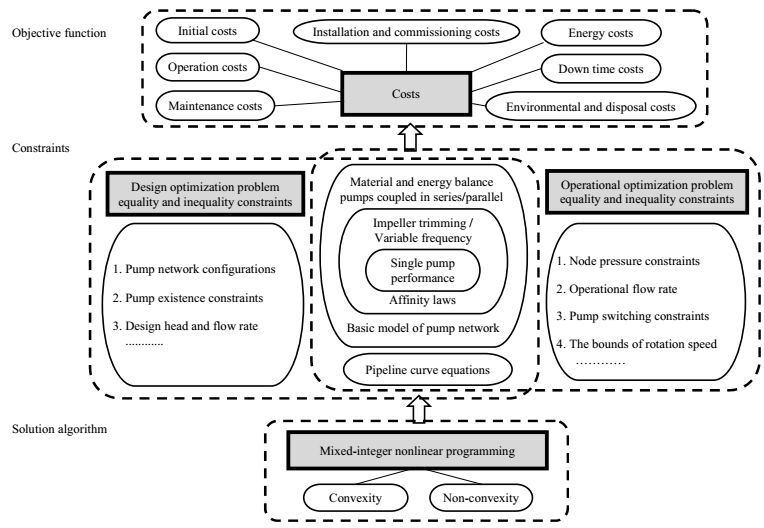
因此命题的建模分成目标函数和约束条件两部分,加上命题的求解算法,构成了如图 1所示的离心泵优化命题研究内容的基本框架。
|
图 1 离心泵网络设计与操作优化命题研究内容框架 Fig.1 Outline of research on design and operational optimization problems of centrifugal pump network |
首先是目标函数。离心泵网络优化的目标始终是成本最小化,研究者们要考虑各种工业用离心泵运行的费用组成,包括初始投资成本、安装和调试费用、操作费用、常规维护维修费用、停车和环境处理在内的所有显性费用,以及泵设备运行效率偏差损耗所引起的隐性特殊维修与折旧费用。
其次是约束条件。优化命题分为设计型和操作型两大类,其公用的约束为泵网络的基础方程和管路特征方程。泵网络由多个单泵构成,所以泵网络基础方程的核心是单泵性能方程:
扬程:
| ${H_i} = {\text{H}}({Q_i})$ | (2) |
功率:
| ${P_i} = {\text{P}}({Q_i})$ | (3) |
效率:
| ${\eta _i} = \eta ({Q_i})$ | (4) |
流量上下限:
| $Q_i^{\text{L}} \leqslant {Q_i} \leqslant Q_i^{\text{U}}$ | (5) |
然后考虑切削及变频比例定律[24]用于表达调整后的单泵性能
切削:
| $\frac{{Q'}}{Q} = \left( {\frac{{D'}}{D}} \right)\quad \frac{{H'}}{H} = {\left( {\frac{{D'}}{D}} \right)^2}\quad \frac{{P'}}{P} = {\left( {\frac{{D'}}{D}} \right)^3}$ | (6) |
变频:
| $\frac{{Q'}}{Q} = \left( {\frac{{n'}}{n}} \right)\quad \frac{{H'}}{H} = {\left( {\frac{{n'}}{n}} \right)^2}\quad \frac{{P'}}{P} = {\left( {\frac{{n'}}{n}} \right)^3}$ | (7) |
单泵串并联是泵网络的基础结构,用等式约束表示如下:
串联物料衡算:
| ${Q_{ij}} = {Q_i} = {Q_j}$ | (8) |
串联能量衡算:
| ${H_{ij}} = {H_i} + {H_j}$ | (9) |
串联流量约束:
| $\max \left( {Q_i^{\text{L}},Q_j^{\text{L}}} \right) \leqslant {Q_{ij}} \leqslant \min \left( {Q_i^{\text{U}},Q_j^{\text{U}}} \right)$ | (10) |
并联物料衡算:
| ${Q_{ij}} = {Q_i} + {Q_j}$ | (11) |
并联能量衡算:
| ${H_{ij}} = {H_i} = {H_j}$ | (12) |
并联扬程约束:
| $\max \left( {H_i^{\text{L}},H_j^{\text{L}}} \right) \leqslant {H_{ij}} \leqslant \min \left( {H_i^{\text{U}},H_j^{\text{U}}} \right)$ | (13) |
管路特征方程可写成如下形式:
| $h{e_{\rm{m}}} = {\left( {\mathit{\Delta }z + \frac{{\mathit{\Delta }p}}{{\rho g}}} \right)_{\rm{m}}} + S \cdot Q_{0{\rm{m}}}^2$ | (14) |
除去上述公用方程之外,设计型问题还需添加描述离心泵网络结构排布[25]的约束方程和泵的存在性约束,并且满足扬程和流量要求,
| ${N_{{\text{p}},i}} \geqslant 0,{N_{{\text{s}},i}} \geqslant 0$ | (15) |
| ${N_{{\text{p}},i}} -{N_{{\text{p}},i\max }} \times {y_k} \leqslant 0$ | (16) |
| ${N_{{\text{s}},i}} -{N_{{\text{s}},i\max }} \times {y_k} \leqslant 0$ | (17) |
| ${y_k} = \left\{ {\begin{array}{*{20}{l}} {\;1,\quad {\rm{k位置存在泵 ;}}} \\ {0,\quad {\rm{k位置不存在泵;}}} \end{array}} \right.$ | (18) |
| ${H_{\text{m}}} \geqslant Coe \cdot h{e_{\text{m}}}$ | (19) |
| ${Q_{\text{m}}} \geqslant {Q_{0{\text{m}}}}$ | (20) |
操作型问题则需添加描述离心泵网络节点压力约束[26]、流量要求和开停、转速约束,
| $p{}_{k,\min } \leqslant {p_k}\left( t \right) \leqslant {p_{k,\max }},\forall k,\forall t$ | (21) |
| ${Q_{\text{m}}} = {Q_{0{\text{m}}}}$ | (22) |
| ${y_k} = \left\{ {\begin{array}{*{20}{l}} {1,\quad {\rm{k位置开泵;}}} \\ {0,\quad {\rm{k位置停泵;}}} \end{array}} \right.$ | (23) |
| ${n_{i,\min }} \times {y_k} -{n_i} \leqslant 0$ | (24) |
| ${n_i} -{n_{i,\max }} \times {y_k} \leqslant 0$ | (25) |
从上述方程可以看出,离心泵网络的设计和操作型问题都包含整型变量,非线性模型方程,是典型的MINLP命题。因此其算法研究都针对MINLP命题,其研究节点自然定位在凸性和非凸性特征,选择或开发合适的求解算法。
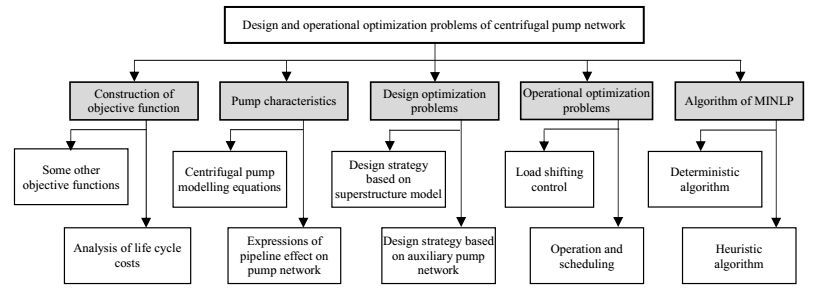
3 泵网络设计与操作优化命题研究现状针对泵网络优化命题研究,国内外有大量文献报道。按照研究主题可以将文献进行如图 2所示归纳整理,主要包括以下五个方向:泵网络系统优化目标研究、基本性能方程的研究、泵网络优化设计研究、泵网络操作优化变负荷控制、优化算法研究。
|
图 2 泵网络设计与操作优化命题研究方向分类 Fig.2 Research category of design and operational optimization of centrifugal pump network |
首先关注优化命题目标研究。学者们从经济成本分析和泵的能量利用出发,分析泵网络各个部分的花费比例、计算离心泵网络的运行效率和能效系数、研究当前操作点在系统各部分的能量分配。通过结果的分析和比较,确定合适的优化目标,为企业挖掘节能潜力提供决策依据。
3.1.1 泵网络寿命周期分析美国水力协会[22]提出了寿命周期成本分析法(Life Cycle Costs,LCC),对泵网络新建和改造进行成本分析。将泵在整个寿命周期中的显性成本消耗总结为初始投资成本、安装调试费用、能耗费用、运行人工成本、维护费用、停运期间费用、环保费用和特殊处置费用,具体内容表示如下:
| ${\rm{LCC = Cic + Cin + Ce + Co + Cm + Cs + Cenv + Cd}}$ | (26) |
其中,Cic表示初始投资成本,比如购置泵、管道和其它辅助设备产生的费用;Cin表示安装调试费用,在新建或扩建过程中,安装和调试设备产生的费用;Ce表示能耗费用,在泵系统中主要指电能的消耗产生的费用;Co表示运行人工成本,对泵系统温度、流量、压力和振动等情况的监测和管理产生的劳动力花费;Cm表示维护费用,对泵、管道和其它辅助设备的定期维修维护所产生费用;Cs表示停运期间费用,由于不可预计的原因导致停车停运,导致在该期间部分产品损失产生的费用;Cenv表示环保费用,泵及其辅助设备在工作过程中可能对环境造成一定的污染和影响而产生的处理费用;Cd表示特殊处置费用,比如泵在输送有毒有害流体过程中产生的处置费用,以及报废处置费用等。
设备寿命一般为15~20年,初始投资成本只是寿命周期成本中的很小一部分,泵网络的能耗、维护费用和其他成本可能远高于初始投资成本。因此,在优化目标中追加泵网络在运行寿命周期内的各项其它费用,会让泵网络总成本更低。他们对一家造纸厂的水循环系统进行分析改造,在原有的泵组基础上并联了一台泵,预期在20年的寿命期内可节约费用70万美元[27]。
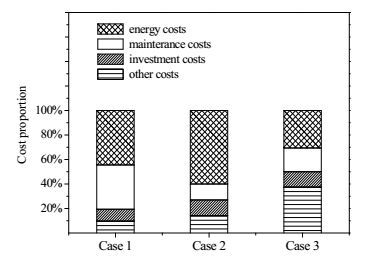
很多研究报道虽然并没有严格采用寿命周期全费用最小作为优化目标,但是会选取费用占比较大的项目作为分析与优化的目标。图 3所示的三个案例分析了泵网络的各项费用组成,由图可知能耗费用和维护费用占比较高,水公用工程年费用的65%消耗在泵运行能耗和维护上[30]。此外,根据不同的考量还可以选择能耗费用最小[31]、能耗费用和维护费用和最小[32]、初始投资成本和能耗费用和最小[33]等作为优化命题的研究目标。
|
图 3 案例1[22]、案例2[28]和案例3[29]离心泵网络费用构成对比 Fig.3 Contributions of centrifugal pump network costs in case 1[22], case 2[28] and case 3[29] |
与LCC法考虑泵网络直接费用不同,部分研究者们将影响各项直接费用的泵效率作为优化目标。泵网络各部分的选型和匹配会影响泵网络的效率[34],单泵和泵网络如果长期运行在非高效区,将会增大机械磨损,减短泵使用寿命,增大维护维修费用的支出。Moreno等[35]模拟泵站,着重强调了优化泵站总费用不仅仅只考虑泵和电机的效率,还需要考虑泵站其它组成部分的效率,比如变频驱动效率和压头在管路的损失效率等,泵的使用寿命会影响整个泵网络的效率。Pascual等[36]介绍了一种新型数学模型,表达了泵效率与泵使用寿命之间的关系,得到泵效率作为泵使用寿命的函数。随着泵运行年份的增加,泵运行效率下降,同时导致能耗费用增加。
除了上述优化目标之外,也有些研究者将泵网络的特殊工艺任务要求添加到优化目标中,例如影响企业能耗费用的最大峰值功率[37]、水系统中水的质量指标[38]以及影响静压头的水源液面高度[39]等,形成多目标优化问题。
3.2 面向建模的离心泵基本性能方程离心泵的单泵性能仍然是泵节能优化的研究重点,如Savar等通过叶轮切削提高泵效率[40],但本文更关注离心泵组合运行时的性能方程如何能够完成建模功能。这一部分的研究主要关注单泵性能如何方便准确地关联?缺乏测量点时以何种方式获得变量值?泵串并联后的实际性能是否需要在单泵基础上修正?
首先是基于建模要求的单泵性能方程研究,离心泵的特性曲线主要包括扬程、功率、效率与流量之间的关系。Ahonen用内插法关联离心泵出厂数据[28]。Chang等[41]用四次多项式拟合。Olszewski等[42]用近似法求功率,关联电机频率、泵的扬程和泵在系统中的位置。Yang等[43, 44]研究关联电机转速的扬程和功率通用方程。
其次工业现场仪表测量点有限,不可能给每台泵装足够的测量点,比如流量。因此,基于泵性能曲线和相似定律[45, 46],根据泵模型进行流量估算是很重要的处理方法,如QH和QP方法[47]。QH法用压头估算流量而QP法用功率估算流量。
此外,一些文献对泵网络中的泵性能和管路性能假设的偏差进行了研究,并提出了相应的简化方法。以并联泵的方式运行,可以使泵网络在更大流量范围内可调。Koor等[48]讨论了并联泵的性能与效率之间的关系,研究了三种泵并联操作工况。Zhang等[49, 50]研究了六种不同类型的污水泵在不同工况下的并联操作。武[51]研究了离心泵并联运行工况的特性,将支路的阀门和管路阻力看作泵的内阻,用虚拟泵的概念简化了并联泵网络工况点的确定方法,便于后期编程中处理支路阻力影响[52]。
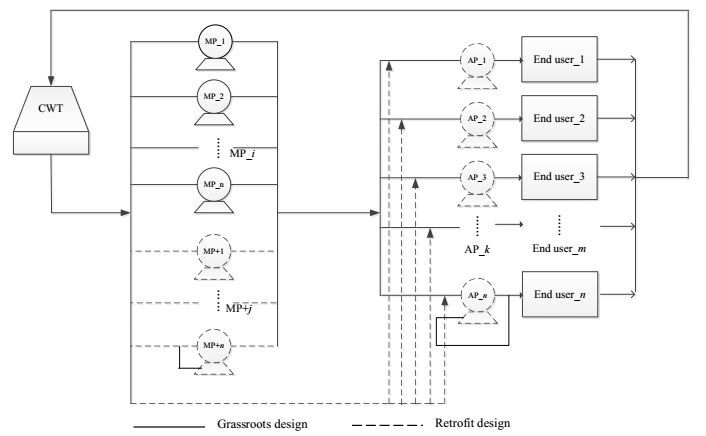
3.3 泵网络设计优化研究泵网络的设计型优化命题通常是在泵网络结构未给定的情况下,通过建模和优化得到合适的排布方案,主要用于新建或者改造现有泵网络[53]。工业装置冷却水泵网络的初始设计中,冷却水槽后设置多泵并联,冷却水经过一排并联泵加压后汇入总管再分支进入终端设备。对于改造设计,往往基于泵的串并联特性,通过增开并联泵数量、添置新管线和泵、以及添置增压泵等方式,实现现存泵网络的改造和扩建。如图 4所示,实线为初始设计,虚线为改造设计。其研究难点在于如何合理地用数学语言描述网络的各种存在可能。典型的设计策略包括,基于超结构模型的设计[25]和基于辅助泵网络的设计[54]。
|
图 4 冷却水系统初始设计和改造设计对比图 Fig.4 Original design vs. retrofit design of pump network for a water cooling system CWT: cooling water tower MPi: main pump i APk: auxiliary pump k |
首先对泵网络独立分析,Westerlund等[25]提出一种基于超结构模型的L层泵网络排布。网络中每层泵型号相同,转速相同,各自并联支路上的泵个数相同,最终计算求解得到总流量、压降与泵配置数量之间的关系图,可用于指导给定流量和压头下泵网络的配置。Westerlund等研究的侧重点在于模型的建立、过程的分析与设计,并没有对化工过程进行操作方面的讨论。若在同一层排布中,泵的型号或者转速不相同的泵网络系统,该模型并不适用。
其次,泵网络是工业循环冷却水系统重要组成部分,许多研究都基于冷却水系统的改造设计[55~57]。对冷却水系统的优化改造可以从冷却水塔[58, 59],泵网络[60]以及换热网络[61]等子系统着手。各个子系统之间相互关联相互影响,用能和用水有较高的耦合度,因此泵网络的新建与改造往往受到冷却水系统中其它部分的影响。在设计改造过程中,需要分析循环水泵网络压力分布[62],同时考虑温度和压降对系统优化的影响[63~65]。热交换网络优化中换热器的排布由简单的并联排布变成串、并联交替排布[66, 67],结果是新鲜冷却水量减小[68],返回冷却水塔的回水温度升高,通过各个支管的压力降增大,需要泵提供的压头将增加。
Sun等[54]在泵网络改造设计方面做了一系列工作。首先基于冷却水系统构建了一个包含主泵网络网络和辅助泵网络网络的超结构模型,描述单冷却水源头多终端用户的分配方式。根据不同换热器的压头需求,通过增加辅助泵来满足流量压头需求,同时减小由于阀门开合度引起的能量损耗,从而减小了泵网络的经济总成本。通过优化求解,得到辅助泵的最优数量以及安装位置。然后,Sun等[69]在此基础上研究了用两步序贯模式对冷却水系统进行经济成本优化计算的策略。第一步使用热力学模型优化换热网络,第二步使用水力学模型优化泵网络。最终,Sun等[70]同步考虑了换热网络的优化和泵网络的优化。与两步序贯法优化冷却水系统结果比较,经济成本节约47.9%。这是一个完整的复杂泵网络设计改造案例。
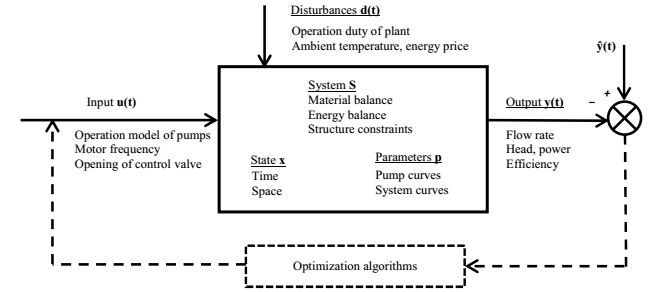
3.4 泵网络操作优化研究泵网络的操作型问题是在给定泵网络结构下,通过变频调速、监测和先进控制等手段,对泵网络的运行数量、转速进行调整,实时优化系统的供应量和操作压降[71]。传统集中式供水的冷却水系统由同一个泵网络通过不同分支管路,向多个终端设备供送冷却水[72],选择其设计目标是让整个终端系统满足时间和空间两个维度上各种操作工况中各种需求条件。在实际工作中,时间维度的变化表示在由于周期/临时的变化或其它原因引起的冷却水温等变量波动。空间维度的变化则表示各个终端需求(流量、扬程)分布。如果设计冷却水装置时按集总和稳态给定负荷要求,那么在某些空间和时间终端就要降压供应。操作问题的目标就是在空间和时间上获得更好的柔性和控制效果。将泵网络操作优化命题的通用建模策略归纳成图 5所示[73]。图中方块表示研究对象方程组S,为给定结构的复杂泵网络,其表达包括物料和能量衡算以及各种约束;输入变量u(t)为泵开停状态、阀门开度、电机频率等;扰动变量d(t)为生产负荷变化、季节温度变化和峰谷电价变化等;状态变量x为时间变量(周期/临时)/和空间变量(需求分布);参数p为泵性能曲线系数、阀门特性系数和其它相关参数;输出变量y(t)为流量、压头、功率、效率、用电量等,ŷ(t)为目标变量。
|
图 5 泵网络操作优化命题通用建模策略示意图 Fig.5 Schematic diagram of modelling of pump network operational optimization |
泵网络的变负荷控制是针对终端需水量变化所产生的变负荷需求,调整当前泵网络中的设备运行台数和工况参数,降低整个网络的操作成本。Koor等[48]基于供水系统,分别研究了相同类型泵并联操作工况、同种型号的新泵和老泵并联操作工况,以及三种不同性能泵并联操作工况,根据排水量和压头的不同,为保证泵网络在高效区运行,可根据转换曲线得到合适的开泵数量。Ma等[74]研究了中央空调的冷却水系统,提出了变速泵的优化控制策略,从而提高能量利用效率。在复杂中央空调系统中,按终端设备不同,两类变速泵使用不同的控制策略,分配水到终端单元的泵的速度通过使用水的在线开放信号控制阀门从而来重新设置压差设定值来控制,而分配水到换热单元的泵的速度则由水流量控制。结果表明通过使用优化控制方案,可以节省12%~32%的泵能量。Tirmizi等[75]基于某大学的中央冷却水系统,考虑外界环境温度对能耗的影响,讨论泵网络的变负荷操作。针对不同泵组合方式,讨论泵网络通过变频调速操作,提高泵网络的运行性能,实现节能降耗的目的。
3.4.2 泵网络的操作调度泵调度问题,包括计划在未来一段时间内泵网络操作问题、最小化能耗费用,综合考虑网络基础元素比如泵、管路、阀门[76]和储槽[38]等,以及考虑由于季节变化的不同水量需求、峰谷电价等因素[77]。泵调度研究中加入了时间变量,进行动态规划,目标是提出调度策略,减少操作费用。操作调度的优点是不需要额外投资,对多泵网络进行优化研究,是实现节能减排不错的选择。Benjamin等[37]研究了包含5台泵的供水调度模型。通过操作优化,选择合适的泵运行组合,满足系统所需的流量和压头。Wang等[78]研究了4台不同性能的水泵分别从不同水源泵送水进入蓄水池的泵网络的操作调度问题。对比Benjamin等研究的操作调度模型,在一天二十四小时中,以1小时作为调度模型的时间间隔,泵的开停只可以发生在每小时间隔时间点上,这样的时间间隔设置过于简单化。Wang等在考虑时间间隔变量时,将时间变量作为连续变量,泵的开停可以发生在任何时间点,而不是只能发生在每小时间隔的间隔点上。在连续时间点对泵网络进行调度操作,与生产生活的实际情况符合度更高,以节能为目标进行操作优化,实现对供水泵的最优排布。
3.5 泵网络设计与操作优化命题的算法研究混合整数非线性规划问题(MINLP)是一类包含连续与离散变量的非线性规划问题。根据工业优化背景构建基本网络图,经过适当筛选并量化相关离散变量和连续变量,确定基本的约束条件,将网络结构模型转化为数学模型,这就是MINLP问题的构建过程。在化学工程领域中很多优化问题都包括了影响设计和操作的离散变量、连续变量以及非线性系统,包括热交换网络[79]、质量交换网络[80]、水网络[81]以及其它网络,如氢网络[82]、反应器网络[83]等,其中以热交换网络的研究与应用最为成熟与广泛[84~86]。本质上各个网络之间存在共性,基本思想就是通过循环、回用和再生回用等方式,使得热量、冷量、未充分利用的物料、公用工程中的冷却循环水和氢气等,实现物流间的能量交换与利用,实现公用工程费用优化,实现装置数量优化,提高能源利用率和减少环境污染物的排放量。在实际工业系统中,各个网络之间有很多交叉[87],在处理优化问题时也常常对多个网络进行集成综合优化。
泵网络模型中包含了泵的基础参数,流量、扬程、功率和效率。对泵网络进行优化配置,通过二元整数变量0和1来表示泵的开停或排布存在性。此外,泵作为增压送能设备,在工业系统中起到中间媒介连接作用。在考虑压降的优化问题中,往往将泵网络的优化与其它网络进行综合优化,比如换热网络[88]和水网络[89]。因此泵网络的设计与操作优化命题是一个典型的MINLP问题。求解MINLP的算法分为两类讨论,凸性MINLP和非凸性MINLP。其中凸性MINLP的算法分为确定型算法和启发式算法,常用确定型算法有分支定界法[90],外逼近法[91],扩展割平面法[25, 92, 93]等;启发式算法有潜水启发式算法和可行性泵启发式算法等[94]。非凸性混合整数非线性规划与凸性混合整数非线性规划相比,很难直接得到全局最优解,因此非凸性MINLP的算法一般可分为直接求解算法和间接求解算法。直接求解算法有空间分支定界法、分支下降算法、αBB等[94];间接求解中,需对非凸性问题进行处理[95],凸性MINLP问题的确定型算法只能作为非凸性MINLP问题的启发式算法。许多研究学者针对泵网络的设计与操作优化命题的求解算法进行研究,将确定型算法与一些智能算法或其它方法结合在一起,比如遗传算法[96~99]、模拟退火算法[100~102]、粒子群算法[103]、蚁群优化算法[104]和模糊优化算法[105]等,用于克服命题的非凸对求解造成的困难,且在运算速度、收敛速度和稳定度等方面表现出了很好的性能。
4 离心泵网络优化研究的展望泵网络优化研究有着良好的工业应用前景,不断发现新需求、提出新命题并探索新方法始终是研究者们工作的方向。前三十年中,工业成本的构成从一次性设备投资最大慢慢向操作能耗最大倾斜,无数最优解因此而改变。近年来人工费用在成本构成中所占比例又不断提高,泵网络优化目标中的管理和维护费用也因此不断增长,这又会给最优解带来什么样的变化?在互联网应用级数增长的大环境下,如何优化设计与操作工厂级泵网络以降低管理成本?如何应对命题大规模化带来的MINLP求解困难?当用电成本和产品市场需求同时发生变化时,如何保证泵网络操作满足需求并达到成本最低?在这些问题中,本文主要整理了如下两点展望。
4.1 泵网络的性能监控和维护调度在泵网络优化的目标函数中,除去能耗和初始投资外,安装和调试、维护维修、停车、环境、停运和处理费用几乎都以人工成本为主。随着企业内部网络信息成本和人工成本的此消彼长,研究者试图让泵正常运行更长时间、减少设备的非正常检修次数,以便减少泵设备管理人数。这就要求针对泵网络建立装置乃至全厂级的智能化管理系统,通过大数据分析监测各台设备的性能指标,合理安排检修时间,降低设备的事故返修率和损毁率,将维护控制在可调度范围内。
这项研究的难点在于,面对种类繁多、测点各异的泵设备,如何高效地确定智能管理的分类原则、完成现场动态数据的滤波和去噪、实施泵性能参数估计和泵设备故障诊断以及面向效率检测的泵设备检修调度。
4.2 考虑时间与空间二维分布式需求的泵网络柔性设计传统的泵网络设计只考虑整个时间周期内和空间分布上的最恶劣工况,是一个不考虑柔性的集总参数命题,在某些空间和时间通过降压供应终端来满足需求,时变问题归属于变负荷控制和调度范畴,而空间变化只能通过能耗实现。进一步的优化设计应该能够考虑柔性并且面向时间与空间二维分布式需求。也就是说,当已知存在空间和时间上的不同需求时,应该首先将集总式命题发展为考虑空间需求差异的分布式命题,其次随时间变化的需求扰动和成本扰动都要进入设计命题。在实际工作中,时间维度的变化表示在由于季节变化而引起的冷却水温相应波动。空间维度的变化则表示各个终端所需的(流量,扬程)各不相同。
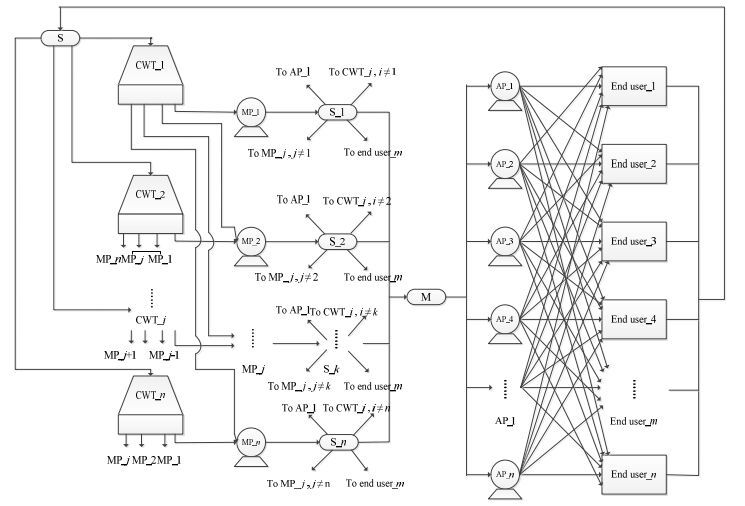
一个包含多个供能源头和多个终端设备的泵网络超结构如图 6所示。这个超结构包含了所有可能的连接,基于超结构模型的设计策略和基于辅助泵网络的设计策略均有体现。按照如下步骤建立超结构:(1)源头(如冷却水塔)后标识的一组箭头表示流股可以去往满足流量和压头的任意主泵;(2)主泵网络后标识的一组箭头,表示流股通过分流单元去往满足压头和流量的其它主泵、任意辅助泵、返回其它源头、与其它主泵流股汇合后进入辅助泵网络或者直接进入终端设备;(3)辅助泵网络后标识的一组箭头表示流股可以去往满足压头和流量的任意终端设备(如换热网络)。主泵网络中的任意主泵和辅助泵网络中的任意辅助泵,本身就是一个泵网络的超结构。图中所示CWT表示源头;MP表示主泵网络;AP表示辅助泵网络;End User表示终端设备;S表示分流单元;M表示混合单元。
|
图 6 考虑空间分布式需求的泵网络超结构 Fig.6 Superstructure of pump network considering distributed load demands and frequency load disturbances CWT_i, i=1, 2, 3, …, n, cooling water tower; MP_j, j=1, 2, 3, …, n, main pump; M, mixer; AP_l, l=1, 2, 3, …, n, auxiliary pump; End User_m, m=1, 2, 3, …, n, end user; |
这项研究的难点在于,空间需求差异的分布式命题采用何种表达方式?考虑扰动的柔性系统设计最终都会成为多层嵌套的MINLP问题,求解难度很高,如何通过变形和算法开发降低求解难度?泵网络的柔性设计问题也有可能非凸,如何求解?这项工作的求解难度最终都会体现在针对MINLP的算法研究上。
5 结论近年来,离心泵节能研究越来越侧重于泵网络的优化,研究者期望通过网络的设计与操作优化命题求解降低成本。研究主要内容集中于(1)设备成本目标构成;(2)实际单泵或多泵的性能表征;(3)基于超结构和辅助泵网络模型的设计优化;(4)变负荷控制和操作调度等操作优化;(5)相关MINLP的算法开发五个方面。在下一阶段的工作中,考虑到人工成本上升以及需求和成本的不断变化,泵网络的性能监控和维护调度以及考虑时间与空间二维分布式需求的泵网络柔性设计将进入工作重点。
符号说明:
| Coe | -比例系数 | η | -效率 |
| D | -叶轮直径,mm | ρ | -密度,kg·m3 |
| g | -重力系数,9.81 m·s-2 | 上标 | |
| H | -扬程,m | L | -下限值 |
| he | -管路扬程,m | U | -上限值 |
| N | -泵的数量 | 下标 | |
| n | -转速,r·min-1 | 0 | -设定值 |
| P | -功率, kW | m | -终端设备位置 |
| p | -压力,Pa | max | -最大值 |
| Q | -流量,m3·h-1 | min | -最小值 |
| S | -管路阻力系数 | i | -第i台泵 |
| t | -时间,s | j | -第j台泵 |
| y | -整型变量 | k | -位置标记 |
| z | -泵位置高度,m | p | -并联 |
| Δ | -差额 | s | -串联 |
| [1] | Abdelaziz E A, Saidur R, Mekhilef S. A review on energy saving strategies in industrial sector[J]. Renewable and Sustainable Energy Reviews , 2011, 15(1): 150-168. DOI:10.1016/j.rser.2010.09.003. |
| [2] | U.S. Energy Information Administration. International energy outlook 2016, 2016. https://www.eia.gov/outlooks/ieo/pdf/0484(2016).pdf. |
| [3] | Waide P, Brunner C U. Energy-efficiency policy opportunities for electric motor-drive systems[M].Paris: International Energy Agency, 2011. |
| [4] | U.S Department of Energy. United States Industrial motor systems market opportunities assessment[M].Washington D.C: U.S. Department of Energy, 1998. |
| [5] | Department of energy, PRC (国家经贸委资源节能综合利用司). The main idea of energy-saving in fans and pumps(关于风机、水泵节能改造的主要思路)[J]. Electronic energy-saving(电子节能) , 1998(3): 5-6. |
| [6] | BonaiutiD , Zangeneh M, Aartojarvi R, et al. Parametric design of a water jet pump by means of inverse design, CFD calculations and experimental analyses[J]. ASME Journal of Fluids Engineering , 2010, 132(3): 031104-1. DOI:10.1115/1.4001005. |
| [7] | Fan J, Eves J, Thompson H M, et al. Computational fluid dynamic analysis and design optimization of jet pumps[J]. Computers and Fluids , 2011, 46(1): 212-217. DOI:10.1016/j.compfluid.2010.10.024. |
| [8] | Motor Project Team (中国电机系统节能项目组). Energy efficiency and market potential of electric motor system in China(中国电机系统能源效率与市场潜力分析)[M].Beijing(北京): China machine press(机械工业出版社), 2001. |
| [9] | Kusiak A, Zeng Y H, Zhang Z J. Modeling and analysis of pumps in a waste water treatment plant:A data-mining approach[J]. Engineering Applications of Artificial Intelligence , 2013, 26(7): 1643-1651. DOI:10.1016/j.engappai.2013.04.001. |
| [10] | Zeng Y H, Zhang Z J, Kusiak A, et al. Optimizing wastewater pumping system with data-driven models and a greedy electromagnetism-like algorithm[J]. Stochastic Environmental Research and Risk Assessment , 2016, 30(4): 1263-1275. DOI:10.1007/s00477-015-1115-4. |
| [11] | Kim J, Smith R. Cooling water system design[J]. Chemical Engineering Science , 2001, 56(12): 3641-3658. DOI:10.1016/S0009-2509(01)00091-4. |
| [12] | Castro M M, Song T W, Pinto J M. Operational cost minimization in cooling water systems[J]. Brazilian Journal of Chemical engineering , 2000, 17(4-7): 649-658. DOI:10.1590/S0104-66322000000400029. |
| [13] | Lu L, Cai W J, Xie L H, et al. HVAC system optimization-in-building section[J]. Energy and Buildings , 2005, 37(1): 11-22. DOI:10.1016/j.enbuild.2003.12.007. |
| [14] | Kusiak A, Xu G L, ZHANG Z J. Minimization of energy consumption in HVAC systems with data-driven models and an interior-point method[J]. Energy Conversion and Management , 2014, 85(9): 146-153. |
| [15] | Goldstein R, Smith W. Water & sustainability (vol.4):U.S. electricity consumption for water supply & treatment-the next half century[M].Washington, DC: Electric Power Research Institute, 2002. |
| [16] | Daw J, Hallett K, Dewolfe J, et al. Energy efficiency strategies for municipal wastewater treatment facilities[R]. Golden, Colorado:National Renewable Energy Laboratory, 2012. |
| [17] | Plappally A K, Lienhard V J H. Energy requirements for water production, treatment, end use, reclamation, and disposal[J]. Renewable & Sustainable Energy Reviews , 2012, 16(7): 4818-4848. |
| [18] | Zhang H H, Qu Y J. MOAR theory:a new system energy-saving method for industrial circulating cooling water system[C]. Proceedings of the International Conference on Advances in Energy, Environment and Chemical Engineering, Paris:Atlantis Press, 2015:90-93. |
| [19] | Perez-lombard L, Ortiz J, Pout C. A review on building energy consumption information[J]. Energy and Buildings , 2008, 40(3): 394-398. DOI:10.1016/j.enbuild.2007.03.007. |
| [20] | ZHOU De-xian(周德贤), YE Wen-biao(叶文彪), ZHANG Tie-cheng(张铁成). Motor project started in China(中国电机系统节能项目正式启动)[J]. Power supply technologies and applications(电源技术应用) , 2002, 5(3): 116-117. |
| [21] | Asdal R, Tutterow V, Mckane A T. Pump systems matter part1[J]. World Pumps , 2006(481): 44-46. |
| [22] | Hydraulic Institute and Europump. Pump life cycle costs:a guide to LCC Analysis for pumping systems[M].Parsippany, N.J.: Hydraulic Institute, 2001. |
| [23] | HE Xiao-rong(何小荣). Optimization of chemical processes(化工过程优化)[M].Beijing(北京): Tsinghua Universitypress(清华大学出版社), 2002. |
| [24] | Seider W D, Seader J D, Lewin D R. Product & process design principles:synthesis, analysis and evaluation[M].New YORK: John Wiley & Sons, 2009. |
| [25] | Westerlund T, Pettersson F, Grossmann I E. Optimization of pump configurations as a MINLP problem[J]. Computers & Chemical Engineering , 1994, 18(9): 845-858. |
| [26] | Boulos P F, Wu Z, Orr C H, et al. Optimal operation of water distribution systems using genetic algorithms[J]. American Water Works Association Distribution System Symposium , 2001(24): 441-447. |
| [27] | YUAN Hai-yu(袁海宇), YUAN Shou-qi(袁寿其), SHI Wei-dong(施卫东). Enlightenment from pump systems matter(美国泵系统节能教育行动计划(PSM)及启示)[J]. Pump Technology(水泵技术) , 2008(6): 23-27. |
| [28] | Ahonen T. Monitoring of centrifugal pump operation[D]. Lappeenranta:Lappeenranta University of Technology, 2011. |
| [29] | Tutterow V, Hovstadius G, Mckane A. Going with the flow:Life cycle costing for industrial pumping systems[J]. Proceedings ACEEE Summer Study on Energy Efficiency in Industry , 2001, 2: 441-449. |
| [30] | Moradijalal M, Rodin S I, Marino M A. Use of genetic algorithm in optimization of irrigation pumping stations[J]. Journal of Irrigation and Drainage Engineering , 2004, 130(5): 357-365. DOI:10.1061/(ASCE)0733-9437(2004)130:5(357). |
| [31] | He X F, Zhang Z J, Kusiak A. Performance optimization of HVAC systems with computational intelligence algorithms[J]. Energy and Buildings , 2014, 81: 371-380. DOI:10.1016/j.enbuild.2014.06.021. |
| [32] | Zhang Z J, He X F, Kusiak A. Data-driven minimization of pump operating and maintenance cost[J]. Engineering Applications of Artificial Intelligence , 2015, 40(C): 37-46. |
| [33] | Alandi P P, Perez P C, Alvarez J F O, et al. Pumping selection and regulation for water distribution networks[J]. Journal of Irrigation and Drainage Engineering , 2005, 131(3): 273-281. DOI:10.1061/(ASCE)0733-9437(2005)131:3(273). |
| [34] | Kaya D, Yagmur E A, Yigit K S, et al. Energy efficiency in pumps[J]. Energy Convers Manage , 2008, 49(6): 1662-1673. DOI:10.1016/j.enconman.2007.11.010. |
| [35] | Moreno M A, Carrion P A, Planells P, et al. Measurement and improvement of the energy efficiency at pumping stations[J]. Biosystems Engineering , 2007, 98(4): 479-486. DOI:10.1016/j.biosystemseng.2007.09.005. |
| [36] | Pascual R, Rey P A, Hodkiewicz M, et al. Integrated model for optimizing strategic overhaul planning of distributed pump stations[J]. Journal of Computing in Civil Engineering , 2011, 25(4): 275-282. DOI:10.1061/(ASCE)CP.1943-5487.0000085. |
| [37] | Baran B, Lucken C V, Sotelo A. Multi-objective pump scheduling optimization using evolutionary strategies[J]. Advanced Software Engineering , 2005, 36(1): 39-47. DOI:10.1016/j.advengsoft.2004.03.012. |
| [38] | Kurek W, Ostfeld A. Multi-objective optimization of water quality, pumps operation, and storage[J]. Journal of Environmental Management , 2013, 115(3): 189-197. |
| [39] | Hu S K, Jia X J, Gao H F. Optimization of the number of multiple pumps running simultaneously in open cycle cooling water system in power plant[J]. Energy Procedia , 2012, 17: 1161-1168. DOI:10.1016/j.egypro.2012.02.222. |
| [40] | Savar M, Kozmar H, Sutlovic I. Improving centrifugal pump efficiency by impeller trimming[J]. Desalination , 2009, 249(2): 654-659. DOI:10.1016/j.desal.2008.11.018. |
| [41] | Chang W, Chang J, Yin H, et al. Energy saving algorithm for pumping systems based on fuzzy decision making[C]. Proceedings 2012 IEEE International Conference on Systems, Man, and Cybernetics, New York:Institute of Electrical and Electrcnics Engineers, 2012, 2(1):2395-2400. |
| [42] | Olszewski P. Genetic optimization and experimental verification of complex parallel pumping station with centrifugal pumps[J]. Applied Energy , 2016, 178: 527-39. DOI:10.1016/j.apenergy.2016.06.084. |
| [43] | Yang Z, Borsting H. Energy efficient control of a boosting system with multiple variable-speed pumps in parallel[C]. 49th IEEE Conference on Decision and Control. New York:Institute of Electrical and Electronics Engineers, 2010, 58(8):2198-2203. |
| [44] | Yang Z, Borsting H. Optimal scheduling and control of a multi-pump boosting system[C]. 2010 IEEE International Conference on Control Applications. New York:Institute of Electrical and Electronics Engineers, 2010, 58(8):2071-2076. |
| [45] | Viholainen J, Sihvonen M, Tolvanen J. Flow control with variable speed drives[C]. IEEE International Conference on Industrial Technology. New Jersey:Institute of Electrical and Electronics Engineers, 2010, 7713(12):350-354. |
| [46] | Bortoni E D C, Almeida R A D, Viana A N C. Optimization of parallel variable-speed-driven centrifugal pumps operation[J]. Energy Efficiency , 2008, 1(3): 167-173. DOI:10.1007/s12053-008-9010-1. |
| [47] | Hammo S, Viholainen J. Testing the accuracy of pump flow calculation without metering[J]. World Pumps , 2005(471): 36-39. |
| [48] | Koor M, Vassiljev A, Koppel T. Optimization of pump efficiencies with different pumps characteristics working in parallel mode[J]. Advances in Engineering Software , 2016, 101: 69-76. DOI:10.1016/j.advengsoft.2015.10.010. |
| [49] | Zhang Z J, Zeng Y H, KUSIAK A. Minimizing pump energy in a wastewater processing plant[J]. Energy , 2012, 47(1): 505-514. DOI:10.1016/j.energy.2012.08.048. |
| [50] | Zhang Z J, Kusiak A, Zeng Y H, et al. Modeling and optimization of a wastewater pumping system with data-mining methods[J]. Applied Energy , 2016, 164: 303-311. DOI:10.1016/j.apenergy.2015.11.061. |
| [51] | WU Peng(武鹏). Study on the parallel pump unit with high efficiency and reliability (并联泵组高效高可靠性运行问题研究) [D]. Hangzhou (杭州):Zhejiang University(浙江大学), 2013. |
| [52] | Izquierdo M D Z, Jimenez J J S, Sol A M D. Matlab software to determine the saving in parallel pumps optimal operation systems, by using variable speed[C]. 2008 IEEE energy 2030 conference. New York:Institute of Electrical and Electronics Engineers, 2008, 2:1-8. |
| [53] | Grossmann I E, Westerberg A W, Biegler L T. Retrofit Design of Processes[C]. 1st International Conference on Foundations of Computer Aided Operations. Netherlands:Elsevier, 1987:403-442. |
| [54] | Sun J, Feng X, Wang Y F, et al. Pump network optimization for a cooling water system[J]. Energy , 2014, 67(4): 506-512. |
| [55] | Kim J K, Smith R. Automated retrofit design of cooling-water systems[J]. AIChE Journal , 2003, 49(7): 1712-1730. DOI:10.1002/(ISSN)1547-5905. |
| [56] | Ponce-Ortega J M, Serna-Gonzalez M, Jimenez-Gutierrez A. Optimization model for re-circulating cooling water systems[J]. Computers and Chemical Engineering , 2010, 34(2): 177-195. DOI:10.1016/j.compchemeng.2009.07.006. |
| [57] | Reddy C, Rangaiah G P, Long L W, . Holistic approach for retrofit design of cooling water networks[J]. Industrial & Engineering Chemistry Research , 2013, 52(36): 13059-13078. |
| [58] | Majozi T, Moodley A. Simultaneous targeting and design for cooling water systems with multiple cooling water supplies[J]. Computers and Chemical Engineering , 2008, 32(3): 540-551. DOI:10.1016/j.compchemeng.2007.03.016. |
| [59] | Rubio-Castro E, Serna-Gonzalez M, Ponce-Ortega J M, et al. Synthesis of cooling water systems with multiple cooling towers[J]. Applied Thermal Engineering , 2013, 50(1): 957-974. DOI:10.1016/j.applthermaleng.2012.06.015. |
| [60] | CHEN Fu-li(陈福利), WANG Yu-fei(王彧斐), FENG Xiao(冯霄). Study on an auxiliary pump network for recirculating cooling water system(带有辅泵的循环水系统研究)[J]. Computers and Applied Chemistry(计算机与应用化学) , 2017, 34(3): 213-216. |
| [61] | SUO Rui-qin(索瑞琴), WANG Yu-fei(王彧斐), FENG Xiao(冯霄). The optimization of the circulating water network considering the heat transfer enhancement(考虑换热强化的循环水网络优化)[J]. Computers and Applied Chemistry(计算机与应用化学) , 2015, 32(12): 1439-1442. |
| [62] | GAO Wei(高伟), FENG Xiao(冯霄). Pressure distribution analysis on circulating water pump networks(循环水泵网络压力分布分析)[J]. Energ Conser Petrol Petroch Ind(石油石化节能) , 2016, 6(12): 12-14. |
| [63] | Nie X R, Zhu X X. Heat exchanger network retrofit considering pressure drop and heat-transfer enhancement[J]. AIChE Journal , 1999, 45(6): 1239-1254. DOI:10.1002/(ISSN)1547-5905. |
| [64] | Gololo K V, Majozi T. Complex cooling water systems optimization with pressure drop consideration[J]. Industrial and Engineering Chemistry Research , 2012, 52(22): 7056-7065. |
| [65] | Sun J, Feng X, Wang Y F. Optimization of cooling-water systems considering temperature-rise and pressure-drop[J]. Chemical Engineering Transactions , 2014, 39: 49-54. |
| [66] | Feng X, Shen R J, Wang B. Recirculating cooling-water network with an intermediate cooling-water main[J]. Energy & Fuels , 2005, 19(4): 1723-1728. |
| [67] | Picon-Nunez M, Morales-Fuentes A, Vazquez-Ramırez E E. Effect of network arrangement on the heat transfer area of cooling networks[J]. Applied Thermal Engineering , 2007, 27(16): 2650-2656. DOI:10.1016/j.applthermaleng.2007.06.006. |
| [68] | Wang Y, Chu K H, Wang Z. Two-step methodology for retrofit design of cooling water network[J]. Industrial & Engineering Chemistry Research , 2013, 53(1): 274-286. |
| [69] | Sun J, Feng X, Wang Y F. Cooling-water system optimization with a novel two-step sequential method[J]. Applied Thermal Engineering , 2015, 89: 1006-1013. DOI:10.1016/j.applthermaleng.2015.01.012. |
| [70] | Sun J, Feng X, Wang Y F. Simultaneous optimization of cooler and pump networks for industrial cooling-water systems[J]. Chemical Engineering Transactions , 2015, 45: 1915-1920. |
| [71] | Zhang H, Xia X, Zhang J. Optimal sizing and operation of pumping systems to achieve energy efficiency and load shifting[J]. Electric Power Systems Research , 2012, 86: 41-50. DOI:10.1016/j.epsr.2011.12.002. |
| [72] | Bonvin G, Demassey S, Pape C L, et al. A convex mathematical program for pump scheduling in a class of branched water networks[J]. Applied Energy , 2017, 185: 1702-1711. DOI:10.1016/j.apenergy.2015.12.090. |
| [73] | Cameron I, Gani R. Product and process modelling. a case study approach[M].Amsterdam: Elsevier, 2011. |
| [74] | Ma Z J, Wang S W. Energy efficient control of variable speed pumps in complex building[J]. Energy and Buildings , 2009, 41(2): 197-205. DOI:10.1016/j.enbuild.2008.09.002. |
| [75] | Tirmizi S A, Gandhidasan P, Zubair S M. Performance analysis of a chilled water system with various pumping schemes[J]. Applied Energy , 2012, 100: 238-248. DOI:10.1016/j.apenergy.2012.05.052. |
| [76] | Kalaiselvan A S V, Umashankar S, Paramasivam S, et al. A comprehensive review on energy efficiency enhancement initiatives in centrifugal pumping system[J]. Applied Energy , 2016, 181: 495-513. DOI:10.1016/j.apenergy.2016.08.070. |
| [77] | Zhuan X T, Xia X H. Optimal operation scheduling of a pumping station with multiple pumps[J]. Applied Energy , 2013, 104: 250-257. DOI:10.1016/j.apenergy.2012.10.028. |
| [78] | Wang J, Chang T, Chen J. An enhanced genetic algorithm for bi-objective pump scheduling in water supply[J]. Expert System with Applications , 2009, 36(7): 10249-10258. DOI:10.1016/j.eswa.2009.01.054. |
| [79] | Linnhoff B, Flower J R. Synthesis of heat exchanger networks(I):systematic generation of energy optimal networks[J]. Chemical Engineering Science , 1978, 24(4): 633-642. |
| [80] | El-Halwagi M M, Manousiouthakis V. Automatic synthesis of mass-exchange networks with single-component targets[J]. Chemical Engineering Science , 1990, 45(9): 2813-2831. DOI:10.1016/0009-2509(90)80175-E. |
| [81] | Alva-Argbez A, Kokossis A C, Smith R. Wastewater minimization of industrial systems using an integrated approach[J]. Computers & Chemical Engineering , 1998, 22(12): S741-S744. |
| [82] | LIANG Xiao-qiang(梁肖强), LIU Yong-zhong(刘永忠). Analysis and improvement of operational flexibility of hydrogen distribution systems(氢气网络系统的操作灵活性分析与改进)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2017, 31(1): 161-169. |
| [83] | Achenie L E K, Biegler L T. Algorithmic synthesis of chemical reactor networks using mathematical programming[J]. Industrial & Engineering Chemistry Fundamentals , 1986, 25(4): 621-627. |
| [84] | Bjork K M, Westerlund T. Global optimization of heat exchanger network synthesis problems with and without the isothermal mixing assumption[J]. Computers & Chemical Engineering , 2002, 26(11): 1581-1593. |
| [85] | CHEN Xi(陈曦), TIAN Da-qing(田大庆), SHAO Zhi-jiang(邵之江). Generalized disjunctive programming for feat exchanger networks synthesis(换热网络综合的广义析取规划模型及求解方法)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2010, 24(4): 670-675. |
| [86] | LEI Yang(雷杨), FAN Bao-an(范宝安), ZENG Dan-lin(曾丹林), et al. Global optimization strategies of heat exchanger network models for typical petrochemical process units(典型石化工艺装置换热网络模型的全局优化策略)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学过程学报) , 2016, 30(3): 686-692. |
| [87] | Jacek J. Review of water network design methods with literature annotations[J]. Industrial & Engineering Chemistry Research , 2010, 49(10): 4475-4516. |
| [88] | Serna-Gonzalez M, Ponce-Ortega J M. Total cost target for heat exchanger networks considering simultaneously pumping power and area effects[J]. Applied Thermal Engineering , 2011, 31(11-12): 1964-1975. DOI:10.1016/j.applthermaleng.2011.02.043. |
| [89] | Kusiak A, Zeng Y H, Zhang Z J. Modeling and analysis of pumps in a waste water treatment plant:a data-mining approach[J]. Engineering Applications of Artificial Intelligence , 2013, 26(7): 1643-1651. DOI:10.1016/j.engappai.2013.04.001. |
| [90] | Dakin R. A tree-search algorithm for mixed integer programming problems[J]. Computer Jounal , 1965, 8(3): 250-255. |
| [91] | Duran M, Grossmann I. An outer approximation algorithm for a class of mixed integer nonlinear problems[J]. Math Program , 1986, 36(3): 307-339. DOI:10.1007/BF02592064. |
| [92] | Westerlund T, Pettersson F. A cutting plane method for solving convex MINLP problems[J]. Computer and Chemical Engineering , 1995, 19(1): 131-136. DOI:10.1016/0098-1354(95)00164-W. |
| [93] | Trespalacios F, Grossmann I E. Cutting planes for improved global logic-based outer-approximation for the synthesis of process networks[J]. Computers and Chemical Engineering , 2016, 90: 201-221. DOI:10.1016/j.compchemeng.2016.04.017. |
| [94] | LIU Ming-ming(刘明明), CUI Chun-feng(崔春风), TONG Xiao-jiao(童小娇), et al. Algorithms, softwares and recentdevelopments of mixed integer nonlinear programming(混合整数非线性规划的算法软件及最新进展)[J]. SCIENTIASINICA :Mathematica(中国科学:数学) , 2016, 46(1): 1-20. |
| [95] | Pettersson F, Westerlund T. Global optimization of pump configurations using binary separable programming[J]. Computer and Chemical Engineering , 1996, 21(5): 521-529. |
| [96] | Zhang G J, Wu T H, Ye R. Global optimization of pump vonfiguration using extended crowding genetic algorithm[J]. Chinese Journal of Mechanical Engineering , 2004, 17(2): 247-252. DOI:10.3901/CJME.2004.02.247. |
| [97] | Young C, Zheng Y, Yeh C, et al. Information-guided genetic algorithm approach to the solution of MINLP problems[J]. Industrial & Engineering Chemistry Research , 2007, 46(5): 1527-1537. |
| [98] | Gogos C, Alefragis P, Housos E. Application of heuristics, genetic algorithms & integer programming at a public enterprise water pump scheduling system[C]. Patras, Greece:11th Panhellenic conference on informatics, 2007. |
| [99] | Moradi-jalal M, Karney B W. Optimal design and operation of irrigation pumping stations using mathematical programming and genetic algorithm GA[J]. Journal of Hydraulic Research , 2008, 46(2): 237-246. DOI:10.1080/00221686.2008.9521858. |
| [100] | DU Hong-bin(杜红彬), XUE Dong-feng(薛东峰), YAO Ping-jing(姚平经). Improved adaptive simulated annealing algorithm for MINLP problems in process synthesis(改进的自适应模拟退火算法及其在过程综合中的应用)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2002, 16(1): 106-110. |
| [101] | Mccormick G, Powell R. Derivation of near-optimal pump schedules for water distribution by simulated annealing[J]. Journal of the Operational Research Society , 2004, 55(7): 728-736. DOI:10.1057/palgrave.jors.2601718. |
| [102] | Shu S, Zhang D, Liu S, et al. Power saving in water supply system with pump operation optimization[C]. 2010 Asia-pacific power and energy engineering conference. New York:Institute of Electrical and Electronics Engineers, 2010:1-4. |
| [103] | Wegley C, Eusuff M, Lansey K. Determining pump operations using particle swarm optimization[C].Joint Conference on Water Resource Engineering & Water Resources Planning & Management. USA:American Society of Civil Engineers, 2000:1-6. |
| [104] | Lopezibanez M, Prasad T D, Paechter B. Ant colony optimization for optimal control of pumps in water distribution networks[J]. Journal of Water Resources Planning and Management , 2008, 134(4): 337-346. DOI:10.1061/(ASCE)0733-9496(2008)134:4(337). |
| [105] | Tang K S, Man K F, Liu Z F, et al. Minimal fuzzy memberships and rules using hierarchical genetic algorithms[J]. IEEE Transactions on Industrial Electronics , 1998, 45(1): 162-169. DOI:10.1109/41.661317. |




