锂离子电池隔膜厚度的均匀性是隔膜重要指标之一，性能优异的隔膜能够大大提高锂离子电池的综合性能。隔膜的生产目前主要有熔融拉伸法和热致相分离法^[1~3]，在这两种加工方法中热风加热系统的温度均匀性，将影响隔膜厚度均匀性。而静压箱是保证热风加热系统出风口的温度均匀的关键设备。

目前，在热风加热系统中的静压箱装置，通常按照经验设计，很难保证在隔膜的宽度方向上风速的均匀性，从而影响温度在此方向上的均匀性，最终影响隔膜的厚度均匀性，拉伸连续性等。在国内最早研究静压箱特性是中国建筑研究院空气调节研究所的王来^[4]，在1991年，基于正交试验回归分析，利用模型实验方法，对等温条件下静压箱静压分布规律进行研究，并给出静压箱静压分布规律的经验公式。2002年，刘泽华等^[5]利用CFD软件对空调系统中静压箱内的空气流动进行仿真试验，是国内最早利用数值模拟方法进行相关研究的学者，他们通过分析模拟得到的速度场和压力场，得出静压箱动力学特性的相关结论。2009年，Mohammadkhah等^[6]使用CFD模拟方法研究八种不同结构的流化床中静压箱的流场，从模拟结果可知气体进口的位置和角度将影响气体分布规律。随后Grace等^[7]通过实验验证静压箱体积和分布板几何结构对于流化床内部流场的影响。同年，Othman等^[8]利用粒子图像测速(PIV)方法，把数值模拟的旋转流化床结构内部的速度场，进行相应的实验，验证了实验与模拟结果基本吻合。

本文借鉴前人研究工作基础上^[9~11]，使用数值模拟研究静压箱内部流场分布，通过实验研究，验证数值模型的准确性，在此基础上，利用数值模拟的方法分析静压箱各结构单因素对出口速度均匀性的影响规律，并对静压箱进行结构优化，找出静压箱结构设计的最优方案。

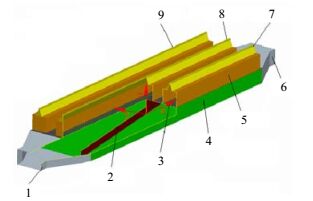
静压箱的结构示意图如图 1所示，主要由进口1、进口2、下箱体、均风板、孔板、上箱体、左侧出口、中间出口和右侧出口组成。由于此静压箱的长度较长，这里采用对称式进口结构。静压箱内气体流动可以归纳为五个环节：进口渐扩结构的导流，下箱体内混合扩散，孔板重新分配，上箱体进一步稳定气流，出口渐缩结构提升气体速度。表 1列出了静压箱主要的结构尺寸。

图 1(Fig. 1)

图 1 静压箱示意图 Fig.1 Schematic diagram of the plenum chamber 1. entrance 2. air distributor 3. orifice plate 4. lower box 5. upper box 6. entrance 7. left outlet 8. intermediate outlet 9. right outlet

表 1(Tab. 1)

表 1 静压箱的主要结构尺寸 Table 1 The main size parameters of the plenum chamber Inlet length k / mm Inlet width w / mm Expanding angle α / ° Upper box height h1/ mm Lower box height h2/ mm Exit height h3/ mm Tapered angle Β / ° Air distributor γ / ° Orifice diameter d / mm Hole center distance l / mm Orifice thickness t / mm 350 200 28 200 200 20 40 15 10 15 6

表 1 静压箱的主要结构尺寸 Table 1 The main size parameters of the plenum chamber

针对静压箱内气体运动的特性和结构特点，选择合理的计算方法和湍流模型是数值计算能够准确预测流场规律的关键。因此本文在计算时选择了能够在数值模拟多孔射流，流线弯曲较高时均能表现出很高精度的Realizable k-ε模型。

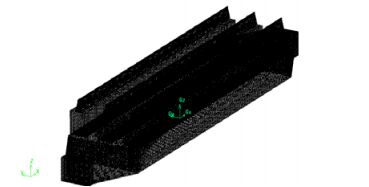
由于静压箱的原型尺寸比较大，为了达到计算精度要求，网格尺寸不能太大，导致网格数量过大，现有计算机资源很难满足其计算要求。在工程实际中，拉伸段静压箱原型的进口总流量是8294.4 m³·h^-1，本文利用流动相似理论^[12]，采用等弗劳德数相似准则，得到缩小五倍的相似模型进行数值模拟，采用的网格尺寸为3 mm(网格数1053252)。整个结构比较复杂，进行分区划分网格，入口箱体和出口箱体的网格形式为结构网格，出口箱体由于尺寸较小，同时对计算值的精度有很高要求，对该区域进行网格加密处理，对出口的边线划分为5份，其他边为3 mm；对于孔板，因孔内流动信息对孔板的整流作用很重要，需要加密划分网格。由于孔板数多，网格划分难度大，因此采用自由划分为非结构性网格，尺寸为0.5 mm。具体模型的网格划分如图 2所示。

图 2(Fig. 2)

图 2 相似模型的网格划分 Fig.2 Mesh design of similar model

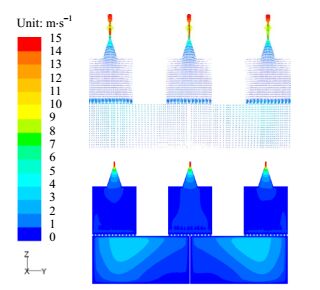
i以下选取具有代表性的X=0，Y=0，Z=0.02 m平面，通过矢量图和云图来分析静压箱内部速度场的分布规律。

(1) X=0平面速度场分析

从图 3可知，下箱体内气体速度分布不均匀，但是经过孔板结构后，在三个上箱体内气体速度的均匀性均得到大大提高。在上箱体内随着高度增加，气体速度的均匀性得到进一步提高。最后经过渐缩型喷嘴结构，气体速度得到提升达到14 m·s^-1左右，以满足工程需要。

图 3(Fig. 3)

图 3 X = 0平面内速度分布 Fig.3 Velocity distribution at X = 0 plane

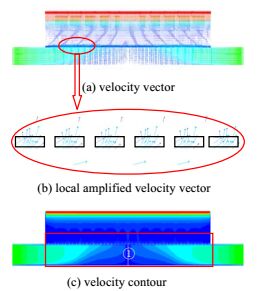
(2) Y=0平面速度场分析

从图 4(a)和图 4(c)中，气体分别从进口1和进口2同时进入各自的楔形渐缩箱体内，往下游发展速度逐渐减小，且速度基本以水平方向为主(X方向)。在图 4(c)中① 区域代表中间区域，这部分区域比较接近均风板，气流运动受到阻力影响最大，速度明显降低，且速度方向从水平方向开始向竖直方向过渡，使得这部分气体更容易进入孔板结构内。

图 4(Fig. 4)

图 4 Y = 0平面内速度分布 Fig.4 Velocity distribution at Y = 0 plane

从4(b)图中，可以清晰看到气体通过孔板的整流作用，气体方向基本上以竖直方向为主。孔板内流动可以理解为气体以一定速度夹角进入短管内流动，如果管子的长度足够长，那么气体经过一定长度后气体速度方向将改变为沿着圆管的轴线方向(Z方向)，这样有利于气体在下游结构中以垂直于出口平面的速度方向上进一步均匀发展，从而提高出口处速度均匀性。但是由于孔板重量和经济性制约，厚度不能太大，故气体很难在孔板内得到充分发展，改变气流方向的作用不能完全体现出来。所以在理论模拟中需要探究孔板的最小厚度，既能满足改变气流方向的作用，也能满足工程实际要求。

(3) Z=0.02 m平面速度场分析

从图 5(a)和图 5(b)中可以看出，整个速度场关于Y=0平面反对称，气体分布在两个楔形渐缩箱体内，因此这两部分气流不发生直接作用。气体从进口进入楔形渐缩箱体后，随着向下游发展速度将沿着均风板倾斜方向流动，在前部分区域速度大小并未有明显衰减，维持在4 m·s^-1左右，后部分区域速度逐渐减小，并且在这个流道内不存在大尺度的漩涡结构。

图 5(Fig. 5)

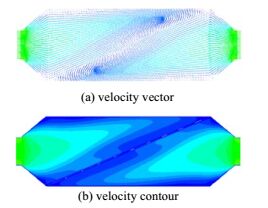
图 5 Z = 0.02 m平面内速度分布 Fig.5 Velocity distribution at Z = 0.02 m plane

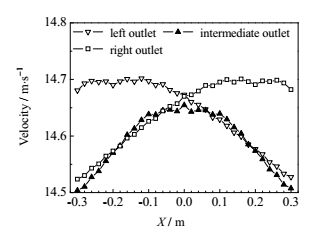
对于静压箱速度均匀性分析，本文选取出口中心线长度上速度点，把最大和最小速度值的偏差，即最大速度偏差定义为出口速度均匀性的评价指标，工程上静压箱的相似模型要求此指标为0.9 m·s^-1。这里主要是分析出口气体沿X方向的速度分布曲线以及气体速度评价指标，从而衡量静压箱工作性能。

从图 6中可以看出，左侧出口与右侧出口速度分布类似，只是呈现反对称特征。这里以右侧出口为例详细说明，当X从-0.3 m增大到0.1 m时，速度也逐渐增大；当X = 0.1 m时，速度比较稳定，维持在14.70 m·s^-1左右。中间出口速度分布为抛物线特征，X=0处为整个出口最大速度点，速度值约为14.65 m·s^-1。左右两出口最大速度偏差约为0.2 m·s^-1，而中间出口最大速度偏差约为0.15 m·s^-1，均满足工程要求的最大速度偏差。

图 6(Fig. 6)

图 6 静压箱出口速度分布 Fig.6 Velocity distribution at the outlet of the plenum chamber d = 5 mm, l = 6 mm, t = 1.2 mm

静压箱出口速度的均匀性，是整个静压箱研究中最重要的目标，故可以通过实验研究出口速度的均匀性，并验证数值模拟结果的准确性。

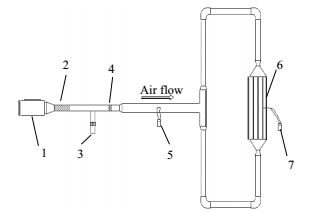
图 7、图 8为静压箱实验流程图，气体从风机送入管网内，为了防止风机工作时振动传递给管网，故在两者之间加入一段软管结构，起到减震作用。由于风机流量可到达1900~2500 m³·h^-1，实验中需要流量只有148.4 m³·h^-1，可以通过支路上的球阀1放空大部分气体，然后再由球阀2来调节到实验所需的流量。图 9为静压箱的实验模型。

图 7(Fig. 7)

图 7 实验流程示意图 Fig.7 Schematic diagram of the experimental setup 1.fan 2.hose 3.globe valve 4.globe valve 5.Pitot tube 6.plenum chamber 7.anemometer

图 8(Fig. 8)

图 8 静压箱实验流程图 Fig.8 Experimental flow chart of the plenum chamber

图 9(Fig. 9)

图 9 静压箱实验模型 Fig.9 Experimental model of the plenum chamber

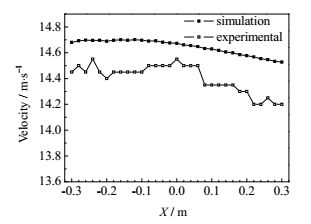
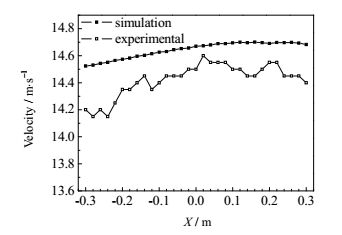
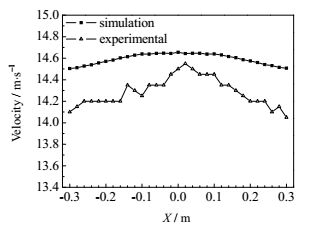
将实验数据和模拟数据进行对比分析，探究实验规律并验证数值模拟的准确性。由图可知，图 10和图 11中模拟值和实验值的相对误差均在3%之内，图 12中模拟值和实验值的相对误差在4%之内，存在一定误差的原因主要是计算过程和实验测量都会存在一定的不可避免的误差，虽然实验中的最大速度偏差均比模拟的大0.3 m³·h^-1左右，但是仍然满足静压箱工程上对速度均匀性的要求。综上可知，模拟结果跟实验结果比较吻合，从而验证了模拟方法的正确性，静压箱三个出口最大速度偏差的实验值为0.5 m·s^-1，速度均匀性满足工程要求。

图 10(Fig. 10)

图 10 左侧出口处速度分布对比 Fig.10 Comparison of velocity distribution at the left outlet d = 5mm, l = 6mm, t = 1.2 mm

图 11(Fig. 11)

图 11 右侧出口处速度分布对比 Fig.11 Comparison of velocity distribution at the right outlet d = 5 mm, l = 6 mm, t = 1.2 mm

图 12(Fig. 12)

图 12 中间出口处速度分布对比 Fig.12 Comparison of velocity distribution at the intermediate outlet d = 5 mm, l = 6 mm, t = 1.2 mm

通过对静压箱内部的流场进行数值模拟可知，孔板结构是影响静压箱的出口速度均匀性的关键结构，本文首先利用“正交试验”方法，确定静压箱孔板结构的正交试验方案，并进行试验结果的统计分析。这里选取孔径(d)、长径比(δ)、厚径比(ε)作为试验因素，在三种因素中，根据工程实际孔的尺寸，确定d的取值范围为5~15 mm，δ在1.2~2.2 (即φ的取值范围为16%~55%)，ε在0.2~1.0。这里选取因素的五个水平。制定试验因素水平表如下表 2，并确定试验方案如下表 3。

表 2(Tab. 2)

表 2 试验因素水平 Table 2 Experimental factor level Level Factor A d / mm B δ C ε 1 5 1.2 0.2 2 8 1.5 0.4 3 10 1.8 0.6 4 12 2.0 0.8 5 15 2.2 1.0

表 2 试验因素水平 Table 2 Experimental factor level

表 3(Tab. 3)

表 3 试验方案 Table 3 Experimental design Experimental code d / mm δ ε Blank column Experimental code d / mm δ ε Blank column 1 5 1.2 0.2 1 14 10 2.0 0.2 3 2 5 1.5 0.4 2 15 10 2.2 0.4 4 3 5 1.8 0.6 3 16 12 1.2 0.8 2 4 5 2.0 0.8 4 17 12 1.5 1.0 3 5 5 2.2 1.0 5 18 12 1.8 0.2 4 6 8 1.2 0.4 3 19 12 2.0 0.4 5 7 8 1.5 0.6 4 20 12 2.2 0.6 1 8 8 1.8 0.8 5 21 15 1.2 1.0 4 9 8 2.0 1.0 1 22 15 1.5 0.2 5 10 8 2.2 0.2 2 23 15 1.8 0.4 1 11 10 1.2 0.6 5 24 15 2.0 0.6 2 12 10 1.5 0.8 1 25 15 2.2 0.8 3 13 10 1.8 1.0 2

表 3 试验方案 Table 3 Experimental design

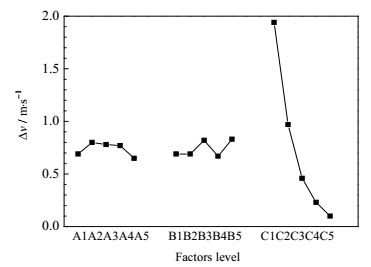
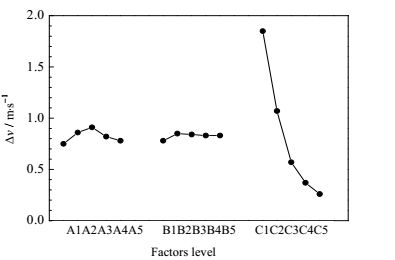
正交试验结果的直观分析方法，也称为极差分析法，其中极差值反映了该因素中最大值与最小值之差，通过极差值可以得出因素之间的主次关系，同时也可以得到最佳的因素水平组合。由于静压箱有三个出口，并且左右两侧出口对称，故正交试验的指标为：中间出口速度偏差、左侧出口速度偏差。

把3个因素分别对应的五个水平的中间出口速度平均偏差和左侧出口速度平均偏差，分别绘制如图 13和图 14所示。

图 13(Fig. 13)

图 13 各因素对中间出口速度偏差的影响 Fig.13 Influence of various factors on intermediate outlet velocity deviation

图 14(Fig. 14)

图 14 各因素对左侧速度偏差的影响趋势 Fig.14 Influence of various factors on left outlet velocity deviation

通过分析，按照左侧出口各因素与速度偏差的规律，很容易得到最佳的水平组合方案A1B1C5即最佳方案是：d = 5 mm，δ = 6 mm，t = 5 mm。此方案t可以满足设备重量要求，但是由于d和δ过小，会造成开孔数量较大，而孔板需要在较大厚度的钢板上，加工大量的孔结构，同时，过厚的孔板需要相应增加其它箱体的厚度，以保证整个结构的稳定性，这样会导致整个箱体重量增加，过重静压箱不利于安装和支撑固定，因此不符合工程实际要求。故通过正交试验得到的最佳水平组合方案，不满足工程实际的要求。

通过以上的直观分析和方差分析，得到各因素水平的对指标影响的规律，但是这些规律只是简单的图表和曲线，并没有能够得出相应的关系式。作者使用量纲分析法—瑞利(Rayleigh)方法来获得孔板参数关联式。根据此方法，首先确定影响出口速度偏差的重要物理参数有几何参数：孔直径(d)、孔中心距(l)、孔板厚度(t)；流体物性参数：密度(ρ)，动力黏度(μ)；流体运动参数：孔内平均流速(v₀)。它们之间的关系式表示为幂函数乘积形式，如下：

式中，m为常数。根据量纲和谐原理，整理得：

通过瑞利方法，得到影响速度偏差的三个无量纲数：长径比(δ)，厚径比(ε)，雷诺数Re。

(1) 多元线性回归

① 中间出口

通过把得到的各系数的估计值，进一步计算并代入公式，可得中间出口速度偏差公式：

回归分析汇总如下，从中可以看到模型拟合概括，回归方程的判定系数为0.888，本次拟合效果非常好。

② 左侧出口

通过把得到的各系数的估计值，进一步计算并代入公式，可得中间出口速度偏差公式：

回归方程的判定系数为0.936，本次拟合效果非常好。但是由于雷诺数系数过小，说明雷诺数对此关联式影响很小，故可以在回归分析时，不考虑雷诺数影响，再次回归得到：

回归方程的判定系数仍为0.936，本次拟合效果非常好。

孔内平均流速(v₀)表达式如下，

同理，式(3) 和式(5) 中各参数的适用范围：d = 5 ~15 mm，δ = 1.2~2.2，ε = 0.2~1.0，Re = 761~7438，v₀ = 2.23 ~8.02 m·s^-1。

(2) 关联式验证

为验证上述孔板参数关联式的准确性，对孔板参数组合方案进行模拟，并与相应的预测值进行对比。对比结果如下图 15所示。

图 15(Fig. 15)

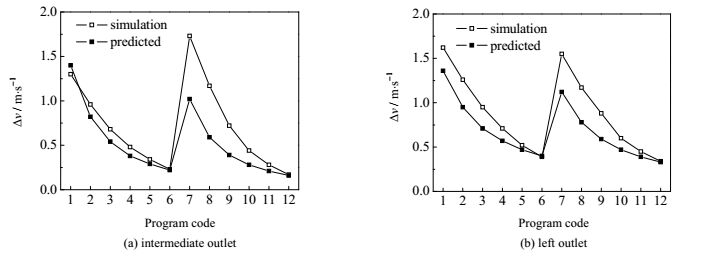
图 15 验证方案的速度分布 Fig.15 Velocity distribution of the validation study

从图 15中可以看出，中间出口和左侧出口的预测值与模拟值变化的趋势相同，预测准确度都比较高，虽然存在一定的偏差，但都在容许的范围内。因此认为此关联式可以用于静压箱的出口速度偏差预测。

正交试验得到静压箱最佳水平组合为A1B1C5，即d = 5 mm，l = 6 mm，t = 5 mm，由于孔板长度较长，此方案需要开孔个数高达51168个。造成孔板的加工难度过大和加工成本过高，不利于工程实际使用。

这里需要结合孔板正交试验的直观分析规律，探究孔个数少，孔板厚度小的方案。按照左侧出口速度偏差规律(图 14)，可知长径比对速度偏差影响很小，这里可以取2.2，而孔径可以选取12 mm，然后选取一系列的厚径比：0.250、0.333、0.417、0.500、0.583、0.667，对应孔厚度为3、4、5、6、7、8 mm。另外，孔中心距为26.4 mm，可圆整为26 mm。以下是优化研究方案及模拟结果：

从表 4可知第四种方案是满足要求的最小厚度方案。此孔板方案具体参数是：d = 12 mm，l = 26 mm，t = 6 mm。静压箱的优化参数如表 5所示。

表 4(Tab. 4)

表 4 静压箱研究方案 Table 4 Experimental design for plenum chamber study No Factor A d / mm B δ C ε Intermediate outlet velocity deviation Left outlet velocity deviation 1 12 2.2 0.250 1.3 1.6 2 12 2.2 0.333 1.0 1.3 3 12 2.2 0.417 0.7 1.0 4 12 2.2 0.500 0.5 0.7 5 12 2.2 0.583 0.3 0.5 6 12 2.2 0.667 0.2 0.4

表 4 静压箱研究方案 Table 4 Experimental design for plenum chamber study

表 5(Tab. 5)

表 5 静压箱优化参数 Table 5 Optimize parameters of the plenum chamber k / mm w / mm α / ° h1/mm h2/ mm h3/ mm Β / ° γ / ° d / mm l / mm t / mm 350 200 28° 200 200 20 40 15 12 26 6

表 5 静压箱优化参数 Table 5 Optimize parameters of the plenum chamber

(1) 通过对静压箱的内部流场进行数值模拟分析，得到静压箱结构内部的整流机理，气体速度从水平方向转变为竖直方向，主要发生在孔板内，孔板是整个结构关键部件。

(2) 模拟和实验的出口速度分布比较吻合，验证了静压箱的数值模型的准确性。静压箱实验结果表明最大速度偏差为0.5 m·s^-1，能够满足工程要求。

(3) 利用数值模拟手段，完成静压箱正交试验的模拟，并进行统计分析，得到直径d、长径比δ和厚径比ε对出口速度偏差的影响规律，模拟结果表明ε和δ对出口速度偏差影响非常显著，而d对出口速度偏差无显著影响。

(4) 基于瑞利量纲分析法，结合正交试验回归理论，得到静压箱的孔板参数与出口速度偏差的经验关联式，结果表明关联式的预测效果较好，可以作为设计孔板的理论依据。

(5) 基于静压箱孔板结构的正交试验直观分析规律，通过模拟得到静压箱最优孔板参数，静压箱孔板几何参数是：d = 12 mm，l = 26 mm，t = 6 mm。

符号说明：