甲醇制丙烯(Methanol to Propene, MTP)是煤化工过程生产丙烯的方法，受到广泛关注^{[1, 2]}。该过程采用H-ZSM-5分子筛催化剂，甲醇通过一系列复杂的反应步骤生成丙烯。MTP是一个分子数增加的强放热快速反应，催化剂易失活，工业上采用常压高温和高空速的反应条件，采用多段固定床和甲醇逐级进料来冷却反应放热，采用大量产物分离-循环来促进中间物向丙烯的转化，采用多个反应器的切换操作来实现催化剂的再生。由于MTP过程复杂，从催化剂、反应器到流程设计都存在很大的改进空间。

化学反应动力学是反应器开发与过程设计的基础信息。MTP涉及甲醇裂解，甲醇与烯烃甲基化，烯烃之间的齐聚、裂化、异构化、芳构化和加氢等^[3~5]反应步骤。现有的动力学研究绝大多数只考虑MTP涉及的部分反应步骤，很少涉及完整的反应网络。Schoenfelder等^[6]只考虑了甲醇转化为烯烃的甲基化反应步骤。姜坤等^[7]在微型固定床反应器中考察了甲醇单独进料的反应规律，仅考虑了甲醇直接裂解和部分烯烃的转化，忽略了甲基化反应步骤。应磊等^[8]研究了C₂~C₇各组分烯烃单独进料时的反应规律，提出了烯烃之间反应的集总反应动力学模型，然而该模型没有考虑烯烃之间的反应受热力学平衡限制。Park和Froment等^{[9, 10]}采用Single-Event方法来构造MTP过程的复杂反应网络，但是其采用的实验数据只包括了部分反应步骤，模型能否用于工业过程存在质疑。已经认识到，甲醇首先是通过与烯烃发生甲基化反应转化为C₂~C₇烯烃，烯烃之间再发生裂化和齐聚反应转化为丙烯，同时还有生成芳烃和烷烃的多步副反应。工业上采用含大量烯烃的循环物料与甲醇共进料，因此只有全面考虑甲醇与烯烃之间的甲基化反应以及烯烃之间的齐聚和裂化反应才能得到有实际应用价值的动力学模型。文献中目前只有吴文章^[11]实验考察了甲醇与C₂~C₇烯烃反应的动力学，提出了比较完整的动力学模型，但其实验中采用C₂~C₇的醇来代替烯烃进料，得到的动力学受醇的裂解影响，其活化能数据与应磊及其他作者的结果不符^{[8, 12]}。应磊指出^[13]，采用醇代替烯烃进料，醇的裂解会掩盖烯烃的裂解与吸附，使实验得到的动力学数据失真。因此，为了获得真实而完整的MTP动力学，应当分别采用甲醇和烯烃混合进料、不同烯烃单独进料的实验条件来获取各反应的动力学数据。

基于上述考虑，本文进一步实验研究甲醇和烯烃混合进料及不同烯烃单独进料条件下在工业H-ZSM-5催化剂上的MTP反应过程，考察反应物类型、空时、反应温度和进料配比的影响。动力学方面拟全面考虑甲醇单独反应、甲醇与烯烃之间的反应、烯烃之间的相互转化及热力学平衡的限制，提出比较完整的反应网络和动力学模型，为深入了解MTP反应机理和动力学、改进现有工业过程并开发新的反应技术提供依据。

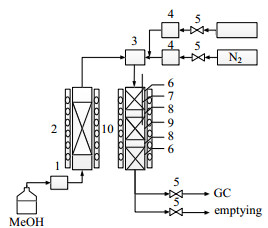
实验装置采用Φ20 mm的不锈钢管式微固定床反应器，如图 1所示。所用的工业H-ZSM-5催化剂由某MTP生产厂家提供，粒径为20~40目，用等量的石英砂进行稀释，装填在反应器的等温段。保持进料流速不变，通过改变催化剂的填装质量来改变空时。甲醇、水以及液体C₅~C₇烯烃用柱塞计量泵进料，气体烯烃C₂~C₄通过质量流量计控制。催化剂在使用前加热至500℃在氮气流中活化1h，然后将温度调至所需要的反应温度。反应后的物质使用配有FID检测器和PoraPLOT Q-HT毛细管柱(25 m×0.53 mm×0.02 mm)的气相色谱在线分析。反应在常压下进行，其它条件列于表 1。

图 1(Fig. 1)

图 1 实验装置 Fig.1 Schematic diagram of the experiment setup 1. pump 2. vaporizer 3. mixer 4. mass flow meter 5. valve 6. SiO2 7.thermometer 8. silica wool 9.catalyst 10. reactor

表 1(Tab. 1)

表 1 反应条件 Table 1 Reaction conditions applied in the study Partial pressure / kPa Temperature/ ℃ Space-time/h(Based on MeOH or CH2) MeOH C2 C3 C4 C5 C6 C7 H2O N2 Methanol feed only 6.93 0 0 0 0 0 0 0 94.4 440;460;480;500 0.04~0.38 C3~C7 feed respectively 0 0 13.1 0 0 0 0 0 88.22 400;425;450; 475;490 0.046~0.227 0 0 13.1 0 0 0 0.031~0.157 0 0 0 13.1 0 0 0.013~0.066 0 0 0 0 13.1 0 0.012~0.099 0 0 0 0 0 13.1 0.005~0.041 Methanol and C2~C7co-feed 6.93 14.48 0 0 0 0 0 65.28 14.63 440;460; 480;500 0.1~0.25 0 14.48 0 0 0 0 0.05~0.15 0 0 14.48 0 0 0 0.025~0.1 0 0 0 14.48 0 0 0.025~0.1 0 0 0 0 14.48 0 0.025~0.125 0 0 0 0 0 14.48 0.025~0.125

表 1 反应条件 Table 1 Reaction conditions applied in the study

反应产物异构体较多，组分浓度采用集总方法处理，归结为以下几类：(1) 甲醇和二甲醚；(2) C₂；(3) C₃；(4) C₄；(5) C₅；(6) C₆；(7) C₇ (包括C₇以上烯烃)；(8) Rest (烷烃Par和芳烃ArH)。

MTP反应路径十分复杂，涉及多个连串/平行/可逆反应步骤，构成了一个复杂网络。本文分别考察甲醇单独进料、烯烃单独进料以及甲醇和烯烃混合进料三种实验条件下的反应规律，以此逐步构建完整的反应网络。

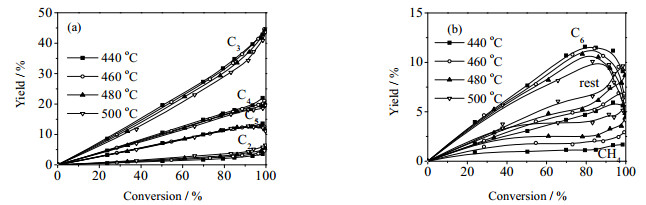
图 2给出了甲醇单独进料条件下的各主要产物收率随甲醇转化率的变化规律。从图中可以看到：低转化率下C₂~C₆烯烃的收率与甲醇转化率之间呈现出很好的线性关系，表明这五种组分是由甲醇平行转化生成^[14]；在高转化率下，C₂和C₃有上升趋势，而C₅和C₆则有下降趋势，说明C₆和C₅不稳定，可以进一步生成低碳烯烃。本节只考虑低转化率情况下呈现的甲醇单独转化为烯烃的动力学，甲醇高转化条件下呈现的烯烃之间的相互转化将在3.2节中详细研究。如果假设低转化率下甲醇单独进料时的反应路径为一级平行反应，以460℃为例，则由实验数据拟合得到的反应速率k₄₆₀和反应活化能Ea列于表 2，其中水浓度的影响借鉴了吴文章^[11]和应磊^[13]的表达式，从表中可以得出甲醇平行生成丙烯的反应速率最快。

图 2(Fig. 2)

图 2 不同温度下产物收率与甲醇转化率的关系 Fig.2 Product yields as a function of methanol conversion under different temperatures

表 2(Tab. 2)

表 2 低空时下甲醇单独进料时的一级平行反应动力学 Table 2 First order kinetics of parallel reactions with only methanol feeding under low space time Reaction equations Kinetic model k460/m3·kgcat-1·h-1 Eai/kJ·mol-1 ${\rm{MeOH}}\xrightarrow{{{k}_{1}}}\frac{1}{2}{{\rm{C}}_{2}} \text{+}{{\rm{H}}_{2}}\rm{O}$ ${{r}_{1}}=\frac{1}{2}\frac{{{k}_{1}}[\rm{MeOH}]}{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}$ 11.66 ± 3.29 79.08 ± 5.02 ${\rm{MeOH}}\xrightarrow{{{k}_{2}}}\frac{1}{3}{{\rm{C}}_{3}} \text{+}{{\rm{H}}_{2}}\rm{O}$ ${{r}_{1}}=\frac{1}{3}\frac{{{k}_{2}}[\rm{MeOH}]}{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}$ 91.08 ± 3.88 32.42 ± 7.8 ${\rm{MeOH}}\xrightarrow{{{k}_{3}}}\frac{1}{4}{{\rm{C}}_{4}} \text{+}{{\rm{H}}_{2}}\rm{O}$ ${{r}_{1}}=\frac{1}{4}\frac{{{k}_{3}}[\rm{MeOH}]}{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}$ 38.24 ± 3.55 29.39 ± 4.03 ${\rm{MeOH}}\xrightarrow{{{k}_{4}}}\frac{1}{5}{{\rm{C}}_{5}} \text{+}{{\rm{H}}_{2}}\rm{O}$ ${{r}_{1}}=\frac{1}{5}\frac{{{k}_{4}}[\rm{MeOH}]}{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}$ 23.31 ± 3.49 32.74 ± 5.97 ${\rm{MeOH}}\xrightarrow{{{k}_{5}}}\frac{1}{6}{{\rm{C}}_{6}} \text{+}{{\rm{H}}_{2}}\rm{O}$ ${{r}_{1}}=\frac{1}{6}\frac{{{k}_{5}}[\rm{MeOH}]}{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}$ 19.18 ± 3.27 19.78 ± 3.92

表 2 低空时下甲醇单独进料时的一级平行反应动力学 Table 2 First order kinetics of parallel reactions with only methanol feeding under low space time

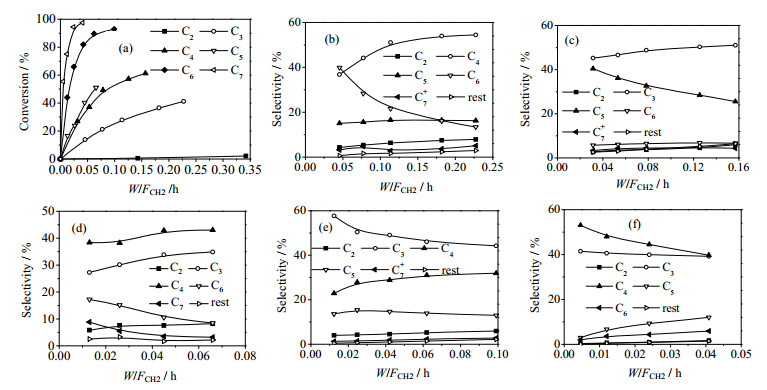
为了研究烯烃之间的相互转化，采用单一烯烃组分分别进料的实验方案(包括C₂、C₃、C₄、C₅、C₆和C₇烯烃分别单独进料)，测定其通过H-ZSM-5催化剂后的反应结果。在475℃条件下，C₂~C₇烯烃单独进料时的转化率和产物选择性随反应空时的变化列于图 3。如图 3(a)所示，随着进料烯烃碳链的增长，烯烃的消耗速率增快。乙烯的转化率最低，其反应速率远小于其它烯烃的反应，在MTP反应网络中可以忽略。

图 3(Fig. 3)

图 3 475℃下C2~C7单独进料时转化率及产物选择性与反应空时的关系 Fig.3 Effects of space time on conversion and product selectivity with C2~C7 feeding at 475℃ (a) conversion (b) C3 (c) C4 (d) C5 (e) C6 (f) C7

图 3(b)表明，低空时下C₃反应的主产物是C₆，随着空时的增加，C₆的选择性迅速降低，C₄的选择性增加，这是由于反应初期C₃发生二聚反应生成C₆，反应后期C₃和C₆发生叠合-裂化生成C₄和C₅。图 3(c)表明，C₄单独进料的主要产物是C₃和C₅，表明两分子C₄发生叠合-裂化生成一分子C₃和一分子C₅，C₅活性较高，又可以和C₄反应生成C₃和C₆。图 3(d)显示，C₅单独反应以叠合-裂化为主，生成C₄和C₆，C₆又会裂解生成C₃；在低空时下C₂的选择性较高，主要是因为C₅发生裂解生成了C₂和C₃。图 3(e)显示，C₆单独反应在低空时下主产物为C₃，选择性接近60%，说明C₆主要发生裂解反应，C₄和C₅烯烃主要是通过C₃和C₆的叠合-裂化生成的；同时，C₆也发生裂解反应生成C₂和C₄。图 3(f)中可以看到，C₇单独反应主产物是C₃和C₄，这是C₇直接裂解的结果，并且在低空时下二者摩尔比接近1:1，随着空时的增大，C₅选择性上升，这是由于C₃和C₇聚合生成C₁₀，进而裂解生成C₅。另外，反应组分中含有少量烷烃和芳烃，而这些副产物都是通过C₂~C₇生成的，因此在反应网络中应加上副产物生成的方程。综合以上分析，可以将烯烃之间的反应归纳为以下主要步骤：

烯烃之间的反应网络在文献中有不少研究，吴文章^[11]给出的反应网络仅考虑了步骤(1)、(3)、(4)、(6) 和(7)，应磊^[8]的反应网络没有包含步骤(8)，本文给出的网络相对更为完整，与图 3给出的反应规律一致。

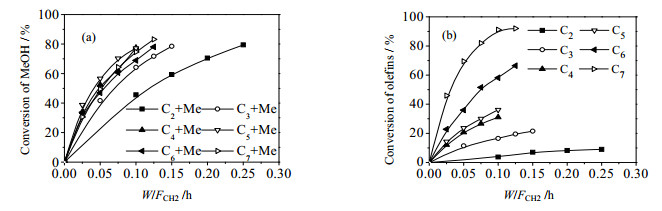
甲醇与单一烯烃混合进料的转化率列于图 4。图 4(a)是甲醇的转化率，图 4(b)是烯烃的转化率，从图中可以看出甲醇与烯烃的反应较快，其中甲醇与戊烯反应最快，甲醇与乙烯反应最慢。甲醇与不同烯烃反应速率的大小顺序为：C₅ > C₄ > =C₇ > C₆ > C₃ > C₂，此结果与吴文章^[11]的实验结果一致。

图 4(Fig. 4)

图 4 480℃下甲醇与烯烃混合进料时的转化率与反应空时的关系 Fig.4 Effects of space time on conversion with methanol/olefin co-feeding at 480℃ (a) methanol (b) olefins

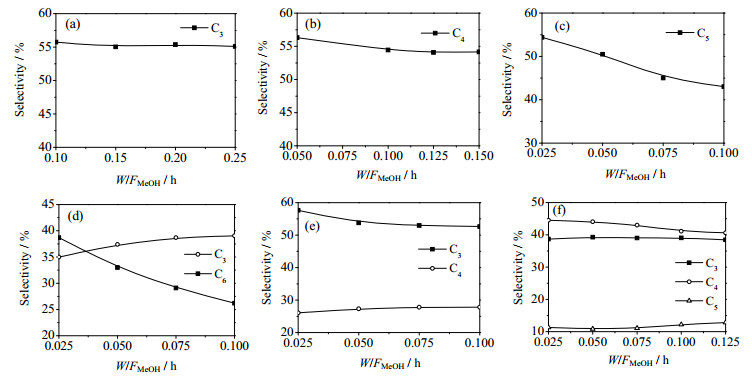
甲醇与不同烯烃反应的主要产物示于图 5。从中可以看到：1) 甲醇与C₂反应的主要产物C₃，随着空时增大C₃选择性基本保持不变；2) 甲醇与C₃反应的主产物是C₄，随着空时增大C₄选择性逐渐降低，这是因为C₄活性较高，更容易发生深度反应；3) 在低空时下甲醇与C₄反应主产物是C₅，随着空时的增加，C₅选择性降低，主要是由于C₅发生叠合-裂化反应；4) 甲醇与C₅发生甲基化反应生成C₆，随着空时的增加，C₆继续发生裂解和叠合-裂化反应导致其选择性降低；5) 甲醇与C₆反应呈现出不同的规律，主要产物为C₃和C₄，这是由于C₆发生甲基化反应生成C₇，C₇迅速裂解生成C₃和C₄；6) 甲醇与C₇共进料反应的主要产物是C₃、C₄和C₅，这是C₇直接裂解的产物，而甲醇主要与C₃和C₄发生甲基化反应。由以上分析可以得出甲醇甲基化反应的步骤可以用式(10) 统一表述：

图 5(Fig. 5)

图 5 480℃下甲醇和C2~C7烯烃反应主产物选择性与反应空时的关系 Fig.5 Effects of space time on main product selectivity with methanol and C2~C7 co-feeding at 480℃ (a) C2 (b) C3 (c) C4 (d) C5 (e) C6 (f) C7

MTP为气固催化反应，原料气在催化剂上发生吸附、反应、脱附等过程，服从经典的Lagmiur-Himshelwood方程，根据式(1)~(10) 构建的反应网络，可列出各步反应的动力学模型，如表 3所示。

表 3(Tab. 3)

表 3 MTP反应动力学模型 Table 3 Kinetic models of MTP Reaction equations Number Kinetic model ${{\rm{C}}_{6}}^{\text{=}}\underset{{{k}_{6}}^{\text{-}1}}{\overset{{{k}_{6}}}{\longleftrightarrow}}2{{\rm{C}}_{3}}^{=}$ (1) ${{r}_{6}}=\frac{{{k}_{6}}[{{\rm{C}}_{6}}]}{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}-\frac{k_{6}^{-1}{{[{{\rm{C}}_{3}}]}^{2}}}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ ${{\rm{C}}_{5}}^{\text{=}}\underset{{{k}_{7}}^{\text{-}1}}{\overset{{{k}_{7}}}{\longleftrightarrow}}{{\rm{C}}_{2}}^{=}\text{+}{{\rm{C}}_{3}}^{=}$ (2) ${{r}_{6}}=\frac{{{k}_{6}}[{{\rm{C}}_{6}}]}{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}-\frac{k_{6}^{-1}{{[{{\rm{C}}_{3}}]}^{2}}}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ ${{\rm{C}}_{6}}^{\text{=}}\underset{{{k}_{8}}^{\text{-}1}}{\overset{{{k}_{8}}}{\longleftrightarrow}}{{\rm{C}}_{2}}^{=}\text{+}{{\rm{C}}_{4}}^{=}$ (3) ${{r}_{8}}=\frac{{{k}_{8}}[{{\rm{C}}_{6}}]}{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}-\frac{k_{8}^{-1}[{{\rm{C}}_{2}}][{{\rm{C}}_{4}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ ${{\rm{C}}_{7}}^{\text{=}}\underset{{{k}_{9}}^{\text{-}1}}{\overset{{{k}_{9}}}{\longleftrightarrow}}{{\rm{C}}_{3}}^{=}\text{+}{{\rm{C}}_{4}}^{=}$ (4) ${{r}_{9}}=\frac{{{k}_{9}}[{{\rm{C}}_{7}}]}{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}-\frac{k_{9}^{-1}[{{\rm{C}}_{3}}][{{\rm{C}}_{4}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ ${{\rm{C}}_{3}}^{\text{=}}\text{+}{{\rm{C}}_{6}}^{\text{=}}\underset{{{k}_{10}}^{\text{-}1}}{\overset{{{k}_{10}}}{\longleftrightarrow}}{{\rm{C}}_{4}}^{=}\text{+}{{\rm{C}}_{5}}^{=}$ (5) ${{r}_{10}}=\frac{{{k}_{10}}[{{\rm{C}}_{3}}][{{\rm{C}}_{6}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}-\frac{k_{10}^{-1}[{{\rm{C}}_{4}}][{{\rm{C}}_{5}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ ${{\rm{C}}_{3}}^{\text{=}}\text{+}{{\rm{C}}_{5}}^{\text{=}}\underset{{{k}_{11}}^{\text{-}1}}{\overset{{{k}_{11}}}{\longleftrightarrow}}2{{\rm{C}}_{4}}^{=}$ (6) ${{r}_{11}}=\frac{{{k}_{11}}[{{\rm{C}}_{3}}][{{\rm{C}}_{5}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}-\frac{k_{11}^{-1}{{[{{\rm{C}}_{4}}]}^{2}}}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ $2{{\rm{C}}_{5}}^{\text{=}}\underset{{{k}_{12}}^{\text{-}1}}{\overset{{{k}_{12}}}{\longleftrightarrow}}{{\rm{C}}_{4}}^{=}\text{+}{{\rm{C}}_{6}}^{=}$ (7) ${{r}_{12}}=\frac{{{k}_{12}}{{[{{\rm{C}}_{5}}]}^{2}}}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}-\frac{k_{12}^{-1}[{{\rm{C}}_{4}}][{{\rm{C}}_{6}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}.$ ${{\rm{C}}_{3}}^{\text{=}}\text{+}{{\rm{C}}_{7}}^{\text{=}}\underset{{{k}_{13}}^{\text{-}1}}{\overset{{{k}_{13}}}{\longleftrightarrow}}2{{\rm{C}}_{5}}^{=}$ (8) ${{r}_{13}}=\frac{{{k}_{13}}[{{\rm{C}}_{3}}][{{\rm{C}}_{7}}]}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}-\frac{k_{13}^{-1}{{[{{\rm{C}}_{5}}]}^{2}}}{{{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}^{2}}}$ ${{\text{C}}_{\text{Rest}}}\xrightarrow{{{k}_{14}}}\text{ArH+Par}$ (9) ${{r}_{\rm{Rest}}}=\frac{{{k}_{14}}\sum\limits_{\rm{n}=2}^{7}{[{{\rm{C}}_{\rm{n}}}]}}{\left(1+{{K}_{\rm{W}0}}[{{\rm{H}}_{2}}\rm{O}] \right)}$ ${\rm{MeOH}}+{{\rm{C}}_{2}}\xrightarrow{{{k}_{15}}}{{\rm{C}}_{3}} $ (10) ${{r}_{15}}=\frac{{{k}_{15}}[\rm{MeOH}][{{\rm{C}}_{2}}]}{{{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}^{2}}}$ ${\rm{MeOH}}+{{\rm{C}}_{3}}\xrightarrow{{{k}_{16}}}{{\rm{C}}_{4}} $ ${{r}_{16}}=\frac{{{k}_{16}}[\rm{MeOH}][{{\rm{C}}_{3}}]}{{{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}^{2}}}$ ${\rm{MeOH}}+{{\rm{C}}_{4}}\xrightarrow{{{k}_{17}}}{{\rm{C}}_{5}} $ ${{r}_{17}}=\frac{{{k}_{17}}[\rm{MeOH}][{{\rm{C}}_{4}}]}{{{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}^{2}}}$ ${\rm{MeOH}}+{{\rm{C}}_{5}}\xrightarrow{{{k}_{18}}}{{\rm{C}}_{6}} $ ${{r}_{18}}=\frac{{{k}_{18}}[\rm{MeOH}][{{\rm{C}}_{5}}]}{{{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}^{2}}}$ ${\rm{MeOH}}+{{\rm{C}}_{6}}\xrightarrow{{{k}_{19}}}{{\rm{C}}_{7}} $ ${{r}_{19}}=\frac{{{k}_{19}}[\rm{MeOH}][{{\rm{C}}_{6}}]}{{{(1+{{K}_{\rm{W}}}[{{\rm{H}}_{2}}\rm{O}])}^{2}}}$

表 3 MTP反应动力学模型 Table 3 Kinetic models of MTP

表中式(1)~式(8) 为可逆反应，利用热力学平衡关系可以减少动力学参数，采用文献[15]中的方法计算热力学平衡常数K_i为：

模型中的动力学参数(反应速率k_i和反应活化能Ea_i)通过实验数据回归确定，实验装置为固定床微分反应器，数学模型可以用下式描述：

式中，V为相应物质的体积流量，W是催化剂的质量，C_i为相应物质的摩尔浓度，r_Ci为相应物质的生成速率。动力学参数的计算采用最小二乘法，目标函数是模型计算值和实验值的浓度偏差最小。

动力学参数与温度的关系采用Arrhenius方程，参考温度为733.15 K(即460℃)，如下所示

计算结果列于表 4中，通过计算结果与文献中的结论比较我们可以得出：1) 甲醇裂解反应：吴文章^[11]认为甲醇裂解平行生成烯烃的反应速率远小于甲基化反应速率，故MTP反应中甲醇裂解反应可以忽略，而从表 2中我们得知，甲醇裂解平行生成烯烃的速率，尤其生成C₃的速率k₂虽然小于甲基化反应k₁₆~k₁₉，但并不可以忽略；甲醇裂解反应活化能均大于零，反应速率随温度升高而加快。2) 烯烃之间的反应：从表 4中可以看出C₇的裂解速率k₉最大，C₅的裂解速率k₇最慢；在叠合-裂化的反应中，C₃与C₆叠合-裂化速率k₁₀最快，C₃与C₇叠合-裂化反应速率k₁₃最慢；而对于C₃，C₄和C₅的自身二聚反应，C₄的二聚反应k₁₂^-1最快。烯烃之间反应速率常数k₆~k₁₃都小于文献[11]给出的值，主要原因是本文采用工业催化剂，含有一定比例的粘合剂，而文献中^[11]大都使用H-ZSM-5催化剂原粉，不含粘合剂。在活化能方面，从表 4中可以发现叠合-裂化的反应表观活化能Ea₆~Ea₁₃均为负值，直接裂解的反应表观活化能为正值，而吴文章^[11]给出的烯烃叠合-裂化反应的表观活化能都为正值。这主要是因为表观活化能的正负是由反应活化能与吸附焓的差值决定的，而根据Corma等^{[16, 17]}的研究证实烯烃在分子筛上的吸附焓为-90~-115 kJ·mol^-1，且吸附焓大小与碳链长度无关，Borges^[12]计算得到烯烃聚合反应(包括叠合和齐聚反应)活化能在30~60 kJ·mol^-1，而裂解反应具有比聚合反应更大的活化能。因此，对于本文研究的聚合反应，由于反应活化能小于吸附焓的绝对值，故表观活化能为负值，而裂解反应则由于反应活化能大于吸附焓的绝对值，所以表观活化能为正值，该结论与本文的计算结果相符。而吴文章在其实验中采用C₂~C₇的醇代替相应的烯烃进料，反应过程中增加了一步醇的水解反应步骤，因此吴文章计算的表观活化能实际是由醇水解、反应活化能和吸附焓三者之和决定的，而醇水解是吸热反应，其活化能较大且为正值^[18]，因此得到的烯烃叠合-裂化反应表观活化能总是为正值，烯烃反应的表观活化能被醇的脱水所掩盖。说明采用醇代替烯烃进料难以获得真实的烯烃叠合-裂化反应动力学数据，应该采用烯烃进料来进行动力学实验研究。

表 4(Tab. 4)

表 4 MTP反应动力学参数 Table 4 Kinetic parameters of MTP ki k460 Eai/kJ·mol-1 ${{\rm{C}}_{6}}^{\text{=}}\underset{{{k}_{6}}^{\text{-}1}}{\overset{{{k}_{6}}}{\longleftrightarrow}}2{{\rm{C}}_{3}}^{=}$ (150.04±5.16) m3·kgcat-1·h-1 41.19±4.33 ${{\rm{C}}_{5}}^{\text{=}}\underset{{{k}_{7}}^{\text{-}1}}{\overset{{{k}_{7}}}{\longleftrightarrow}}{{\rm{C}}_{2}}^{=}\text{+}{{\rm{C}}_{3}}^{=}$ (3.82±3.41) m3·kgcat-1·h-1 218.94±43.46 ${{\rm{C}}_{6}}^{\text{=}}\underset{{{k}_{8}}^{\text{-}1}}{\overset{{{k}_{8}}}{\longleftrightarrow}}{{\rm{C}}_{2}}^{=}\text{+}{{\rm{C}}_{4}}^{=}$ (42.59±3.99) m3·kgcat-1·h-1 39.32±13.37 ${{\rm{C}}_{7}}^{\text{=}}\underset{{{k}_{9}}^{\text{-}1}}{\overset{{{k}_{9}}}{\longleftrightarrow}}{{\rm{C}}_{3}}^{=}\text{+}{{\rm{C}}_{4}}^{=}$ (641.91±27.32) m3·kgcat-1·h-1 26.08±5.29 ${{\rm{C}}_{3}}^{\text{=}}\text{+}{{\rm{C}}_{6}}^{\text{=}}\underset{{{k}_{10}}^{\text{-}1}}{\overset{{{k}_{10}}}{\longleftrightarrow}}{{\rm{C}}_{4}}^{=}\text{+}{{\rm{C}}_{5}}^{=}$ (74.54±5.16) m6·mol-1·kgcat-1·h-1 -45.92±9.23 ${{\rm{C}}_{3}}^{\text{=}}\text{+}{{\rm{C}}_{5}}^{\text{=}}\underset{{{k}_{11}}^{\text{-}1}}{\overset{{{k}_{11}}}{\longleftrightarrow}}2{{\rm{C}}_{4}}^{=}$ (25.16±1.12) m6·mol-1·kgcat-1·h-1 -6.81±5.71 $2{{\rm{C}}_{5}}^{\text{=}}\underset{{{k}_{12}}^{\text{-}1}}{\overset{{{k}_{12}}}{\longleftrightarrow}}{{\rm{C}}_{4}}^{=}\text{+}{{\rm{C}}_{6}}^{=}$ (8.86±2.13) m6·mol-1·kgcat-1·h-1 -9.57±5.68 ${{\rm{C}}_{3}}^{\text{=}}\text{+}{{\rm{C}}_{7}}^{\text{=}}\underset{{{k}_{13}}^{\text{-}1}}{\overset{{{k}_{13}}}{\longleftrightarrow}}2{{\rm{C}}_{5}}^{=}$ (9.09±2.17) m6·mol-1·kgcat-1·h-1 -24.29±3.19 ${{\text{C}}_{\text{Rest}}}\xrightarrow{{{k}_{14}}}\text{ArH+Par}$ (1.59±0.45) m6·mol-1·kgcat-1·h-1 -30.37±8.52 ${\rm{MeOH}}+{{\rm{C}}_{2}}\xrightarrow{{{k}_{15}}}{{\rm{C}}_{3}} $ (13.68±6.44) m6·mol-1·kgcat-1·h-1 108.42 ±17.91 ${\rm{MeOH}}+{{\rm{C}}_{3}}\xrightarrow{{{k}_{16}}}{{\rm{C}}_{4}} $ (110.32±9.63) m6·mol-1·kgcat-1·h-1 15.48±5.29 ${\rm{MeOH}}+{{\rm{C}}_{4}}\xrightarrow{{{k}_{17}}}{{\rm{C}}_{5}} $ (249.02±7.31) m6·mol-1·kgcat-1·h-1 21.59±2.35 ${\rm{MeOH}}+{{\rm{C}}_{5}}\xrightarrow{{{k}_{18}}}{{\rm{C}}_{6}} $ (246.01±10.58) m6·mol-1·kgcat-1·h-1 9.96 ±1.40 ${\rm{MeOH}}+{{\rm{C}}_{6}}\xrightarrow{{{k}_{19}}}{{\rm{C}}_{7}} $ (110.56±9.11) m6·mol-1·kgcat-1·h-1 19.78±3.67 KW (0.0578±0.0013) m3·mol-1 -42.77±6.07 KW0 (0.0077±0.0001) m3·mol-1 -48.77±4.74

表 4 MTP反应动力学参数 Table 4 Kinetic parameters of MTP

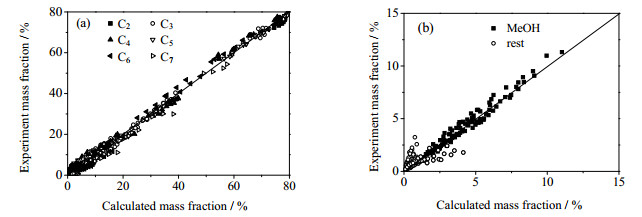
如图 6所示对实验值和模型计算值进行了统计。由图 6可知，MTP反应动力学模型计算值和实验值符合较好，其中C₃、C₄、C₅、C₆、C₇烯烃拟合计算结果最佳，甲醇次之，拟合相对误差范围都在5~15%之间。C₂烯烃和Rest组分的拟合计算结果较差，平均相对误差范围为20%~40%，这主要是一方面反应网络十分复杂，涉及的模型参数较多，准确拟合有一定困难；另一方面小组分测量误差也较大。Rest组分的拟合计算结果较差的另一个原因是因为采用的模型比较简单，所有副反应均采用同一个参数进行拟合，误差较大。

图 6(Fig. 6)

图 6 实验值与模型计算值的比较 Fig.6 Comparison of experimental and calculated results

表 5为对拟合计算结果进行的决定性指标ρ²(线性相关系数)检验和F(方差)检验，得到可靠实验数据252组，需要拟合的参数共计42个。FT值为F检验值取置信度T为5.0 %相应自由度下的临界值。从表 5可以看出, 决定性指标ρ² > 0.95, F > 10F_0.05，置信区间95%，因此认为该反应动力学模型和参数估值可靠。

表 5(Tab. 5)

表 5 统计检验表 Table 5 Analysis of error statistics Component MeOH C2 C3 C4 C5 C6 C7 Rest ρ2 0.992 0.971 0.997 0.995 0.990 0.988 0.976 0.913 F 270 213 715 466 223 183 87 41 10FT 14.6 14.6 14.6 14.6 14.6 14.6 14.6 14.6 R2 0.964 0.908 0.988 0.991 0.986 0.984 0.983 0.804

表 5 统计检验表 Table 5 Analysis of error statistics

(1) MTP是个复杂的反应过程，主要反应路径有三类：甲醇裂解反应、甲醇与C₂~C₆烯烃发生的甲基化反应、C₂~C₇烯烃的叠合-裂化及裂解反应。通过甲醇单独进料、烯烃单独进料、甲醇和烯烃混合进料的实验，分析反应的主要产物及变化规律，提出了较为全面的MTP反应网络。

(2) 针对所提出的MTP反应网络，建立了Lagmiur-Himshelwood形式的动力学模型，考察了反应空时、温度的影响和热力学平衡的限制。通过实验数据回归，确定了模型中的动力学参数，模型计算值和实验值吻合较好，该模型可用于工业MTP反应过程的模拟。

(3) 实验表明，在H-ZSM-5催化剂上，甲醇自身既可以发生裂解反应，也可以和C₂~C₆烯烃发生甲基化反应；C₂~C₅等低碳烯烃主要发生叠合-裂化反应，C₆~C₇等主要发生裂解反应。温度升高，有利于甲醇裂解、甲基化和烯烃裂解反应，不利于烯烃的叠合-裂化反应。在MTP反应中，C₃主要是通过甲醇裂解和高碳烯烃裂解生成的，而由C₂甲基化生成C₃的量很少。

[C_i]        -组分i的摩尔浓度，mol·m^-3

Ea_i        组分i反应活化能，kJ·mol^-1

F_CH2        烯烃进料流量，kg·h^-1

F_MeOH        甲醇进料流量，kg·h^-1

K        热力学平衡常数

k_i        反应速率常数

k_i^*        指前因子

K_W，K_W0        水浓度影响参数，m³·mol^-1

R        摩尔气体常量，J·mol^-1·K^-1

r_Ci        组分i的生成速率，mol·kg_cat^-1·h^-1

T        温度，K

V        物质的体积流量，m³·h^-1

W/ F_MeOH        基于甲醇的反应空时，h

W/F_CH2        基于烯烃的反应空时，h

i, j        组分或数字

[MeOH]        甲醇的摩尔浓度，mol·m^-3