稀土金属被广泛应用于传统及高新产业领域,市场对其需求日益增长,我国作为世界上最大的稀土资源生产和消费国家,在稀土熔盐电解产业方面得到迅猛发展[1-3]。但由于我国稀土电解槽存在早期破损严重、槽寿命偏短等缺陷[4-5],容易导致工厂非计划停槽,生产工作量增加,能源及原材料消耗增加,严重影响了电解槽的经济技术指标,制约了我国稀土熔盐电解生产。而在大量电解槽早期破损事故[6]中,屡屡发现石墨内衬先行失效,作为电解槽关键且薄弱环节,石墨内衬重要性不言而喻。
稀土熔盐电解槽石墨内衬服役期间处于复杂的环境下,不仅受到槽壳约束力作用[7-9],而且受到活性气氛的氧化腐蚀[10]作用,不仅严重影响稀土熔盐电解槽石墨内衬材料的力学性能及寿命,而且其先行失效会引发碳杂质污染产品[11]。因此研究石墨内衬材料力学性能劣化情况时需要考虑载荷-氧化腐蚀损伤耦合作用,然而近年来国内外学者对石墨阳极和石墨内衬等碳素材料性能研究仍侧重于研究破损机理及抗腐蚀性等方面[12-14],并未对复杂环境中碳素材料损伤本构模型进行深入研究。使得稀土熔盐电解槽石墨内衬在进行优化设计缺乏科学理论依据,与实际破损情况不符,无法准确表征出石墨内衬的实际力学劣化过程。
本文利用自行研发的高温氧化环境下石墨内衬试样力学实验系统,针对稀土熔盐电解槽石墨内衬在复杂环境下服役工况进行模拟实验,分别对不同氧化时间下石墨内衬试样进行单轴压缩试验,在力学损伤本构模型中引入氧化腐蚀-应力耦合损伤变量,建立稀土熔盐电解环境下石墨内衬氧化腐蚀—应力损伤耦合本构关系模型,为石墨内衬的耐久性设计、施工和电解操作生产提供可靠的力学参数,其理论、实际工程意义重大。
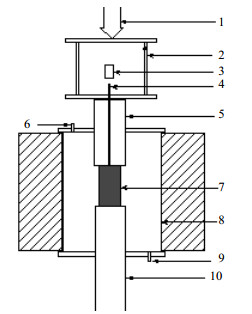
2 石墨内衬氧化腐蚀作用下单轴压缩试验 2.1 试验方法试验选用试样为全石墨质(HC100)内衬,根据力学试验试样的尺寸标准要求,石墨试样径高比为1:2的Ф25 mm×50 mm圆柱体。设备是自行研制的高温氧化气氛下石墨内衬单轴压缩实时试验系统,采用材料试验机与之相配套的高温炉实现,结构示意图如图 1。实验分为两组进行,每组5个试样,试样分别在通入二氧化碳与氮气混合气体且温度为1 000 ℃环境下氧化0.5、1、1.5、2和2.5 h,其中一组试样冷却至室温后,用nano Voxel-2000型显微CT设备进行CT层析成像试验,并对石墨内衬试样CT图像进行二值化分割处理,统计计算二值化CT图像孔隙率;另一组试样氧化后紧接着采用位移控制方式对试样实施加载,直至炭块试样破坏为止,位移加载速率为0.002 mm·s-1。
|
图 1 石墨内衬力学性能实时测试装置结构示意图 Fig.1 Schematic diagram of experimental setup for real-time mechanical property measurements of graphite lining 1. load 2. loaded steel frame 3. laser range finder 4. ranging rod 5. upper pressure head 6. exhalation hole 7. graphite sample 8. high temperature furnace tube 9. inlets 10. lower head |
图 2为石墨内衬显微CT图像,图 3为二值化处理后石墨内衬显微CT图像。稀土电解槽石墨内衬在复杂环境下受到氧化腐蚀及外力作用, 宏观上表现为石墨内衬力学性能劣化,微细观上表现为石墨内衬孔隙或裂隙细观结构演化,孔隙细观结构演化是宏观力学性能劣化的内在原因,宏观力学性能劣化是孔隙细观结构演化的外在表现。因此为了深入研究石墨内衬损伤破裂过程,需从宏观力学性能参数变化及微观结构变化两方面进行研究。在碳素材料宏观力学性质劣化研究方面,通过进行力学实验,利用宏观力学参数变化来表述其损伤劣化过程,取得了一定成果,但关于其微细观结构演化规律研究极少。石墨内衬由骨料、沥青粘结剂及孔隙组成,其孔隙结构作为二氧化碳扩散通道与反应场所,孔隙结构演化不仅影响反应扩散过程,同时反映了材料力学性能变化。

|
图 2 石墨内衬氧化后显微CT图像 Fig.2 CT micrographs of graphite lining after oxidation |

|
图 3 二值化处理后石墨内衬CT图像 Fig.3 CT micrographs of graphite lining before and after binary processing |
由石墨内衬显微CT图可知,骨料及沥青黏结剂结构在CT图像上表现为高密度带,近于灰色,灰度值较大;孔隙结构在CT图像上表现为低密度带,近于黑色,灰度值较小。图像在二值化处理后,可以清晰地看到孔隙结构及孔隙演化过程,孔隙呈现较为密集的点状。随着氧化腐蚀时间增加,石墨内衬试样由边缘向轴心方向,孔隙结构增多,有效承载面积减小。石墨内衬孔隙结构演化规律在一定程度上反映其力学性能的变化。由于石墨内衬孔隙位置强度低,在孔隙处易发生应力集中现象,因此在外力作用下易导致局部孔隙部位石墨破裂。石墨内衬有效承载面积随着孔隙率增大而减小,抗压强度随孔隙率增大而减小,所以随着氧化扩散与孔隙结构演化进行,孔隙率增大,石墨内衬抗压强度越小,越容易在载荷作用下破裂损伤。
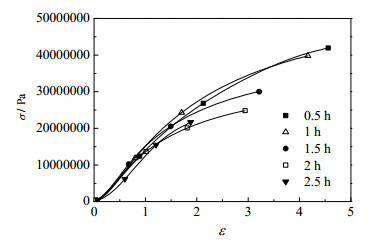
2.2.2 石墨内衬试样应力-应变曲线变化规律由图 4可以看出,石墨内衬单轴受压应力-应变曲线大致经历3个阶段:压密阶段、线弹性阶段和破坏阶段。
|
图 4 石墨内衬单轴压缩实验应力-应变曲线 Fig.4 Stress-strain curves of uni-axial compression test of graphite lining |
第1阶段:压密阶段。应变增长速率随应力增大而减小,初始阶段石墨内衬试样内部存在的孔隙结构逐渐闭合。随着氧化时间增加,压密阶段在整个应力-应变曲线中所占比例越大,石墨内衬试样内部孔隙率随着氧化时间增加而增大,试样微观表现为孔隙结构增大,宏观表现为力学性能劣化,压密阶段应变相应增大。
第2阶段:线弹性阶段。细观损伤变化不大,应力和应变呈线性相关,此阶段斜率近似为石墨内衬试样平均线弹性模量,随着氧化时间增大,斜率随之减小。
第3阶段:破坏阶段。随着应力的增长,应变增长速率亦增长,曲线呈凸起状(部分曲线不明显),达到峰值应力后,试样破碎,加载进程结束。对石墨内衬试样加载过程观察发现,石墨内衬在张力破裂和挤压破碎共同作用下发生破坏现象,当加载到接近石墨内衬峰值强度时裂纹沿压向迅速扩展,从裂纹开始出现至破坏几乎瞬间发生,破坏过程伴随有较大的能量释放,加载结束时产生较大响声,同时产生裂纹一侧有小块崩落。随着石墨内衬氧化腐蚀时间的增加,其力学性能发生较为显著地劣化现象,加载过程变形缓慢,峰值强度及峰值应变降低,从裂纹产生到完全破坏时间减少,破坏过程伴随响声减小,突然释放应变能减弱。
由图可知,随着石墨内衬氧化腐蚀时间增加,其初始压密阶段、屈服段越长,弹性阶段越短。石墨内衬内部微孔隙结构随着氧化腐蚀时间增加而增加,随着有效面积减小,力学性能劣化越显著。
3 石墨内衬损伤本构模型 3.1 损伤本构关系由Lemaitre应变等价假设[15]可知,全应力σ作用于受损石墨内衬引起的应变等价于有效应力σ'作用于无损石墨内衬引起的应变,可得单轴压缩下石墨内衬材料内部损伤型本构关系为:
| $ \sigma {\rm{ = }}\left( {1 - D} \right){E_{\left( 0 \right)}}\varepsilon $ | (1) |
式中E(0)为无损状态下石墨内衬的弹性模量,D为石墨内衬氧化腐蚀-应力损伤耦合变量。
石墨内衬氧化腐蚀型本构关系为:
| $ \sigma = \left( {1 - {D_{\rm{m}}}} \right){E_{\left( {\rm{b}} \right)}}\varepsilon $ | (2) |
| $ {E_{\left( {\rm{b}} \right)}} = {E_{\left( 0 \right)}}\left( {1 - {D_{\rm{c}}}} \right) $ | (3) |
式中Dm为石墨内衬应力损伤变量,E(b)为氧化腐蚀损伤状态下的石墨内衬弹性模量,Dc为石墨内衬氧化腐蚀损伤变量。
由式(1)、(2)、(3)得到用氧化腐蚀-应力损伤变量表示石墨内衬本构关系为:
| $ \begin{aligned} \sigma &=(1-D) E_{(0)} \varepsilon \\ &=\left(1-D_{\mathrm{m}}\right)\left(1-D_{\mathrm{c}(\mathrm{b})}\right) E_{(0)} \varepsilon \\ &=\left(1-D_{\mathrm{m}}+D_{\mathrm{c}(\mathrm{b})}-D_{\mathrm{m}} D_{\mathrm{c}(\mathrm{b})}\right) E_{(0)} \varepsilon \end{aligned} $ | (4) |
式中
将石墨内衬氧化腐蚀-应力耦合损伤变量D定义为:
| $ D = 1 - \left( {1 - {D_{\rm{c}}}} \right)\left( {1 - {D_{\rm{m}}}} \right) = 1 - \frac{{{E_{\left( {{\rm{b, t}}} \right)}}}}{{{E_{\left( 0 \right)}}}} $ | (5) |
式中:E(0)为石墨内衬无损伤状态瞬时弹性模量,E(b, t)为石墨内衬氧化腐蚀-应力损伤状态下瞬时弹性模量。
3.2 应力损伤演化方程石墨材料试件成型时,内部不可避免地存在微观缺陷, 并且在氧化腐蚀作用下会产生新的缺陷,在载荷作用下,石墨内衬材料内部的微观缺陷不断的产生、扩展、贯通,导致材料力学性能不断劣化。为了便于统计量化这些微观缺陷,基于连续损伤力学对离散随机的微观损伤进行连续化处理,利用损伤变量表示微观缺陷演化过程。将连续损伤理论与概率理论相结合,假定石墨内衬微元强度或石墨内衬微元破坏损伤服从Weibull分布[16-17],则其强度概率密度函数可以表示为:
| $ \omega \left( \varepsilon \right) = \frac{m}{{{x_0}}}{\left( {\frac{\varepsilon }{{{x_0}}}} \right)^{m - 1}}\exp \left[ { - {{\left( {\frac{\varepsilon }{{{x_0}}}} \right)}^m}} \right] $ | (6) |
式中:m、x0分别为Weibull分布标度和形态函数,表示石墨内衬的均匀性特征;ε为石墨内衬微元体的应变。
根据连续介质损伤力学,力学损伤变量Dm可定义为力学损伤面积S和无损伤面积Sm之比。假设初始条件下无力学损伤,即ε = 0,Dm= 0,则可得到:
| $ {D_{\rm{m}}} = \frac{S}{{{S_{\rm{m}}}}} = \int_0^\varepsilon {\omega \left( \varepsilon \right)} {\rm{d}}\varepsilon = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{{{x_0}}}} \right)}^m}} \right] $ | (7) |
石墨材料的氧化腐蚀损伤是指在稀土熔盐电解环境下,阳极产生的CO2气体会与石墨内衬发生氧化反应,使得槽体氧化腐蚀破损,导致石墨内衬力学性能劣化。考虑石墨内衬中氧化反应、气体扩散和孔隙结构演化耦合作用,建立稀土熔盐电解环境下的石墨内衬试样的氧化扩散与孔隙结构演化数学模型,得到石墨内衬氧化腐蚀模型一维偏微分方程组为:
| $ \left\{ \begin{array}{l} \frac{{\partial \left( {\varphi \left( {r, t} \right){C_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\left( {r, t} \right)} \right)}}{{\partial t}} = \nabla \left( {\varphi \left( {r, t} \right){D_{\rm{s}}} \cdot \nabla {C_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\left( {r, t} \right)} \right) - {R_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\\ \varphi \left( {r, t} \right) = {\varphi _0} + \left( {1 - {\varphi _0}} \right)b\left( {r, t} \right)\\ {D_s} = {\left[ {\varphi \left( {r, t} \right)} \right]^2}\left( {\frac{1}{{{D_{{\rm{AB}}}}}} + \frac{1}{{{D_{{\rm{kn}}}}}}} \right)\\ {R_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = \frac{{{\rho _{\rm{c}}}}}{{{M_{\rm{c}}}}}A{{\rm{e}}^{{\raise0.7ex\hbox{${ - {E_{\rm{a}}}}$} \!\mathord{\left/ {\vphantom {{ - {E_{\rm{a}}}} {{R_{\rm{g}}}T}}}\right.} \!\lower0.7ex\hbox{${{R_{\rm{g}}}T}$}}}}{R_g}T{F_{\rm{b}}}{C_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\left( {r, t} \right)\\ \frac{{\partial b\left( {r, t} \right)}}{{\partial t}} = A{{\rm{e}}^{{\raise0.7ex\hbox{${ - {E_{\rm{a}}}}$} \!\mathord{\left/ {\vphantom {{ - {E_{\rm{a}}}} {{R_{\rm{g}}}T}}}\right.} \!\lower0.7ex\hbox{${{R_{\rm{g}}}T}$}}}}{R_{\rm{g}}}T{F_{\rm{b}}}{C_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}\left( {r, t} \right) \end{array} \right. $ | (8) |
式中:φ为石墨内衬孔隙率,C为稀土电解槽石墨内衬二氧化碳瞬时浓度,mol·m-3;C0为稀土电解槽石墨内衬外表边缘二氧化碳初始浓度,mol·m-3;r为稀土电解槽石墨内衬圆柱体截面径向长度,m;t为石墨内衬氧化时间,s;b为石墨内衬的失重率,%;Ds为二氧化碳在稀土电解槽石墨内衬内部扩散系数,m2·s-1;RCO2为二氧化碳与稀土电解槽石墨内衬的反应速率,mol·(m3·s)-1;τ为石墨材料的曲折率,定义为多孔材料内部真实孔长度与表现孔长度之比,随石墨氧化消耗而变化,近似于孔隙率倒数,即
边界条件及初始条件如式(9)所示:
| $ \left\{\begin{array}{l}{C_{\mathrm{CO}_{2}}(R, \mathrm{t})=C_{0}} \\ {C_{\mathrm{CO}_{2}}(r, 0)=0 \quad 0 \leqslant r \leqslant R} \\ {b(r, 0)=0 \quad 0 \leqslant r \leqslant R}\end{array}\right. $ | (9) |
稀土电解槽石墨内衬在高温氧化性环境中受到氧化腐蚀作用,在微观上表现为内部微细观结构改变,具体体现在其孔隙率变化;在宏观上表现为力学参数变化。宏观力学性质劣化的外在表现为石墨内衬表观损伤,其实质就是材料微细观结构变化。在氧化腐蚀作用下,石墨内衬损伤引起材料微结构的变化和材料受力性能的劣化,且损伤劣化程度与氧化腐蚀过程密切相关。石墨内衬在氧化腐蚀作用下微细观结构发生不同程度的损伤,引起石墨内衬试样的孔隙率变化, 通过分析氧化腐蚀作用对其微细观结构的影响效应,可基于氧化腐蚀后内部孔隙的变化建立氧化损伤变量[18-20],定量描述氧化腐蚀引起试样内部微细观结构化学损伤程度。
| $ D_{c}=\frac{\varphi-\varphi_{0}}{1-\varphi_{0}} $ | (10) |
式中:φ0为石墨内衬试样氧化腐蚀前的孔隙率,φ为石墨内衬试样氧化腐蚀后的孔隙率。
将式(7)和(10)代入式(4)中,得出用氧化腐蚀损伤变量和外力载荷损伤变量表示的本构关系:
| $ \sigma=\left(1-D_{\mathrm{m}}\right)\left(1-D_{\mathrm{c}}\right) E_{(0)} \varepsilon=\frac{1-\varphi}{1-\varphi_{0}} \exp \left[-\left(\frac{\varepsilon}{x_{0}}\right)^{m}\right] E_{(0)} \varepsilon $ | (11) |
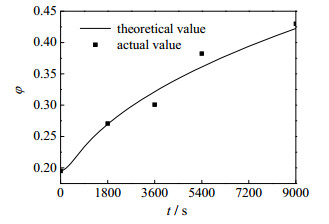
为了得到Weibull参数x和m变化规律,首先对石墨内衬在不同氧化时间下CT显微图像进行二值化处理,统计计算孔隙率,验证氧化腐蚀模型,得到不同氧化时间下化学损伤变量Dc。表 1为模型计算基本输入参数。图 5为石墨内衬孔隙率实际值与理论值对比曲线图。由图 5可知,氧化腐蚀模型计算值与实验值基本一致,该模型可以用来预测石墨内衬氧化扩散及孔隙演化过程。
|
|
表 1 模型计算基本输入参数 Table 1 Basic input parameters of model calculation |
|
图 5 石墨内衬孔隙率实际值与理论值对比曲线图 Fig.5 Comparison of experimental and theoretical values of graphite lining porosity |
然后通过对石墨内衬在不同氧化腐蚀时间下进行单轴压缩试验,得到不同氧化腐蚀时间下单轴压缩应力-应变曲线。根据氧化腐蚀作用下石墨内衬单轴压缩试验应力-应变曲线拟合求得初始性弹性E0、Weibull分布标度m和形态函数x0,然后分析Weibull分布标度m和形态函数x0受氧化腐蚀变化影响的规律。氧化-应力损伤耦合模型主要参数见下表 2。
|
|
表 2 单轴压缩下损伤本构模型参数拟合值 Table 2 Fitting parameters of damage constitutive models under uniaxial compression |
由表 2可知石墨内衬随着氧化腐蚀时间增大,Weilbull参数值x0增大,m减小,反映出其在不同化学损伤状态下,表征其强度的Weibull分布参数值会发生变化。因此引入Weibull分布来表征石墨内衬力学损伤时,应考虑氧化腐蚀损伤状态对Weibull分布参数值的影响,建立参数值x0、m与氧化腐蚀损伤变量Dc关系式,准确表征氧化腐蚀作用下石墨内衬力学损伤变量Dm。通过对石墨内衬Weibull参数x0、m与化学损伤变量Dc进行曲线拟合,得到Weibull参数x0、m变化规律:
(1) Weibull分布形态函数x
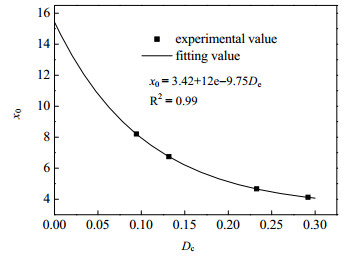
图 6为Weibull分布参数x0随化学损伤Dc变化曲线。由图可知,Weibull分布参数x0随化学损伤Dc增大而减小,二者呈负指数关系。Weibull分布参数x0与化学损伤Dc的关系式可表示为:
|
图 6 Weibull分布参数x0随化学损伤Dc变化曲线 Fig.6 Profile of Weibull distribution parameter x0 as a function of chemical damage Dc |
| $ x_{0}=3.42+12 \mathrm{e}^{-9.75 D_{\mathrm{c}}} $ | (12) |
(2) Weibull分布标度m
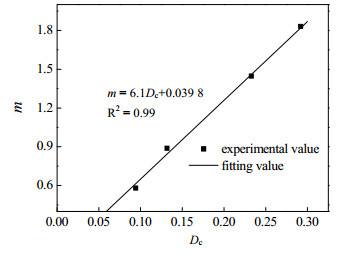
图 7为Weibull分布参数m随化学损伤Dc变化曲线。由图可知,Weibull分布参数m随化学损伤Dc增大而增大,二者呈线性相关。Weibull分布参数m与化学损伤Dc的关系式可表示为:
|
图 7 Weibull分布参数m随化学损伤Dc变化曲线 Fig.7 Profile of Weibull distribution parameter m as a function of chemical damage Dc |
| $ m=6.1 D_{\mathrm{c}}+0.0398 $ | (13) |
将式(12)和式(13)带入式(11)中,得出石墨内衬氧化腐蚀-应力损伤耦合本构关系式:
| $ \begin{array}{l} \sigma {\rm{ = }}\frac{{1{\rm{ - }}\varphi }}{{1{\rm{ - }}{\varphi _0}}}\exp \left[ { - {{\left( {\frac{\varepsilon }{{3.42 + 12{{\rm{e}}^{ - 9.75{D_{\rm{c}}}}}}}} \right)}^{6.1{D_{\rm{c}}} + {{0.039}_{}}8}}} \right]{E_{\left( 0 \right)}}\varepsilon \\ = \frac{{1{\rm{ - }}\varphi }}{{1{\rm{ - }}{\varphi _0}}}\exp \left[ { - {{\left( {\frac{\varepsilon }{{3.42 + 12{{\rm{e}}^{ - 9.75\left( {\frac{{{\varphi _0} - \varphi }}{{1 - {\varphi _0}}}} \right)}}}}} \right)}^{6.1\left( {\frac{{{\varphi _0} - \varphi }}{{1 - {\varphi _0}}}} \right) + {{0.039}_{}}8}}} \right]{E_{\left( 0 \right)}}\varepsilon \end{array} $ | (14) |
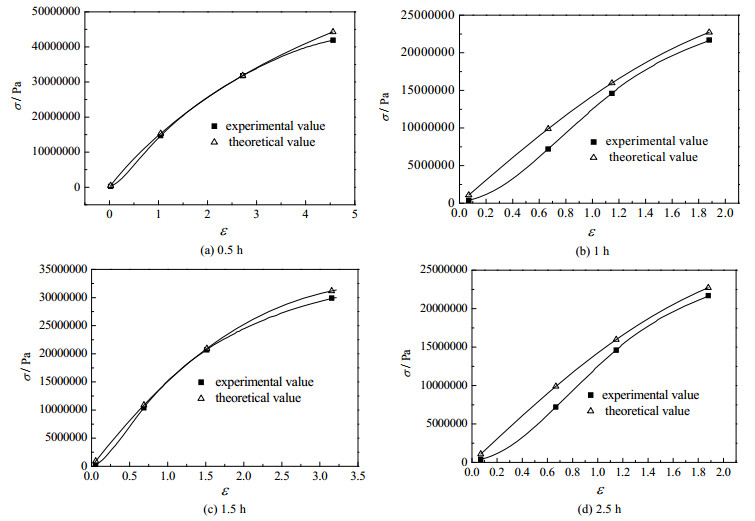
为了验证石墨内衬氧化腐蚀-力学损伤耦合本构模型的合理性,根据所得模型参数,利用已建立的氧化腐蚀-力学损伤耦合本构模型,得到氧化腐蚀作用下石墨内衬单轴压缩过程的应力-应变预测曲线,将试验曲线与模型预测曲线进行对比分析,图 8为氧化腐蚀作用下石墨内衬理论值和试验值对比曲线。由图 8可知:石墨内衬氧化腐蚀-应力损伤耦合本构模型能够较为准确反映石墨内衬氧化腐蚀状态下单轴压缩过程中力学特征变化趋势,模型预测曲线和试验曲线趋势线相近,拟合程度较高,较客观地表征石墨内衬单轴压缩过程。与实验值相比,氧化0.5 h时模拟计算值的最大偏差为2.39×106 Pa,平均偏差为7.36×105 Pa;氧化1 h时模拟计算值的最大偏差为2.22×106 Pa,平均偏差为1.22×106 Pa;氧化1.5 h时模拟计算值的最大偏差为1.48×106 Pa,平均偏差为7.06×105 Pa;氧化2.5 h时模拟计算值的最大偏差为2.90×106 Pa,平均偏差为1.87×106 Pa。从图 8看,随着氧化时间的延长,到2.5 h时模型与实验值之间偏差较大,原因可能是由于随着氧化时间的增加,石墨内部孔隙增多,而孔隙的大量增加会影响气体传输的氧化路径,从而导致孔隙在石墨内部分布不均匀,进而使石墨内衬在单轴压缩过程中受力不均匀,石墨内衬的力学性能发生复杂性变化,宏观上表现为试验的应力-应变曲线与理论的应力-应变曲线有所差距。但两者趋势上依然具有一致性,说明模型的合理性、有效性。同时由于氧化腐蚀损伤变量的引入,模型真实地反映了氧化腐蚀时间对石墨内衬力学性质的影响,石墨内衬单轴抗压强度随着氧化腐蚀时间增加而降低,其力学性能劣化与氧化腐蚀-应力耦合作用密切相关,模型更真实表征稀土电解槽石墨内衬实际服役情况。
|
图 8 氧化腐蚀作用下石墨内衬理论值和试验值对比曲线 Fig.8 Comparison of theoretical and experimental values of graphite lining under oxidation corrosion |
(1) 考虑到石墨内衬内部微观缺陷结构非均匀性,基于连续损伤理论与概率理论,采用Weibull分布函数描述其微元强度分布特征,将Weibull分布函数引入单轴压缩下石墨内衬力学损伤本构模型中,较真实地表征了石墨内衬力学损伤演化过程。结果表明:石墨内衬随着氧化腐蚀时间增大,Weilbull参数值x0增大,m减小,反映出其在不同化学损伤状态下,表征其强度的Weibull分布参数值会发生变化。Weibull分布参数x0随化学损伤Dc增大而减小,二者呈负指数相关;Weibull分布参数m随化学损伤Dc增大而增大,二者呈线性相关。
(2) 考虑氧化腐蚀对石墨内衬力学性质的影响,在力学损伤本构关系中引入基于孔隙率变化的氧化腐蚀损伤变量,基于Lemaitre应变等效原理建立氧化腐蚀-应力损伤耦合本构模型。该模型考虑了氧化腐蚀-应力耦合作用对石墨内衬力学性能劣化影响,其理论、实际工程意义重大。
(3) 稀土熔盐电解槽石墨内衬在复杂环境下受到二氧化碳气体的氧化腐蚀,造成了石墨内衬内部孔隙结构增大,有效承载面积减少,导致其力学性能劣化,弹性模量及峰值应力降低。实际实验结果同氧化腐蚀-应力损伤耦合本构模型数值模拟结果基本吻合,表明石墨内衬氧化腐蚀-应力耦合本构模型合理性,可以真实地描述在稀土熔盐电解槽复杂环境下石墨内衬损伤破裂演化过程,为石墨内衬的耐久性设计、施工和电解操作生产提供可靠的力学参数,为延长稀土电解槽寿命提供理论依据。
| [1] |
周俏华. 中国现代稀土金属产业发展概述[J]. 价值工程, 2011(29): 276-277. ZHOU Q H. Overview of development of China's modern rare earth metal industry[J]. Value Engineering, 2011(29): 276-277. |
| [2] |
张卫平, 杨庆山, 陈建军. 高纯稀土金属制备方法与发展趋势[J]. 金属材料与冶金工程, 2007, 35(3): 62-64. ZHANG W P, YANG Q S, CHEN J J. Preparation method and development trend of high purity RE materials[J]. Metal Materials and Metallurgy Engineering, 2007, 35(3): 62-64. |
| [3] |
刘建刚. 稀土熔盐电解炉筑炉工艺改进[J]. 广东化工, 2015, 42(6): 52-59. LIU J G. Improvement on molten salt electrolytic furnace for preparing rare earth[J]. Guangdong Chemical Industry, 2015, 42(6): 52-59. |
| [4] |
王永良, 铁军, 薛济来. 铝电解槽内衬材料破损及数据挖掘诊断技术的探讨[J]. 轻金属, 2010(12): 25-33. WANG Y L, TIE J, XUE J L. Failure of the potlining aluminium reduction cells and discussion on diagnostic technique of datamining[J]. Light Metals, 2010(12): 25-33. |
| [5] |
杜继红, 奚正平, 鞠鹤, 等. 稀土钕电解用陶瓷坩埚的研制[J]. 稀有金属材料与工程, 2001(6): 457-459. DU J H, XI Z P, JU H, et al. Preparation of rare earth Nd electrolysis crucibles[J]. Rare Metal Materials and Engineering, 2001(6): 457-459. |
| [6] |
尹书奎, 邵勇, 曹继明, 等. 大型预焙铝电解槽阴极内衬破损特征及检测[J]. 轻金属, 2005(12): 29-32. YIN S K, SHAO Y, CAO J M, et al. The characteristic of the damages and the maintenance measures of the cathode liners in large pre-baked anode aluminium[J]. Light Metals, 2005(12): 29-32. |
| [7] |
石富. 稀土电解槽的研究现状及发展趋势[J]. 中国稀土学报, 2007, 25(S1): 70-76. SHI F. Present condition of research and developing trend in the rare earth electrolysis cell[J]. Journal of the Chinese Rare Earth Society, 2007, 25(S1): 70-76. |
| [8] |
HIRSCHHORN I S. Commercial production of rare earth metals by fused salt electrolysis[J]. The Journal of the Metal & Material Society, 1968, 20(3): 19-22. |
| [9] |
王维, 薛济来, 朱骏, 等. 铝电解槽石墨化阴极和槽壳的变形[J]. 北京科技大学学报, 2012, 34(6): 695-700. WANG W, XUE J L, ZHU J, et al. Deformation in the graphitized cathodes and on the shells of aluminum reduction cells[J]. Journal of University of Science and Technology Beijing, 2012, 34(6): 695-700. |
| [10] |
陈德宏, 颜世宏, 李宗安, 等. Si3N4结合SiC材料在稀土电解槽中的应用及效果[J]. 稀土, 2012, 33(3): 12-15. CHEN D H, YAN S H, LI Z A, et al. Evaluation of Si3N4 bonded SiC used in the rare earth electrolysis cell[J]. Chinese Rare Earths, 2012, 33(3): 12-15. |
| [11] |
薛娟琴, 刘妮娜, 刘志飞, 等. 熔盐电解Nd用石墨阳极失效及浸渍硼酸盐防护[J]. 稀有金属, 2016, 40(8): 806-815. XUE J Q, LIU N N, LIU Z F, et al. Failure and borate impregnation protection of graphite anode for neodymium electrodeposition in Molt[J]. Chinese Journal of Rare Metals, 2016, 40(8): 806-815. |
| [12] |
刘中兴, 徐子娟, 王伟, 等. 稀土电解槽石墨阳极的研究[J]. 有色金属(冶炼部分), 2014(1): 45-49. LIU Z X, XU Z J, WANG W, et al. Study on graphite anode of rare earth electrolytic cell[J]. Nonferrous Metals (Extractive Metallurgy), 2014(1): 45-49. |
| [13] |
杜继红, 奚正平, 武宏让, 等. 稀土熔盐电解中新型阳极的研制及耐蚀性能[J]. 中国有色金属学报, 1998, 8(S2): 240-241. DU J H, XI Z P, WU H R, et al. Development and corrosion resistance of new anode in rare earth molten salt electrolysis[J]. The Chinese Journal of Nonferrous Metals, 1998, 8(S2): 240-241. |
| [14] |
侯复生, 汪进宝. 涂层材料对石墨阳极抗氧化性能影响的研究[J]. 稀土, 2012, 33(6): 94-96. HOU F S, WANG J B. Study of the influence of coating materials on anti-oxidation of graphite anodes[J]. Chinese Rare Earths, 2012, 33(6): 94-96. |
| [15] |
LEMAITRE J, CHABOCHE J L. Mechanics of solid materials[M]. Cambridge: Cambridge University Press, 1990: 159-168.
|
| [16] |
EIBLJ, SCHMIDT-HURTIENNE B. Strain-rate-sensitive constitutive law for concrete[J]. Journal of Engineering Mechanics, 1999, 125(12): 1411-1420. DOI:10.1061/(ASCE)0733-9399(1999)125:12(1411) |
| [17] |
KHAN M S, KING R. Transmuted modified Weibull distribution: A generalization of the modified Weibull probability distribution[J]. European Journal of Pure and Applied Mathematics, 2013, 6(1): 66-88. |
| [18] |
韩铁林, 师俊平, 陈蕴生, 等. 化学侵蚀后砂浆力学特性的劣化及其细观结构损伤定量化方法[J]. 材料研究学报, 2015, 29(12): 921-930. HAN T L, SHI J P, CHEN Y S, et al. Salt solution attack induced mechanical property degradation and quantitative analysis method for evolution of meso-structure damages of mortar[J]. Chinese Journal of Materials Research, 2015, 29(12): 921-930. |
| [19] |
PIGNATELLI R, COMI C, MONTEIRO P J M. A coupled mechanical and chemical damage model for concrete affected by alkali-silica reaction[J]. Cement and Concrete Research, 2013, 53: 196-210. DOI:10.1016/j.cemconres.2013.06.011 |
| [20] |
丁梧秀, 冯夏庭. 灰岩细观结构的化学损伤效应及化学损伤定量化研究方法探讨[J]. 岩石力学与工程学报, 2005, 24(8): 1283-1288. DING W X, FENG X T. Study on chemical damage effect and quantitative analysis method of meso-steucture of limestone[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1283-1288. |




