1 引言

国内近几年对固体垃圾问题，包括高危固体废弃物的重视，使探索出一种高效、清洁的处理方法变得日益重要。而等离子体技术具有能源利用率高、处理效果突出的特点，能够满足这一需求。目前在国外该技术已应用到包括城市生活、医院卫生、工业废置等诸多领域^[1-2]。而该技术在应用中却存在一个问题，即由于等离子体温度高于电极金属的熔点，导致设备寿命减小，工作效率降低^[3]。所以发展一种简便可靠的耦合电极-电弧的研究方法则成为关键。

由于等离子体发生装置尺寸小、结构复杂，在实验或生产操作中难以对其电极状态进行观测。除此之外，其具有的高温-电磁相互耦合的特点更使得数据测量工作难以进行。因此，数值模拟计算成为解决该问题的主要研究方法^[4-6]。但同时，由于人们更多关注等离子体主体内的物理场分布，而忽略了电极本身热电子发射机制带来的热效应，因此在传统计算结果中对于电极温度的计算需要改进。有鉴于此，且考虑转移弧与非转移弧发生原理相似，因此本文针对自由燃烧电弧等离子体，将电极与电弧区耦合建立二维轴对称的磁流体动力学(magnetohydrodynamic, MHD)计算模型，并通过合理的设计方法，通过求解电子连续方程与附加面热源将电弧对电极的热效应、流体域的电导率修正包含在内，得到了与实验测量相近的温度场分布。该模型的建立可以为工业用直流电弧等离子体炬的设计改良提供方法基础。

2 数学模型 2.1 基本假设

研究宏观条件下发生装置内部的温度场分布，因此通过下面的合理假设对复杂的电弧模型进行简化，具体包括：

1) 在电弧区域采用局域热平衡(local thermodynamic equilibrium, LTE)假设；

2) 等离子体为光学薄；

3) 等离子体的密度、比热、速度、黏度、热导率、电导率、双极扩散系数、净辐射系数、气体粒子数密度分布等热力学参数和输运系数都仅为温度的函数；

4) 忽略重力和黏性耗散；

5) 由于等离子体温度高，对应的声速也高，使得当地流动马赫数并不高，非特别说明时等离子体流动是远低于声速的，视为不可压缩流动，可忽略压力功；

以上假设可以将耦合模型中控制方程的诸多项进行简化，并能够合理地选择需要的变物性函数关系。

2.2 控制方程

本文计算模型以自由燃烧电弧为基础，使用定常、二维轴对称条件，通过对纳维-斯托克斯方程组、Maxwell方程组各项进行增减，并补充近电极区的电导率修正以及电极表面热源，得到以下耦合电极的磁流体动力学方程组(MHD)。

(1) 纳维-斯托克斯方程组

$ \frac{\partial }{{\partial z}}\left( {\rho {v_{\rm{z}}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho {v_{\rm{r}}}} \right) = 0 $

(1)

$ \frac{\partial }{{\partial z}}\left( {\rho {v_{\rm{r}}}{v_{\rm{z}}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho v_{\rm{r}}^2} \right) = \\- \frac{{\partial p}}{{\partial r}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {2r\mu \frac{{\partial {v_{\rm{r}}}}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left[ {\mu \left( {\frac{{\partial {v_{\rm{z}}}}}{{\partial r}} + \frac{{\partial {v_{\rm{r}}}}}{{\partial z}}} \right)} \right] - 2\mu \frac{{{v_{\rm{r}}}}}{{{r^2}}} - {j_{\rm{r}}}{B_{\rm{ \mathsf{ θ} }}} $

(2)

$ \frac{\partial }{{\partial z}}\left( {\rho v_{\rm{z}}^2} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho {v_{\rm{r}}}{v_{\rm{z}}}} \right) = - \frac{{\partial p}}{{\partial z}} + \frac{\partial }{{\partial z}}\left( {2\mu \frac{{\partial {v_{\rm{z}}}}}{{\partial z}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r\mu \left( {\frac{{\partial {v_{\rm{z}}}}}{{\partial r}} + \frac{{\partial {v_{\rm{r}}}}}{{\partial z}}} \right)} \right] + {j_{\rm{r}}}{B_{\rm{ \mathsf{ θ} }}} $

(3)

$ \frac{\partial }{{\partial z}}\left( {\rho {v_{\rm{z}}}{c_{\rm{p}}}T} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho {v_{\rm{r}}}{c_{\rm{p}}}T} \right) = \frac{\partial }{{\partial z}}\left( {k\frac{{\partial T}}{{\partial z}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {rk\frac{{\partial T}}{{\partial r}}} \right) - 4\pi {\varepsilon _{\rm{N}}} + \\\frac{{j_{\rm{r}}^2 + j_{\rm{z}}^2}}{\sigma } + \frac{5}{2}\frac{{{k_{\rm{B}}}}}{e}\left( {\frac{{{j_{\rm{z}}}}}{{{C_{\rm{p}}}}}\frac{{\partial h}}{{\partial z}} + \frac{{{j_{\rm{r}}}}}{{{C_{\rm{p}}}}}\frac{{\partial h}}{{\partial r}}} \right) $

(4)

式中v_z、v_r分别为速度的轴向与径向分量；B_θ为磁感应强度的周向分量；j_z、j_r分别为电流的轴向与径向分量；T为温度；k_e为工质气体的导热系数；c_p为定压比热；σ为电导率；ε_N为净辐射系数；k_B为玻尔茲曼常数；e为电子电荷。物理量单位均使用国际单位制。

式(2)、(3)为动量方程，添加了洛仑兹力项，以实现磁场中带电粒子受到洛仑兹力作用而产生的“箍缩”现象，这一现象发生在自由燃烧电弧中时，由于电弧受力向轴线方向压缩，导致电流流通面积变小，电流密度增大，其产生的焦耳热也会增大，因此不可忽略。而发生在非转移弧时，由于存在固壁约束，电流的流通面积在气流与洛仑兹力的共同作用下减少，此时洛仑兹力项可忽略。

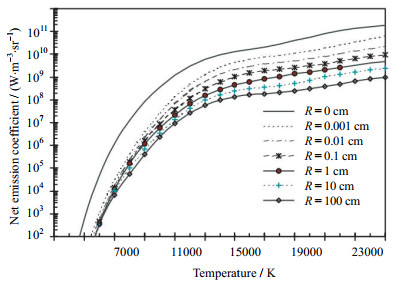
式(4)为能量方程，添加了热辐射项、焦耳热项、电子焓输运项，以满足等离子体的光学薄且辐射不可忽略、电流热效应以及碰撞支配能量传递的特殊性质。其中，由于等离子体主体温度高达10⁴数量级，热辐射在能量传递过程起着重要作用因而不可忽略。在弧柱中心区域呈现光学薄特性，发射率远大于吸收率，而到弧柱边缘区域温度降低，呈光学厚状态，辐射又被很快吸收，因此热辐射整体增加了等离子体能量传递过程。在本文模拟计算中，采用简化的辐射模型，即净辐射系数ε_N^[7-8]，其中纵坐标数值单位中的sr为球面度，如图 1可知^[9]，净辐射系数随着温度升高而升高，随等温球半径R增大而减小，其中R = 0对应光学薄状态，并且由MURPHY研究^[10]得到等温球半径R = 0.01 cm时可以吸收90%以上的辐射，本文也采用该数组。

(2) Maxwell方程组

$ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\sigma \frac{{\partial \varphi }}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {\sigma \frac{{\partial \varphi }}{{\partial z}}} \right) = 0 $

(5)

$ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {A_{\rm{z}}}}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\partial {A_{\rm{z}}}}}{{\partial z}}} \right) = - {\mu _0}{j_{\rm{z}}} $

(6)

$ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial A{\rm{r}}}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\partial {A_{\rm{r}}}}}{{\partial z}}} \right) = - {\mu _0}{j_{\rm{r}}} $

(7)

式(5)为电流连续方程，式(6)、(7)分别为径向和轴向的磁矢量势方程。其中，欧姆定律为${j_{\rm{z}}}{\rm{ = }} - \sigma \frac{{\partial \varphi }}{{\partial z}}$、${j_{\rm{r}}} = - \sigma \frac{{\partial \varphi }}{{\partial r}}$。式中，$\varphi $为电势。

磁矢量势与磁感应强度转化关系为

$ {B_{\rm{ \mathsf{ θ} }}} = \frac{{\partial {A_{\rm{r}}}}}{{\partial z}} - \frac{{\partial {A_{\rm{z}}}}}{{\partial r}} $

式中A_z、A_r分别为磁矢量势的轴向与径向分量。

(3) 近电极区修正

近电极区模型包含两部分内容，一是计算电子连续性方程得到空间中的电子数密度分布，从而修正电导率；二是增加电弧对电极表面的热效应。两部分协同作用，重新定性电极内部的温度分布。

根据LOWKE等^[11]研究，假设近电极区域的等离子体为电中性，则采用以下方程形式求解电子数密度：

$ \nabla \cdot \left( {{D_{\rm{A}}}\nabla {n_{\rm{e}}}} \right) = \gamma \left( {n_{\rm{e}}^2 - n_{{\rm{eq}}}^2} \right) $

(8)

其中$n_{\mathrm{e}}$为电子数密度，$D_{\mathrm{A}}$为双极扩散系数，$\gamma$为电子离子结合系数，$n_{\mathrm{cq}}$为局域热平衡下的电子数密度。电子离子结合系数$\gamma=1.1 \times 10^{-12} n_{\mathrm{e}} T^{-4.5} \mathrm{cm}^{3} \cdot \mathrm{s}^{-1}$，其中也包含有一项电子数密度$n_{\mathrm{e}}$，因此式(8)方程源项为非线性源项，在采用有限体积法求解前需要进行非线性化处理。除此之外，双极扩散系数${D_{\rm{A}}} = 2kT{\mu _i}/e$、局域热平衡电子数密度n_eq均可作为温度的单值函数。

得到电子数密度后，根据欧姆定律，在低温区域中，由于电离度很小，电导率本应也很低，然而本文模型中，低温区域位于电极表面，由于此处具有较大的电势梯度，即电场强度E，因此即便电离度低，其实际具有的电导率会大于热平衡状态下的电导率值，高温与低温区域的电导率分别为$j=-\sigma \nabla \varphi=\sigma E$、$j=n_{\mathrm{e}} e \mu_{\mathrm{e}} E$。

整合后可以得到

$ j = - {\sigma _{{\rm{eff}}}}\nabla \varphi = - \frac{{{n_{\rm{e}}}e}}{{{n_0}/\left( {{n_{\rm{T}}}{\mu _{\rm{e}}}} \right) + \left( {2e{n_{\rm{e}}}{n_{{\rm{eq}}}}} \right)/\left( {{n_{\rm{T}}}\sigma } \right)}}\nabla \varphi $

其中${\sigma _{{\rm{eff}}}}$为有效电导率，${{n_0}}$为中性粒子数密度，${{n_{\rm{T}}}}$为总粒子数，${{\mu _{\rm{e}}}}$为电子迁移率，$\sigma $为热平衡状态下的电导率。值得注意的是，除了电子迁移率${{\mu _{\rm{e}}}}$以外，粒子数密度等都可以看作温度的函数，而电子迁移率，根据其定义

$ {\mu _{\rm{e}}} = \frac{e}{{{m_{\rm{e}}}{\nu _{\rm{e}}}}} = \frac{e}{{{m_{\rm{e}}}{v_{{\rm{th}}}}\left( {{n_{\rm{i}}}A{Q_{{\rm{ei}}}} + {n_{\rm{a}}}B{Q_{{\rm{ea}}}}} \right)}} $

其中，${{m_{\rm{e}}}}$为电子质量，${{\nu _{\rm{e}}}}$为粒子碰撞频率，${{v_{{\rm{th}}}}}$为电子热运动速度，${{Q_{{\rm{ei}}}}}$为电子-离子碰撞截面，${{Q_{{\rm{ea}}}}}$为电子-原子碰撞截面，这些参数并没有温度函数关系，意味电子迁移率${\mu _{\rm{e}}}$需要用额外的方法去求解，本文使用了Bolsig程序^[12]求解玻尔兹曼方程得到了系列电子迁移率${\mu _{\rm{e}}}$，用来修正电导率。

除了宏观等离子体对电极的热传导、热辐射外，电弧的行为也影响到电极的能量传递过程。阴极的过程具体表现为阴极金属发射的电子具有一定的电子焓热，使阴极表面温度降低。同时阴极表面的电离层产生的离子，将会在较大的电场作用下向阴极表面运动从而带来一定的离子焓热，使阴极表面温度升高，除此之外还有本身的热辐射，几种因素共同作用，作为电极表面的额外能量输入。阳极的过程表现为电子运动到阳极表面释放焓热，存在热辐射，而没有离子焓。电极的面热源形式如下^[13]：

$ {F_{\rm{c}}} = - \left| {{j_e}} \right|{\phi _{\rm{c}}} + \left| {{j_{\rm{i}}}} \right|{V_{\rm{i}}} - \varepsilon \alpha {T^4} $

(9)

$ {F_a} = \left| {{j_e}} \right|{\phi _{\rm{c}}} - \varepsilon \alpha {T^4} $

(10)

其中，${{j_e}}$为近阴极区的电子电流，${\phi _{\rm{c}}}$为阴极的逸出功，${{j_{\rm{i}}}}$为近阴极区的离子电流，${V_{\rm{i}}}$为工质气体一次电离电势，$\varepsilon $为表面发射系数，$\alpha $为斯特藩-玻尔兹曼常数。

在具体计算中，由于离子电流无法提前得知，需要根据电流连续性条件，将阴极金属发射产生的热电子电流与弧柱区求解Maxwell方程组得到的电弧电流做比较，继而通过离子电流补全守恒关系。热电子发射方程(Richardson方程)为

$ \left| {{j_{\rm{R}}}} \right| = A{T^2}\exp \frac{{ - {\phi _{\rm{c}}}e}}{{{k_{\rm{B}}}T}} $

其中，$A$为热发射常数，${{k_{\rm{B}}}}$为玻尔兹曼常数。离子电流${{j_{\rm{r}}}}$计算方法为，当弧区电流大于发射电流时$\left( {{j_{\rm{n}}} > {j_{\rm{R}}}} \right), \quad {j_{\rm{e}}} = {j_{\rm{R}}}, \quad {j_{\rm{i}}} = {j_{\rm{n}}} - {j_{\rm{R}}}$；当弧区电流小于发射电流时$\left( {{j_{\rm{n}}} < {j_{\rm{R}}}} \right), \quad {j_{\rm{e}}} = {j_{\rm{n}}}, \quad {j_{\rm{i}}} = 0$。

但由于在Fluent软件中，无法进行面热源的设置，式(9)、(10)无法直接使用，因此采用另外一种，类似激光加热金属表面的处理方法^[14]对其进行等效转化，从而能够正常加载。

2.3 模型归纳

2.2节对该耦合模型的内容以及设置方法进行了描述，在此，为了方便与Fluent软件程序相接，将上述方程组归纳为统一的控制方程形式，即基本的NS方程形式。

$ \frac{{\partial (\rho \phi )}}{{\partial t}} + \nabla \cdot (\rho \vec u\phi ) = \nabla \cdot \left( {{\mathit{\Gamma }_\phi }\nabla \phi } \right) + {S_\phi } $

(11)

其中，${\vec u}$为速度矢量，$\phi $为自定义标量，${{\mathit{\Gamma }}_{\phi }}$为广义扩散系数，${{S}_{\phi }}$为广义源项。式(11)中各项依次是瞬态项、对流项、扩散项和源项，本文基于二维稳态假定，故瞬态项忽略，下面给出MHD方程组中各方程的形式归纳。

根据以上归纳，即可使用户自定主标量(user-defined scalar，UDS)定义新的控制方程，使用用户自定义函数(user-defined function，UDF)写入物性函数、边界条件等。

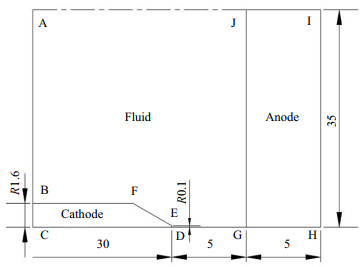
3 计算模型 3.1 模型划分及边界条件

本文采用二维轴对称模型，图 2为模型结构，为了显示阴极平台，图示已作适当放缩，取半径35 mm，长40 mm的计算域，其中包含阴极固体域、流体域、阳极固体域3个部分。阴极固体域主体半径1.6 mm，尖端平台为30度半锥角，平台半径为0.1 mm，材料为钍钨合金；流体域使用氩气工质气体；阳极固体域为大平板，材料为铜。由于本文只探究电极温度分布，对于温度超过金属熔点的情况不添加熔化-凝固模型，一律默认水冷材料，同时水冷材料不会影响电弧特性^[9]。

网格建立过程中，采取先疏后密，并不断调节亚松弛因子，每阶段计算收敛后，使用自适应网格，将温度梯度较大区域以及电弧主要分布区域网格加密，不断调整计算最终达到要求。

图 2中，阴极固体域为BCDF，BC为阴极冷壁面，DEFB为阴极-电弧共轭传热面，流体域为ABFEDGJA，阳极固体域为GHIJ，HIJ为阳极冷壁面，GJ为阳极-电弧共轭传热面，CDGH为对称轴，AB为氩气进口，AJ为氩气出口。具体边界条件见表 2，通量为0的项均使用Ω表示，$\Omega=\partial \phi / \partial \vec{n}=0$。

本文采用200 A弧电流，电流连续方程与磁矢量势方程在全计算域计算，电子连续方程只在流体域计算，使用的工质气热力学参数与输运参数分别来自MURPHY ^[15]与张晓宁^[16]。

所用程序使用Visual Studio2017编写，Fluent18.1求解，除了直接得到上述标量值，对计算域中总(分)电流值、焦耳热值、热辐射值、电场强度等黑箱值均单独分配存储空间UDM以便分析。

3.2 计算过程

该模型需要将电磁场与一般流场涉及到的物理模型耦合计算，需要使用Fluent软件的UDF与UDS功能，用以引入某些物性参数随温度变化的函数，并添加自定义标量电势$\ \varphi $、磁矢量势的轴向与径向分量${{A}_{\text{z}}}$、${{A}_{\text{r}}}$，以及电子数密度${{n}_{\text{e}}}$对应的标量方程。

通过上文对控制方程组的描述可以得知，除了电子连续方程较为特殊之外，其余方程求解中需要使用到的物性参数均与温度分布密切相关，因此从温度来设想一次迭代过程如下：由初始流场温度计算出局域热平衡电导率$\sigma $，同时得到当前温度下的双极扩散系数${{D}_{\text{A}}}$、局域热平衡电子数密度${{n}_{\text{eq}}}$用以求解式(8)电子连续方程，得到当前温度下的电子数密度${{n}_{\text{e}}}$，该温度下还可求解出${{\sigma }_{1}}$参与的电流连续方程得到电势，即得到电场强度分布，以上计算结果可以得到有效电导率${{\sigma }_{\text{eff}}}$，于是其他过程均以有效电导率${{\sigma }_{\text{eff}}}$为基础继续计算。可以发现，虽然电磁场与流场耦合计算，但是电子方程和以电势为基础的方程组的求解相对独立，温度作为影响因素仅对电导率的计算有影响，而电子方程的求解反过来又会影响电势方程的求解，所以在大的耦合模型下，这两个方程又作为另一对耦合形式出现。此外，各方程添加的源项，极易引起迭代计算的震荡或者发散，因此为了得到稳定且较为准确的物理场分布，一方面需要保证高质量的网格以及合理的亚松弛因子，另一方面各项参数采集以及形式变化需要经过仔细斟酌。

4 计算结果分析 4.1 速度-压力分布

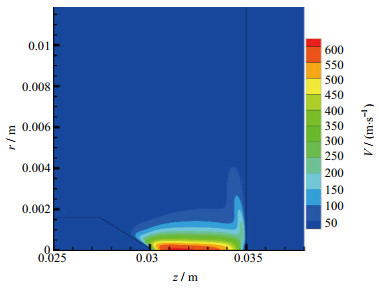
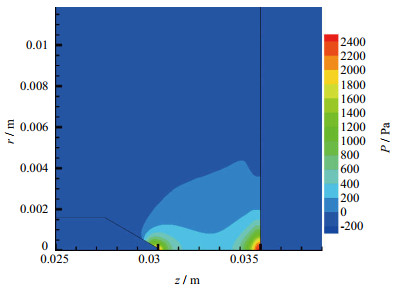
气体进口处速度较低，但由于阴极端部电流密度很大，工质气被迅速加热电离后，等离子体在洛仑兹力的作用下压缩，热量集中，从而使等离子体加速形成射流。如图 3、4，在阴极附近，即温度最高的区域形成了一个由于热膨胀造成的高压区与阳极轴线附近形成了动能-势能转化高压区。

4.2 温度分布

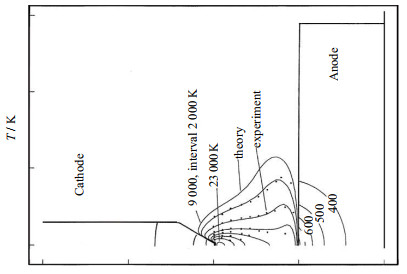
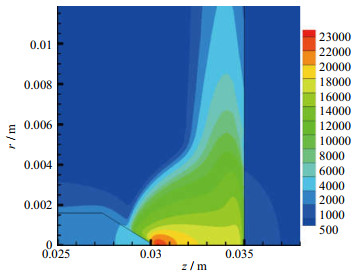
电极耦合模型的固体域温度分布是预估阴极寿命的重要依据，因此在自由燃烧电弧模型的基础上需要补充阴极金属发射电子对流体域电弧计算的影响，以及阴极弧根的形位对阴极表面的附近热源的影响。图 5中该模型计算得到流体域最高温度位于阴极尖端附近，约为23 150 K，阴极最高温度位于阴极尖端，约为4 000 K，阳极最高温度位于轴线附近，且呈近二次项分布，约为850 K。温度分布范围与图 6中前人研究结果基本一致。可以发现，在不采用电极水冷或添加剂熔融扩散的前提下^[13]，采用200 A电流强度势必会造成阴极的烧蚀。由于在计算过程中，气体逐渐电离，电极温度逐渐升高，可以设想，在此计算模型的基础上，如果采用非稳态模型计算，当阴极温度升高至熔点时所用计算时间即为电极的工作寿命，继而可以加入水冷与熔化-凝固模型对实际设备进行较为准确的设计优化，这也是本文的出发点。

4.3 电子数密度分布

此处的电子数密度为求解电子连续性方程得到，由于该标量方程涉及到的物性参数较多，数量级普遍较大，采集时存在一定误差，此处不再展示其余粒子数密度等分布图。

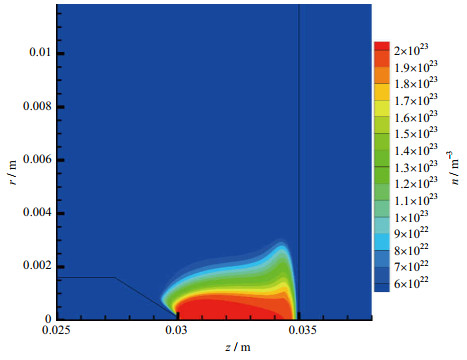
由图 7中计算结果可知，电子数密度分布规律与温度分布规律近似，并且16 000~23 000 K区域对应电子数密度最大的区域，这是因为一次电离的氩离子在14 000 K左右会发生二次电离，但在25 000 K以下由二次电离产生的电子数与一次电离提供的电子存在数量级的差别，直到高于25 000 K时，一次电离的氩原子数才会呈现明显下降。所以，虽然本文中计算温度最高达到了23 000 K，但是使用的粒子数相关物性仍采用一次电离数据，使用的氩气电离能也采用了一次电离能，计算电子数密度分布规律基本合理。

4.4 电势-电流密度分布

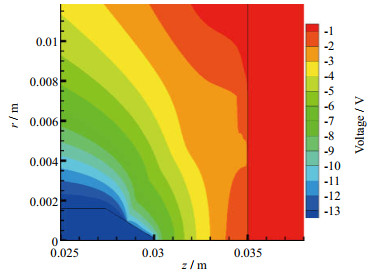
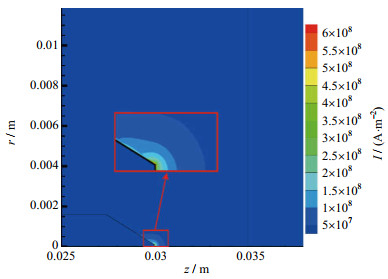
与电势、电流密切相关的参数是电导率，由以上计算得到的电子数密度对局域热平衡电导率进行修正，最终得到电势为13.6 V(图 8)，电流密度最大为7x10⁸ A×m^-2位于阴极尖端附近(图 9)。由于本文关于近阴极区的计算未包含鞘层的电位降计算，所以采用电势补偿的方法^[17]，由ZHOU等^[18]的研究，当电流为200 A大小时，鞘层内电势差约为11.7 V，则补偿后电势差为25.3 V，与实验测量值26 V较为接近。相较于一般电导率$\sigma $为温度的单调函数，有效电导率${{\sigma }_{\text{eff}}}$在修正过程中需要使用电子迁移率${{\mu }_{\text{e}}}$，这一参数在很大程度上与电场强度E大小相关。由电弧的结构可知，在近电极区的较小轴向距离内存在很高的电势差，这意味着该区域的场强较大，因此，场强分布非线性，导致除了气体完全未电离和完全电离两种情况外，修正后的电导率分布关于温度并不是单调关系，由此导致计算结果里电势的数值会低于一般自由燃烧电弧，而电弧主体温度值接近，其中差别最明显的就是在近阴极区的温度分布。

5 结论

针对耦合电极的直流等离子体进行了二维轴对称数值模拟。主要结论如下：

1) 速度-压力变化关系与一般自由燃烧电弧相似，速度高值位于电弧中心，压力高值位于电弧两端；

2) 流体域的温度-电子数密度分布规律基本一致，符合氩气正常电离过程的数量变化规律；固体域温度结果合理，可以近似预测电极寿命；

3) 提出了针对Fluent软件功能的计算模型，以及在实验数据缺乏下的近似处理方法。