气隙式膜蒸馏(air gap membrane distillation, AGMD)能够明显降低分离过程中因热传导而损失的热量、可分离高盐浓度料液、可利用低温热源、且具有膜不易污染等优点[1]。但是目前该技术存在渗透通量低[2]等问题,从而限制了其工业应用。增大料液的扰动程度、强化传质过程、提高渗透通量是解决该问题的常见方法之一。研究表明,在膜蒸馏过程中引入气体可有效提高渗透通量,因此可认为气液两相流技术能够用于强化膜蒸馏过程[3-6]。
但是,由于两相间的相互作用伴随着相间的动量传递、热量传递与质量传递过程,故定量分析两相流问题的难度较大[7]。而随着计算流体动力学(CFD)的不断发展,通过计算机建模分析液相中气泡等“细”观物质的运动现象、探索多相间的相互作用规律已被证明是一种分析该问题十分有效的方法,如FLUENT、ANSYS等成熟的商业软件已被广泛应用于该研究领域。TAHA等[8]在超滤(UF)过程中以间歇鼓泡的方式形成气液两相流,通过控制鼓泡频率及气体流量的方法保持塞状流型(slug flow),使渗透通量明显增加;在此基础上,此文应用FLUENT软件,结合VOF (volume of fluid)模型完成了对该强化传质过程的量化计算及分析。Ndinisa等[9]应用CFX软件对膜管中以层流方式流动的气液两相流进行分析,分别采用VOF模型、两相流欧拉(two fluid Eulerian)模型和二者相结合的方法研究有、无流体透过膜孔两种情况下泰勒气泡与料液间的相互作用,总结出应用不同模型分析此类问题的优势与劣势。GUPTA等[10]应用FLUENT软件对水平微通道中的泰勒气泡进行模拟,重点研究气泡周围薄层液膜的运动形态,分析气泡形态对其周围薄层液膜的影响。SMITH等[11]在中空纤维膜超滤过程中引入气体,结合实验探讨操作条件对气泡形态及运动的影响,并利用CFD模拟方法分析塞状气泡的运动性质,认为利用该方法可计算出宏观实验无法获得的重要参数,也为深入理解中空纤维膜中塞状气泡的运动规律提供了依据。由上可知,CFD模拟方法适用于分析气液相间的作用规律,可用于计算通过宏观实验无法测定的剪应力、相对速度等参数,可辅助两相流强化机理的分析过程。
目前,两相流强化膜蒸馏过程的机理研究并不完善,从流型角度分析两相间相互作用的研究报道相对较少,因此探讨两相流参数(如流型、气含率等)对强化效果的影响,对进一步提高渗透通量、完善两相流强化传质机理十分必要。本文以膜蒸馏海水淡化为研究背景,针对气隙式膜蒸馏过程渗透通量低的问题,通过将氮气引入实验体系的方法进行气液两相流强化传质实验,并结合CFD技术对强化过程进行模拟研究。本文利用FLUNET6.3软件的VOF模型,计算出通气强化后的瞬态局部膜壁剪应力、膜管内气液相的分布形式、速度分布与湍流强度,定性分析气相对料液的扰动作用,探讨两相流强化效果,为进一步探究两相流强化传质机理提供依据。
2 实验条件与模拟参数 2.1 实验条件利用课题组前期研究结果[12],实验操作参数确定为:NaCl溶液浓度35 g·L-1(wNaCl = 3.5%)、入口温度60 ℃、流量40 L·h-1,冷却水入口温度20 ℃、流量120 L·h-1,N2流量10~80 L·h-1。自制的管状煤基炭膜参数见表 1。仪器设备参数、实验装置及流程与课题组前期研究内容相同[12]。
|
|
表 1 膜参数 Table 1 Parameters of the membrane used in the study |
膜的分离性能常用渗透通量与截留率表示。课题组前期研究结果[13]表明,在本文的实验参数及装置条件下,系统连续运行10 h过程中对NaCl的截留率均超过99%,说明本文的分离体系脱盐效果较好。故此处的分离性能只考察渗透通量(J),其计算式如下:
| $J = \frac{m}{{A \times t}}$ | (1) |
根据实验流体情况设定模拟所需的物性参数,见表 2。
|
|
表 2 流体物性参数 Table 2 Physical properties of fluids |
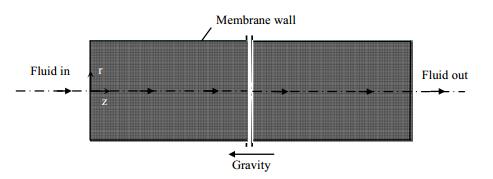
图 1为利用GAMBIT 2.4软件建立的膜管内部二维物理模型与结构化网格划分示意图。在气含率为0.2条件下进行网格无关性检验,结果如表 3所示。结果表明当网格尺寸小于0.19 mm ×0.05 mm时,模拟出的出口温度、平均剪应力、平均湍流强度值差异不大(< ±5%)。因此,确定出较为适宜的网格尺寸为0.19 mm×0.05 mm,此条件下对应的计算域网格总数为54 000。在此基础上,选择FLUENT 6.3软件中的VOF模型、k-ε湍流模型,采用QUICK格式对控制方程进行离散化处理,使用压力耦合方程组的半隐式方法(SIMPLE算法)求解离散后的方程组,设置计算收敛残差值为10-5。
|
图 1 CFD模拟膜管二维物理模型与结构化网格划分示意图 Fig.1 CFD simulation of two dimensional tubular membrane geometry with structured mesh |
|
|
表 3 网格无关性检验 Table 3 Grid independence check |
在VOF模型中,不同的流体组分共用着一套动量、热量方程,因此需要根据引进的相体积分数变量(第q相流体体积分数为
(1) 体积分数方程(连续性方程)
| $\frac{{\partial \alpha_{\text{q}}}}{{\partial t}} + \overrightarrow v \cdot \nabla \alpha_{\text{q}} = \frac{{S\alpha_{\text{q}}}}{{\rho_{\text{q}}}}$ | (2) |
其中:
对本文的两相系统,体积分数的计算基如下约束:
| $\sum\limits_{q{\text{ = }}1}^2 {\alpha_{\text{q}}} {\text{ = }}1$ | (3) |
(2) 动量方程
求解整个区域内单一的动量方程,可得到由各相共享的速度场。动量方程取决于所有相的容积比率,方程如下:
| $\frac{\partial }{{\partial {\text{t}}}}\left( {\rho \overrightarrow v } \right) + \nabla \cdot \left( {\rho \overrightarrow v \overrightarrow v } \right) = - \nabla p + \nabla \cdot \left[ {\mu \left( {\nabla \overrightarrow v + \nabla {{\overrightarrow v }^{\text{T}}}} \right)} \right] + \rho \overrightarrow g + \overrightarrow F $ | (4) |
其中:F为自定义源项,式(4)中该项为零。
对本文的两相系统,式(4)的容积比率平均密度与黏度分别采用如下形式:
| $\rho {\text{ = }}\sum\limits_{q = 1}^2 {\alpha_{\text{q}}\rho_{\text{q}}} $ | (5) |
| $\mu {\text{ = }}\sum\limits_{q = 1}^2 {\alpha_{\text{q}}\mu_{\text{q}}} $ | (6) |
(3) 能量方程
能量方程在各相中也是共享的,表示如下:
| $\frac{\partial }{{\partial t}}\left( {\rho E} \right) + \nabla \cdot \left[ {\overrightarrow v \left( {\rho E + p} \right)} \right] = \nabla \cdot \left( {k_{\text{eff}}\nabla T} \right) + S_{\text{h}}$ | (7) |
其中:keff为有效热导率;Sh为热源项,式(7)中该项为零;E为总能量。
对本文的两相系统,式(7)的能量E与温度T均采用质量平均值,分别表示如下:
| $E = \frac{{\sum\limits_{q = 1}^n {\alpha_{\text{q}}\rho_{\text{q}}E_{\text{q}}} }}{{\sum\limits_{q = 1}^n {\alpha_{\text{q}}\rho_{\text{q}}} }}$ | (8) |
| $T = \frac{{\sum\limits_{q = 1}^2 {\alpha_{\text{q}}\rho_{\text{q}}T_{\text{q}}} }}{{\sum\limits_{q = 1}^2 {\alpha_{\text{q}}\rho_{\text{q}}} }}$ | (9) |
式(7)的有效热导率keff采用如下形式:
| $k{\text{eff = }}\sum\limits_{q = 1}^2 {\alpha_{\text{q}}k_{\text{q}}} $ | (10) |
根据图 1,建立如下柱坐标体系的边界条件。
(1) 入口边界条件
当z = 0 mm、-2.5 mm < r < 2.5 mm时,定义为抛物线形入口速度分布形式:
| $u_{\text{r }} ={u_{\max }} \cdot [{\text{1}} - {{\text{(}}\frac{r}{R}{\text{)}}^{\text{2}}}{\text{]}}$ | (11) |
其中,根据实验条件取管中心料液的流速
(2) 出口边界条件
当z = 100 mm、-2.5 mm < r < 2.5 mm时,定义出口压力为常压(0.1 MPa)。
(3) 壁面边界条件
当0 mm < z < 100 mm、r = 2. 5 mm或r =-2.5 mm时,定义壁面流速为0。
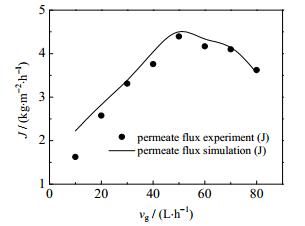
3 结果与讨论 3.1 模拟可靠性验证实验条件下,将不同流量N2通入膜管后得到的渗透通量实验值与模拟值对比结果见图 2。图中渗透通量的模拟值是采用出口温度模拟值,通过对膜管内部进行热量衡算而得,计算式如(12)所示。由图可以发现,二者吻合较好;渗透通量随N2流量的增大先增大后减小;N2流量为50 L·h-1时,渗透通量达到实验条件下的最大值(4.4 kg·m-2·h-1)。
| $J = \frac{{{N_{\rm{L}}} \cdot ({H_{{\rm{L,i}}}} - {H_{{\rm{L,o}}}}) + {N_{\rm{G}}} \cdot ({H_{{\rm{G,i}}}} - {H_{{\rm{G,o}}}})}}{{{H_{{\rm{vap}}}} - {H_{{\rm{L,o}}}}}}$ | (12) |
|
图 2 N2流量对渗透通量的影响及模型验证 Fig.2 Effects of N2 flow on permeation flux and model validation |
其中,下标L、G、vap、i、o分别为溶液、气体、水蒸气、进口、出口;N表示单位膜面积的流体质量流量,kg·m-2·h-1;H表示焓,kJ·kg-1。
图 3为高速摄像仪拍摄的气液两相流型照片与不同气体流量条件下瞬态流型模拟结果。可以发现,实拍照片与模拟结果相对应;随着N2流量增大,流型依次经历了泡状流(10~30 L·h-1)、塞状流(40 L·h-1)、团状流(50 L·h-1)、乳沫流(60~70 L·h-1)与环状流(80 L·h-1),该发展规律与相关文献研究结果[16-18]一致。当N2流量小于40 L·h-1时,流量增大导致气泡体积变大,由此可加剧对料液的扰动程度,使液体分子间相互作用增强,促进传质过程,进而使渗透通量增大;当N2流量为40 L·h-1时,管内气液两相流型为塞状流,此时管内既有体积较大的塞状气泡也有流速较大的小气泡,故对原有料液的扰动程度大于单一泡状流的情况,因而可继续强化传质过程使渗透通量增大。当N2流量为50 L·h-1时,对应团状流,该流型与塞状流类似,但气团分布形式更加紧凑,气团间小气泡数量明显增多,故对料液的扰动程度最大,渗透通量可达到最大值。当N2流量大于50 L·h-1时,随着流量增大,管内流体的流动形式依次经历了乳沫流与环状流,通入的气体对料液的扰动程度相对团状流时减弱,对传质过程的强化作用变小,故渗透通量相对团状流时有所降低。综上,本文采用的模拟方法与计算结果可靠。

|
图 3 N2流量对瞬态两相流型的影响及模型验证
Fig.3 Effects of N2 flow on two-phase flow pattern and model validation
(a) 10 L·h-1 (b) 20 L·h-1 (c) 30 L·h-1 (d) 40 L·h-1
(e) 50 L·h-1 (f) 60 L·h-1 (g) 70 L·h-1 (h) 80 L·h-1
 photo photo  simulated flow pattern (red/light-gas phase; blue/dark-liquid simulated flow pattern (red/light-gas phase; blue/dark-liquid
|
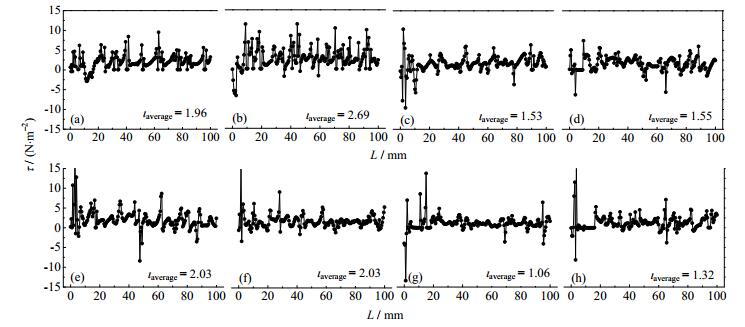
图 4为不同气含率条件下瞬态膜壁剪应力(流体施加于膜壁的应力)分布模拟结果,图中横坐标表示膜管内部距离溶液入口的长度。图 5为相同实验条件下无气体强化过程的膜壁剪应力模拟结果。对比可知,经两相流强化后的膜壁剪应力明显大于无强化过程,并且前者的剪应力分布规律与后者有显著区别。在两相流强化过程中,因存在气体的扰动作用,膜壁剪应力的大小与方向(剪应力值的正、负值代表相反方向)均会沿流动方向发生变化;而在无强化过程中,膜壁剪应力仅在溶液入口附近受流动边界层发展的影响,先迅速减小最终趋于一个稳定值,其方向保持不变(剪应力值恒为正值),符合传统传递过程膜壁剪应力的发展规律。
|
图 4 气含率对瞬态膜壁剪应力的影响 Fig.4 Effects of gas holdup on membrane wall shear stress (a) 0.20 (b) 0.33 (c) 0.43 (d) 0.50 (e) 0.56 (f) 0.60 (g) 0.64 (h) 0.67 |

|
图 5 无气体强化过程的膜壁剪应力 Fig.5 Profile of membrane wall shear stress under no-enhancement process |
由图 4还可看出,当气含率变化时,膜管相同位置处的膜壁剪应力大小略有差异,但大多集中在0~5 N·m-2范围内,平均值约为1.77 N·m-2,普遍大于无气体强化过程的膜壁剪应力(约0.015 N·m-2),故可认为两相流技术能够有效增大膜蒸馏过程的膜壁剪应力。此外,两相流强化过程膜壁剪应力的大小与方向会发生变化,该规律与文献[19-20]结果一致。此现象是由于气相引入膜管后形成的气泡(或气团等)形状并不规整且在流动过程中容易变形,而溶液与气泡(或气团等)不同部位接触的过程中所受到的扰动作用会有差异,故膜壁剪应力的大小会发生变化;同时由于气泡(或气团等)在膜管内移动过程中还存在随机的脉动现象,因此气泡施加于溶液作用力的方向并不固定,导致膜壁剪应力的方向会发生变化。无论是膜壁剪应力较大还是其方向发生变化,流体对膜壁的冲刷作用均会增强,因此可在一定程度上降低膜污染程度,减弱因浓度极化现象而导致的分离效果变差的趋势,有助于延长分离膜的使用时间,强化膜蒸馏传质过程、提高渗透通量。
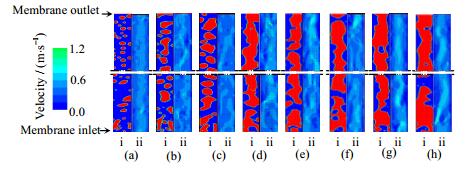
3.3 两相流强化对流型、流速及湍流强度的影响图 6为不同气含率条件下瞬态气液两相流型及流速模拟结果。由图可知,当气含率小于0.50时对应泡状流,且随着气含率增大,体积变大的气泡可增强对料液的扰动作用,进而使气液两相混合得更加均匀、增大整体流速、强化传质效果;当气含率等于0.50时,对应塞状流,膜管内既存在体积较大的塞状气泡也存在小气泡,气泡群对料液的扰动作用继续增强、整体流速变大;当气含率等于0.56时,对应团状流,膜管中心以团状气泡为主,周围也存在少量小气泡,气泡群对料液的扰动作用继续增强、整体流速明显变大;当气含率大于0.56时,对应乳沫流与环状流,随着气含率增大,流速较大的气相由占据膜管中心位置逐渐发展至整个膜管空间,液相仅能沿着膜壁附近的狭小空间以相对较低的流速移动,气相与液相的速度差变大并各自发展至连续流动状态,两相间出现较为明显且稳定的相界面,故气相对液相的扰动作用减弱,两相流强化效果相对团状流时变小。
|
图 6 气含率对瞬态流型及速度分布的影响
Fig.6 Effects of gas holdup on flow pattern and velocity
Gas holdup: (a) 0.20 (b) 0.33 (c) 0.43 (d) 0.50 (e) 0.56 (f) 0.60 (g) 0.64 (h) 0.67 ⅰ. Transient flow pattern (red/light-gas phase; blue/dark-liquid phase) ⅱ. Velocity |
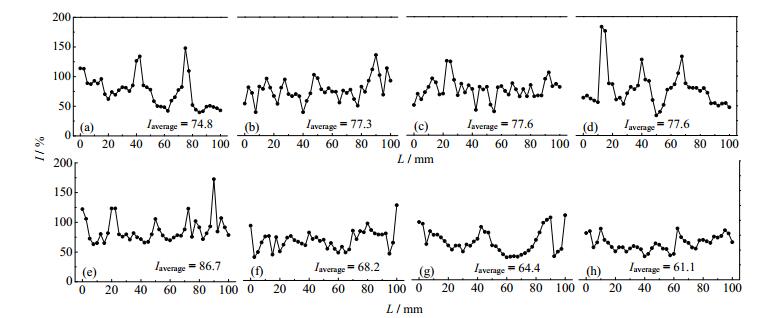
图 7为不同气含率条件下局部湍流强度(I)的模拟结果,图中横坐标表示膜管内部距离溶液入口的长度。由图可知,通气强化后因存在气体的扰动作用,膜管内流体的瞬态湍流强度沿流动方向不断发生变。当气含率不大于0.56时,随着气含率增大,瞬态湍流强度变大(74.8%~86.7%),说明湍流脉动程度增大;而当气含率大于0.56时,瞬态湍流强度随气含率增大而减少(86.7%~61.1%),表示湍流脉动程度降低。该变化规律与不同气含率条件下膜蒸馏渗透通量的变化规律一致,表明通气强化可通过增大膜管内流体的脉动程度,强化传递过程,提高渗透液产量。
|
图 7 气含率对瞬态湍流强度的影响 Fig.7 Effects of gas holdup on turbulence intensity (a) 0.20 (b) 0.33 (c) 0.43 (d) 0.50 (e) 0.56 (f) 0.60 (g) 0.64 (h) 0.67 |
对气隙式膜蒸馏氯化钠水溶液的两相流强化过程进行实验与模拟研究,探讨两相流强化传质机理,得到以下结论:
(1) 当进料流量为40 L·h-1、氮气流量为50 L·h-1时,对应团状流,此时气相对液相的强化传质效果最好,水渗透通量可达到4.4 kg·m-2·h-1。
(2) 两相流强化过程的平均膜壁剪应力(1.77 N·m-2)明显大于无强化过程(约0.015 N·m-2);前者的大小与方向均会沿流动方向发生变化,而后者先迅速减小最终趋于一个稳定值、方向保持不变;两相流强化过程变化的膜壁剪应力可强化膜壁附近流体的扰动作用、提高渗透通量,也可在一定程度上降低膜污染、浓度极化程度,有助于延长分离膜的使用时间;气含率不大于0.56(泡状流、塞状流与团状流)时,随着气含率增大,气泡群对溶液的扰动作用增强、湍流强度增大、气液相混合更加均匀、整体流速变大、传质效果变好;气含率大于0.56(乳沫流与环状流)时,两相间出现较为明显且稳定的界面,气相对液相的扰动作用减弱,湍流强度减弱、两相流强化效果相对变差。
(3) 利用CFD模拟方法可得到膜壁剪应力、气液两相流型、速度分布与湍流强度规律,模拟结果可用于定性分析两相流强化膜蒸馏过程中气相对液相的扰动情况、两相间的相互作用等,在此基础上可进一步探讨两相流强化传质机理。
符号说明:
|
|
| [1] |
BAGHBANZADEH M, RANA D, LAN C Q. Zero thermal input membrane distillation, a zero-waste and sustainable solution for freshwater shortage[J]. Applied Energy, 2017, 187: 910-928. DOI:10.1016/j.apenergy.2016.10.142 |
| [2] |
ALSAADI A S, FRANCIS L, MAAB H, et al. Evaluation of air gap membrane distillation process running under sub-atmospheric conditions: experimental and simulation studies[J]. Journal of Membrane Science, 2015, 489: 73-80. DOI:10.1016/j.memsci.2015.04.008 |
| [3] |
DING Z, LIU L, LIU Z, et al. The use of intermittent gas bubbling to control membrane fouling in concentrating TCM extract by membrane distillation[J]. Journal of Membrane Science, 2011, 372(1/2): 172-181. |
| [4] |
CHEN G, YANG X, LU Y, et al. Heat transfer intensification and scaling mitigation in bubbling-enhanced membrane distillation for brine concentration[J]. Journal of Membrane Science, 2014, 470: 60-69. DOI:10.1016/j.memsci.2014.07.017 |
| [5] |
WU C R, JIA Y, CHEN H Y, et al. Study on air-bubbling strengthened membrane distillation process[J]. Desalination and Water Treatment, 2011, 34(1/2/3): 2-5. |
| [6] |
WU C R, LI Z G, ZHANG J H, et al. Study on the heat and mass transfer in air-bubbling enhanced vacuum membrane distillation[J]. Desalination, 2015, 373: 16-26. DOI:10.1016/j.desal.2015.07.001 |
| [7] |
AZBEL D. Two-phase flows in chemical engineering[M]. Cambridge: Cambridge University Press, 1981.
|
| [8] |
TAHA T, CUI Z F. CFD modelling of gas-sparged ultrafiltration in tubular membranes[J]. Journal of Membrane Science, 2002, 210(1): 13-27. |
| [9] |
NDINISA N V, WILEY D E, FLETCHER D F. Computational fluid dynamics simulations of Taylor bubbles in tubular membranes model validation and application to laminar flow systems[J]. Chemical Engineering Research and Design, 2005, 83(A1): 40-49. |
| [10] |
GUPTA R, FLETCHER D F, HAYNES B S. On the CFD modelling of Taylor flow in microchannels[J]. Chemical Engineering Science, 2006, 64(12): 2941-2950. |
| [11] |
SMITH S, TAHA T, CUI Z F. Enhancing hollow fibre ultrafiltration using slug-flow-a hydrodynamic study[J]. Desalination, 2002, 146(1/2/3): 69-74. |
| [12] |
张金赫, 李花, 沈驭臣, 等. 膜蒸馏海水淡化过程中的两相流强化实验研究[J]. 高校化学工程学报, 2018, 32(1): 38-43. ZHANG J H, LI H, SHEN Y C, et al. Experimental investigation on two-phase flow enhancement of desalination processes via membrane distillation[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 38-43. |
| [13] |
沈驭臣.膜蒸馏海水淡化过程两相流强化与CFD模拟[D].大连: 大连理工大学, 2016. SHEN Y C. Two-phase flow enhancement and CFD simulation of membrane distillation process for seawater desalination[D]. Dalian: Dalian University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10141-1017823857.htm |
| [14] |
WU C, LI Z, ZHANG J, et al. Study on the heat and mass transfer in air-bubbling enhanced vacuum membrane distillation[J]. Desalination, 2015, 373: 16-26. DOI:10.1016/j.desal.2015.07.001 |
| [15] |
Fluent Inc. Fluent 6.3 user's guide[Z]. America: Fluent Inc, 2006.
|
| [16] |
WANG T, ZHANG Z G, REN X J, et al. Direct observation of single- and two-phase flows in spacer filled membrane modules[J]. Separation and Purification Technology, 2014, 125: 275-283. DOI:10.1016/j.seppur.2014.01.040 |
| [17] |
WIBISONO Y, CORNELISSEN E R, KEMPERMAN A J, et al. Two-phase flow in membrane processes: a technology with a future[J]. Journal of Membrane Science, 2014, 453: 566-602. DOI:10.1016/j.memsci.2013.10.072 |
| [18] |
CUI Z F, CHANG S, FANE A G. The use of gas bubbling to enhance membrane processes[J]. Journal of Membrane Science, 2003, 221(1/2): 1-35. |
| [19] |
SMITH S R, FIELD R W, CUI Z F. Predicting the performance of gas-sparged and non-gas-sparged ultrafiltration[J]. Desalination, 2006, 191(1/2/3): 376-385. |
| [20] |
TAHA T, CHEONG W L, FIELD R W, et al. Gas-sparged ultrafiltration using horizontal and inclined tubular membranes—A CFD study[J]. Journal of Membrane Science, 2006, 279(1/2): 487-494. |




