气泡在黏弹性流体中的运动现象在许多工业过程中普遍存在,如化工、食品、环境、高分子等[1]。在这些过程中,单气泡的运动速度对气液两相间的传递现象具有非常重要的影响[2]。与牛顿流体、幂律流体等其他流变特性的流体相比,气泡在黏弹性流体中的运动具有某些特殊的行为,例如,HASSAGER等[3]发现在黏弹性流体中上升的气泡尾部的流体的流动方式向下,即产生所谓的“负尾流”。LIU等[4]则发现,与其他流体相比,气泡在黏弹性流体中的形状呈倒泪滴形,具有一个尖尾。此外,在牛顿流体或其他类型的非牛顿流体中,气泡的速度往往与体积呈线性比例关系,气泡的速度随体积单调递增。但许多研究者发现,在黏弹性流体中,气泡存在着一个临界体积,在临界体积处,速度的递增不连续,突然发生了跃迁,换言之,在微小的气泡体积增加幅度下,速度则增加幅度很大[5-7]。气泡发生速度跃迁后,造成气泡在液相中的停留时间减小,影响气液两相的传质和传热过程,因此,对黏弹性流体中气泡速度的研究具有非常重要的意义。BELMONTE等[8]实验研究了气泡在黏弹性流体中的气泡速度跃迁现象,并将此现象归因于气泡尾部尖端的出现。HERRERA-VELARDE等[9]观察了气泡跃迁前后的流场变化,发现气泡跃迁后,在其尾部出现了负尾流。RODRIGUE等[10]则将气泡速度的跃迁归因于Marangoni效应和弹性效应间的不稳定平衡。近来,RODRIGO等[11]对Boger流体(黏度恒定的黏弹性流体)中的气泡运动进行了研究,同样发现气泡速度的跃迁伴随着其尾部尖端的形成。尽管上述学者对黏弹性流体中的气泡运动行为进行了大量的研究,但相关知识仍十分匮乏。因此,本文利用高速摄像机对黏弹性流体中单气泡上升过程进行了研究,探讨了气泡体积、流体的浓度和表面张力对气泡上升速度的影响,对气泡的速度跃迁的机理进行了初步的讨论,并给予实验数据,提出了一个包含气泡体积、流体流变性质和物理性质等因素的关联式,用于预测黏弹性流体中气泡速度发生跃迁的临界条件,实验范围内,关联式的预测值与实验值重现性较好。
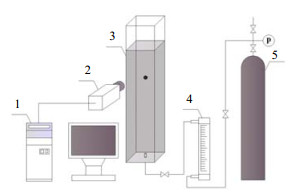
2 实验(装置与材料) 2.1 实验装置实验装置如图 1所示,主要由方形有机玻璃鼓泡塔、氮气瓶、管路系统以及数据采集系统组成。其中,鼓泡塔尺寸为0.15 m×0.15 m×1.5 m。氮气由氮气瓶经管路系统到达鼓泡塔底部的不锈钢喷嘴(内径:1 mm),在管路中通过转子流量计控制进气量,进而产生不同大小的气泡。气泡上升运动的图像由德国MV-GX1050高速摄像机采集,分辨率为500×1 728像素。摄像机位于喷嘴上方0.6 m处,在这个高度上,气泡的速度达到了稳定状态,高速摄像机的采样帧频为100 f·s-1,拍摄到的图片通过采集软件直接储存在计算机中,最终由Matlab处理得到形状、速度及体积等参数。在前期的研究中,已采用落球法验证了高速摄像机和Matlab处理方法的准确性:即利用高速摄像机采集不同尺寸的不锈钢小球在不同浓度的溶液中自由沉降的过程,采用Matlab处理得到钢球的体积,并与小球实际体积做比较,发现测量及图像处理的总误差在5%以内,说明图片采集和处理方法是可行的[12]。所有的实验均在室温及常压下进行。
|
图 1 实验装置示意图 Fig.1 Schematic diagram of the experimental setup 1. computer 2. camera 3. bubble column 2, 4. rotameter 5. nitrogen container |
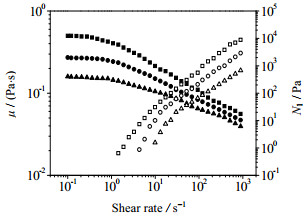
实验所用黏弹性流体为聚丙烯酰胺(PAA)水溶液(优级纯,Sigma),水为自制的双蒸水,氮气为高纯氮,纯度为99.999%,表面活性剂为十二烷基硫酸钠(SDS),表面活性剂浓度分别为0、5、10 mg·L-1。实验中PAA溶液的浓度分别为:w = 0.5%、1.0%和1.5 %。表面张力由表面张力仪(DCAT21, dataphysics, Austria)测定,精度为± 0.1 mN·m-1。流变性由可编程流变仪(Reologica, Instruments AB, 瑞典)测定,剪切速率为0.1~1 000 s-1,测定结果如图 2所示。由图 2可以看出实验所用PAA水溶液具有明显的剪切变稀性,表观黏度随剪切速率的变化由幂律模型表示:
|
图 2 黏度(实心符号)及第一法向应力(空心符号)随剪切速率的变化 Fig.2 Profiles of viscosity μ (solid symbols) and first normal stress difference N1 (empty symbols) under different shear rates ▲△ w(PAA)-0.5% ●○ w(PAA)-1.0% ■ □ w(PAA)-1.5% |
| $ \mu = K{\dot \gamma ^n} $ | (1) |
式中K、n为表征流体剪切变稀性的参数。PAA溶液具有黏弹性,第一法向应力差N1随剪切速率
| $ {N_1} = A{\dot \gamma ^b} $ | (2) |
式中A、b为表征流体黏弹性的参数。拟合得到的系数K、n、A、b见表 1。
|
|
表 1 实验流体的流变性质及物理性质 Table 1 Rheological and physical properties of the experimental liquids |
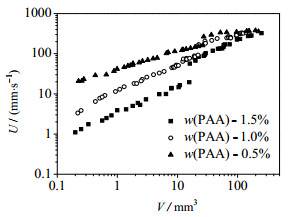
图 3表示PAA溶液浓度对气泡终端速度及跃迁变化的影响,终端速度是指气泡达到稳定运动状态下的最终速度,由于气泡的运动图像的采集点位于喷嘴上方0.6 m处,根据黄程蓉等[13]的研究,这个距离足以保证气泡达到稳定上升状态。由图 3可知,相同尺寸下的气泡最终上升速度随着PAA溶液浓度的增大而减小。气泡终端速度发生跃迁时的气泡体积通常被称为临界体积,用Vc表示。由于非常精确地观察到气泡恰好发生跃迁十分困难,本实验将Vc定义为气泡发生速度跃迁前后的体积平均值。由图 3可以看出,随着PAA溶液浓度的降低,Vc逐渐增大,表明随着黏弹性的降低,气泡速度跃迁的发生越来越困难。此外,为考察PAA溶液浓度对气泡跃迁程度的大小的影响,以跃迁前后速度的差值与跃迁前速度之比表征气泡跃迁幅度F,其计算表达式为:
|
图 3 PAA溶液浓度对气泡上升速度和跃迁速度的影响 Fig.3 Effects of PAA concentrations on velocity and velocity transition discontinuity |
| $ F = \left( {{U_{\rm{a}}} - {U_{\rm{b}}}} \right)/{U_{\rm{b}}} $ | (3) |
其中F为气泡跃迁幅度,Ua和Ub分别为气泡跃迁后和跃迁前的速度。由图 3发现,在未添加表面活性剂时,气泡跃迁幅度随着PAA溶液浓度的增大而增大,当PAA浓度为0.5%时,F为0.64,当PAA浓度为1.0%时,F为0.82,当PAA浓度为1.5%时,F为1.92,RODRIGUE等[14]也得到了类似的趋势。气泡在PAA溶液中的跃迁现象可能与流体本身的性质有关,由图 2可知,PAA溶液同时表现出黏性和弹性,由于弹性的存在,PAA溶液中的聚合物分子形变具有松弛特征,即随着时间的变化而变化。PAA溶液中的PAA分子相互之间缠绕连接,当由于流体的流动使高聚物被拉长时,其分子处于不平衡的构象,由于分子弹性的存在,不平衡的分子构象需逐步过渡到平衡的构象,也就是分子链不得不沿着外力的方向运动,从而产生了内部应力,随着时间的发展,聚合物分子逐渐恢复到卷曲的原状,由于流体运动产生的内应力逐渐耗散并消失[15]。气泡在黏弹性流体中上升时,带动气泡周围流体向上流动,使得聚合物沿运动方向被拉长,产生了作用于气泡表面的法向应力,当气泡较小时,气泡运动时间大于聚合物的松弛时间,法向应力很快的耗散掉,随着气泡的增大,气泡的运动速度以及聚合物的形变程度均随之增大,当气泡的运动时间小于聚合物的松弛时间时,气泡尾部的流体产生了应力残留,对气泡产生了一个向上挤压的力,使得气泡的速度突然增大,发生跃迁现象。
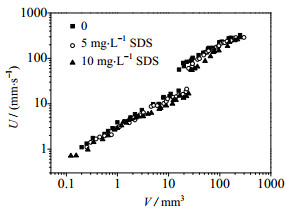
3.2 表面活性剂的影响图 4表示1.5%PAA溶液中表面活性剂SDS浓度对气泡速度的影响,由图可看出,与不含表面活性剂的PAA溶液相比,表面活性剂SDS的存在对气泡的终端速度具有明显的减少作用。但当气泡的体积较小时,3种不同的SDS浓度之间对气泡速度的影响并没有明显的差别,随着气泡体积的增大,SDS浓度对气泡速度影响开始显现,即气泡速度随SDS浓度的增大而降低,DEWSBURY[16]认为表面活性剂分子覆盖在气泡表面上,阻止了气泡表面的内环流,使气泡类似于固体小球,进而降低了气泡的速度。当气泡体积较小时,不同的SDS浓度下的表面活性剂分子均可覆盖满气泡界面,此时,SDS浓度对气泡速度的影响并没有明显的差别。随着气泡体积的增大,SDS浓度较低时,其分子开始不足以完全覆盖气泡表面,不同的SDS浓度对气泡速度影响开始显现。同时,由图 4还可发现,表面活性剂对气泡的跃迁速度有一定的影响,随着SDS浓度的增大,气泡发生跃迁时的临界体积Vc明显增大。根据作者前期的研究,在其他类型的流体中,表面活性剂分子的存在仅会造成气泡的速度降低,并未有跃迁现象发生[17],由此可知,表面活性剂仅会影响气泡的跃迁时的临界体积及跃迁幅度,并非气泡发生跃迁的主因。不同液相条件下的气泡临界体积,跃迁前速度、跃迁后速度以及跃迁幅度如表 2所示,由表 2可知,随着PAA溶液浓度的增大,气泡的临界体积逐渐减小,跃迁幅度则逐渐增大,随着SDS浓度的增大,气泡的临界体积逐渐增大,而跃迁幅度也逐渐增大。
|
图 4 表面活性剂浓度对w =1.5% PAA溶液中气泡速度的影响 Fig.4 Effects of SDS concentrations on velocity and velocity trasition discontinuity in w =1.5% PAA solution |
|
|
表 2 不同溶液中气泡运动参数实验测定值 Table 2 Parameters of bubble motion measured in different experimental liquids |
气泡的速度跃迁与其形状具有一定的关系。为气泡在发生跃迁前后的形状对比图,由图 5可知,当体积较小时,气泡呈球形(V = 0.25 mm3);随着体积的增大,气泡呈鸭蛋形(V = 6.08 mm3);随着体积的增大,气泡呈瓜子型,但气泡的上部为圆形,整体均为向外的凸面(V = 19.08 mm3);随着气泡体积的进一步增大,气泡开始发生速度的跃迁,此时气泡的尾部出现了尖端,且尖端两侧的界面向气泡内部凹进,即所谓的倒泪滴状,如当气泡体积为25.50 mm3时,气泡的尖端的两侧已经略微的向内凹进,随着气泡体积的继续增大,气泡的上半部开始变扁,尖端及其两侧的凹进更为明显(V = 66.14 mm3,V = 138.24 mm3)。因此,从上述可以发现,在气泡速度发生跃迁前后,气泡形状出现了两点不同,即尖端的尾部和尾部两侧的凹进。

|
图 5 w(PAA) = 1.0%溶液中气泡的形状 Fig.5 Bubble shapes in w(PAA) = 1.0% solution (critical volumn, Vc = 22.29 mm3) |
由上述的讨论可知,影响气泡跃迁的因素主要有气泡的体积,流体的流变性、黏弹性以及表面张力等。其中气泡发生跃迁时的体积以临界直径表征,其计算式如下:
| $ {d_{\rm{c}}} = \sqrt[3]{{{{6{V_{\rm{c}}}} / \pi }}} $ | (4) |
流体的流变性由稠度指数K和流动指数n表示;黏弹性由参数A和b表征。
通常,气泡在流体中的运动可由无量纲数表征,常用的无量纲数为Morton数(Mo)和Eötvös数(Eo),对于剪切变稀流体而言,由于Mo数和Eo数均与气泡直径有关,且随着气泡直径的变化而变化。临界速度Uc为气泡跃迁前后的速度平均值,因此,气泡恰好发生跃迁时的临界Eo数和临界Mo数如式(5)、(6):
| $ E{o_{\rm{c}}} = \frac{{{\rho _L}gd_{\rm{c}}^{\rm{2}}}}{\sigma } $ | (5) |
| $ M{o_{\rm{c}}} = \frac{{g{\mu ^4}}}{{{\rho _L}{\sigma ^3}}} $ | (6) |
Moc数包含流体的黏度,由图 2可知,PAA溶液的黏度随着剪切速率的增加而降低,即,
| $ M{o_{\rm{c}}} = \frac{g}{{{\rho _l}{\sigma ^3}}}{\left[ {K{{\left( {\frac{{{U_{\rm{c}}}}}{{{d_{\rm{c}}}}}} \right)}^{n - 1}}} \right]^4} $ | (7) |
由于气泡发生跃迁与流体的黏弹性直接相关,因此,为量化气泡发生跃迁情况,必须考虑流体黏弹性的影响,表征流体黏弹性的无量纲数为Deborah数(De),定义为材料的弛豫时间与运动过程时间的对比,其另一种形式为第一法向应力差与剪切应力之比[18],据此所得的临界的Deborah数(Dec)如下所示:
| $ D{e_{\rm{c}}} = \frac{A}{K}{\left( {\frac{{{U_{\rm{c}}}}}{{{d_{\rm{c}}}}}} \right)^{b - n}} $ | (8) |
上述3个无量纲数群包括了影响气泡跃迁的几种因素,其相互规律可由下式表示:
| $ f\left( {E{o_{\rm{c}}}, M{o_{\rm{c}}}, D{e_{\rm{c}}}} \right) = 0 $ | (9) |
利用MATLAB软件,通过多项式拟合回归分析,得到下面无量纲关系式:
| $ E{o_{\rm{c}}} = 1.24D{e_{\rm{c}}}^{0.03}M{o_{\rm{c}}}^{0.48} $ | (10) |
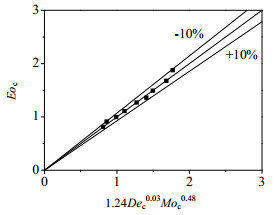
图 6为新关联式计算得到的Eoc值与实验值的对比图,图 6表明通过式(10)得到的计算值与实验值能够得到很好的重现。
|
图 6 实验测定值与式(10)的预测值的对比 Fig.6 Comparison of experimental and Eq. (10) calculated results |
(1) 黏弹性流体中,随着气泡体积的增大,气泡速度会在某个临界体积发生跃迁现象。
(2) 气泡速度发生跃迁时的临界体积随PAA溶液浓度的增大而减小,随SDS浓度的增大而增大,发生跃迁前后气泡的形状发生显著变化,跃迁后的气泡出现了尖端尾部。
(3) 提出了一个预测气泡跃迁的临界条件的经验关联式,实验范围内关联式的预测值与实验值吻合良好。研究结果对涉及到黏弹性流体中气液两相流动的工业过程的优化设计具有重要的指导意义。
|
|
| [1] |
CHHABRA R P. Bubbles, drops, and particles in non-Newtonian fluids[M]. 2nd ed. Boca Raton: Taylor & Francis Group Crc, Press, 2007.
|
| [2] |
SUH I S, SCHUMPE A, DECKWER W D, et al. Gas-liquid mass transfer in the bubble column with viscoelastic liquid[J]. Canadian Journal of Chemical Engineering, 2010, 69(2): 506-512. |
| [3] |
HASSAGER O. Negative wake behind bubbles in non-Newtonian liquids[J]. Nature, 1979, 279(5712): 402-403. DOI:10.1038/279402a0 |
| [4] |
LIU Y J, LIAO T Y, JOSEPH D D. A two-dimensional cusp at the trailing edge of an air bubble rising in a viscoelastic liquid[J]. Journal of Fluid Mechanics, 2006, 304: 321-342. |
| [5] |
FUNFSCHILLING D, LI H Z. Effects of the injection period on the rise velocity and shape of a bubble in a non-Newtonian fluid[J]. Chemical Engineering Research & Design, 2006, 84(10): 875-883. |
| [6] |
PILLAPAKKAM S B, SINGH P, BLACKMORE D, et al. Transient and steady state of a rising bubble in a viscoelastic fluid[J]. Journal of Fluid Mechanics, 2007, 589: 215-252. DOI:10.1017/S0022112007007628 |
| [7] |
ASTARITA G, APUZZO G. Motion of gas bubbles in non-Newtonian liquids[J]. AIChE Journal, 1965, 11(5): 815-820. DOI:10.1002/aic.690110514 |
| [8] |
BELMONTE A. Self-oscillations of a cusped bubble rising through a micellar solution[J]. Rheologica Acta, 2000, 39(6): 554-559. DOI:10.1007/s003970000098 |
| [9] |
HERRERA-VELARDE J R, ZENIT R, CHEHATA D, et al. The flow of non-Newtonian fluids around bubbles and its connection to the jump discontinuity[J]. Journal of Non-Newtonian Fluid Mechanics, 2003, 111(2/3): 199-209. |
| [10] |
RODRIGUE D, KEE D D, FONG C F C M. Bubble velocities:further developments on the jump discontinuity[J]. Journal of Non-Newtonian Fluid Mechanics, 1998, 79(1): 45-55. DOI:10.1016/S0377-0257(98)00072-X |
| [11] |
VÉLEZ-CORDERO J R, SÁMANO D, ZENIT R. Study of the properties of bubbly flows in Boger-type fluids[J]. Journal of Non-Newtonian Fluid Mechanics, 2012, 175/176: 1-9. DOI:10.1016/j.jnnfm.2012.03.008 |
| [12] |
范俊赓.屈服应力流体中单气泡运动行为的研究[D].沈阳: 沈阳航空航天大学, 2018. FAN J G. Study on motion behavior of single bubbles in yield-stress fluid[D]. Shenyang: Shenyang Aerospace University, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10143-1018012627.htm |
| [13] |
黄程蓉, 陈小鹏, 周丹, 等. 黏性溶液中单个气泡的运动形变[J]. 高校化学工程学报, 2018, 32(5): 1012-1018. HUANG C R, CHEN X P, ZHOU D, et al. Shape evolution of a single rising bubble in viscous solutions[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(5): 1012-1018. DOI:10.3969/j.issn.1003-9015.2018.05.004 |
| [14] |
RODRIGUE D, DE KEE D. Bubble velocity jump discontinuity in polyacrylamide solutions:A photographic study[J]. Rheologica Acta, 1999, 38(2): 177-182. DOI:10.1007/s003970050167 |
| [15] |
PILZ C, BRENN G. On the critical bubble volume at the rise velocity jump discontinuity in viscoelastic liquids[J]. Journal of Non-Newtonian Fluid Mechanics, 2007, 145(2/3): 124-138. |
| [16] |
DEWSBURY K, KARAMANEV D, MARGARITIS A. Hydrodynamic characteristics of free rise of light solid particles and gas bubbles in non-Newtonian liquids[J]. Chemical Engineering Science, 1999, 54(21): 4825-4830. DOI:10.1016/S0009-2509(99)00200-6 |
| [17] |
LI S, FAN J, XU S, et al. Effect of the surfactants on hydrodynamics characteristics of bubble in shear-thinning fluids at low Reynolds number[J]. Journal of Central South University, 2018, 25(3): 534-542. DOI:10.1007/s11771-018-3758-z |
| [18] |
LEIDER P J, BIRD R B. Squeezing flow between parallel disks. I. Theoretical analysis[J]. Industrial & Engineering Chemistry Fundamentals, 1974, 13(4): 336-341. |




