2. 中国科学院电工研究所,北京 100190;
3. 上海交通大学 内燃机研究所,上海 200240
2. Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China;
3. Institute of Internal Combustion Engine, Shanghai Jiaotong University, Shanghai 200240, China
燃油雾化好坏关系内燃机能否实现高效、清洁燃烧,而液体射流稳定性对射流的破碎雾化具有决定性作用,其研究对于内燃机燃烧技术的发展具有重要的理论意义和实际应用价值。
压力旋流喷嘴具有可靠性高、雾化效果好、所需泵端压力低等优点[1],已广泛应用于航空和船用发动机、燃气轮机及工业窑炉等喷射系统[2-3]。随着技术的不断发展,压力旋流喷嘴也逐渐用在内燃机,特别是汽油缸内直喷(GDI)发动机的燃油喷射中[4]。
在内燃机中,压力旋转喷嘴形成的圆环旋转黏性液体射流与环境存在温度差异。射流液体与周围环境气体间存在温差时,温度扰动的存在能导致液体射流界面稳定性发生变化。虽然作者已研究了黏性、表面张力、旋流强度等对圆环旋转黏性液体射流稳定性的影响[5-7],但并未考虑温度扰动的影响。
近年来,国内外一些学者采用射流线性稳定性分析方法,对存在温度扰动的液体射流稳定性问题进行了研究,分析非均匀液体温度、均匀环境温度、周期性变化环境温度等条件下的温度扰动对液体射流稳定性的影响,取得了重要研究成果[8-13]。研究表明,当射流表面存在温度扰动时,射流表面将产生热毛细力,进而产生Marangoni流动,从而对射流稳定性产生影响;另外,射流液体的黏性、导热率、比热容等物性参数不同时,温度扰动对射流稳定性的影响会发生变化。目前,采用射流稳定性方法对存在温度扰动的液体射流稳定性问题的研究,均是在比较简单的条件下进行,如存在温度扰动的二维平面液体射流或圆柱轴对称液体射流稳定性问题的研究等。存在温度扰动的压力旋流喷嘴或空气助力旋流喷嘴等形成的圆环旋转黏性液体射流稳定性问题的研究还未见报道。
本文采用射流稳定性方法对存在温度扰动的圆环旋转黏性液体射流稳定性问题进行研究。建立同时存在速度扰动、压力扰动以及温度扰动的圆环旋转黏性液体射流稳定性色散方程,并对色散方程进行空间模式下的数值求解。在此基础上分析存在温度扰动的圆环旋转黏性液体射流的稳定性,研究温度扰动强度对圆环旋转黏性液体射流稳定性的作用,以及射流液体热量传递特性对温度扰动与圆环旋转黏性液体射流稳定性作用的影响。
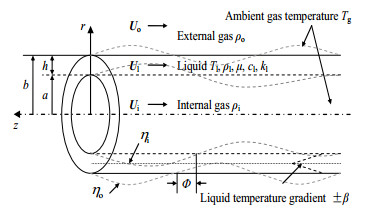
2 色散方程的建立本文讨论的圆环旋转黏性液体射流是具有两个自由液面的中空环状射流。图 1给出的是柱坐标系(r, θ, z)下圆环旋转黏性液体射流示意图。
|
图 1 圆环旋转黏性液体射流示意图 Fig.1 Schematic diagram of annular swirl viscous liquid sheet |
假定射流方向与z轴相反;气液流体均为不可压缩牛顿流体;圆环射流液体内半径为a,外半径为b,厚度为h;液体两侧相位差为Φ;射流液体动力黏度为μ,射流周围气体为无黏流体;气液界面处表面张力系数为σ;射流液体密度为ρl,圆环射流内部气体密度为ρi,外部气体密度为ρo;射流液体初始温度为Tl0,环形射流内外部气体具有相同温度Tg,液体内部具有双线性温度分布;液体射流旋转速度分布采用固体涡核型旋转速度分布Ar,A为液体旋转角速度,r为半径。
对射流控制方程组(N-S方程组)进行扰动,并对扰动后的射流控制方程组进行线性化和无量纲化处理,经过推导得到无量纲形式的线性化射流扰动控制方程:
| $\frac{{\partial v{'_{{\rm{l}}r}}}}{{\partial r}} + \frac{1}{r}v{'_{{\rm{l}}r}} + \frac{1}{r}\frac{{\partial v{'_{{\rm{l}}\theta }}}}{{{\partial _\theta }}} + \frac{{\partial v{'_{{\rm{l}}z}}}}{{\partial z}} = 0$ | (1) |
| $\frac{{\partial v{'_{{\rm{l}}r}}}}{{\partial t}} + E\frac{{\partial v{'_{{\rm{l}}r}}}}{{\partial \theta }} - \frac{{\partial v{'_{{\rm{l}}r}}}}{{\partial z}} - 2Ev{'_{{\rm{l}}\theta }} = - \frac{{\partial p{'_{\rm{l}}}}}{{\partial r}} + \frac{1}{{Re}}\left( {{\nabla ^2}v{'_{{\rm{l}}r}} - \frac{{v{'_{{\rm{l}}r}}}}{{{r^2}}} - \frac{2}{{{r^2}}}\left. {\frac{{\partial v{'_{{\rm{l}}\theta }}}}{{\partial \theta }}} \right)} \right.$ | (2) |
| $\frac{{\partial v{'_{{\rm{l}}\theta }}}}{{\partial t}} + E\frac{{\partial v{'_{{\rm{l}}\theta }}}}{{\partial \theta }} - \frac{{\partial v{'_{{\rm{l}}\theta }}}}{{\partial z}} - 2Ev{'_{{\rm{l}}r}} = - \frac{{\partial p{'_{\rm{l}}}}}{{\partial \theta }} + \frac{1}{{Re}}\left( {{\nabla ^2}v{'_{{\rm{l}}\theta }} - \frac{{v{'_{{\rm{l}}\theta }}}}{{{r^2}}} + \frac{2}{{{r^2}}}\left. {\frac{{\partial v{'_{{\rm{l}}r}}}}{{\partial \theta }}} \right)} \right.$ | (3) |
| $\frac{{\partial v{'_{{\rm{l}}z}}}}{{\partial t}} + E\frac{{\partial v{'_{{\rm{l}}z}}}}{{\partial \theta }} - \frac{{\partial v{'_{{\rm{l}}z}}}}{{\partial z}} = - \frac{{\partial p{'_{\rm{l}}}}}{{\partial z}} + \frac{1}{{Re}}{\nabla ^2}v{'_{{\rm{l}}z}}$ | (4) |
| $\frac{{\partial {T_1}^\prime }}{{\partial t}} + E\frac{{\partial {T_1}^\prime }}{{\partial \theta }} - \frac{{\partial {T_1}^\prime }}{{\partial z}} + Bu{'_{{\rm{l}}r}} = \frac{1}{{Pe}}{\nabla ^2}{T_1}^\prime \;\;\;\left( {{A_h} + \frac{1}{2} < r < {B_h}} \right)$ | (5) |
| $\frac{{\partial {T_1}^\prime }}{{\partial t}} + E\frac{{\partial {T_1}^\prime }}{{\partial \theta }} - \frac{{\partial {T_1}^\prime }}{{\partial z}} + Bu{'_{{\rm{l}}r}} = \frac{1}{{Pe}}{\nabla ^2}{T_1}^\prime \;\;\;\left( {{A_h} \le r \le {A_h} + \frac{1}{2}} \right)$ | (6) |
其中,$\overline {v_{_{\rm{j}}}'} $为无量纲扰动速度;$p_{\rm{j}}'$为无量纲扰动压力;Wj为射流内外部气体轴向速度与射流液体轴向速度比;Qj为气液密度比;δl = 1,δi = δo = 0。
| $\begin{array}{l} Re = \frac{{{\rho _{\rm{l}}}Uh}}{\mu }, \;{Q_{\rm{i}}} = \frac{{{\rho _{\rm{i}}}}}{\rho }, \;{Q_{\rm{o}}} = \frac{{{\rho _{\rm{o}}}}}{\rho }, \;E = \frac{{Ah}}{U}, \;{W_{\rm{i}}} = \frac{{{U_{\rm{i}}}}}{U}, \;\\ {W_{\rm{o}}} = \frac{{{U_{\rm{o}}}}}{U}, \;Pe = \frac{{{\rho _{\rm{l}}}{c_{\rm{l}}}Uh}}{{{\lambda _{\rm{l}}}}}, \;B = \frac{{\beta h}}{{{T_{{\rm{l}}0}}}}, \;{A_h} = \frac{a}{h}, \;{B_h} = \frac{b}{h}。\end{array} $ |
依据简正模态法,设无量纲扰动速度、扰动压力及扰动温度有如下形式的解[14]:
| $\begin{array}{*{35}{l}} {{{\bar{v}}}_{\text{j}}}^{\prime }={{{\hat{\bar{v}}}}_{\text{j}}}^{\prime }(r)\exp [\omega t+\text{i}(kz+m\theta )] \\ {{p}_{\text{j}}}^{\prime }={{{\hat{p}}}_{\text{j}}}^{\prime }(r)\exp [\omega t+\text{i}(kz+m\theta )] \\ {{T}_{\text{l}}}^{\prime }(r,\theta ,z,t)={{{\hat{T}}}_{\text{l}}}^{\prime }(r)\exp [\omega t+\text{i}(kz+m\theta )] \\ \end{array}$ | (7) |
其中,${{\hat{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}}'}}_{\text{j}}}\left(r \right)$、${\hat p'_{\rm{j}}}\left(r \right)$、${\hat T'_{\rm{l}}}\left(r \right)$分别为初始无量纲扰动矢量速度、压力及温度幅值;k = kr + iki,kr为实波数,与波长λo的关系为kr = 2π/λo,ki为扰动空间增长率;ω = ωr + iωi,ωr为扰动时间增长率,ωi为扰动频率;实数m为角向模数,表征扰动角向变化。
将无量纲扰动速度、扰动压力及扰动温度代入射流扰动控制方程中,求解可得扰动量:
| $\hat v{'_{{\rm{l}}r}} = \frac{1}{2}\left[ {{c_{{\rm{l}}1}}{I_{m + 1}}\left( {{l_1}r} \right) + {e_{{\rm{l}}1}}{I_{m - 1}}\left( {{l_2}r} \right)} \right] + \frac{1}{2}\left[ {{c_{{\rm{l}}2}}{K_{m + 1}}\left( {{l_1}r} \right) + {e_{{\rm{l}}2}}{K_{m - 1}}\left( {{l_2}r} \right)} \right] - \frac{{Rek}}{{2\left( {{l^2} + 2{\rm{i}}ERe} \right)}} \cdot $ | (8) |
| $\begin{array}{l} \;\;\;\;\;\;\left[ {{d_{{\rm{l1}}}}{I_{m + 1}}\left( {kr} \right) - {d_{{\rm{l2}}}}{K_{m + 1}}\left( {kr} \right)} \right] - \frac{{Rek}}{{2\left( {{l^2} - 2{\rm{i}}ERe} \right)}}\left[ {{d_{{\rm{l1}}}}{I_{m - 1}}\left( {kr} \right) - {d_{{\rm{l2}}}}{K_{m - 1}}\left( {kr} \right)} \right]\\ \hat v{'_{{\rm{l}}\theta }} = \frac{1}{{2{\rm{i}}}}\left[ {{c_{{\rm{l1}}}}{I_{m + 1}}\left( {{l_1}r} \right) - {e_{{\rm{l1}}}}{I_{m - 1}}\left( {{l_2}r} \right)} \right] + \frac{1}{{2{\rm{i}}}}\left[ {{c_{{\rm{l2}}}}{K_{m + 1}}\left( {{l_1}r} \right) - {e_{{\rm{l2}}}}{K_{m - 1}}\left( {{l_2}r} \right)} \right] - \frac{{Rek}}{{2{\rm{i}}\left( {{\lambda ^2} + 2{\rm{i}}ERe} \right)}} \cdot \end{array}$ | (9) |
| $\begin{array}{l} \hat v{'_{{\rm{l}}z}} = - {\rm{i}}{d_{{\rm{l}}1}}\frac{{k{l^2}Re{I_m}\left( {kr} \right)}}{{{l^4} + 4{E^2}R{e^2}}} + \frac{1}{{2k}}{\rm{i}}{c_{{\rm{l}}1}}{l_1}{I_m}\left( {{l_1}r} \right) + \frac{1}{{2k}}{\rm{i}}{e_{{\rm{l}}1}}{l_2}{I_m}\left( {{l_2}r} \right)\\ - {\rm{i}}{d_{{\rm{l}}2}}\frac{{k{l^2}Re{K_m}\left( {kr} \right)}}{{{\lambda ^4} + 4{E^2}R{e^2}}} - \frac{1}{{2k}}{\rm{i}}{c_{{\rm{l}}2}}{l_1}{K_m}\left( {{l_1}r} \right) - \frac{1}{{2k}}{\rm{i}}{e_{{\rm{l}}2}}{l_2}{K_m}\left( {{l_2}r} \right) \end{array}$ | (10) |
| $\hat p{'_{\rm{j}}}\left( r \right) = {d_{{\rm{j}}1}}{I_m}\left( {kr} \right) + {d_{{\rm{j}}2}}{K_m}\left( {kr} \right)$ | (11) |
| $\begin{array}{c} {{\hat T}_{\rm{l}}}'(r) = {c_{T1}}{I_m}(\alpha r) + {c_{T2}}{K_m}(\alpha r)\\ { + _{}}{c_{{\rm{l}}1}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{I_{m + 1}}({l_1}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m + 1}}({l_1}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { + _{}}{e_{{\rm{l1}}}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{I_{m - 1}}({l_2}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m - 1}}({l_2}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { + _{}}{c_{{\rm{l2}}}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{K_{m + 1}}({l_1}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m + 1}}({l_1}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { + _{}}{e_{{\rm{l2}}}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{K_{m - 1}}({l_2}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m - 1}}({l_2}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { - _{}}{d_{{\rm{l1}}}}\frac{{PeBRek}}{{{l^2} + 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{I_{m + 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m + 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { + _{}}{d_{{\rm{l2}}}}\frac{{PeBRek}}{{{l^2} + 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{K_{m + 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m + 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { - _{}}{d_{{\rm{l1}}}}\frac{{PeBRek}}{{{l^2} - 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{I_{m - 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m - 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ \begin{array}{*{20}{c}} {{ + _{}}{d_{{\rm{l2}}}}\frac{{PeBRek}}{{{l^2} - 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{K_{m - 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m - 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]}&{\left( {{A_h} + \frac{1}{2} < r \le {B_h}} \right)} \end{array} \end{array}$ | (12) |
| $\begin{array}{c} {{\hat T}_{\rm{l}}}'(r) = {c_{T1}}{I_m}(\alpha r) + {c_{T2}}{K_m}(\alpha r)\\ { - _{}}{c_{{\rm{l}}1}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{I_{m + 1}}({l_1}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m + 1}}({l_1}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { - _{}}{e_{{\rm{l}}1}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{I_{m - 1}}({l_2}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m - 1}}({l_2}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { - _{}}{c_{{\rm{l2}}}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{K_{m + 1}}({l_1}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m + 1}}({l_1}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { - _{}}{e_{{\rm{l2}}}}PeB\left[ {{I_m}(\alpha r)\int_0^r {{K_{m - 1}}({l_2}t){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m - 1}}({l_2}t){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { + _{}}{d_{{\rm{l1}}}}\frac{{PeBRek}}{{{l^2} + 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{I_{m + 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m + 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { - _{}}{d_{{\rm{l2}}}}\frac{{PeBRek}}{{{l^2} + 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{K_{m + 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m + 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ { + _{}}{d_{{\rm{l1}}}}\frac{{PeBRek}}{{{l^2} - 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{I_{m - 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{I_{m - 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]\\ \begin{array}{*{20}{c}} {{ - _{}}{d_{{\rm{l2}}}}\frac{{PeBRek}}{{{l^2} - 2{\rm{i}}ERe}}\left[ {{I_m}(\alpha r)\int_0^r {{K_{m - 1}}(kt){K_m}(\alpha t)t{\rm{d}}t + {K_m}(\alpha r)\int_0^r {{K_{m - 1}}(kt){I_m}(\alpha t)t{\rm{d}}t} } } \right]}&{\left( {{A_h} \le r \le {A_h} + \frac{1}{2}} \right)} \end{array} \end{array}$ | (13) |
按照射流液体控制方程的求解过程,同样可以求解得到气体的扰动速度、扰动压力及扰动温度。
对射流扰动控制方程的运动学、动力学及热力学边界条件进行扰动、线性化及无量纲化处理,得到无量纲线性化扰动控制方程的边界条件。
无量纲Marangoni数表征表面张力随温度的变化率,具有式(14)的形式。
| $Ma = \frac{{\gamma {T_{{\rm{l0}}}}}}{{{\rho _{\rm{l}}}{U^2}h}}$ | (14) |
圆环液膜内自由液面动力学边界条件(r = Ah):
| $\frac{{\partial v_{\rm lz}'}}{{\partial r}} + \frac{{\partial v_{\rm lr}'}}{{\partial z}} = - Ma \cdot Re\frac{{\partial T_1'}}{{\partial z}}$ | (15) |
| $\frac{{\partial v_{\rm lr}'}}{{\partial \theta }} + {A_\rm h}\frac{{\partial v_{l\theta }'}}{{\partial r}} - v_{l\theta }' = - {A_\rm h}MaRe\frac{{\partial T_1'}}{{\partial \theta }}$ | (16) |
| ${p_1}^\prime - {p_\rm 1}^\prime - \frac{2}{{Re}}\frac{{\partial v_{{\rm l}r}'}}{{\partial r}} + {E^2}{A_\rm h}{\eta _{\rm{i}}} - \frac{1}{{W{e_\rm T}A_\rm h^2}}\left( {{\eta _{\rm{i}}} + A_\rm h^2\frac{{{\partial ^2}{\eta _{\rm{i}}}}}{{\partial {z^2}}} + \frac{{{\partial ^2}{\eta _{\rm{i}}}}}{{\partial {\theta ^2}}}} \right) = 0$ | (17) |
其中,WeT = We/(1-We·Ma)。
圆环液膜外自由液面动力学边界条件(r = Bh):
| $\frac{{\partial v_{\rm lz}'}}{{\partial r}} + \frac{{\partial v_{\rm lr}'}}{{\partial z}} = - Ma \cdot Re\frac{{\partial {T_1}^\prime }}{{\partial z}}$ | (18) |
| $\frac{{\partial v_{\rm lr}'}}{{\partial \theta }} + {B_\rm h}\frac{{\partial v_{l\theta }'}}{{\partial r}} - v_{l\theta }' = - {B_\rm h}MaRe\frac{{\partial {T_1}^\prime }}{{\partial \theta }}$ | (19) |
| $p{'_{\rm{l}}} - p{'_{\rm{o}}} - \frac{2}{{Re}}\frac{{\partial v_{\rm lr}'}}{{\partial r}} + {E^2}{B_\rm h}{\eta _{\rm{o}}} + \frac{1}{{W{e_\rm T}B_\rm h^2}}\left( {{\eta _{\rm{o}}} + B_\rm h^2\frac{{{\partial ^2}{\eta _{\rm{o}}}}}{{\partial {z^2}}} + \frac{{{\partial ^2}{\eta _{\rm{o}}}}}{{\partial {\theta ^2}}}} \right) = 0$ | (20) |
圆环旋转黏性液体射流无量纲线性化扰动控制方程的热力学边界条件包括温度连续性条件和热流密度连续性条件。
无量纲化的温度连续性条件:
| $\left\{ \begin{array}{l} {\left. {{{T'}_{\rm{l}}}_{}} \right|_{r = {A_{\rm{h}}}}} = {\left. {{{T'}_i}_{}} \right|_{r = {A_{\rm{h}}}}}\\ {\left. {{{T'}_{\rm{l}}}_{}} \right|_{r = {B_{\rm{h}}}}} = {\left. {{{T'}_o}_{}} \right|_{r = {B_{\rm{h}}}}} \end{array} \right.$ | (21) |
无量纲化的热流密度连续性条件:
| $\left\{ \begin{array}{l} \frac{{\partial {{\left. {{T_{\rm{l}}}{{^\prime }^{}}} \right|}_{r = {A_{\rm{h}}}}}}}{{\partial r}} = {\Lambda _{\rm{i}}}\frac{{\partial {{\left. {{T_{\rm{l}}}{{^\prime }_{}}} \right|}_{r = {A_{\rm{h}}}}}}}{{\partial r}}\\ \frac{{\partial {{\left. {{T_{\rm{l}}}{{^\prime }^{}}} \right|}_{r = {B_\rm h}}}}}{{\partial r}} = {\Lambda _{\rm{o}}}\frac{{\partial {{\left. {{T_{\rm{l}}}{{^\prime }_{}}} \right|}_{r = {B_{\rm{h}}}}}}}{{\partial r}} \end{array} \right.$ | (22) |
其中,${\Lambda _{\rm{i}}}{\rm{ = }}{{\lambda / {{\lambda _{\rm{l}}}}}_{\rm{i}}}$和${\Lambda _{\rm{o}}} = {{{\lambda _o}} / {{\lambda _{\rm{l}}}}}$分别为内部和外部气体液体导热系数比。
通过整理得到12个无量纲射流边界条件。将扰动速度、扰动压力、扰动温度代入12个无量纲射流边界条件中,经整理得到如下齐次方程组:
| $\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}(\omega , k, m)\mathit{\boldsymbol{X}} = 0$ | (23) |
其中,X= [c11, c12, e11, e12, d11, d12, d21, d22, cT1, cT2, cg1, cg2] T;Λ(ω, k, m)是一个12阶方阵。
式(23)为齐次线性代数方程组,有非零解的条件是方程组系数行列式为零;由此可得:
| $\left| {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}(\omega , k, m)} \right| = 0$ | (24) |
式(24)即为建立的描述存在温度扰动的圆环旋转黏性液体射流自由表面扰动发展的色散方程。
鉴于色散方程的严重非线性及复杂性,只能对其进行数值求解。以往研究者对该类问题的数学模型进行迭代求解时,大都采用抛物线法(亦称Müller法)。然而,与弦截法相比,虽然抛物线法的收敛速度略快,但其算法比较复杂,既要处理符号问题,还要考虑复数的运算。为此,本文采用弦截法对色散方程进行空间模式数值求解。色散方程是一个12阶行列式,数值求解结果对初值十分敏感;初值选定不合适的话,有可能导致计算结果的不收敛。通过大量的数值计算发现,对于一定的扰动波数,求解扰动频率比直接求解扰动增长率更容易收敛。因此,本文在数值求解扰动增长率时,首先确定一定扰动波数所对应的扰动频率,然后再求解扰动增长率。
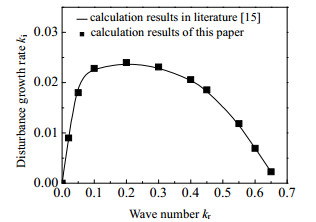
图 2给出的是Ma、Β、Λi和Λo、Pei和Peo为0时,射流扰动增长率的计算结果与文献[14]给出的计算结果的比较。从图 2中可以看到,两个计算结果相同。这从一定角度说明存在温度扰动的圆环旋转黏性液体射流稳定性色散方程以及色散方程数值求解方法的正确性。
|
图 2 射流扰动增长率的计算结果与文献[15]中的结果对比 Fig.2 Comparison of calculation results of disturbance growth rate with the results in the literature [15] |
简单条件下的温度扰动对液体射流稳定性影响的研究,如存在温度扰动的二维平面液体射流或圆柱轴对称液体射流稳定性问题等,已经证实温度扰动的存在会导致液体射流界面的稳定性发生变化;对存在温度扰动的圆环旋转黏性液体射流稳定性问题进行研究,研究过程中选择的工质为水与乳化剂的混合溶液,其动力黏度为0.006 kg·m-1·s-1,初始入口速度为6 m·s-1。
由于建立的描述存在温度扰动的圆环旋转黏性液体射流稳定性的色散方程中假设压力扰动、速度扰动及温度扰动皆具有相同的扰动频率,因此下述分析中提到的扰动频率是指压力扰动、速度扰动以及温度扰动的共同扰动频率。
目前,射流线性稳定性分析方法还无法直接对扰动强度与射流稳定性之间的关系进行研究。但有研究认为,射流液体与周围气体间的温差越大,温度扰动强度越大[16]。因此,本文通过气液温差对射流稳定性的影响来间接反映温度扰动强度对射流稳定性的作用,主要讨论射流周围气体温度高于射流液体温度的情况。
最大扰动增长率反映的是射流的不稳定程度。将最大扰动增长率对应的波数称为最不稳定波数,它与射流破碎液滴粒径具有一定的对应关系[1]:
| $d_{\rm{D}}^3 = \frac{{3\pi d_{\rm{L}}^2}}{{{k_{\rm{L}}}}}$ | (25) |
其中,kL为最不稳定波数;
| ${d_{\rm{L}}} = 2{\left( {\frac{4}{{3f}}} \right)^{1/3}}{\left( {\frac{{C_t^2{\sigma ^2}}}{{{\rho _{\rm{g}}}{\rho _{\rm{l}}}{U^2}}}} \right)^{1/6}}{\left[ {1 + 2.6{\mu _{\rm{l}}}\sqrt[3]{{\left( {\frac{{{C_t}\rho _{\rm{g}}^{\rm{4}}{U^8}}}{{6f\rho _{\rm{l}}^{\rm{2}}{\sigma ^5}}}} \right)}}} \right]^{1/5}}$ |
Ct为常数;f为与雷诺数和韦伯数有关的待定系数。
从式(25)中可以看到,最不稳定波数越大,射流破碎液滴粒径越小。
将射流最大扰动增长率对应的频率称为最不稳定频率,射流最不稳定频率与最不稳定波数具有线性对应的关系。
不稳定截断频率指的是不稳定频率的最大值,反映的是射流不稳定频率范围和射流破碎液滴粒径范围。不稳定截断频率越大,射流不稳定频率范围越大、射流破碎产生的最小液滴粒径越小、射流破碎液滴粒径范围越大。
通过最大扰动增长率、最不稳定频率以及不稳定截断频率对存在温度扰动的圆环旋转黏性液体射流稳定性进行研究。为了表达上的简洁,将轴对称扰动下的射流稳定性和非轴对称扰动下的射流稳定性简称为轴对称稳定性和非轴对称稳定性。
3.1 射流的轴对称稳定性与非轴对称稳定性射流是否旋转是射流轴对称稳定性和非轴对称稳定性的重要影响因素。
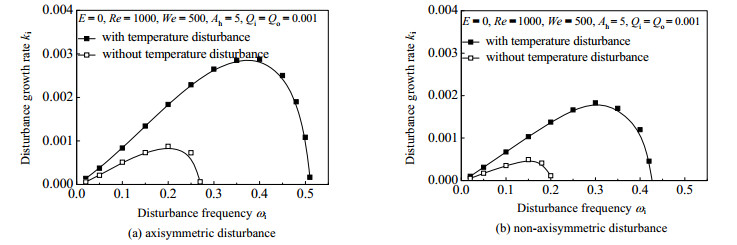
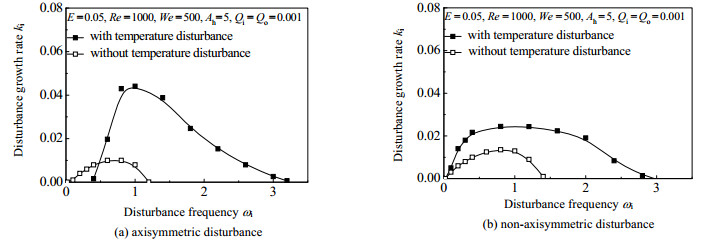
图 3和图 4分别是射流不旋转和旋转条件下,存在温度扰动与不存在温度扰动时圆环黏性液体射流的扰动增长率随扰动频率变化的比较。
|
图 3 射流不旋转时温度扰动对射流扰动增长率随扰动频率变化的影响 Fig.3 Effects of temperature disturbance on disturbance growth rate without liquid swirling |
|
图 4 射流旋转时温度扰动对射流扰动增长率随扰动频率变化的影响 Fig.4 Effects of temperature disturbance on disturbance growth rate with liquid swirling |
从图 3可以看到,射流不旋转时,无论是轴对称扰动还是非轴对称扰动,存在温度扰动时的扰动增长率随扰动频率的变化规律与不存在温度扰动时的变化规律基本相同。然而,存在温度扰动时,射流的最大扰动增长率、最不稳定频率以及不稳定截断频率明显大于不存在温度扰动时的相应参数。说明温度扰动的存在有利于圆环黏性液体射流的失稳及破碎,也有利于射流破碎液滴粒径的减小以及破碎液滴粒径范围的增大。
对于无旋转圆环黏性液体射流来说,不论是否存在温度扰动,轴对称扰动射流的最大扰动增长率皆大于非轴对称扰动射流。说明无旋转圆环黏性液体射流的占优模式为轴对称扰动模式,温度扰动不改变无旋转圆环黏性液体射流的占优模式。
从图 4中可以看到,与射流不旋转时相比,在射流旋转条件下,温度扰动的存在对圆环黏性液体射流稳定性产生更大的影响。
从图 4(a)中可以发现,在射流旋转条件下,不存在温度扰动时,不稳定扰动频率的变化范围从零开始。而存在温度扰动时,不稳定扰动频率的变化范围则从一定扰动频率开始。说明射流旋转时,温度扰动使得频率低于一定值的扰动不会对射流的轴对称不稳定性产生影响,温度扰动的存在有利于提高一定扰动频率下(主要是扰动频率较低情况下)圆环旋转黏性液体射流的轴对称稳定性。这有可能是在较低的扰动频率下温度扰动与速度扰动及压力扰动产生相互抵消的结果。另外,从图 4(a)中还可以看到,在射流旋转条件下,存在温度扰动时,不仅射流的最大扰动增长率、最不稳定频率以及不稳定截断频率会显著增大,而且扰动增长率随扰动频率的变化规律也会发生一定的变化。从图 4(b)中可以看到,在射流旋转条件下,温度扰动对非轴对称扰动也有类似的影响。温度扰动的存在同样有利于射流旋转时圆环黏性液体射流的失稳及破碎、射流破碎液滴粒径的减小以及破碎液滴粒径范围的增大。
对比图 4(a)和(b)可见温度扰动时,非轴对称扰动的不稳定频率范围略大于轴对称扰动的不稳定频率范围,而不稳定起始频率和不稳定截断频率皆小于轴对称扰动的不稳定起始频率和不稳定截断频率。
另外,对比图 4(a)和(b)还可以发现,不存在温度扰动时,轴对称扰动射流的最大扰动增长率小于非轴对称扰动射流,非轴对称扰动模式占优。而存在温度扰动时,轴对称扰动射流的最大扰动增长率却明显大于非轴对称扰动射流,轴对称扰动模式占优。说明在射流旋转条件下,温度扰动使圆环旋转黏性液体射流的占优模式发生改变,即由非轴对称扰动模式转变为轴对称扰动模式。这可能是由于温度扰动与角向模数(反映扰动的类型)相互作用的结果。
3.2 射流温差对射流稳定性的作用有研究认为,射流液体与周围气体间温差在一定程度上反映了温度扰动强度[13]。以无量纲参数B = βh/Tl0表征气液温差,Β越大,气液温差越大。
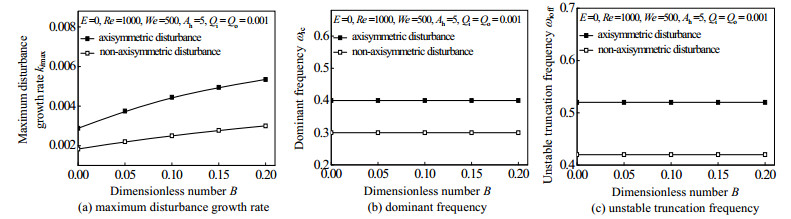
图 5和6分别给出的是射流不旋转和旋转时,圆环黏性液体射流的最大扰动增长率、最不稳定频率及不稳定截断频率随Β的变化。
|
图 5 射流不旋转时扰动参数随无量纲数Β的变化 Fig.5 Variation of the disturbance frequency characteristics as a function of B without liquid swirling |
|
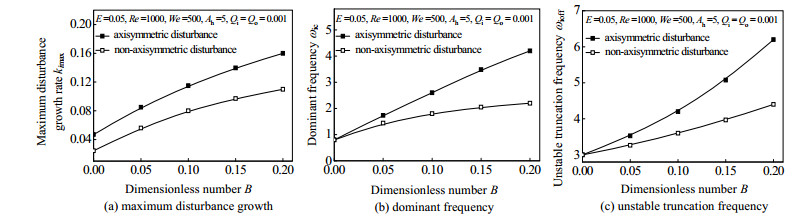
图 6 射流旋转时扰动参数随无量纲数Β的变化 Fig.6 Variation of the disturbance frequency characteristics as a function of B with liquid swirling |
从图 5可见,射流不旋转时,Β对轴对称扰动和非轴对称扰动射流的最大扰动增长率具有基本相同的作用,即Β增加,最大扰动增长率增大;Β对轴对称扰动的影响略大;不同Β时,轴对称扰动射流的最大扰动增长率总是大于非轴对称扰动射流。说明射流不旋转时,气液温差,即温度扰动强度增大有利于射流的失稳及破碎。这与一般的理解基本一致,气液温差不改变射流的占优模式。
射流不旋转时,Β对轴对称扰动射流和非轴对称扰动射流最不稳定频率和不稳定截断频率几乎没有影响。说明射流不旋转时,气液温差,亦即温度扰动强度对射流破碎液滴粒径以及射流不稳定频率范围和破碎液滴粒径范围没有影响。
射流不旋转时,轴对称扰动射流的最不稳定频率和不稳定截断频率总是大于非轴对称扰动射流。说明不同气液温差,亦即不同温度扰动强度时,轴对称扰动射流的破碎液滴粒径总是小于非轴对称扰动射流,轴对称扰动射流的破碎液滴粒径范围总是大于非轴对称扰动射流。
通过图 6和图 5的比较可以看到,射流旋转时,除了最大扰动增长率明显增大以外,轴对称扰动和非轴对称扰动射流的最大扰动增长率随Β的变化规律几乎与射流不旋转时完全相同。
与射流不旋转时Β对射流最不稳定频率和不稳定截断频率几乎没有影响不同,射流旋转时,随着Β的增加,射流最不稳定频率和不稳定截断频率增大。说明射流旋转时,气液温差,亦即温度扰动强度的增加有利于射流破碎液滴粒径的减小及射流破碎液滴粒径范围的增大。为此,为获得更好的雾化效果,在工程应用时可考虑增加圆环射流周围气体的温度。
射流旋转时,虽然轴对称扰动和非轴对称扰动射流的最不稳定频率和不稳定截断频率皆随Β的增加而增大,但轴对称扰动射流最不稳定频率和不稳定截断频率受Β的影响更大。
射流旋转时,不同Β下轴对称扰动射流最不稳定频率和不稳定截断频率总是大于非轴对称扰动射流,并且两者间的差值随着Β的增加而增大,说明随着气液温差,亦即温度扰动强度增加,轴对称扰动射流破碎液滴粒径小于非轴对称扰动射流破碎液滴粒径的程度以及破碎液滴粒径范围大于非轴对称扰动射流破碎液滴粒径范围的程度增大。
3.3 贝克来数对射流稳定性的作用贝克来数Pe反映的是射流液体的热量传递特性与温度扰动对圆环旋转黏性液体射流稳定性作用的影响。
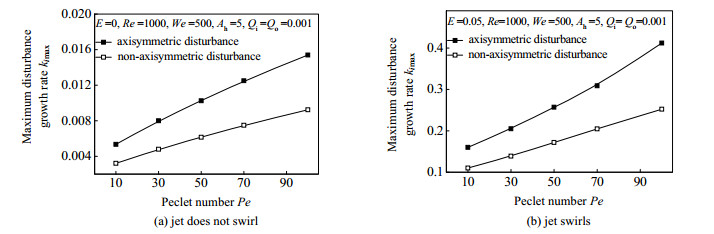
图 7给出的是射流不旋转和旋转时,圆环黏性液体射流最大扰动增长率随贝克来数Pe的变化。
|
图 7 最大扰动增长率随贝克来数Pe的变化 Fig.7 Variation of the maximum disturbance growth rate as a function of Peclet number |
从图 7中可以看到,随着Pe增加,不论是轴对称扰动还是非轴对称扰动,射流最大扰动增长率皆呈增大趋势;说明射流液体的热量传递特性越差,圆环黏性液体射流越容易失稳。随着Pe的增加,不旋转射流最大扰动增长率的增大幅度略有减小,而旋转射流最大扰动增长率的增大幅度略有增大。在不同Pe下,轴对称扰动射流最大扰动增长率总是大于非轴对称扰动射流,且随着Pe的增加,轴对称扰动与非轴对称扰动射流最大扰动增长率之间的差值增大。说明射流液体的热量传递特性对圆环黏性液体射流的占优模式没有影响,且射流液体热量传递特性越差,轴对称扰动模式占优程度越高。
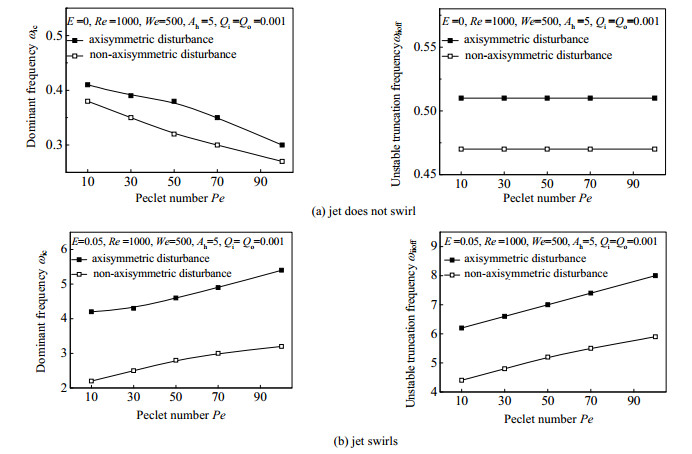
图 8给出的是射流不旋转和旋转时,圆环黏性液体射流的最不稳定频率和不稳定截断频率随Pe的变化。从图 8可以看到,射流旋转和不旋转两种情况下,Pe对圆环黏性液体射流最不稳定频率和不稳定截断频率的影响表现出明显不同特性。
|
图 8 最不稳定频率和不稳定截断频率随贝克来数Pe的变化 Fig.8 Variation of the disturbance frequency characteristics as a function of Peclet number |
需要说明的是,式(25)反映了最不稳定波数与射流破碎液滴粒径的关系,而射流最不稳定频率与最不稳定波数具有线性对应的关系。所以本小节的叙述中将根据射流最不稳定频率的大小及范围来反映射流破碎液滴粒径及分布。从图 8(a)中可以看到,射流不旋转时,随着Pe的增加,轴对称扰动射流最不稳定频率减小,且减小趋势逐渐加快;非轴对称扰动射流最不稳定频率减小,但减小趋势逐渐变慢;轴对称扰动射流最不稳定频率始终大于非轴对称扰动射流。说明射流不旋转时,射流液体的热量传递特性越差,射流破碎液滴粒径越大,而轴对称扰动射流的破碎液滴粒径总是小于非轴对称扰动射流。
射流不旋转时,随着Pe的增加,轴对称扰动和非轴对称扰动射流的不稳定截断频率皆基本保持不变,且轴对称扰动射流不稳定截断频率总是大于非轴对称扰动射流。说明射流不旋转时,射流液体的热量传递特性对射流破碎液滴粒径范围没有影响,轴对称扰动射流的破碎液滴粒径范围总是大于非轴对称扰动射流。
从图 8(b)中可以看到,射流旋转时,最不稳定频率随Pe的变化趋势与射流不旋转时完全不同。随着Pe的增加,射流最不稳定频率增大,且轴对称扰动射流最不稳定频率的增大有加快趋势,而非轴对称扰动射流最不稳定频率的增大有减慢趋势;轴对称扰动射流的最不稳定频率总是大于非轴对称扰动射流。说明射流旋转时,射流液体的热量传递特性越差,射流破碎液滴粒径越小;轴对称扰动射流的破碎液滴粒径总是小于非轴对称扰动射流,这一点与射流不旋转时相同。
射流旋转时,不稳定截断频率随Pe的变化与射流不旋转时完全不同。随着Pe的增加,不稳定截断频率增大。轴对称扰动射流不稳定截断频率总是大于非轴对称扰动射流。说明射流旋转时,射流液体的热量传递特性越差,破碎液滴粒径范围越大,而破碎液滴粒径范围总是大于非轴对称扰动射流,这一点与射流不旋转时相同。
4 结论(1) 推导出存在温度扰动的圆环旋转黏性液体射流扰动控制方程的解析解和边界条件,建立了同时存在速度扰动、压力扰动以及温度扰动的圆环旋转黏性液体射流稳定性色散方程,对色散方程进行了空间模式求解,并进行了验证分析。
(2) 温度扰动的存在使得圆环旋转黏性液体射流的最大扰动增长率、最不稳定频率和不稳定截断频率增大,并使射流扰动增长率随扰动频率的变化规律改变。温度扰动的存在有利于提高一定扰动频率下射流的轴对称扰动稳定性,并使射流扰动的占优模式发生变化。
(3) 对于旋转射流,随气液温差的增加,射流最大扰动增长率、最不稳定频率和不稳定截断频率增大。轴对称扰动射流最不稳定频率和不稳定截断频率受气液温差影响更大。
(4) 在相同温度扰动下,圆环旋转射流的最大扰动增长率、最不稳定频率以及不稳定截断频率皆随Pe的增加而增大。轴对称扰动射流的最大扰动增长率、最不稳定频率以及不稳定截断频率总是大于非轴对称扰动射流,且差值随Pe的增加而增大。
| [1] |
ASHGRIZ N. Handbook of atomization and sprays: Theory and applications[M]. New York: Springer Verlag, 2011.
|
| [2] |
IBRAHIM A A. Comprehensive study of internal flow field and linear and nonlinear instability of an annular liquid sheet emanating from an atomizer[D]. Cincinnati: University of Cincinnati, 2006.
|
| [3] |
YOON S. A fully nonlinear model for atomization of high-speed jets[D]. West Lafayette: Purdue University, 2002.
|
| [4] |
MA Z H. Investigation on the internal flow characteristics of pressure-swirl atomizer[D]. Cincinnati: University of Cincinnati, 2001.
|
| [5] |
阎凯, 宁智, 吕明. 圆环旋转黏性液膜射流三维不稳定性研究[J]. 计算力学学报, 2012, 29(6): 893-900. YAN K, NING Z, LV M. Three-dimensional instability analysis of an annular swirling viscous liquid sheet[J]. Chinese Journal of Computational Mechanics, 2012, 29(6): 893-900. |
| [6] |
阎凯.圆环旋转黏性液体射流稳定性及破碎研究[D].北京: 北京交通大学, 2014. YAN K. Study on stability and breakup of an annular swirling viscous liquid sheet [D]. Beijing: Beijing Jiaotong University, 2014. |
| [7] |
阎凯, 宁智, 吕明. 圆环旋转黏性液体射流空间不稳定性研究[J]. 力学学报, 2012, 44(4): 687-693. YAN K, NING Z, LV M. Spatial instability analysis of an annular swirling viscous liquid jet[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(4): 687-693. DOI:10.6052/0459-1879-11-197 |
| [8] |
FURLANI E P. Temporal instability of viscous liquid microjets with spatially varying surface tension[J]. Journal of Physics A: Mathematical and General, 2005, 38(1): 263-276. |
| [9] |
MASHAYEK F, ASHGRIZ N. Nonlinear instability of liquid jet with thermocapillarity[J]. Journal of Fluid Mechanics, 1995, 283: 97-123. DOI:10.1017/S0022112095002242 |
| [10] |
XU J J, DAVIS S H. Instability of capillary jets with thermocapillarity[J]. Journal of Fluid Mechanics, 1985, 161: 1-25. DOI:10.1017/S0022112085002798 |
| [11] |
DIJKSTRA H A, STEEN P H. Thermocapillary stabilization of the capillary breakup of an annular film of liquid[J]. Journal of Fluid Mechanics, 1991, 229: 205-228. DOI:10.1017/S0022112091003002 |
| [12] |
WANG Z L, ZHOU Z W. Effect of heat exchange on the interfacial instability of gas-liquid jet[J]. Applied Mathematics and Mechanics, 2003, 24(7): 747-755. DOI:10.1007/BF02437806 |
| [13] |
丁宁.加热条件下液体射流破碎机理的研究[D].天津: 天津大学, 2002. DING N. Study on the mechanism of liquid jet breakup under heating conditions[D]. Tianjin: Tianjin University, 2002. |
| [14] |
IBRAHIM A A, JOG M A, JENG S M. Effect of liquid swirl velocity profile on the instability of a swirling annular liquid sheet[J]. Atomization and Spray, 2006, 16(3): 237-263. DOI:10.1615/AtomizSpr.v16.i3.10 |
| [15] |
YAN K, Ning Z, LYU M, et al. Spatial instability in annular swirling viscous liquid sheet[J]. Physics of Fluids, 2015, 27(2): 024101-1 _024101-15.
|
| [16] |
PRUDHOMME R, ORDONNEAU G. The maximum entropy method applied to liquid jet atomization[C]//15th annual conference on liquid atomization and spray systems. Toulouse: Proceedings of ICLASS-Europe, 1999.
|




