2. 陕西省能源化工过程强化重点实验室, 陕西 西安 710049
2. Shaanxi Key Laboratory of Energy Chemical Process Intensification, Xi'an 710049, China
有机朗肯循环(organic Rankine cycle,ORC)已被证实是实际回收利用低温余热最有效的方式之一[1]。近年来,为了最大限度地提升ORC系统性能,各种不同类型的ORC结构相继被提出和应用,如同流回热结构[2]、侧线回热结构[3]、双(多)压蒸发结构[4]、有机闪蒸结构[5]、超临界循环结构[6]等,极大地推动了ORC在余热回收领域的进一步发展和应用[7]。针对ORC系统结构的选择和优化也成为研究者们关注的重点之一。
基础ORC结构主要包含工质泵、蒸发器、透平机和冷凝器4个单元模块。双压蒸发循环结构是在此基础上,将整个热回收过程分成2个压力级,分别产生不同品质的蒸气,不但可以提升工质与余热流股的换热效率,提高余热回收量,还可进一步减小系统的不可逆损失[8],是目前ORC系统中最具潜力的结构之一。Du等[4]构建了双压蒸发ORC循环中各单元模块的数学模型,并以系统的发电输出为目标对双压力系统进行分析。结果表明,双压蒸发ORC系统的输出功比基础结构高18.9%,传热面积增加42.14%,且随着热源流量的上升,高压蒸发级与低压蒸发级的输出功比值降低。Li等[9]以总输出和总导热之比为目标,建立了双压蒸发ORC系统的火积理论模型,对比和分析了串联和并联2种不同的双压力蒸发循环结构。结果表明,串联结构相对于并联结构更优,也更适合工业推广,且串联的双压蒸发ORC结构相较于单压蒸发结构有更好的热力学性能,但单压蒸发ORC结构的经济性优于双压蒸发ORC结构[10]。Li等[11]通过对小规模串联双压蒸发结构的热力学和经济性分析指出,热源温度的升高和流量的增加可有效降低双压蒸发结构的总费用,使特定工况下双压蒸发结构的经济性优于单压蒸发结构。
Manente等[12]在热源进口温度为100~200 ℃时,对单压和串联双压蒸发结构热力学性能进行了对比研究。结果表明,热源进口温度在100~125 ℃时,双压蒸发ORC结构下系统输出最高可提升29%,但在热源进口温度位于150~200 ℃时,双压蒸发ORC系统的优势减弱。特别地,当工质的临界温度低于热源进口温度40 ℃以上时,双压蒸发结构将不再适用。在此基础上,Li等[13]提出了热源温度与工质临界温度的定量表达式来确定单/双压蒸发结构的适用性。除此之外,他们还将串联双压蒸发ORC结构拓展到高压蒸发为超临界状态,低压蒸发为亚临界状态的结构[14]。该结构的发电输出较单一的超临界ORC循环和基础ORC循环提升19.9% 和48.9%。Wang等[15]以系统输出为目标,构建了双压蒸发结构和超临界结构下ORC系统的数学模型。计算结果表明,高压力级对整个ORC系统的性能影响更大,且随着高压力级蒸发压力的不断提升,双压力结构下热回收部分的热量交换更加充分。此外,还定义了边界温度用于判断双压力结构和超临界结构的适用性,高于边界温度,超临界结构更适用,反之,则双压力结构更适用。
综上所述,目前针对双压蒸发ORC循环系统的研究多关注系统的热力学性能或经济性能分析,缺少统一的结构选择依据。尽管部分研究者[12-13]提出了定性规则或定量的关系式,用于判断单/双压蒸发ORC结构在不同热源温度下的适用性,但研究方法以热力学建模分析为主,缺少对系统内部机理的深入探究和分析,加之研究中选择的候选流体有限,使得确定的规则准确性和普适性不足。为此,本研究针对实际工业生产中最常见的低温热源温度范围,挑选了尽可能多的候选流体,通过对单双压蒸发ORC结构在不同热源进口温度下适用性的模拟研究和分析,阐明了单/双压蒸发结构选择的内部机理和系统结构对系统性能的影响,并总结了单/双压蒸发ORC结构的选择原则。
2 单/双压蒸发ORC系统模拟 2.1 单/双压蒸发ORC系统结构本研究中所探究的单压蒸发循环(single pressure evaporation cycle,SPEC)和双压蒸发循环(dual pressure evaporation cycle,DPEC)结构及其对应的t-s(温-熵)图如图 1和2所示,图中t为温度。在SPEC中,工质泵(1→2)将冷凝器出口的液体加压并输送到热回收装置,热回收装置包括预热器(2→3)和蒸发器(3→4) 2部分,在热回收装置中,工质回收余热中的热量,由过冷液体变成高温高压蒸气状态。热回收装置出口的高温高压蒸气进入透平机(4→5)膨胀后变成低温低压乏气,同时产生发电输出,透平机出口的乏气进入冷凝器(4→5→1),被公用工程冷凝成饱和液体,如图 1所示。
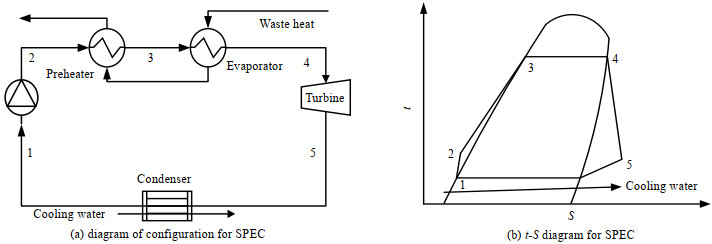
|
图 1 单压蒸发循环结构图和t-S图 Fig.1 Configuration and t-S diagram for SPEC |
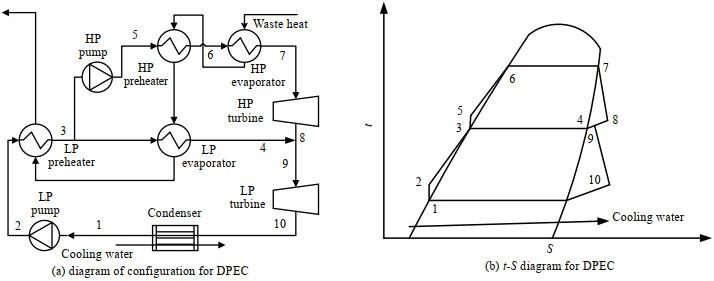
|
图 2 双压蒸发循环结构和t-S图 Fig.2 Configuration and t-S diagram for DPEC |
|
|
表 1 候选工质的物性 Table 1 Properties of candidate working fluids |
研究采用的双压蒸发循环结构为串联的双压力蒸发结构,该结构在单压蒸发ORC结构的基础上增加了一个压力级(3→5→6→7→8),将热回收装置分为高压(high pressure,HP)和低压(low pressure,LP) 2个部分,产生2种不同品质的工质蒸气,并分别进入高压透平机(7→8)和低压透平机(9→10),高压透平机出口的蒸气压力与低压热回收装置的蒸发压力相等,低压部分预热器出口的饱和液体分流一部分通过高压工质泵进入高压热回收部分。需要注意的是,该串联蒸发结构较并联蒸发结构具有更好的热回收性能[9],且其中透平机的布置方式也选择了热力学性能和经济性更优的交互透平机布置方式[16],如图 2所示。
2.2 候选工质工质的选择直接影响ORC系统的热回收性能。大量研究表明干、等熵工质具有更好的热回收性能,而且能够有效避免透平机出口的液相流体对透平机造成损害[18]。在挑选工质时,有机工质的临界温度与热源温度也存在一定的匹配关系,即低临界温度的工质适用于温度较低的热源,而高温热源更适合选择临界温度较高的工质[19],最优的工质的临界温度低于热源的进口温度约30~50 ℃,临界温度相近的工质,其饱和蒸气曲线的斜率越小,也就是临界压力越高的工质有更高的输出[20],当工质的临界温度低于热源进口温度55 ℃以上时,热回收效率会变得很低[21]。
在工业领域,一般的低温余热为生产过程产生的低于200 ℃的余热气、冷凝水、热水等。为此,依据以上的工质选择原则,研究选取了如表 1所示的17种干、等熵工质作为候选工质,表 1还给出了候选工质临界温度tc和临界压力pc。17种工质的临界温度为204.35~85.8 ℃,可适用于绝大多数200 ℃以下的低温热源。
2.3 ORC系统模拟 2.3.1 基本假设鉴于其详尽的物性数据库、精确的物性计算方法、成熟完备的单元模型以及广泛的工业应用,研究采用Aspen软件对单/双压力蒸发ORC系统进行模拟。根据表 1中候选流体的性质,选用Peng-Robinson(P-R)方程作为物性方程[22],因为P-R方程在临界区域内有较高的准确性,同时也能对物质的液相密度等物性能进行较好的预测[23],在有机流体物性模拟预测方面有广泛的应用[24-25]。
模拟中用到的假设条件归纳如下:
1) 选取入口温度为120~200 ℃水作为热源流股,压力为20 × 105 Pa;模拟中以10 ℃为步长提高热源入口温度;热源流量为1 kg·s-1,不限制热源的出口温度。
2) 除了透平机和工质泵的压力变化外,只考虑蒸发器和冷凝器的压降,且设定为10 kPa [26],忽略系统中其他附属设备(如管道等)的压降。
3) 考虑到干、等熵工质的过热对系统的热回收性能影响较小[3],忽略工质的过热,假设蒸发器出口为饱和蒸气。
4) 冷凝器出口的工质状态为40 ℃的饱和液体,且为了适应实际工业场景,整个装置的压力应大于等于大气压。
5) 系统的最小传热温差为5 ℃,透平机和工质泵的等熵效率为常数,取值为0.8,透平机出口气相分率为1。
2.3.2 评价指标1) 系统效率
ORC系统效率,ηsys定义为系统的总输出(Wtur-Wpum)与可回收余热总量Qav的比值,如式(1)所示:
| ${\eta _{{\rm{sys}}}} = \frac{{{W_{{\rm{tur}}}} - {W_{{\rm{pum}}}}}}{{{Q_{{\rm{av}}}}}}$ | (1) |
因为高于工质冷凝温度5 ℃(最小传热温差)的热源皆具有被回收利用的潜力,因此文中高于45 ℃的余热均是可回收余热。特别地,对于双压蒸发结构而言,系统的净输出功应是所有透平机输出功和所有工质泵消耗功率的差值。
2) 热回收效率
系统的热回收效率,ηthm定义为系统的总输出(Wtur-Wpum)与实际回收余热Qre的比值,如式(2)所示:
| ${\eta _{{\rm{thm}}}} = \frac{{{W_{{\rm{tur}}}} - {W_{{\rm{pum}}}}}}{{{Q_{{\rm{re}}}}}}$ | (2) |
其中,系统实际回收的余热量可表示为蒸发器负荷和预热器负荷的总和。
3) 其他约束
本文将蒸发器出口温度定义为决策变量,且蒸发温度应介于工艺限制的最高温度和冷凝温度之间,如式(3)所示。
| ${t_{{\rm{con}}}} \le {t_{{\rm{eva}}}} \le \min \left\{ {{t_{{\rm{WH}},{\rm{in}}}} - \Delta {t_{{\rm{pp}}}},{t_{\rm{c}}} - \Delta {t_{\rm{d}}}} \right\}$ | (3) |
对双压蒸发循环而言,低压蒸发级的蒸发温度应介于高压力级蒸发温度和冷凝温度之间,如式(4)所示。
| ${t_{{\rm{con}}}} \le t_{{\rm{eva}}}^{{\rm{LP}}} \le t_{{\rm{eva}}}^{{\rm{HP}}}$ | (4) |
式(3)和(4)中,tcon和teva分别表示冷凝和蒸发温度;tWH, in为热源进口温度;tc为工质临界温度;Δtpp和Δtd分别为最小传热温差、工质的最高蒸发温度与其临界温度的最小差值;上标LP和HP分别为低压和高压蒸发过程。需要注意的是,为了获得最优的操作条件,在模拟过程中,将在以上给定的变化范围内,以2 ℃为步长对蒸发温度进行离散。
3 单压蒸发ORC系统分析 3.1 固定热源的单压蒸发ORC系统分析在固定热源入口温度为200 ℃时,对单压蒸发的基础ORC结构进行模拟,得到不同候选工质下对应的最优蒸发温度和最大的系统效率,如图 3所示,图中横坐标的工质依照其临界温度由高到低排列。
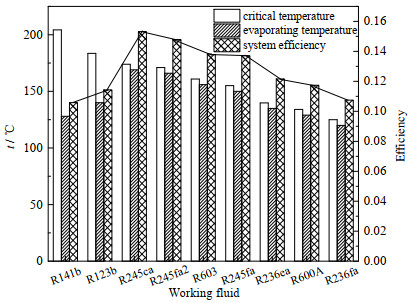
|
图 3 热源进口温度200℃下不同工质对应的最优蒸发温度和系统效率 Fig.3 Optimal evaporating temperature and system efficiency of different working fluids at waste heat inlet temperature of 200 ℃ |
由图 3可以看出当热源进口温度为200 ℃时,系统效率最大时对应的工质为R245ca,最大的系统效率为0.153,当热源进口温度为200 ℃时,系统对应的可用热源的热量为730 kW,系统最大的输出为111.89 kW。同时从图 3可以看出,R245ca的最优蒸发温度也是最高的,为169 ℃,意味着使用工质R245ca可以产生最高品质的蒸气。由图 3还可看出,ORC的系统效率随工质临界温度降低呈现先增大后减小的趋势,在工质为R245ca时出现一个极大值,对应最大的系统效率为0.153。除R245ca外,R245fa2,R603,R245fa等工质下对应的系统效率也较高,其临界温度与热源进口温度的温差在26~45 ℃。温差超出该范围时系统效率都较低。特别地,工质R603的临界温度R245fa高约6 ℃,但两者对应的系统效率和发电输出却基本相同,这是因为R603的临界压力高于R245ca,说明工质的临界压力较高也有利于提升系统效率。因此,在候选工质的临界温度相近时,应优先选择临界压力较大的工质。图 4给出了部分候选工质下系统热回收的t-Q图。其中,工质的温度变化都由一个线性增长的预热阶段和一个温度恒定的等温蒸发阶段构成。
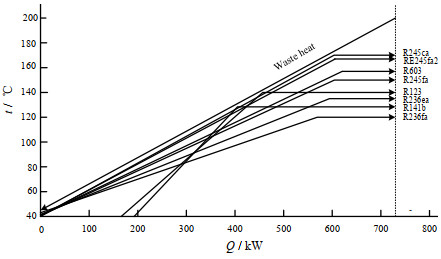
|
图 4 热源进口温度200 ℃下部分工质的系统热回收t-Q图 Fig.4 Diagram of system heat recovery of some working fluids at waste heat inlet temperature of 200 ℃ |
由图 4可以看出,在最优条件下,临界温度较高的工质与热源流股换热时形成的夹点类型为泡点夹点(vaporization pinch point,VPP)[27],工质预热段的负荷曲线偏离热源负荷曲线较远,余热出口温度较高;随着工质临界温度的下降,工质的蒸发温度升高,工质等温蒸发部分的负荷曲线上移,预热部分的负荷曲线逐渐靠近热源负荷曲线,当工质为R245ca时形成VPP和进口夹点(preheating pinch point,PPP)[27]双夹点,随着工质临界温度进一步降低,工质等温蒸发部分的负荷曲线逐渐下移,蒸发温度降低,工质与热源仅在进口处形成PPP。因此,对于给定进口温度的热源,在单压蒸发系统的最优条件下,工质与热源形成的夹点类型随着工质的临界温度降低的变化趋势为:VPP→VPP & PPP→PPP,其系统效率随着工质临界温度的降低先增大,后减少,并在形成VPP & PPP双夹点时达到最大,此时回收的热量最多,产生的蒸气品质也最高。当工质与热源形成VPP夹点时,工质预热部分负荷曲线与热源负荷曲线相距较远,热源出口温度与工质进口温度间温差较大,可通过增加一级低温蒸发,进一步回收余热,提升系统输出和系统效率。然而,当工质与热源形成PPP夹点时,仅使用单压力级就可将余热回收完全,对应的热源出口温度较低,此时添加第2级蒸发将影响第1级蒸发产生的蒸气品质和数量,从而降低整个系统的发电输出和系统效率。因此,当工质与热源形成VPP夹点时,系统具备多级蒸发潜力,而形成PPP夹点时,则不具备该潜力。换言之,VPP & PPP双夹点状态既是单压蒸发结构下系统所能达到的最优状态,也是判断系统是否具有双压蒸发潜力的临界状态。因此,对于给定进口温度的热源,若其最优工质已知,则当候选工质的临界温度高于单压蒸发的最优工质的临界温度时,系统可利用多级蒸发提升系统的效率和输出,反之则不可。
3.2 热源温度变化对单压蒸发ORC系统的影响以表 1中的候选工质数据为基础,讨论热源进口温度变化对单压蒸发ORC系统工质选择和性能指标的影响。设热源的进口温度从200 ℃开始,以10 ℃为步长依次降低直至120 ℃,最终的优化结果分别汇总在表 2和图 5中。
|
|
表 2 不同热源进口温度下的最优的操作参数 Table 2 Optimal operation parameters under different heat source inlet temperatures |
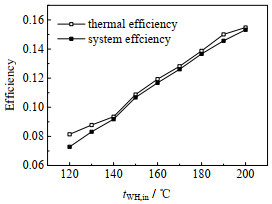
|
图 5 不同热源进口温度下最大的系统效率和热回收效率 Fig.5 Maximum system and thermal efficiencies under different heat source inlet temperatures |
由表 2的结果可知,固定热源进口温度下得到的工质选择原则和夹点变化规律在热源进口温度变化的条件下仍然是适用的。即不同热源温度下选择的最优工质仍然满足热源进口与工质临界温度的温差(26~45 ℃),且热源流股与工质形成VPP & PPP双夹点时,单压蒸发系统效率达到最大,如200 ℃和160 ℃下的结果所示。当然该状态仍可作为判断系统是否具有双压蒸发潜力的临界状态。
由图 5也可看出,热源的入口温度越高,其系统效率和热回收效率越高,且系统效率曲线和热回收效率曲线非常接近。这是因为,在最优操作点下,工质的负荷曲线与热源流股的负荷曲线无限接近而形成VPP & PPP双夹点,使得系统效率和热回收效率也无限接近,且偏离双夹点状态越远,系统效率和热回收效率的差距越大。同时,从工质的临界温度和蒸发温度的温差(5 ℃)也可看出,在最优工作状态下,工质被加热到临界温度附近以获取尽可能高品质的蒸气,使系统效率最大化。而工质的临界温度和蒸发温度的温差是为了保证整个过程的绝对亚临界状态而给定的工艺限制,见式(3)。
需要特别指出的是,表 2和图 5中都只有200 ℃和160 ℃时形成的VPP & PPP双夹点,其他热源温度下系统效率达到最大时并未形成双夹点,而是无限接近双夹点。这是因为候选工质的临界温度是不连续的,而表 2中热源流股的进口温度也都是以一定步长离散的,从而无法保证工质的临界温度与热源温度能够完全按照“双夹点规则”实现匹配和对应,而是尽可能地接近。为了验证这一点,对热源温度进行微调,以使其与对应的工质达到VPP & PPP双夹点状态,如表 3所示。
|
|
表 3 调整后不同热源进口温度下的最优的操作参数 Table 3 Optimal operation parameters under different heat source inlet temperatures after modification |
由表 3可知,对热源进口温度进行微调后,所有热源温度下都可与其对应的工质达到双夹点最优状态。同时,在最优工况下,工质的临界温度随着热源入口温度的升高而升高,两者存在一定的数学关系,拟合结果如图 6所示。可以看出,最优工质的临界温度与热源的进口温度基本呈线性关系,两者的拟合关系式为
| ${t_{\rm{c}}} = 0.929\;17{t_{{\rm{WH}},{\rm{in}}}} - 11.278\;06,{R^2} = 0.996$ | (5) |
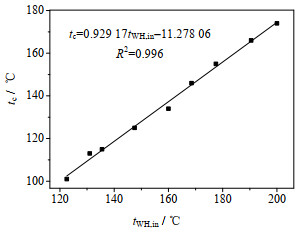
|
图 6 热源进口温度与其最优工质临界温度的关系 Fig.6 Relationship between the critical temperature of optimal working fluids and heat source inlet temperature |
由上一节的分析可知,如果工质的临界温度高于单压蒸发最优工质的临界温度,则系统具有双压蒸发的潜力,反之则不具备双压蒸发的潜力。那么,对于变热源进口温度的情况,如果工质的临界温度位于图 6中曲线下方,则系统不具备双压蒸发的潜力,反之,则系统具备双压蒸发潜力。因此,该线性关系式可用于任意热源进口温度下的单压蒸发和双压蒸发结构的选择。
4 双压蒸发ORC系统分析 4.1 双压蒸发工艺讨论双压蒸发ORC结构是在基础ORC结构的基础上增加了一个压力级,将热回收分为高压和低压两部分,同时产生两种不同品质的蒸气,其结构和t-S图如图 2所示。双压力结构中换热部分的t-H(温-焓)图如图 7所示,包含2段预热和2段等温蒸发部分。
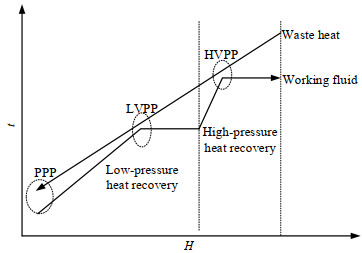
|
图 7 双压蒸发ORC热回收部分的t-H图 Fig.7 t-H diagram of heat recovery process for DPEC |
由图 7中工质负荷曲线的拐点可知,双压力过程可能产生3类夹点,即高压泡点夹点(HVPP),低压泡点夹点(LVPP)和PPP。不难看出,在HVPP & LVPP & PPP 3夹点情况下,两级蒸发都能够产生尽可能高品质的蒸气,系统的热回收也最完全,是双压蒸发循环的最理想的工况点。然而,由单压力级情况的分析可知,在仅形成VPP时系统才具备2级蒸发的潜力。换言之,选择双压力结构的前提是单压蒸发系统形成VPP,且无法形成PPP。因此,对于适用于双压蒸发系统的流体来说,其最优工况只可能是同时形成LVPP & HVPP双夹点。那么,双压力系统中低压力回路的功能就是在保证蒸气品质的基础上,尽可能增加热回收,以提升总的系统效率。
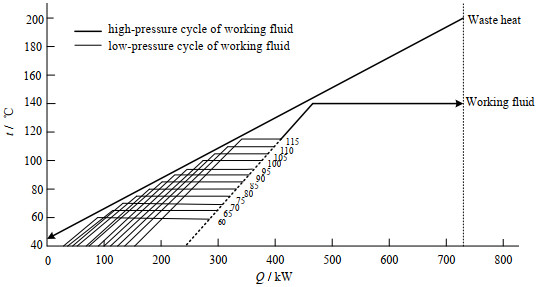
4.2 低压级蒸发温度对系统的影响在固定高压力级蒸发温度的基础上,分析低压蒸发级蒸发温度对系统性能的影响。本节选取热源进口温度为200 ℃,工质为R141b,高压力级的蒸发温度为140 ℃。分析结果如图 8所示。换热部分的t-Q图见图 9。
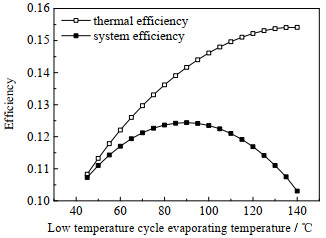
|
图 8 不同低压蒸发级蒸发温度下最大的系统效率和热回收效率 Fig.8 Maximum system and thermal efficiencies of different low pressure evaporating temperatures |
|
图 9 双压蒸发结构不同低压蒸发温度对应的换热回收部分的t-Q图 Fig.9 t-Q diagram of heat recovery process of different low pressure evaporating temperatures for DPEC |
由图 8可以看出,双压蒸发ORC结构下的系统效率随着低压蒸发级的蒸发温度的增加先增大后减小,存在最大的系统效率,为0.124 4,较单压蒸发循环下的系统效率提升20.78%。需要注意的是,系统效率变化曲线两个端点处的低压蒸发温度分别为冷凝温度(40 ℃)和高压蒸发温度(140 ℃),对应的ORC系统为单压蒸发循环结构。因此,该变化曲线的含义是:当低压蒸发温度高于40 ℃时,系统可考虑添加低压蒸发级,且随着低压蒸发温度升高,双压蒸发ORC系统效率逐渐提升,在低压蒸发温度为90 ℃时达到最大;此时若继续升高低压蒸发温度,双压蒸发ORC的系统效率将开始降低,直至低压蒸发温度达到140 ℃时,系统重新变为单压力级结构。除此之外,双压蒸发ORC结构下的系统效率随低压蒸发级蒸发温度的变化幅度不大,不超过13.7%。换言之,在双压蒸发ORC结构中,低压蒸发级对系统性能的影响较小,高压力级才是决定双压蒸发循环热回收性能的关键。
由图 8中还可看出,系统的热回收效率随着低压蒸发级的蒸发温度的提升而增大。这是因为随着低压蒸发级蒸发温度的升高, 系统的热回收量减少,使得系统的热回收效率得以提升,如图 9所示。图 9中蓝色曲线为高压部分的工质负荷曲线,黑色曲线为低压部分的工质负荷曲线。由图 9可知,双压蒸发循环相比单压蒸发循环可回收更多的余热,降低热源出口温度,提升热回收效率。低压蒸发级蒸发温度在40~140 ℃内变化时,双压蒸发循环可比单压蒸发循环多回收204 kW余热热量,占总的可用热量的27.9%,且热回收量随着低压蒸发级蒸发温度的升高而减少,低压蒸发级蒸发温度越高,热源的出口温度越高,回收的热量越少,使得系统的热回收效率越高。
5 结论针对单压和双压蒸发ORC系统的工质和结构选择问题,在热源进口温度为200~120 ℃,选取了17种候选工质,对单压和双压蒸发ORC结构适用条件进行模拟研究,得到如下结论:
(1) 对于单压蒸发ORC结构,随着工质临界温度的降低,工质与热源流股在最优情况下形成的夹点类型由VPP逐渐变为VPP & PPP双夹点,并最终形成单独的PPP;在形成VPP & PPP双夹点时,系统效率达到最大。
(2) 热源和工质形成的夹点类型是ORC系统结构选择的关键指标。在单压蒸发最优条件下,夹点类型为VPP时,可选择双压力结构进一步提升系统效率,而夹点类型为PPP时,系统并不具备通过双压蒸发结构提升效率的潜能,采用单压蒸发结构更优。
(3) 不同热源条件下,热源进口温度与其单压蒸发结构下的最优工质的临界温度呈线性关系,该关系式也可作为任意热源进口温度下ORC系统结构选择的依据。
(4) 双压蒸发循环可有效地提升系统的热回收量,降低热源出口温度,提升系统效率和发电输出。对于双压蒸发结构的系统,其系统效率最大时对应的换热夹点类型为HVPP & LVPP双夹点。
(5) 在双压蒸发ORC结构中,高压蒸发级是决定热回收性能的关键,低压蒸发级对系统性能的影响较小。
| [1] |
ZIVIANI D, BEYENE A, VENTURINI M. Advances and challenges in ORC systems modeling for low grade thermal energy recovery[J]. Applied Energy, 2014, 121: 79-95. DOI:10.1016/j.apenergy.2014.01.074 |
| [2] |
SALEH B, KOGLBAUER G, WENDLAND M, et al. Working fluids for low-temperature organic Rankine cycles[J]. Energy, 2007, 32(7): 1210-1221. DOI:10.1016/j.energy.2006.07.001 |
| [3] |
MAGO P J, CHAMRA L M, SRINIVASAN K K, et al. An examination of regenerative organic Rankine cycles using dry fluids[J]. Applied Thermal Engineering, 2008, 28(8): 998-1007. |
| [4] |
DU Y, YANG Y, HU D, et al. Off-design performance comparative analysis between basic and parallel dual-pressure organic Rankine cycles using radial inflow turbines[J]. Applied Thermal Engineering, 2018, 138: 18-34. DOI:10.1016/j.applthermaleng.2018.04.036 |
| [5] |
HO T, MAO S S, GREIF R. Increased power production through enhancements to the organic flash cycle (OFC)[J]. Energy, 2012, 45(1): 686-695. DOI:10.1016/j.energy.2012.07.023 |
| [6] |
LE V L, FEIDT M, KHEIRI A, et al. Performance optimization of low-temperature power generation by supercritical ORCs (organic Rankine cycles) using low GWP (global warming potential) working fluids[J]. Energy, 2014, 67: 513-526. DOI:10.1016/j.energy.2013.12.027 |
| [7] |
LECOMPTE S, HUISSEUNE H, BROEK M, et al. Review of organic Rankine cycle (ORC) architectures for waste heat recovery[J]. Renewable & Sustainable Energy Reviews, 2015, 47: 448-461. |
| [8] |
LI T L, WANG Q, ZHU J, et al. Thermodynamic optimization of organic Rankine cycle using two-stage evaporation[J]. Renewable Energy, 2015, 75(C): 654-664. |
| [9] |
LI T L, ZHANG Z, LU J, et al. Two-stage evaporation strategy to improve system performance for organic Rankine cycle[J]. Applied Energy, 2015, 150: 323-334. |
| [10] |
LI T L, MENG N, LIU J, et al. Thermodynamic and economic evaluation of the organic Rankine cycle (ORC) and two-stage series organic Rankine cycle (TSORC) for flue gas heat recovery[J]. Energy Conversion and Management, 2019, 183: 816-829. DOI:10.1016/j.enconman.2018.12.094 |
| [11] |
LI J, YANG Z, HU S, et al. Thermo-economic analyses and evaluations of small-scale dual-pressure evaporation organic Rankine cycle system using pure fluids[J]. Energy, 2020, 206: 413-431. |
| [12] |
MANENTE G, LAZZARETTO A, BONAMICO E. Design guidelines for the choice between single and dual pressure layouts in organic Rankine cycle (ORC) systems[J]. Energy, 2017, 123: 413-431. DOI:10.1016/j.energy.2017.01.151 |
| [13] |
LI J, GE Z, DUAN Y, et al. Parametric optimization and thermodynamic performance comparison of single-pressure and dual-pressure evaporation organic Rankine cycles[J]. Applied Energy, 2018, 217: 409-421. DOI:10.1016/j.apenergy.2018.02.096 |
| [14] |
LI J, GE Z, DUAN Y, et al. Design and performance analyses for a novel organic Rankine cycle with supercritical-subcritical heat absorption process coupling[J]. Applied Energy, 2019, 235: 1400-1414. DOI:10.1016/j.apenergy.2018.11.062 |
| [15] |
WANG M, ZHANG J, ZHAO S, et al. Performance investigation of transcritical and dual-pressure organic Rankine cycles from the aspect of thermal match[J]. Energy Conversion and Management, 2019, 197: 111850. DOI:10.1016/j.enconman.2019.111850 |
| [16] |
LI J, GE Z, LIU Q, et al. Thermo-economic performance analyses and comparison of two turbine layouts for organic Rankine cycles with dual-pressure evaporation[J]. Energy Conversion and Management, 2018, 164: 603-614. DOI:10.1016/j.enconman.2018.03.029 |
| [17] |
CHEN H J, GOSWAMI D Y, STEFANAKOS E K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat[J]. Renewable & Sustainable Energy Reviews, 2010, 14(9): 3059-3067. |
| [18] |
BROWN J S, BRIGNOLI R, QUINE T. Parametric investigation of working fluids for organic Rankine cycle applications[J]. Applied Thermal Engineering, 2015, 90: 64-74. DOI:10.1016/j.applthermaleng.2015.06.079 |
| [19] |
LONG R, BAO Y J, HUANG X M, et al. Exergy analysis and working fluid selection of organic Rankine cycle for low grade waste heat recovery[J]. Energy, 2014, 73: 475-483. DOI:10.1016/j.energy.2014.06.040 |
| [20] |
HAERVIG J, SORENSEN K, CONDRA T J. Guidelines for optimal selection of working fluid for an organic Rankine cycle in relation to waste heat recovery[J]. Energy, 2016, 96: 592-602. DOI:10.1016/j.energy.2015.12.098 |
| [21] |
VIVIAN J, MANENTE G, LAZZARETTO A. A general framework to select working fluid and configuration of ORCs for low-to-medium temperature heat sources[J]. Applied Energy, 2015, 156: 727-746. DOI:10.1016/j.apenergy.2015.07.005 |
| [22] |
PENG D, ROBINSON D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 59-64. |
| [23] |
KAMATH R S, BIEGLER L T, GROSSMANN I E. An equation-oriented approach for handling thermodynamics based on cubic equation of state in process optimization[J]. Computers & Chemical Engineering, 2010, 34(12): 2085-2096. |
| [24] |
CHEN C L, LI P Y, LE S N T. Organic rankine cycle for waste heat recovery in a refinery[J]. Industrial & Engineering Chemistry Research, 2016, 55(12): 3262-3275. |
| [25] |
YU H S, EASON J, BIEGLER L T, et al. Process integration and superstructure optimization of organic Rankine cycles (ORCs) with heat exchanger network synthesis[J]. Computers & Chemical Engineering, 2017, 107(S1): 257-270. |
| [26] |
TCHANCHE B F, PAPADAKIS G, LAMBRINOS G, et al. Fluid selection for a low-temperature solar organic Rankine cycle[J]. Applied Thermal Engineering, 2009, 29(11/12): 2468-2476. |
| [27] |
YU H S, FENG X, WANG Y F. A new pinch based method for simultaneous selection of working fluid and operating conditions in an ORC (organic Rankine cycle) recovering waste heat[J]. Energy, 2015, 90: 36-46. DOI:10.1016/j.energy.2015.02.059 |




