2. 青海黄河上游水电开发有限责任公司光伏产业技术分公司,青海 西宁 810007;
3. 陕西省能源化工过程强化重点实验室,陕西 西安 710049;
4. 热流科学与工程教育部重点实验室,陕西 西安 710049
2. Qinghai Huanghe Hydropower Development Co., Photovoltaic Industry Technology Branch, Xining 810007, China;
3. Shaanxi Key Laboratory of Energy Chemical Process Intensification, Xi'an 710049, China;
4. Key Laboratory of Thermo-Fluid Science and Engineering, Xi'an 710049, China
具有随机性和波动性的可再生能源大规模并网将加剧用户侧和发电侧的用电不匹配[1],主要表现为用户负荷峰谷期与发电峰谷期的错位。而采用电池储能对用户负荷进行削峰填谷减小用户负荷波动是解决上述问题的途径之一[2-3],即采用电池储能系统(battery energy storage system, BESS)在用电负荷高峰期放电,低谷期充电,改变用户负荷特性,缓解用电负荷的大幅度波动[4-5]。
由于电池类型、生产厂家和生产批次等方面的差异,电池的操作性能(如循环寿命、日历寿命和充放电效率等)和投资及维护费用存在显著差异[6],这意味着在实际配置电池储能系统时需要涉及性能和费用上具有差异的多种类储能电池的集成。因此,电池储能系统的操作或设计问题实际上是一个多种类电池储能系统的操作或设计优化问题[7-10]。对于采用电池储能系统在负荷侧的削峰填谷,目前主要采用单种类电池进行储能系统设计[11]。然而,由于用户侧的负荷特性多变,单种类电池储能系统具有其局限性且灵活性不足,而采用多种类电池则具有较大的灵活性和适应性,但采用多种类电池储能系统进行负荷侧削峰填谷的研究还罕见报道。
对于电池储能系统的削峰填谷研究,目前主要有两类。一类是关注以减小用电负荷波动为目标的电池储能系统削峰填谷设计或操作[12-13]。另一类则是关注削峰填谷的经济性能,利用分时电价等电价机制来操作电池储能系统实现套利,间接地达到削峰填谷效果[14-15]。上述两类方法均可在一定程度上实现电池储能系统对用户负荷的削峰填谷作用,但关注以减小用电负荷波动为目标的方法忽视了高昂的电池费用,而关注经济性的方法却又可能会引起新的用户负荷高峰期和低谷期。虽然采用多目标优化方法可同时考虑削峰填谷能力和经济性的影响[16],但是对于存在强非线性的大规模电池储能系统而言,多目标优化问题的求解则带来极大困难。因此,对于同时兼顾削峰填谷作用和系统经济性的多电池储能系统,需要针对多电池储能系统的多目标设计和操作构建有效的求解方法。
为了解决以上问题,针对多种类电池储能系统在削峰填谷场景下的容量配置和功率调度优化问题,本文提出一种多电池储能系统实现削峰填谷的多目标优化分步求解方法。在该方法中,首先以系统的负荷标准差最小为优化目标,旨在最大化削减用户的负荷波动;在此基础上,以总费用最小为目标,确保系统的经济性运行。最后,以一个实际光-储供电系统案例验证了该方法的有效性,并获得多种类电池储能系统在削峰填谷场景中最优的容量配置和功率调度。
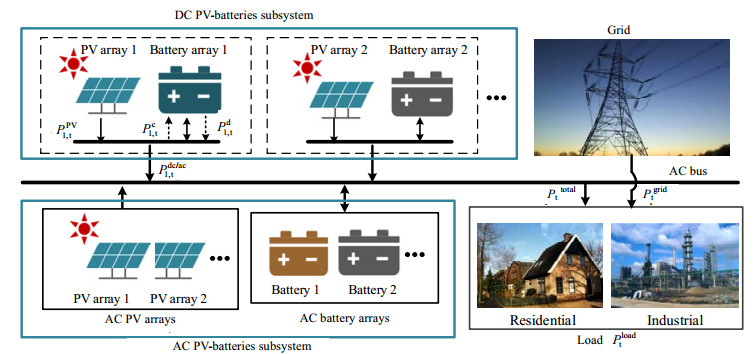
2 问题描述图 1为光(photovoltaic, PV)-储供电系统的结构示意图。在图 1中,光-储供电系统由光伏子阵、电池子阵、电网和用户4个子系统组成。其中,根据光伏子阵和储能电池子阵的物理连接关系可分为直流(direct current, DC)光-储和交流(alternating current, AC)光-储子系统两类。在直流光-储子系统中,储能电池子阵与光伏子阵具有一一对应的关系。如光伏子阵1和电池子阵1,电池子阵1只能储存光伏子阵1所发的电能。而在交流光-储子系统中,光伏子阵与电池子阵则是统一分配的关系,即所有的光伏子阵发的电统一分配给储能电池子阵。本文中,交流电池子阵也可用于储存来自直流光伏子阵的电能。用户的用电需求则由光伏、电池和电网3者共同满足。图 1中的标识符号解释可见本文的3.1和3.2节。
|
图 1 光-储供电系统的结构示意图 Fig.1 A schematic diagram of PV-batteries power supply system |
针对多种类电池储能系统在削峰填谷场景下的容量配置和功率调度多目标优化问题可描述为:已知(1)任一光伏子阵的发电功率曲线和用户的用电功率曲线;(2)电池储能系统的电池种类和电池参数(循环次数、充放电效率、充放电倍率、荷电状态(state of charge,SOC)上下限、购置单价和维护操作成本等);(3)电网的电价信息。目标为在综合考虑储能系统的削峰填谷作用和经济性的基础上,构建多种类电池储能系统的容量配置和功率调度优化数学模型,以确定供电系统的容量配置方案和功率调度策略。
3 多种类电池储能系统电池容量配置和调度优化数学模型及求解 3.1 目标函数 3.1.1 负荷标准差最小本文采用用户功率与其平均值偏离程度,即负荷标准差,表征系统的削峰填谷效果。因此,光-储供电系统的负荷标准差可表示为
| $\min \; {\rm TP} = \sum\limits_{t \in T} {\sqrt {{{\left( {P_t^{{\rm{load}}} - \sum\limits_{i \in {\mathit{\boldsymbol{I}}_1}} {{\eta ^{{\rm{dc/ac}}}}P_{i, t}^{\rm{d}}} - \sum\limits_{i \in {\mathit{\boldsymbol{I}}_2}} {{\eta ^{{\rm{ac/dc}}}}P_{i, t}^{\rm{d}}} + \sum\limits_{i \in {\mathit{\boldsymbol{I}}_1}} {{\eta ^{{\rm{dc/ac}}}}P_{i, t}^{\rm{c}}} + \sum\limits_{i \in {\mathit{\boldsymbol{I}}_2}} {{\eta ^{{\rm{ac/dc}}}}P_{i, t}^{\rm{c}}} - {{\bar P}^{{\rm{load}}}}} \right)}^2}} } $ | (1) |
式中:
用户的平均用电功率可表示为
| ${\bar P^{{\rm{load}}}} = \frac{1}{T}\sum\limits_{t \in T} {\left( {P_t^{{\rm{load}}} - \sum\limits_{i \in {\mathit{\boldsymbol{I}}_1}} {{\eta ^{{\rm{dc/ac}}}}P_{i, t}^{\rm{d}}} - \sum\limits_{i \in {\mathit{\boldsymbol{I}}_2}} {{\eta ^{{\rm{ac/dc}}}}P_{i, t}^{\rm{d}}} + \sum\limits_{i \in {\mathit{\boldsymbol{I}}_1}} {{\eta ^{{\rm{dc/ac}}}}P_{i, t}^{\rm{c}}} + \sum\limits_{i \in {\mathit{\boldsymbol{I}}_2}} {{\eta ^{{\rm{ac/dc}}}}P_{i, t}^{\rm{c}}} } \right)} $ | (2) |
式中:T为时间间隔的总数。
3.1.2 总费用最低光-储供电系统的总费用包括电池储能系统费用和购电费用,可表示为
| $\min {\rm TC }= \frac{1}{{365L}}\left[ {\sum\limits_{t \in T} {\sum\limits_{i \in \mathit{\boldsymbol{I}}} {C_i^{\rm{E}}{E_i}\left( {1{\rm{ + }}{f_i}} \right)} } {\rm{ + }}\sum\limits_{t \in T} {{\rho _t}P_t^{{\rm{grid}}}\Delta {t_t}} } \right]$ | (3) |
式中:
对直流光-储子系统而言,在时间间隔t上,任意光伏子阵的发电功率与相应电池子阵的放电功率之和应等于相应电池子阵的充电功率与输入交流母线的功率之和。于是该功率平衡可表示为
| $P_{j, t}^{{\rm{pv}}} + P_{i, t}^{\rm{d}} = P_{i, t}^{\rm{c}} + P_{j, t}^{{\rm{dc/ac}}}i = j, i \in {\mathit{\boldsymbol{I}}_1}, j \in {\mathit{\boldsymbol{J}}_1}$ | (4) |
式中:
在交流母线上的功率平衡:在时间间隔t上,所有交流光伏子阵的发电功率和所有交流储能电池子阵的放电功率与直流光-储输入交流母线的功率之和,应等于所有交流储能电池子阵的充电功率、上网功率与废弃功率之和。于是该功率平衡可表示为
| $\sum\limits_{j \in {{\bf{J}}_2}} {{\eta ^{{\rm{dc/ac}}}}P_{j, t}^{{\rm{pv}}}} + \sum\limits_{i \in {{\bf{I}}_2}} {{\eta ^{{\rm{dc/ac}}}}P_{i, t}^{\rm{d}}} {\rm{ + }}\sum\limits_{j \in {{\bf{J}}_1}} {P_{j, t}^{{\rm{dc/ac}}}{\eta ^{{\rm{dc/ac}}}}} = \sum\limits_{i \in {{\bf{I}}_2}} {{\eta ^{{\rm{ac/dc}}}}P_{i, t}^{\rm{c}}} + P_t^{{\rm{total}}} + P_t^{\rm{w}}\;\;\;\;t \in T$ | (5) |
式中:
对于用户而言,用户的用电需求由光伏,电池和电网满足,于是有
| $P_t^{{\rm{load}}} = P_t^{{\rm{total}}}{\rm{ + }}P_t^{{\rm{grid}}}{\rm{ \;\;\;\; }}t \in T$ | (6) |
(1) 电池储能系统电量平衡约束
| ${B_{i, t}} = {B_{i, t - 1}} + \eta _i^{\rm{c}}P_{i, t}^{\rm{c}}\Delta {t_t} - P_{i, t}^{\rm{d}}\Delta {t_t}/\eta _i^{\rm{d}}{\rm{ \;\;\; }}t \in T, i \in \mathit{\boldsymbol{I}}$ | (7) |
式中:
(2) 储能电池电量约束
储能电池的电量应满足以下约束
| ${\rm SOC}_i^{\min }{E_i} \leqslant {B_{i, t}} \leqslant {\rm SOC}_i^{\max }{E_i} {\rm{ \;\;\;\; }}t \in T, i \in \mathit{\boldsymbol{I}}$ | (8) |
式中:
且储能电池的电量也应满足
| ${B_{i, 1}} = {B_{i, T}}{\rm{ \;\;\;\; }}i \in \mathit{\boldsymbol{I}}$ | (9) |
式中:1和T分别为研究周期的开始和结束时刻。
(3) 储能电池容量约束
| $E_i^{\min } \leqslant {E_i} \leqslant E_i^{\max }{\rm{ \;\;\;\; }}i \in \mathit{\boldsymbol{I}}$ | (10) |
式中:
(4) 储能电池功率约束
储能电池子阵的功率应满足以下约束
| $P_i^{{\rm{min}}} \leqslant P_{i, t}^{\rm{c}} \leqslant P_i^{{\rm{max}}}{\rm{ \;\;\;\; }}t \in T, i \in \mathit{\boldsymbol{I}}$ | (11) |
| $P_i^{{\rm{min}}} \leqslant P_{i, t}^{\rm{d}} \leqslant P_i^{{\rm{max}}}{\rm{ \;\;\;\; }}t \in T, i \in \mathit{\boldsymbol{I}}$ | (12) |
式中:
(5) 储能电池充放电状态约束
电池储能系统的充放电状态约束可表示为
| $\sum\limits_{i \in \mathit{\boldsymbol{I}}} {P_{i, t}^{\rm{d}}} \cdot \sum\limits_{i \in \mathit{\boldsymbol{I}}} {P_{i, t}^{\rm{c}}} \le 0\;\;\;\;\;\;t \in T$ | (13) |
该式表示电池储能系统不能在同一时间同时处于充电和放电状态。由式(13)可知,只要系统有任一电池子阵处于充电状态(放电状态)则认为电池储能系统处于充电状态(放电状态)。所以在本文中,不存在一个电池子阵处于充电状态和另一电池子阵处于放电状态的情况。
电池储能系统除了需要满足不能在同一时间同时处于充放电状态的约束,其放电电量也不应废弃,所以有
| $\sum\limits_{i \in \mathit{\boldsymbol{I}}} {P_{i, t}^{\rm{d}}} \cdot P_t^{\rm{w}} \leqslant 0{\rm{ \;\;\;\; }}t \in T$ | (14) |
(6) 储能电池容量衰退
为了考虑电池容量衰退对电池储能系统的容量配置和功率调度的影响,并同时简化电池容量衰退过程,在本文中对电池的容量衰退过程假设如下:
1) 仅考虑电池充放电过程对电池容量的影响,即只考虑电池的循环容量衰退;
2) 假定电池的容量衰退量与电池的吞吐量呈正比。
电池的容量衰退可表示为
| $Q_{i, t}^{{\rm{loss}}} = Q_{i, t{\rm{ - }}1}^{{\rm{loss}}}{\rm{ + }}\frac{{\left( {P_{i, t}^{\rm{c}} + P_{i, t}^{\rm{d}}} \right)\Delta {t_t}}}{{2{N_i}{E_i}}}{\rm{ \;\;\;\; }}t \in T, i \in \mathit{\boldsymbol{I}}$ | (15) |
式中:
储能电池在研究时间长度内不能超过电池本身循环次数要求,于是有
| $Q_{i, T}^{{\rm{loss}}} \leqslant 100{\rm{\% }}t \in T, i \in \mathit{\boldsymbol{I}}$ | (16) |
式(1)~(16)即是在削峰填谷场景下多种类电池储能系统的容量配置和功率调度优化的多目标优化数学模型。
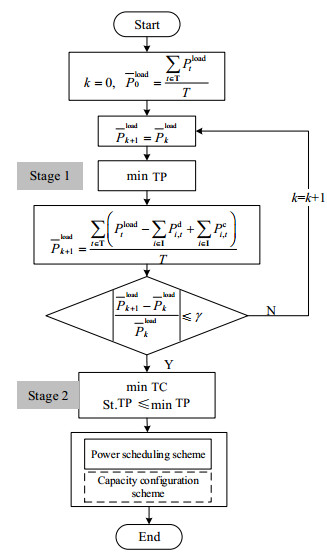
3.3 分步求解方法针对上述模型,为了同时保证电池储能系统的削峰填谷效果和系统运行的经济性,本文提出了分步求解的方法,具体步骤如图 2所示。该方法主要包括以下2步:
|
图 2 分步求解流程图 Fig.2 Flow chart of the step-wise optimization approach |
第1步:以光-储供电系统的负荷标准差最小为目标,以最大程度实现多电池储能系统的削峰填谷效果。在第1步的计算模型中,待求变量Y1和可行域D1分别可表示为
| $Y1 = \left\{ \begin{gathered} {B_{i, t}}, {E_i}, P_{i, t}^{\rm{c}}, P_{i, t}^{\rm{d}}, P_{j, t}^{{\rm{dc/ac}}}, P_t^{{\rm{grid}}}, \\ {\overline P ^{{\rm{load}}}}, P_t^{{\rm{total}}}, P_t^{\rm{w}}, Q_{i, t}^{{\rm{loss}}}, {\rm TP}, \\ i \in \mathit{\boldsymbol{I}}, j \in \mathit{\boldsymbol{J}}, t \in T, \\ \end{gathered} \right\}$ | (17) |
| $D1{\rm{ = }}\left\{ {Y1|{\rm{Eq}}{\rm{.}}(1)\sim(2), {\rm{Eq}}{\rm{.}}(4)\sim(16)} \right\}$ | (18) |
第2步:以第1步中的最小负荷标准差为约束,再以系统的总费用最小为优化目标,使得光-储供电系统经济运行,并获得多种类储能电池系统的最优容量配置和功率调度方案。故系统的负荷标准差应满足
| ${\rm TP} \leqslant {{\rm TP}^{{\rm{min}}}}$ | (19) |
式中:
在第2步的计算模型中,待求变量Y2和可行域D2分别可表示为
| $Y2 = \left\{ \begin{gathered} {B_{i, t}}, {E_i}, P_{i, t}^{\rm{c}}, P_{i, t}^{\rm{d}}, P_{j, t}^{{\rm{dc/ac}}}, P_t^{{\rm{grid}}}, \\ P_t^{{\rm{total}}}, P_t^{\rm{w}}, Q_{i, t}^{{\rm{loss}}}, {\rm TC}, {\rm TP}, \\ i \in \mathit{\boldsymbol{I}}, j \in \mathit{\boldsymbol{J}}, t \in T, \\ \end{gathered} \right\}$ | (20) |
| $ D2\rm{=}\left\{Y2|\rm{Eq}\rm{.}(3)\sim(16),\rm{Eq}\rm{.}(19)\right\}$ | (21) |
需要说明的是在该分步求解方法中,第1步优化的目的在于获取最小的系统负荷标准差,以最大化削减负荷的波动。其他所有的待求变量值由第2步优化获得。
以上所得的待求变量和可行域针对的是设计优化问题,当对光-储供电系统进行操作优化时,电池子阵的容量即为常数。
4 案例分析为了验证本文方法的有效性,本节以一个光-储系统的多种类电池储能系统的容量配置和功率调度问题为例,研究在削峰填谷场景下储能电池系统的削峰填谷效果和系统的经济性,以确定在满足系统削峰填谷效果和经济性要求下的多种类电池储能系统的电池容量和功率调度。
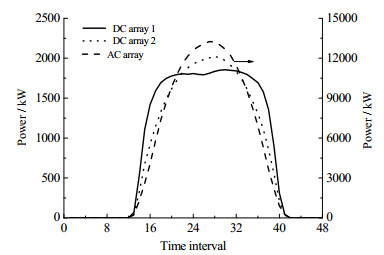
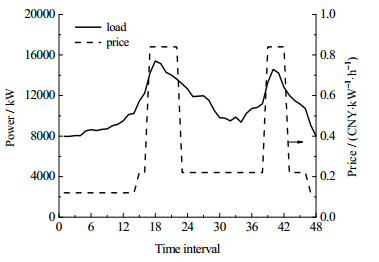
4.1 基础数据以中国青海省某光-储发电厂为例来阐述本文方法。图 3给出了该光-储发电厂直流光伏子阵和交流光伏子阵的出力曲线。该发电厂的电池储能系统由6种电池组成,各电池的相关参数如表 1所列。用户负荷曲线和电网电价信息可见图 4。在计算中假设现在电池容量保持率均为100%,各电池的操作维护成本均取投资成本的1%。各电池的荷电状态上下限为5%和95%。且假定光-储供电系统进行容量配置时,各储能电池子阵的容量上下限为原额定容量的50%和150%。在本文中,假设全年的光伏发电数据和用户需求数据如图 3和图 4所示。并将一天划分为48个时间间隔,每个时间间隔的持续时间均为0.5 h。且假定电池储能系统更换电池的时间为4年。假设直流与交流相互转换的效率均为95 %。
|
图 3 光伏出力曲线 Fig.3 Power supply curves of PV arrays |
|
|
表 1 电池参数 Table 1 Parameters of the batteries |
|
图 4 用户功率曲线和电价曲线 Fig.4 Power demand and price curve |
本文所有计算在GAMS平台上实现,CPU为Intel(R) Core(TM) i5-8400@2.80 GHz。该NLP模型采用求解器CONOPT进行求解。本文所得解均为局部最优解。
4.2 多种类电池储能系统的优化结果分析表 2给出了该光-储供电系统多种类电池储能系统的优化结果。其中,Stage 1表示系统以负荷标准差最小为目标进行优化;Stage 2则表示系统首先以负荷标准差最小为目标进行优化,然后再以系统总费用最低为目标进行优化。操作优化是指对原光-储供电系统进行调度优化,设计优化则是指对原光-储供电系统进行改造,同时优化电池储能系统的容量配置和功率调度。
|
|
表 2 光-储供电系统的优化结果 Table 2 Optimization results of the PV-batteries power supply system |
由表 2可知,与未配置电池储能系统的光伏供电系统比较,配置电池储能系统的光伏供电系统,利用电池储能系统对电能在时间和空间的转移特性,可以实现其削峰填谷的作用,且一定程度上降低系统的弃电率。但从费用上来看,配置电池储能系统的光伏供电系统降低了系统的电费,但由于配置电池储能系统而产生了更高的费用,从而使总费用有所增加。
在表 2中的操作优化中,由于操作优化未改变原来的电池容量,所以与原有配置保持一致。对比操作优化中在不同目标下的优化结果可知,在只考虑削峰填谷效果时,系统会优先选择充放电效率高的电池,如编号为直流2的NCR电池;而较少考虑电池充放电效率最差的,如编号为直流1的VRB电池。在Stage 2中,系统通过优化光-储供电系统的功率调度策略,在保证系统的削峰填谷的效果的同时,通过降低电费使得总费用降低,同时也降低了系统的弃电率。
在表 2的设计优化中,需要说明的是括号内表示直接采用分步求解方法得到的结果。计算中发现,编号为直流1的VRB电池无论在Stage 1还是在Stage 2中,其容量衰退量均为0。这表明该电池储能系统没有必要采用VRB电池,故将VRB电池从电池储能系统中去除。在表 2的设计优化中,对电池容量配置而言,无论是Stage 1还是Stage 2所配置的电池容量均大于原系统的电池容量。与操作优化的最后结果(Stage 2)相比,增加了交流4的NCM电池的容量。其中直流2的NCR电池和交流2的LFP电池容量为系统允许容量的上限值,这表明系统对这两种电池的选择优先级是最高的。而交流1的LFP电池和交流3的NCM电池的容量是下降的,且均为系统允许容量的下限值,这也表明了系统对这两种电池的选择优先级是最低的(当然除了直流1的VRB电池)。由表 1可知,交流2~4电池子阵充放电效率是相等的。对于Stage 1而言,这4种电池的优先级是一样的。但是在Stage 2中所配置的电池容量却并不一致。这是由于Stage 2的目标为总费用最小,电池选择的另一个指标便是经济性。由表 1可知,电池的经济性由电池的购置费用和性能(循环次数、放电深度和循环倍率等)决定的。对比操作优化,设计优化可以根据系统对各电池的经济优先级优化电池的容量,虽然设计优化中所配置的电池容量高于原电池容量,却获得了更优的削峰填谷效果。
总而言之,在操作优化和设计优化中,Stage 2优化后的总费用比Stage 1优化后的费用降低了约3%和1%。这就说明了采用分步方法对光-储供电系统进行操作优化和设计优化,可一定程度降低系统的总费用。而经Stage 2优化后,设计优化所得到的总费用比操作优化所得到的总费用降低了3%。这是因为优化了电池容量,从而进一步降低了系统的总费用。
图 5给出了在操作和设计优化中不同目标下的用户功率变化曲线。
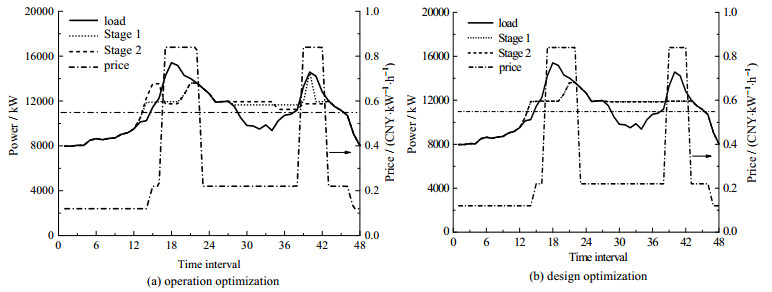
|
图 5 不同目标下用户功率变化曲线的对比 Fig.5 Comparison of power demand curves under different targets |
由图 5可知,无论是操作优化还是设计优化,电池储能系统都有一定的削峰填谷效果。例如,在时间间隔17~22和时间间隔39~42的用电高峰期就被“削减”一部分,而低谷期(时间间隔29~37)的用电负荷就被“填补”了。
在图 5(a)中,在操作优化中,Stage 1只关注系统的削峰填谷效果,削减了峰值负荷,增大了谷值负荷;Stage 2则在分时电价的指引下对用电负荷进行了“移动”(Stage 1中时间间隔39~41的小峰转移到Stage 2中时间间隔14~16的小峰),再次对系统的功率调度策略进行了优化,在保证系统削峰填谷效果的同时降低了系统的费用。在图 5(b),Stage 1和Stage 2下的用户负荷曲线则相差无几。这是由于分时电价峰谷期与用户的峰谷期是基本一致的。当松弛电池容量时,在Stage 1中,所选取电池的容量使得系统的削峰填谷效果最好,只要在系统所允许的电池容量范围内,系统可以选择适合系统的任意电池容量,从而存在电池容量冗余的现象。而Stage 2是在Stage 1基础上,以系统总费用最低为优化目标的。进行Stage 2后,冗余的电池容量被消除,功率调度策略进一步得到优化。但由表 2可以得知,在设计优化中Stage 2和Stage 1的电费相差不大,这也说明了系统的功率调度策略变化不大,因而导致在Stage 1和Stage 2下用户负荷曲线相差无几。
削峰填谷的效果主要是由电池储能系统的充放电实现的。下面以设计优化Stage 2的结果为例来说明电池储能系统的调度情况,具体结果如图 6所示。
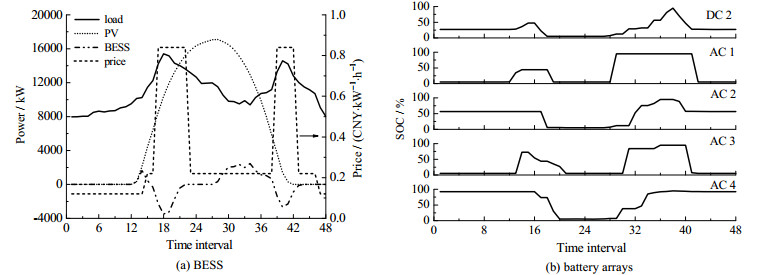
|
图 6 电池储能系统的功率调度曲线(设计优化Stage 2) Fig.6 Power scheduling curves of BESS (Stage 2 in design optimization) |
由图 6(a)可知,在用户负荷或电价低谷的时间间隔时,电池储能系统储存光伏所发的电能,如时间间隔28~38;在用户负荷或电价处于高峰的时间间隔时,电池储能系统放电以削减用户的负荷并同时降低系统的电费,如时间间隔16~21。在图 6(a)中,电池储能系统一天两充两放,这是因为用户负荷有两个高峰期导致的。图 6(b)给出了各电池子阵SOC的变化情况。由图 6(b)可知,各电池均为一天两充两放,且各电池子阵的SOC均在系统所要求的5 %~95 %。
5 结论对于存在强非线性的大规模电池储能系统而言,多目标优化问题的求解带来极大困难。为了同时兼顾削峰填谷作用和系统经济性,针对多种类电池储能系统在削峰填谷场景下的容量配置和功率调度优化问题,本文提出了一种多电池储能系统实现削峰填谷多目标优化的分步求解方法。在分步求解方法中,首先以电池储能系统的负荷标准差最小为优化目标,旨在最大化削减用户的负荷波动;在此基础上,以电池储能系统的总费用最小为目标,确保系统的经济性运行。本文以一个实际光-储供电系统案例验证了方法的有效性,并获得多种类电池储能系统在削峰填谷场景中最优的容量配置和功率调度。研究结果表明,采用本文方法可对原光-储供电系统中的多种类电池储能系统进行操作优化和设计优化,并最大化电池储能系统的削峰填谷作用和最小化系统的总费用。在第1步中,无论是操作优化还是设计优化,系统均优先选择充放电效率高的电池子阵;在第2步中,操作优化则是在分时电价的指引下采用电池储能系统中各电池子阵对用电负荷进行平移,以减少系统的电费;而设计优化,电池容量是松弛变量,系统在第1步的电池充放电效率优先级基础上,再增添经济性优先级,对电池子阵进行选取,同时优化电池子阵的容量和功率调度策略。采用本文分步求解方法不仅可获得多种类电池储能系统的容量配置和功率调度策略,还能在保证系统的削峰填谷效果的同时降低系统的总费用。
| [1] |
MARARAKANYE N, BEKKER B. Renewable energy integration impacts within the context of generator type, penetration level and grid characteristics[J]. Renewable and Sustainable Energy Reviews, 2019, 108: 441-451. DOI:10.1016/j.rser.2019.03.045 |
| [2] |
XU L, PAN Y, LIN M, et al. Community load leveling for energy configuration optimization: Methodology and a case study[J]. Sustainable Cities and Society, 2017, 35: 94-106. DOI:10.1016/j.scs.2017.07.017 |
| [3] |
LI Y, GAO W, RUAN Y. Performance investigation of grid-connected residential PV-battery system focusing on enhancing self-consumption and peak shaving in Kyushu, Japan[J]. Renewable Energy, 2018, 127: 514-523. DOI:10.1016/j.renene.2018.04.074 |
| [4] |
GARC A-PLAZA M, ELOY-GARC A CARRASCO J, ALONSO-MART NEZ J, et al. Peak shaving algorithm with dynamic minimum voltage tracking for battery storage systems in microgrid applications[J]. Journal of Energy Storage, 2018, 20: 41-48. DOI:10.1016/j.est.2018.08.021 |
| [5] |
韩晓娟, 田春光, 张浩, 等. 用于削峰填谷的电池储能系统经济价值评估方法[J]. 太阳能学报, 2014, 35(9): 1634-1638. HAN X J, TIAN C G, ZHANG H, et al. Economic evaluation method of battery energy storage system in peak load shifting[J]. Acta Energiae Solaris Sinica, 2014, 35(9): 1634-1638. |
| [6] |
ZHAO H, GUO S, ZHAO H. Comprehensive assessment for battery energy storage systems based on fuzzy-MCDM considering risk preferences[J]. Energy, 2019, 168: 450-461. DOI:10.1016/j.energy.2018.11.129 |
| [7] |
HAJIAGHASI S, SALEMNIA A, HAMZEH M. Hybrid energy storage system for microgrids applications: A review[J]. Journal of Energy Storage, 2019, 21: 543-570. DOI:10.1016/j.est.2018.12.017 |
| [8] |
蒋迎花, 康丽霞, 刘永忠. 考虑日历和循环衰退的多种类电池储能系统的功率调度优化[J]. 高校化学工程学报, 2019, 33(4): 895-902. JIANG Y H, KANG L X, LIU Y Z. Power dispatch optimization of a multi-type battery energy storage system considering calendar and cycle degradation[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(4): 895-902. |
| [9] |
JIANG Y, KANG L, LIU Y. A unified model to optimize configuration of battery energy storage systems with multiple types of batteries[J]. Energy, 2019, 176: 552-560. DOI:10.1016/j.energy.2019.04.018 |
| [10] |
JACOB A S, BANERJEE R, GHOSH P C. Sizing of hybrid energy storage system for a PV based microgrid through design space approach[J]. Applied Energy, 2018, 212: 640-653. DOI:10.1016/j.apenergy.2017.12.040 |
| [11] |
PAPIC I. Simulation model for discharging a lead-acid battery energy storage system for load leveling[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 608-615. DOI:10.1109/TEC.2005.853746 |
| [12] |
CHUA K H, LIM Y S, MORRIS S. A novel fuzzy control algorithm for reducing the peak demands using energy storage system[J]. Energy, 2017, 122: 265-273. |
| [13] |
IOAKIMIDIS C S, THOMAS D, RYCERSKI P, et al. Peak shaving and valley filling of power consumption profile in non-residential buildings using an electric vehicle parking lot[J]. Energy, 2018, 148: 148-158. DOI:10.1016/j.energy.2018.01.128 |
| [14] |
YAN X, OZTURK Y, HU Z, et al. A review on price-driven residential demand response[J]. Renewable and Sustainable Energy Reviews, 2018, 96: 411-419. DOI:10.1016/j.rser.2018.08.003 |
| [15] |
IMANI M H, GHADI M J, GHAVIDEL S, et al. Demand response modeling in microgrid operation: a review and application for incentive-based and time-based programs[J]. Renewable and Sustainable Energy Reviews, 2018, 94: 486-499. DOI:10.1016/j.rser.2018.06.017 |
| [16] |
ROSS M, ABBEY C, BOUFFARD F, et al. Multiobjective optimization dispatch for microgrids with a high penetration of renewable generation[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1306-1314. DOI:10.1109/TSTE.2015.2428676 |
| [17] |
GALLO A B, SIM ES-MOREIRA J R, COSTA H K M, et al. Energy storage in the energy transition context: A technology review[J]. Renewable and Sustainable Energy Reviews, 2016, 65: 800-822. DOI:10.1016/j.rser.2016.07.028 |




