2. 浙江大学衢州研究院, 浙江 衢州 324000;
3. 浙江中烟工业有限责任公司, 浙江 杭州 310024;
4. 宁波工程学院 材料与化学工程学院, 浙江 宁波 315211
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China;
3. Technology Center, China Tobacco Zhejiang Industrial Co. Ltd., Hangzhou 310024, China;
4. School of Materials and Chemical Engineering, Ningbo University of Technology, Ningbo 315211, China
细颗粒物(fine particulate matter,PM2.5)是影响大气环境质量的重要污染物之一,控制排放是治理PM2.5问题的主要途径[1]。旋风分离器通过离心力分离气流中的颗粒物,被广泛用于工业烟道气的初步除尘,但存在对细颗粒物分离效率低的问题[2]。PM2.5空气动力学直径小、重量轻,会随着气流运动而很难被离心分离。通过颗粒凝并技术可以使细颗粒物粒径变大,这是强化旋风分离器分离性能的有效方法。
在众多凝并技术中,双极荷电凝并技术在凝并效果和经济性上都具有优势[3],受到研究者的广泛关注。有研究[4]表明,当荷电电压高于起晕电压时,电极附近的气体介质会发生电离,产生的带电离子与颗粒物发生碰撞,从而使颗粒物负荷异种电荷。Eliasson等[5]研究发现,双极荷电细颗粒物的凝并速率比中性颗粒高出2~4个数量级。张向荣等[6]和谭百贺等[7]分别研究了直流电场和交流电场下双极荷电颗粒的碰撞凝并规律。相比于外加电场,湍流凝并通过流场扰流增大颗粒碰撞凝并几率,具有能耗低的优点。INDIGO公司[8]最早开发了运用双极荷电-湍流凝并技术的凝聚器,通过设置扰流柱使荷电颗粒产生速度差。Wang等[9]提出一种耦合电晕电场和湍流的凝并装置,可使颗粒荷电与湍流凝并过程同步进行。目前,旋风分离器的研究多与结构优化相关[10-11],很少有将双极荷电技术用于强化旋风分离器的报道。侯广信等[12]的研究表明旋风分离器中存在湍流凝并。因此,可使用双极荷电-湍流凝并技术强化旋风分离器。
荷电颗粒在旋风分离器中的运动非常复杂,经典分级效率模型[13]难以用于颗粒凝并较强的情况。Wang等[14]研究发现,旋风分离器分级效率曲线存在明显的“鱼钩”现象(当颗粒尺寸小于临界值时,分级效率在一定范围内随着颗粒尺寸的减小而增加),这种现象可认为是由颗粒凝并产生。梅芳等[15]考虑颗粒的破碎,修正了原有分级模型,导出“鱼钩效应”的计算式,但未考虑具体的颗粒凝并方式,且计算式只与颗粒尺寸相关。旋风分离器中还存在较强的旋流,旋流也会影响颗粒的选择性混合和碰撞凝并[16-17]。因此,在现有模型的基础上,引入旋流、库仑力作用下的颗粒凝并,建立双极荷电-旋风分离器分级效率模型,具有较大的实用价值。
为研究双极荷电技术对旋风分离器的强化效果,探究荷电电压、入口流速对旋风分离器分离效率的影响规律,本研究进行了不同操作条件下的旋风分离实验,建立了双极荷电-旋风分离器的分级效率模型,以期为双极荷电-旋风分离器的设计提供相关的技术支撑。
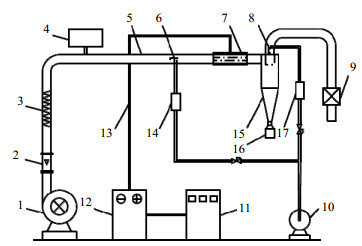
2 实验装置与方法 2.1 实验装置双极荷电-旋风分离器实验装置如图 1所示,主要由颗粒发生系统、采样测试系统、双极荷电装置及旋风分离器组成。
|
图 1 双极荷电-旋风分离实验装置示意图 Fig.1 Schematic diagram of bipolar charging-cyclone separation experimental setup 1. compressor 2. flowmeter 3. electric heating wire 4. particle generator 5. rectifying section 6, 8. sampling head 7. bipolar charging region 9. bag-type dust remover 10. sucking pump 11. control cabinet 12. high voltage DC power supply 13. high voltage cable 14, 17. sampling tube 15. cyclone separator 16. dust collection chamber |
颗粒发生装置采用循环流化床发尘系统。在风机作用下,颗粒以流化状态在发尘回路中循环。可通过流量计控制进入主系统管路的气体流量,从而控制颗粒物浓度。为模拟烟道气真实情况,选用粉煤灰为发尘物料,主要成分为SiO2、Al2O3、Fe2O3、CaO等,密度约为2.4 g·cm−3,比电阻为1010~1011 Ω·cm,相对介电常数为6.4。
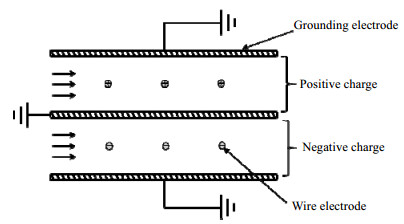
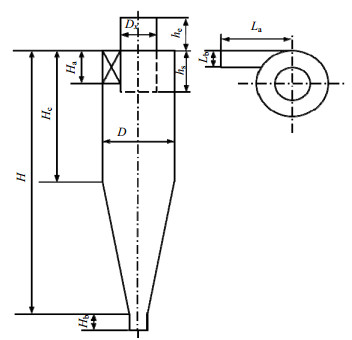
双极荷电装置如图 2所示,采用线板式结构,细钨丝作为电晕丝与高压直流电源连接,电极板接地,正负荷电区长100 mm,高50 mm,板间距20 mm,相邻电晕丝距离20 mm,电晕丝距离电极板10 mm。旋风分离器如图 3所示,结构尺寸见表 1。
|
图 2 双极荷电区示意图 Fig.2 Schematic diagram of bipolar charging region |
|
图 3 旋风分离器示意图 Fig.3 Schematic diagram of the cyclone separator |
|
|
表 1 旋风分离器结构尺寸 Table 1 Structure dimensions of the cyclone separator mm |
测量系统采用Dekati DLPI+型低压撞击器,用于测量气流中颗粒的质量浓度。各级撞击板所对应颗粒中位径D50值如表 2所示,撞击器基于颗粒惯性和质量,将颗粒粒径分为14级,可测粒径为0.016~10 μm,误差在±5%。实验使用等速采样法进行采样,采样探头位于中心位置。管道截面积小于0.1 m2,同一截面采样点数通常为1,管道中心处的颗粒物浓度即可代表该截面处的颗粒浓度。
|
|
表 2 DLPI+各级撞击板对应颗粒参数 Table 2 Impact plate parameters of DLPI+ |
为防止实验过程中产生的细颗粒物污染环境,使用布袋收集废弃粉煤灰颗粒。
2.2 实验方法在工程应用中,旋风分离器入口流速通常在15~25 m·s−1,在此流速下,大部分细颗粒物会随着气流从旋风分离器中逸出,并且高流速下,颗粒容易发生破碎造成颗粒凝并效果减弱。而研究颗粒凝并时,通常会选择在较低的流速下进行[18]。为研究荷电颗粒在旋风分离器中的凝并、分离过程,参照文献[16, 18],选择流速7~9 m·s−1,并选取荷电电压0~6 kV,进行双极荷电-旋风分离实验。风机启动一段时间,待各流量计显示稳定后,在荷电区入口和旋风分离器出口进行采样测试,采样时间3 min。按照入口-出口的顺序连续重复采样3次取平均值,通过入口和出口处采样颗粒的质量,可以确定旋风分离器的总分离效率η:
| $ \eta {\text{ = }}\frac{{{m_{{\text{in}}}} - {m_{{\text{out}}}}}}{{{m_{{\text{in}}}}}} $ | (1) |
通过对比每一级撞击板上收集到的颗粒质量,可确定旋风分离器分级效率ηi:
| $ {\eta _i}{\text{ = }}\frac{{{m_{{\text{in, }}i}} - {m_{{\text{out, }}i}}}}{{{m_{{\text{in, }}i}}}} $ | (2) |
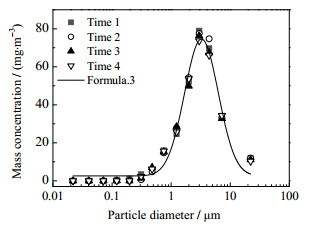
在旋风分离器中,颗粒物的凝并和分离与颗粒分布状态有关。如图 4所示为初始颗粒的质量-粒径分布,单次实验数据由3次重复实验取平均值获得。Time1~4实验点较为接近,这说明循环流化床发尘装置具有较好的重复性。通过拟合实验数据发现,入口处颗粒粒径分布近似服从对数正态分布,用gin(x)表示:
|
图 4 入口颗粒的质量-粒径分布 Fig.4 Mass concentration distribution of the inlet particle |
| $ {g_{{\text{in}}}}(x) = \frac{{{\rho _0}}}{{x\ln \sigma \sqrt {2\pi } }}{\exp _{}}[ - \frac{{{{\ln }^2}(x/{\alpha _{{\text{in}}}})}}{{2{{\ln }^2}\sigma }}] $ | (3) |
荷电电压U和对应的电流如表 3所示,说明起晕电压在5 kV附近,荷电电压达到6 kV后,空气介质被击穿。表 4为不同荷电电压及入口流速ν下,双极荷电-旋风分离器的总分离效率。从表 4可见,在同一流速下,荷电电压在0~5 kV,旋风分离器的总分离效率变化很小。荷电电压达到5 kV后,电极刚开始产生电晕,电离产生的带电离子较少,荷电电压对旋风分离器的分离性能影响不明显。
|
|
表 3 各荷电电压对应电流 Table 3 Current values corresponding to each charging voltage |
|
|
表 4 不同荷电电压、入口流速下旋风分离器总分离效率 Table 4 Total separation efficiency of the cyclone separator under different charging voltages and inlet flow rates |
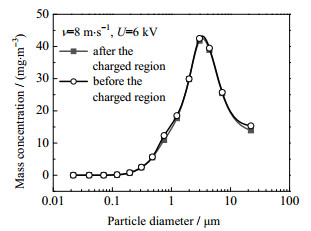
还可观察到,随着电压从5提高到6 kV,旋风分离器的总分离效率有明显的提升,这说明双极荷电技术对旋风分离器具有较好的强化效果。颗粒凝并和静电吸附都会影响分离效率,通过比较荷电区前后的颗粒粒径分布如图 5所示,可以发现颗粒凝并是分离效率提高的主要原因。荷电电压增加,电极丝附近的电晕效果增强,产生更多的带电离子,随着气流经过的颗粒物通过碰撞捕获带电离子,因此颗粒荷电量变大。进入旋风分离器后,库仑力在短距离内促进颗粒凝并,颗粒荷电量越大,颗粒凝并效果就越强。凝并后的颗粒在旋风分离器中更容易被分离。旋风分离器中也存在带有同种电荷的颗粒,颗粒之间存在排斥力,不利于颗粒的凝并,但有实验证明荷电颗粒仍比不带电颗粒更容易凝并[19]。
|
图 5 荷电区前后颗粒的质量-粒径分布 Fig.5 Mass concentration distribution before and after the charged region |
随着入口流速的增加,旋风分离器的总分离效率增大。这是因为旋风分离器中颗粒所受离心力与颗粒运动速度的平方成正比,在较高的入口流速下,颗粒更容易被离心力甩向壁面而捕集下来。
为了更直观地了解入口流速对颗粒凝并的影响,以相对于未荷电时的分离效率增加量表示双极荷电的强化效果。当荷电电压为6 kV、流速在7、8、9 m·s−1下的分离效率增加量分别为25.32%、14.04%、10.26%,在较低流速下,颗粒荷电对旋风分离器的强化效果更显著。流速影响颗粒在荷电区和旋风分离器内的停留时间,颗粒在以电场荷电为主要荷电方式时,可以认为颗粒荷电量在很短时间内达到饱和,颗粒荷电时长对颗粒凝并的影响可以忽略。而在较低流速下,颗粒物在旋风分离器中有更长的停留时间,颗粒发生库仑凝并的几率更大,荷电的强化效果更好。
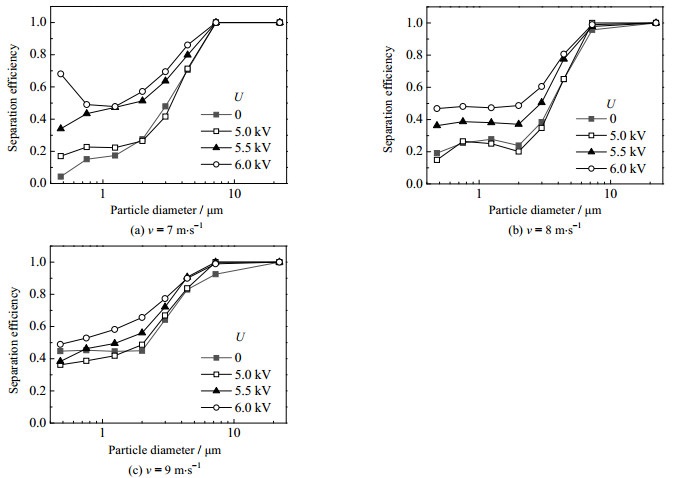
3.3 荷电电压、入口流速对旋风分离器分级效率的影响旋风分离器分级效率曲线有助于分析细颗粒物在旋风分离器中的凝并、分离过程。旋风分离器中,不同粒径颗粒受到的离心力不同,若只考虑这个因素,分级效率曲线应为S型曲线,且旋风分离器对细颗粒物的分离效果较弱。这与图 6所示的类似“鱼钩”的现象不一致,说明在细颗粒物尺寸范围,分级效率不是由旋风分离器的分离特性决定,而是由颗粒凝并决定。
|
图 6 荷电电压、入口流速对旋风分离器分级效率的影响 Fig.6 Effects of different charging voltages and flow rates on fractional efficiency of the cyclone separator |
由图 6可知,当荷电电压U为0 kV、入口流速ν为7 m·s−1时,细颗粒物的分级效率较低,旋风分离器难以分离气流中的细颗粒物。随着入口流速的提高,细颗粒物的分级效率有所提高,说明旋风分离器内可能存在湍流凝并。分级效率曲线随着荷电电压的增加而向上移动,尤其是细颗粒物的分级效率,提升效果更明显,说明双极荷电加剧了颗粒间的凝并,即存在库仑凝并。当入口流速为7 m·s−1、荷电电压为6 kV时,粒径为0.47 μm的颗粒所对应的分离效率与其他数据相比较大,呈现明显的鱼钩现象,这是因为小粒径颗粒具有更高的扩散系数,会加速细颗粒物的凝并进程[20],并且随着粒径的减小,颗粒间吸引力和质量力之比增大,凝并后的颗粒难以破碎。对于鱼钩现象,有很多不同的解释,有研究者认为这是由于不完善的实验和测量导致的偶然、随机的现象[21],Majumder等[22]将这现象归因于大颗粒尾迹的夹带作用,而通过以上对实验结果的分析,“鱼钩效应”也可能是由颗粒凝并产生的。
4 物理模型 4.1 双极荷电-旋风分离器分级效率模型双极荷电-旋风分离器的分级效率可通过入口和出口处的颗粒质量-粒径分布进行计算:
| $ \omega (x, v, U) = \frac{{{g_{{\text{in}}}}(x) - {g_{{\text{out}}}}(x, v, U)}}{{{g_{{\text{in}}}}(x)}} $ | (4) |
颗粒在旋风分离器中的运动过程非常复杂,同时涉及颗粒的凝并和分离。为简化模型,对于确定粒径分布的颗粒群,研究假设荷电颗粒在旋风场中先完成整个凝并过程再进行分离。该假设下,分离过程单独进行,即不考虑颗粒凝并,此时的分级效率用ψ(x, v)表示。旋风分离器分离的对象是经过凝并后的颗粒群,可用gagg(x, v, U)表示凝并后颗粒的质量-粒径分布,旋风分离器出口处颗粒质量-粒径分布如式(5)所示:
| $ {g_{{\text{out}}}}(x, v, U) = {g_{{\text{agg}}}}(x, v, U) - {g_{{\text{agg}}}}(x, v, U)\psi (x, v) $ | (5) |
结合式(4)、(5),双极荷电-旋风分离器的分级效率可表示为
| $ \omega (x, v, U) = 1 - \frac{{{g_{{\text{agg}}}}(x, v, U)[1 - \psi (x, v)]}}{{{g_{{\text{in}}}}(x)}} $ | (6) |
式(6)中的ψ(x, v)不考虑颗粒凝并,可采用Barth模型,详见文献[13],ψ(x, v)与入口流速v、颗粒粒径x及旋风分离器结构参数有关。
根据实验结果,入口颗粒的质量-粒径分布可认为是对数正态分布,如式(3)所示。Vemury等[23]研究表明,颗粒分布越接近对数正态分布,凝并前后颗粒分布的几何标准差σ越接近常数。鉴于颗粒总质量浓度不变,凝并后颗粒粒径分布如式(7)所示:
| $ {g_{{\text{agg}}}}(x, v, U) = \frac{{{\rho _0}}}{{x\ln \sigma \sqrt {2\pi } }}{\exp _{}}[ - \frac{{{{\ln }^2}[x/{\alpha _{{\text{agg}}}}(v, U)]}}{{2{{\ln }^2}\sigma }}] $ | (7) |
将式(3)、(7)代入式(6),得
| $ \omega (x, v, U) = 1 - {\exp _{}}[\frac{{{{\ln }^2}(x/{\alpha _{{\text{in}}}}) - {{\ln }^2}[x/{\alpha _{{\text{agg}}}}(v, U)]}}{{2{{\ln }^2}\sigma }}][1 - \psi (x, v)] $ | (8) |
从上式可见,分级效率模型的关键是确定凝并前后颗粒质量中位径的关系。通过凝并系数可联系凝并前后颗粒状态变化,进而得到颗粒质量中位径关系。凝并系数K指颗粒在单位时间内能够进行碰撞凝并的有效体积。向晓东等[24]采用单分散性颗粒的凝并系数近似计算多分散性颗粒的凝并系数,提出了凝并前后颗粒的数量中位径关系,如式(9)所示:
| $ {a_{{\text{agg}}}} = {(1 + \frac{{3{\rho _0}Kt}}{{\pi {\rho _p}{{\exp }_{}}(3\ln {a_{{\text{in}}}} + 4.5{{\ln }^2}\sigma )}})^{1/3}}{a_{{\text{in}}}} $ | (9) |
式中:t表示颗粒在旋风分离器内的平均停留时间,可用旋风分离器体积与流量比值表示:
| $ t = \frac{{{V_{{\text{cyc}}}}}}{Q} = \frac{{\frac{1}{4}\pi {D^2}{H_{\text{c}}} + \frac{1}{{12}}\pi {D^2}(H - {H_{\text{c}}})}}{{vS}} $ | (10) |
当颗粒粒径分布遵循对数正态分布时,颗粒质量中位径与数量中位径存在以下关系[25]:
| $ {\alpha _{{\text{in}}}} = {a_{{\text{in}}}}{\exp _{}}(3{\ln ^2}\sigma ) $ | (11) |
将式(11)代入式(9),得到式(12):
| $ {\alpha _{{\text{agg}}}} = {[1 + \frac{{3{\rho _0}Kt}}{{\pi {\rho _{\text{p}}}\exp (3\ln {\alpha _{{\text{in}}}} - 4.5{{\ln }^2}\sigma )}}]^{1/3}}{\alpha _{{\text{in}}}} $ | (12) |
由式(8)、(12)可发现,确定分级效率还需要引入凝并系数模型。荷电颗粒在旋风场中的凝并主要有湍流凝并和库仑凝并,湍流和库仑力作用具有不同的运动尺度,可认为是相互独立的,凝并系数K采用文献[26]中的方式,由湍流凝并系数和库仑凝并系数进行计算:
| $ K = \sqrt {{K_{{\text{TS}}}}^2 + {K_{\text{c}}}^2} $ | (13) |
在忽略旋流影响的情况下,可采用Saffman[27]提出的湍流凝并系数模型,如式(14)所示:
| $ {K_{{\text{TS}}}} = {\left( {\frac{{8\pi {\varepsilon _{{\text{dis}}}}}}{{15\mu }}} \right)^{\frac{1}{2}}}{(\frac{{{x_1} + {x_2}}}{2})^3} $ | (14) |
实际上,旋风分离器中湍流凝并会受到旋风场的影响,颗粒在旋风场中做螺旋运动,加剧颗粒的湍流混合,延长颗粒运动轨迹,从而影响湍流凝并系数。故需对式(14)进行校正,本研究引入一个表示旋流增强效果的系数ξtra,如式(15)所示:
| $ {K_{{\text{TS}}}} = {\xi _\text{tra}}{{\cdot}}{\left( {\frac{{8\pi {\varepsilon _{{\text{dis}}}}}}{{15\mu }}} \right)^{\frac{1}{2}}}{(\frac{{{x_1} + {x_2}}}{2})^3} $ | (15) |
显然,在一定的流速范围内,ξtra随入口流速的增大而增大,可近似用式(16)表示,其中A1是与旋风分离器结构相关的系数。
| $ {\xi _\text{tra}} = {A_1}\frac{v}{{{v_{{\text{se}}}}}} $ | (16) |
当入口流速较大时,旋流场较强的剪切力会使颗粒破碎,从而减弱颗粒在旋风分离器中的凝并作用,此时的颗粒破碎核函数由文献[16]给出。在本实验中,入口流速为7~9 m·s−1,并且引入了库仑力的影响,细颗粒物的库仑力要大于颗粒所受到的剪切应力,因此没有考虑颗粒破碎的影响。
颗粒库仑凝并系数Kc则采用Williams提出的模型[28]:
| $ {K_{\text{c}}} = \frac{{z({\text{e}^z} + 1)}}{{2({\text{e}^z} - 1)}}{K_{\text{t}}} $ | (17) |
| $ z = \frac{{{q_1}{q_2}}}{{2\pi {k_{\text{B}}}T{\varepsilon _0}({x_1} + {x_2})}} $ | (18) |
式(17)中,布朗凝并系数Kt由文献[28]给出,主要变量有颗粒粒径x1和x2,颗粒荷电量q1、q2,温度T等。
研究对象的粒径在0.48 μm以上,因此只考虑场致荷电的情况,并假设颗粒荷电在极短的时间内完成,颗粒荷电量可以表示为[29]
| $ q = 3\pi {\varepsilon _0}E{x^2}(\frac{\varepsilon }{{\varepsilon + 2}}) $ | (19) |
E为平均电场强度,与电流密度的平方根呈线性关系,借鉴线筒式电晕放电中电流与电压的关系[30],近似用式(20)表示,其中荷电电压U大于等于起晕电压Uc。
| $ E = {A_2}\sqrt {(U - {U_{\text{c}}})U} $ | (20) |
以上的湍流凝并和库仑凝并都使用了2种颗粒粒径,由于式(9)中对所有颗粒均采用了同一凝并系数,粒径为αin的单分散性颗粒的凝并系数可近似表示多分散性颗粒的凝并系数[24],故x1、x2均取为αin。
综上,双极荷电-旋风分离器分级效率可通过式(8)、(10)、(12)、(13)、(15)、(17)~(20)进行计算,其中拟合参数A1、A2为可调参数,需通过拟合实验数据得到。
4.2 物理模型计算结果与分析双极荷电-旋风分离器分级效率模型涉及的参数如表 5所示。
|
|
表 5 已知参数 Table 5 Known parameter values in the study |
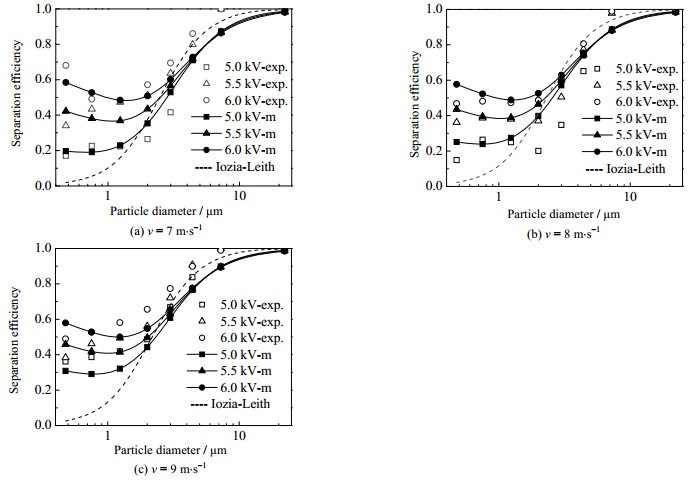
使用1stOpt软件对实验数据进行拟合,优化算法采用麦夸特法(LM)+通用全局优化法(UGO),以残差平方和最小作为拟合准则。收敛判断指标为10−10,拟合参数A1=0.146,A2=636。此时分级效率的模型计算值与实验值对比,平均绝对偏差0.071,最大绝对偏差0.223,相关系数R2=0.92。如图 7所示为模型计算得到的不同入口流速、荷电电压对应的分级效率曲线。图中,5.0 kV-m、5.5 kV-m、6.0 kV-m是荷电电压分别为5.0、5.5、6.0 kV时,使用本研究模型计算的分级效率曲线。作为对比,本研究也使用了Iozia-Leith模型[13]对各个流速下分级效率进行计算,计算值与实验值平均绝对偏差0.124,最大绝对偏差0.34。此外模型引入了颗粒凝并对分级效率的影响,细颗粒物分级效率的计算结果与实验结果更加吻合。模型适用条件如下:低浓度微米级颗粒,颗粒粒径分布近似为对数正态分布,旋风分离器入口流速在5~15 m·s−1,颗粒荷电方式为线筒式或线板式荷电。
|
图 7 本研究模型计算得到的旋风分离器分级效率 Fig.7 Fractional efficiency of the cyclone separator calculated by the model in this study |
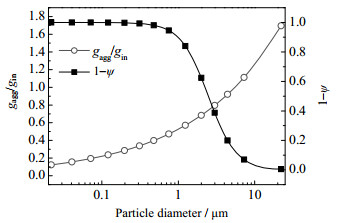
从图 7可见,双极荷电对旋风分离器的强化主要在于对细颗粒物分离效率的提升,可以有效改善传统旋风分离器难以分离细颗粒物的缺点。并且分级效率曲线呈现明显的“鱼钩效应”,在一定粒径范围内,颗粒粒径越小,分离效率越高。式(6)中,凝并前后颗粒的质量-粒径分布的比值gagg/gin反映了凝并效果的强弱,1−ψ反映了颗粒分离效果,以荷电电压6 kV,入口流速7 m·s−1为例,两者计算结果如图 8所示。随着颗粒粒径变小,gagg/gin减小,gagg/gin表示凝并后某粒径颗粒质量与原始质量的比值,说明颗粒粒径越小,颗粒受凝并过程影响越显著。从1−ψ曲线可以看到,粒径小于1 μm的颗粒物几乎不能被分离,在此区间内的颗粒物分离主要靠颗粒凝并,因此出现分离效率随粒径减小而增大的现象。颗粒尺寸较大时,gagg/gin接近于1,凝并效果较差,分级效率由颗粒分离过程决定。本研究考虑了颗粒凝并,且结果与“鱼钩现象”相符,随着颗粒凝并系数的增大,“鱼钩”现象越显著,说明此现象很可能是因颗粒间凝并形成大颗粒所导致。
|
图 8 gagg/gin与1−ψ Fig.8 Profiles of gagg/gin and 1−ψ as a function of particle diameter |
采用双极荷电技术强化了旋风分离器对细颗粒物的分离能力,进行了不同荷电电压、入口流速下的旋风分离实验,以此研究荷电电压、入口流速对颗粒在旋风场中凝并、分离过程的影响,结论如下:
(1) 双极荷电技术可以有效提高旋风分离器的总分离效率,荷电电压从0 kV提高到6 kV,入口流速为7、8、9 m·s−1时分离效率分别从44.44%、58.38%、65.07% 提升至69.76%、72.42%、75.33%。双极荷电-旋风分离器对细颗粒物具有较好的分离效率,分级效率曲线呈现类似“鱼钩”的现象,“鱼钩”效应可能是由颗粒凝并产生的。
(2) 荷电电压达到起晕电压后,颗粒荷电量随着电压的增加而增加,颗粒间库仑力的增大有利于颗粒库仑凝并,从而提高分离效率;入口流速增大后,一定程度上加强了颗粒湍流凝并,但会缩短颗粒停留时间,减弱颗粒凝并效果,降低双极荷电对旋风分离器的强化效果。
(3) 引入旋流、库仑力作用下的颗粒凝并,建立了双极荷电-旋风分离器分级效率模型。分级效率的模型计算值与实验值比较,平均绝对偏差为0.071,最大绝对偏差为0.223,模型较为可靠,可用于估计双极荷电-旋风分离器分级效率。
符号说明:
A1, A2 — 拟合参数 Vp — 颗粒总体积,m3
a — 数量中位径,m v — 入口流速,m·s−1
Cμ — 湍流相关常数 vse — 颗粒沉降速度,m·s−1
D50 — 颗粒中位径,μm x — 颗粒粒径,m
E — 平均电场强度,V·m−1 z — 无因次量
f — 摩擦系数 α — 质量中位径,m
g — 颗粒质量-粒径分布 ε0 — 真空介电常数,F·m−1
Hcs — 延伸面高度,m ε — 相对介电常数
I — 电流,mA εdis — 湍流耗散率
K — 总凝并系数,m3·s−1 η — 分离效率
Kc — 库仑凝并系数,m3·s−1 λ — 平均自由程,m
KTS — 湍流凝并系数,m3·s−1 μ — 气体黏度,Pa·s
Kt — 布朗凝并系数,m3·s−1 ξtra — 旋流增强效果系数
kB — 玻耳兹曼常数,J·K−1 ρ0 — 初始颗粒总质量浓度,mg·m−3
l — 湍流尺度,m ρg — 空气密度,kg·m−3
m — 颗粒质量,mg ρp — 颗粒密度,kg·m−3
mcyc — 旋风分离器结构相关常数 σ — 几何标准差
n — 颗粒数量 ψ — 不考虑颗粒凝并时的分级效率
q — 颗粒荷电量,C ω — 双极荷电-旋风分离器分级效率
Q — 体积流量,m3·s−1 下标
S — 入口截面积,m2 i — 撞击盘序号
T — 温度,K in — 双极荷电-旋风分离器入口
t — 平均停留时间,s out — 双极荷电-旋风分离器出口
U — 荷电电压,V agg — 凝并后
Uc — 起晕电压,V 1 — 小颗粒
Vcyc — 旋风分离器体积,m3 2 — 大颗粒
| [1] |
YAO Q, LI S Q, XU H W, et al. Studies on formation and control of combustion particulate matter in China: A review[J]. Energy, 2010, 35(11): 4480-4493. DOI:10.1016/j.energy.2010.08.009 |
| [2] |
孙国刚, 时铭显. 提高旋风分离器捕集细粉效率的技术研究进展[J]. 现代化工, 2008, 28(7): 64-69. SUN G G, SHI M X. Progress in improving removal efficiency of gas cyclones for free particles[J]. Modern Chemical Industry, 2008, 28(7): 64-69. DOI:10.3321/j.issn:0253-4320.2008.07.016 |
| [3] |
李宁, 袁伟锋, 刘含笑, 等. 基于电湍耦合凝并机制的PM2.5捕集增效装置的开发及应用[J]. 中国电力, 2018, 51(6): 17-25. LI N, YUAN W F, LIU H X, et al. Development and application of PM2.5 trapping and removal device based on turbulence coupled with bipolar-charged particle coagulation[J]. Electric Power, 2018, 51(6): 17-25. |
| [4] |
INTRA P. Corona discharge in a cylindrical triode charger for unipolar diffusion aerosol charging[J]. Journal of Electrostatics, 2012, 70(1): 136-143. DOI:10.1016/j.elstat.2011.11.007 |
| [5] |
ELIASSON B, EGLI W. Bipolar coagulation-modeling and applications[J]. Journal of Aerosol Science, 1991, 22(4): 429-440. DOI:10.1016/0021-8502(91)90003-Z |
| [6] |
张向荣, 王连泽. 外电场对双极荷电颗粒碰撞及凝聚的影响[J]. 北京理工大学学报, 2012, 32(1): 91-94. ZHANG X R, WANG L Z. Effects of an external electric field on the collision and agglomeration between bipolarly charged particles[J]. Journal of Beijing Institute of Technology (Natural Science Edition), 2012, 32(1): 91-94. |
| [7] |
谭百贺, 王连泽, 吴子牛. 双极荷电颗粒在外加交变电场中的静电凝聚[J]. 清华大学学报(自然科学版), 2009, 49(2): 301-304. TAN B H, WANG L Z, WU Z N. Electrostatic coagulation of bipolar-charged particles in an external AC electric field[J]. Journal of Tsinghua University (Science and Technology), 2009, 49(2): 301-304. DOI:10.3321/j.issn:1000-0054.2009.02.036 |
| [8] |
TRUCE R. Enhanced fine particle and mercury emission control using the indigo agglomerator[J]. VGB PowerTech, 2008, 88(3): 6-101. |
| [9] |
WANG J N, HUANG W J, XU H M, et al. Coagulation and capture of fine particles in the coupling system of corona discharge and embedded turbulence[J]. Powder Technology, 2020, 382: 85-94. |
| [10] |
陈伟, 冯健美, 韩济泉, 等. 分离层数对多层分离结构旋风分离器性能的影响[J]. 高校化学工程学报, 2019, 33(6): 1378-1385. CHEN W, FENG J M, HAN J Q, et al. Effects of separation layer on the performance of multi-layer cyclone separators[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(6): 1378-1385. |
| [11] |
钟欣, 杜浩宇, 朱诗杰, 等. 不同数量并联微旋风分离器分离性能影响研究[J]. 高校化学工程学报, 2019, 33(3): 548-556. ZHONG X, DU H Y, ZHU S J, et al. Effects of numbers of parallel micro-cyclone separators on separation performance[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 548-556. DOI:10.3969/j.issn.1003-9015.2019.03.006 |
| [12] |
侯广信, 陈建义. 颗粒碰撞团聚对旋风分离器分离性能影响研究[J]. 石油机械, 2008, 36(5): 1-4. HOU G X, CHEN J Y. Study on effect of particles collision and agglomeration on separation performance of cyclone separator[J]. China Petroleum Machinery, 2008, 36(5): 1-4. |
| [13] |
钱付平, 章名耀. 旋风分离器分离性能的经验模型与数值预测[J]. 东南大学学报(自然科学版), 2005, 35(1): 35-39. QIAN F P, ZHANG M Y. Empirical model and numerical prediction for separation performance of cyclone separator[J]. Journal of Southeast University (Natural Science Edition), 2005, 35(1): 35-39. |
| [14] |
WANG B, YU A B. Computational investigation of the mechanisms of particle separation and "fish-hook" phenomenon in hydrocyclones[J]. AIChE Journal, 2009, 56(7): 1703-1715. DOI:10.1002/aic.12114 |
| [15] |
梅芳, 张庆红, 陆厚根. 气流分级"鱼钩效应"的研究[J]. 硅酸盐学报, 1996, 24(6): 10-15. MEI F, ZHANG Q H, LU H G. Study on the "fish-hook effect" of airflow classification[J]. Journal of Chinese Ceramic Society, 1996, 24(6): 10-15. |
| [16] |
吴然, 张琳, 许伟刚, 等. 旋流场中小颗粒污染物凝并及运动特性研究[J]. 高校化学工程学报, 2019, 33(2): 338-345. WU R, ZHANG L, XU W G, et al. Coagulation and motion characteristics of small particle pollutants in swirling flow field[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 338-345. |
| [17] |
刘定平, 罗伟乐. 基于旋流与声波的颗粒复合凝并建模与运动轨迹仿真[J]. 动力工程学报, 2017, 37(5): 413-417. LIU D P, LUO W L. Moving trajectory simulation of particles and modeling of the complex coagulation based on swirl and acoustic wave[J]. Journal of Chinese Society of Power Engineering, 2017, 37(5): 413-417. |
| [18] |
冯鹏, 盛虎, 周虎, 等. 亚微米颗粒物湍流团聚数值模拟研究[J]. 洁净煤技术, 2020, 26(5): 181-187. FENG P, SHENG H, ZHOU H, et al. Numerical simulation on the characteristics of submicron particle turbulence agglomeration[J]. Clean Coal Technology, 2020, 26(5): 181-187. |
| [19] |
周建刚, 刘栋, 白敏菂, 等. 烟道中同极性荷电粉尘的凝并研究[J]. 环境工程, 2009, 27(2): 12-14, 62. ZHOU J G, LIU D, BAI M D, et al. Study on agglomeration of homo-polarity particles in flue[J]. Environmental Engineering, 2009, 27(2): 12-14, 62. |
| [20] |
陈厚涛, 赵兵, 徐进, 等. 燃煤飞灰超细颗粒物声波团聚清除的实验研究[J]. 中国电机工程学报, 2007, 27(35): 28-32. CHEN H T, ZHAO B, XU J, et al. Experimental study on acoustic agglomeration of ultrafine fly ash particles[J]. Proceedings of the Chinese Society for Electrical Engineering, 2007, 27(35): 28-32. |
| [21] |
GUIMARAES A A, KLEIN T S, MEDRONHO R A. Fish-hook effect in granulometric efficiency curves of hydrocyclones: A misuse of laser diffraction particle size analysers[J]. Powder Technology, 2020, 374: 185-189. |
| [22] |
MAJUMDER A K, YERRISWAMY P, BARNWAL J P. The "fish hook" phenomenon in centrifugal separation of fine particles[J]. Minerals Engineering, 2003, 16(10): 1005-1007. |
| [23] |
VEMURY S, CHRISTIAN J, PRATSINIS S E. Coagulation of symmetric and asymmetric bipolar aerosols[J]. Journal of Aerosol Science, 1997, 28(4): 599-611. |
| [24] |
向晓东, 陈旺生, 幸福堂, 等. 烟尘在交变电场中电凝并收集的实验研究[J]. 武汉冶金科技大学学报(自然科学版), 1999, 22(3): 252-255. XIANG X D, CHEN W S, XING F T, et al. Particle agglomeration in an aiternating electric field[J]. Journal of Wuhan University of Science and Technology, 1999, 22(3): 252-255. |
| [25] |
郝吉明, 马广大, 王书肖. 大气污染控制工程[M]. 3版. 北京: 高等教育出版社, 2010. HAO J M, MA G D, WANG S X. Air pollution control engineering[M]. 3rd ed. Beijing: Higher Education Press, 2010. |
| [26] |
FLAGAN R C, SAROFIM A F. Coal generated inorganic aerosol: A review: First international Aerosol Conference [C]. Minneapolis: American Association for Aerosol Research, 1984, 23(4): 778-782.
|
| [27] |
SAFFMAN P G, TURNER J S. On the collision of drops in turbulent clouds[J]. Journal of Fluid Mechanics, 1956, 1(1): 16-30. |
| [28] |
WILLIAMS M M R, LOYALKA S K. Aerosol science: Theory and practice, with special reference to the nuclear industry[M]. Oxford: Pergamon Press, 1991.
|
| [29] |
高梦翔, 姚鑫, 朱勇, 等. 双区静电除尘模拟设计中的颗粒荷电模型选用[J]. 工业催化, 2018, 26(10): 124-129. GAO M X, YAO X, ZHU Y, et al. Particle charging models selection in two-stage electrostatic precipitator simulation design[J]. Industrial Catalysis, 2018, 26(10): 124-129. |
| [30] |
刘志强, 何寿杰, 冯晓军, 等. 线筒式电晕放电伏安特性关系的研究[J]. 河北大学学报(自然科学版), 2008, 28(6): 604-607. LIU Z Q, HE S J, FENG X J, et al. Current-voltage characteristic of wire-cylinder type negative corona discharge[J]. Journal of Hebei University (Natural Science Edition), 2008, 28(6): 604-607. |




