2. 浙江大学衢州研究院,浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
硫酸铵[(NH4)2SO4]作为一种氮肥,具有低水分、不结团、强化学稳定性以及适用于碱性土壤等优点。然而近年来,由于尿素行业的迅速发展,硫酸铵肥料的市场空间受到挤压,其市场需求量逐年下降[1]。而另一方面,硫酸铵作为己内酰胺[2]和氨法脱硫[3]等行业的副产品,其年产量却随着这些行业的发展而迅速增加。因此,如何将过剩的硫酸铵资源化利用成为目前亟待解决的关键问题。
针对上述问题,本课题组提出在氨肟法生产己内酰胺的过程中,将副产物硫酸铵加热分解为氨和硫氧化物(SO2或SO3),硫氧化物经进一步加工制得硫酸,这两种产品可作为已内酰胺的原料在系统内循环使用。改进后的氨肟法工艺能够实现闭路循环,整个过程只有己内酰胺作为产品输出,不再有任何其它副产品,与原工艺相比更具有经济竞争力。其中,硫酸铵的热分解是实现上述工艺的关键步骤。
硫酸铵的热分解是典型的固体分解反应。KIYOURA等[4]于上世纪70年代研究了硫酸铵热分解的平衡、机理和动力学,利用热重分析结合XRD提出硫酸铵的分解可分为3个阶段:
Ⅰ:硫酸铵脱氨生成硫酸氢铵
| $ {{\text{(N}{{\text{H}}_{\text{4}}}\text{)}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\xrightarrow{{}}\text{N}{{\text{H}}_{\text{4}}}\text{HS}{{\text{O}}_{\text{4}}}\text{+N}{{\text{H}}_{\text{3}}}\text{(g)} $ | (1) |
Ⅱ:硫酸氢铵脱水生成焦硫酸铵
| $ \text{2N}{{\text{H}}_{\text{4}}}\text{HS}{{\text{O}}_{\text{4}}}\xrightarrow{{}}{{\text{(N}{{\text{H}}_{\text{4}}}\text{)}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{7}}}\text{+}{{\text{H}}_{\text{2}}}\text{O(g)} $ | (2) |
Ⅲ:焦硫酸铵分解
| $ \text{3(N}{{\text{H}}_{\text{4}}}{{\text{)}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{7}}}\xrightarrow{{}}\text{2N}{{\text{H}}_{\text{3}}}\text{(g)+2}{{\text{N}}_{\text{2}}}\text{(g)+6S}{{\text{O}}_{\text{2}}}\text{(g)+9}{{\text{H}}_{\text{2}}}\text{O(g)} $ | (3) |
总反应
| $ \text{3(N}{{\text{H}}_{\text{4}}}{{\text{)}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\xrightarrow{{}}\text{4N}{{\text{H}}_{\text{3}}}\text{(g)+}{{\text{N}}_{\text{2}}}\text{(g)+3S}{{\text{O}}_{\text{2}}}\text{(g)+6}{{\text{H}}_{\text{2}}}\text{O(g)} $ | (4) |
刘科伟[5]于本世纪初通过研究硫酸铵在管式炉中的恒温失重并结合红外光谱对产物的分析,提出与KIYOURA等相同的反应历程。近年来,范芸珠[6]通过热重分析,运用单一扫描速率法对上述3个阶段逐一进行动力学分析,得到了各个阶段对应的温度区间和动力学3因子(活化能、指前因子和反应级数)。
热分析动力学的基本方法[7]可分为等温法、单一扫描速率法和多重扫描速率法。等温法由于其不可避免的局限性,如总是存在一个升温过程,在实际当中较少使用。单一扫描速率法则是在一个常升温速率下,对热失重数据进行热动力学分析的方法。近年来,用该方法处理数据得到的结果其可靠性受到学者们的普遍质疑,认为其不能反映出固态反应的复杂本质[8-12]。为此,国际热分析及量热学学会(ICTAC)动力学分会组织呼吁应采用多重扫描速率法来处理热分析数据[13]。多重扫描速率法是指对不同升温速率所得多条热分析曲线进行热动力学分析的方法,通过重复温度扫描技术来揭示简单背后多步反应的复杂本质,还可以在不涉及动力学机理函数的前提下获得较为可靠的活化能,因此也常被称为无模式函数法(model-free method)。
本文将多重扫描速率法运用于硫酸铵热分解过程动力学分析,补充和完善已有的动力学数据。首先通过对比硫酸铵和硫酸氢铵的热失重过程,验证了硫酸铵的热分解机理;然后采用多重扫描速率法研究了硫酸铵的受热分解过程,计算得到了反应的活化能、指前因子和最概然机理函数。
2 实验部分硫酸铵和硫酸氢铵(国药集团化学试剂有限公司),AR纯,质量分数大于99%。TA-Q500热重分析仪(TA Instruments)。实验所用温度范围40~550 ℃,分别采用升温速率β为5、7.5、10、12.5和15 ℃×min-1线性升温,以高纯氮气做载气,流速40 mL×min-1,样品量约为3 mg。
3 数据处理在热分析动力学中,固体反应物转化率α的表达式为[7]:
| $ \alpha = \frac{{{m_0} - {m_t}}}{{{m_0} - {m_e}}} $ | (5) |
分别采用积分Kissinger-Akahira-Sunose(KAS)法[14]和微分Friedman法[15]计算硫酸铵热分解的活化能,各自的计算方法如下:
Ⅰ:KAS法[14](积分法)
| $ \ln (\frac{{{\beta _i}}}{{T_{\alpha , i}^2}}) = {\rm{Const}} - \frac{{{E_\alpha }}}{{R{T_{\alpha , i}}}} $ | (6) |
将
Ⅱ:Friedman法[15](微分法)
| $ \ln \left[ {\beta {{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)}_{\alpha , i}}} \right] = {\rm{Const}} - \frac{{{E_\alpha }}}{{R{T_{\alpha , i}}}} $ | (7) |
活化能计算方法类似KAS法,将
Ⅲ:方法比较
积分KAS法在推导过程中引入了温度积分近似,所以数值准确度理论上不如微分Friedman法。但是,微分法在实际运用过程中也存在基线确定困难等问题,与积分法相比不一定具有优越性。因此,两种方法可作为各自的补充,互为参考,从而求得更加准确的活化能。
3.2 机理函数精选采用Coats-Redfern法[16]为硫酸铵热分解过程精选机理函数,方程表达式如下:
| $ \ln \left[ {\frac{{G(\alpha )}}{{{T^{\rm{2}}}}}} \right] = \ln \left( {\frac{{AR}}{{\beta E}}} \right) - \frac{E}{{RT}} $ | (8) |
由上式可知,在一定的升温速率下
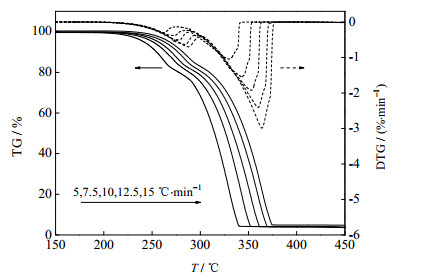
图 1是硫酸铵分别在5、7.5、10、12.5、15 ℃×min-1升温速率下的热重(TG)曲线。由图 1可知,硫酸铵热分解的起始温度约为200 ℃,整个热分解过程可分为3个阶段,分别与方程(1)、(2)和(3)相对应。将各阶段的实验失重值(ΔWE)与理论值(ΔWT)和文献[6](ΔWL)的实验值相比较,结果列于表 1中。
|
图 1 不同升温速率下硫酸铵的TG/DTG曲线 Fig.1 TG/DTG curves of ammonium sulfate at different heating rates |
|
|
表 1 硫酸铵的实验失重值与理论值和文献值的比较 Table 1 Comparison of experimental weight loss results of ammonium sulfate with theoretical and literature values |
表 1表明,实验失重值与文献值相差不大,与理论值略有偏差。原因可能为各反应阶段之间的交叉,即反应(1)尚未完全结束,反应(2)就已经开始进行,所以实验值与理论值并不完全一致。本文与文献[6]的不同之处在于3个阶段的区间划分方式。文献[6]以温度T为自变量划分区间,而从图 1中可以看出,随着升温速率的提高各阶段所对应的温度区间也随之向右偏移,以T为自变量不能准确的划分各个区间。然而,不同阶段之间所对应的转化率α是相同的,即无论升温速率如何变化,当反应进行到一定程度时,反应过程的控制步骤就会发生变化,从一个阶段转变到另一个阶段。因此,本文以转化率α为自变量划分3个阶段,为了便于使用,分别取α = 0.14和α = 0.2为区间端点;当α < 0.14时为第1阶段,式(1)即硫酸铵脱氨生成硫酸氢铵是过程的控制步骤;当0.14 < α < 0.2时为第2阶段,式(2)即硫酸氢铵脱水生成焦硫酸铵是过程的控制步骤;当α > 0.2时为第3阶段,式(3)即焦硫酸铵分解是过程的控制步骤。
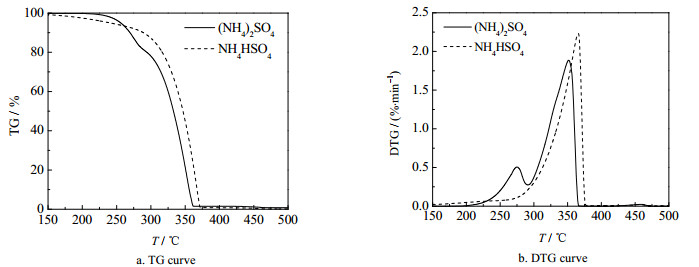
图 2为10 ℃×min-1升温速率下硫酸铵和硫酸氢铵热失重过程的TG和DTG对比。可以看到,硫酸氢铵的TG和DTG曲线形状与硫酸铵后两个阶段的曲线形状基本一致,但硫酸氢铵的起始分解温度要略低于硫酸铵第2阶段的起始温度,而热解终止温度却高于硫酸铵,曲线的形状整体有所滞后。原因可能是由于硫酸铵热分解作为一个串联反应,第2步热解反应的速率会受到第1步反应的影响,所以由硫酸铵生成的硫酸氢铵起始热解温度要低于硫酸氢铵单独热分解时的温度,但此时第1步反应生成的硫酸氢铵已经处于活化状态,所以比硫酸氢铵单独热解时更容易分解,终止热解温度相应有所降低。然而从TG和DTG的曲线形状可以断定,硫酸铵生成硫酸氢铵后的热分解与硫酸氢铵单独热分解的反应机理是一样的。因此,下文得到的硫酸铵的热分析动力学也可以用来预测硫酸氢铵的热分解过程,而不会引起太大的误差。
|
图 2 硫酸铵和硫酸氢铵热失重过程的对比 Fig.2 Comparison of thermogravimetric processes of ammonium sulfate and ammonium hydrogen sulfate |
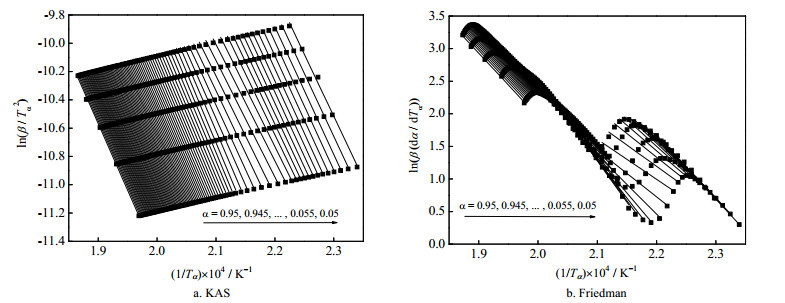
将不同升温速率下的TG和DTG数据分别代入式(6)和(7)中,得到不同转化率下的拟合直线如图 3所示。在图 3中,各拟合直线与实验点之间的相关系数R2均大于0.99,线性相关性良好。两种方法线性回归曲线斜率计算得到的不同阶段平均活化能以及文献[6]的计算结果列于表 2中。
|
图 3 不同转化率下活化能的拟合结果 Fig.3 Fitting results of activation energy at different conversions |
|
|
表 2 KAS法和Friedman法计算所得3个阶段的平均活化能 Table 2 Mean activation energies of the three stages calculated by the KAS and Friedman methods |
表 2表明,采用两种方法计算得到的3个阶段的活化能,除了第2阶段的计算结果略有偏差外,其余两个阶段的活化能差异都不大,并且第2阶段活化能的偏差也小于10%。而文献[6]中采用单一扫描速率法计算出来的活化能与本文采用多重扫描速率法计算得到的活化能有较大差异,单一扫描速率法仅用到一条热分析曲线,即使是良好的线性也未必能保证所选机理函数的合理性和参数的准确性[17],因为同一组数据可能同时有几种机理函数能与之相匹配[18],而不同机理函数得到的活化能却千差万别,因此,单一扫描速率法得到的结果理论参考意义不大。多重扫描速率法计算活化能不依赖机理函数的选择,并且本文采用微分法和积分法两种方法计算得到的活化能可以相互验证,所以结果更加准确可靠。下文也将以此计算所得活化能为基础选择机理函数。
4.3 机理函数的选择以第1阶段为例,说明机理函数的选择过程。首先,将不同升温速率下0 < α < 0.14转化率区间的热重数据和41种常用机理函数代入式(8)中,作线性回归,直线斜率即为活化能,截距为指前因子,不同升温速率下拟合结果的平均值列于表 3中;然后,将计算得到的平均活化能与表 2中KAS法和Friedman法所得活化能的平均值相比较,选取活化能相差不超过10%且相关系数最好的机理函数为最概然机理函数。比较表 2和表 3可知,第34号机理函数最为符合,为n=3反应级数机理,活化能E=96.47 kJ×mol-1,指前因子ln(A/min-1)=19.13。
|
|
表 3 第一阶段Coats-Redfern法计算结果 Table 3 Results of the Coats-Redfern method for the first stage |
用同样的方法确定确定其余阶段的最概然机理函数以及计算出相应的动力学参数,结果如表 4所示。
|
|
表 4 硫酸铵热分解的最概然机理函数和动力学参数 Table 4 Most probable mechanism functions and kinetic parameters of ammonium sulfate thermal decomposition |
采用TG-DTG技术对硫酸铵热分解过程进行多重扫描速率分析,并分别用积分KAS法和微分Friedman法计算不同阶段的活化能,然后由Coats-Redfern法推导最概然机理函数。结果表明,硫酸铵的非等温热分解分为3阶段。其中,第1阶段转化率区间为0~0.14,活化能E = 96.47 kJ×mol-1,指前因子ln(A/min-1)=19.13,符合n=3收缩圆柱体相边界反应机理;第2阶段转化率区间为0.14~0.2,E=79.47 kJ×mol-1,ln(A/min-1)=13.79,符合n=3/2随机成核和随后生长机理;第3阶段转化率为0.2~1,E=98.30 kJ×mol-1,ln(A/min-1)=18.00,符合n=3收缩球体相边界机理。上述得到的硫酸铵热解动力学也可用于硫酸氢铵热解过程的研究。
|
|
| [1] |
SONG X F, ZHAO J C, LI Y Z, et al. Thermal decomposition mechanism of ammonium sulfate catalyzed by ferric oxide[J]. Frontiers of Chemical Science and Engineering, 2013, 7(2): 210-217. DOI:10.1007/s11705-013-1320-y |
| [2] |
何晓辉, 雍玉梅, 禹耕之, 等. 己内酰胺在硫酸铵晶体表面吸附特性[J]. 化工学报, 2010, 61(11): 2849-2854. HE X H, YONG Y M, YU G Z, et al. Adsorption of caprolactam on surface of ammonium sulfate crystal[J]. CIESC Journal, 2010, 61(11): 2849-2854. |
| [3] |
葛能强, 邵永春. 湿式氨法脱硫工艺及应用[J]. 硫酸工业, 2006(6): 10-15. GE N Q, SHAO Y C. Application of wet ammonia desulphurization process[J]. Sulphuric Acid Industry, 2006(6): 10-15. DOI:10.3969/j.issn.1002-1507.2006.06.003 |
| [4] |
KIYOURA R, URANO K. Mechanism, kinetics, and equilibrium of thermal decomposition of ammonium sulfate[J]. Industrial & Engineering Chemistry Process Design & Development, 1970, 9(4): 489-494. |
| [5] |
刘科伟, 陈天朗. 硫酸铵的热分解[J]. 化学研究与应用, 2002, 14(6): 737-738. LIU K W, CHEN T L. Studies on the thermal decomposition of ammonium sulfate[J]. Chemical Research and Application, 2002, 14(6): 737-738. DOI:10.3969/j.issn.1004-1656.2002.06.038 |
| [6] |
范芸珠, 曹发海. 硫酸铵热分解反应动力学研究[J]. 高校化学工程学报, 2011, 25(2): 341-346. FAN Y Z, CAO F H. Thermal decomposition kinetics of ammonium sulfate[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(2): 341-346. DOI:10.3969/j.issn.1003-9015.2011.02.028 |
| [7] |
胡祖荣. 热分析动力学[M]. 北京: 科学出版社, 2008. HU Z R. Thermal analysis kinetics[M]. Beijing: Science Press, 2008. |
| [8] |
BROWN M E, MACIEJEWSKI M, VYAZOVKIN S, et al. Computational aspects of kinetic analysis:Part A:The ICTAC kinetics project-data, methods and results[J]. Thermochimica ACTA, 2000, 355(1): 125-143. |
| [9] |
MACIEJEWSKI M. Computational aspects of kinetic analysis:Part B:The ICTAC kinetics project-the decomposition kinetics of calcium carbonate revisited, or some tips on survival in the kinetic minefield[J]. Thermochimica ACTA, 2000, 355(1): 145-154. |
| [10] |
VYAZOVKIN S. Computational aspects of kinetic analysis.:Part C. The ICTAC kinetics project-the light at the end of the tunnel?[J]. Thermochimica ACTA, 2000, 355(1): 155-163. |
| [11] |
BURNHAM A K. Computational aspects of kinetic analysis.:Part D:The ICTAC kinetics project-multi-thermal-history model-fitting methods and their relation to isoconversional methods[J]. Thermochimica ACTA, 2000, 355(1): 165-170. |
| [12] |
RODUIT B. Computational aspects of kinetic analysis.:Part E:The ICTAC kinetics project-numerical techniques and kinetics of solid state processes[J]. Thermochimica ACTA, 2000, 355(1): 171-180. |
| [13] |
VYAZOVKIN S, BURNHAM A K, CRIADO J M, et al. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data[J]. Thermochimica ACTA, 2011, 520(1): 1-19. |
| [14] |
AKAHIRA T, SUNOSE T. Method of determining activation deterioration constant of electrical insulating materials[J]. RES REP Chiba INST Technol (Sci Technol), 1971(16): 22-31. |
| [15] |
FRIEDMAN H L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic[J]. Journal of Polymer Science Part C:Polymer Symposia, 1964, 6(1): 183-95. |
| [16] |
COATS, AMP A W, REDFERN J P. Kinetic parameters from thermogravimetric data[J]. Nature, 1964, 201(4914): 68-69. DOI:10.1038/201068a0 |
| [17] |
王文钊, 刘朝, 唐经文. 动力学参数的补偿效应及改进的求解方法[J]. 生物质化学工程, 2008, 42(4): 13-16. WANG W Z, LIU C, TANG J W. Compensation effect and an improved computing method of kinetic parameter[J]. Biomass Chemical Engineering, 2008, 42(4): 13-16. DOI:10.3969/j.issn.1673-5854.2008.04.004 |
| [18] |
CRIADO J M, MORALES J. Thermal decomposition reactions of solids controlled by diffusion and phase-boundary processes:Possible misinterpretation of the mechanism from thermogravimetric data[J]. Thermochimica ACTA, 1977, 19(3): 305-317. DOI:10.1016/0040-6031(77)80006-3 |




