1 引言

注塑成型(plastic injection molding，PIM)因其生产效率高、成本低、产品柔韧性好等优点广泛应用于各种塑料制品的制造中^[1]。PIM是一个多参数相互耦合的非线性复杂过程，对工艺参数的要求高，对工艺条件的变化敏感^[2]。PIM工艺参数的设置与产品质量和生产效率密切相关^[3]。传统参数优化方法需要进行大量试模，造成了时间成本浪费，采用正交实验设计可以在较少的实验次数下有效分析参数影响^[4-6]。Oktem等^[7]在正交实验设计的基础上使用信噪比(signal to noise，S/N)和方差分析(analysis of variance，ANOVA)确定工艺参数对翘曲和收缩的影响。

解决高分子注塑成型制品的质量缺陷工程优化问题，关键在于选择高适配性关系模型和高保真度优化算法^[8-9]。代理模型可以替代繁琐的计算机分析，建立产品质量与工艺参数间的关系函数，大幅缩短了研究时间，在PIM优化中已有广泛应用^[10-14]。与其他代理模型相比，梯度增强型Kriging(gradient-enhanced Kriging，GEK)模型^[15]在Kriging模型的基础上充分利用样本梯度信息，在少量样本时具有显著的收敛速度和模型精度，能够有效替代Moldflow等注塑模流分析软件建立质量指标预测模型。PIM参数优化需要同时考虑产品质量和生产效率，因此需要可靠有效的多目标优化算法进行全局优化^[16-17]。多目标差分进化算法(multi-objective differential evolution，MODE)与其他优化算法相比，在处理全局优化问题时收敛速度快，具有较强的鲁棒性，适用于PIM优化问题^[18-19]。

为了实现注塑过程的高质量和高效率生产，本研究提出了一种注塑成型产品质量关键工艺参数的多目标优化设计方法。针对空调外罩的注塑成型过程，通过正交实验设计和Moldflow2019软件进行数值模拟获取原样本数据；通过信噪比和方差分析确定对产品质量影响显著的参数；采用GEK模型建立产品质量预测模型，其预测精度优于Kriging模型；以最小翘曲、体积收缩率和周期时间为优化目标，采用MODE算法进行多目标优化，通过加权法选取最优参数组合并输入Moldflow进行验证。

2 注塑成型工艺参数多目标优化设计方法 2.1 注塑成型工艺分析

PIM是典型的离散工业，每个生产周期的过程大致为：塑料颗粒经螺杆挤压和加热熔融为可流动的熔体；随后熔体经螺杆推动进入喷嘴、流道和浇口直至模腔；待熔体填满模腔后经保压、冷却完全成形，最终弹出具有预期形状的制品。一般将其分为闭模、注射、保压、冷却、开模5个阶段。

PIM工艺参数主要分为温度、压力、时间3大类，这些工艺参数会影响产品质量和生产效率。翘曲和收缩是最主要的质量缺陷，指制品内外弯曲程度和体积减少程度，分别用翘曲量(warpage)和体积收缩率(volume shrinkage)来表示。生产效率指标一般选择周期时间，表示注射、保压、冷却过程的总耗时，周期时间越短，生产效率越高。

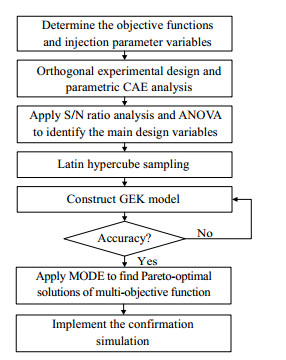
2.2 参数优化方法流程

为了提升PIM过程的产品质量和生产效率，本研究提出了一种注塑工艺参数多目标优化设计方法，用以求解翘曲量、体积收缩率和周期时间综合最小时的工艺参数组合。该方法流程如图 1所示，具体步骤如下：

步骤1：确定产品质量指标和生产效率指标，并选择相关的工艺参数，以各参数的取值范围作为设计空间。

步骤2：根据参数取值范围设计正交实验，并基于Moldflow进行数值模拟，计算得到每个正交实验的质量指标值。

步骤3：对正交实验结果进行信噪比分析和方差分析，确定各参数对质量指标的影响率，剔除对质量影响较小的参数。

步骤4：选择对质量指标影响显著的参数，通过拉丁超立方采样随机生成实验，并进行Moldflow模拟，根据模拟结果建立GEK预测模型，并与Kriging模型的精度进行对比。

步骤5：将得到的GEK预测模型作为目标函数，通过MODE算法进行多目标全局优化，得到Pareto最优解集。

步骤6：通过加权法从Pareto最优解集中选取最优参数组合，代回Moldflow进行数值模拟，验证方法的有效性。

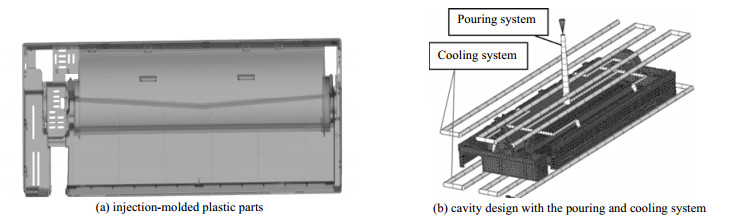
3 注塑成型模流分析与质量评价 3.1 空调外罩注塑成型模流分析模型

由于其轻量化、定制化、成本低、效率高、对复杂结构变化适应性好等特点，注塑成型技术广泛应用于空调制造行业。本研究以某空调外罩作为研究对象，其尺寸为798 mm×285 mm×135 mm，平均壁厚为5 mm，3D模型如图 2(a)所示，所用材料为聚碳酸酯和丙烯腈-丁二烯-苯乙烯共聚物和混合物(PC/ABS)材料。将空调外罩三维模型导入Moldflow软件，通过网格划分将3D模型转化为三角形单元模型。软件版本为Autodesk Moldflow (2019版)，使用Inter Core™i9-9900K CPU @ 3.60 GHz计算机处理器。网格划分后，将模型转化为完整的型腔设计，包括浇注和冷却系统，如图 2(b)所示。

3.2 正交实验设计与模拟计算

本研究在正交实验的基础上，通过S/N和ANOVA确定工艺参数对翘曲量和体积收缩率的影响关系。根据Moldflow推荐值和实际生产经验，选取模具温度θ_mo、熔体温度θ_me、注射时间t_in、注射压力p_in、保压时间t_pm、保压压力p_pm和冷却时间t_c这7个参数为最初的设计变量，将其分为3个水平，如表 1所示。

3.3 影响因素显著性分析

通过计算模拟结果的信噪比均值来确定参数对质量的影响程度。信噪比定义如式(1)所示：

$ \eta = - 10{\log _{}}({\text{MSD}}) = - 10{\log _{}}\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {Y_i^2} } \right] $

(1)

式中：$\eta $为信噪比；MSD为均方偏差；$ {Y_i} $为第i次实验的结果；$ N $为实验次数。

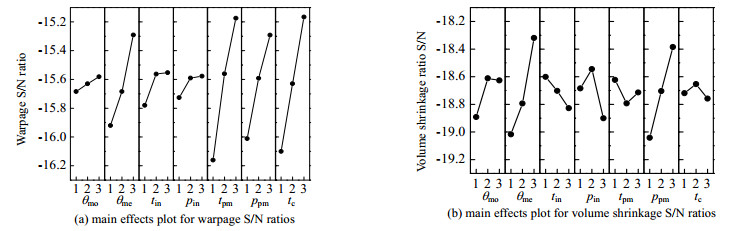
图 3分别为不同水平参数下翘曲量、体积收缩率的信噪比大小。线段跨度越大，表示信噪比的极差越大，该参数对质量的影响程度越高。因此可以推断出，参数对翘曲量影响显著顺序为：t_pm > t_c > p_pm > θ_me > t_in > θ_mo > p_in；对体积收缩率影响显著顺序为：θ_me > p_pm > p_in > θ_mo > t_in > t_pm > t_c。

为了定量比较参数对产品质量的影响程度，需要对正交结果进行ANOVA分析，分别计算各参数的自由度f、连续平方和Seq SS、翘曲的参数影响率C_wp、体积收缩率的参数影响率C_vs和总影响率C_t，见表 2。根据表 2结果可以推断出，t_pm、t_c、p_pm、θ_me是对翘曲量影响较大的主要参数。θ_me、p_pm、p_in、θ_mo的贡献率是对体积收缩率影响较大的主要参数。为了降低计算量的同时保证模型精度，需要缩减后参数的总影响率大于90%。因此选取θ_mo、θ_me、p_in、t_pm、p_pm、t_c用于建立质量预测模型。

4 基于GEK代理模型的多目标参数优化 4.1 梯度增强型Kriging模型

Kriging代理模型作为一种半参数化的插值技术，可通过部分已知的信息去模拟某一点的未知信息^[20]。假定有m个变量，需要拟合未知映射y对变量组合x=[x₁, x₂, …, x_m]^T的关系模型。拟合模型可表示为

$ y\left( \mathit{\boldsymbol{x}} \right) = {f^{\rm{T}}}(\mathit{\boldsymbol{x}})\beta + z(\mathit{\boldsymbol{x}}) $

(2)

式中：β是回归系数；上标T为转置；$ {f^{\rm{T}}}(\mathit{\boldsymbol{x}}) $是$ \mathit{\boldsymbol{x}} $的多项式，可以是0阶、一阶或二阶多项式；$ z(\mathit{\boldsymbol{x}}) $为随机分布的函数，反映局部偏差的近似，具有如下统计特性^[21]：

$ \left\{ \begin{array}{l} E\left[ {z(\mathit{\boldsymbol{x}})} \right] = 0 \hfill \\ {\rm{Va}}{{\rm{r}}_{}}\left[ {z(\mathit{\boldsymbol{x}})} \right] = {\sigma ^2} \hfill \\ {\rm{Co}}{{\rm{v}}_{}}[z({x^{\left( i \right)}}), z({x^{\left( j \right)}})] = {\sigma ^2}\left[ {R({x^{\left( i \right)}}, {x^{\left( j \right)}})} \right] \hfill \end{array} \right. $

(3)

式中：E为期望函数；Var为方差函数；Cov为协方差函数；$ {x^{\left( i \right)}} $和$ {x^{\left( j \right)}} $是训练样本中任意2个点；R是带有参数$ \theta $的相关函数，表征训练样本点间的空间相关性，常用高斯指数函数来表示，如式(4)所示。

$ R({x^{\left( i \right)}}, {x^{\left( j \right)}}) = {\exp _{}}\left( { - \sum\limits_{k = 1}^m {{\theta _k}{{\left| {x_k^{\left( i \right)} - x_k^{\left( j \right)}} \right|}^2}} } \right) $

(4)

GEK模型利用梯度信息来提高Kriging模型的精度。假设对未知函数y在n个样本处取得m个函数值及$ n \times m $个偏导数值。则训练样本的输入集$ \mathit{\boldsymbol{S}} $及对应的输出集$ {\mathit{\boldsymbol{y}}_s} $分别为

$ \mathit{\boldsymbol{S}} = {\left[ {{x^{(1)}}, \ldots , {x^{(n)}}, {x^{(1)}}, \ldots , {x^{(1)}}, \ldots , {x^{(n)}}, \ldots , {x^{(n)}}} \right]^{\rm{T}}} $

(5)

$ {\mathit{\boldsymbol{y}}_s} = {\left[ {{y^{\left( 1 \right)}}, \ldots , {y^{\left( n \right)}}, \frac{{\partial {y^{\left( 1 \right)}}}}{{\partial {x_1}}}, \ldots , \frac{{\partial {y^{\left( 1 \right)}}}}{{\partial {x_m}}}, \ldots , \frac{{\partial {y^{\left( n \right)}}}}{{\partial {x_1}}}, \ldots , \frac{{\partial {y^{\left( n \right)}}}}{{\partial {x_m}}}} \right]^{\rm{T}}} $

(6)

则拟合的GEK模型如式(7)所示：

$ y\left( \mathit{\boldsymbol{x}} \right) = {f^{\rm{T}}}(\mathit{\boldsymbol{x}})\beta + {\mathit{\boldsymbol{r}}'^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{R}}'^{ - 1}}\left( {{\mathit{\boldsymbol{y}}_s} - \beta \mathit{\boldsymbol{F}}} \right) $

(7)

$ \mathit{\boldsymbol{F}} = {[\underbrace {1{\text{ }} \cdots {\text{ }}1}_n{\text{ }}\underbrace {{\text{0 }} \ldots {\text{ 0}}}_{nm}]^{\rm{T}}} $

(8)

式中：$ \mathit{\boldsymbol{R}}' $和$ \mathit{\boldsymbol{r}}' $分别为GEK模型的相关矩阵和相关矢量；F为预估矩阵，定义如式(9)所示：

$ \mathit{\boldsymbol{R}}' = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}&{\partial \mathit{\boldsymbol{R}}} \\ {\partial {\mathit{\boldsymbol{R}}^{\rm{T}}}}&{{\partial ^2}\mathit{\boldsymbol{R}}} \end{array}} \right] \mathit{\boldsymbol{r}}' = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{r}} \\ {\partial \mathit{\boldsymbol{r}}} \end{array}} \right] $

(9)

式中：$ \partial \mathit{\boldsymbol{R}} $为Jacobi矩阵，$ {\partial ^2}\mathit{\boldsymbol{R}} $为Hessian矩阵，相关矢量$ \mathit{\boldsymbol{r}} $及其一阶导数$ \partial \mathit{\boldsymbol{r}} $定义如式(10)、(11)所示。

$ \mathit{\boldsymbol{r}} = {\left[ {\begin{array}{*{20}{c}} {R({x^{\left( 1 \right)}}, \mathit{\boldsymbol{x}})}& \cdots &{R({x^{\left( n \right)}}, \mathit{\boldsymbol{x}})} \end{array}} \right]^{\rm{T}}} $

(10)

$ \partial \mathit{\boldsymbol{r}} = {\left[ {\begin{array}{*{20}{c}} {\frac{{\partial R({x^{\left( 1 \right)}}, \mathit{\boldsymbol{x}})}}{{\partial x_1^{\left( 1 \right)}}}}& \cdots &{\frac{{\partial R({x^{\left( 1 \right)}}, \mathit{\boldsymbol{x}})}}{{\partial x_m^{\left( 1 \right)}}}}& \cdots &{\frac{{\partial R({x^{\left( n \right)}}, \mathit{\boldsymbol{x}})}}{{\partial x_1^{\left( n \right)}}}}& \cdots &{\frac{{\partial R({x^{\left( n \right)}}, \mathit{\boldsymbol{x}})}}{{\partial x_m^{\left( n \right)}}}} \end{array}} \right]^{\rm{T}}} $

(11)

4.2 模型精度验证

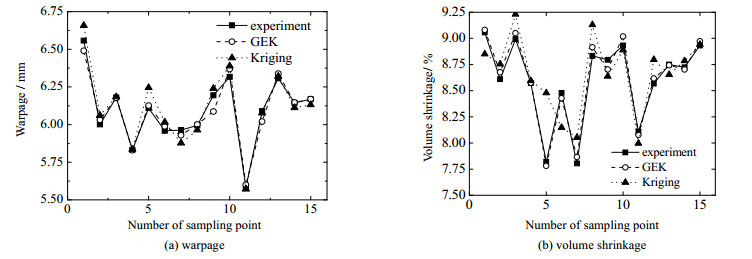
根据正交实验结果分析，选取θ_mo、θ_me、p_in、t_pm、p_pm、t_c作为建立翘曲量和体积收缩率预测模型的设计变量，t_in取翘曲量和体积收缩率综合最小时的值(3 s)。采用拉丁超立方抽样产生30组样本数据点进行模拟实验，实验结果用于建立GEK和Kriging拟合模型。另取15组模拟实验，将模拟结果与GEK模型和Kriging模型的预测结果进行对比，如图 4所示。可以发现，在整体预测精度上GEK模型优于Kriging模型。

同时采用均方根误差RMSE、平均绝对百分比误差MAPE、决定系数R²来评估GEK和Kriging模型的预测精度，MAPE和RMSE越小，R²越接近1，模型的预测精度越高。最终的评价指标值如表 3所示，可以发现，GEK模型的MAPE和RMSE值小于Kriging模型，R²大于Kriging模型，GEK预测模型精度优于Kriging模型。

4.3 多目标差分进化计算分析

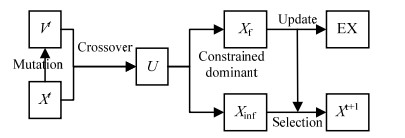
在上述GEK模型的翘曲量和体积收缩率预测模型分析基础上，采用MODE算法对注塑成型工艺参数进行优化。MODE算法的基本框架如图 5所示。

其中$ {X^t} $表示$ t $时刻的种群，$ {V^t} $表示$ t $时刻对$ {X^t} $执行变异操作后的群体，$ U $表示$ t $时刻对$ {X^t} $和$ {V^t} $执行交叉操作后的群体，$ {X^{t + 1}} $表示对$ U $进行约束支配处理和拥挤度评价之后进行选择操作得到的下一时刻的种群，由满足约束部分X_f和不满足约束部分X_inf组成，EX表示最优个体的存档集，该存档集通过与X_f中的个体比较进行实时更新。达到迭代条件后，将EX中的个体作为Pareto解集输出。

针对空调外罩的注塑成型过程，建立以产品最小翘曲量、最小体积收缩率、最短周期时间为目标的多目标优化数学模型。

$ \begin{array}{l} F(\mathit{\boldsymbol{x}}){{ = {\rm{minimiz}}}}{{\text{e}}_{}}{\text{(}}{\rm{wp}}(\mathit{\boldsymbol{x}}), {\rm{vs}}(\mathit{\boldsymbol{x}}), T(\mathit{\boldsymbol{x}}){\text{)}} \hfill \\ \left[ {\begin{array}{*{20}{c}} {{\rm{wp}}(\mathit{\boldsymbol{x}})} \\ {{\rm{vs}}(\mathit{\boldsymbol{x}})} \end{array}} \right] = {f^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\left[ {\begin{array}{*{20}{c}} {{\beta _1}} \\ {{\beta _2}} \end{array}} \right] + {{\mathit{\boldsymbol{r}}'}^{\rm{T}}}\left( \mathit{\boldsymbol{x}}\right){{\mathit{\boldsymbol{R}}'}^{ - 1}}\left( {{y_s} - \left[ {\begin{array}{*{20}{c}} {{\beta _1}} \\ {{\beta _2}} \end{array}} \right]\mathit{\boldsymbol{F}}} \right) \hfill \\ T(\mathit{\boldsymbol{x}}) = {t_{{\rm{pack}}}} + {t_{{\rm{cool}}}} + 3 \hfill \end{array} $

(12)

式中：$ F(\mathit{\boldsymbol{x}}) $为优化目标函数集合；$ {\rm{wp}}(\mathit{\boldsymbol{x}}) $、$ {\rm{vs}}(\mathit{\boldsymbol{x}}) $、$ T(\mathit{\boldsymbol{x}}) $分别为翘曲量、体积收缩率和周期时间与设计变量的关系式；$ {\beta _1} $、$ {\beta _2} $分别为翘曲量和体积收缩率的回归系数。将上述求得的GEK模型作为翘曲量和体积收缩率的关系式代入。全局设计空间如式(13)所示，其中t_ct为周期时间：

$ \begin{array}{l}{\text{50}}\ ^\circ {\text{C}}\le {\theta }_{{\rm{mo}}}\le {80}\ ^\circ {\text{C}}\\ {\text{250}}\ ^\circ {\text{C}}\le {\theta }_{{\rm{me}}}\le {280}\ ^\circ {\text{C}}\\ {120}\ {\rm{MPa}}\le {p}_{{\rm{in}}}\le {150}\ {\rm{MPa}}\\ {15}\ {\rm{s}}\le {t}_{{\rm{pm}}}\le {35}\ {\rm{s}}{\rm{}}\\ {70}\ {\rm{MPa}}\le {p}_{{\rm{pm}}}\le {90}\ {\rm{MPa}}\\ {20}\ {\rm{s}}\le {t}_{{\rm{c}}}\le {40}\ {\rm{s}}\\ {t}_{{\rm{ct}}}={t}_{{\rm{pm}}}+{t}_{{\rm{c}}}+{t}_{{\rm{in}}}\end{array} $

(13)

利用MODE算法定位多目标优化问题Pareto最优解集的过程如下：

步骤1：随机生成包含$ N $个个体的初始种群，其中$ N $为种群大小。

步骤2：评价初始种群中所有个体的目标值F和约束水平度。将满足约束的非支配最优个体加入存档集EX中。

步骤3：对剩余个体通过随机选择、二项交叉和多项式变异操作来生成子代种群$ U $。评价子代种群中每个个体的目标函数值F和约束水平度。

步骤4：根据每个个体的约束水平度，将U分为满足约束的子集X_f和不满足约束的子集X_inf，对于X_f中的个体依据支配关系和拥挤度进行非支配排序分级，对X_inf中的个体依据约束水平度进行排序。依次从X_f和X_inf中选择最优个体进入下一代种群。

步骤5：检查是否满足收敛条件。如果满足收敛条件，则EX中的最优个体为Pareto最优解集，优化过程结束；否则，将步骤4中选择的最优个体作为下一代的原始种群，重新定向到步骤2。

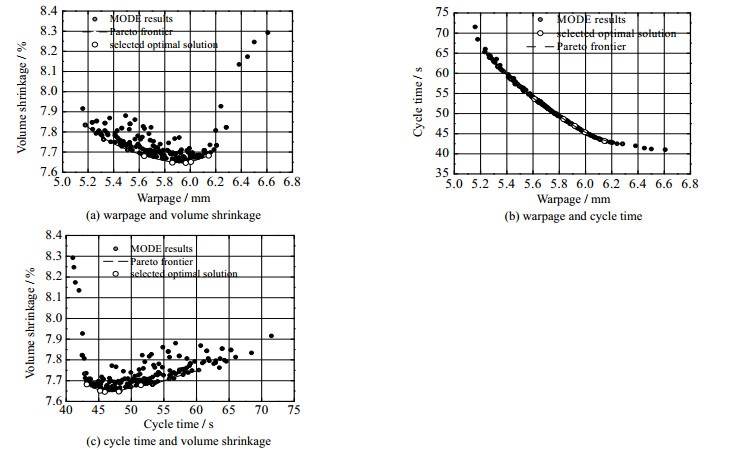
4.4 优化计算结果分析

将MODE算法的种群数量设定为200，交叉率为0.6，变异率为0.2，最大迭代次数为1 000次，最终得到的二维Pareto前沿如图 6所示。观察图 6(a)可以发现翘曲量和体积收缩率之间存在明显的折中点。从图 6(b)中可以看出，翘曲量与周期时间呈显著的线性关系，翘曲量降低，周期时间延长，Pareto前沿较为平缓，没有明显突出的部分。如图 6(c)所示，体积收缩率与周期时间之间的关系存在明显的转折。

为了从三优化目标的Pareto最优解集中得到最终的理想解，将最终解的翘曲值限定在6.2 mm内，体积收缩率限定在7.7% 内，选取5组候选解，如图 6中空心圆表示，具体数值见表 4。为了评价候选解的优劣，对5个候选解的3个指标(翘曲值、体积收缩率、周期时间)进行标准化处理：

$ {r_{ij}} = ({f_{ij}} - \mathop {\min }\limits_{1 \leqslant i \leqslant 5} \left\{ {{f_{ij}}} \right\})/(\mathop {\max }\limits_{1 \leqslant i \leqslant 5} \left\{ {{f_{ij}}} \right\} - \mathop {\min }\limits_{1 \leqslant i \leqslant 5} \left\{ {{f_{ij}}} \right\}) $

(14)

式中：f_ij为第i个候选解第j个指标的数值；r_ij为第i个候选解第j个指标标准化后的数值。

根据式(15)计算每个候选解的综合评价指数$ {r_i} $，指数越小代表候选解越优秀。

$ {r_i} = \sum\limits_{j = 1}^3 {{\lambda _j}{r_{ij}}} $

(15)

式中：λ_j为第j个指标的加权系数，用来描述指标的重要程度。根据工程师经验和产品要求，分别取翘曲值、体积收缩率、周期时间的加权系数为0.5、0.3、0.2。最终5个候选解的综合评价指数如表 4所示，第4个候选解的综合评价指数最低，因此选择候选解4的工艺参数作为优化后的最佳工艺参数。

4.5 优化结果验证

将优化后的最优工艺参数带回Moldflow软件进行模流分析，并与Moldflow推荐设定参数(θ_mo：75 ℃；θ_me：270 ℃；t_in：2 s；p_in：130 MPa；t_pm：25 s；p_pm：80 MPa；t_c：30 s)的分析结果进行对比，如图 7所示。优化后的翘曲值为5.852 mm，与模型预测值的误差为0.13%，相比优化前减少了0.88%；优化后的体积收缩率为7.554%，与模型预测值的误差为1.21%，相比优化前减少了4.68%；优化后的周期时间为48.56 s，相比优化前(52 s)降低了14.81%。

根据对比结果可以推断出：采用GEK-MODE方法得到的参数组合可实现翘曲、体积收缩率和周期时间的同步减小，在提高产品质量的同时提高生产效率，注射成型参数的最优取值：模具温度为76.85 ℃、熔体温度为279.95 ℃、注射时间为3 s、注射压力为146.68 MPa、保压时间为15.75 s、保压压力为89.99 MPa、冷却时间为26.29 s。

5 结论

本研究提出了一种包含正交实验设计、Moldflow模流分析、GEK模型和MODE算法的注塑成型工艺参数优化设计方法，以空调外罩为研究对象，通过调整模具温度、熔体温度、注射时间、注射压力、保压时间、保压压力、冷却时间7个工艺参数最小化产品的翘曲量、体积收缩率和周期时间。首先在正交实验设计的基础上，对7个变量进行影响显著性分析，发现影响翘曲值的主要因素是保压时间、冷却时间、保压压力和熔体温度，影响体积收缩率的主要因素是熔体温度、保压压力、注射压力和模具温度。然后利用GEK模型建立产品质量与工艺参数间的关系模型，其精度优于Kriging模型，且预测误差较小，能够替代Moldflow软件进行结果预测。最后利用MODE算法得到的最优参数组合，可实现翘曲量、体积收缩率和周期时间分别降低0.88%、4.68% 和14.81%。结果证明提出的参数优化设计方法能够准确分析工艺参数与产品质量的影响关系，可以有效地定位最优工艺参数设置，实现产品质量和生产效率的提高，为实际注塑工艺提供理论依据和参考。