2. 浙江创立汽车空调有限公司,浙江 龙泉 323000
2. Zhejiang Chuangli Automotive Air Conditioner Co. Ltd., Longquan 323000, China
随着社会的发展,节约能源、提高能源的利用率日趋迫切,因此改善换热器流动与换热性能是一个备受关注的课题[1-3]。平行流换热器是一种由扁管和翅片组成的高效换热器,具有体积小、重量轻、换热效率高等特点,广泛应用于汽车空调领域[4],其百叶窗翅片通过扰动流体流动以达到破坏流体边界层和强化传热的效果。因此,研究平行流换热器百叶窗翅片的流动状态以及换热强度是优化其换热性能的重要途径[5]。
目前,国内外许多学者对百叶窗翅片换热器的流动、传热和阻力特性进行大量试验和模拟研究,其中,CHANG等[6-7]根据经验和调研整理出91种百叶窗翅片模型的实验数据,拟合了传热和阻力性能关联式。该公式综合考虑了各种结构参数,关联度很高,为进一步研究提供了理论依据。YUN等[8]在低空气流速工况下对不同翅片间距和开窗角度的百叶窗翅片进行了实验研究,结果表明翅片间距对百叶窗翅片换热性能影响更大,并引入无量纲因子j/f1/3对百叶窗翅片换热器的性能进行综合评价。
虽然研究者对百叶窗进行了全面研究,但是换热性能仍然不能满足实际应用的需求[9-10],鉴此, 本文提出一种新型变截面百叶窗翅片。通过数值模拟研究变截面百叶窗翅片的流动与传热特性,并将新型变截面百叶窗翅片和矩形翅片的模拟结果进行对比。分别研究曲率数R*、百叶窗角度θ、百叶窗间距Lp等参数对其内部的流动与传热特性的影响,以综合性能因子JT最大为评价指标,筛选得出一组最优结构参数,为后续的研究提供理论依据。
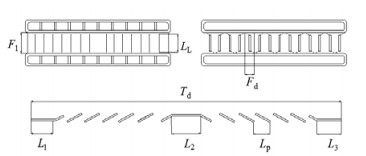
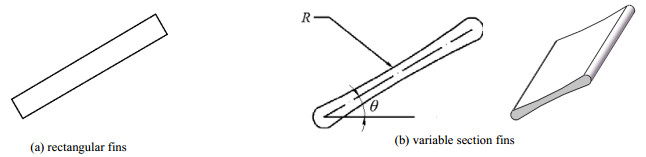
2 物理模型变截面百叶窗翅片的整体结构布局如图 1所示,图 2给出了变化前后翅片的形状示意图。变截面百叶窗翅片是在矩形百叶窗翅片的基础上提出的,通过变换矩形翅片的长边,使其弯曲一定的弧度,矩形翅片的短边用光滑的圆弧代替。变截面百叶窗翅片截面为收腰型形状,两端厚,中间薄,沿中线对称。与矩形翅片相比,变截面百叶窗翅片中间的圆弧导致空气流经百叶窗的倾角不断变化,入口进风的流动状态持续改变,加强空气在百叶窗间的扰动,强化换热效果。同时,变截面百叶窗翅片采用圆弧形表面,增大空气与翅片的接触面积,进一步加强了换热。几何模型参数如表 1所示。
|
图 1 百叶窗翅片结构 Fig.1 The structure of louver fins |
|
图 2 矩形翅片与变截面翅片结构示意图 Fig.2 Structural sketch of rectangular fins and variable section fins |
|
|
表 1 模型的基本参数 Table 1 Basic structural data of the model |
为简化计算,对物理问题进行如下假设:1)流体为不可压缩流体;2)忽略重力对传热和阻力影响;3)壁面为无滑移边界条件。基于以上假设,本研究采用三维不可压缩、稳态空气层流流动与传热模型。其连续方程、动量守恒方程、能量守恒方程如下:
连续方程:
| $ \rho \frac{{\partial {u_i}}}{{\partial {x_j}}} = 0 $ | (1) |
动量守恒方程:
| $ \rho \frac{\partial }{{\partial {x_i}}}({u_i}{u_j}) = \mu \frac{\partial }{{\partial {x_i}}}\left( {\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{{\partial p}}{{\partial {x_j}}} $ | (2) |
能量守恒方程:
| $ \rho \frac{\partial }{{\partial {x_i}}}({u_i}T) = \frac{\lambda }{{{c_p}}}\frac{\partial }{{\partial {x_i}}}\left( {\frac{{\partial T}}{{\partial {x_i}}}} \right) $ | (3) |
式中:ρ为流体密度,取值为1.225 kg·m-3;ui、uj为i,j方向的速度,m·s-1;μ为动力黏度,Pa·s;cp为流体的比定压热容,取值为1 006 J·kg-1·K-1;T为热力学温度,K;p为压力,Pa;λ为流体的导热系数,W·m-1·K-1。
3.2 边界条件模型通过基于有限元法(FEM)的FLUENT进行求解,选用压力基求解器,控制方程中的速度-压力耦合采用SIMPLE算法;能量和动量方程采用二阶迎风差分格式,边界条件具体设置如下。
入口采用速度进口,温度T=299 K,出口设置为压力出口,与流体平行的面采用对称性边界条件。平行流换热器中翅片呈周期性布置,流动和换热具有周期性,故与流体垂直方向的上下2个面设置为周期性边界条件;百叶窗的翅片表面与流体接触,设置为流固耦合面;固体区域的材料为铝,由翅片和扁管组成,扁管壁设置为恒壁温。
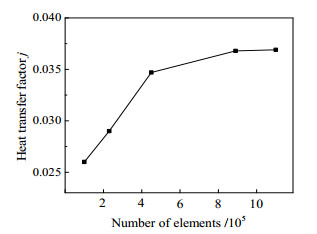
3.3 网格独立性考核图 3给出了传热因子j随网格数目的变化趋势。百叶窗翅片的几何结构具有对称性与周期性,因此可以取多元扁管间单元的一半作为计算区域以减小网格数目,节约计算时间。从图 3中可以看出,当网格数目达到89万时,传热因子j不再随网格数目变化而变化。因此,本文模拟采用的网格数目为89万。
|
图 3 网格数目对传热因子的影响 Fig.3 Effects of grid numbers on the heat transfer factor |
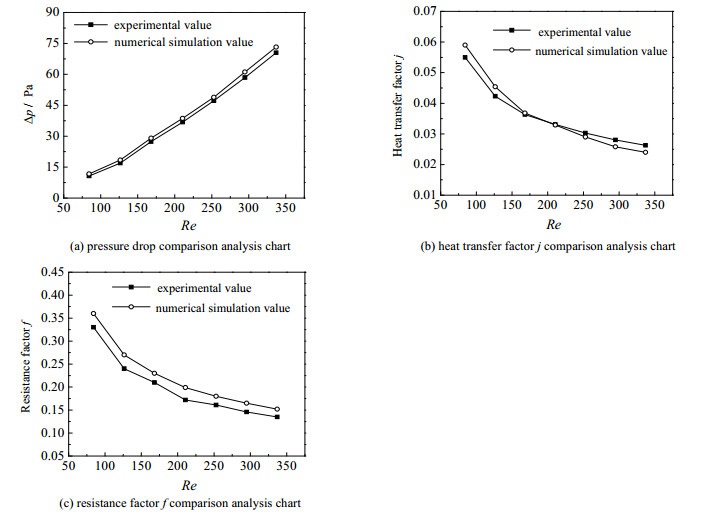
图 4给出了空气侧压降Δp、传热因子j和阻力因子f随雷诺数Re变化的计算结果。为了验证模拟方法的准确性,图中将模拟结果与CHANG等[6-7]实验关联式计算值进行比较。由图 4(a)中可以看出,随着雷诺数Re增大,空气侧压降Δp升高。由图 4(b)中可以看出,当Re < 200时,模拟得到的传热因子j值大于实验关联式计算值;当Re > 200时,实验关联式计算得到的传热因子j值高于数值模拟结果。其主要原因是:随着Re增大,流经百叶窗翅片间的流体增多,部分流体的流型发生了改变,进出口温差减小,导致模拟值的传热因子j先大于实验式值而后小于实验式值。由图 4(c)中看出,数值模拟的阻力因子f值高于实验关联式计算出的阻力因子f值,并且其差值随着Re的增大而减小。
|
图 4 模拟验证对比图 Fig.4 Verification of simulated and experimental results |
经过计算,两者之间空气侧压降Δp最大误差为9.56%,传热因子j最大误差为7.2%,阻力因子f最大误差为9.1%。这种误差产生的主要原因是实验关联式是通过大量实验研究总结而成的,在实验中会存在参数测量以及仪器不精准造成的误差,所以在其适用范围内会存在一定的误差值。其次,数值模拟在模型和计算方面采取了一些假设,例如假设空气为常物性等也会造成误差。但是偏差均在10%以内,因此模拟结果是接近真实值的。
4 数据处理基于FLUENT软件对平行流换热器空气侧的换热和流动性能进行仿真模拟,计算不同雷诺数下百叶窗翅片的j和f。j越大,换热性能越好;f越小,摩擦阻力越小;JF越大,换热器整体换热性能越好。采用的数据处理公式如下:
传热因子表达式:
| $ j = \frac{h}{{{c_p}{q_{m{\rm{a}}}}}}P{r^{{2 / 3}}} $ | (4) |
| $ h = \frac{\phi }{{{A_{\rm{a}}}\Delta {T_{{\rm{lm}}}}}} $ | (5) |
| $ \phi = {c_p}{q_{m{\rm{a}}}}\left( {{T_{{\rm{in}}}} - {T_{{\rm{out}}}}} \right) $ | (6) |
| $ \Delta {T_{{\rm{lm}}}} = \frac{{\left( {{T_{{\rm{in}}}} - {T_{{\rm{out}}}}} \right)}}{{\ln \frac{{\left( {{T_{{\rm{in}}}} - {T_{\rm{w}}}} \right)}}{{\left( {{T_{{\rm{out}}}} - {T_{\rm{w}}}} \right)}}}} $ | (7) |
式中:ua为空气进口速度,m·s-1;qma为空气质量流量,kg·s-1;Pr取0.7;ΔTlm为平均温差,K;φ为热流量,W;Aa为百叶窗翅片空气侧的换热面积,取值为173 mm2;Tin为进口温度,取值为299 K;Tout为出口温度,K;Tw为蒸发剂的温度,取值为278 K。
阻力因子表达式:
| $ f = 2\frac{{\Delta p}}{{\rho {u_{\rm{a}}}^2}} \cdot \frac{{{A_{\rm{c}}}}}{{{A_{\rm{a}}}}} $ | (8) |
| $ \Delta p = {p_{{\rm{in}}}} - {p_{{\rm{out}}}} $ | (9) |
式中:Ac为最窄处空气流通面积,取值为7.9 mm2;pin为空气进口压力,Pa;pout为空气出口压力,Pa。
综合性能因子表达式:
| $ {\rm{JF}} = {j / {{f^{1/3}}}} $ | (10) |
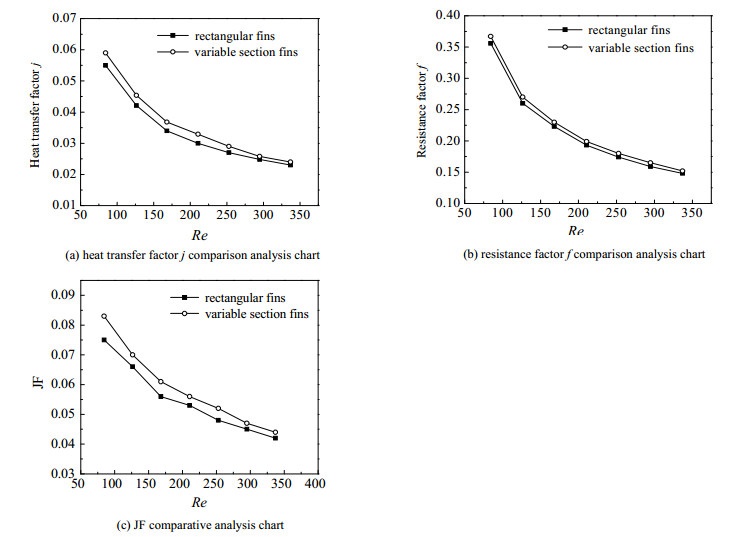
图 5给出了百叶窗矩形翅片与变截面翅片传热因子j、阻力因子f、综合性能因子JF随雷诺数Re的变化规律。从图 5中可以看出,随着Re的增大,矩形百叶窗翅片与变截面百叶窗翅片的传热因子j都减小,阻力因子f也减小。这是因为随着Re降低,迎面风速变小,空气流经百叶窗时与百叶窗换热充分,传热因子j增大,但同时流体流经百叶窗时边界层变厚,流动阻力增加,阻力因子f增大。
|
图 5 流动与传热特性对比分析 Fig.5 Comparative of flow and heat transfer characteristics |
通过比较发现,变截面翅片的传热因子j较矩形翅片提高了7.3%,但阻力因子f却增大了2.6%。导致这种现象的原因是:变截面翅片中间有一定的弧度,当气体从百叶窗翅片间流过时,具有一定弧度的百叶窗翅片会对空气流动产生扰动,增强换热。此外,曲面的设计使得翅片中间厚度变小,与空气接触的换热面积增大,更利于散热,增强了换热效果。但是流经变截面百叶窗翅片间的空气受到的扰动增大,导致流动阻力增加,压降增加。
因此,为了评价2种类型翅片的性能,采用式(10)中的综合性能因子JF进行进一步评价分析。从图 5(c)中可以看出,变截面百叶窗翅片的综合性能因子JF一直大于矩形百叶窗翅片的综合性能因子JF,平均提高了7.65%,所以变截面百叶窗翅片的换热效果更佳。
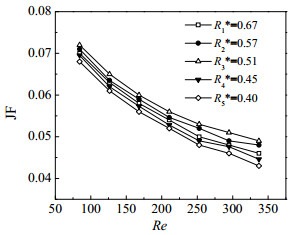
5.2 曲率数对百叶窗性能的影响图 6给出了百叶窗翅片综合性能因子JF随R*变化规律。曲率数R*是由曲率半径R与百叶窗宽度LL作比值得到的无量纲数。曲率半径R分别取2.82、3.14、3.53、4.03、4.71 mm,则曲率数R*分别为0.4、0.45、0.51、0.57、0.67。从图 6中可以看出,通过比较不同曲率数R*的综合性能因子JF,发现当曲率数R*=0.51时综合换热性能最好,曲率数R*=0.4时综合换热性能最差。这主要是因为曲率数R*减小意味着曲率半径R减小,变截面翅片中间厚度减小,百叶窗的倾角变大,空气在百叶窗间的扰动增强,加强了换热。但并不是曲率数R*越小越好,主要是因为曲率数R*过小,扰动增大的同时阻力也在增大,增大到一定程度时,换热系数增加幅度减小,但阻力系数依然在增大,所以综合性能会下降。
|
图 6 改变曲率数对比分析图 Fig.6 Profiles of results with different curvature numbers |
从图 6中还可以看出,随着Re的增大,综合性能因子JF呈下降趋势。导致这种现象的主要原因是随着Re的增大,迎面风速增大,空气在百叶窗间停留的时间变短,空气与翅片换热不充分,传热因子j减小,所以综合性能因子JF降低。
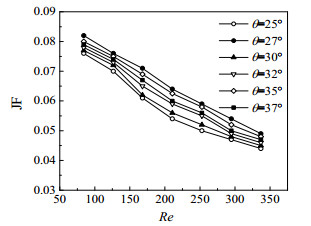
5.3 百叶窗角度对百叶窗性能的影响图 7显示了百叶窗翅片综合性能因子JF随百叶窗角度θ变化的曲线。从图 7中可以看出,百叶窗角度θ与综合性能因子JF并不是一种正比关系。说明在其他工况都一致的情况下,只改变百叶窗角度θ时,存在一个最佳百叶窗角度θ,使变截面百叶窗翅片的换热效果达到最佳,综合性能达到最优。其主要原因是百叶窗角度θ对空气在百叶窗内部流动的轨迹有影响。当百叶窗角度θ增大时,相应百叶窗高度就有所增大,相邻百叶窗间的流道宽度增加,进而增加了流场的扰动,使流动效率增大,换热效果增强。当百叶窗角度θ继续增加时,相应百叶窗高度会继续增大,到达一定高度时会阻碍流体的流动,导致流体的速度有所减小,换热效果下降。
|
图 7 改变百叶窗角度对比分析图 Fig.7 Profiles of results with different louver angles |
综上所述,从图 7中可以看出,当百叶窗角度θ = 27°时,变截面百叶窗翅片的综合性能最优;当百叶窗角度θ = 25°时,变截面百叶窗翅片的综合性能最差。
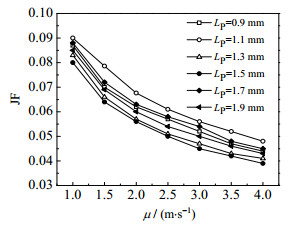
5.4 百叶窗间距对百叶窗性能的影响图 8显示了百叶窗翅片综合性能因子JF随百叶窗间距Lp变化的曲线。从图 8中可以看出,当百叶窗间距Lp=1.1 mm时,变截面百叶窗翅片综合性能最好;当百叶窗间距Lp=1.5 mm时,变截面百叶窗翅片综合性能最差。导致这一现象的原因是:在相同的迎风面速度下,当百叶窗间距Lp较小时,只有少部分空气流经百叶窗,其余大部分空气沿百叶窗轴向流动,阻力较小,换热系数较低。随着百叶窗间距Lp的增大,流经百叶窗间的空气增多,换热效果增强,但同时阻力也在增加。当百叶窗间距Lp达到某一值后继续增加,空气侧的水力直径增大,空气流经百叶窗翅片时流速减小,换热效果下降,阻力减小。
|
图 8 改变百叶窗间距对比分析图 Fig.8 Profiles of results with different louver spacing |
本文通过数值模拟研究了变截面百叶窗翅片的流动与传热特性,分析了曲率数R*、百叶窗角度θ、百叶窗间距Lp等参数分别变化时对变截面百叶窗翅片传热及流动阻力的影响规律,得到以下结论:
(1) 通过与实验关联式对比,数值模拟得到的变化规律与实验关联式相同,其传热因子j最大偏差为7.2%,阻力因子f最大偏差为9.1%,验证了变截面百叶窗翅片计算模型的正确性。
(2) 变截面百叶窗翅片与矩形翅片相比,综合性能因子JF平均提高了7.65%,强化了换热效果,具有一定的理论指导意义和广泛的应用价值。
(3) 在本文研究范围内,当曲率数R*在0.4~0.67变化时,曲率数R*=0.51时综合性能最优;当百叶窗角度θ在25°~37°变化时,百叶窗角度θ=27°时综合性能最优;当百叶窗间距Lp在0.9~1.9 mm变化时,百叶窗间距Lp=1.1 mm时综合性能最优。
| [1] |
李亚子, 雷勇刚, 吕永康, 等. 斜百叶片支撑多管束受限外流传热和阻力特性[J]. 高校化学工程学报, 2017, 31(3): 579-585. LI Y Z, LEI Y G, LV Y K, et al. Heat transfer and flow resistance of confined external flow in louver baffle supported tube bundles[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(3): 579-585. DOI:10.3969/j.issn.1003-9015.2017.00.029 |
| [2] |
夏春杰, 王定标, 董永申, 等. 基于遗传算法的蜂窝板换热器多目标优化[J]. 高校化学工程学报, 2015, 29(5): 1201-1206. XIA C J, WANG D B, DONG Y S, et al. Multi-objective optimization of honeycomb plate heat transfer exchangers using a genetic algorithm method[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1201-1206. DOI:10.3969/j.issn.1003-9015.2015.00.024 |
| [3] |
李文江, 张井志, 吕迪, 等. 百叶窗板翅式换热器换热与阻力性能数值模拟研究[J]. 热能动力工程, 2019, 34(2): 101-108. LI W J, ZHANG J Z, LV D, et al. Numerical simulation of heat transfer and resistance performance of louver fin heat exchanger[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(2): 101-108. |
| [4] |
邓敏锋.多元平行流蒸发器数值模拟及性能优化[D].长沙: 中南大学, 2007. DENG M F. Numerical simulation and performance optimization of multi-parallel flow evaporator[D]. Changsha: Central South University, 2007. http://d.wanfangdata.com.cn/thesis/Y1084903 |
| [5] |
崔晓梅.多元平行流蒸发器换热特性研究[D].大连: 大连理工大学, 2012. CUI X M. Study on heat transfer characteristics of multi-parallel flow type evaporator[D]. Dalian: Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012395426.htm |
| [6] |
CHANG Y J, HSU K C, LIN Y T, et al. A generalized friction correlation for louver fin geometry[J]. International Journal of Heat & Mass Transfer, 2000, 43(12): 2237-2243. |
| [7] |
CHANG Y J, WANG C C. A generalized heat transfer correlation for louver fin geometry[J]. International Journal of Heat & Mass Transfer, 1997, 40(3): 533-544. |
| [8] |
KIM J H, CHANG S L, YUN J H. Heat-transfer and friction characteristics for the louver-fin heat exchanger[J]. Journal of Thermophysics & Heat Transfer, 2012, 18(1): 58-64. |
| [9] |
张丽娜, 高长银, 刘敏珊. 新型百叶窗翅片对流换热特性研究[J]. 压力容器, 2014, 31(5): 46-50. ZHANG L N, GAO C Y, LIU M S. Research on convective heat transfer characteristics of new kinds of louver fins[J]. Pressure Vessel Technology, 2014, 31(5): 46-50. DOI:10.3969/j.issn.1001-4837.2014.05.007 |
| [10] |
周光辉, 胡亚晗, 曹侃, 等. 椭圆形百叶窗翅片传热强化数值分析[J]. 低温与超导, 2018, 46(6): 71-75, 81. ZHOU G H, HU Y H, CAO K, et al. Numerical analysis of heat transfer enhancement of elliptical louver fins[J]. Cryogenics & Superconductivity, 2018, 46(6): 71-75, 81. |




