2. 陕西省洁净煤转化工程技术中心, 陕西 西安 710069
2. Shaanxi Research Center of Engineering Technology for Clean Coal Conversion, Xi′an 710069, China
与常规喷动床相比,多喷嘴喷动流化床具有颗粒相与气相混合更均匀、流动更快、颗粒死区更小、壁面黏结更少等优点[1],具有良好的研发优势。计算流体力学-离散单元(CFD-DEM)耦合模型对连续相求解N-S方程,对颗粒相求解牛顿第二定律,在喷动床研究中广泛应用[2]。Yue等[3]用CFD-DEM模型研究喷动床内颗粒密度对喷动偏转的影响,用喷动偏转角度量化喷动偏转行为,结果表明交替喷动偏转的流体力学特性与初始状态和颗粒密度关系不大。Liu等[4]用CFD-DEM耦合方法研究了不同密度颗粒的喷动特性,得到了不同密度和流速下的流型图,结果表明,最小喷动气速、床层压降和稳态喷动气速范围随颗粒密度的增加而增加。目前,采用CFD-DEM方法对多喷嘴喷动流化床内颗粒流体力学和传热特性的研究未见报道。本研究基于欧拉-拉格朗日框架下的CFD-DEM方法,采用Fluent15.0分析多喷嘴喷动流化床内颗粒的流动及混合特性,并引入Li和Mason[5]传热模型研究不同操作参数对传热的影响,将模拟结果与常规喷动床比较,为多喷嘴喷动流化床的推广应用提供理论和应用参考。
2 模型方程 2.1 固相CFD-DEM模拟方法对固相采用离散单元法(DEM)求解。通过牛顿第二定律和角动量守恒对单个颗粒进行受力分析,计算公式如下[6]:
| $m_i \frac{\mathrm{d} \boldsymbol{v}_i}{\mathrm{d} t}=m_i \boldsymbol{g}+\boldsymbol{F}_{\mathrm{n}}+\boldsymbol{F}_{\mathrm{t}}+\boldsymbol{F}_{\mathrm{drag}}+\boldsymbol{F}_{\mathrm{p}}$ | (1) |
| $ I_i \frac{\mathrm{d} \omega_i}{\mathrm{d} t}=\boldsymbol{M}_i $ | (2) |
式中:
| $\boldsymbol{F}_{\mathrm{n}}=\frac{4}{3} E^* \sqrt{R^*} \delta_{\mathrm{n}}^{3/2} \boldsymbol{n}+2 \sqrt{\frac{5}{6}} \zeta \sqrt{S_{\mathrm{n}} m^*} \boldsymbol{v}_{\mathrm{n}}^{\mathrm{rel}}$ | (3) |
式中:n为法向单位矢量;
| $ \frac{1}{{{E^*}}} = \frac{{\left( {1 - v_i^2} \right)}}{{{E_i}}} + \frac{{\left( {1 - v_j^2} \right)}}{{{E_j}}} $ | (4) |
| $ \frac{1}{{{R^*}}} = \frac{1}{{{R_i}}} + \frac{1}{{{R_j}}} $ | (5) |
| $ \frac{1}{{{m^*}}} = \frac{1}{{{m_i}}} + \frac{1}{{{m_j}}} $ | (6) |
| $ \zeta=\frac{\ln e}{\sqrt{\ln ^2 e+\pi^2}} $ | (7) |
| $ S_{\mathrm{n}}=2 E^* \sqrt{R^* \delta_{\mathrm{n}}}$ | (8) |
式中:
| $\boldsymbol{F}_{\mathrm{t}}=-8 G^* \sqrt{R^{*} \delta_{\mathrm{n}}} \delta_{\mathrm{t}} \boldsymbol{t}+2 \sqrt{\frac{5}{6}} \zeta \sqrt{S_{\mathrm{t}} m^*} \boldsymbol{v}_{\mathrm{t}}^{\mathrm{rel}} $ | (9) |
| $\boldsymbol{F}_{\mathrm{drag}}=\frac{\zeta}{1-\varphi_{\mathrm{g}}}\left(\boldsymbol{u}_{\mathrm{g}}-\boldsymbol{v}_i\right) \frac{\pi}{6} d_{\mathrm{p}}^3$ | (10) |
| $\boldsymbol{M}_i=-\mu_{\mathrm{r}} \boldsymbol{F}_{\mathrm{n}} R_i \omega_i$ | (11) |
| $ \boldsymbol{F}_{\mathrm{p}}=-V_{\mathrm{p}, i} \nabla p_{\mathrm{g}}$ | (12) |
式中:
气相被当作连续相,通过N-S方程获得每相的运动信息。质量和动量守恒方程如下[11]:
| $\frac{\partial}{\partial t}\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}}\right)+\nabla \cdot\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{u}_{\mathrm{g}}\right)=0$ | (13) |
| $\frac{\partial}{\partial t}\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{u}_{\mathrm{g}}\right)+\nabla \cdot\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{u}_{\mathrm{g}} \boldsymbol{u}_{\mathrm{g}}\right)=-\varphi_{\mathrm{g}} \nabla p_{\mathrm{g}}+\nabla \cdot\left[\varphi_{\mathrm{g}}\left(\boldsymbol{\tau}_{\mathrm{g}}+\boldsymbol{\tau}_{\mathrm{g}}^{\prime \prime}\right)\right]+\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{g}-\boldsymbol{F}_{\mathrm{d}}$ | (14) |
| $ \frac{\partial}{\partial t}\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} c_{\mathrm{g}} T_{\mathrm{g}}\right)+\nabla \cdot\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} u_{\mathrm{g}} c_{\mathrm{g}} T_{\mathrm{g}}\right)=\nabla \cdot\left[\varphi_{\mathrm{g}}\left(k_{\mathrm{g}}+k_{\mathrm{t}}\right) \nabla T_{\mathrm{g}}\right]+\sum\nolimits_{i=1}^{k_v} Q_{\mathrm{g}, i}$ | (15) |
式中:
| $ \boldsymbol{\tau}_{\mathrm{g}}=\mu_{\mathrm{g}}\left[\left(\nabla \boldsymbol{u}_{\mathrm{g}}\right)+\left(\nabla \boldsymbol{u}_{\mathrm{g}}\right)^{-1}\right]-\frac{2}{3} \mu_{\mathrm{g}}\left(\nabla \cdot \boldsymbol{u}_{\mathrm{g}}\right) \boldsymbol{I}$ | (16) |
| $ \boldsymbol{\tau}_{\mathrm{g}}^{\prime \prime}=\mu_t\left[\left(\nabla \boldsymbol{u}_{\mathrm{g}}\right)+\left(\nabla \boldsymbol{u}_{\mathrm{g}}\right)^{-1}\right]-\frac{2}{3} \mu_t\left(\nabla \cdot \boldsymbol{u}_{\mathrm{g}}\right) \boldsymbol{I}-\frac{2}{3}$ | (17) |
| $ \boldsymbol{F}_{\mathrm{d}}=\beta\left(\boldsymbol{u}_{\mathrm{g}}-\boldsymbol{u}_{\mathrm{s}}\right)$ | (18) |
式中:μg为气体黏度,Pa·s;I为颗粒应力张量;μt为湍流黏度,kg·m−1·s−1;us为固相速度,m·s−1。
同时,引入Gidaspow曳力模型进行计算,计算公式如下[14-15]:
| $\beta=\left\{\begin{array}{ll} \frac{3}{4} \frac{\varphi_{\mathrm{g}}\left(1-\varphi_{\mathrm{g}}\right) \rho_{\mathrm{g}}\left|\boldsymbol{u}_{\mathrm{g}}-\boldsymbol{u}_{\mathrm{s}}\right|}{d_{\mathrm{p}}} C_{\mathrm{D} 0} \varphi_{\mathrm{g}}{ }^{-2.7} & \varphi_{\mathrm{g}}>0.8 \\ 150 \frac{\left(1-\varphi_{\mathrm{g}}\right)^2}{\varphi_{\mathrm{g}} d_{\mathrm{p}}{ }^2}+1.75 \frac{\left(1-\varphi_{\mathrm{g}}\right) \rho_{\mathrm{g}}\left|\boldsymbol{u}_{\mathrm{g}}-\boldsymbol{u}_{\mathrm{s}}\right|}{d_{\mathrm{p}}} & \varphi_{\mathrm{g}} \leqslant 0.8 \end{array}\right. $ | (19) |
| $C_{\mathrm{D} 0}=\left\{\begin{array}{ll} \frac{24}{R e_{\mathrm{p}}}\left(1+0.15 R e_{\mathrm{p}}^{0.687}\right) & R e_{\mathrm{p}}<1\;000 \\ 0.44 & R e_{\mathrm{p}} \geqslant 1\;000 \end{array}\right.$ | (20) |
式中:
气相湍流用
| $\frac{\partial}{\partial t}\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} k\right)+\nabla \cdot\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} k \boldsymbol{u}_{\mathrm{g}}\right)=\nabla \cdot\left[\varphi_{\mathrm{g}}\left(\mu_{\mathrm{g}}+\frac{\mu_t}{\sigma_{\mathrm{k}}}\right) \nabla k\right]+\varphi_{\mathrm{g}} G_{\mathrm{k}}-\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \varepsilon$ | (21) |
| $ \frac{\partial}{\partial t}\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \varepsilon\right)+\nabla \cdot\left(\varphi_{\mathrm{g}} \rho_{\mathrm{g}} \varepsilon \boldsymbol{u}_{\mathrm{g}}\right)=\nabla \cdot\left[\varphi_{\mathrm{g}}\left(\mu_{\mathrm{g}}+\frac{\mu_t}{\sigma_{\varepsilon}}\right) \nabla \varepsilon\right]+\varphi_{\mathrm{g}} C_{1 \mathtt{ε}} \frac{\varepsilon}{k} G_{\mathrm{k}}-C_{2 \mathtt{ε}} \rho_{\mathrm{g}} \frac{\varepsilon^2}{k} $ | (22) |
式中:
气体的能量方程的求解形式为[17]
| $ \frac{\partial}{\partial t}(\rho E)+\nabla(\boldsymbol{v}(\rho E+p))=\nabla\left(k_{\mathrm{eff}} \nabla T-\sum\limits_j h_j \boldsymbol{J}_j+\left(\boldsymbol{\tau}_{\mathrm{eff}} \boldsymbol{v}\right)\right)+S_{\mathrm{h}}$ | (23) |
式中:
| $ {Q_{i.j}} = {h_{i, j}}\left( {{T_j} - {T_i}} \right) $ | (24) |
式中:
通过Li和Mason[5]提出的传热模型对对流换热系数
| $h_{\mathrm{pg}, i}=\frac{N u_{\mathrm{p}, i} k_{\mathrm{g}}}{d_{\mathrm{p}, i}}$ | (25) |
| $N u_{\mathrm{p}, i}=\left\{\begin{array}{lr} 2+0.6 \varphi_{\mathrm{g}}^{3.5} Re_{\mathrm{p}, i}^{1/2} Pr^{1/3} & Re_{\mathrm{p}, i}<200 \\ 2+0.5 \varphi_{\mathrm{g}}^{3.5} Re_{\mathrm{p}, i}^{1/2} Pr^{1/3}+0.02 \varphi_{\mathrm{g}}^{3.5} R e_{\mathrm{p}, i}^{0.8} P r^{1/3} & 200 <R e_{\mathrm{p}, i} <1\;500 \\ 2+0.000\;045 \varphi_{\mathrm{g}}^{3.5} Re_{\mathrm{p}, i}^{1.8} & R e_{\mathrm{p}, i}>1\;500 \end{array}\right.$ | (26) |
| $P r=\frac{\mu_{\mathrm{g}} C_{p, \mathrm{~g}}}{k_{\mathrm{g}}}$ | (27) |
式中:
单个颗粒的温度随时间的变化[19]与气体和颗粒之间的对流传热[17]公式表示为
| $ m_{\mathrm{p}} C_{\mathrm{p}} \frac{\mathrm{d} T}{\mathrm{d} t}=\sum Q_{\text {heat }} $ | (28) |
| $Q_{i, \mathrm{~g}}=h_{\mathrm{pg}, i} A_{\mathrm{p}, i}\left(T_{\mathrm{g}}-T_{\mathrm{p}, i}\right)$ | (29) |
式中:
颗粒-流体-颗粒间的热传导的计算公式为[18]:
| $ Q_{\mathrm{pgp}, i j}=k_{\mathrm{g}}\left(T_{\mathrm{p}, j}-T_{\mathrm{p}, i}\right) \int\limits_{R_{\mathrm{in}}}^{R_{\mathrm{out}}} \frac{2 \pi x}{l_{i j}-\left(\sqrt{r_i^2-x^2}+\sqrt{r_j^2-x^2}\right)} \mathrm{d} x$ | (30) |
式中:
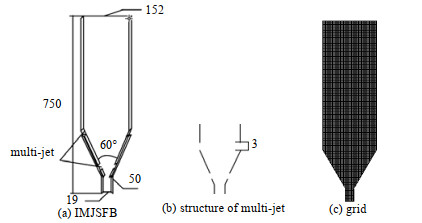
本研究的多喷嘴喷动流化床为侧壁开孔,喷嘴数量为1对,喷嘴的直径为3 mm,如图 1所示,颗粒属性以及模拟参数见表 1。恢复系数及摩擦系数与文献[20]一致,通过FFT功率谱分析实验和模拟的压力波动情况,结果表明实验和模拟结果吻合,参数选取合理。在颗粒混合过程中,2个喷动床的总气体体积流量一致,进气速度为1.875 m·s−1。为了更好地比较颗粒的流动特性,颗粒特性与杨春玲[21]的研究保持一致。初始与边界条件设置如表 2所示。采用
|
图 1 多喷嘴喷动流化床的示意图(unit: mm) Fig.1 Schematic diagram of multi-jet spout-fluidized bed (unit: mm) |
|
|
表 1 模拟使用颗粒的详细属性和模拟参数 Table 1 Detailed properties and particle parameters used in simulation |
|
|
表 2 初始和边界条件的设置 Table 2 Setting of initial and boundary conditions |
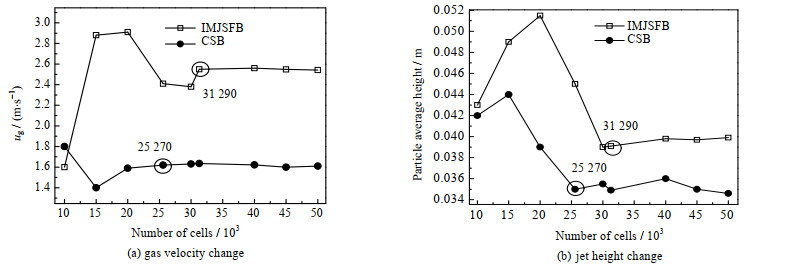
通过分析网格独立性和时间步长验证模型的准确性。根据Liu等[22]的实验数据,对喷动床内的颗粒进行模拟。图 2为CSB和IMJSFB的网格独立性的测试结果。图 2(a)和(b)分别表示同一截面处气体最高流速和颗粒平均喷流高度的大小。在验证网格独立性时,计算网格数越多,仿真精度越高。综合考虑计算精度、计算时间以及计算成本,当网格数为31 290时可以实现网格独立性。
|
图 2 网格独立性测试 Fig.2 Grid independence test |
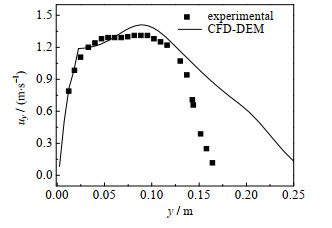
图 3为CSB内颗粒速度沿床层轴线分布的实验与模拟对比,颗粒速度的变化基本保持一致。颗粒以一定速度从入口边界被夹带到喷射区中心区域,并在短时间内加速到最大速度,随后进入喷泉区,颗粒的垂直速度uy逐渐减小。
|
图 3 颗粒沿床层轴线的平均时间垂直速度 Fig.3 Profile of the time-averaged particles vertical velocity along bed axis |
从颗粒流动、混合和传热3个方面比较IMJSFB和CSB,模拟工况如表 3所示。
|
|
表 3 模拟工况汇总 Table 3 Summary of simulated working conditions |
颗粒的碰撞和能量特性能在很大程度上反映其流动特性,对床层压降的分析能很好地体现喷动床内的气泡行为。
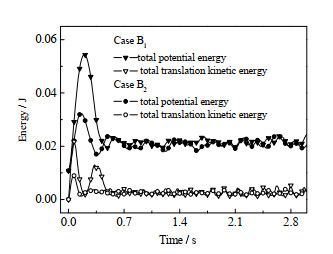
颗粒总势能和总平移动能随时间变化如图 4所示。曲线的峰值在喷动的初始阶段出现,当颗粒喷动稳定后,曲线呈周期性波动。整体来看,IMJSFB的颗粒平均总势能和平均总平移动能均比CSB低,这是由侧壁开孔对主喷嘴气体的分流作用引起的。
|
图 4 颗粒总势能和总平移动能随时间变化 Fig.4 Changes in total potential energy and total translational kinetic energy of particles with time |
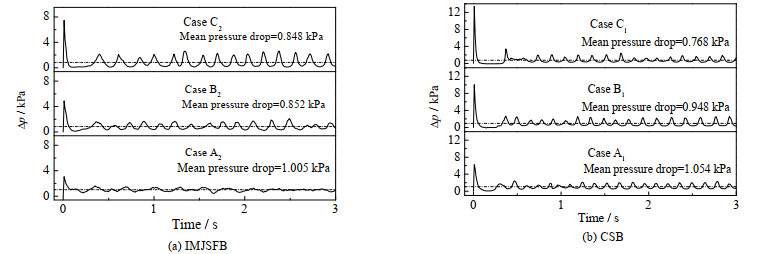
图 5为3种工况下床层压降Δp随时间的变化。初始阶段,床层压降随气速增大而增大。原因是颗粒在床内密集堆积,床层为固定床,床层阻力随气速增大而增大,床层压降随之增大。在同一工况下,当气速较低时IMJSFB的床层压降比CSB小,气速较大时情况相反。这是因为气速低时侧开孔的存在使IMJSFB实现了分级喷动,气速增大时分级喷动转换为整体抬升。
|
图 5 不同床内不同气速下床层压降随时间的变化 Fig.5 Changes of bed pressure drop with time at different gas velocities |
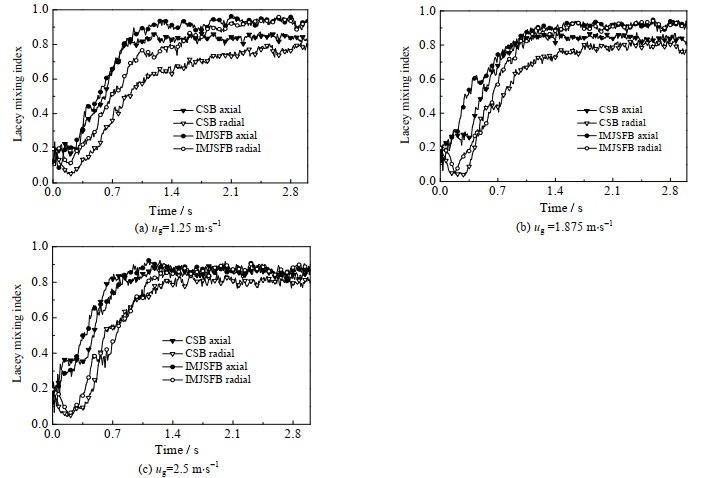
引入Lacey指数表征颗粒从初始离散状态到理想混合过程的演变。图 6为不同气速下喷动床内颗粒的轴径向混合指数随时间的变化。颗粒轴向混合指数均高于径向,因此喷动床的全床混合效果取决于径向混合。同时,侧壁开孔对环隙区的扰动改善了颗粒的混合效果,从而IMJSFB的混合效果优于CSB。
|
图 6 不同气速下2种床内颗粒的轴径向混合指数随时间的变化 Fig.6 Variation of axial-radial mixing index of particles with time under different gas velocities in two kinds of beds |
引入混合强化因子
| $ \eta_{\mathrm{M}}=\frac{\overline{M_{\mathrm{IMJSFB}}}}{\overline{M_{\mathrm{CSB}}}} \times 100 \%$ | (31) |
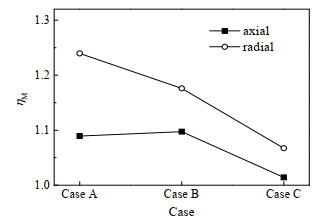
图 7为IMJSFB在不同气速下混合强化因子ηM的变化。不同工况下的混合强化因子均大于1,在侧喷嘴的作用下轴径向混合效果更好。CSB的径向混合主要受环隙区颗粒死区的影响,而侧壁开孔在一定程度上可以改善这种现象。
|
图 7 不同气速下混合强化因子 Fig.7 Mixed enhancement factor at different gas velocities |
传热过程的模拟参数设置情况汇总于表 4。
|
|
表 4 模拟传热参数的设置 Table 4 Setting of heat transfer parameters |
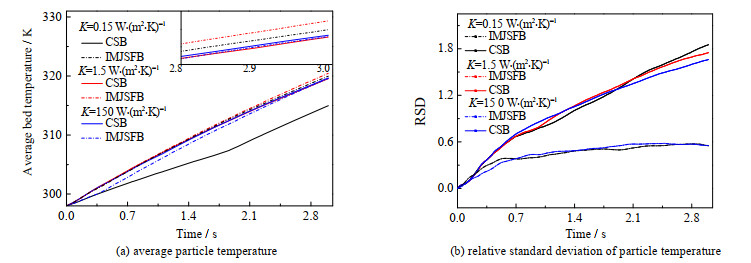
不同传热系数对喷动床传热的影响如图 8所示。其中,进气温度、进气速度、颗粒比热容分别为373 K、1.875 m·s−1、344 J·(kg·K)−1。IMJSFB中侧开孔对壁面的扰动作用改善了颗粒与热气体之间的对流传热。颗粒的传热效果随传热系数的增大而增大,当传热系数较低时,IMJSFB的优势更明显。IMJSFB的颗粒温度相对标准偏差远小于CSB,说明在IMJSFB中颗粒混合更均匀,有利于传热。
|
图 8 传热系数对颗粒平均温度与颗粒温度相对标准偏差影响 Fig.8 Effect of heat transfer coefficient on average particle temperature and relative standard deviation of particle temperature |
颗粒热容值对喷动床传热的影响如图 9所示。其中,进气温度、进气速度、颗粒传热系数分别为373 K、1.875 m·s−1、1.5 W·(m2·K−1)。颗粒热容值较小时,IMJSFB的颗粒升温速度更快。颗粒热容值一定时,IMJSFB的颗粒温度相对标准偏差低于CSB,说明侧开孔的存在提高了颗粒间的传热效果。

|
图 9 颗粒热容值对颗粒平均温度与颗粒温度相对标准偏差影响 Fig.9 Effect of heat capacity of particle on average particle temperature and relative standard deviation of particle temperature |
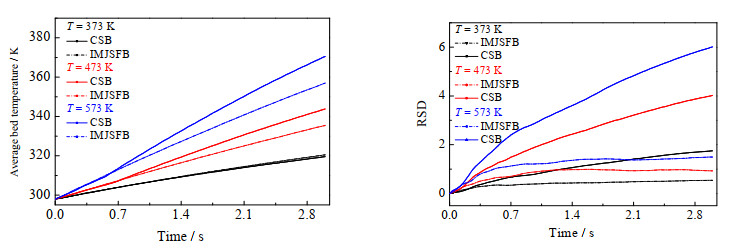
进气温度对喷动床传热的影响如图 10所示。其中,进气速度、颗粒比热容、颗粒传热系数分别为1.875 m·s−1、344 J·(kg·K)−1、1.5 W·(m2·K)−1。进气温度越高,颗粒的升温速度越快,传热效果越好。IMJSFB的颗粒温度相对标准偏差随温度变化不明显,全床温度均匀性更好。此外,当颗粒温度较低时,2种床的颗粒平均温度差异不大,且IMJSFB的颗粒温度相对标准偏差低于CSB,因此IMJSFB适合处理进气温度低的颗粒。
|
图 10 进气温度对喷动床内颗粒平均温度与颗粒温度相对标准偏差影响 Fig.10 Effect of inlet temperature on average particle temperature and relative standard deviation of particle temperature in spouted bed |
多喷嘴喷动流化床有效消除了喷动床内锥体流动死区,气-固两相流动状态实现了整体优化。与常规喷动床相比,多喷嘴结构能够有效强化床内颗粒的流动与混合,进而提升了床内颗粒、流体相间的传热传质效率与反应效率。研究结果对多喷嘴喷动流化床烟气脱硫脱碳过程强化与工程应用具有一定的参考价值。
(1) 多喷嘴喷动流化床中侧开孔的存在改善了颗粒流动死区的现象,同时实现了分级喷动过程,在一定程度上减小了颗粒的喷动阻力。
(2) 多喷嘴喷动流化床的径向与轴向混合指数均高于常规喷动床,喷动床内颗粒的流动状态与颗粒的能量值密切相关,气体传给颗粒的能量随气速的增大而增大。
(3) 与常规喷动床相比,多喷嘴喷动流化床的全床温度均匀性更好,颗粒温差更小。
(4) 多喷嘴喷动流化床在处理传热系数低、进气温度低的颗粒时更占优势。
| [1] |
祝京旭, 洪江. 喷动床发展与现状[J]. 化学反应工程与工艺, 1997, 13(2): 96-119. ZHU J X, HONG J. Development and present situation of spouted bed[J]. Chemical Reaction Engineering and Technology, 1997, 13(2): 96-119. |
| [2] |
ZHU H P, ZHOU Z Y, YANG R Y, et al. Discrete particle simulation of particulate systems: Theoretical developments[J]. Chemical Engineering Science, 2006, 62(13): 3378-3396. |
| [3] |
YUE Y H, WANG T Y, SHEN Y S. CFD-DEM study of effects of particle density on spout deflection behavior in a spout fluidized bed[J]. Powder Technology, 2020, 366(3): 736-746. |
| [4] |
LIU X J, GAN J Q, ZHONG W Q, et al. Particle shape effects on dynamic behaviors in a spouted bed: CFD-DEM study[J]. Powder Technology, 2020, 361(7): 349-362. |
| [5] |
LI J, MASON D J. A computational investigation of transient heat transfer in pneumatic transport of granular particles[J]. Powder Technology, 2000, 112(3): 273-282. DOI:10.1016/S0032-5910(00)00302-8 |
| [6] |
XU Y P, GAO X, LI T W. Numerical study of the bi-disperse particles segregation inside a spherical tumbler with Discrete Element Method (DEM)[J]. Computers & Mathematics with Applications, 2021, 81(7): 588-601. |
| [7] |
HERTZ H. On the contact of elastic solids[J]. Journal fur die Reine und Angewandte Mathematik, 1882, 92: 156-171. |
| [8] |
MINDLIN R D. Compliance of elastic bodiesin contact[J]. Journal of Applied Mechanics, 1949, 16(3): 259-268. DOI:10.1115/1.4009973 |
| [9] |
白谨豪. 多喷嘴喷动床内干、湿颗粒流动与传热过程CFD-DEM数值模拟[D]. 西安: 西北大学, 2021. BAI J H. CFD-DEM simulation of wet granular-fluid flows and heat transfer in an integral multi-jet spouted bed [D]. Xi′an: Northwest University, 2021. |
| [10] |
HU C S, LUO K, WANG S, et al. The effects of collisional parameters on the hydrodynamics and heat transfer in spouted bed: A CFD-DEM study[J]. Powder Technology, 2019, 353(5): 132-144. |
| [11] |
雷琨, 宋海萍, 高亚平, 等. 基于CFD-DEM法的矩形喷动床与柱锥形喷动床颗粒喷动特性模拟[J]. 天津科技大学学报, 2019, 34(6): 48-54. LEI K, SONG H P, GAO Y P, et al. Simulation of particle spouting characteristics of rectangular spouted bed and cylindrical spouted bed based on CFD-DEM method[J]. Journal of Tianjin University of Science and Technology, 2019, 34(6): 48-54. |
| [12] |
DU J L, YUE K, WU F, et al. Numerical study on the water vaporization during semi dry flue gas desulfurization in a three-dimensional spouted bed[J]. Powder Technology, 2021, 383(4): 471-483. |
| [13] |
MARCHELLI F, HOU Q F, BOSIO B, et al. Comparison of different drag models in CFD-DEM simulations of spouted beds[J]. Powder Technology, 2020, 360(10): 1253-1270. |
| [14] |
TAKABATAKE K, MORI Y, KHINAST J G, et al. Numerical investigation of a coarse-grain discrete element method in solid mixing in a spouted bed[J]. Chemical Engineering Journal, 2018, 346(4): 416-426. |
| [15] |
MOLINER C, MARCHELLI F, BOSIO B, et al. Modelling of spouted and spout-fluid beds: Key for their successful scale up[J]. Energies, 2017, 10(11): 1729-1729. |
| [16] |
杨春玲, 白谨豪, 吴峰, 等. 三维整体式喷动-流化床结构优化与流动数值模拟[J]. 高校化学工程学报, 2019, 33(6): 1415-1423. YANG C L, BAI J H, WU F, et al. Numerical simulation and structure optimization on fluid flow behavior of three-dimensional integral multi-jet spout-fluidized bed[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(6): 1415-1423. |
| [17] |
LIU M L, CHEN M, LI T T, et al. CFD-DEM-CVD multi-physical field coupling model for simulating particle coating process in spout bed[J]. Particuology, 2019, 42(3): 67-78. |
| [18] |
CHAUDHURI B, MUZZIO F J, TOMASSONE M S. Modeling of heat transfer in granular flow in rotating vessels[J]. Chemical Engineering Science, 2006, 61(19): 6348-6360. |
| [19] |
WEI G C, ZHANG H, AN X Z, et al. CFD-DEM study on heat transfer characteristics and microstructure of the blast furnace raceway with ellipsoidal particles[J]. Powder Technology, 2019, 346(2): 350-362. |
| [20] |
SALIKOV V, ANTONYUK S, HEINRICH S, et al. Characterization and CFD-DEM modelling of a prismatic spouted bed[J]. Powder Technology, 2015, 270(5): 622-636. |
| [21] |
杨春玲. 三维整体式多喷嘴喷动-流化床内气固两相流动实验与数值模拟研究[D]. 西安: 西北大学, 2020. YANG C L. Numerical and experimental study of integral multi-jet structure impact on gas-solid flow in a 3D spout-fluidized bed [D]. Xi' an: Northwest University, 2020. |
| [22] |
LIU G Q, LI S Q, ZHAO X L, et al. Experimental studies of particle flow dynamics in a two-dimensional spouted bed[J]. Chemical Engineering Science, 2007, 63(4): 1131-1141. |




