2. 重庆建筑工程职业学院 轨道与机电工程系,重庆 400072;
3. 重庆机床(集团)有限责任公司,重庆 401336
2. Department of Track and Electrical Engineering, Chongqing Jianzhu College, Chongqing 400072, China;
3. Chongqing Machine Tool(Group) Co. Ltd., Chongqing 401336, China
带时间延迟最优控制问题(time-delay optimal control problem,TDOCP)的求解是实现时滞工业过程对象最优控制的一个核心[1-2]。在当前最优控制问题数值求解算法中,控制变量参数化(control variable parameterization,CVP)方法因具有求解精度高、离散化后非线性规划(nonlinear programming,NLP)问题规模较小等优点,在工业过程控制领域得到了众多学者的青睐[3-5]。近年来,国内外学者提出了诸多改进方法用于TDOCP问题的求解。比如,Gui等[6]基于CVP方法推导了带时间延迟系统的协态方法,并在锌冶炼过程TDOCP问题中进行仿真试验,结果显示优化计算后锌粉原料可以有效减少;Yu等[7]研究了混合时间尺度变换(hybrid time-scaling,HTS)HTS-CVP方法进行时间延迟尺度转化,从而实现了TDOCP问题的有效求解;Lin等[8]提出了2种用于计算TDOCP问题目标函数梯度信息的方法,实现了时滞非线性系统的参数预估。此外,Jajarmi等[9]基于庞特里亚金极大值原理将TDOCP问题转换为耦合两点边值问题,并推导了有限差分求解方法;文献[10]和文献[11]分别提出了单时间转化和终值时间转换算法用于终值时间不固定TDOCP问题的求解。
对于传统CVP方法,动态系统时间延迟的存在让状态变量和梯度信息的求解变得困难,进而影响到TDOCP问题的高效求解,因此状态变量转化与梯度信息计算一直是研究的热点。然而,以传统CVP方法为基础的目标函数和约束条件梯度求取方法[6-8]在算法复杂性和效率方面存在一定的不足,比如,协态方法通过构造Hamilton函数得到协态系统进行梯度求取,但迟滞系统和协态系统因为初始值不同并不能同时求解,需要引入插值方法进行近似;时间尺度转化方法引入时间尺度变换可以实现时间节点的精确控制,但也增加了系统梯度信息求解的复杂度。因此,本文提出了一种求解TDOCP问题的扩展控制向量参数化方法。首先,采用控制变量参数化技术和光滑化罚函数法将TDOCP问题近似转化为不含路径约束的有限维NLP问题;进一步,引入扩展变分系统通过辅助状态变量分析时间延迟状态变量扩展变分系统求解方法,以此实现迟滞系统与变分系统在统一初始时刻下求解;同时,针对扩展变分系统直接推导出目标函数和约束函数对于控制参数的梯度信息求解公式,为基于梯度信息的NLP求解器提供高效梯度信息求取方法;最后,在两个典型工业过程TDOCP问题上进行测试以验证所提方法的正确性和有效性。
2 问题描述考虑控制变量和状态变量同时存在时间延迟的工业过程最优控制问题,其优化过程为对延迟系统中的控制变量实施控制,使目标性能函数达到最优,该类问题数学描述如下(问题P1):
| $\begin{array}{l} \min \;{g_0} = {\mathit{\Phi}_0}(\mathit{\boldsymbol{x}}(T|\mathit{\boldsymbol{u}})) + \int_0^T {{L_0}(\mathit{\boldsymbol{x}}(t - h|\mathit{\boldsymbol{u}}),\mathit{\boldsymbol{x}}(t|\mathit{\boldsymbol{u}}),\mathit{\boldsymbol{u}}(t))} {\rm{d}}t\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\mathit{\boldsymbol{\dot x}}(t) = \mathit{\boldsymbol{f}}[\mathit{\boldsymbol{x}}(t - h),\mathit{\boldsymbol{x}}(t),\mathit{\boldsymbol{u}}(t - h),\mathit{\boldsymbol{u}}(t),t],\;\;t \in [0,T]\\ \;\;\;\;\;\;\mathit{\boldsymbol{x}}(t) = \phi(t),\;\;t \in [ - h,0],\;\;\mathit{\boldsymbol{x}}(0){\rm{ = }}{\mathit{\boldsymbol{x}}_0};\;\;\mathit{\boldsymbol{u}}(t) = \varphi (t),\;\;t \in [ - h,0];\;\;{\mathit{\boldsymbol{u}}_{\min }} \le \mathit{\boldsymbol{u}}(t) \le {\mathit{\boldsymbol{u}}_{\max }}\\ \;\;\;\;\;\;{g_i} = {\mathit{\Phi }_i}(\mathit{\boldsymbol{x}}(T|u)) + \int_0^T {{L_i}(\mathit{\boldsymbol{x}}(t - h|u),\mathit{\boldsymbol{x}}(t|u),\mathit{\boldsymbol{u}}(t))} {\rm{d}}t = 0,\;\;i \in E\\ \;\;\;\;\;\;{g_j} = {\mathit{\Phi }_j}(\mathit{\boldsymbol{x}}(T|u)) + \int_0^T {{L_j}(\mathit{\boldsymbol{x}}(t - h|u),\mathit{\boldsymbol{x}}(t|u),\mathit{\boldsymbol{u}}(t))} {\rm{d}}t \ge 0,\;\;j \in I \end{array} $ | (1) |
式中:
针对问题(P1),将控制时域
| $u_j^k(t) \approx \tilde u_j^k(t) = \sum\limits_{r = 1}^{{M_{jk}} + 1} {{\sigma _{jkr}}} \phi _{jkr}^{({M_{jk}})}(t){\rm{ }}\;\;t \in [{t_{k - 1}}, {t_k})$ | (2) |
式中:
| ${u_j}(t) \approx {\tilde u_j}(t) = \sum\limits_{k = 1}^N {{\sigma _{j, k}}{\chi _{\left[ {{t_{k - 1}}, {t_k}} \right)}}(t)} , {\rm{ }}t \in [{t_{k - 1}}, {t_k})$ | (3) |
| ${\chi _{_{\left[ {{t_{k - 1}}, {t_k}} \right)}}}(t) = \left\{ \begin{gathered} 1, {\rm{ }}t \in \left[ {{t_{k - 1}}, {t_k}} \right), {\rm{ }} \\ 0, {\rm{ }}t \notin \left[ {{t_{k - 1}}, {t_k}} \right). \\ \end{gathered} \right.$ | (4) |
式中:
| $\begin{gathered} \min \;{g_0}(\mathit{\boldsymbol{\sigma}} ) = {\mathit{\Phi} _0}(\mathit{\boldsymbol{x}}(T|\mathit{\boldsymbol{\sigma}} )) + \sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {{L_0}(\mathit{\boldsymbol{x}}({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} ){\rm{d}}t} } \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\mathit{\boldsymbol{\dot x}}(t) = \left\{ \begin{gathered} \mathit{\boldsymbol{f}}[\mathit{\boldsymbol{x}}({t_\rm{delay}}), \mathit{\boldsymbol{x}}(t), {\mathit{\boldsymbol{\sigma}} _j}, {\mathit{\boldsymbol{\sigma}} _k}, t], \;\;t \in [{t_{k - 1}}, {t_k}], \;\;{t_\rm{delay}} \in [{t_{j - 1}}, {t_j}] \\ \mathit{\boldsymbol{f}}[\phi (t), \mathit{\boldsymbol{x}}(t), \varphi (t), {\mathit{\boldsymbol{\sigma}} _k}, t], \;\;t < h, \;\;t \in [{t_{k - 1}}, {t_k}] \\ \end{gathered} \right. \\ \;\;\;\;\;\mathit{\boldsymbol{x}}(t) = \phi (t), \;\;t \in [ - h, 0];\;\;\mathit{\boldsymbol{x}}(0) = {\mathit{\boldsymbol{x}}_0}, \;\;\mathit{\boldsymbol{u}}(t) = \varphi (t);\;\;t \in [ - h, 0], \;\;{\mathit{\boldsymbol{u}}_{\min }} \leqslant \mathit{\boldsymbol{\sigma}} \leqslant {\mathit{\boldsymbol{u}}_{\max }} \\ \;\;\;\;\;{g_i}(\mathit{\boldsymbol{\sigma}} ) = {\mathit{\Phi} _i}(\mathit{\boldsymbol{x}}(T|\mathit{\boldsymbol{\sigma}} )) + \sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {{L_i}(\mathit{\boldsymbol{x}}({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} ){\rm{d}}t} } = 0, \;\;i \in E \\ \;\;\;\;\;{g_j}(\mathit{\boldsymbol{\sigma}} ) = {\mathit{\Phi} _j}(\mathit{\boldsymbol{x}}(T|\mathit{\boldsymbol{\sigma}} )) + \sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {{L_j}(\mathit{\boldsymbol{x}}({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{x}}(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} ){\rm{d}}t} } \leqslant 0, \;\;j \in I \\ \end{gathered} $ | (5) |
有关控制变量参数化后问题(P2)与最优控制问题(P1)的收敛性可由定理1保证,鉴于定理1已经在文献[12]中进行了详细证明,本文省略其证明过程,给出具体定理描述如下:
定理1.设
| $\mathop {\lim }\limits_{N \to \infty } {g_0}({\mathit{\boldsymbol{\tilde u}}^{\rm{*}}}(t)) = {g_0}({\mathit{\boldsymbol{\tilde u}}^ * }(t))$ | (6) |
经过控制变量参数化后,问题(P2)的目标函数值将收敛到问题(P1)的目标函数值,但经过控制变量参数化处理后,问题(P2)依旧包含不等式路径约束,这使得问题(P2)求解变得困难。因此,结合文献[13]提出的光滑化罚函数法,本文引入max函数,将不等式路径约束
| $\max \{ {g_j}(\mathit{\boldsymbol{\sigma}} ), 0\} = 0{\rm{\;\;\;}}j \in I$ | (7) |
通过引入文献[14]提出的光滑化函数,式(7)可以通过定理2近似得到,其证明过程可参阅文献[12]。
定理2.对于不等式路径约束
| $\max \{ {g_j}(\mathit{\boldsymbol{\sigma}} ), 0\} \approx p\{ {g_j}(\mathit{\boldsymbol{\sigma}} ), \varepsilon \} = {g_j}(\mathit{\boldsymbol{\sigma}} ) + \sqrt {{g_j}{{(\mathit{\boldsymbol{\sigma}} )}^2} + 4{\varepsilon ^2}} )/2$ | (8) |
进一步,引入路径约束惩罚因子
| $\min \;{\bar g_0}(\mathit{\boldsymbol{\sigma}} ) = {\mathit{\Phi}_0}(x(T|\mathit{\boldsymbol{\sigma}} )) + \sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {{L_0}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} ){\rm{d}}t} } + \rho \sum\limits_{j \in I} {\sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {p\{ {g_j}(\mathit{\boldsymbol{\sigma}} ), \varepsilon \} {\rm{d}}t} } } $ | (9) |
设
分析可知,由于时间延迟微分方程组的存在,问题(P2)中目标函数和约束函数对于控制参数
| $\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( t \right) = \partial \mathit{\boldsymbol{x}}\left( t \right)/\partial \mathit{\boldsymbol{\sigma , \boldsymbol{\varGamma} }}\left( {{t_{{\rm{delay}}}}} \right) = \partial \mathit{\boldsymbol{x}}\left( {{t_{{\rm{delay}}}}} \right)/\partial \mathit{\boldsymbol{\sigma }} $ | (10) |
则带时间延迟状态变量变分系统可由定理3和定理4推导得到。
定理3.假设
| $\begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\dot \varGamma} }}\left( t \right) = \partial \mathit{\boldsymbol{f}}\left[ {\mathit{\boldsymbol{x}}\left( {{t_{{\rm{delay}}}}} \right),\mathit{\boldsymbol{x}}\left( t \right),{\mathit{\boldsymbol{\sigma }}_j},{\mathit{\boldsymbol{\sigma }}_k}} \right]/\partial \mathit{\boldsymbol{x}}\left( t \right) \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( t \right) \times \partial \mathit{\boldsymbol{f}}\left[ {\mathit{\boldsymbol{x}}\left( {{t_{{\rm{delay}}}}} \right),\mathit{\boldsymbol{x}}\left( t \right),{\mathit{\boldsymbol{\sigma }}_j},{\mathit{\boldsymbol{\sigma }}_k},t} \right]/\partial \mathit{\boldsymbol{x}}\left( {{t_{{\rm{delay}}}}} \right) \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {{t_{{\rm{delay}}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\partial \mathit{\boldsymbol{f}}\left[ {\mathit{\boldsymbol{x}}\left( {{t_{{\rm{delay}}}}} \right),\mathit{\boldsymbol{x}}\left( t \right),{\mathit{\boldsymbol{\sigma }}_j},{\mathit{\boldsymbol{\sigma }}_k},t} \right]/\partial \mathit{\boldsymbol{\sigma }}\\ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( 0 \right) = {\bf{0}} \end{array} $ | (11) |
证明.由问题(P2)可知,
| $\frac{\partial \boldsymbol{x}(t)}{\partial \mathit{\boldsymbol{ \boldsymbol{\sigma} }}}=\frac{\boldsymbol{x}_{0}}{\partial \mathit{\boldsymbol{ \boldsymbol{\sigma} }}}+\int_{0}^{t_{f}}\left\{\partial \boldsymbol{f}\left[\boldsymbol{x}\left(t_{\text {delay }}\right), \boldsymbol{x}(t), \mathit{\boldsymbol{ \boldsymbol{\sigma} }}_{j}, \mathit{\boldsymbol{ \boldsymbol{\sigma} }}_{k}, t\right] / \partial \boldsymbol{x}(t) \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}(t)+\right.\\ \left.\partial \boldsymbol{f}\left[\boldsymbol{x}\left(t_{ {delay}}\right), \boldsymbol{x}(t), \mathit{\boldsymbol{ \boldsymbol{\sigma} }}_{j}, \mathit{\boldsymbol{ \boldsymbol{\sigma} }}_{k}, t\right] / \partial \boldsymbol{x}\left(t_{\text {delay }}\right) \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left(t_{\text {delay }}\right)+\partial \boldsymbol{f}\left[\boldsymbol{x}\left(t_{\text {delay }}\right), \boldsymbol{x}(t), \mathit{\boldsymbol{ \boldsymbol{\sigma} }}_{j}, \mathit{\boldsymbol{ \boldsymbol{\sigma} }}_{k}, t\right] / \partial \mathit{\boldsymbol{ \boldsymbol{\sigma} }}\right\} \mathrm{d} t $ | (12) |
式(12)对时间t求导得到:
| $\frac{{\rm{d}}}{{{\rm{d}}t}}\left\{ {\frac{{\partial x(t)}}{{\partial \mathit{\boldsymbol{\sigma}} }}} \right\} = \frac{{\partial f[x({t_\rm{delay}}), x(t), {\mathit{\boldsymbol{\sigma}} _j}, {\mathit{\boldsymbol{\sigma}} _k}, t]}}{{\partial x(t)}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} (t) + \frac{{\partial f[x({t_\rm{delay}}), x(t), {\mathit{\boldsymbol{\sigma}} _j}, {\mathit{\boldsymbol{\sigma}} _k}, t]}}{{\partial x({t_\rm{delay}})}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} ({t_\rm{delay}}) + \frac{{\partial f[x({t_\rm{delay}}), x(t), {\mathit{\boldsymbol{\sigma}} _j}, {\mathit{\boldsymbol{\sigma}} _k}, t]}}{{\partial \mathit{\boldsymbol{\sigma}} }}$ | (13) |
可知,
定理4.定义
| $\begin{gathered} \frac{{\partial {{\tilde g}_l}(\mathit{\boldsymbol{\sigma}} )}}{{\partial \mathit{\boldsymbol{\sigma}} }} = \frac{{\partial {\mathit{\tilde \Phi }_l}(x(T|\mathit{\boldsymbol{\sigma}} ))}}{{\partial x}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} (T) + \frac{{\partial {\mathit{\tilde \Phi }_l}(x(T|\mathit{\boldsymbol{\sigma}} ))}}{{\partial \mathit{\boldsymbol{\sigma}} }} + \sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {\{ \frac{{\partial {{\tilde L}_l}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} )}}{{\partial x}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} (t)} } + \\ \frac{{\partial {{\tilde L}_l}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} )}}{{\partial x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} )}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} ({t_\rm{delay}}) + \frac{{\partial {{\tilde L}_l}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} )}}{{\partial \mathit{\boldsymbol{\sigma}} }}\} {\rm{d}}t \\ \end{gathered} $ | (14) |
证明.采用链式法则对函数
| $\begin{gathered} \frac{{\partial {{\tilde g}_l}(\mathit{\boldsymbol{\sigma}} )}}{{\partial \mathit{\boldsymbol{\sigma}} }} = \frac{{\partial {\mathit{\tilde \Phi }_l}(x(T|\mathit{\boldsymbol{\sigma}} ))}}{{\partial x}}\frac{{\partial x}}{{\partial \mathit{\boldsymbol{\sigma}} }} + \frac{{\partial {\mathit{\tilde \Phi }_n}(x(T|\mathit{\boldsymbol{\sigma}} ))}}{{\partial \mathit{\boldsymbol{\sigma}} }} + \sum\limits_{k = 1}^N {\int_{{t_{k - 1}}}^{{t_k}} {\{ \frac{{\partial {{\tilde L}_l}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} )}}{{\partial x}}\frac{{\partial x}}{{\partial \mathit{\boldsymbol{\sigma}} }}} } + \\ \frac{{\partial {{\tilde L}_l}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} )}}{{\partial x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} )}}\frac{{\partial x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} )}}{{\partial \mathit{\boldsymbol{\sigma}} }} + \frac{{\partial {{\tilde L}_l}(x({t_\rm{delay}}|\mathit{\boldsymbol{\sigma}} ), x(t|\mathit{\boldsymbol{\sigma}} ), \mathit{\boldsymbol{\sigma}} )}}{{\partial \mathit{\boldsymbol{\sigma}} }}\} {\rm{d}}t \\ \end{gathered} $ | (15) |
将式(10)入式(15),即可得到定理4式(14),证毕。
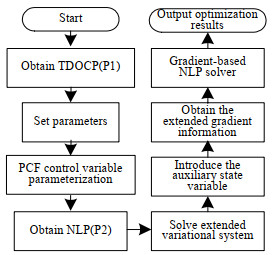
3.3 算法步骤结合3.1节和3.2节算法推导,给出时间延迟最优控制问题扩展控制变量参数化算法(extended control variable parameterization, Extended-CVP)实现过程,其算法流程如图 1所示,主要步骤为:
|
图 1 扩展控制变量参数化算法流程图 Fig.1 Flow chart of extended control variable parameterization approach |
步骤1.输入带时间延迟最优控制问题(P1),设置控制时域分段数
步骤2.在分段数
步骤3.求解时间延迟状态变量扩展变分系统,得到辅助状态变量
步骤4.采用式(14)得到
步骤5.选择NLP求解器求解问题(P2),得到优化后最优控制参数
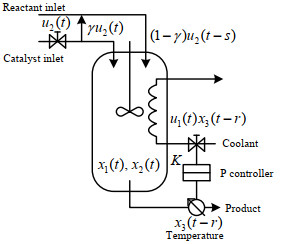
该连续搅拌釜反应器生产模型由Soliman和Ray[16]提出,其生产过程如图 2所示,图中
|
图 2 Soliman和Ray连续搅拌釜反应器生产过程 Fig.2 Continuous stirred tank reactor of Soliman and Ray process |
| $\begin{gathered} \min \;{g_0}(u) = \int_0^{0.2} {(\left\| {\mathit{\boldsymbol{x}}(t)} \right\|_2^2 + 0.01\left\| {\mathit{\boldsymbol{u}}(t)} \right\|_2^2){\rm{d}}t} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;{{\dot x}_1}(t) = - {x_1}(t) - R(t), \;\;{{\dot x}_2}(t) = - {x_2}(t) + 0.9{u_2}(t - s) + 0.1{u_2}(t) \\ \;\;\;\;\;\;\;\;{{\dot x}_3}(t) = - 2{x_3}(t) + 0.25R(t) - 1.05{u_1}(t){x_3}(t - r) \\ \;\;\;\;\;\;\;\;R(t) = (1 + {x_1}(t))(1 + {x_2}(t)){\exp _{}}(25{x_3}(t)/(1 + {x_3}(t))) \\ \;\;\;\;\;\;\;\;{x_3}(t) = - 0.02, \;\; - r \leqslant t \leqslant 0, \;\;{u_2}(t) = 1, \;\; - s \leqslant t \leqslant 0, \;\;|{u_1}| \leqslant 5 \\ \;\;\;\;\;\;\;\;r = 0.015, \;\;s = 0.02, \;\;\mathit{\boldsymbol{x}}(0) = [0.49\; - 0.0002\; - 0.02] \\ \end{gathered} $ | (16) |
采用Extended-CVP方法对该问题进行求解,控制时域采用均匀时间网格划分,分别设置20和40两种分段数,初始控制参数取
|
|
表 1 连续搅拌釜反应器最优控制问题结果对比 Table 1 Result comparison of continuous stirred tank reactor optimal control problem |
|
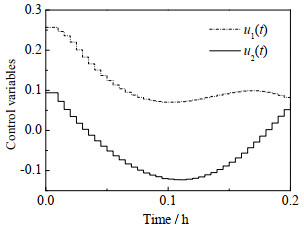
图 3 连续搅拌釜反应器最优控制曲线 Fig.3 Optimal control curves of continuous stirred tank reactor |
|
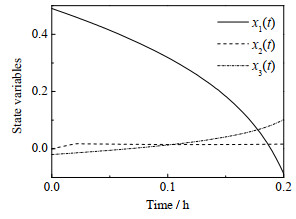
图 4 连续搅拌釜反应器最优状态曲线 Fig.4 Optimal state curves of continuous stirred tank reactor |
本例以Jajarmi等[20]研究的带状态延迟线性二次型调节器(linear quadratic regulator,LQR)为对象进行测试,其TDOCP问题模型如下所示,模型中所采用的参数数值见表 2。表中a、c为状态变量x(t)输入矩阵的取值参数,b为延迟状态变量x(t-h)输入矩阵的取值参数,h为时间延迟量,tf为最优控制终值时间,S为终值状态加权矩阵,Q为状态变量加权矩阵,R为控制变量加权矩阵。
|
|
表 2 状态延迟LQR问题参数值 Table 2 Parameters of state time-delay LQR optimal control problem |
| $\begin{gathered} \min \;{g_0}(u) = \frac{1}{2}{x^{\rm{T}}}({t_f})\mathit{\boldsymbol{Sx}}({t_f}) + \frac{1}{2}\int_0^{{t_f}} {({x^{\rm{T}}}(t)\mathit{\boldsymbol{Qx}}(t){\rm{ + }}{\mathit{\boldsymbol{u}}^{\rm{T}}}(t)\mathit{\boldsymbol{Ru}}(t)){\rm{d}}t} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{\mathit{\boldsymbol{\dot x}}}(t) = {A_1}(t)\mathit{\boldsymbol{x}}(t) + {A_2}(t)\mathit{\boldsymbol{x}}(t - h) + B(t)\mathit{\boldsymbol{u}}(t);\;\;\mathit{\boldsymbol{x}}(t) = {[1, 0]^{\rm{T}}}, \;\; - h \leqslant t \leqslant 0 \\ \;\;\;\;\;\;{A_1}(t) = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - 4{\pi ^2}(a + c\cos 2\pi t)}&0 \end{array}} \right], \;\;{A_2}(t) = \left[ {\begin{array}{*{20}{c}} 0&0 \\ { - 4{\pi ^2}b\cos 2\pi t}&0 \end{array}} \right], \;\;B(t) = {\left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right]^{\rm{T}}} \\ \end{gathered} $ | (17) |
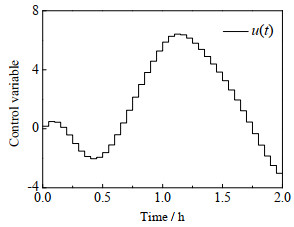
测试中,控制时域采用等间隔方式划分,分段数设置为21、40和150,初始控制参数取
|
|
表 3 状态延迟LQR问题结果对比 Table 3 Result comparison of state time-delay LQR optimal control problem |
|
图 5 状态延迟LQR问题最优控制曲线 Fig.5 Optimal control curve of state time-delay LQR optimal control problem |
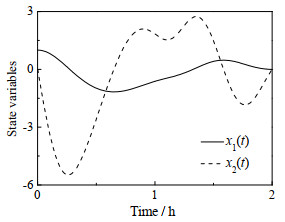
|
图 6 状态延迟LQR问题最优状态曲线 Fig.6 Optimal state curves of state time-delay LQR optimal control problem |
本文提出了一种用于求解工业过程TDOCP问题的扩展控制变量参数化算法。该方法通过引入辅助状态变量推导了时间延迟状态变量扩展变分系统,拓展了传统CVP方法对于带时间延迟最优控制问题的求解能力;同时,给出了目标函数和约束函数对控制参数梯度信息的求解方法,为基于梯度信息的NLP求解器高效求解提供了支撑,保证了优化求解的精度和效率。所提出的方法针对连续搅拌釜反应器和LQR控制器两个典型TDOCP问题进行了测试,结果显示提出方法能在较少优化参数下取得与文献结果相近甚至更优的结果,表明了本文方法的有效性和正确性。考虑非均匀时间间隔控制变量参数化和不确定参数进一步提升本文方法对TDOCP问题的适用性是下一步工作计划开展的课题。
| [1] |
邹雄, 王兵, 张毅, 等. 基于广义析取动态优化模型综合间歇精馏系统[J]. 高校化学工程学报, 2015, 29(3): 634-641. ZOU X, WANG B, ZHANG Y, et al. Optimal synthesis of batch distillation systems based on a general disjunctive dynamic optimization model[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(3): 634-641. |
| [2] |
MA Y, CHEN X, EASON J P, et al. Dynamic optimization for grade transition processes using orthogonal collocation on molecular weight distribution[J]. AIChE Journal, 2019, 65(4): 1198-1210. DOI:10.1002/aic.16524 |
| [3] |
陈特欢, 任志刚. 流体管道水锤抑制的时间尺度变换控制[J]. 控制理论与应用, 2018, 35(2): 198-206. CHEN T H, REN Z G. Control of water hammer suppression via time-scaling technique[J]. Control Theory & Applications, 2018, 35(2): 198-206. |
| [4] |
张兵, 俞欢军, 陈德钊. 序贯优化化工动态问题的蚁群算法[J]. 高校化学工程学报, 2006, 20(1): 120-125. ZHANG B, YU H J, CHEN D Z. Sequential optimization of chemical dynamic problems by ant-colony algorithm[J]. Journal of Chemical Engineering of Chinese Universities, 2006, 20(1): 120-125. |
| [5] |
LIU P, LI G D, LIU X G, et al. Novel non-uniform adaptive grid refinement control parameterization approach for biochemical processes optimization[J]. Biochemical Engineering Journal, 2016, 111: 63-74. DOI:10.1016/j.bej.2016.03.006 |
| [6] |
GUI W H, SHEN X Y, CHEN N, et al. Optimal control of multiple-time delayed systems based on the control parameterization method[J]. ANZIAM Journal, 2011, 53(1): 68-86. DOI:10.1017/S1446181112000053 |
| [7] |
YU C, LIN Q, LOXTON R, et al. A hybrid time-scaling transformation for time-delay optimal control problems[J]. Journal of Optimization Theory and Applications, 2016, 169(3): 876-901. DOI:10.1007/s10957-015-0783-z |
| [8] |
LIN Q, LOXTON R, XU C, et al. Parameter estimation for nonlinear time-delay systems with noisy output measurements[J]. Automatica, 2015, 60: 48-56. DOI:10.1016/j.automatica.2015.06.028 |
| [9] |
JAJARMI A, HAJIPOUR M. An efficient finite difference method for the time-delay optimal control problems with time-varying delay[J]. Asian Journal of Control, 2017, 19(2): 554-563. DOI:10.1002/asjc.1371 |
| [10] |
DI W, BAI Y. Time-scaling transformation for optimal control problem with time-varying delay problem with time-varying delay[J/OL]. Discrete & Continuous Dynamical Systems-S, 2019[2019-08-29]. http://dx.doi.org/10.3934/dcdss.2020098.
|
| [11] |
LIU C, LOXTON R, TEO K L. A computational method for solving time-delay optimal control problems with free terminal time[J]. Systems & Control Letters, 2014, 72: 53-60. |
| [12] |
刘平, 李国栋, 杨金凤, 等. 集装箱装卸摆动最优控制快速数值求解算法[J]. 控制理论与应用, 2019, 36(8): 1275-1282. LIU P, LI G D, YANG J F, et al. Fast optimal control numerical approach for the swing control of container load[J]. Control Theory & Applications, 2019, 36(8): 1275-1282. |
| [13] |
胡云卿, 刘兴高, 薛安克. 带不等式路径约束最优控制问题的惩罚函数法[J]. 自动化学报, 2013, 39(12): 1996-2001. HU Y Q, LIU X G, XUE A K. A penalty method for solving inequality path constrained optimal control problems[J]. Acta Automatica Sinica, 2013, 39(12): 1996-2001. |
| [14] |
LIU X, HU Y, FENG J, et al. A novel penalty approach for nonlinear dynamic optimization problems with inequality path constraints[J]. IEEE Transactions on Automatic Control, 2014, 59(10): 2863-2867. DOI:10.1109/TAC.2014.2317293 |
| [15] |
LIU P, LI X, LIU X, et al. An improved smoothing technique-based control vector parameterization method for optimal control problems with inequality path constraints[J]. Optimal Control Applications and Methods, 2017, 38(4): 586-600. DOI:10.1002/oca.2273 |
| [16] |
SOLIMAN M A, RAY W H. Optimal control of multivariable systems with pure time delays[J]. Automatica, 1971, 7(6): 681-689. DOI:10.1016/0005-1098(71)90006-9 |
| [17] |
HIRMAJER T, BALSA-CANTO E, BANGA J R. DOTcvp: Application to biochemical engineering problems[R]. Vigo: Instituto de Investigaciones Marinas, Investigaciones Marinas-Council for Scientific Research, 2009.
|
| [18] |
BETTS J T, CAMPBELL S L, THOMPSON K C. Optimal control software for constrained nonlinear systems with delays[C]//Computer-Aided Control System Design (CACSD), 2011 IEEE International Symposium, Denver: IEEE, 2011: 444-449.
|
| [19] |
BETTS J T, CAMPBELL S L, THOMPSON K C. Simulation and optimization of systems with delays[C]//Proceedings of the 2013 Spring Simulation Multi-conference Poster Session, San Diege: Society for Compater Simulation International, 2013: 1084-1085.
|
| [20] |
JAJARMI A, HAJIPOUR M. An efficient recursive shooting method for the optimal control of time-varying systems with state time-delay[J]. Applied Mathematical Modelling, 2016, 40(4): 2756-2769. DOI:10.1016/j.apm.2015.09.072 |
| [21] |
PENG H, WANG X, ZHANG S, et al. An iterative symplectic pseudospectral method to solve nonlinear state-delayed optimal control problems[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 48: 95-114. DOI:10.1016/j.cnsns.2016.12.016 |




