2. 上海电器科学研究所(集团)有限公司, 上海 200063
2. Shanghai Electric Appliance Science Research Institute Co. Ltd., Shanghai 200063, China
化工行业中,安全仪表系统(safety instrumented system,SIS)的不可用性在很大程度上决定着企业的安全生产水平,SIS通过检测危险事件、执行所需的安全动作将化工装置维持在安全的状态;一旦此类设备发生故障,装置的动态风险水平就会受到影响[1]。因此,对SIS设备进行不可用性分析、实时掌握装置生产状况具有十分重要的意义。
安全完整性等级(safety integrity level,SIL)是衡量SIS安全性能评估的重要指标之一,需求失效概率(probability of failure on demand,PFD)的计算是确定SIL等级的基础[2],IEC标准中将PFD作为SIS不可用性的性能指标。IEC61508中计算PFD的前提为SIS处于低需求的操作模式中,即:需求频率不超过每年一次并且最多为检验测试频率的2倍[3]。然而,许多研究表明[4-6],现有的操作模式分类标准中对需求频率划分的理论依据是不明确的,并且该分类标准忽略了需求持续时间对操作模式的影响,Bukowski等[7]认为马尔可夫(Markov)模型是处理以上问题的最合适方法,Alizadeh等[8-9]认为需要通过在Markov模型中考虑工艺安全需求率与需求持续时间量化低需求模式下的PFD,而不是按照IEC标准对操作模式进行分类。IEC标准模型中,没有体现出工艺安全需求率、需求持续时间对SIS不可用性的综合影响[9]。
现有的PFD计算模型多针对同型冗余设备,但在实际生产中,厂区出于安全和法规要求等考虑也涉及使用异型冗余设备[10],王海清等[11]提出了相应的异型冗余设备计算公式,但这些方法中,共因失效(common cause failure,CCF)的计算方法均依据IEC标准中的β因子模型,但该模型对不同冗余结构没有区分度。
为解决上述问题,对IEC标准中的β因子模型进行了改进,提出考虑工艺安全需求的异型冗余设备PFD计算模型,该模型综合考虑了工艺安全需求率、需求持续时间、共因失效、修复率等相关要素,以期为SIL评估提供更为准确的PFD。
2 基于齐次马尔可夫链的PFD计算方法齐次马尔可夫链常用于设备失效率与修复率均为恒定的可修系统的可用性建模分析中[12]。齐次马尔可夫链的转移概率pij与时间无关,仅取决于状态i与状态j,且失效率与修复率均为恒定。由所有的pij(r×r)构成的转移矩阵P可以表示为
| $ \mathit{\boldsymbol{P}} = [{p_{ij}}] = \left[ \begin{array}{l} {p_{11}}\;\;\;\;{p_{{\text{12 }}\;\;\;\;...\;\;\;\;}}{p_{1r}} \hfill \\ {p_{21}}\;\;\;\;{p_{{\text{22 }}\;\;\;\;...\;\;\;\;}}{p_{2r}} \hfill \\ ....\;\;....\;\;...\;\;.... \hfill \\ {p_{r1}}\;\;\;\;{p_{r2}}_{\;\;\;\;...\;\;\;\;}{p_{rr}} \hfill \end{array} \right] $ | (1) |
假设集合P(t)={P1(t), …., Pr(t)},Pr(t)表示为t时刻系统处于r状态的概率,考虑到P矩阵的每一行之和均为1且所有pij都大于等于0,Pr(t)可以表示为
| $ {P_r}(t) = \sum\limits_i {{P_i}(t - 1){p_{ij}}} $ | (2) |
如果P(0)={P1(0), …., Pr(0)},Pr(0)表示为初始时刻系统处于r状态的概率,则查普曼-科尔莫格洛夫方程为
| $ {P_r}(t) = P(0){\mathit{\boldsymbol{P}}^t} $ | (3) |
式中:Pt为t时刻的状态转移矩阵。由于齐次马尔可夫链转移矩阵P的幂收敛于一个概率向量M,向量M=[π1, …., πr]表示为稳态概率,M可以由线性方程(4)得到
| $ \mathit{\boldsymbol{MP}} = 0 $ | (4) |
假设πi是系统处于状态i的稳态概率,由于所有稳态概率之和为1,那么
| $ \sum\limits_{i{ = 1}}^r {{\pi _i} = 1} $ | (5) |
假设
| $ {\rm{PFD}} = \sum\limits_{j = {1}}^r {{\pi _j}} $ | (6) |
为了量化共因失效对冗余结构MooN的影响,IEC61508中给出了β因子模型,但该方法只考虑到同型冗余设备且对不同冗余结构没有区分度。相对于同型冗余设备,异型冗余设备的共因失效系数更小[11]。由A、B这2个异型设备构成的1oo2冗余结构(M=1,N=2)的共因失效系数β为[11]
| $ \beta = d{\min _{}}({\beta _{\rm{A}}}, {\beta _{\rm{B}}}){\text{ }} $ | (7) |
式中:βA为2个A设备构成的1oo2结构的共因失效系数,βB为2个B设备构成的1oo2结构的共因失效系数,d为异型冗余结构修正因子,其定性赋值方法见文献[10]。
引入冗余结构修正系数CMooN对式(7)进行改进,改进后的共因失效系数βA, B为[13]
| $ {\beta _{{\rm{A, B}}}} = {C_{{\rm{MooN}}}}\beta $ | (8) |
冗余结构MooN的修正系数见表 1,表中的M与N均为冗余结构的个数,“−”为此结构下的修正系数在IEC标准中未给出。由共因失效引起的危险未检测失效率λC, DU为
| $ {\lambda _{{\rm{C, DU}}}} = \sqrt {{\lambda _{{\rm{DUA}}}}{\lambda _{{\rm{DUB}}}}} $ | (9) |
|
|
表 1 冗余结构修正系数 Table 1 Redundant structure correction coefficients |
式中:λDUA为设备A危险未检测的失效率,λDUB为设备B危险未检测的失效率。
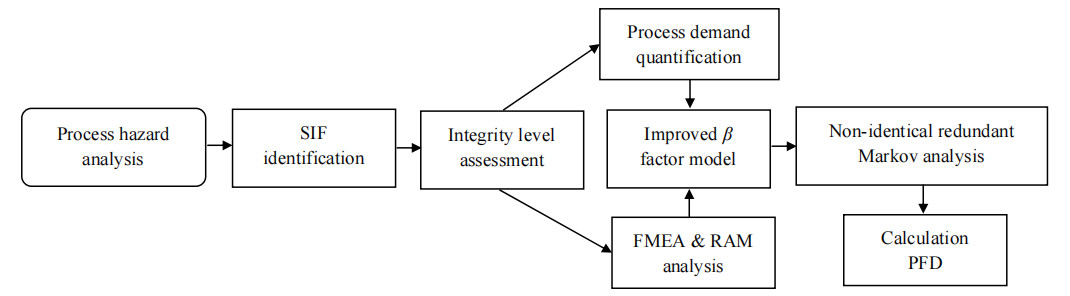
3.2 异型冗余设备PFD计算模型在齐次马尔可夫链的基础上,不失一般性,以1oo2异型冗余系统为例,提出一种考虑工艺安全需求的异型冗余设备PFD计算模型,系统中的2个设备均发生危险失效时,才会导致系统的安全功能失效,模型计算流程如图 1所示,该模型满足以下假设:
|
图 1 考虑工艺安全需求的异型冗余设备PFD计算流程 Fig.1 PFD calculation process of non-identical redundant equipment considering process safety demand |
1) 诊断测试中的危险未检测失效率λDUA、λDUB,设备修复率μDU、需求恢复率μDE、共因失效修复率μCC、需求率λDE均恒定;
2) 危险状态下的工艺安全需求持续时间和恢复时间呈指数分布,即平均需求持续时间为1/μDE;
3) 检验测试可以发现所有危险未检测(dangerous undetected,DU)的失效,但忽视检测的时间,因为测试时间远小于测试周期;
4) 在维修或检验测试后,系统修旧如新;
5) 危险事件发生后,系统能够恢复到正常状态,系统恢复率μT恒定;
6) 使用改进β因子模型计算冗余系统的共因失效率。
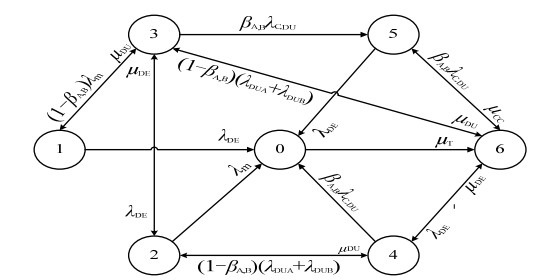
基于以上假设,图 2为1oo2异型冗余结构Markov模型状态转移图,该冗余系统可能出现的状态见表 2。
|
图 2 Markov模型状态转移图 Fig.2 Markov model state transition diagram |
|
|
表 2 1oo2异型冗余系统可能的状态 Table 2 Possible states of 1oo2 non-identical redundant system |
从图 2中可得冗余系统处于稳态时的概率πi(i=0, 1, ...6),相对应的稳态方程为
| $ \left\{ {\begin{array}{*{20}{l}} {((1 - {\beta _{\rm{A, B}}}){\lambda _{\rm{m}}} + {\beta _{\rm{A, B}}}{\lambda _{{\rm{C, DU}}}} + {\mu _{\rm{DU}}} + {\lambda _{DE}}){\pi _3} = (1 - {\beta _{\rm{A, B}}})({\lambda _{\rm{DUA}}} + {\lambda _{\rm{DUB}}}){\pi _6} + {\mu _{DE}}{\pi _2} + {\mu _{\rm{DU}}}{\pi _1}}\\ {({\mu _{{\rm{DE}}}} + {\mu _{{\rm{DU}}}} + {\lambda _{\rm{m}}}){\pi _2} = (1 - {\beta _{{\rm{A, B}}}})({\lambda _{{\rm{DUA}}}} + {\lambda _{{\rm{DUB}}}}){\pi _4} + {\lambda _{{\rm{DE}}}}{\pi _3}}\\ {({\mu _{{\rm{DE}}}} + (1 - {\beta _{{\rm{A, B}}}})({\lambda _{{\rm{DUA}}}} + {\lambda _{{\rm{DUB}}}}) + {\beta _{{\rm{A, B}}}}{\lambda _{{\rm{C, DU}}}}){\pi _4} = {\lambda _{{\rm{DE}}}}{\pi _6} + {\mu _{{\rm{DU}}}}{\pi _2}}\\ {{\mu _{\rm{T}}}{\pi _0} = {\lambda _{{\rm{DE}}}}({\pi _5} + {\pi _1}) + {\lambda _{\rm{m}}}{\pi _2} + {\beta _{{\rm{A, B}}}}{\lambda _{{\rm{C, DU}}}}{\pi _4}}\\ {({\lambda _{{\rm{DE}}}} + {\mu _{{\rm{CC}}}}){\pi _5} = {\lambda _{{\rm{C, DU}}}}{\beta _{{\rm{A, B}}}}({\pi _6} + {\pi _3})}\\ {({\lambda _{{\rm{DE}}}} + {\mu _{{\rm{DU}}}}){\pi _1} = (1 - {\beta _{{\rm{A, B}}}}){\lambda _{\rm{m}}}{\pi _3}} \end{array}} \right. $ | (10) |
从状态3和6转移到状态5、或从状态4转移到状态0时,冗余系统发生共因失效,与同型冗余结构共因失效率βDUλDU的不同之处在于:异型冗余结构的共因失效系数和失效率均需要做出一定的修正[11]。由式(8)和(9)可得,异型冗余结构的共因失效率为
| $ {\rm{CC}}{{\rm{F}}_{\rm{A, B}}} = {\beta _{\rm{A, B}}}{\lambda _{{\rm{C, DU}}}} $ | (11) |
由状态6转移到状态3或由状态4转移到状态2时,冗余系统只发生了单个设备DU失效。表决结构为1oo2,因此,状态转移率为两个设备独立危险失效的概率之和[9],即(1−βA, B)(λDUA+λDUB)。当λDUA=λDUB=λDU时,βA, B=βDU,状态转移率简化为2λDU(1−βDU)[9]。
由状态3转移到状态1时,冗余系统中的另一个设备也发生DU失效[9],由条件概率公式可得状态转移率p31为
| $ {p_{31}} = (1 - {\beta _{\rm{A, B}}}){\lambda _{\rm{m}}} = 2(1 - {\beta _{\rm{A, B}}})\frac{{{\lambda _{\rm{DUA}}}{\lambda _{\rm{DUB}}}}}{{{\lambda _{\rm{DUA}}} + {\lambda _{\rm{DUB}}}}} $ | (12) |
若λDUA=λDUB=λDU,p31=(1−βDU)λDU[9]。
设备修复率μDU可表示为[9]
| $ {\mu _{\rm{DU}}} = \frac{1}{{{t_{\rm{MDT}}}}} = \frac{1}{{\tau - {\lambda _{\rm{f}}} + {t_{{\rm{MTTR}}}}}} $ | (13) |
式中:tMDT为系统平均停车时间(h),tMTTR为平均修复时间(h),τ为检测周期(h),λf为冗余结构的平均失效概率,可以表示为
| $ {\lambda _{\rm{f}}} = \int_0^\tau {tf(t)} {\rm{d}}t/\int_0^\tau {f(t)} {\rm{d}}t $ | (14) |
其中,概率密度函数f(t)为:
| $ f(t) = {\lambda _{\rm{DUA}}}{\rm{ex}}{{\rm{p}}_{}}( - {\lambda _{\rm{DUA}}}t)[1 - {\rm{ex}}{{\rm{p}}_{}}( - {\lambda _{\rm{DUB}}}t)] + {\lambda _{\rm{DUB}}}{\rm{ex}}{{\rm{p}}_{}}( - {\lambda _{\rm{DUB}}}t)[1 - {\rm{ex}}{{\rm{p}}_{}}( - {\lambda _{\rm{DUA}}}t)] $ | (15) |
若λDUA=λDUB=λDU,f(t)简化为2λDUexp(−λDUt)[1−exp(−λDUt)][9]。由等价无穷小可得,1−exp(−λDUAt)≈λDUAt,代入计算可得λf≈2τ/3。
系统处于稳态的概率之和为1,因而
| $ \sum\limits_{i{ = 0}}^6 {{\pi _i} = 1} $ | (16) |
当系统处于状态1和5时,将无法响应工艺安全需求,因而异型冗余系统的PFD为
| $ {\rm{PFD}} = {\pi _1} + {\pi _5} $ | (17) |
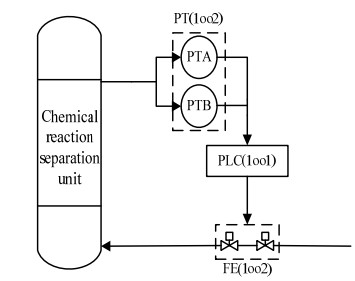
某化学反应分离装置的压力控制保护回路如图 3所示,该装置用于处理挥发性烃类的多相流体,该流体在放热反应完成后分离成气体和液体产物,主要应用于炼油厂等设施中[8]。该SIS由二取一(1oo2)异型表决结构的压力传感器(PT),一取一(1oo1)表决结构的逻辑控制器(PLC)和二取一(1oo2)表决结构的最终执行元件(FE)构成。
|
图 3 化学反应分离单元压力保护SIF回路 Fig.3 Pressure protection SIF function of chemical reaction/separation unit |
主要的安全仪表功能(safety instrumented function,SIF)为:反应器中压力达到预设高触发值时,逻辑控制器发送关断信号给执行元件,执行元件关闭阀门,保证反应器内压力正常。上游流体组分的变化可能导致反应装置内产生剧烈的放热反应,当装置内的压力迅速上升时会对SIS产生工艺安全需求,但在本研究的案例中,放热化学反应导致压力升高的工艺安全需求只会施加在压力传感器上,SIS的PLC和FE仅在高压超过设定界限时才会触发相应的安全功能[8],因而在计算PT的PFD时使用工艺安全需求Markov模型,计算LS和FE的PFD时使用IEC标准模型。
该SIS失效数据来自OREDA等数据库[14],具体数据见表 3。由于化学反应分离装置的实际工艺流程设计中包含了各种独立保护层,导致生产作业中对联锁SIF回路产生需求的频率较低,如果产生需求,考虑到系统的可操作性,需求持续时间较短,因而,λDE=1×10−5 h−1,μDE=1×10−4 h−1,μT=1×10−3 h−1的选取是合理的[8]。
|
|
表 3 化学反应分离装置压力保护系统失效数据 Table 3 Failure data of pressure protection system of chemical reaction/separation unit |
由于PTA与PTB的失效率数量级相似程度较大,因而取d=0.9,由式(7)~(9)可得βA, B=0.18,λC, DU=3.116×10−6 h−1。将PT的失效数据代入式(10),解方程组可以得到系统处于每个状态时的概率,计算结果代入式(17)可得相应的PFD。
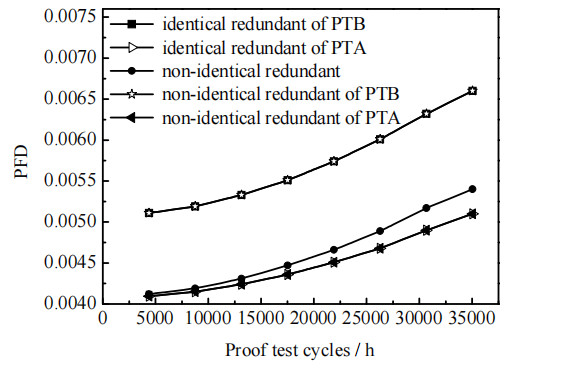
文献[8-9]已经证明了工艺安全需求Markov模型的准确性,但研究对象针对同型冗余设备,以检测周期τ为指标(检测时间间隔为4 380 h)对传感器(同型冗余设备计算模型来源于文献[8],假设2个传感器类型均为PTA或PTB)的PFD进行对比分析,结果如图 4所示。
|
图 4 传感器的PFD的对比 Fig.4 Comparison of PFD of sensor |
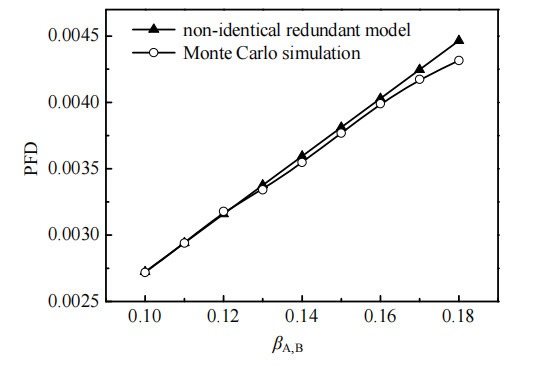
由图 4可知,当传感器类型均为PTA或PTB时,文中模型计算结果与同型冗余设备模型计算结果相一致,且随着检测周期的不断增加,PFD值不断增大。当传感器类型不同时,2个模型之间的计算差值不断增大,这与文献[11]中的变化趋势一致。对图 4中PFD的计算结果进行相对误差分析(以异型冗余设备计算结果为基准),结果如图 5所示。蒙特卡洛模拟[15-16]是一种随机的抽样模拟方法,能够灵活描述冗余系统的相关操作(设备失效和维护等)以及状态转移过程,被广泛应用于设备可靠性分析中,IEC61508中建议应用蒙特卡洛模拟验证从其他分析方法所得的结果[17]。为验证模型的准确性,需要将2种方法所得结果进行对比。图 6为不同βA, B值下的异型冗余模型计算结果与蒙特卡洛模拟结果的对比情况。
|
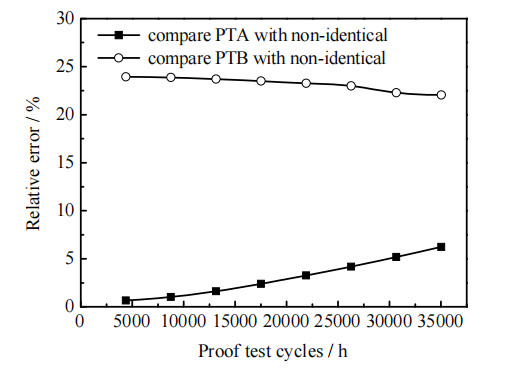
图 5 PFD计算的相对误差 Fig.5 Relative error of PFD calculation |
|
图 6 2种方法计算结果对比 Fig.6 Comparison of calculation results of two methods |
由图 5可知,在4 380~35 040 h的检测周期内,异型冗余设备与类型均为PTA的同型冗余设备的PFD计算相对误差最大为6.23%,且检测周期越长,误差越大;异型冗余设备与类型均为PTB的同型冗余设备的PFD计算相对误差随检测周期的增长,略有下降,但均在20% 以上。以上结果表明,现有的工艺安全需求Markov模型(适用于同型冗余设备)应用于异型冗余设备时,会出现较大的PFD计算误差。由图 6可知,文中模型计算结果与蒙特卡洛模拟结果的相对误差范围为0.03%~3.36%,符合IEC标准中的计算要求[3]。该结果证明了本研究模型的准确性。
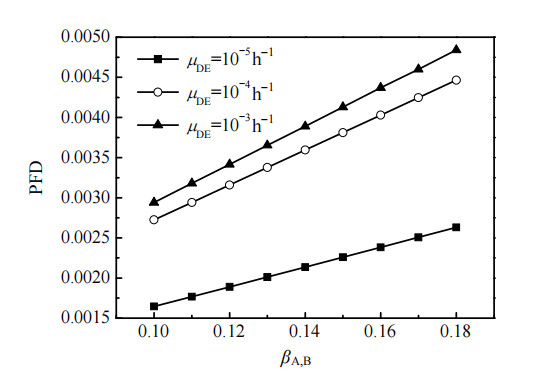
为了进一步研究λDE与μDE对PFD计算结果的影响,改变λDE和μDE的取值,λDE分别为10−6、10−5、10−4 h−1,μDE分别为10−5、10−4、10−3 h−1。λDE的增加意味着SIS需要更频繁地响应过程工业中产生的工艺安全需求,μDE的增加意味着需求持续时间的缩短。图 7为λDE的变化对传感器PFD计算的影响,图 8为μDE的变化对传感器PFD计算的影响。

|
图 7 λDE的变化对传感器PFD的影响 Fig.7 Effect of varying λDE on PFD of sensor |
|
图 8 μDE的变化对传感器PFD的影响 Fig.8 Effect of varying μDE on PFD of sensor |
从图 7中可知,SIS在更频繁响应工艺安全需求的同时,其PFD值是减少的,PFD值的变化可以通过Markov状态转移图来解释。由于PFD值等价于系统在状态1、5时的概率,因此PFD值的任何变化都意味着系统处于这2个状态概率的增加或减少。当λDE增大时,系统处于0、2、4状态的概率会增大,处于1、5状态的概率会减少,进而导致PFD值减少。从图 8中可知,需求持续时间缩短(μDE增大)时,其PFD值是增加的,该变化也可以通过Markov状态转移图来解释。当μDE增大时,系统处于4、2状态的概率会减小,处于3、6状态的概率会增加,因而更容易转变为1、5状态,进而导致PFD值增加。以上结论与文献[18]中给出的PFD变化趋势相似。
5 结论(1) 现有的工艺安全需求Markov模型应用于异型冗余设备时会出现较大的计算误差,文中模型提高了PFD计算的精度,避免由于SIL定级过高、过低导致的安全事故和不必要损失。
(2) 通过蒙特卡洛模拟验证了文中模型的准确性,并进一步研究了工艺安全需求率和需求持续时间对PFD计算的影响,参数灵敏度分析结果也与预期相一致。
(3) 该计算模型的不足在于假设维修或检验测试后,系统修旧如新,但在某些情况下,系统很难恢复到之前的状态。因此,下一步研究方向将考虑不完美维修对异型冗余设备PFD计算的影响。
| [1] |
屈持, 王海清, 刘建利, 等. 基于最小维修的石化安全设备区间截尾寿命数据分析[J]. 化工进展, 2020, 39(11): 4384-4390. QU C, WANG H Q, LIU J L, et al. Interval censored life data of petrochemical safety equipment based on minimal maintenance[J]. Chemical Industry and Engineering Progress, 2020, 39(11): 4384-4390. |
| [2] |
刘荫, 王海清, 许小林, 等. 考虑火炬负荷风险的关联联锁回路SIL定级方法[J]. 化工学报, 2021, 72(5): 2754-2762. LIU Y, WANG H Q, XU X L, et al. SIL grading method of associated overpressure interlock protection circuit considering flare load risk[J]. CIESC Journal, 2021, 72(5): 2754-2762. |
| [3] |
International Electrotechnical Commission (IEC). Functional safety of electrical/electronic/programmable electronic safety related systems: IEC61508 [S]. Switzerland: IEC, 2010.
|
| [4] |
JIN H, LUNDTEIGEN M A, RAUSAND M. Reliability performance of safety instrumented systems: A common approach for both low- and high-demand mode of operation[J]. Reliability Engineering and System Safety, 2011, 96(3): 365-373. DOI:10.1016/j.ress.2010.11.007 |
| [5] |
LIU Y L, RAUSAND M. Reliability assessment of safety instrumented systems subject to different demand modes[J]. Journal of Loss Prevention in the Process Industries, 2011, 24(1): 49-56. DOI:10.1016/j.jlp.2010.08.014 |
| [6] |
MISUMI Y, SATO Y. Estimation of average hazardous-event-frequency for allocation of safety-integrity levels[J]. Reliability Engineering and System Safety, 1999, 66(2): 135-144. DOI:10.1016/S0951-8320(99)00030-7 |
| [7] |
BUKOWSKI J V, GOBLE W M. Using Markov models for safety analysis of programmable electronic systems[J]. ISA Transactions, 1995, 34(2): 193-198. DOI:10.1016/0019-0578(95)00008-N |
| [8] |
ALIZADEH S, SRIRAMULA S. Unavailability assessment of redundant safety instrumented systems subject to process demand[J]. Reliability Engineering and System Safety, 2018, 171: 18-33. DOI:10.1016/j.ress.2017.11.011 |
| [9] |
ALIZADEH S, SRIRAMULA S. Impact of common cause failure on reliability performance of redundant safety related systems subject to process demand[J]. Reliability Engineering and System Safety, 2018, 172: 129-150. |
| [10] |
靳江红, 吴宗之, 赵寿堂, 等. 异型设备冗余和多重表决结构的可靠性计算[J]. 自动化与仪表, 2010, 25(10): 11-15. JIN J H, WU Z Z, ZHAO S T, et al. Reliability calculation of non-identical redundant components and multiple voting configurations[J]. Automation & Instrumentation, 2010, 25(10): 11-15. |
| [11] |
王海清, 乔丹菊, 刘祥妹, 等. 异型冗余设备KooN结构通用PFD计算模型[J]. 中国安全科学学报, 2016, 26(8): 90-94. WANG H Q, QIAO D J, LIU X M, et al. Model for calculating generalizing PFD of non-identical redundant KooN configurations[J]. China Safety Science Journal, 2016, 26(8): 90-94. |
| [12] |
RAUSAND M, HøYLAND A. System reliability theory: Models, statistical methods, and applications[M]. 2nd ed. New Jersey: Wiley, 2004.
|
| [13] |
李宏浩. 储气库安全仪表系统SIL提升与安全维保优化研究[D]. 青岛: 中国石油大学(华东), 2018. LI H H. Study on safety instrumented system SIL promotion and maintenance optimization of gas storage [D]. Qingdao: China University of Petroleum (East China), 2018. |
| [14] |
ORED A. Offshore reliability data handbook[M]. 6th ed. Trondheim: Det Norske Veritas, 2015.
|
| [15] |
刘睿, 陈曦. 聚合反应过程中的蒙特卡洛方法[J]. 高校化学工程学报, 2021, 35(3): 389-399. LIU R, CHEN X. Review on the Monte Carlo method in polymerization processes[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(3): 389-399. |
| [16] |
高晓浩, 张桃红, 杨智勇, 等. 可降解高聚物的降解跨尺度建模研究[J]. 高校化学工程学报, 2016, 30(6): 1419-1426. GAO X H, ZHANG T H, YANG Z Y, et al. Trans-Scale modeling on degradation of biodegradable polymers[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(6): 1419-1426. |
| [17] |
WU S N, ZHANG L B, LUNDTEIGEN M A, et al. Reliability assessment for final elements of SISs with time dependent failures[J]. Journal of Loss Prevention in the Process Industries, 2018, 56: 186-199. |
| [18] |
ALIZADEH S, SRIRAMULA S. Reliability modelling of redundant safety systems without automatic diagnostics incorporating common cause failures and process demand[J]. ISA Transactions, 2017, 71(2): 599-614. |




