换热网络(heat exchange network,HEN)由于其合理的能源利用和可观的经济性,在化工领域得到广泛的应用。换热网络的优化是在20世纪40年代首次提出的[1]。早期的优化主要依靠工程师的经验,采用夹点分析法、数学规划法以及启发式算法进行换热合成[2]。Linnhoff等[3]首先提出一种基于热力学原理的夹点设计法。数学规划法可以更加精确地描述换热网络模型,通过直接求解模型可以避免图解法存在的问题出现。Yee等[4-5]提出了分级超结构(stage-wise superstructure,SWS)模型,该模型考虑了更多可能存在的换热匹配,但由于其复杂程度,常规方法较难求解。随着计算机技术提高,启发式算法由于其对超结构模型的要求低并且全局搜索能力强而在HEN合成中得到了广泛应用。例如,刘凯等[6]使用离散AEA和PSO双层算法进行同步优化寻优,优化有分流换热网络的分级超结构模型。Toimil等[7]总结了启发式算法在HEN合成中的相关应用,给出了混合方法在换热匹配和面积优化中的发展趋势。
常规换热网络合成是基于操作参数都固定在标称值的假设下。而在化工过程中,可能会面临来自环境或工厂操作的一些不确定因素。柔性换热网络合成能够在不确定参数下仍保持换热网络的最优和可操作性,具有很大研究价值。柔性HEN合成的研究包括多周期综合和柔性分析[8]。
Floudas等[9]首先提出了一种多周期顺序合成方法,利用线性规划(linear programming,LP)模型将公用减到最小,利用混合整数线性规划(mixed integer linear programming,MILP)模型使换热器数量达到最少,并采用非线性规划(nonlinear programming,NLP)模型优化换热面积。李志红等[10-12]总结了多周期HEN优化设计方法,提出用专家系统求解换热网络超结构模型,并拓展到各种多周期HEN中。肖丰等[13-14]将结垢热阻生长过程分为4个阶段,分别进行柔性HEN初步综合和同步优化,以年度总费用最小为目标,对网络结构、换热器面积和清洗时序进行优化。针对结垢热阻随运行时间不断增大的问题,朱真等[15]提出一种基于持续节能的多周期HEN综合设计方法,考虑了换热器结垢对多周期HEN优化结果的影响,进而实现多周期HEN的最优综合。Pavão等[16]开发了一种使用元启发式算法的多周期HEN优化方案,同时考虑了成本节约,工业实现以及计算效率等。以上大部分多周期换热网络只考虑了3或4个工况,不确定的参数的变化必须由几个离散点描述,增加了工业应用的限制性[8]。
Marselle等[17]建立了弹性分析的概念,该方法的主要思想是在标准状态设计初始的换热网络,并检查其是否满足弹性要求。Saboo等[18-19]定义一个弹性指数来测量当前HEN能够承受的最大干扰。指标大于1,则满足弹性要求,否则,通过将原始结构与临界点的设计相结合来改变弹性。柔性分析方法类似于弹性分析,但柔性测试和网络更新等更依赖于数学模型。Swaney等[20]定义了柔性指数,即使换热网络仍能满足可行操作的不确定参数与标称点的最大偏差。康丽霞等[21]提出一种控制面积冗余的换热网络设计方法,该方法分为2个合成阶段,首先进行初始换热网络结构的获得,再确定换热网络结构和面积的修正方案。以上文献中采用的顺序合成法将结构优化与面积优化分开,通常在标准工况下得到初始结构,随后通过柔性检验修正HEN面积,但顺序合成可能陷入局部最优。
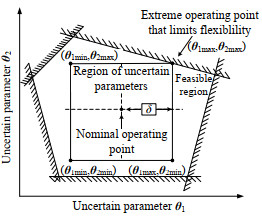
为了解决以上问题,本研究提出了一种允许操作参数连续变化的柔性同步合成方法,基于分流分级超结构模型,采用双层优化策略对换热网络模型结构和换热器面积进行同步优化。外层采用离散粒子群(binary partide swarm optimization,BPSO)算法优化HEN的拓扑结构,内层采用基于模拟退火思想的进化算法(aploex evolation algorthm,AEA)对换热量和热容流率等连续变量进行优化。同步优化方法需要找到限制HEN柔性的临界点,对一个网络结构在标准点和临界点下优化,将所得结果合并,再根据年度总费用(total annual cost,TAC)优化网络结构,以摆脱固定结构的限制。在柔性约束构成的可行域中,非凸可行域的临界点位于不确定参数构成超矩形的边界上,不同换热网络的临界点不同,寻找临界点计算量巨大。而凸可行域的临界点位于不确定参数波动的角点,在优化过程中可以简化寻找临界点的步骤。对于如图 1所示的凸可行域设计问题[22],标准点为所有波动均为0的点,如图 1中矩形的中点;影响柔性的极限点(临界点)为各个不确定参数的最大波动点,如图 1中矩形的各个顶点,通过已知的换热网络数据及波动最大数值可以直接获取标准点和极限点。在各点已知情况下,采用同步优化方法可以有效寻找到最优的柔性换热网络设计。
|
图 1 柔性HEN的凸可行域 Fig.1 Convex feasible region of flexible HENs |
简单地描述如下:给定一组基本数据,包括热容流率、工艺流和公用工程的进出口温度以及冷、热公用工程的价格。给定换热设备的传热膜系数。对于凸可行域下的柔性HEN优化问题,为了处理不确定参数影响,同时考虑标准和极限情况合成换热网络,以最小化TAC为目标对结构和面积同步优化,然后计算柔性指数来判断得到的结果是否可行。
柔性指数F的定义[21]即在可行操作下能够偏离标称点的最长距离,其模型如式(1)所示。
| $\begin{array}{l} F = \max \;\delta \\ \;\;\;\;\;\;\;{\rm{s}}.{\rm{t}}.\\ \;\;\;\;\;\;\;H({\boldsymbol{p}}, {\boldsymbol{z}}, {\boldsymbol{x}}, {\boldsymbol{\theta }}) = 0\\ \;\;\;\;\;\;\;g({\boldsymbol{p}}, {\boldsymbol{z}}, {\boldsymbol{x}}, {\boldsymbol{\theta }}) \le 0\\ \;\;\;\;\;\;\;R(\delta ) = \left\{ {\left( {{{\boldsymbol{\theta }}^N} - \delta \times \Delta {{\boldsymbol{\theta }}^ - }} \right) \le {\boldsymbol{\theta }} \le \left( {{{\boldsymbol{\theta }}^N} + \delta \times \Delta {{\boldsymbol{\theta }}^ + }} \right)} \right\}\\ \;\;\;\;\;\;\;\delta \ge 0 \end{array}$ | (1) |
式中:H为等式约束,包括质量守恒以及能量守恒约束,g为换热量、热容流率以及换热温差非负约束等来自物理操作以及物质特性限制的不等式约束。约束变量包含p,z,x和θ。p为定义HEN结构构造和换热器设备参数的设计变量的矢量,z为控制变量的矢量,表示操作自由度,其数值随不确定参数变化而变化,使过程满足约束条件。x为状态变量的矢量,如出口温度。θ为不确定参数的向量,如入口温度波动,传热膜系数波动等。δ为可行操作下的最大偏差与预期波动的比值。R(δ)为由不确定参数θ所构成的超矩形即不确定参数的波动范围。
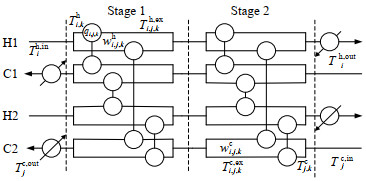
2.2 柔性换热网络的SWS模型柔性换热网络模型采用Yee等[4-5]提出的SWS模型,如图 2所示。q为换热量,T为物流进出口温度;w为各物流的分流量;H1、H2为热流;C1、C2为冷流;上标h、c分别为热流、冷流;上标in、out分别为进口、出口;上标ex为换热器;下标i、j、k分别为热流符号、热流序号、换热级数。换热网络各条工艺流在每一级上都可分流,理论上所有冷热物流在每一级上都存在相互换热的可能。分流后的物流会在每级的末端非等温混合。
| $\begin{array}{l} \min \;{\rm{TAC}} = {\rm{mean}}({C_{{\rm{cu}}}}\sum\limits_{i = 1}^{{\rm{HN}}} {q_i^{{\rm{cu}}}} + {C_{{\rm{hu}}}}\sum\limits_{j = 1}^{{\rm{CN}}} {q_j^{{\rm{hu}}}} ){\rm{ + }}\sum\limits_{k = 1}^{{\rm{ST}}} {\sum\limits_{i = 1}^{{\rm{HN}}} {\sum\limits_{j = 1}^{{\rm{CN}}} {{C_{{\rm{ef}}}} \times {Z_{i, j, k}}} } } + C_{{\rm{ef}}}^{{\rm{cu}}}\sum\limits_{i = 1}^{{\rm{HN}}} {Z_i^{{\rm{cu}}}} + C_{ef}^{{\rm{hu}}}\sum\limits_{j = 1}^{{\rm{CN}}} {Z_i^{{\rm{hu}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_{{\rm{Af}}}}\sum\limits_{k = 1}^{{\rm{ST}}} {\sum\limits_{i = 1}^{{\rm{HN}}} {\sum\limits_{j = 1}^{{\rm{CN}}} {{{(S_{i, j, k}^{{\rm{max}}})}^\beta }} } } + C_{{\rm{Af}}}^{{\rm{cu}}}\sum\limits_{i = 1}^{{\rm{HN}}} {{{(S_i^{{\rm{cu, max}}})}^\beta }} + C_{{\rm{Af}}}^{{\rm{hu}}}\sum\limits_{j = 1}^{{\rm{CN}}} {{{(S_i^{{\rm{hu, max}}})}^\beta }} \\ i = 1, 2, ..., {\rm{HN}};j = 1, 2, ..., {\rm{CN}};k = 1, 2, ..., {\rm{ST}} \end{array}$ | (2) |
|
图 2 非等温混合的分级超结构 Fig.2 Stage-wise superstructure for non-isothermal mixing |
换热网络优化通常以TAC作为优化目标,包括换热器及换热面积费用和公用费用。TAC的计算方法如公式(2)所示,式中:S为换热面积,m2;Ccu和Chu分别为冷热公用的单价,Cef为每台换热器的固定价格,CAf为换热面积的单价;Zi, j, k、
以上述TAC为目标函数,柔性HEN在各个工况下的数学模型应满足如下等式或不等式约束。
各条物流的热量守恒方程:
| $f_i^{\rm{h}}\left( {T_i^{{\rm{h}}, {\rm{in}}} - T_i^{{\rm{h}}, {\rm{out }}}} \right) = \sum\limits_{k = 1}^{{\rm{ST}}} {\sum\limits_{j = 1}^{{\rm{CN}}} {{q_{i, j, k}}} } + q_i^{{\rm{cu}}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (3) |
| $f_j^{\rm{c}}\left( {T_j^{{\rm{c}}, {\rm{ out }}} - T_j^{{\rm{c}}, {\rm{ in }}}} \right) = \sum\limits_{k = 1}^{{\rm{ST}}} {\sum\limits_{j = 1}^{{\rm{CN}}} {{q_{i, j, k}}} } + q_j^{{\rm{hu}}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (4) |
式中:f为热容流率。
各级的热量守恒方程:
| $f_i^{\rm{h}}\left( {t_{i, k}^{\rm{h}} - t_{i, k + 1}^{\rm{h}}} \right) = \sum\limits_{j = 1}^{{\rm{CN}}} {{q_{i, j, k}}} \;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (5) |
| $f_j^{\rm{c}}\left( {t_{j, k}^{\rm{c}} - t_{j, k + 1}^{\rm{c}}} \right) = \sum\limits_{i = 1}^{{\rm{HN}}} {{q_{i, j, k}}} \;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (6) |
每台换热器的换热量平衡方程,
| $w_{i, j, k}^{\rm{h}}\left( {t_{i, k}^{\rm{h}} - t_{i, j, k}^{{\rm{h}}, {\rm{out }}}} \right) = {q_{i, j, k}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (7) |
| $w_{i, j, k}^{\rm{c}}\left( {t_{i, j, k}^{{\rm{c}}, {\rm{ out }}} - t_{i, k + 1}^{\rm{c}}} \right) = {q_{i, j, k}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (8) |
各物流分流质量守恒方程:
| $f_i^{\rm{h}} = \sum\limits_{j = 1}^{{\rm{CN}}} {w_{i, j, k}^{\rm{h}}} \;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (9) |
| $f_j^{\rm{c}} = \sum\limits_{i = 1}^{{\rm{HN}}} {w_{i, j, k}^{\rm{c}}} \;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (10) |
入口温度约束:
| $t_{i, 1}^{\rm{h}} = T_i^{{\rm{h}}, {\rm{in }}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}}$ | (11) |
| $t_{j, k + 1}^{\rm{c}} = T_i^{{\rm{c}}, {\rm{in}}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (12) |
混合温度约束:
| $f_i^{\rm{h}}t_{i, k}^{\rm{h}} = \sum\limits_{j = 1}^{{\rm{CN}}} {w_{i, j, k}^{\rm{h}}} t_{i, j, k}^{{\rm{h}}, {\rm{out }}}\;\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (13) |
| $f_j^{\rm{c}}t_{j, k}^{\rm{c}} = \sum\limits_{i = 1}^{{\rm{HN}}} {w_{i, j, k}^{\rm{c}}} t_{i, j, k}^{{\rm{c}}, {\rm{out}}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (14) |
换热量、热容流率以及换热温差非负约束:
| ${q_{i, j, k}} \ge 0, w_{i, j, k}^{\rm{c}} \ge 0, w_{i, j, k}^{\rm{h}} \ge 0\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (15) |
| $t_{i, j, k}^{{\rm{h}}, {\rm{out}}} - t_{j, k + 1}^{\rm{c}} \ge 0, t_{i, k}^{\rm{h}} - t_{i, j, k}^{{\rm{c}}, {\rm{out}}} \ge 0\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (16) |
| $q_i^{{\rm{cu}}} \ge 0, q_j^{{\rm{hu}}} \ge 0\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}$ | (17) |
| ${T^{{\rm{cu}}, {\rm{in}}}} - T_i^{{\rm{h}}, {\rm{out}}} \ge 0, {T^{{\rm{cu}}, {\rm{out}}}} - T_{i, k + 1}^{\rm{h}} \ge 0\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};k = 1, 2, \ldots , {\rm{ST}}$ | (18) |
| ${T^{{\rm{hu}}, {\rm{in}}}} - T_j^{{\rm{c}}, {\rm{in}}} \ge 0, {T^{{\rm{hu}}, {\rm{out}}}} - T_{j, 1}^{\rm{c}} \ge 0\;\;\;\;j = 1, 2, \ldots , {\rm{CN}}$ | (19) |
换热网络结构约束:
| $\left\{ {\begin{array}{*{20}{l}} {{q_{i, j, k}} = 0}&{}\\ {w_{i, j, k}^{\rm{c}} = 0, }&{{\rm{ if}}\;\;\;\;w_{i, j, k}^{\rm{c}} \times w_{i, j, k}^{\rm{h}} = 0}\\ {w_{i, j, k}^{\rm{h}} = 0}&{} \end{array}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}}} \right.$ | (20) |
各工况下换热面积计算公式如式(21)~(23):
| $\begin{array}{l} \;{S_{i, j, k}} = \frac{{{q_{i, j, k}}\left( {h_{{\rm{h}}, i}^{ - 1} + h_{{\rm{c}}, j}^{ - 1}} \right)}}{{{{\left( {\Delta T_{i, j, k}^1\Delta T_{i, j, k}^2\left( {\Delta T_{i, j, k}^1 + \Delta T_{i, j, k}^2} \right)/2} \right)}^{1/3}}}}\\ i = 1, 2, \ldots , {\rm{HN}};j = 1, 2, \ldots , {\rm{CN}};k = 1, 2, \ldots , {\rm{ST}} \end{array}$ | (21) |
| $S_i^{{\rm{cu}}} = \frac{{q_{\rm{i}}^{{\rm{cu}}}\left( {h_{{\rm{h}}, i}^{ - 1} + h_{{\rm{c}}, {\rm{cu}}}^{ - 1}} \right)}}{{{{\left( {\Delta T_{i, {\rm{cu}}}^1\Delta T_{i, {\rm{cu}}}^2\left( {\Delta T_{i, {\rm{cu}}}^1 + \Delta T_{i, {\rm{cu}}}^2} \right)/2} \right)}^{1/3}}}}\;\;\;\;i = 1, 2, \ldots , {\rm{HN}}$ | (22) |
| $S_j^{{\rm{hu}}} = \frac{{q_j^{{\rm{hu}}}\left( {h_{{\rm{h}}, {\rm{hu}}}^{ - 1} + h_{{\rm{c}}, j}^{ - 1}} \right)}}{{{{\left( {\Delta T_{j, {\rm{hu}}}^1\Delta T_{j, {\rm{hu}}}^2\left( {\Delta T_{j, {\rm{hu}}}^1 + \Delta T_{j, {\rm{hu}}}^2} \right)/2} \right)}^{1/3}}}}\;\;\;\;j = 1, 2, \ldots , {\rm{CN}}$ | (23) |
式中:hh、hc为热冷物流的传热膜系数,ΔT表示换热温差。
柔性指数约束:
| $F \ge 1$ | (24) |
柔性指数约束可以验证HEN是否满足柔性要求,而柔性过大会增加换热网络成本,因此通过柔性指数也可以直观反映所得HEN的经济性。柔性指数大于且接近1时,具有更好的经济性。
3 柔性SWS模型双层同步优化策略 3.1 BPSO和AEA算法简介BPSO算法最早由Eberhart和Kennedy[23]提出,具有与PSO算法相同的速度更新机制。在粒子群算法中,粒子速度
| $m = {m_{{\rm{min}}}} + \left( {{m_{{\rm{max}}}} - {m_{{\rm{min}}}}} \right) \times ({\rm{PSOStep}} - {\rm{iter}})/{\rm{PSOStep}}$ | (25) |
| ${v_o} = m \cdot {v_{o - 1}} + {c_1} \cdot {\mathop{\rm rand}\nolimits} () \cdot \left( {{p_{o - 1}} - {x_{o - 1}}} \right) + {c_2} \cdot {\mathop{\rm rand}\nolimits} () \cdot \left( {{p_{\rm{g}}} - {x_{o - 1}}} \right)$ | (26) |
式中:c1、c2为学习因子,PSOStep为算法的最大迭代次数,iter为算法的当前迭代次数。
而在BPSO算法中,由于粒子均为二进制数值,因此在更新粒子位置时不能直接将速度与当前位置相加。在离散算法中,粒子的速度
| $s{v_o} = \frac{1}{{1 + \exp \left( { - {v_o}} \right)}}$ | (27) |
| ${x_o} = \left\{ {\begin{array}{*{20}{c}} {1, }&{{\rm{ if }}\;\;\;\;{\rm{rand }}()s{v_o}}\\ 0&{\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}}} \end{array}} \right.$ | (28) |
AEA算法将群体智能与自适应模拟退火策略相结合,保证了更好的全局搜索能力和计算效率[24-25]。假设
| $C_{o, l}^r = \left( {x_{o, l}^r - y_{o, l}^r} \right) \cdot \left[ {F\left( {X_o^r} \right) - F\left( {Y_o^r} \right)} \right.$ | (29) |
| ${T^r} = \frac{1}{{MN}}\sum\limits_{o = 1}^M {\sum\limits_{l = 1}^N {C_{o, l}^r} } $ | (30) |
| $P_{o, l}^r = \left( {1 + {\rm{exp}}{{\left( {\frac{{C_{o, l}^k}}{{{T^k}}}} \right)}^{ - 1}}} \right.$ | (31) |
式中:
假设当前是最小化目标函数问题,AEA算法的更新机制是基于原始种群和重新排序的种群之间的差异,如式(29)所示。相关系数
| $\delta _{o, l}^r = \left\{ {\begin{array}{*{20}{l}} {1, }&{P_{o, l}^r \ge {\rm{rand}}(0, 1)}\\ { - 1, }&{{\rm{ otherwise }}} \end{array}} \right.$ | (32) |
| $\Delta _{o, l}^r = \left| {x_{o, l}^r - y_{o, l}^r} \right| \cdot \delta _{o, l}^r \cdot {\rm{rand}}(0, 1)$ | (33) |
| $x_{o, l}^{r + 1} = \left\{ {\begin{array}{*{20}{l}} {x_{o, l}^r + \Delta _{o, l}^r, }&{F\left( {x_{o, l}^r + \Delta _{o, l}^r} \right) \le F\left( {x_{o, l}^r} \right)}\\ {x_{o, l}^r, }&{\;\;\;\;{\rm{otherwise}}} \end{array}} \right.$ | (34) |
在处理外层离散变量时,相较于遗传算法等启发式算法,BPSO算法有更好的平均收敛率及平均收敛代数,且对复杂程度较高问题具有更好的优化效果;而内层AEA根据个体差异优化换热量等连续变量,具有高效的搜索效率,并且其反向搜索能力也有助于跳出局部最优解。BPSO算法与AEA的双层算法适用于HEN问题的求解。
3.2 优化策略双层优化策略可以在考虑标称和极限条件的情况下,求解凸可行域的柔性HEN综合问题。利用BPSO算法在外层搜索最优的HEN结构,并在内层采用AEA算法对换热量
Step 1:首先给出物流详细数据,确定HEN级数
Step 2:在外层BPSO算法中,首先随机生成一组HEN结构作为初始种群。每个HEN结构用矩阵Z表示,其维度是
| ${z_{i, j, k}} = \left\{ {\begin{array}{*{20}{l}} 1&{{\rm{rand}}(0, 1) > 0.5}\\ 0&{{\rm{rand}}(0, 1) < 0.5} \end{array}} \right.$ | (35) |
Step 3:将外层的HEN结构输入内层,根据Z初始化冷热流股的分流量
每台换热器的换热量
| $\begin{array}{l} Q = \left\{ {{q_{1, 1, 1}}, \ldots , {q_{i, j, k}}, \ldots , {q_{{\rm{HN}}, {\rm{CN}}, {\rm{ST}}}};w_{1, 1, 1}^{\rm{h}}, \ldots , w_{i, j, k}^{\rm{h}}, \ldots , w_{{\rm{HN}}, {\rm{CN}}, {\rm{ST}}}^{\rm{h}};w_{1, 1, 1}^{\rm{c}}, \ldots , w_{i, j, k}^{\rm{c}}, \ldots , w_{{\rm{HN}}, {\rm{CN}}, {\rm{ST}}}^{\rm{c}}} \right\}\\ t_{\max , j, k}^{\rm{c}} = \mathop {\max }\limits_{i = 1, 2, \ldots , {\rm{HN}}} \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\frac{{f_j^{\rm{c}}\left( {t_{j, k}^{\rm{c}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right)}}{{w_{i, j, k}^c}} + {T_{{\rm{c}}, {\rm{in}}, j}}}&{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1} \end{array}\\ \begin{array}{*{20}{c}} {\left[ {f_j^{\rm{c}}\left( {t_{j, k}^{\rm{c}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right) - \sum\limits_{{\rm{n}} = 1}^{i - 1} {\left( {{q_{n, j, k}}} \right)} } \right] + {T_{{\rm{c}}, {\rm{in}}, j}}}&{i = 2, 3, \ldots , {\rm{HN}}} \end{array} \end{array} \right\} \end{array}$ | (36) |
| $\begin{array}{l} i{\rm{f}}\;t_{i, k}^{\rm{h}} < {T_{{\rm{c}}, {\rm{in}}, j}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_{\max , i, j, k}} = 0\\ \;{\rm{elseif }}\left( {{T_{{\rm{h}}, {\rm{out}}, i}} < {T_{{\rm{c}}, {\rm{in}}, j}}} \right)\& \left( {w_{i, j, k}^{\rm{c}} \ge w_{i, j, k}^{\rm{h}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_{\max , i, j, k}} = {\rm{min}}\left\{ {w_{i, j, k}^{\rm{h}}\left( {t_{i, k}^{\rm{h}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right), w_{i, j, k}^{\rm{c}}\left( {t_{\max , j, k}^{\rm{c}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right)} \right\}\\ \;{\rm{elseif }}\left( {{T_{{\rm{h}}, {\rm{out}}, i}} \ge {T_{{\rm{c}}, {\rm{in}}, j}}} \right)\& \left( {t_{i, k}^{\rm{h}} \ge t_{\max , j, k}^{\rm{c}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_{\max , i, j, k}} = \min \left\{ {w_{i, j, k}^{\rm{h}}\left( {t_{i, k}^{\rm{h}} - {T_{{\rm{h}}, {\rm{out}}, i}}} \right), w_{i, j, k}^{\rm{c}}\left( {t_{\max , j, k}^{\rm{c}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right)} \right\}\\ \;{\rm{elseif }}\left( {{T_{{\rm{h}}, {\rm{out}}, i}} < {T_{{\rm{c}}, {\rm{in}}, j}}} \right)\& \left( {w_{i, j, k}^{\rm{c}} < w_{i, j, k}^{\rm{h}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_{\max , i, j, k}} = \min \left\{ {w_{i, j, k}^{\rm{c}}\left( {t_{i, k}^{\rm{h}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right), w_{i, j, k}^{\rm{h}}\left( {t_{\max , j, k}^{\rm{c}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right)} \right\}\\ \;{\rm{elseif }}\left( {{T_{{\rm{h}}, {\rm{out}}, i}}} \right.\left. { \ge {T_{{\rm{c}}, {\rm{in}}, j}}} \right){\rm{\& }}\left( {t_{i, k}^{\rm{h}} < t_{\max , j, k}^{\rm{c}}} \right)\& \left( {w_{i, j, k}^{\rm{c}} < w_{i, j, k}^{\rm{h}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_{\max , i, j, k}} = \min \left\{ {w_{i, j, k}^{\rm{h}}\left( {t_{i, k}^{\rm{h}} - {T_{{\rm{h}}, {\rm{out}}, i}}} \right), w_{i, j, k}^{\rm{c}}\left( {t_{i, k}^{\rm{h}} - {T_{{\rm{c}}, {\rm{in}}, j}}} \right)} \right\}\\ \;{\rm{else}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_{\max , i, j, k}} = w_{i, j, k}^{\rm{h}}\left( {t_{i, k}^{\rm{h}} - {T_{{\rm{h}}, {\rm{out}}, i}}} \right) \end{array}$ | (37) |
Step 4:在内层算法中,会得到在标准及极限点下的个体Q。如果极点的数目等于n,则个体将是
Step 5:根据式(21)~(23)计算各换热器在不同操作条件下的换热面积。在计算投资成本和操作成本时,考虑每台换热器的最大换热面积和在不同条件下的平均公用。如果满足AEA算法终止条件,则返回TAC。
Step 6:重复步骤3至步骤5,直至得到BPSO种群中的每个粒子的TAC值。依据粒子的TAC值,按照式(25)~(28)生成一个新的HEN拓扑结构种群,并获得每个个体的TAC,依据TAC值更新种群,直至满足终止条件。
Step 7:计算柔性指数,并输出换热网络。
4 案例研究 4.1 案例一案例一包含有3条热物流及2条冷物流,如表 1所示物流数据及价格来自文献[26]。其波动为所有物流的入口温度±10 K,为凸可行域问题。外层BPSO算法的动态权重范围是0.4~1.2,学习因子为1.4。BPSO种群设为200个,迭代50次。内层AEA算法种群为120个,迭代50次。代码运行于Windows 7 x64-Intel Xeon E5645 2.4GH环境下Matlab软件中,计算时间为6 h 14 min。换热网络级数设为3级(ST=3),最小传热温差为3 K。目标函数选取了标准点及{438 K, 363 K, 483 K, 303 K, 303 K},{438 K, 363 K, 483 K, 283 K, 283 K},{418 K, 343 K, 463 K, 303 K, 303 K},{418 K, 343 K, 463 K, 283 K, 283 K}的平均值进行计算。
|
|
表 1 案例一物流数据 Table 1 Streams data of case 1 |
为证明同步合成的有效性,案例一分别给出了顺序综合法及双层同步优化方法的柔性HEN。顺序综合法的设计步骤如下所示:
Step 1:使用SWS模型在正常情况下以TAC值为目标函数优化换热网络,优化结果作为柔性设计的初始结构。
Step 2:计算现有结构的柔性指数,若不小于1则结构满足柔性;否则,该结构不满足柔性,找到限制柔性的极限点并重新优化,取得换热器的最大换热面积。
Step 3:重复Step 2操作,直至柔性指数不小于1,得到满足柔性的换热网络。
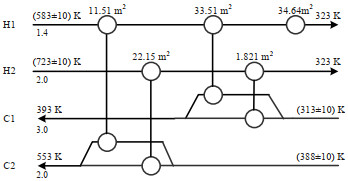
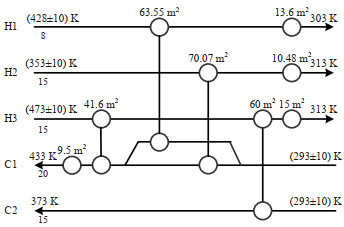
该方法所得HEN如图 3所示。图 4为双层同步优化策略得到的HEN结构。表 2为两种方法的对比结果。此案例中,顺序综合法得到的初始HEN可以实现完全换热。但是存在波动时,必须添加冷却器及加热器,并增大部分换热器的面积以满足柔性要求,该方法的TAC为174 839.86 $·a-1。本方法结果TAC值为154 145.59 $·a-1,可以节省20 694.27 $·a-1。如表 2所示,同步方法结果的公用工程成本较高,但投资成本可以从144 427.59 $·a-1大幅度降低到115 603.21 $·a-1。顺序综合法得到的结构能在标准状态下完全换热,且有分流,能够实现更多的热交换,操作费用较低。但该结构中换热器的换热温差较小,存在波动时需要增加更多换热面积,且添加多台公用换热器,导致投资成本更大。比较柔性指数也可以看出,同步方法所得结果满足柔性要求且柔性指数较小,避免了不必要的成本。通过结果对比,可以发现具有固定结构的方法在合成HEN时存在更多的局限性,同步方法有更大的搜索潜力,可以得到更好的HEN配置。
|
图 3 案例一顺序综合法HEN结构 Fig.3 Sequential synthesis HEN for case 1 |
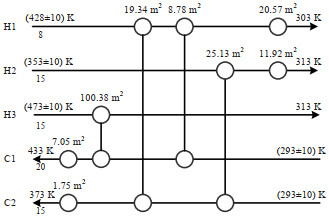
|
图 4 案例一同步综合法HEN结构 Fig.4 Simultaneous synthesis HEN for case 1 |
|
|
表 2 案例一对比结果 Table 2 Comparison results of case 1 |
案例二的物流数据及价格来自文献[27],包含2条热物流及2条冷物流,如表 3所示。所有物流的入口温度存在±10 K的波动,为凸可行域问题。外层BPSO种群设为200个,迭代40次。内层AEA算法种群为80个,迭代50次。计算时间为2 h 49 min。级数为2级(ST=2)。最小传热温差为10 K。
|
|
表 3 案例二物流数据 Table 3 Streams data of case 2 |
文献采用多周期综合方法合成柔性HEN,TAC值为130 474.08 $·a-1,柔性指数为1.429。文献中公用费用为标准点和极值点{573 K,713 K,303 K,378 K}的平均值。案例采用了相同方式计算TAC值,TAC为125 740.23 $·a-1且柔性指数为1.008。案例结果与文献的HEN分别如图 5和图 6所示,表 4给出了结果对比。
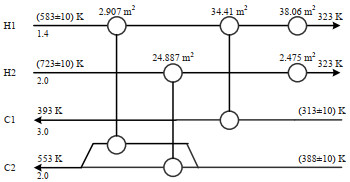
|
图 5 案例二HEN结构 Fig.5 Structure of case 2 |
|
|
表 4 案例二对比结果 Table 4 Comparison results of case 2 |
比较结果可以发现,两者具有相同的换热设备数目,且公用工程总量相同,不同点在于换热设备的位置与面积。两个结构均能使得两条冷流完全换热,实现相同的换热量,同步方法的结果使用了更少的换热面积。其原因在于文献首先确定初始结构,重复引入关键点设计并检验柔性至满足要求,在此过程中可能会导致柔性指数较大,使得部分换热器面积过大。双层优化策略会根据目标函数值对结构进行优化,使得所得结果在结构上更加合理,在满足了柔性指数约束的同时使其尽可能小,具有更好的经济性。同时经过验证,文献结果的冷却器H1-CU换热面积为标况下换热面积,而存在波动时该冷却器的面积应当比文献给出面积更大。冷公用量最大的情况出现在极值点{593 K, 733 K, 323 K, 398 K}处,此时的冷公用量为218 kW,冷却器H1-CU的面积应为41.97 m2。将面积扩大后文献的TAC为134 911.33 $·a-1,而同步方法总费用减少了9 171.1 $·a-1,也证明了双层同步优化策略的有效性。
5 结论针对柔性换热网络设计问题,提出了一种双层同步优化方法,该方法可以同步求解凸可行域问题的柔性换热网络结构及换热面积。分别在外层和内层使用了BPSO算法和AEA算法优化HEN的结构和换热面积,并对结果进行了柔性检验。两个案例研究结果表明双层同步优化方法能够克服固定结构优化的限制,通过内外层的信息传输实现对网络结构的更新,具有更大的搜索潜力。同时,在内层优化中综合了考虑了标准和极限情况,能够避免柔性指数过大情况发生,能够使总成本达到较为满意的结果。
| [1] |
GROSSMANN I, APAP R, CALFA B. Mathematical programming techniques for optimization under uncertainty and their application in process systems engineering[J]. Theoretical Foundations of Chemical Engineering, 2017, 51(6): 893-909. DOI:10.1134/S0040579517060057 |
| [2] |
FURMAN K, SAHINIDIS N. A Critical review and annotated bibliography for heat exchanger network synthesis in the 20th century[J]. Industrial & Engineering Chemistry Research, 2002, 41(10): 2335-2370. |
| [3] |
LINNHOFF B, FLOWER J. Synthesis of heat exchanger networks: Ⅰ, Systematic generation of energy optimal networks[J]. AIChE Journal, 1978, 24(4): 633-642. DOI:10.1002/aic.690240411 |
| [4] |
YEE T F, GROSSMANN I. Simultaneous optimization models for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(10): 1165-1184. |
| [5] |
YEE T F, GROSSMANN I, KRAVANIA Z. Simultaneous optimization models for heat integration-Ⅰ. Area and energy targeting and modeling of multi-stream exchangers[J]. Computers & Chemical Engineering, 1990, 14(10): 1151-1164. |
| [6] |
刘凯, 杜红彬, 金宇辉, 等. 基于AEA和PSO的双层同步换热网络综合方法研究[J]. 高校化学工程学报, 2017, 36(6): 1395-1403. LIU K, DU H B, JIN Y H, et al. A bi-level algorithm based on AEA and PSO algorithm for simultaneous synthesis of heat exchanger network[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 36(6): 1395-1403. DOI:10.3969/j.issn.1003-9015.2017.06.019 |
| [7] |
TOIMIL D, GOMEZ A. Review of metaheuristics applied to heat exchanger network design: International transactions in operations research[J]. International Transactions in Operational Research, 2016, 24(1/2): 7-26. |
| [8] |
KANG L, LIU Y. Synthesis of flexible heat exchanger networks: A review[J]. Chinese Journal of Chemical Engineering, 2019, 27(7): 1485-1497. DOI:10.1016/j.cjche.2018.09.015 |
| [9] |
FLOUDAS C, GROSSMANN I. Synthesis of flexible heat exchanger networks for multiperiod operation[J]. Computers & Chemical Engineering, 1986, 10(2): 153-168. |
| [10] |
李志红, 华贲. 有分流换热网络的弹性设计-基于温度波动情形[J]. 高校化学工程学报, 2000, 14(2): 151-155. LI Z H, HUA B. Synthesis of flexible heat exchanger network with stream splitting based on stream temperature perturbation[J]. Journal of Chemical Engineering of Chinese Universities, 2000, 14(2): 151-155. DOI:10.3321/j.issn:1003-9015.2000.02.009 |
| [11] |
李志红, 华贲. 多周期操作工况下换热网络的弹性设计[J]. 高校化学工程学报, 1999, 13(3): 252-258. LI Z H, HUA B. Flexible synthesis of heat exchanger networks for multiperiod operation[J]. Journal of Chemical Engineering of Chinese Universities, 1999, 13(3): 252-258. DOI:10.3321/j.issn:1003-9015.1999.03.012 |
| [12] |
李志红, 华贲. 无分流换热网络的弹性设计(Ⅰ)基于温度波动情形[J]. 高校化学工程学报, 1999, 13(3): 317-325. LI Z H, HUA B. Synthesis of flexible heat exchanger networks with stream no-splitting (Ⅰ) based on ranges of stream supply temperatures[J]. Journal of Chemical Engineering of Chinese Universities, 1999, 13(3): 317-325. |
| [13] |
肖丰, 姚平经. 多周期换热网络柔性综合与维护同步优化[J]. 华东理工大学学报, 2009, 35(5): 783-787. XIAO F, YAO P J. Simultaneous optimization of synthesis and maintenance for flexible heat exchanger network[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2009, 35(5): 783-787. DOI:10.3969/j.issn.1006-3080.2009.05.024 |
| [14] |
肖丰, 都健, 陈理, 等. 柔性换热网络综合与清洗时序安排同步优化[J]. 化工学报, 2009, 60(10): 2529-2535. XIAO F, DU J, CHEN L, et al. Simultaneous optimization of synthesis and cleaning schedule for flexible heat exchanger network[J]. CIESC Journal, 2009, 60(10): 2529-2535. |
| [15] |
朱真, 孙琳, 罗雄麟. 基于持续节能的多周期换热网络优化设计[J]. 化工学报, 2016, 67(12): 5176-5182. ZHU Z, SUN L, LUO X L. Design optimization of multi-period heat exchanger networks based on continuous energy saving[J]. CIESC Journal, 2016, 67(12): 5176-5182. |
| [16] |
PAVÃO L, MIRANDA C, COSTA C, et al. Synthesis of multiperiod heat exchanger networks with timesharing mechanisms using meta-heuristics[J]. Applied Thermal Engineering, 2018, 128(9): 637-652. |
| [17] |
MARSELLE D, MORARI M, RUDD D. Design of resilient processing plants-Ⅱ. Design and control of energy management systems[J]. Chemical Engineering Science, 1982, 37(2): 259-270. DOI:10.1016/0009-2509(82)80160-7 |
| [18] |
SABOO A, MORARI M. Design of resilient processing plants-Ⅳ. Some new results on heat exchanger network synthesis[J]. Chemical Engineering Science, 1984, 39(3): 579-592. DOI:10.1016/0009-2509(84)80054-8 |
| [19] |
SABOO A, MORARI M, Woodcock D. Design of resilient processing plants-Ⅷ. A resilience index for heat exchanger networks[J]. Chemical Engineering Science, 1985, 40(8): 1553-1565. DOI:10.1016/0009-2509(85)80097-X |
| [20] |
SWANEY R, GROSSMANN I. An index for operational flexibility in chemical process design. Part Ⅰ: Formulation and theory[J]. AIChE Journal, 1985, 31(4): 621-630. DOI:10.1002/aic.690310412 |
| [21] |
康丽霞, 刘永忠. 考虑冗余控制的多周期换热网络设计[J]. 化工学报, 2018, 69(3): 1022-1029. KANG L X, LIU Y Z. Design of multi-period heat exchanger networks for overdesign control[J]. CIESC Journal, 2018, 69(3): 1022-1029. |
| [22] |
KONUKMAN A, CAMURDAN M, AKMAN U. Simultaneous flexibility targeting and synthesis of minimum-utility heat-exchanger networks with superstructure-based MILP formulation[J]. Chemical Engineering and Processing: Process Intensification, 2002, 41(6): 501-518. DOI:10.1016/S0255-2701(01)00171-4 |
| [23] |
KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm algorithm[C]. 1997 IEEE International Conference on Systems, Man, and Cybernetics Computational Cybernetics and Simulation, USA, 1997, 5: 4104-4108.
|
| [24] |
LI S J, LI F. Alopex-based evolutionary algorithm and its application to reaction kinetic parameter estimation[J]. Computers & Industrial Engineering, 2011, 60(2): 341-348. |
| [25] |
YANG Y H, ZONG X P, YAO D C, et al. Improved Alopex-based evolutionary algorithm (AEA) by quadratic interpolation and its application to kinetic parameter estimations[J]. Applied Soft Computing, 2016, 51(11): 23-38. |
| [26] |
PAVÃO L, MIRANDA C, COSTA C A.S.S., RAVAGNANI M. Automated heat exchanger network synthesis by using hybrid natural algorithms and parallel processing[J]. Computers & Chemical Engineering, 2016, 94(8): 370-386. |
| [27] |
ESCOBAR M, TRIERWEILER J O. Simultaneous synthesis of heat exchanger networks with operability considerations: Flexibility and controllability[J]. Computers & Chemical Engineering, 2013, 55(4): 158-180. |