经典成核理论(classical nucleation theory,CNT)忽略了表面张力的曲率修正(修正首项由Tolman长度表示)[1],成核速率的计算结果与实验值存在明显偏差[2]。目前,Tolman长度还不能实验测定,通常采用密度泛函理论(density functional theory,DFT)或梯度平方理论(square gradient theory,SGT)进行理论计算[3-4]。但是,DFT和SGT只适用于远离临界点的两相平衡区,在临界点附近两者都失效。Blokhuis等[5]将Tolman长度与流体的容积性质相联系,使得可以用状态方程预测Tolman长度。但是常用的状态方程没有考虑临界密度涨落对热力学性质的影响,因此需要采用重正化群理论。但是由White建立的全局重正化群理论(global renormalization group,GRG)[6]及其推广[7]没有正确反映流体的临界非对称性[8-9],不能用来计算和非对称性有关的Tolman长度[10-11]。最近,作者改进了GRG理论[12],并将改进的GRG理论与阱宽可变的统计缔合流体(statistical associating fluid theory for molecules with variable range,SAFT-VR)方程[13]结合,计算了几种简单有机分子的临界表面张力和Tolman长度[14]。然而,SAFT-VR方程对于强极性和缔合流体不够准确,而微扰链-SAFT方程(Perturbed-chain SAFT, PC-SAFT)[15-16]更严格地考虑了分子间的色散相互作用,因此本研究将改进的GRG方法与PC-SAFT方程结合,用于醇、醋酸、水等工业上有着广泛应用的缔合流体,为修正经典成核理论提供理论依据。
2 理论和计算方法 2.1 重正化计算方法原始全局重正化群虽然能正确描述流体的多数临界性质,但是未能正确描述临界非对称性,因此不能用来计算Tolman长度。场论分析[17]和实例计算[12, 14]都表明,为正确描述临界非对称性,需将原始GRG的哈密顿量改为如下形式:
| $ H = \int {\left\{ {{f_{^{{\text{EOS}}}}}n({\mathit{\boldsymbol{r}}}) + [{a_{{\text{vdw}}}} + {u_1}{k_{\text{B}}}Tn({\mathit{\boldsymbol{r}}})]L_0^2{{\left| {\nabla n({\mathit{\boldsymbol{r}}})} \right|}^2}} \right\}} {\text{d}}r $ | (1) |
式中:H为哈密顿量;f为自由能密度,是摩尔Helmholtz自由能与摩尔体积之比;fEOS为由状态方程计算的自由能密度;n为分子数密度,n(r)表示n是位置矢量r的函数;
由于临界非对称性由分子间相互作用决定,因此,如果在建立状态方程时准确考虑了分子间相互作用,则完整标度理论[18]中表征临界非对称性的关键参数——场混合系数a3就可由状态方程直接求出[10]。因此本研究采用这样的方法确定u1的值:选取合适的u1,使得由式(1)结合重正化群理论计算得到的a3与直接由fEOS预测的a3一致。u1的这种取法使得式(1)从临界非对称的角度看是自洽的。由重正化群理论计算a3实质上就是计算气液平衡压力和定容热容,在临界点附近二者存在如下所示的线性关系[10]:
| $ \hat P'' \approx \frac{1}{{1 + {a_3}}}\frac{{\hat C_{V, {\text{m}}}^{{\text{res}}}}}{{\hat T}} $ | (2) |
式中:
实际计算中将密度区间[0, nmax] 50 000等分(nmax为体系允许的最大数密度),计算的是每个等分点上的f和e。详细过程如下:
| $ {\tilde f_i}(n) = {\tilde f_{i - 1}}(n) + {\text{δ }}{\tilde f_i}(n){, _{}}{\tilde f_0}(n) = {\tilde f_{^{_{{\text{EOS}}}}}}(n){;_{}}i = 1, 2, \cdots {;_{}}\tilde f(n) = \mathop {\lim }\limits_{i \to \infty } {\tilde f_i}(n), $ | (3a) |
| $ {\text{δ }}{\tilde f_i}(n) = - \frac{1}{{L_i^3}}\ln \frac{{\int_0^{{{\min }_{}}(n, {n_{\max }} - n)} {\exp \left\{ { - L_i^3{{\tilde G}_{i, s}}(n, x)} \right\}{\text{d}}x} }}{{\int_0^{{{\min }_{}}(n, {n_{\max }} - n)} {\exp \left\{ { - L_i^3{{\tilde G}_{i, l}}(n, x)} \right\}{\text{d}}x} }}{, _{}}{L_i} = {2^i}{L_0}, $ | (3b) |
| $ {\tilde G_{i, s}}(n, x) = \frac{{{{\tilde f}_{i - 1}}(n + x) + {{\tilde f}_{i - 1}}(n - x)}}{2} - {\tilde f_{i - 1}}(n) + \left( {\frac{{{a_{{\text{vdw}}}}}}{{{k_{\text{B}}}T}} + {u_1}n} \right)\frac{{{x^2}\mathit{\Delta} }}{{{2^{2i}}}}, $ | (3c) |
| $ {\tilde G_{i, l}}(n, x) = \frac{{{{\tilde f}_{i - 1}}(n + x) + {{\tilde f}_{i - 1}}(n - x)}}{2} - {\tilde f_{i - 1}}(n) + \frac{{{a_{{\text{vdw}}}}{x^2}}}{{{k_{\text{B}}}T}}, $ | (3d) |
| $ {e_i} = \frac{{\partial {{\tilde f}_i}}}{{\partial {{({k_{\text{B}}}T)}^{ - 1}}}} = \frac{{\partial ({{\tilde f}_{i - 1}} + {\text{δ }}{{\tilde f}_i})}}{{\partial {{({k_{\text{B}}}T)}^{ - 1}}}} = {e_{i - 1}} + {\text{δ }}{e_i}{, _{}}{e_0} = {e^{{\text{EOS}}}} = \frac{{\partial {{\tilde f}_{^{{\text{EOS}}}}}}}{{\partial {{({k_{\text{B}}}T)}^{ - 1}}}}{;_{}}i = 1, 2, \cdots {;_{}}e = \mathop {\lim }\limits_{i \to \infty } {e_i}, $ | (4a) |
| $ {\text{δ}}{e_i} = \frac{{\partial ({\text{δ }}{{\tilde f}_i})}}{{\partial {{({k_{\text{B}}}T)}^{ - 1}}}} = \frac{{\int_0^{{{\min }_{}}(n, {n_{\max }} - n)} {{g_{i, s}}{{\exp }_{}}\left\{ { - L_i^3{{\tilde G}_{i, s}}} \right\}{\text{d}}x} }}{{\int_0^{{{\min }_{}}(n, {n_{\max }} - n)} {{{\exp }_{}}\left\{ { - L_i^3{{\tilde G}_{i, s}}} \right\}{\text{d}}x} }} - \frac{{\int_0^{{{\min }_{}}(n, {n_{\max }} - n)} {{g_{i, l}}{{\exp }_{}}\left\{ { - L_i^3{{\tilde G}_{i, l}}} \right\}{\text{d}}x} }}{{\int_0^{{{\min }_{}}(n, {n_{\max }} - n)} {{{\exp }_{}}\left\{ { - L_i^3{{\tilde G}_{i, l}}} \right\}{\text{d}}x} }}, $ | (4b) |
| $ {g_{i, s}} = \frac{{\partial {{\tilde G}_{i, s}}}}{{\partial {{({k_{\text{B}}}T)}^{ - 1}}}} = \frac{{{e_{i - 1}}(n + x) + {e_{i - 1}}(n - x)}}{2} - {e_{i - 1}}(n) + \frac{{{a_{{\text{vdw}}}}{x^2}\mathit{\Delta} }}{{{2^{2i}}}}, $ | (4c) |
| $ {g_{i, l}} = \frac{{\partial {{\tilde G}_{i, l}}}}{{\partial {{({k_{\text{B}}}T)}^{ - 1}}}} = \frac{{{e_{i - 1}}(n + x) + {e_{i - 1}}(n - x)}}{2} - {e_{i - 1}}(n) + {a_{{\text{vdw}}}}{x^2}, $ | (4d) |
式中:字符顶上的“∼”表示除以kBT,例如
| $ {a_{{\text{vdw}}}} = - \frac{{{m^2}}}{2}\int {{u_{{\text{att}}}}(r){\text{d}}r} , \;\;\mathit{\Delta} = \frac{{5\int {{u_{{\text{att}}}}(r){r^2}{\text{d}}r} }}{{3L_0^2\int {{u_{{\text{att}}}}(r){\text{d}}r} }} $ | (5) |
式中:m为分子的等效链节数;uatt(r)为等效链节间的吸引势,r为位置矢量r的模,是标量。重正化迭代的收敛判据为两次迭代的自由能之间相对误差小于10−12。
2.2 表面张力和Tolman长度Tolman[1]在Gibbs表面热力学理论的框架下推导出了球形液滴的表面张力与曲率半径的关系:
| $ \sigma ({R_e}) = {\sigma _\infty }\left( {1 - \frac{{2{\delta _T}}}{{{R_e}}} + \cdots } \right) $ | (6) |
式中:σ(Re)为计入了曲率修正的表面张力;Re为液滴半径;σ∞为平坦表面张力;δT为Tolman长度。Blokhuis和Kuipers给出了球形液滴Tolman长度近似表达式[5]:
| $ - {\hat \delta _T} \approx \frac{{{{\hat \sigma }_\infty }}}{{{{({{\hat n}_{\text{l}}} - {{\hat n}_{\text{g}}})}^2}}}\left( {\hat n_{\text{l}}^2{{\hat \kappa }_{\text{l}}} - \hat n_{\text{g}}^2{{\hat \kappa }_{\text{g}}}} \right) $ | (7) |
式中:
| $ {\hat \sigma _\infty } = 0.274\;7{\left( {{{B_0^2} \mathord{\left/ {\vphantom {{B_0^2} {\mathit{\Gamma} _0^ - }}} \right. } {\mathit{\Gamma} _0^ - }}} \right)^{2/3}}{\left| {{\Delta}\hat T} \right|^{2\nu }} $ | (8) |
式中:v为临界指数,ν ≈0.6;临界振幅B0和
进一步可计算Tolman长度对成核功ΔW的修正,如式(9)所示;ΔW关系到成核速率J的大小[19],如式(10)所示,其中J0是与过饱和度或过冷度有关的系数:
| $ \Delta W = \frac{4}{3}\pi {\sigma _\infty }R_{\text{e}}^2\left( {1 - \frac{{4{\delta _{\text{T}}}}}{{{R_{\text{e}}}}}} \right) $ | (9) |
| $ J = {J_0}\exp \;( - {{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {({k_{\text{B}}}T)}}} \right. } {({k_{\text{B}}}T)}}) $ | (10) |
对于普通的弱极性、非缔合流体,SAFT-VR方程已经足够准确,但是对于强极性、缔合流体,以水为例,SAFT-VR方程预测水的a3为−0.030 9[20],但由两相平衡数据[21]可以推算出其a3应大于零,若用SAFT-VR+GRG计算,则水的Tolman长度在临界点将趋于正无穷,与完整标度理论预言(趋于负无穷)完全相反。而PC-SAFT方程预测的a3与相平衡实验结果吻合,因此,本研究选用PC-SAFT方程,uatt(r)取为Lennard-Jones势的吸引部分,d为Lennard-Jones势表征分子大小的特征参数;ε为能量特征参数。
| $ {u_{{\text{att}}}}(r) = \left\{ \begin{array}{l} 0, \;\;\;r < d \hfill \\ 4\varepsilon \left[ {{{(d/r)}^{12}} - {{(d/r)}^6}} \right], \;\;r \geqslant d \hfill \\ \end{array} \right. $ | (11) |
本研究考察的流体包括正构烷醇、醋酸和水。表 1给出计算所需的参数[16],包括2个和缔合有关的参数:缔合能εHB、有效缔合体积κHB。L0*为L0的约化,L0*=L0/d,a3, EOS为状态方程预测的a3,u1为式(1)中的待定参数。流体的缔合类型都取2B模型[22]。
|
|
表 1 缔合流体的方程参数 Table 1 Equation parameters of the associating fluids |
临界指数和振幅[12]、另一个场混合系数b2的计算结果列于表 2。
|
|
表 2 缔合流体的临界参数 Table 2 Critical parameters of the associating fluids |
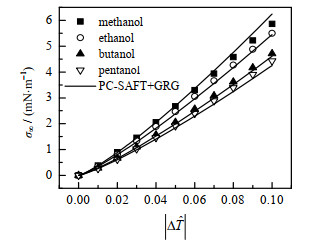
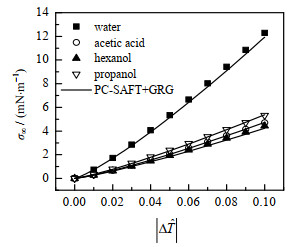
图 1、2显示了各种缔合流体表面张力σ∞的计算结果(实线)和较准确的经验公式[26](数据点)的对比。严格说式(8)只有在临界点附近才准确,但由图可以看出,PC-SAFT+GRG计算的σ∞在外推到远离临界点时依然和经验公式保持较高的一致。
|
图 1 甲醇、乙醇、丁醇、戊醇的表面张力σ∞ Fig.1 Planar surface tensions of methanol, ethanol, butanol and pentanol |
|
图 2 水、醋酸、丙醇、己醇的表面张力σ∞ Fig.2 Planar surface tensions of water, acetic acid, propanol and hexanol |
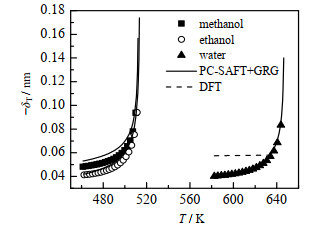
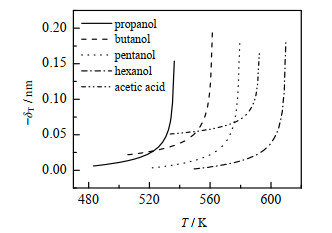
图 3、4为PC-SAFT+GRG对从甲醇到己醇的正构烷醇、醋酸和水的Tolman长度的计算结果(实线)。由于缺乏Tolman长度的实验数据,本研究将取自NIST数据库[21]的气液平衡数据以及由经验公式[26]计算的σ∞代入式(7),估算其值(记作Eq+NIST,以数据点表示),可以看出PC-SAFT+GRG与Eq+NIST符合良好。图中还用点虚线给出了水的DFT计算结果[27],可以看出DFT不能反映Tolman长度的临界发散行为,而改进的重正化群方法的结果与完整标度理论的预测一致。由于缺乏准确的近临界相平衡实验数据,图 4只画出了PC-SAFT+GRG计算结果。
|
图 3 甲醇、乙醇、水的Tolman长度−δT Fig.3 Profiles of Tolman length −δT of methanol, ethanol and water |
|
图 4 丙醇、丁醇、戊醇、己醇、醋酸的Tolman长度−δT Fig.4 Profiles of Tolman length −δT of propanol, butanol, pentanol, hexanol and acetic acid |
将计算所得σ∞和δT代入式(9)便能计算成核功。以Re = 0.5 nm的微小水滴为例,图 5显示了本研究的计算结果(实线)和Eq+NIST(数据点)、DFT(点线)以及经典成核理论(即完全忽略Tolman修正,虚线)的对比,其中Eq+NIST、DFT、CNT用到的σ∞均由经验公式[26]计算。从图中可以看出考虑了Tolman修正的3种方法计算的成核功比较接近,它们都与经典成核理论的计算结果有显著差异,这将显著影响成核速率的预测。
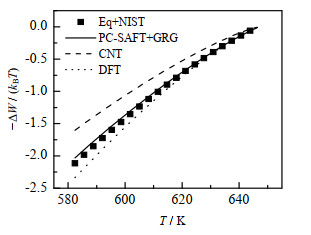
|
图 5 水(Re = 0.5 nm)的−ΔW / (kBT)随温度T的函数关系 Fig.5 Profiles of −ΔW / (kBT) as a function of water temperature (Re = 0.5 nm) |
本研究将改进的重正化群理论与PC-SAFT方程结合,预测了包括醇、醋酸、水在内的各种缔合流体的表面张力和Tolman长度。PC-SAFT+GRG对缔合流体的表面张力与Tolman长度的描述不仅在临界点符合完整标度理论的预测,也能外推至非临界区,依然保持较高的准确性。经过Tolman修正的表面张力能对经典成核理论预测的成核速率作出改进。
| [1] |
TOLMAN R C. The effect of droplet size on surface tension[J]. Journal of Chemical Physics, 1949, 17(3): 333-337. DOI:10.1063/1.1747247 |
| [2] |
WÖLK J, STREY R. Homogeneous nucleation of H2O and D2O in comparison: the isotope effect[J]. Journal of Physical Chemistry B, 2001, 105(47): 11683-11701. DOI:10.1021/jp0115805 |
| [3] |
BLOKHUIS E M, VAN GIESSEN A E. Density functional theory of a curved liquid-vapor interface: Evaluation of the rigidity constants[J]. Journal of Physics: Condensed Matter, 2013, 25: 225003-225014. DOI:10.1088/0953-8984/25/22/225003 |
| [4] |
WILHELMSEN Ø, BEDEAUX D, REGUERA D. Tolman length and rigidity constants of the Lennard-Jones fluid[J]. Journal of Chemical Physics, 2015, 142(6): 064706-064715. DOI:10.1063/1.4907588 |
| [5] |
BLOKHUIS E M, KUIPERS J. Thermodynamic expressions for the Tolman length[J]. Journal of Chemical Physics, 2006, 124(7): 074701-074708. DOI:10.1063/1.2167642 |
| [6] |
WHITE J A. Contribution of fluctuations to thermal properties of fluids with attractive forces of limited range: Theory compared with PρT and CV data for argon[J]. Fluid Phase Equilibria, 1992, 75: 53-64. DOI:10.1016/0378-3812(92)87006-9 |
| [7] |
LUE L, PRAUSNITZ J M. Renormalization-group corrections to an approximate free-energy model for simple fluids near to and far from the critical region[J]. Journal of Chemical Physics, 1998, 108(13): 5529-5536. DOI:10.1063/1.475942 |
| [8] |
ZHAO W, WU L, WANG L, et al. Critical asymmetry in renormalization group theory for fluids[J]. Journal of Chemical Physics, 2013, 138(23): 234502-234513. DOI:10.1063/1.4810809 |
| [9] |
WANG L, ZHAO W, WU L, et al. Improved renormalization group theory for critical asymmetry of fluids[J]. Journal of Chemical Physics, 2013, 139(12): 124103-124111. DOI:10.1063/1.4821599 |
| [10] |
WANG J T, ANISIMOV M A. Nature of vapor-liquid asymmetry in fluid criticality[J]. Physical Review E, 2007, 75(5): 051107-051125. DOI:10.1103/PhysRevE.75.051107 |
| [11] |
ANISIMOV M A. Divergence of Tolman's length for a droplet near the critical point[J]. Physical Review Letters, 2007, 98(3): 035702-035705. DOI:10.1103/PhysRevLett.98.035702 |
| [12] |
ZHOU Z Y, CAI J, HU Y. A self-consistent renormalization group theory for critical asymmetry of one-component fluids[J]. Molecular Physics, 2022, 120(3): e1987541-1987551. DOI:10.1080/00268976.2021.1987541 |
| [13] |
GIL-VILLEGAS A, GALINDO A, WHITEHEAD P J, et al. Statistical associating fluid theory for chain molecules with attractive potentials of variable range[J]. Journal of Chemical Physics, 1997, 106(10): 4168-4186. DOI:10.1063/1.473101 |
| [14] |
ZHOU Z Y, CAI J, HU Y. Application of the renormalization group theory for critical asymmetry to surface criticality of one-component fluids[J]. Fluid Phase Equilibria, 2021, 544-545: 113114-113122. DOI:10.1016/j.fluid.2021.113114 |
| [15] |
GROSS J, SADOWSKI G. Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules[J]. Industrial & Engineering Chemistry Research, 2001, 40(4): 1244-1260. |
| [16] |
GROSS J, SADOWSKI G. Application of the perturbed-chain SAFT equation of state to associating systems[J]. Industrial & Engineering Chemistry Research, 2002, 41(22): 5510-5515. |
| [17] |
BERTRAND C E, NICOLL J F, ANISIMOV M A. Comparison of complete scaling and a field-theoretic treatment of asymmetric fluid criticality[J]. Physical Review E, 2012, 85(3): 031131-031140. DOI:10.1103/PhysRevE.85.031131 |
| [18] |
KIM Y C, FISHER M E, ORKOULAS G. Asymmetric fluid criticality. I. Scaling with pressure mixing[J]. Physical Review E, 2003, 67(6): 061506-061526. DOI:10.1103/PhysRevE.67.061506 |
| [19] |
WILHELMSEN Ø, BEDEAUX D, REGUERA D. Communication: Tolman length and rigidity constants of water and their role in nucleation[J]. Journal of Chemical Physics, 2015, 142(17): 171103-171107. DOI:10.1063/1.4919689 |
| [20] |
FORTE E, LLOVELL F, MARTIN TRUSLER J P, et al. Application of the statistical associating fluid theory for potentials of variable range (SAFT-VR) coupled with renormalization-group (RG) theory to model the phase equilibria and second-derivative properties of pure fluids[J]. Fluid Phase Equilibria, 2013, 337: 274-287. DOI:10.1016/j.fluid.2012.09.022 |
| [21] |
LEMMON E W, HUBER M L, MCLINDEN M O. NIST Standard Reference Database [DB/OL]. (2010) [2022-2-26]. http://webbook.nist.gov/.
|
| [22] |
HUANG S H, RADOSZ M. Equation of state for small, large, polydisperse, and associating molecules[J]. Industrial & Engineering Chemistry Research, 1990, 29(11): 2284-2294. |
| [23] |
FISHER M E, ZINN S Y. The shape of the van der Waals loop and universal critical amplitude ratios[J]. Journal of Physics A: Mathematical and General, 1998, 31: L629-L635. DOI:10.1088/0305-4470/31/37/002 |
| [24] |
WILSON K G. Renormalization group and critical phenomena. Ⅱ. Phase-space cell analysis of critical behavior[J]. Physical Review B, 1971, 4(9): 3184-3205. DOI:10.1103/PhysRevB.4.3184 |
| [25] |
BERTRAND C E. Asymmetric fluid criticality[D]. City of College Park: University of Maryland, 2011.
|
| [26] |
SOMAYAJULU G R. A generalized equation for surface tension from the triple point to the critical point[J]. International Journal of Thermophysics, 1988, 9(4): 559-566. DOI:10.1007/BF00503154 |
| [27] |
REHNER P, AASEN A, WILHELMSEN Ø. Tolman lengths and rigidity constants from free-energy functionals-general expressions and comparison of theories[J]. Journal of Chemical Physics, 2019, 151: 244710-244722. DOI:10.1063/1.5135288 |




