2. 山东大学 动力工程及工程热物理博士后科研流动站, 山东 济南 250061
2. Power Engineering and Engineering Thermal Physics Postdoctoral Research Station, Shandong University, Jinan 250061, China
由于具有能耗低、响应快等诸多优势,微小通道广泛应用于化工[1-3]、能源[4-5]、航空航天[6-7]等各种领域。随着通道尺寸减小,重力作用削弱,表面张力、黏度等影响逐渐增大,微小通道中两相流型特征和流型转换边界等参数的变化规律与常规管道有较大的差别。
流型是两相流研究和工程应用的基础,直接影响两相流动的传热、传质及阻力特性。Taitel等[8]基于理论推导,获得了水平管内间歇流、光滑层状流、波状层状流、分散泡状流和环状流的流型转换边界。该理论转换边界与常规通道内的实验结果吻合较好[9],但由于未考虑表面张力的作用,对于小管径内两相流型的预测偏差较大[10]。Triplett等[11]测定了内径1.45和1.1 mm水平圆管内两相流动,结果表明常规通道的流型转换边界无法预测实验结果。Coleman等[12]实验测定了内径为5.5至1.3 mm的微小圆管及方管内两相流型特征,并指出管径、物性对当量直径小于10 mm的通道有着重要的影响。
作为两相流的重要参数之一,含气率是确定其他参数的关键。随着计算机图像处理技术的高速发展,图形处理技术在含气率的测量中得到广泛应用。Serizawa等[13]研究了微通道中的空气-水的两相流动,通过假设气泡具有轴对称形状分析含气率的变化规律。付鑫[14]通过虚拟双目系统构建了三维可视化光路,还原了液氮两相流动三维气液界面。Zhang等[15]提出了虚拟双目立体视觉系统,并进行泡状流的三维重建。Li等[16]通过正交平面的双目立体视觉系统对内径2~4 mm的水平和垂直圆管内含气率进行了测量,并与快关阀测量的数据进行对比,二者误差在±6% 以内。含气率预测模型主要包括滑移率模型、KαH模型、漂移通量模型等[16],Woldesemayat等[17]基于文献中不同流型对应的含气率数据(2 845个数据点),讨论了68个含气率相关模型的预测性能,并指出漂移通量模型的效果较好。
虽然已有一些小通道内两相流型的研究,但在三维气液界面特征以及含气率预测方面的分析仍有不足。本文主要对内径为5.16和3.14 mm的小通道内气液两相流动进行可视化研究,以空气和去离子水作为两相工质,改进实验系统的光路设计,获得流型的正视图与俯视图,并重构三维气液界面,计算含气率,使用电磁阀进行含气率的标定,并分析流型转换边界及含气率的变化规律。
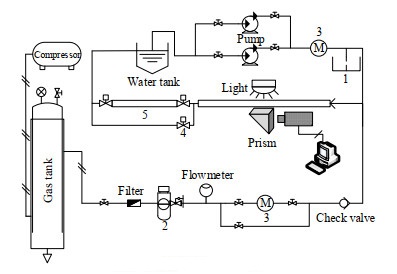
2 实验系统及三维重构方法简介如图 1所示为小通道两相流实验系统图,主要包含水循环和空气循环。水路的循环动力由MG204XK与MG209XK 2种型号磁力驱动齿轮泵提供,根据实验工况,选择性开启。连续相介质流经齿轮泵以后,进入高精度科里奥利质量流量计(HK-CMF-D-DN6),并流入可视化实验段,经过含气率标定段流入水箱,完成水路循环。气路部分的动力由空压机(OTS-1500×3)提供,在300 L固定式大型储气罐存储后,经空气滤清器和减压阀,根据实验工况选择气体流量计(型号MF5706,量程0 ~ 25 L·min-1;型号DO7-19B,量程0 ~ 2 L·min-1),随后通过单向阀门进入实验段。
|
图 1 小通道两相流实验系统图 Fig.1 Schematic diagram of the experimental setup of two-phase flows in mini channels 1. sewage outlet 2. pressure reducting valve 3. mass flowmeter 4. solenoid valve 5. calibration section |
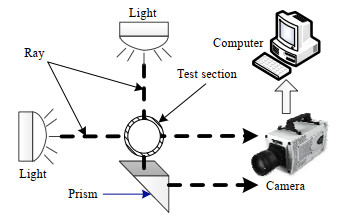
如图 2所示,实验段由透光性良好的石英玻璃管构成,实验段正下方放置一两直角边相等的三棱镜,尺寸为30 mm × 30 mm × 100 mm。为使流型稳定,棱镜始端与入口距离为350 mm。该三棱镜的反射平面与水平面呈45°夹角,可以将俯视图像反射成平行图像。基此,可以利用单一的高速摄像机,从正面和顶部2个垂直的角度出发,对两相流型的二维图像进行拍摄,获取同一位置正交平面的流型特征图像。实验段的后部和上部采用200 W的相同型号LED灯进行照明,满足拍摄的光照需求。可视化实验段后部连接电磁快关阀标定实验段,称取标定段内液体质量,求出工况对应的含气率。为保证标定值稳定,一组标定值至少测量5次。
|
图 2 虚拟双目系统示意图 Fig.2 Schematic diagram of the virtual multi-vision setup |
由于空气、水、石英管不同的折射率n以及圆弧形的壁面,拍摄尺寸与真实尺寸存在一定的偏差。当偏离管道中心时,光路与管道壁面呈一定角度,光线发生偏折。偏离管道中心距离越大,光路与管道接触点法线的夹角θ越小,光线偏移程度也会越大。当管内流体为水时,偏移程度较大,与文献[14]中管路折射修正公式进行对比,发现内径放大了33% 左右,因此后续气液界面三维重构以及含气率测量,均采用文献[14]中公式修正光线折射引起的误差。
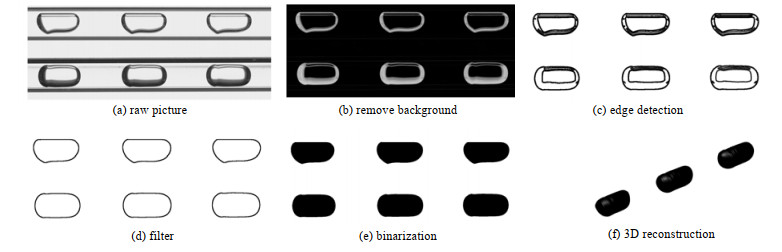
以弹状流为例,如图 3所示为在Matlab软件中进行气液界面三维重构的具体过程。首先,利用虚拟双目图像采集单元,获得2个正交平面的流型图片。如图 3(a)所示,其中上部分区域为正视图对应的流型,下部分区域为俯视图对应的流型。针对图像边缘信息模糊的问题,通过分割、滤波,并利用全液相背景图像去除背景,得到不含光源等噪声的图像,如图 3(b)所示。随后通过边缘检测(Canny算法)、腐蚀滤波变换、填充等步骤,使图片转化为二值化图像。由于表面张力的作用,气泡在管内流动头部与尾部会趋向于半球形或圆帽型,因此假设三维气液界面垂直于流动方向截面形状为椭圆,将2个正交化平面的每一个截面方向的气相长度,定义为椭圆的长轴a和短轴b[16]。对二维截面沿流动方向进行拉伸,长度为1个像素点,从而得到沿流动方向,每个像素点对应的三维气液界面。在整个计算域迭代重构,从而获得完整的三维气液界面,如图 3(f)所示。
|
图 3 弹状流三维重构技术流程 Fig.3 3D reconstruction process of slug flows |
根据图 3(f)得到的二值化图像对,采用文献[14]计算含气率方法,对图像中每个横坐标处假想气泡椭圆模型与管道截面积A的比值,通过积分式叠加可以得到整个计算域长度L的含气率α的数值。
| $ \alpha = \int\limits_0^L {\frac{{{\rm{ \mathsf{ π} }}ab}}{A}} $ | (1) |
式中:a为椭圆模型长轴像素长度,b为椭圆模型短轴像素长度,L为管道长度像素数量,α为含气率。
在实际的计算中,气液两相流动流型复杂多变,选取连续的N张图片组成时间序列,批量处理获得平均含气率,N值根据具体实验工况确定。如式(2)所示:
| $ {\alpha _{{\rm{ave}}}} = \sum\limits_{i = 1}^N {{\alpha _i}} /N $ | (2) |
式中:αi为第i张图片的含气率,αave为N张图片的含气率平均值。
3 实验结果与讨论 3.1 小通道流型特点两相流型的类别受管径尺寸、流动参数及物性等多种因素影响,文献中对于流型的划分有多种不同的标准。本文将实验获得的流型分为泡状流、弹状流和环状流3种。
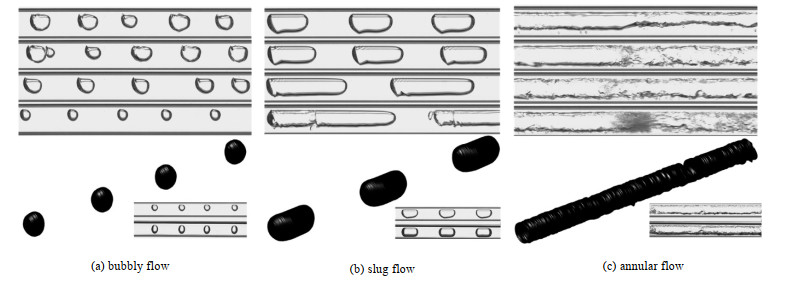
泡状流:如图 4(a)所示,大量小气泡分散在连续的液体中,气相的当量直径小于通道内径。随流量参数的变化,气泡在径向的发展不受壁面的限制。与大通道相比,小通道内泡状流分布更为均匀。
|
图 4 二维及三维流型(5.16 mm) Fig.4 2D and 3D flow patterns (5.16mm) |
弹状流:如图 4(b)所示,当气泡长度大于通道内径时,气泡垂直于流动方向的发展受到壁面的限制,形成弹状流,也被称为Taylor流型。气弹周围覆盖一层薄薄的液膜,由于重力原因,底层液膜较厚,二者的差距随通道直径的减小而逐渐降低。
环状流:如图 4(c)所示,当气相流量较大时,液膜附在管壁,中心形成气芯,气液两相界面存在波动和较强的剪切作用。随着惯性力及表面张力的增强,重力的减弱,环状流是微小通道内的两相流动的主要流型,在流型图上占据较大的区域。
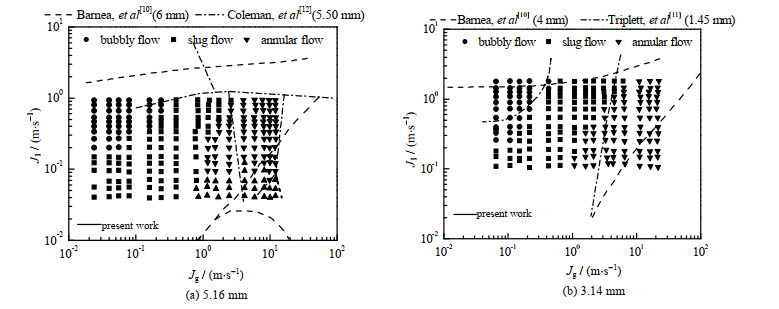
3.2 流型图及转换边界如图 5所示为内径为5.16和3.14 mm的水平圆管内,空气与水两相流型图及Barnea等[10]、Triplett等[11]及Coleman等[12]的流型转换边界对比情况。Jg为空气的表观速度,Jl为水的表观速度。受限于实验条件,本文5.16 mm管径内气相最大表观速度为12 m·s-1,液相最大表观速度为0.934 m·s-1。3.14 mm通道内气相和液相最大表观速度分别为27和2 m·s-1。由图 5(a)可得,相比Barnea等[10]的实验结果(6 mm内径),环状流出现在更低的气相流速下。实验数据与Coleman等[12]的分界线整体吻合较好。不同之处在于环状流与弹状流的分界线,造成这种差异的主要原因是入口段的类型以及对于过渡区域流型的定义不同。
|
图 5 小管径两相流动流型图及分界线 Fig.5 Flow pattern maps and transitional lines of two-phase flows in mini tubes |
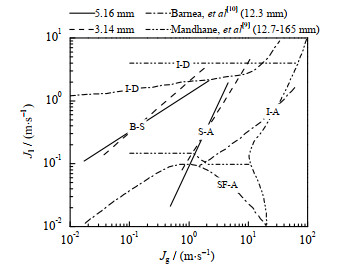
如图 6所示为不同管径流型转换边界的对比,Mandhane等[9]和Barnea等[10]的流型图,将泡状流与弹状流统称为间歇流。由图可得,管径对于流型转换起着重要的作用。与常规通道相比,微小通道内泡状流出现在更低的液相表观速度下,弹状流向环状流的转变所要求的气相流量也有所下降,导致环状流在流型图上所占的比重随管径的减小逐渐增大。管径对流型转换边界的影响主要是因为:重力作用随管径减小而降低,表面张力的作用逐渐增强,微小通道内液膜附着壁面的能力增强,通道顶部更容易被液膜占据,更容易形成环状流。
|
图 6 不同管径下流型分界线对比 Fig.6 Comparison of flow pattern transitional lines with different tube diameters (B: bubbly flow, S: slug flow, SF: stratified flow, A: annular flow, I: intermittent flow, D: dispersed flow) |
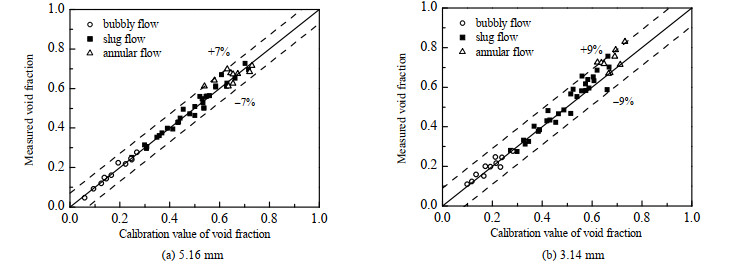
如图 7所示为快关阀所获得的含气率与图像处理含气率的对比情况。从图中可以看出,对于5.16 mm的通道,通过图像处理与快关阀实验得到的含气率的绝对误差最大为7%,而3.14 mm管径,二者最大绝对误差为9%,因此可以认为三维重构技术计算含气率的方法是有效的。
|
图 7 快关阀实验含气率与图像处理实验含气率对比 Fig.7 Comparison of gas content results from fast-closing valve experiments and image processing experiments |
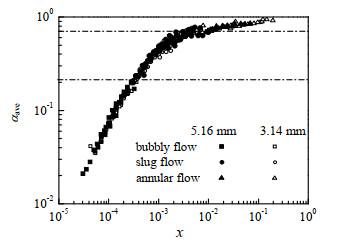
如图 8所示为含气率随干度x的变化趋势,其中x为空气质量与两相总质量的比值。由图 8可得,管径对含气率的影响较小。当干度较低时,含气率随干度的增加而快速升高。对于泡状流和弹状流,气泡长度随干度增加而迅速增大,气相占据通道的比例升高。由于水与空气的密度差较大,空气质量流量的少量增加就会导致空气所占截面积大幅增加。当干度增加到0.01左右,流型变为环状流,液体呈环形附在管壁,气相位于管道中心。连续相在运动过程中会受到摩擦力和虚拟质量力等力的作用,气液两相的相间滑移增大,因此相对于干度增加的速率,含气率的变化率逐渐放缓。
|
图 8 含气率随干度变化规律 Fig.8 Profiles of void fractions as a function of gas qualities |
如表 1所示,选取了4组不同预测模型,对比实验结果与公式预测值的相对大小。为了更好地对4组含气率相关性进行评估,本文引入了平均绝对误差(MAD)和平均相对误差(MRD)。
| ${\rm{MAD}} = \frac{1}{M}\sum\limits_{{\rm{ }}\lambda = 1}^M {|\frac{{{y_{\lambda ,{\rm{pred}}}} - {y_{\lambda ,\exp }}}}{{{y_{\lambda ,\exp }}}}|} $ | (3) |
| ${\rm{MRD}} = \frac{1}{M}\sum\limits_{\lambda = 1}^M {\frac{{{y_{\lambda ,{\rm{pred}}}} - {y_{\lambda ,\exp }}}}{{{y_{\lambda ,\exp }}}}} $ | (4) |
|
|
表 1 不同含气率模型公式 Table 1 Formula of different void fraction models |
式中:yλ, pred和yλ, exp分别为第λ个实验点的预测值和实验值,M是实验点的数量。
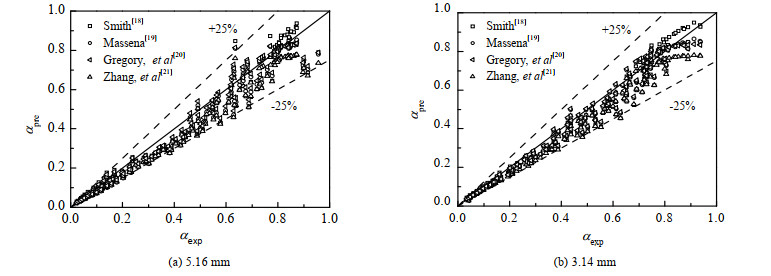
从表中可以看出,无论绝对误差还是相对误差,4种含气率模型均能很好地对实验含气率进行预测,其中Gregory等[20]模型总体绝对误差为8.9%,相对误差为-6.6%。如图 9所示为图像处理实验含气率与公式预测值的对比,图中αpre为公式预测含气率,αexp为图像处理实验含气率。由图 9可得,4组含气率模型吻合度较好,基本所有实验数据都在预测值的±25% 误差带以内,Gregory等[20]模型的预测性能最好,对于5.16 mm管径圆管,超过70.3% 的实验数据在±15% 误差带以内,而对于内径3.14 mm的通道,86.1 %的数据落在±15% 误差带以内。
|
图 9 图像处理实验含气率与公式预测值的对比 Fig.9 Comparison from experimental void fractions and predicted values |
研究内径为5.16和3.14 mm的水平圆管内气液两相流动,利用三棱镜改进光路,同时获得了俯视图与正视图,利用Matlab软件,修正折射影响、重构三维气液界面,并计算含气率。分析了小通道内的流型、流型转换边界、三维气液界面以及含气率变化规律,得到主要结论如下:
(1) 水平小通道内的流型主要为泡状流、弹状流和环状流。相较于常规管道,小通道内重力作用减弱。由于随管径的减小,表面张力作用增强,弹状流向环状流转变所要求的气相流量逐渐下降,环状流在流型图上占据的比例随管径的减小而逐渐上升。
(2) 使用快关阀的方法进行含气率标定,对比了快关阀与三维重构技术得到的含气率,二者吻合较好,最大绝对误差均不超过10%。
(3) 对于泡状流和弹状流,含气率随干度的增大而线性升高;对于环状流,含气率随干度的升高增加速率较低。管径对含气率的影响较弱,基于三维气液界面所获得的含气率与经验公式的吻合度较好,基本所有数据都在公式预测值的±25%误差带以内。
| [1] |
黄莹, 高璞珍, 徐鹏, 等. 水平分布双气泡运动特性的可视化实验[J]. 高校化学工程学报, 2019, 33(3): 557-563. HUANG Y, GAO P Z, XU P, et al. Visualization study on dynamic behaviors of horizontal arranged bubbles[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 557-563. DOI:10.3969/j.issn.1003-9015.2019.03.007 |
| [2] |
李花, 潘艳秋, 俞路, 等. 气液两相流强化气隙式膜蒸馏脱盐实验及CFD模拟[J]. 高校化学工程学报, 2019, 33(1): 55-62. LI H, PAN Y Q, YU L, et al. Gas-liquid two-phase flow intensified air gap membrane distillation for desalination and its CFD simulation[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(1): 55-62. DOI:10.3969/j.issn.1003-9015.2019.01.007 |
| [3] |
王晓军, 张林, 吴苏晨, 等. T型微通道内液-液两相流流型研究[J]. 高校化学工程学报, 2017, 31(1): 13-20. WANG X J, ZHANG L, WU S C, et al. Study on liquid-liquid two-phase flow patterns in a T-shaped microchannel[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(1): 13-20. |
| [4] |
陈珉芮, 钱锦远, 李晓娟, 等. 十字型微通道中非定常分散相速度下液滴生成的数值分析[J]. 高校化学工程学报, 2018, 32(3): 522-528. CHEN M R, QIAN J Y, LI X J, et al. Numerical simulation of droplet Generation in cross-junction microchannel under changing dispersion phase velocities[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 522-528. DOI:10.3969/j.issn.1003-9015.2018.03.005 |
| [5] |
唐苇羽, 陈景祥, 韩锦程, 等. 不同强化换热管内流动沸腾换热特性对比[J]. 浙江大学学报(工学版), 2018, 52(6): 1216-1222. TANG W Y, CHEN J X, HAN J C, et al. Comparison of flow boiling heat transfer characteristics inside different enhanced heat transfer tubes[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(6): 1216-1222. |
| [6] |
KONISHI C, MUDAWAR I. Review of flow boiling and critical heat flux in microgravity[J]. International Journal of Heat and Mass Transfer, 2015, 80: 469-493. DOI:10.1016/j.ijheatmasstransfer.2014.09.017 |
| [7] |
高超, 朱志冰, 李海旺. 宽高比及表面粗糙度对矩形微尺度通道流动特性的影响[J]. 航空动力学报, 2018, 33(5): 158-162. GAO C, ZHU Z B, LI H W. Influence of aspect ratio and roughness on flow behavior in rectangle microchannels[J]. Journal of Aerospace Power, 2018, 33(5): 158-162. |
| [8] |
TAITEL Y, DUKLER A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AICHE Journal, 1976, 22(1): 47-55. DOI:10.1002/aic.690220105 |
| [9] |
MANDHANE J M, GREGORY G A, AZIZ K. A flow pattern map for gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow, 1974, 1(4): 537-553. DOI:10.1016/0301-9322(74)90006-8 |
| [10] |
BARNEA D, LUNINSKI Y, TAITEL Y. Flow pattern in horizontal and vertical two phase flow in small diameter pipes[J]. The Canadian Journal of Chemical Engineering, 1983, 61(5): 617-620. DOI:10.1002/cjce.5450610501 |
| [11] |
TRIPLETT K, GHIAASIAAN S, ABDEL-KHALIK S, et al. Gas-liquid two-phase flow in microchannels Part Ⅰ: Two-phase flow patterns[J]. International Journal of Multiphase Flow, 1999, 25(3): 377-394. DOI:10.1016/S0301-9322(98)00054-8 |
| [12] |
COLEMAN J W, GARIMELLA S. Characterization of two-phase flow patterns in small diameter round and rectangular tubes[J]. International Journal of Heat and Mass Transfer, 1999, 42(15): 2869-2881. DOI:10.1016/S0017-9310(98)00362-7 |
| [13] |
SERIZAWA A, FENG Z, KAWARA Z. Two-phase flow in microchannels[J]. Experimental Thermal and Fluid Science, 2002, 26(6/7): 703-714. |
| [14] |
付鑫. 微细通道内液氮流动沸腾热物理特性与机理的可视化研究[D]. 上海: 上海交通大学, 2011. FU X. Visualization study on thermo-physical characteristics and mechanism of convective boiling of liquid nitrogen in mini/micro-channels[D]. Shanghai: Shanghai Jiao Tong University, 2011. |
| [15] |
ZHANG T, QIAN Y, YIN J, et al. Experimental study on 3D bubble shape evolution in swirl flow[J]. Experimental Thermal and Fluid Science, 2019, 102: 368-375. DOI:10.1016/j.expthermflusci.2018.12.007 |
| [16] |
LI H, ZHENG X, JI H, et al. Void fraction measurement of bubble and slug flow in a small channel using the multivision technique[J]. Particuology, 2017, 33: 11-16. DOI:10.1016/j.partic.2016.11.004 |
| [17] |
WOLDESEMAYAT M A, GHAJAR A J. Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes[J]. International Journal of Multiphase Flow, 2007, 33(4): 347-370. DOI:10.1016/j.ijmultiphaseflow.2006.09.004 |
| [18] |
SMITH S. Void fractions in two-phase flow: A correlation based upon an equal velocity head model[J]. Proceedings of the Institution of Mechanical Engineers, 1969, 184(1): 647-664. DOI:10.1243/PIME_PROC_1969_184_051_02 |
| [19] |
MASSENA W A. Steam-water pressure drop and critical discharge flow[R]. Washington DC: Hanford Press, 1960.
|
| [20] |
GREGORY G A, SCOTT D S. Correlation of liquid slug velocity and frequency in horizontal cocurrent gas-liquid slug flow[J]. AIChE Journal, 1969, 15(6): 933-935. DOI:10.1002/aic.690150623 |
| [21] |
ZHANG W, HIBIKI T, MISHIMA K. Correlations of two-phase frictional pressure drop and void fraction in mini-channel[J]. International Journal of Heat and Mass Transfer, 2010, 53(1/2/3): 453-465. |




