2. 中国石油大学(华东) 新能源学院, 山东 青岛 266580;
3. 中国石化青岛炼油化工有限责任公司, 山东 青岛 266500
2. College of New Energy, China University of Petroleum(East China), Qingdao 266580, China;
3. Sinopec Qingdao Refining & Chemical Co. Ltd., Qingdao 266500, China
再生器是催化裂化工艺中的重要设备[1-3],主要作用是烧除催化剂上的结炭从而恢复催化剂的活性。再生器内部通常采用两级串联多组并联的旋风分离器。旋风分离器的正常工作是保证催化裂化装置长期安全运行的关键[4]。旋风分离器结构简单,但内部流场却非常复杂[5-7]。旋流中心以一定的频率和振幅旋转,即旋进涡核(processing vortex core,PVC)现象[8]。多家石化公司多次出现旋风分离系统开裂[9-11],1、2级旋风分离器连接部位以及旋风分离器与筒体的连接部位开裂[12]、料腿多处穿孔[13]等现象。
吴小林等[8]利用雷诺应力横型(Reynolds stress model,RSM)模拟单级旋风分离器内三维非稳态流场,介绍了旋进涡核现象以及旋进涡核中心运动规律。Yazdabadi等[14]建立了用于描述旋进涡核的实验模型,实验清楚地表明PVC现象是涡核中心的瞬时位置偏移几何中心引起的。Gao等[15]采用相位多普勒粒子分析仪(phase Doppler particle analyzer,PDPA)对旋风分离器内流场进行测量,发现旋风分离器内部涡核运动伴随着能量的损失,随着高度的减小,涡能量损失减小。Brar等[16]研究了旋进涡核与进口气速的关系,从数据分析可以看出:随着入口气速的增加,轴向速度和切向速度脉动频率都随之增加,两者之间存在近似线性关系。Hoekstra等[17]利用激光多普勒测速仪(laser Doppler velocimetry,LDV)技术测得旋流器中的轴向速度和切向速度分布,并对比了3种不同湍流模型模拟结果,发现RSM模型结果与实验数据基本吻合。以上学者对单级旋风器内部流场进行了详尽的研究。但是,工业生产中常常采用两级乃至多级串联的旋风分离器。本文研究了再生器内两级串联旋风分离器的旋进涡核现象,为旋风分离器的工程设计与应用提供参考。
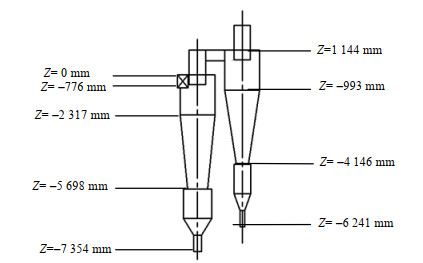
2 计算模型和数值方法 2.1 几何模型以工业现场再生器内两级串联旋风分离器的真实尺寸建立模型。如图 1所示,第1级旋风分离器中心轴与Z=0 mm平面交点为几何原点,第1、2级旋风分离器均采用蜗壳式入口,两级分离器筒体直径一致,延长第2级旋风分离器的排气管长度至其半径8倍,以保证出口界面的流动参数扩散通量为零。具体几何尺寸如表 1。
|
图 1 二级旋风分离器几何模型 Fig.1 Geometric diagram of a two-stage cyclone separator |
|
|
表 1 几何模型参数 Table 1 Parameters of geometry model |
采用Gambit软件对模型进行网格划分。整个模型从上到下采用cooper格式获得六面体网格,网格单元扭曲度在0.5以下。对水平面中心处进行加密,以便更好地捕捉旋进涡核现象。
按上述方法分别绘制了280万、210万和178万网格,采用相同计算方法比较了3组网格的分离效率(表 2)。可以看出网格数量对计算结果的影响小于1%,为了保证计算的精确性和成本,在网格数为210万条件下进行计算。
|
|
表 2 不同网格数分离效率 Table 2 Separation efficiency of different meshes |
采用Fluent软件对旋风分离器内三维流场进行模拟计算,三维黏性流动纳维-斯托克斯方程为
| $ \rho \frac{{d\mathit{\boldsymbol{u}}}}{{dt}} = - \nabla p + \mu {\nabla ^2}\mathit{\boldsymbol{u}} + \frac{1}{3}\mu \nabla \left( {\nabla \mathit{\boldsymbol{u}}} \right) + \rho F $ | (1) |
式中:ρ为流体密度,u为速度矢量,p为压力,μ为动力黏度,F为体积力,数学符号▽为哈密顿算子。
压力速度耦合选项采用SIMPLEC算法,压力梯度项采用PRESTO!方法,各项流采用QUICK差分格式。湍流模型采用RSM湍流模型。
2.4 边界条件第1级旋风分离器的入口设置为velocity inlet,分别设置入口速度为17、20、25、30 m·s-1。第2级旋风分离器出口边界条件为outflow。壁面采用无滑移边界条件,壁面函数采用标准壁面函数。
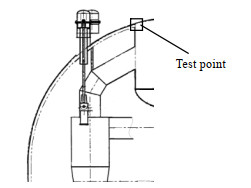
2.5 实验方法旋风分离器内非稳态脉动诱发系统产生振动,旋风分离器处于再生器内部,无法直接测量工作状态下旋风分离器壁面的振动情况。再生器顶部集气室焊缝处是测试旋风系统振动信号的最佳位置。测试设备采用上海澄科机电设备有限公司(CHENGTEO)的T1010L型和ICP/IEPE压电加速度传感器,测量位置如图 2所示。
|
图 2 再生器振动测试位置图 Fig.2 Schematic diagram of the test point at the regenerator |
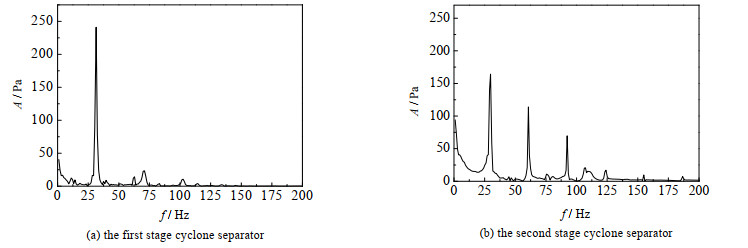
Z=-1 000 mm截面位于直筒段上部,图 3为入口速度为30 m·s-1时静压力脉动频谱图。可以看出:第1级旋风分离器的静压力脉动主频为31.44 Hz,振动幅度为241.01 Pa。第2级旋风分离器内压力脉动主要由31.44、62.89、94.69 Hz 3个频率的信号叠加,主频脉动幅度最大,为176.22 Pa,二倍频振幅为113.61 Pa,三倍频振幅为69.76 Pa。第2级分离器振动信号复杂,不仅与自身非对称式蜗壳式入口结构有关,还受第1级分离器出口影响。第2级分离器入口包含许多涡流,使得第2级分离器内流动变得复杂。
|
图 3 压力脉动频谱图 Fig.3 Spectra results of pressure pulsation |
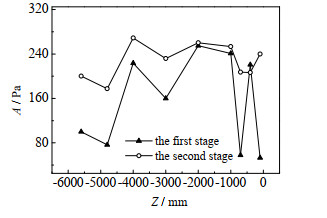
图 4、5分别表示第1、2两级分离器内气相脉动频率与幅度的轴向分布。可以看出当入口速度与结构参数一定时,1、2级分离器内不同高度的脉动主频一致,均为31.44 Hz左右。这说明流体在旋转运动时,具有固定的频率,该频率与结构和边界有关,与空间位置无关。第2级旋风分离器的脉动幅度整体高于第1级,1、2级旋风分离器在排气管部分的脉动幅度波动都比较大。造成这种现象一方面是因为旋风分离器都采用90°蜗壳单侧入口结构,这种非对称性结构是导致内部流场不均匀分布的主要原因。另一方面是由于排气管管径小,内旋流扭曲程度较大,使得排气管内气流的压力脉动振幅在此处变得敏感。
|
图 4 脉动主频轴向分布图 Fig.4 Axial distribution of pulsation main frequency |
|
图 5 脉动幅值轴向分布图 Fig.5 Axial distribution of pulsation amplitude |
旋风分离器内部气相流场符合Rankin涡结构[18],是由外部的准自由涡和内部刚性自由涡构成。以水平截面压力最低点坐标表示涡核中心位置。定义Rx,Ry为旋进涡核在X方向和Y方向的最大位移,计算式如式(2)、(3),以0.002 s为时间间隔,绘制0.05 s内涡核中心的轨迹图。
| $ {R_x} = \frac{{({x_{\max }} - {x_{\min }})}}{2} $ | (2) |
| $ {R_y} = \frac{{({y_{\max }} - {y_{\min }})}}{2} $ | (3) |
式中:xmax为X坐标方向涡核中心偏离分离器几何中心的最大值,mm;xmin为X坐标方向涡核中心偏离分离器几何中心的最小值,mm;ymax:Y坐标方向涡核中心偏离分离器几何中心的最大值,mm;ymin:Y坐标方向涡核中心偏离分离器几何中心的最小值,mm;
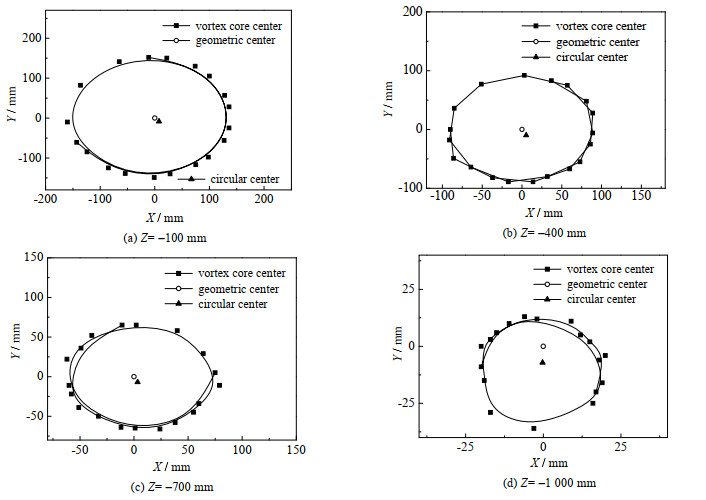
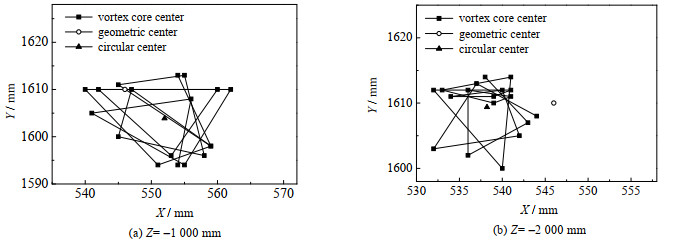
图 6、7分别为第1、2级旋风分离器内涡核轨迹追踪示意图。第1级分离器涡核围绕几何中心做近似圆周运动,且随着轴向高度的降低,涡核的摆动幅度逐渐减小。对比第1级分离器,可以发现第2级分离器内涡核的摆动幅度明显减小,且不再近似圆周运动,随机性更强,这主要是因为第2级分离器内流场更为复杂,呈现出强烈的不稳定性,从而导致旋进涡核运动的随机发散。
|
图 6 第1级分离器内涡核轨迹追踪示意图 Fig.6 Trajectory tracking of vortex core in the first stage separator |
|
图 7 第2级分离器内涡核轨迹追踪示意图 Fig.7 Trajectory tracking of vortex core in the second stage separator |
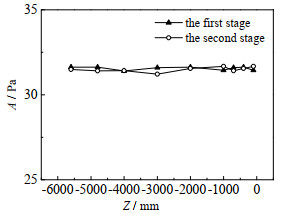
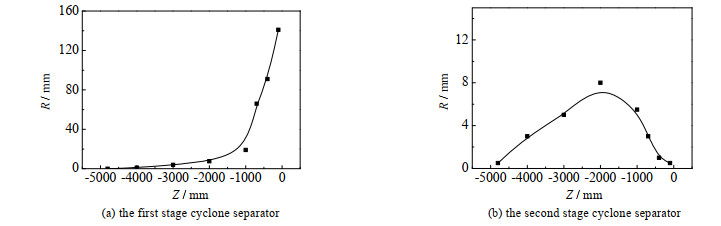
以X方向和Y方向最大位移的平均值作为涡核中心摆动半径,图 8为1、2级旋风分离器涡核摆动半径轴向分布。可以看出,第1级旋风分离器内摆动半径大于第2级旋风分离器。第1级旋风分离器从直筒段上部随着高度的上升摆动半径迅速增大,在Z=-100 mm处达到最高值142 mm。在Z= -4 000 mm(灰斗段)截面以下观察不到涡核摆动。第2级旋风分离器涡核摆动最大处为直筒段中部,偏移距离为9 mm,在Z= -4 800 mm(灰斗段)开始检测不到涡核摆动。这是由于灰斗处气量小、空间大以及底部返混现象使得在灰斗区内无法观测到涡核摆动。
|
图 8 涡核摆动半径的轴向分布图 Fig.8 Axial distribution of vortex core motion radius |
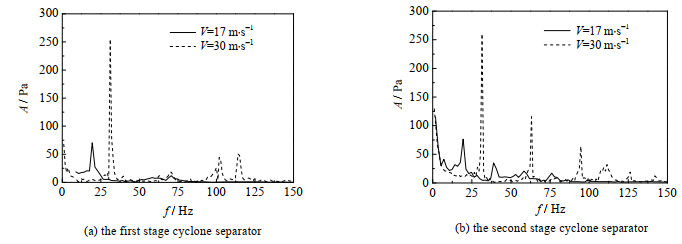
图 9为入口气速对压力脉动主频的影响。从图中可以看出,随着入口气速的增加,脉动频率呈线性增加。主要是因为入口速度的增加提高了入口的流量,气体在分离器内停留时间更短,切向速度也随之增加,从而提高了涡核的旋进频率。图 10为Z= -2 000 mm处1、2级旋风分离器直筒段截面几何中心处脉动幅度。可以看出:1、2级分离器脉动幅度也呈一定比例增加。入口速度增加的同时加剧了内旋流的扭曲,使得压力脉动幅度发生改变。

|
图 9 入口气速对脉动主频的影响 Fig.9 Effects of inlet velocity on the dominant frequency |
|
图 10 入口速度对脉动幅值的影响 Fig.10 Effects of inlet velocity on amplitude |
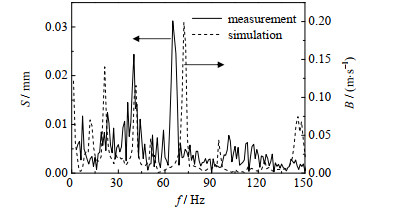
图 11为再生器与集气室焊缝处振动信号与第2级旋风排气管处气流切向速度脉动模拟结果的对比。从图中可以看出模拟数据得到的频谱图与工业现场测量的振动信号吻合较好,脉动频率主要分布在21.28、41.39和68.24 Hz,振幅的分布趋势与工业现场的实测信号较为吻合,数值模拟频率与工业现场实测相比高5%左右。主要原因有2个方面:1) 忽略了催化剂对气相振动频率的抑制作用,后续通过模拟气固两相流对流场脉动的影响发现,固相的加入会使流动脉动频率在一定范围内减小。2) 气体的脉动传递给壁面时,流固耦合作用会使壁面的振动频率略低于气相的脉动频率。
|
图 11 数值结果与现场振动信号的对比 Fig.11 Comparison of numerical results with on-site vibration signals/ |
采用RSM对两级串联旋风分离器内部三维非稳态流场进行了数值计算,并将计算结果与现场测试结果进行了对比,得到如下结论:
(1) 两级串联旋风分离器空间内都存在旋进涡核现象,且存在周期性振荡规律。1、2级分离器内脉动主频均为31.44 Hz。第2级分离器内存在较强的二倍频、三倍频分量,其幅值不断减小。
(2) 第1级分离器涡核中心围绕几何中心做近似圆周运动,第2级分离器由于内部流场的复杂,涡核中心轨迹无明显规律,旋进涡核的摆动幅度随着轴向高度的降低而逐渐减小。
(3) 随着入口气速的增加,入口流量提高,1、2级分离器内压力脉动主频呈直线增加,脉动幅度也显著增加。
(4) 通过模拟计算与现场测试频域图的对比可见,在主频的分布以及幅值上吻合良好,证明了本文计算结果的可靠性。
|
|
| [1] |
王正则. 催化裂化装置反应再生工艺设备的大型化[J]. 炼油设计, 1996, 26(3): 37-41. WANG Z Z. Problems of processing equipment in reaction-regeneration section of large-scale FCCU[J]. Petroleum Refinery Engineering, 1996, 26(3): 37-41. |
| [2] |
陈俊武. 催化裂化在炼油厂中的地位和作用展望--催化裂化仍将发挥主要作用[J]. 石油学报(石油加工), 2003, 19(1): 1-11. CHEN J W. Prospects of status and role of FCC in refinery-FCC will continue to play a leading role in petroleum industry[J]. ACTA Petrolei Sinica (Petroleum Processing Section), 2003, 19(1): 1-11. DOI:10.3969/j.issn.1001-8719.2003.01.001 |
| [3] |
山红红, 李春义, 钮根林, 等. 流化催化裂化技术研究进展[J]. 石油大学学报(自然科学版), 2005, 29(6): 135-150. SHAN H H, LI C Y, NIU G L, et al. Research progress in fluid catalytic cracking technology[J]. Journal of China University of Petroleum (Edition of Natural Science), 2005, 29(6): 135-150. DOI:10.3321/j.issn:1000-5870.2005.06.032 |
| [4] |
程光旭, 刘亚杰, 李春树, 等. 催化裂化反应-再生系统的失效模式、效应和危害度分析[J]. 化学工程, 2003, 31(2): 55-60. CHENG G X, LIU Y J, LI C S, et al. Analysis on fault modes, effect and criticality of reactor-regenerator system in fluid catalytic cracking unit[J]. Chemical Engineering, 2003, 31(2): 55-60. DOI:10.3969/j.issn.1005-9954.2003.02.012 |
| [5] |
胡小康, 刘小成, 徐俊, 等. 循环流化床提升管内压力脉动特性[J]. 化工学报, 2010, 61(4): 825-831. HU X K, LIU X C, XU J, et al. Characteristics of pressure fluctuations in CFB riser[J]. CIESC Journal, 2010, 61(4): 825-831. |
| [6] |
王江云, 毛羽, 孟文, 等. 旋风分离器内非轴对称旋转流场的测量[J]. 石油学报(石油加工), 2015, 31(4): 920-929. WANG J Y, MAO Y, MENG W, et al. Experiment measurement of non-axisymmetric rotating flow field in cyclone separator[J]. ACTA Petrolei Sinica (Petroleum Processing Section), 2015, 31(4): 920-929. DOI:10.3969/j.issn.1001-8719.2015.04.013 |
| [7] |
王甜, 徐俊, 宋健斐, 等. 旋风分离器内旋转流的不稳定性[J]. 化工学报, 2010, 61(2): 317-322. WANG T, XU J, SONG J F, et al. Instability of swirling flow in cyclone[J]. CIESC Journal, 2010, 61(2): 317-322. |
| [8] |
吴小林, 熊至宜, 姬忠礼, 等. 旋风分离器旋进涡核的数值模拟[J]. 化工学报, 2007, 58(2): 383-390. WU X L, XIONG Z Y, JI Z L, et al. Numerical simulation of processing vortex core in cyclone separator[J]. Journal of Chemical Industry and Enginering (China), 2007, 58(2): 383-390. DOI:10.3321/j.issn:0438-1157.2007.02.019 |
| [9] |
刘国荣, 赵延灵, 李国成, 等. 再生器旋风分离器系统开裂原因分析[J]. 压力容器, 2005, 22(6): 46-48. LIU G R, ZHAO Y L, LI G C, et al. Cracking analysis of cyclone separator system regenerator[J]. Pressure Vessel Technology, 2005, 22(6): 46-48. DOI:10.3969/j.issn.1001-4837.2005.06.012 |
| [10] |
曹晖, 刘雁. 催化裂化装置再生器旋风分离器故障原因及措施[J]. 广东化工, 2013, 40(1): 136-137. CAO H, LIU Y. FCC regenerator cyclone separator fault reasons and measures[J]. Guangdong Chemical Industry, 2013, 40(1): 136-137. DOI:10.3969/j.issn.1007-1865.2013.01.074 |
| [11] |
张红. 反应器内旋风分离器工况异常原因分析及解决方法[J]. 石油化工设备技术, 2000, 21(5): 12-14. ZHANG H. Reason analysis om abnormal working condition of inner cyclone for reactor and its solution[J]. Petro-chemical Equipment Technology, 2000, 21(5): 12-14. DOI:10.3969/j.issn.1006-8805.2000.05.004 |
| [12] |
韩立清, 李开歧, 罗杰英, 等. 重油催化裂化单旋壳体疲劳断裂失效分析[J]. 石油化工设备, 2008, 37(S1): 11-14. HAN L Q, LI K Q, LUO J Y, et al. Failure analysis of fatigue cracks of single stage cyclone shell in heavy oil catalytic cracking unit[J]. Petro-chemical Equipment, 2008, 37(S1): 11-14. |
| [13] |
杨永国, 王兹尧, 张永宏, 等. 催化裂化装置再生器催化剂跑损原因分析及控制措施[J]. 炼油技术与工程, 2004, 34(3): 9-11. YANG Y G, WANG Z R, ZHANG Y H, et al. Analysis of catalyst loss in FCC regenerator and the countermeasures[J]. Petroleum Refinery Engineering, 2004, 34(3): 9-11. DOI:10.3969/j.issn.1002-106X.2004.03.003 |
| [14] |
YAZDABADI P A, GRIFFITHS A J, SYRED N. Characterization of the PVC phenomena in the exhaust of a cyclone dust separator[J]. Experiments in Fluids, 1994, 17(1/2): 84-95. DOI:10.1007/BF02412807 |
| [15] |
GAO Z W, WANG J, Wang J Y, et al. Analysis of the effect of vortex on the flow field of a cylindrical cyclone separator[J]. Separation and Purification Technology, 2018, 210(1): 438-447. |
| [16] |
BRAR L S, SHARMA R P, ELSAYED K. The effect of the cyclone length on the performance of stairmand high-efficiency cyclone[J]. Powder Technology, 2015(286): 668-677. |
| [17] |
HOEKSTRA A J, DERKSEN J J, AKKER H E A V D. An experimental and numerical study of turbulent swirling flow in gas cyclones[J]. Chemical Engineering Science, 1999, 54(S 13/14): 2055-2065. |
| [18] |
毛羽, 庞磊, 王小伟, 等. 旋风分离器内三维紊流场的数值模拟[J]. 石油炼制与化工, 2002, 32(2): 1-6. MAO Y, PANG L, WANG X W, et al. Numerical modelling of three-dimension turbulent field in cyclone separator[J]. Petroleum Processing and Petrochemicals, 2002, 32(2): 1-6. DOI:10.3969/j.issn.1005-2399.2002.02.001 |




