热裂解是氨制氢反应最常用的技术[1]。目前,用于热解氨制氢的反应器主要有固定床、膜反应器(如固定床膜反应器和催化膜反应器)、微反应器等。对于规模化工业生产,一般采用固定床式反应器[2]。氨制氢反应是吸热且化学计量数增加的,提高温度有利于提高氨的平衡转化率,相应地,氨的平衡转化率随着压力的增加而降低[3],因此,氨分解过程中需要通过高温和低压来保证氨的产率。然而,受反应动力学的限制,固定床中氨制氢反应需在极高的温度下进行(873~1 173 K)[4]。氨制氢反应器的热源温度是影响反应器能量效率极为重要的参数,因为降低热源温度可以降低热源所提供能量的品位,等于减少了的消耗。因此,很多关于氨分解制氢的研究致力于在保证反应速率和产率的前提下,尽可能降低制氢反应温度[3, 5]。例如,通过采用新型的高效低温钌基催化剂[4],可以将反应器操作温度降低到773 K,使间接式氨燃料电池系统运行所需热能减少29 %,将系统总能量效率提升2 % [5]。也有研究对反应器参数进行优化[6-8],或者采用多级反应器等方案以提高反应器热效率[7, 9]。此外,系统上改变反应器加热回路,利用分解反应器产物回热进料气体[5, 10-12];建立放热反应与氨分解反应耦合的反应器替代电加热反应器等方案[5, 7, 10-12],在提升分解反应器能量效率上也取得了很好的效果。
现有研究大多是从热力学第一定律出发对影响反应器的单个或多个参数进行参数敏感性分析。然而,由于反应器本身是一个较为复杂的过程装置,针对固定参数的评判指标受到诸如进料成分、压力、温度、加热形式和反应器尺寸等复杂因素影响,往往难以对各项优化结果权衡考虑。此外,过程或过程单元的能源效率最好用热力学第二定律来评估[13-14]。评估方法的核心是明确这一过程中所损失的有用功,而这些损失的有用功可以通过熵产率来衡量[15-16]。熵产率作为标准的优点在于其与参考环境等因素无关,是一种纯粹衡量过程的不可逆性热力学目标函数,能够反映系统节能的长期目标[13-14, 16-17]。Nummedal等和Kjelstrup等[18-20]最早使用数值方法开始了对一维化学反应器模型的熵产优化工作。Johannessen等[15]利用最优控制理论,获得了SO2氧化反应器的最优温度配置。Chen等[17]对CO2加氢制轻质烯烃反应器进行了熵产分析,获得了最佳反应器内径和最佳催化剂床密度。在反应器优化方面的既有研究结果表明,该方法可以有效提升反应器能量利用效率,但目前还没有研究者将其用于优化氨分解制氢反应过程。同时,反应器熵产最优化研究受限于一维模型,各种变量的径向梯度对仿真结果的影响一直无法探讨,特别是在氨制氢固定床这种温度梯度较大的反应器中,反应场分布受温度梯度影响显著[4]。最后,缺乏对此前熵产分析优化结果进行验证的研究支撑。
本研究基于熵产分析对氨制氢反应器进行了一维建模和优化,对氨制氢反应过程的热力学不可逆性进行详细地讨论,得到了反应器最优热源配置。同时,通过三维计算流体动力学(CFD)仿真结果与一维模型进行跨维度比较,验证了优化策略的可行性[21];分析了径向温度梯度等一维模型无法表征的因素对仿真结果的影响。熵产分析优化降低了反应器由化学反应、黏性流动、热量和质量传输现象的不可逆性导致的有用功损失,从而为工业氨制氢反应器设计提供理论基础;同时,深层次的热力学理论分析可以为进一步的生产优化和研究提供支持。
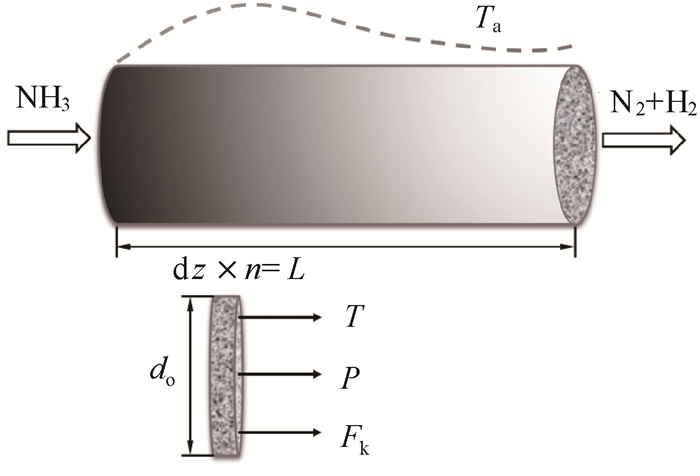
2 一维模型 2.1 反应器数学模型图 1为固定床式氨分解制氢反应器原理图。圆柱形固定床反应器内填充有球形催化剂颗粒,使氨在高温条件下分解为氮和氢。在均匀分布的颗粒床层阻塞作用下,床内气体可维持稳定的平推流,故可用一维模型对上述反应过程进行简化分析[6, 16, 18-19, 22-23]。采用Co0.5Ce0.1Al0.4O(sa)催化剂,反应速率模型由文献[8, 24]得到。其他相关假设总结如下:(1)气体在轴向方向没有返混;(2)忽略径向方向的温度和浓度分布;(3)化学反应为受动力学控制反应;(4)反应气体为理想气体;(5)反应器床层简化为多孔介质反应通道。
|
图 1 模型示意图 Fig.1 Schematic diagram of reactor |
氨分解制氢反应方程如式(1)。
| $ \begin{aligned} & \mathrm{NH}_3(\mathrm{~g}) \rightleftharpoons \frac{1}{2} \mathrm{~N}_2(\mathrm{~g})+\frac{3}{2} \mathrm{H}_2(\mathrm{~g}) \\ & \Delta_{\mathrm{r}} H_{\text {ref }}=+4.622 \times 10^4 \mathrm{~J} \cdot \mathrm{~mol}^{-1}, T_{\text {ref }}=298.15 \mathrm{~K} \end{aligned} $ | (1) |
反应器温度分布微分方程如式(2)。
| $ \frac{\mathrm{d} T}{\mathrm{~d} z}=\frac{\pi d_{\mathrm{o}} q-A_{\mathrm{c}} r \Delta_{\mathrm{r}} H}{\sum\limits_{\mathrm{k}} F_{\mathrm{k}} C_{p_{-} \mathrm{k}}} $ | (2) |
热流密度由式(3)确定。
| $ q=U \Delta(T)=U\left(T_{\mathrm{a}}-T\right) $ | (3) |
压力分布微分方程采用Ergun经验公式,如式(4)。
| $ \frac{\mathrm{d} P}{\mathrm{~d} z}=-\left(\frac{150 \mu}{d_{\mathrm{p}}^2} \frac{(1-\varepsilon)^2}{\varepsilon^3}+\frac{1.75 G}{d_{\mathrm{p}}} \frac{1-\varepsilon}{\varepsilon^3}\right) v $ | (4) |
表观质量流量G和表观气速v可由式(5)和式(6)计算得到。
| $ G=\sum_{\mathrm{k}} F_{\mathrm{k}} M_{\mathrm{k}} / A_{\mathrm{c}} $ | (5) |
| $ v(z)=F_{\mathrm{T}}(z) R T(z) /\left[P(z) A_{\mathrm{c}}\right] $ | (6) |
组分摩尔流率分布微分方程如式(7),氨分解制氢反应速率r可通过式(8)计算,式中A和Ea的取值见2.3节中表 1。
| $ \frac{\mathrm{d} F_{\mathrm{k}}}{\mathrm{~d} z}=a_{\mathrm{k}} A_{\mathrm{c}} r(1-\varepsilon) $ | (7) |
| $ r=A \exp \left(\frac{-E_{\mathrm{a}}}{R T}\right) C_{\mathrm{NH}_3}=k_{\mathrm{R}} C_{\mathrm{NH}_3} $ | (8) |
|
|
表 1 反应器主要参数 Table 1 Reactor parameters |
对于固定床反应器,其熵产主要来自化学反应、黏性流动、热量传输的不可逆损失。因此,可将反应器微元熵产率表达如式(9)。
| $ \sigma=A_{\mathrm{c}} r(T)\left(-\frac{\Delta_{\mathrm{r}} G(T)}{T}\right)+A_{\mathrm{c}} v\left[-\frac{1}{T}\left(\frac{\mathrm{~d} P}{\mathrm{~d} z}\right)\right]+\pi d_{\mathrm{o}} U\left(T_{\mathrm{a}}-T\right)\left(\frac{1}{T}-\frac{1}{T_{\mathrm{a}}}\right) $ | (9) |
由微元熵产率可得到反应器总熵产率如式(10)。
| $ \frac{\mathrm{d} S_{\mathrm{irr}}}{\mathrm{~d} t}=\int\limits_0^t \sigma \mathrm{~d} z $ | (10) |
对于氨分解制氢反应器,建立约束条件下反应器总熵产率最小的最优化问题如式(11),即以式(10)为优化目标。
| $ f=\min \left(\frac{\mathrm{d} S_{\mathrm{irr}}}{\mathrm{~d} t}\right) $ | (11) |
对总熵产率的优化,以反应器温度分布、压力分布、组分分布、热源温度分布、进出口温度、压力和组分为操作变量。进一步,将优化目标函数表达为反应器温度分布、压力分布、组分分布和热源温度分布的泛函,如式(12)。
| $ \frac{\mathrm{d} S_{\mathrm{irr}}}{\mathrm{~d} t}=\int\limits_0^L \sigma\left[T(z), P(z), F_{\mathrm{N}_2}(z), F_{\mathrm{H}_2}(z), F_{\mathrm{NH}_3}(z), T_{\mathrm{a}}(z)\right] \mathrm{d} z $ | (12) |
优化问题在一定约束条件下进行:(a)优化问题的求解需要满足能量、动量和质量守恒关系,即式(2)、(4)、(7);(b)反应器的进出口需要满足生产条件约束,即对进出口边界条件进行等式约束。本研究规定氢气产率保持不变,故优化后反应器的氢气产量等于初始条件参考值,如式(13)。
| $ F_{\mathrm{H}_2-\text { out }}-F_{\mathrm{H}_2-\text { in }}=F_{\mathrm{H}_2-\text { out }}^{\text {ref }}-F_{\mathrm{H}_2-\text { in }}^{\text {ref }} $ | (13) |
采用Euler-Lagrange方法求解上述熵产最小化问题。构建与目标函数和约束条件相对应的Euler-Lagrange函数,如式(14)。
| $ \zeta=\left\{\begin{array}{l} \sigma\left[T(z), P(z), F_{\mathrm{N}_2}(z), F_{\mathrm{H}_2}(z), F_{\mathrm{NH}_3}(z), T_{\mathrm{a}}(z)\right] \\ +\lambda_q(z)\left[\frac{\mathrm{d} T}{\mathrm{~d} z}-\frac{\pi d_{\mathrm{o}} q-A_c r \Delta_{\mathrm{r}} H}{\sum_{\mathrm{k}} F_{\mathrm{k}} C_{\mathrm{p}, \mathrm{k}}}\right] \\ +\lambda_p(z)\left[\frac{\mathrm{d} P}{\mathrm{~d} z}+\left(\frac{150 \mu}{d_{\mathrm{p}}{ }^2} \frac{(1-\varepsilon)^2}{\varepsilon^3}+\frac{1.75 G}{d_{\mathrm{p}}} \frac{1-\varepsilon}{\varepsilon^3}\right) v\right] \\ +\lambda_{\mathrm{NH}_3}(z)\left[\frac{\mathrm{d} F_{\mathrm{NH}_3}}{\mathrm{~d} z}+A_{\mathrm{e}} r(1-\varepsilon)\right] \\ +\lambda_{\mathrm{N}_2}(z)\left[\frac{\mathrm{d} F_{\mathrm{N}_2}}{\mathrm{~d} z}-\frac{1}{2} A_{\mathrm{e}} r(1-\varepsilon)\right] \\ +\lambda_{\mathrm{H}_2}(z)\left[\frac{\mathrm{d} F_{\mathrm{H}_2}}{\mathrm{~d} z}-\frac{3}{2} A_{\mathrm{c}} r(1-\varepsilon)\right] \\ +\lambda_{F_{\mathrm{H}_2}}\left[\left(F_{\mathrm{H}_2 \text {-out }}-F_{\mathrm{H}_2 \text {-in }}\right)-\left(F_{\mathrm{H}_2 \text {-out }}^{\text {ref }}-F_{\mathrm{H}_2 \text {-in }}^{\text {ref }}\right)\right] \end{array}\right\} \mathrm{d} z $ | (14) |
式中:λFH2是与氢气总产率相关的拉格朗日乘子;λq(z)、λp(z)、λNH3(z)、λN2(z)、λH2(z)是与守恒方程相关的拉格朗日乘子函数。
采用数值方法对Euler-Lagrange函数进行求解。首先,对计算域进行离散,将反应器沿轴向离散为n个计算节点;然后,对Euler-Lagrange函数中各微分方程分别进行离散,得到一组代数方程;最后,使用Matlab R2024a优化工具箱函数fmincon对代数方程组进行求解。
2.3 模型设置与验证一维流化床式氨分解制氢反应器的关键参数设置如表 1所示,各参数的取值参考已有文献[8]。需要说明的是,本研究基于对反应器的DaI数(Damköhler I number)的计算结果对反应器长度进行了修正[24],以保证氨气在设计工况下可实现完全转化。参考案例计算时,反应器进气温度与恒温热源温度保持一致(Tin=Ta)。反应模型的关键参数Arrhenius常数A和反应活化能Ea均与文献[8, 24]保持一致。
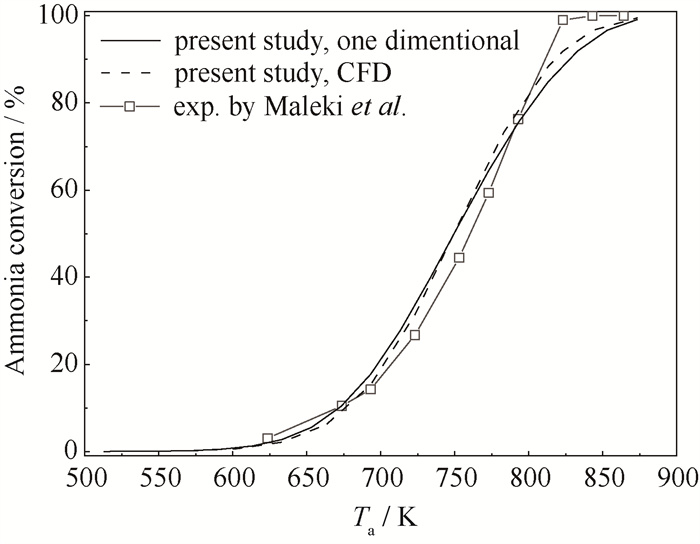
对采用数值方法求解的一维模型进行计算节点无关性验证,得到氨气转化率计算结果的相对误差随节点数增加快速降低,当节点数达到500时,相对偏差已降至0.6 % 以内,而进一步增加节点数对误差的降低作用极为有限,同时,节点数过多会影响计算速度。综上,最终将节点数设置为500。此外,将一维模型的计算结果与已有文献[24]中相同条件下的实验结果进行比较,结果如图 2所示。可以看到,在整个温度范围内,一维模型模拟结果与文献数据转化率的最大误差为10.65 %,满足计算精度要求。
|
图 2 本研究获得的结果与文献实验数据比较 Fig.2 Model validation by compare with literature experimental data |
将一维模型仿真结果与CFD多维模型进行跨维度比较,是验证一维模型的一种重要方法[21]。采用三维CFD模型对氨制氢反应熵产优化结果进行验证,对比优化前后反应器熵产,可证实优化结果的有效性。此外,可以探明导致模型误差的原因,并对反应器径向分布差异给计算结果造成的影响进行分析。
3.1 CFD仿真数学模型针对多孔介质区域,建立质量守恒、动量守恒、能量守恒和组分守恒方程[24]。质量守恒方程如式(15)。
| $ \nabla \cdot(\varepsilon \rho \boldsymbol{v})=0 $ | (15) |
使用Brinkman-Forchheimer扩展的Darcy方程进行流动和压力的耦合计算,如式(16)。
| $ \boldsymbol{v} \cdot \nabla(\varepsilon \rho \boldsymbol{v})=-\nabla P+\nabla \cdot\left(\frac{\mu}{\varepsilon} \nabla \boldsymbol{v}\right)-\frac{\mu}{\kappa} \boldsymbol{v}-\frac{1}{2} \rho C_F|\boldsymbol{v}| \boldsymbol{v} $ | (16) |
基于热平衡传热模型建立能量守恒方程,如式(17)。
| $ \nabla \cdot\left(\varepsilon \rho c_p \boldsymbol{v} T\right)=S_f^h+\nabla \cdot\left(k_{\text {eff }} \nabla T-\sum\limits_{\mathrm{k}} h_{\mathrm{k}} J_{\mathrm{k}}\right)+\Delta_{\mathrm{r}} H \rho_{\mathrm{s}} R_{\mathrm{r}} $ | (17) |
黏性耗散项Sfh反映了多孔介质阻塞作用引起的能量损失,由Darcy项、Brinkman项和Forchheimer项组成[25-26],其中,Brinkman耗散项由Brinkman阻力项的幂表示[25, 27-28],如式(18)。
| $ S_f^h=\frac{\mu}{\kappa} \boldsymbol{v} \cdot \boldsymbol{v}-\frac{\mu}{\varepsilon} \boldsymbol{v} \cdot \nabla^2 \boldsymbol{v}+\frac{1}{2} \rho C_F|\boldsymbol{v}| \boldsymbol{v} \cdot \boldsymbol{v} $ | (18) |
组分守恒方程如式(19)。
| $ \nabla \cdot\left(\varepsilon \rho y_{\mathrm{k}} \boldsymbol{v}\right)=\nabla \cdot J_{\mathrm{k}}+\sum\limits_{\mathrm{k}} a_{\mathrm{k}} M_{\mathrm{k}} g \rho_{\mathrm{s}} R_{\mathrm{r}} $ | (19) |
三维CFD仿真模型条件与一维模型保持一致,具体参数如表 1所示。CFD仿真平台采用商业软件FLUENT 23.1。反应速率方程与本研究一维模型相同,采用均匀速度入口条件,将出口压力设为大气压,壁面设为无滑移边界,热边界条件设为第一类温度边界。压力项离散采用PRESTO!格式,速度项离散采用QUICK格式,温度项离散采用QUICK格式,组分项均采用二阶迎风格式离散。利用Coupled算法求解压力-速度耦合。
如图 3所示,几何模型采用三维结构化网格,为减小仿真误差,对入口区域进行了网格加密。网格无关性验证结果如表 2所示。选择不同网格数的氨转化率计算结果与网格数足够大(网格数为3 888 000)的结果进行比较,当网格数为486 000时,认为相对偏差可以接受。CFD模型验证结果如图 2所示,可以看到三维CFD仿真模型对反应器的还原度优于一维模型,特别是高温工况下与文献结果更为接近。温度为823.15 K时,三维CFD仿真得到的转化率和Maleki等[24]的实验结果相对误差为7.2 %,小于一维模型偏差10.7 %。

|
图 3 CFD仿真网格示意图 Fig.3 Mesh scheme utilized in the 3 dimensional CFD model |
|
|
表 2 网格无关性验证结果 Table 2 Mesh independence test result |
基于三维数值模型计算反应器内的熵产分布时,除了一维模型中已考虑的由化学反应、
黏性流动、热量传输导致的不可逆性外,还引入了由质量扩散造成的熵产。因此,单位体积熵产率可表达为式(20)。
| $ \sigma_{\mathrm{TOT}}=\sigma_{\mathrm{RE}}+\sigma_{\mathrm{HT}}+\sigma_{\mathrm{FF}}+\sigma_{\mathrm{MT}} $ | (20) |
化学反应引起的熵产如式(21)~(24)。
| $ \sigma_{\mathrm{RE}}=-\varepsilon r \frac{\Delta_{\mathrm{r}} G(T)}{T} $ | (21) |
| $ -\frac{\Delta_{\mathrm{r}} G(T)}{T}=R \ln \frac{x_{\mathrm{NH}_3} K_{\mathrm{p}}}{x_{\mathrm{N}_2}^{1 / 2} x_{\mathrm{H}_2}^{3 / 2}} $ | (22) |
| $ K_{\mathrm{p}}=\exp \left[-\frac{\sum_{\mathrm{k}=1}^n a_{\mathrm{k}} E_{\mathrm{k}}^0(T)}{R T}\right] $ | (23) |
| $ E_{\mathrm{k}}^0(T)=h_{\mathrm{k}}^0(T)-T \cdot s_{\mathrm{k}}^0(T) $ | (24) |
多孔介质流动导致的熵产如式(25)。
| $ \sigma_{\mathrm{FF}}=\frac{\mu}{\kappa T} \boldsymbol{v} \cdot \boldsymbol{v}-\frac{\mu}{\varepsilon T} \boldsymbol{v} \cdot \nabla^2 \boldsymbol{v}+\frac{1}{2 T} \rho C_F|\boldsymbol{v}| \boldsymbol{v} \cdot \boldsymbol{v} $ | (25) |
传热引起的熵产如式(26)。
| $ \sigma_{\mathrm{HT}}=\frac{k_{\text {eff }}}{T^2}(\nabla T)^2 $ | (26) |
质量扩散引起的熵产[29]如式(27)。
| $ \sigma_{\mathrm{MT}}=\rho R \sum_{\mathrm{k}} \frac{D_{\mathrm{km}}}{x_{\mathrm{k}}}\left(\nabla x_{\mathrm{k}} \cdot \nabla y_{\mathrm{k}}\right) $ | (27) |
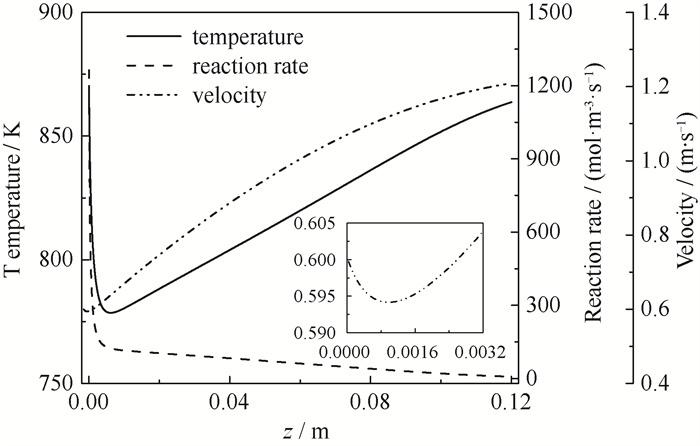
图 4展示了温度、混合气体流速和反应速率沿反应器轴向方向上的分布(一维,U=350 W ·m-2 ·K-1,Ta=Tin=873.15 K)。氨气进入反应器后快速反应,同时吸收大量热量,使气体温度从873.15 K降至最低778.52 K。氨分解制氢是化学计量系数增加的反应,且填料床的阻塞作用使混合气体通过床体后出现2 600 Pa左右的压降,导致气体体积膨胀、对应体积流量增大,使得整体上混合气体流动速度沿轴向增加。但由于入口段温度骤降,混合气体的流速从入口速度的0.6 m ·s-1先微弱下降至最小值0.594 m ·s-1,之后恢复上升并保持单调递增(如图 4放大图窗)。沿轴向方向上入口段混合气体温度下降,导致反应速率快速下降;而在轴向距离(z)超过0.006 m后,反应速率保持缓慢下降。混合气体温度在z超过0.006 m后逐渐回升,但氨的浓度随反应逐渐进行而不断减小。分别对反应速率式(8)中温度T和氨浓度CNH3求偏导,发现温度项偏导小于浓度项。因此,当z超过0.006 m后,在温度上升和浓度下降的综合作用下,反应速率随z的增加而减小。
|
图 4 氨制氢反应器的温度、反应、流动分布 Fig.4 Reaction mixture temperature, reaction rate and velocity profiles in the ammonia decomposition reactor |
比熵产率(Sspec,反应器熵产/氢的产率)能够直观反映生产单位摩尔氢的有用功损耗,可以作为评价氨制氢的过程不可逆性的理想指标。
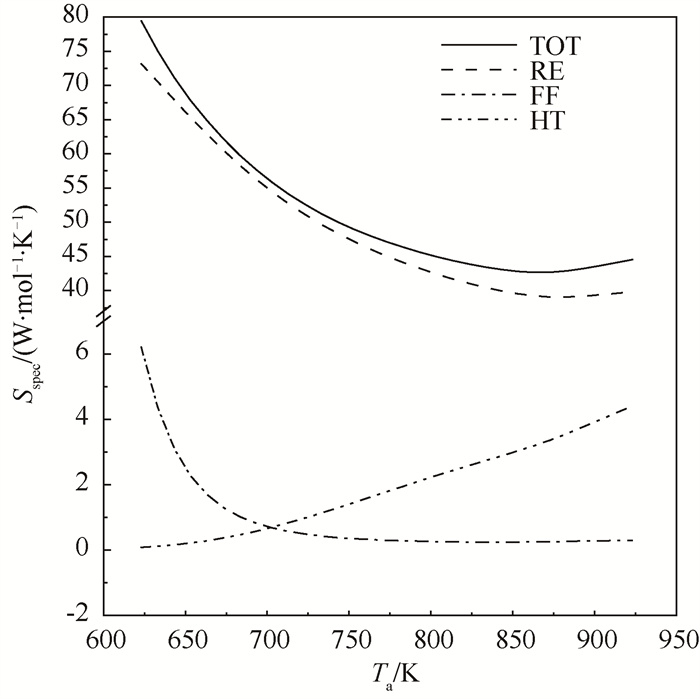
4.2.1 热源温度和传热系数的影响在总传热系数U=350 W ·m-2 ·K-1,其他参数与表 1相同的条件下,比熵产率与热源温度的关系如图 5所示,传热造成的比熵产率随温度升高单调上升,流动造成的比熵产率随温度升高单调下降,同时流动和传热造成的比熵产率在总比熵产率中占比较小,二者之和在总比熵产率中占比在10 % 以内。反应造成的比熵产率随温度先下降后上升,在880 K时达到最小值。总比熵产率的变化规律与此类似,存在总比熵产率最低的最佳操作温度,U=350 W ·m-2 ·K-1时,最佳操作温度出现在860 K附近。
|
图 5 热源温度对比熵产率的影响 Fig.5 Variations of the specific entropy generation rate Sspec versus the reactor wall temperature Ta |
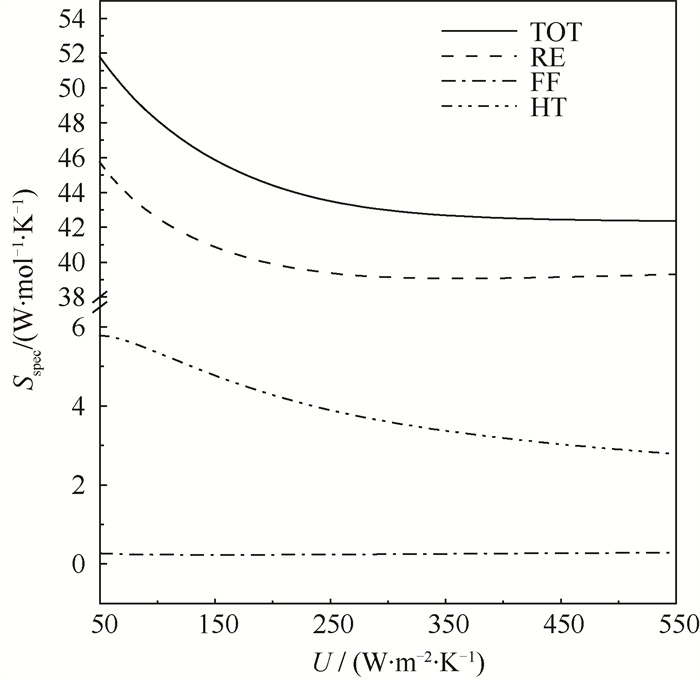
图 6展示了总传热系数对比熵产率的影响(Tin=Ta=873.15 K),从图中看到流动造成的比熵产率随总传热系数增加而先下降再上升;传热造成的比熵产率随总传热系数增加而下降;反应造成的比熵产率随总传热系数增加而先剧烈地下降后缓慢地上升。总比熵产率随总传热系数增加先剧烈下降、后缓慢下降,在U<250 W ·m-2 ·K-1时,随总传热系数增加,总熵产率降低非常显著。而在总传热系数超过250 W ·m-2 ·K-1这一拐点之后,增大总传热系数带来的边际效应变得明显,继续增加总传热系数对降低总比熵产率的作用变得十分微弱。
|
图 6 换热系数对比熵产率的影响 Fig.6 Variations of the specific entropy generation rate Sspec versus the overall heat transfer coefficient U (Tin=Ta=873.15 K) |
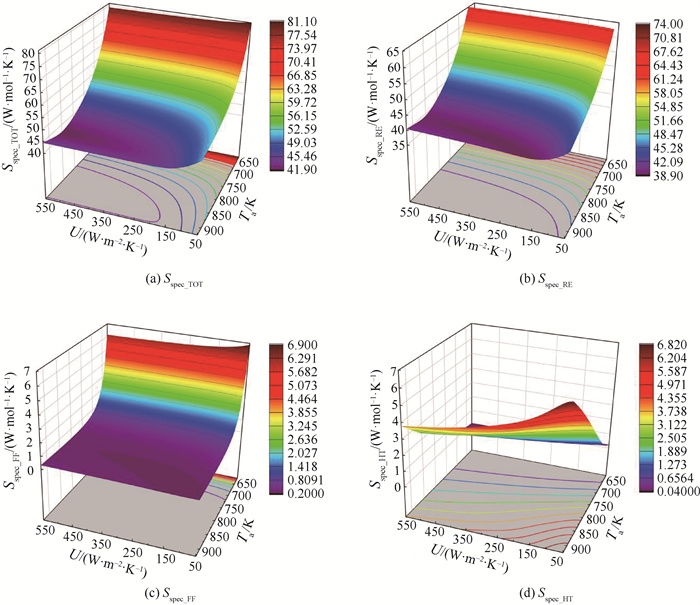
综合考虑改变操作温度和总传热系数对比熵产率的影响,得到结果如图 7所示。对比图 7(a)~(d)可以看出,比熵产率在温度变量方向上的梯度基本大于总传热系数方向,即温度对比熵产率的影响作用更大。从图 7(a)所展示的总比熵产率云图中可以看到,在不同传热系数下,随温度上升,总熵产率均呈先下降后上升的趋势,对应不同传热系数的反应器可以找到其最佳操作温度。而不同温度下总比熵产率随传热系数仍为负相关,但同样存在使边际效应变得显著的拐点。如图 7(a)底部等值线图所示,当总比熵产率等值线与总传热系数轴平行时,总比熵产率沿总传热系数轴方向没有梯度分量,总比熵产率不再随传热系数改变而变化。对比图 7(a)~(b)发现反应造成的比熵产率在总比熵产中占比最大,且分布规律基本一致。
|
图 7 温度和换热系数对比熵产率的综合影响 Fig.7 Variations of the specific entropy generation rate Sspec versus the reactor wall temperature Ta and overall heat transfer coefficient U |
图 7(c)流动造成的比熵产率云图中显示在温度高于723.15 K时,流动造成的比熵产率在1 W ·mol-1 ·K-1内,在总比熵产率中占比小于2 %,而反应器在运行时,为保证氨的转化率,实际操作温度通常高于723.15 K,因此,流动造成的比熵产率基本可以忽略不计。如图 7(d)所示,换热造成的比熵产率与温度的关系与其他方面不同,从比熵产率等值线的分布可以看出,总传热系数和温度对换热造成比熵产的影响相比其他因素更加线性。
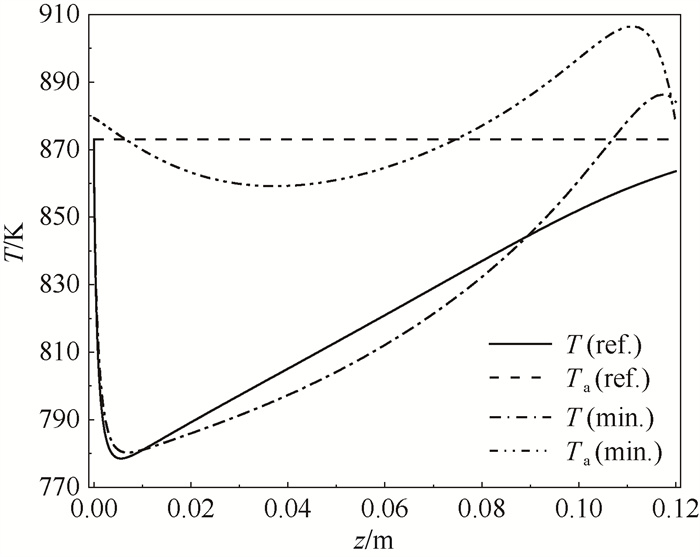
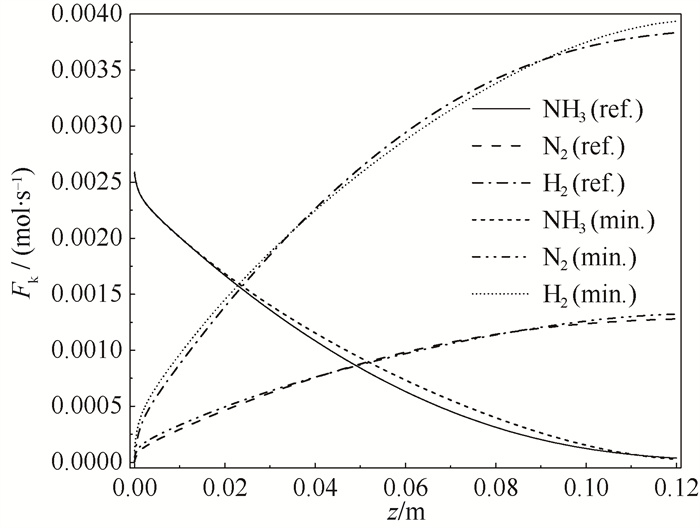
4.3 熵产优化分析基于熵产优化分析获得了氨制氢反应器的最优热源温度分布以及其入口条件。如图 8所示,U=350 W ·m-2 ·K-1,Tinref=Taref=873.15 K的参考案例热源从恒温边界优化为先降后升再降的温度分布曲线,从图 9中可见优化后增加了氮、氢的入口摩尔流率,反应器内气体摩尔流速增加。流动造成的比熵产率增加了4.51 %,但由于流动造成的比熵产在总比熵产中占比小于1 %,对总比熵产率影响微弱。优化后反应和传热比熵产率下降更多,总比熵产率从42.69 W ·m-2 ·K-1降到41.31 W ·mol-1 ·K-1,相对减小3.23 % (表 3)。
|
|
表 3 参考案例优化前后反应器比熵产值对比 Table 3 Specific entropy generation rate in reactor |
如图 8所示,优化后反应器内大部分区域温度与热源温度之差减小。结合图 9可看出,入口段温度降低导致反应速率减小,出口段温度升高提升了反应速率。综合结果是使得气体摩尔流率分布更接近于一条直线,即缩小了反应器各段反应速率的差距。对反应器一维模型内反应速率求变异系数(变异系数是微元反应速率标准差除以其平均值,能直观反映数据偏差程度),得到变异系数从82.96 % 降至76.23 %,说明优化后反应速率分布变得更加均匀,内部空间利用更为充分。
|
图 8 优化前后温度T和热源温度Ta分布 Fig.8 Reaction mixture temperature T and Reactor wall temperature Ta distribution in the reference (ref.) and minimized (min.) reactors |
|
图 9 优化前后组分摩尔流率分布 Fig.9 Molar flow rate of component Fk distribution in the reference (ref.) and minimized (min.) reactors |
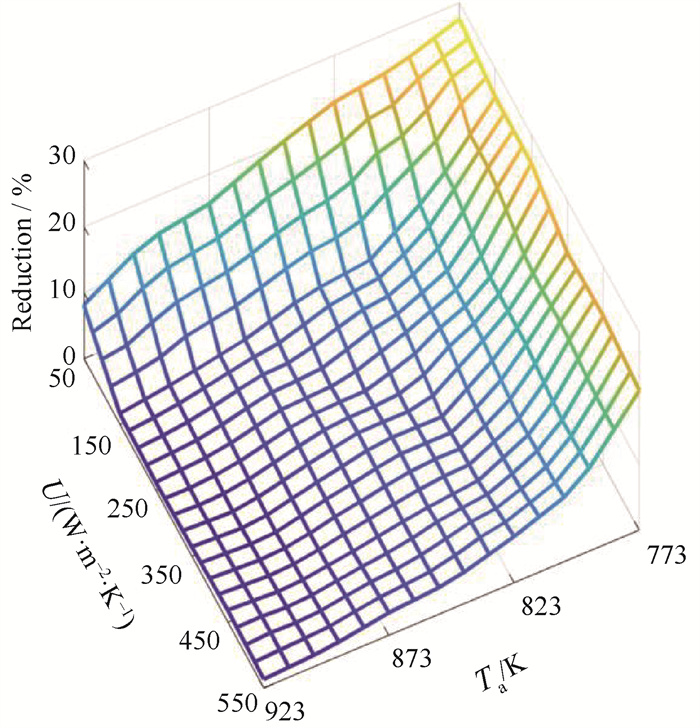
如图 10所示,对参考温度取值为773.15~923.15 K、总传热系数为50~550 W ·m-2 ·K-1的不同参数配置情况进行熵产优化分析,得到的优化结果显示在此参考工况范围内,采用最优热源温度配置能将比熵产率降低1.00 % ~27.48 %。对比发现低温和低传热系数工况优化幅度较大,因为在相同氢气产率的条件约束下,降低气体摩尔流率并优化热源分布提高转化率,即可显著减小单位比熵产率。
|
图 10 比熵产率的优化幅度 Fig.10 Specific entropy generation rate reduction |
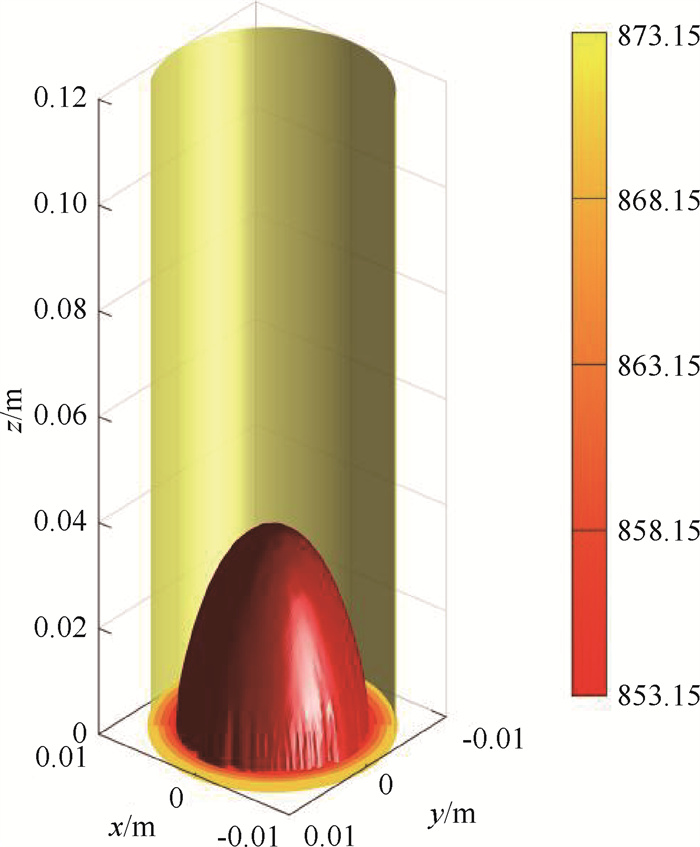
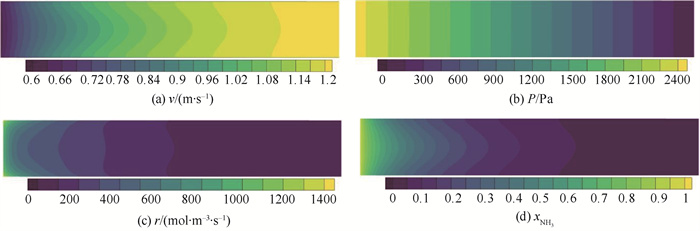
三维CFD仿真得到的温度场如图 11所示,在考虑反应器径向温度、浓度和速度等变量分布差异的情况下,温度场与一维模型求解结果有明显差异。从图中T=853.15 K的半纺锤体型等值面可以看出,反应器内温度梯度并非简单的沿径向方向,在沿轴向也具有一定的分量,因此,反应器传热简化为径向导热是存在一定偏差的。由于反应器内气体保持平推流,轴向速度差异较小(图 12(a)),且从图 12(b)可见,几乎只有轴向方向存在压力梯度,因此,一维模型在流动、压降计算上与三维模型更为接近。图 12(c)显示反应器内进口中心反应速度略小于壁面处,出口段则与之相反;反应速度随轴向距离增加而减小。这是因为入口段温度梯度较大,温度是影响反应的主要因素,贴近壁面处靠近热源,温度更高,反应更剧烈;出口段径向温差小,径向温度差异不再是反应的决定因素,而中心区域入口段的反应较慢,导致残余的氨浓度更高,反应速率高于外侧区域。
|
图 11 氨制氢反应器三维等温分布图 Fig.11 Ammonia decomposition reactor three dimensional temperature filed (CFD result, Ta=Tin=873.15 K) |
|
图 12 氨制氢反应器速度、压力、反应和组分分布 Fig.12 Ammonia decomposition reactor velocity, pressure, reaction rate and ammonia more fraction filed (CFD result, Ta=Tin=873.15 K) |
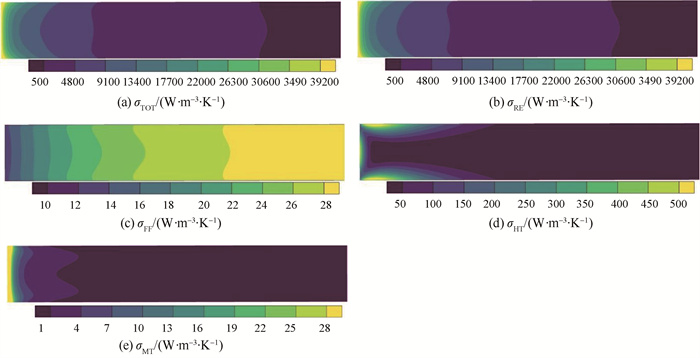
CFD仿真得到的熵产分析结果如图 13~14所示,从图 13中可以看出,造成熵产的主要区域是反应发生较为剧烈的入口段,且反应熵产在总熵产中占主导地位。总熵产沿轴向分布规律与一维模型分析结果基本一致,优化后熵产分布更为均匀,总比熵产值从43.67 W ·mol-1 ·K-1下降到41.14 W ·mol-1 ·K-1 (表 3),三维仿真得到的优化幅度5.779 % 大于一维模型的3.233 %。从图 13(a)中可以看出,在入口段贴近壁面处反应造成熵产大于中心区域,而出口段则与之相反,与图 12(c)反应速率分布规律大致相同。
|
图 13 参考案例CFD仿真微元熵产率 Fig.13 Reference case local entropy production rate in CFD study |
|
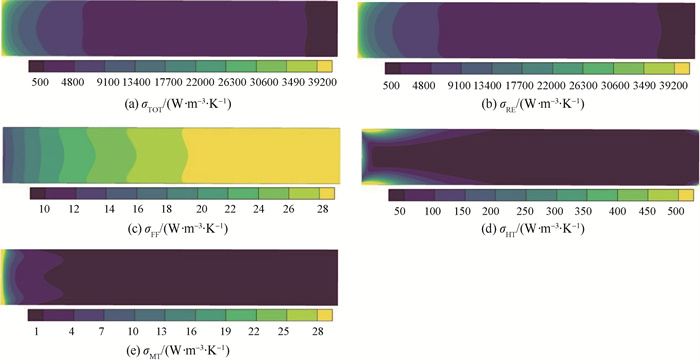
图 14 优化后CFD仿真微元熵产率 Fig.14 Minimized case local entropy production rate in CFD study |
图 13(c)显示流动熵产在轴向上随距离增加而增大,这一分布规律不同于其他部分。由流动造成熵产的式(25)可知,μ/κ和ρCF/2均在104数量级,μ/ε则在10-5数量级,因此,Darcy黏性损失项和Forchheimer惯性损失项是起决定性作用的。由于平推流特性,径向速度相较于轴向速度可以忽视,轴向速度在同一横截面内分布也较为均匀,Darcy项可近似为与轴向速度的平方成正比,Forchheimer项可近似为与轴向速度的立方成正比。所以随着轴向距离增加,轴向流动速度上升(如图 12(a)),流动熵产快速上升。一维与三维模型仿真流动熵产结果非常接近,如表 3所示一维模型和三维模型优化前的比熵产率分别为0.257 1 W ·mol-1 ·K-1和0.248 9 W ·mol-1 ·K-1,二者的相对偏差仅有3 %。
由式(26)可知,传热熵产的主要推动力是温度梯度,从图 13~14可以看出,温度梯度更大的入口段传热熵产更多。由图 11及其对应分析可知,一维与三维模型在传热仿真上存在较大差异,一维模型未考虑的轴向温度梯度和径向差异使仿真反应器最低温度远低于三维模型,因此,三维模型中传热熵产不到一维模型仿真结果的20 % (表 3)。CFD仿真得到扩散熵产主要出现在反应剧烈、浓度梯度较大的入口段。扩散熵产占比小于0.2 %,一维模型忽略扩散熵产,对仿真影响很小。由式(27)可知,扩散对熵产的影响形式与传热相似,二者的熵产推动力分别来自浓度梯度和温度梯度。随着反应轴向推进,扩散熵产仅随反应进程的改变而变化,而传热熵产还受反应器表面热源的影响。因此,除进口位置之外,在壁面附近也有明显的传热熵产,而扩散熵产则主要出现在进口段。传热熵产在优化前后变化较小,一维和三维模型均在±2 % 左右。图 14(d)显示三维模型优化后,出口段出现了较为明显的传热熵产,因此,优化后的传热熵产高于优化前。而如表 3所示,扩散熵产优化幅度非常明显,相较于优化前减小了80.57 %。
5 结论对一维氨制氢反应器模型进行了参数分析和以熵产率为目标函数的最小优化,并通过三维模型进行了结果验证,得到以下结论:
(1) 在参考温度取值为773.15~923.15 K、总传热系数为50~550 W ·m-2 ·K-1工况内,一维模型熵产优化能将比熵产率降低1.00 % ~27.48 %,优化后反应分布更均匀,反应器内部空间利用更充分;
(2) 在723.15~923.15 K温度内,反应熵产在总熵产中占比在90 % 左右,传热熵产占比在10 % 以内,而流动熵产占比小于2 %,基本可以忽略不计;
(3) CFD仿真结果显示扩散熵产主要出现在入口段,且在总熵产中占比小于0.2 %,忽略扩散熵产对计算结果的影响很小。
本研究通过熵产分析优化,使反应器比熵产率降低,反应器内部空间利用更充分,从而降低氨制氢生产能耗,体现了优化后反应器在反应性能和经济性上的优势。后续研究将在此基础上考虑新一代反应器构型,针对性地探究如耦合放热反应的氨制氢反应器的设计和优化方案。
|
|
| [1] |
LUCENTINI I, GARCIA X, VENDRELL X, et al. Review of the decomposition of ammonia to generate hydrogen[J]. Industrial & Engineering Chemistry Research, 2021, 60(51): 18560-18611. |
| [2] |
MORLANÉS N, KATIKANENI S P, PAGLIERI S N, et al. A technological roadmap to the ammonia energy economy: Current state and missing technologies[J]. Chemical Engineering Journal, 2021, 408: 127310. DOI:10.1016/j.cej.2020.127310 |
| [3] |
ANDRIANI D, BICER Y. A review of hydrogen production from onboard ammonia decomposition: Maritime applications of concentrated solar energy and Boil-off gas recovery[J]. Fuel, 2023, 352: 128900. DOI:10.1016/j.fuel.2023.128900 |
| [4] |
ASIF M, SIDRA BIBI S, AHMED S, et al. Recent advances in green hydrogen production, storage and commercial-scale use via catalytic ammonia cracking[J]. Chemical Engineering Journal, 2023, 473: 145381. DOI:10.1016/j.cej.2023.145381 |
| [5] |
LIN L, ZHANG L X, LUO Y, et al. Highly-integrated and cost-efficient ammonia-fueled fuel cell system for efficient power generation: A comprehensive system optimization and techno-economic analysis[J]. Energy Conversion and Management, 2022, 251: 114917. DOI:10.1016/j.enconman.2021.114917 |
| [6] |
BADESCU V. Optimal design and operation of ammonia decomposition reactors[J]. International Journal of Energy Research, 2020, 44(7): 5360-5384. DOI:10.1002/er.5286 |
| [7] |
JANG J, HAN M. Ammonia autothermal reformer with air side-stream distribution for hydrogen production[J]. International Journal of Hydrogen Energy, 2024, 49: 1468-1481. DOI:10.1016/j.ijhydene.2023.09.157 |
| [8] |
POURALI M, ESFAHANI J A, JAHANGIR H, et al. Ammonia decomposition in a porous catalytic reactor to enable hydrogen storage: Numerical simulation, machine learning, and response surface methodology[J]. Journal of Energy Storage, 2022, 55: 105804. DOI:10.1016/j.est.2022.105804 |
| [9] |
ABASHAR M E E. Ultra-clean hydrogen production by ammonia decomposition[J]. Journal of King Saud University - Engineering Sciences, 2018, 30(1): 2-11. DOI:10.1016/j.jksues.2016.01.002 |
| [10] |
CHA J, JO Y S, JEONG H, et al. Ammonia as an efficient COX-free hydrogen carrier: Fundamentals and feasibility analyses for fuel cell applications[J]. Applied Energy, 2018, 224: 194-204. DOI:10.1016/j.apenergy.2018.04.100 |
| [11] |
YE M N, SHARP P, BRANDON N, et al. System-level comparison of ammonia, compressed and liquid hydrogen as fuels for polymer electrolyte fuel cell powered shipping[J]. International Journal of Hydrogen Energy, 2022, 47(13): 8565-8584. DOI:10.1016/j.ijhydene.2021.12.164 |
| [12] |
ZHAO J F, LIANG Q C, LIANG Y F. Simulation and study of PEMFC system directly fueled by ammonia decomposition gas[J]. Frontiers in Energy Research, 2022, 10: 819939. DOI:10.3389/fenrg.2022.819939 |
| [13] |
BEJAN A. Entropy generation minimization: The method of thermodynamic optimization of finite-size systems and finite-time processes[M]. Boca Raton: CRC Press, 1995.
|
| [14] |
BEJAN A, TSATSARONIS G, MORAN M. Thermal design and optimization[M]. Hoboken: Wiley, 1995.
|
| [15] |
JOHANNESSEN E, KJELSTRUP S. Minimum entropy production rate in plug flow reactors: An optimal control problem solved for SO2 oxidation[J]. Energy, 2004, 29(12/15): 2403-2423. |
| [16] |
KONG R, CHEN L G, XIA S J, et al. Minimization of entropy generation rate in hydrogen iodide decomposition reactor heated by high-temperature helium[J]. Entropy, 2021, 23(1): 82. DOI:10.3390/e23010082 |
| [17] |
CHEN L G, ZHANG L, XIA S J, et al. Entropy generation minimization for CO2 hydrogenation to light olefins[J]. Energy, 2018, 147: 187-196. DOI:10.1016/j.energy.2018.01.050 |
| [18] |
NUMMEDAL L, KJELSTRUP S, COSTEA M. Minimizing the entropy production rate of an exothermic reactor with a constant heat-transfer coefficient: The ammonia reaction[J]. Industrial & Engineering Chemistry Research, 2003, 42(5): 1044-1056. |
| [19] |
KJELSTRUP S, JOHANNESSEN E, RøSJORDE A, et al. Minimizing the entropy production of the methanol producing reaction in a methanol reactor[J]. International Journal of Applied Thermodynamics, 2000, 3(4): 147-153. |
| [20] |
NUMMEDAL L, RøSJORDE A, JOHANNESSEN E, et al. Second law optimization of a tubular steam reformer[J]. Chemical Engineering and Processing: Process Intensification, 2005, 44(4): 429-440. DOI:10.1016/j.cep.2004.06.005 |
| [21] |
YUAN Q, LUO Y Y, SHI T, et al. Investigation into the heat transfer models for the hot crude oil transportation in a long-buried pipeline[J]. Energy Science & Engineering, 2023, 11(6): 2169-2184. |
| [22] |
VAN DER HAM L V, GROSS J, VERKOOIJEN A, et al. Efficient conversion of thermal energy into hydrogen: Comparing two methods to reduce exergy losses in a sulfuric acid decomposition reactor[J]. Industrial & Engineering Chemistry Research, 2009, 48(18): 8500-8507. |
| [23] |
王一帆, 段学志, 吴炜, 等. 管壳式自热型氨分解反应器模拟分析[J]. 化工学报, 2015, 66(8): 3169-3176. WANG Y F, DUAN X Z, WU W, et al. Modeling and analysis of concentric self-thermal fixed-bed reactor for ammonia decomposition[J]. CIESC Journal, 2015, 66(8): 3169-3176. |
| [24] |
MALEKI H, FULTON M, BERTOLA V. Kinetic assessment of H2 production from NH3 decomposition over CoCeAlO catalyst in a microreactor: Experiments and CFD modelling[J]. Chemical Engineering Journal, 2021, 411: 128595. |
| [25] |
NIELD D A, BEJAN A. Convection in porous media[M]. New York: Springer, 2013: 537-605.
|
| [26] |
NIELD D A. Resolution of a paradox involving viscous dissipation and nonlinear drag in a porous medium[J]. Transport in Porous Media, 2000, 41(3): 349-357. |
| [27] |
NIELD D A. The modeling of viscous dissipation in a saturated porous medium[J]. Journal of Heat Transfer, 2007, 129(10): 1459-1463. |
| [28] |
HOOMAN K, GURGENCI H. Effects of viscous dissipation and boundary conditions on forced convection in a channel occupied by a saturated porous medium[J]. Transport in Porous Media, 2007, 68(3): 301-319. |
| [29] |
BRIONES A M, MUKHOPADHYAY A, AGGARWAL S K. Analysis of entropy generation in hydrogen-enriched methane-air propagating triple flames[J]. International Journal of Hydrogen Energy, 2009, 34(2): 1074-1083. |




