2. 青岛科技大学 过程系统工程研究所, 山东 青岛 266042;
3. 齐鲁师范学院 化学与化工学院, 山东 济南 250200
2. Institute of Process Systems Engineering, Qingdao University of Science & Technology, Qingdao 266042, China;
3. College of Chemistry and Chemical Engineering, Qilu Normal University, Jinan 250200, China
化工生产过程中,原料的预处理、反应物、产物与副产物的分离均基于相平衡计算结果。相平衡包括汽液平衡、液液平衡、汽液液和固液相平衡。汽液平衡在化工过程中的应用最为广泛,液液平衡常用于萃取过程,固液平衡常用于结晶过程、冶金和炼油过程。固液平衡可分为2类,一类是溶解平衡,不同化学物质在液相和固体间的平衡,本质是固体在液体中的溶解度问题,多用于电解质体系;另一类是熔融平衡,是相同化学物质的熔融态和固态间的平衡,多用于非电解质体系。
非电解质固液相平衡计算模型主要包括2类方法:一种是基于正规溶液理论的方法。Won[1]提出用溶解度参数表示固相和液相活度系数,并用熔点温度和组分的分子量估算熔化焓以计算相平衡的平衡常数;Pedersen等[2]修正Won模型的溶解度参数表达式,优化固相和液相活度系数的计算模型,并在相平衡模型中添加了以组分的分子量和熔点温度为变量的固液相焓差修正项,提高了对固液相平衡的预测能力,将模型的应用范围从正构烷烃扩展到异构烷烃、环烷烃、芳香烃;Zuo等[3]考虑了Poynting因子对固相逸度的影响,用实沸点和石油重馏分的可调参数估算烷烃-环烷烃-芳烃的分布,该模型可在较宽压力范围内计算C7~C80油气体系固体析出温度和固体析出量;陈五花[4]在相平衡模型中考虑了有序固相与无序固相的转换焓项,并建立组分的固-固转换焓、固-固转换温度、熔化焓和熔点温度等新关系式;杨居衡[5]将正规溶液模型和Wilson模型统一起来描述固相的非理想性,建立了IRSW模型,模型对不同体系的固体析出温度、固体析出量和不同温度下的固相碳数质量分布均能得出准确的计算值。另一类是基于局部组成理论的模型,Coutinho等[6-10]提出用纯组分的升华热估算局部组成模型的相互作用能量参数,将Wilson、NRTL、UNIQUAC局部组成模型用于固相计算。Ji等[11]在模型中添加了熔点温度和压力之间的线性表达式,改进正构烷烃的熔化焓、热容参数的计算公式,提出HWWAX-UNIQUAC模型,用于固相活度系数的计算;Ghanaei等[12]基于基团贡献模型,提出了新的热容关联式,并改进P-UNIQUAC模型的交互作用能量参数;Silva等[13]在交互作用能量参数中增加校正参数
研究者在改进相平衡计算模型时,对相同类别的模型进行了比较和评价,但同时参与评价的相平衡模型较少[12-13]。本研究拟对基于正规溶液理论和局部组成理论的非电解质固液相平衡模型进行评价,分析相平衡模型的特点,并对计算结果偏差较大的相平衡模型进行改进,为非电解质体系固液相平衡的计算提供模型和方法。
2 数据来源及方法 2.1 数据来源使用Pauly等[16]在常压和不同温度条件下以正构烷烃C10为溶剂、正构烷烃C18~C30为溶质的2个固液混合物体系的相平衡实验数据,包括以质量为基准的固相分率、流量和组成。2个固液混合物体系中各组分质量分数的实验数据见表 1。
|
|
表 1 2个固液混合物体系的实验值(质量分数) Table 1 Experimental data of the composition of the two solid-liquid mixtures (mass fraction) |
Won[1]基于正规溶液理论,假设所有组分都是可结晶的,用纯组分的升华热估算固相溶解度参数,并用溶解度参数分别表示液相和固相的活度系数。
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = {\exp _{}}\left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) + \frac{{{V_i}}}{{RT}}{{\left( {{{\overline \delta }^{\rm L}} - \delta _i^{\rm L}} \right)}^2} - {{\left( {{{\overline \delta }^{\rm S}} - \delta _i^{\rm S}} \right)}^2}} \right) $ | (1) |
Pedersen等[2]修正了Won[1]溶解度参数的模型,提高了对固相非理想性的描述,将模型的应用范围从正构烷烃扩展到异构烷烃、环烷烃、芳香烃。Pedersen等[2]在计算溶解度时未忽略固液相焓差修正项,计算结果更加准确。
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = \frac{{\gamma _i^{\rm L}}}{{\gamma _i^{\rm S}}}{\exp _{}}\left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) - \frac{{{a_4}{M_{{\rm r},i}}}}{R}\left( {\frac{{T_i^f}}{T} - 1 - {{\ln }_{}}\frac{{T_i^f}}{T}} \right) - \frac{{{a_5}{M_{{\rm r},i}}}}{{2R}}\left( {{{\left( {T_i^f} \right)}^2} + T - 2T_i^f} \right)} \right) $ | (2) |
陈五花[4]根据结晶理论考虑了有序固相与无序固相之间的转换,结合正规溶液理论建立组分的固-固转换焓、固-固转换温度、熔化焓和熔点温度等新关系式,固相和液相活度系数计算公式均采用正规溶液理论的方法。并在K值模型中加入了Pedersen固液相焓差修正项。
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = \frac{{\gamma _i^{\rm L}}}{{\gamma _i^{\rm S}}}\exp \left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) - \frac{{{a_4}{M_{{\rm r},i}}}}{R}\left( {\frac{{T_i^f}}{T} - 1 - \ln \frac{{T_i^f}}{T}} \right) - \frac{{{a_5}{M_{{\rm r},i}}}}{{2R}}\left( {{{\left( {T_i^f} \right)}^2} + T - 2T_i^f} \right) + \frac{{\Delta H_i^t}}{{RT}}\left( {1 - \frac{T}{{T_i^t}}} \right)} \right) $ | (3) |
Coutinho等[6-10]基于局部组成理论开发了适用于正构烷烃体系的固相活度系数模型,并对二元体系的实验数据进行了测试,可用于石油烃类体系固液相平衡的计算。Coutinho等[8-10]将纯组分的升华热估算局部组成模型的相互作用能量参数,对有序固相与无序固相间的分离进行建模,将局部组成模型(UNIQUAC)的适用范围扩展到固相,计算结果准确。
| $ \ln \gamma _i^{\rm S} = \ln \left( {\frac{{{{\bar \varphi }_i}}}{{x_i^{\rm S}}}} \right) + 1 - \frac{{{{\bar \varphi }_i}}}{{x_i^{\rm S}}} - \frac{Z}{2}{q_i}\left( {{{\ln }_{}}\left( {\frac{{{{\bar \varphi }_i}}}{{{{\bar \theta }_i}}}} \right) + 1 - \frac{{{{\bar \varphi }_i}}}{{{{\bar \theta }_i}}}} \right) + {q_i} - {q_i}\ln \left( {\sum\limits_{j = 1}^n {{{\bar \theta }_j}} {\tau _{ji}}} \right) - {q_i}\sum\limits_{j = 1}^n {\frac{{{{\bar \theta }_j}{\tau _{ij}}}}{{\sum\limits_{k = 1}^m {{{\bar \theta }_k}{\tau _{kj}}} }}} $ | (4) |
| $ {\lambda _{ij}} = - \frac{2}{Z}\left( {\Delta H_i^{\rm{sub}} - RT} \right) $ | (5) |
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = \frac{{\gamma _i^{\rm L}}}{{\gamma _i^{\rm S}}}{\exp _{}}\left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) + \frac{{\Delta H_i^t}}{{RT}}\left( {1 - \frac{T}{{T_i^t}}} \right)} \right) $ | (6) |
陈五花[17]采用新的固-固转换焓、固-固转换温度、熔化焓和熔点温度等关系式,并在K值模型中加入了Pedersen固液相焓差修正项,修正了P-UNIQUAC模型。
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = \frac{{\gamma _i^{\rm L}}}{{\gamma _i^{\rm S}}}\exp \left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) - \frac{{{a_4}{M_{{\rm r},i}}}}{R}\left( {\frac{{T_i^f}}{T} - 1 - \ln \frac{{T_i^f}}{T}} \right) - \frac{{{a_5}{M_{{\rm r},i}}}}{{2R}}\left( {{{\left( {T_i^f} \right)}^2} + T - 2T_i^f} \right) + \frac{{\Delta H_i^t}}{{RT}}\left( {1 - \frac{T}{{T_i^t}}} \right)} \right) $ | (3) |
Ghanaei等[12]基于基团贡献模型,提出新的热容关联式,改进P-UNIQUAC模型的交互作用能量参数,并对影响液固标准态逸度比值的因素进行灵敏度分析,得出熔化焓项对相平衡计算的影响最大,固-液相间热容差的影响和固-固相转化带来的影响与熔化焓项对比可以忽略,因此Ghanaei等[12]在模型中忽略了固液相焓差修正项和固-固相转化焓项,且认为正构烷烃的液相溶液接近于理想溶液,将i组分的液相活度系数的值设为1。P-UNIQUAC方程的配位数是Z=6,Ghanaei等[12]令2/Z=0.48,配位数是根据假设的正构烷烃分子间的二元能量参数来确定的。
| $ \frac{{c_p^{\rm L}}}{R} = 2\left( {3.92 + 4.81 \times {{10}^{ - 4}}T} \right) + \left( {{n_{{\rm C},i}} - 2} \right)\left( {2.04 + 5.62 \times {{10}^{ - 3}}T} \right) $ | (7) |
| $ \frac{{c_p^{\rm S}}}{R} = 2\left( {2.40 \times {{10}^{ - 2}}T} \right) + \left( {{n_{{\rm C},i}} - 2} \right)\left( {3.41{T^{ - 1}} - 6.13 \times {{10}^{ - 1}} + 2.93 \times {{10}^{ - 2}}T - 1.44 \times {{10}^{ - 4}}{T^2} + 2.84 \times {{10}^{ - 7}}{T^3}} \right) $ | (8) |
| $ {\lambda _{ij}} = - 0.48\left( {\Delta H_i^{\rm{sub}} - RT} \right) $ | (9) |
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = \frac{{\gamma _i^{\rm L}}}{{\gamma _i^{\rm S}}}{\exp _{}}\left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) + \frac{{\Delta H_i^t}}{{RT}}\left( {1 - \frac{T}{{T_i^t}}} \right)} \right) $ | (10) |
目前非电解质固液相平衡计算模型包括基于正规溶液理论方法和基于局部组成理论方法。正规溶液理论方法是用溶解度参数算出活度系数,溶解度参数模型决定了活度系数的准确性;局部组成理论方法是在UNIQUAC方法的基础上,改进模型的交互作用能量参数,将模型扩展应用于固相,交互作用参数的准确决定了固相活度系数的准确性。在K值模型中,活度系数、熔化焓、熔点温度、固液相焓差修正项、有序固相到无序固相转化焓等性质的准确决定了非电解质固液相平衡的准确性。通过优化固相热力学性质改进模型,优化非电解质固液相平衡模型的计算结果。
3 计算结果与评价采用Pauly等[16]固液相平衡实验数据评价Won等6种模型对固液相平衡固相分率和固相组成的计算效果。
3.1 模型对体系A固相分率计算结果评价体系A以质量分数为基准的固相分率的实验值与6种模型计算值的绝对偏差(AD)、最大绝对偏差(MAD)和平均绝对偏差(AAD)见表 2。
|
|
表 2 6种模型对体系A固相分率的计算结果 Table 2 Prediction results of the six models for solid phase fraction of system A |
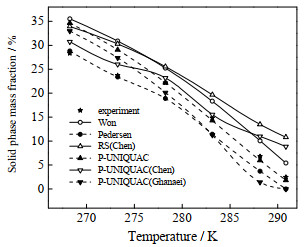
由图 1可以看出,在体系A中,6种模型计算值的固相分率与实验值平均偏差为(2.17%~5.90%)。在268.25~273.25 K,Pedersen模型计算的固相分率的结果与实验值非常接近(AAD为0.40%);除Pedersen模型外,P-UNIQUAC(Chen)模型的计算值也比较接近实验值(AAD为2.37%);在此温度区间内体系温度相对较低,与各组分熔点温度相差较大,加入固液相焓差修正项可提高模型计算值的准确性,在此温度范围内,Pedersen和P-UNIQUAC(Chen)计算值优于其他4种方法,其他模型对固相分率的计算值AAD均小于6%。在278.25~290.85 K,P-UNIQUAC模型对固相分率的计算值与实验值的AAD为0.53%;其他模型对固相分率的计算值的AAD均小于7%,在此温度区间内,溶质组分C20~C22含量相对较多,有序固相与无序固相间的转换焓项的影响较大,因此K值模型中考虑有序固相与无序固相间转换焓项的P-UNIQUAC模型计算值较好。
|
图 1 体系A固相分率的实验数据与6种模型的预测结果 Fig.1 Comparison of experimental and predictive results of the six models for system A on solid phase fractions |
体系B以质量分数为基准的固相分率的实验值与6种模型计算值的绝对偏差、最大绝对偏差和平均绝对偏差见表 3。
|
|
表 3 6种模型对体系B固相分率的计算结果 Table 3 Prediction results of the six models for solid phase fraction of system B |
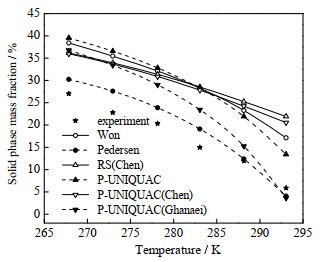
由图 2可以看出,6种模型对体系B固相分率的计算值均高于实验值。6种模型中最接近实验值的是Pedersen模型,AAD为2.99%。Pedersen模型中包含固液两相之间热容的差值,体现了模型考虑固液相焓差修正项的必要性。其次为P-UNIQUAC(Ghanaei)模型,计算结果的AAD为7.18%。P-UNIQUAC(Ghanaei)模型改进了交互作用能量参数,计算结果优于P-UNIQUAC模型。对于体系B,溶质组分C20~C22含量相对较少,固-固相转化焓在K值模型中的影响不大,增加固-固相转化焓反而使计算值与实验值的结果偏差增大,由图 2中可以看出,P-UNIQUAC(Ghanaei)的固液相平衡预测结果中混合物的液相更接近理想溶液的行为。
|
图 2 体系B固相分率的实验数据与6种模型的预测结果 Fig.2 Comparison of experimental and predictive results of the six models for system B on solid phase fractions |
在267.85~283.05 K,RS(Chen)模型、P-UNIQUAC(Chen)模型、Won模型和P-UNIQUAC模型计算结果的AAD分别为11.22%、10.81%、12.28% 和13.00%。在283.05~293.05 K,Won模型、P-UNIQUAC模型、RS(Chen)和P-UNIQUAC(Chen)模型计算结果的AAD分别为11.97%、10.26%、14.30% 和13.28%。
3.3 模型对固相分率计算结果的总体评价以质量分数为基准的2个体系固相分率的实验值与6种模型计算值的平均绝对偏差见表 4。由表 4可以看出,6种模型对固相分率总体计算结果的AAD最小的是Pedersen模型(2.58%)。对比Won模型发现,Pedersen模型考虑了固液相焓差修正项,且对碳原子个数大于6的固相和液相溶解度参数采用新关联式,计算得到的固相和液相活度系数更准确;偏差较大的是RS(Chen)和P-UNIQUAC(Chen)模型,AAD分别为9.14%和7.27%,陈五花模型在温度大于288.15 K时计算
|
|
表 4 6种模型对固相分率总体预测结果的平均绝对偏差 Table 4 Average absolute deviations of overall prediction results by the six models on solid phase fraction |
Pedersen模型适用于测试温度相对较低、与各组分的熔点温度相差较大的体系,该模型的固液相焓差修正项及溶解度参数关联式有助于提高模型计算值的准确性;P-UNIQUAC模型适用于溶质组分C20~C22质量分数大于22%,测试温度大于0 ℃的体系,在此条件下,有序固相与无序固相间的转换焓项的影响较大,在K值模型中加入固-固相转换焓项后的计算结果更接近实验值。
4 方法改进当体系温度高于或低于熔点温度时,固液两相的焓差会影响K值模型的计算结果,若K值模型只考虑熔化焓项而忽略固液相焓差修正项,会影响固相分率计算结果的准确性。
4.1 模型改进方法由于RS(Chen)模型、Pedersen和P-UNIQUAC(Chen)模型都已经考虑了固液相焓差修正项的影响,本研究仅对Won、P-UNIQUAC和P-UNIQUAC(Ghanaei) 3种方法的K值模型进行改进。通过增加3种不同的固液相焓差修正项改进K值计算模型,并用实验数据对改进方法对固相分率的计算精度进行评价。
下面分别对3种固液相焓差修正项进行介绍。
Pedersen固液相焓差修正项为式(11),修正项以组分的分子量和熔点温度为变量。
| $ \left( { - \frac{{{a_4}{M_{{\rm r},i}}}}{R}\left( {\frac{{T_i^f}}{T} - 1 - \ln \frac{{T_i^f}}{T}} \right) - \frac{{{a_5}{M_{{\rm r},i}}}}{{2R}}\left( {{{\left( {T_i^f} \right)}^2} + T - 2T_i^f} \right)} \right) $ | (11) |
| $ {a_4} = {1.255_{}}J \cdot {\left( {g \cdot K} \right)^{ - 1}} $ |
| $ {a_5} = - 1.94 \times {10^{ - 3}}_{}J \cdot {\left( {g \cdot {K^2}} \right)^{ - 1}} $ |
DIPPR固液相焓差修正项和Ghanaei固液相焓差修正项均基于K值模型式(13)中后两项热容积分项。
| $ K_i^{\rm{SL}} = \frac{{x_i^{\rm S}}}{{x_i^{\rm L}}} = \frac{{\gamma _i^{\rm L}}}{{\gamma _i^{\rm S}}}{\exp _{}}\left( {\frac{{\Delta H_i^f}}{{RT}}\left( {1 - \frac{T}{{T_i^f}}} \right) - \frac{1}{{RT}}\int\limits_T^{T_i^f} {\left( {c_p^{\rm L} - c_p^{\rm S}} \right)dT + \frac{1}{R}} \int\limits_T^{T_i^f} {\frac{{\left( {c_p^{\rm L} - c_p^{\rm S}} \right)}}{T}} dT} \right) $ | (12) |
其中DIPPR固液相焓差修正项中的固相热容和液相热容关联式分别采用DIPPR数据库中的关联式形式,即式(13)和(14)。
| $ c_p^S = {C_{1i}} + {C_{2i}}T + {C_{3i}}{T^2} + {C_{4i}}{T^3} + {C_{5i}}{T^4} $ | (13) |
| $ c_p^L = {C_{1i}} + {C_{2i}}T + {C_{3i}}{T^2} + {C_{4i}}{T^3} + {C_{5i}}{T^4} $ | (14) |
Ghanaei固液相焓差修正项中的热容关联式见式(8)和(9)。分别将Pedersen、Ghanaei和DIPPR固液相焓差修正项用于Won、P-UNIQUAC和P-UNIQUAC(Ghanaei)模型,得到9种不同的改进模型,见表 5。
|
|
表 5 9种改进的用于K值计算的固液相平衡模型 Table 5 Nine modified solid-liquid equilibrium models for K value calculation |
体系A、B以质量分数为基准的固相分率的实验值与9种改进模型的计算值的绝对偏差见表 6。
|
|
表 6 9种改进模型对体系A和B固相分率的绝对偏差 Table 6 Absolute deviations of the nine modified models on solid phase fraction simulation of systems A and B |
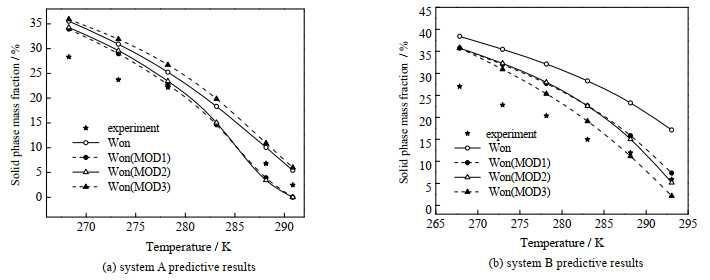
体系A和B以质量分数为基准的固相分率的实验值与Won改进模型的计算值见图 3。由图 3(a)可以看出,Won(MOD1)和Won(MOD2)的模型比未改进的Won模型与计算值的误差更小,计算结果更准确。3种改进方法对固相分率计算结果的AAD分别为2.83%、3.18% 和4.52%。在283.15和278.25 K时,优化模型的计算值与实验值的AAD均小于1.30%。Won(MOD3)的计算结果偏差略大于Won(MOD1)和Won(MOD2),AAD为5.49%。
|
图 3 不同体系固相分率的实验数据与Won改进模型的计算结果 Fig.3 Comparison of solid fraction between experimental data and calculated results of the Won modified model for different systems |
由图 3(b)可以看出,在267.85~293.05 K,Won(MOD3)模型对固相分率的计算值与实验值最接近,AAD为5.08%;Won(MOD1)与Won(MOD2)模型对固相分率的预测结果基本相同,AAD分别为6.37% 和6.20%;Won的3种改进模型均比未改进的Won模型准确(11.95%)。
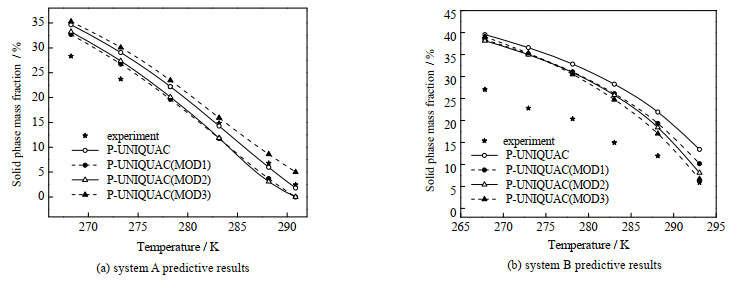
4.2.2 P-UNIQUAC方法改进效果体系A和B以质量分数为基准的固相分率的实验值与P-UNIQUAC改进模型的计算值见图 4。由图 4(a)可以看出,未改进的P-UNIQUAC模型对固相分率结果的计算值在278.25~290.85 K已经非常准确,AAD为0.53%,但在268.25~273.25 K,P-UNIQUAC(MOD1)与P-UNIQUAC(MOD2)模型对固相分率结果的计算值比未改进的P-UNIQUAC更加准确,AAD分别为3.68%、4.27% 和5.84%。P-UNIQUAC(MOD3)模型的计算值略差于MOD1和MOD2,AAD为6.67%。
|
图 4 不同体系固相分率的实验数据与P-UNIQUAC改进模型的计算结果 Fig.4 Comparison of solid fraction between experimental data and calculated results of the P-UNIQUAC modified models for different systems |
由图 4(b)可以看出,P-UNIQUAC的3种改进模型的计算值都比未改进的P-UNIQUAC模型(11.59%)更准确。在267.85~293.05 K,P-UNIQUAC(MOD3)模型对固相分率的计算结果优于P-UNIQUAC(MOD1)和P-UNIQUAC(MOD2),但AAD较大,为8.38%;P-UNIQUAC(MOD1)与P-UNIQUAC(MOD2)对固相分率的计算值与实验值的AAD分别为9.53% 和8.89%。
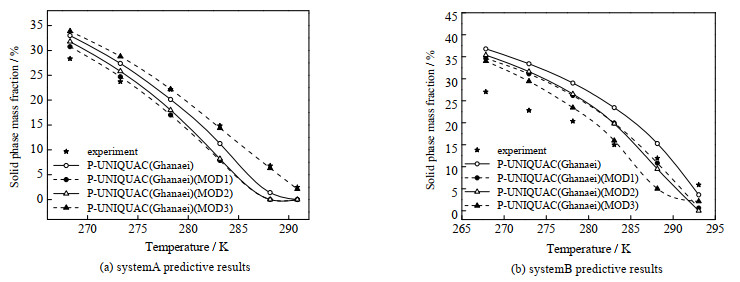
4.2.3 P-UNIQUAC(Ghanaei)方法改进效果体系A和B以质量分数为基准的固相分率的实验值与P-UNIQUAC(Ghanaei)改进模型的计算值见图 5。
|
图 5 不同体系固相分率的实验数据与P-UNIQUAC(Ghanaei)改进模型的计算结果 Fig.5 Comparison of solid fraction between experimental data and calculated results of the P-UNIQUAC(Ghanaei) modified models for different systems |
由图 5(a)可以看出,在278.25~290.85 K,P-UNIQUAC(Ghanaei)(MOD3)的模型比未改进的P-UNIQUAC(Ghanaei)模型(3.38%)的预测结果更准确,AAD为0.34%。在268.25~273.25 K,P-UNIQUAC(Ghanaei)(MOD1)模型对固相分率的计算值与实验值接近,AAD为1.71%;P-UNIQUAC(Ghanaei)(MOD2)对固相分率的计算值的AAD为2.77%;P-UNIQUAC(Ghanaei)(MOD3)模型的预测结果偏差略大,AAD为5.30%。
由图 5(b)可以看出,在267.85~283.05 K,P-UNIQUAC(Ghanaei)(MOD3)模型对固相分率的计算值与实验值最接近,AAD为4.42%;P-UNIQUAC(Ghanaei)(MOD1)与(MOD2)模型对固相分率的计算值的AAD分别为6.68% 和7.04%;P-UNIQUAC(Ghanaei)的3种改进模型都比未改进的P-UNIQUAC(Ghanaei)模型(9.37%)的计算值更准确。在288.15~293.05 K,P-UNIQUAC(Ghanaei)(MOD1)对固相分率预计算值的偏差(3.18%)略大于未改进的P-UNIQUAC(Ghanaei)的计算值(2.78%);P-UNIQUAC(Ghanaei)(MOD2)与P-UNIQUAC(Ghanaei)(MOD3)模型对固相分率计算值的AAD分别为4.16% 和5.34%,均大于P-UNIQUAC(Ghanaei)(MOD1)和未改进方法P-UNIQUAC(Ghanaei)。
4.3 改进模型对固相分率计算结果的总体评价Won等改进模型对以质量分数为基准的2个体系固相分率计算值的平均绝对偏差结果见表 7。从表 7中可以看出,在Won方法中,MOD1、MOD2和MOD3对固相分率计算值与实验值相比,AAD分别为4.60%、4.69% 和5.29%,均优于未改进的Won模型(8.24%)。Won(MOD1)对固相分率的计算值与实验值的AAD最小,说明在Won方法中添加Pedersen固液相焓差修正项对原模型的优化效果最好。
|
|
表 7 改进模型对固相分率的计算值与实验值的平均绝对偏差 Table 7 Average absolute deviations of solid fraction between calculated results of the modified models and the experimental data |
在P-UNIQUAC方法中,MOD1、MOD2和MOD3对固相分率的预测结果的AAD分别为6.31%、6.1%和5.86%,优于未改进的P-UNIQUAC模型(6.95%)。P-UNIQUAC(MOD3)对固相分率的计算值与实验值的AAD最小,说明在P-UNIQUAC方法中添加DIPPR热容估算模型的固液相焓差修正项对原模型的优化效果最好。
在P-UNIQUAC(Ghanaei)方法中,MOD1、MOD2和MOD3对固相分率的计算值与实验值的AAD分别为4.83%、5.18% 和3.36%,同样优于未改进的P-UNIQUAC(Ghanaei)(5.41%)。P-UNIQUAC(Ghanaei)(MOD3)对固相分率的计算值与实验值的AAD最小,说明在P-UNIQUAC(Ghanaei)方法中添加DIPPR热容估算模型的固液相焓差修正项对原模型的优化效果最好。
总体来看,在Won方法中添加Pedersen固液相焓差修正项,在P-UNIQUAC、P-UNIQUAC(Ghanaei)方法中采用DIPPR热容关联式并增加固液相焓差修正项,对固相分率的计算结果最准确。
在体系A、B中,P-UNIQUAC(Ghanaei)(MOD3)是9种改进模型中对固相分率预测结果最好的,在体系A中AAD为2.00%,在体系B中AAD为4.72%。一方面是因为P-UNIQUAC(Ghanaei)模型对交互作用能量参数进行了改进,提高了固相活度系数的计算精度。另一方面是因为在P-UNIQUAC(Ghanaei)模型中添加DIPPR热容估算模型的固液相焓差修正项对原模型的优化效果最好。
P-UNIQUAC(Ghanaei)(MOD3)模型在体系A中,AAD为2.00%,优于Pedersen模型(AAD为2.17%),其他8种改进模型对固相分率的计算值均不如Pedersen模型准确,AAD介于2.83%~4.28%,这说明当溶质组分C20~C22质量分数大于22% 时,基于局部组成理论的P-UNIQUAC(Ghanaei)模型求解固相活度系数并结合DIPPR热容估算模型的固液相焓差修正项改进的模型可以提高预测结果的准确性。Pedersen模型在体系B中,AAD为2.99%,优于9种改进模型(4.72%~9.53%),这说明当溶质组分C20~C22质量分数小于22%时,用Pedersen溶解度参数关联式模型可以准确求解固相、液相活度系数。
因此,当溶质组分C20~C22质量分数大于22% 时,建议采用P-UNIQUAC(Ghanaei)(MOD3)模型;当溶质组分C20~C22质量分数小于22% 时,建议采用Pedersen模型。
5 结论本研究采用2个不同体系的实验数据对6种非电解质固液相平衡模型进行了评价。通过增加固液相焓差修正项对Won等3种非电解质固液相平衡模型进行改进,并评价了改进模型对K值计算结果的准确性,得到如下结论:
(1) 评价了基于正规溶液理论及基于局部组成理论共6种非电解质固液相平衡的K值模型。结果表明,Pederson模型对固相分率预测结果AAD最小(2.58%);其次是P-UNIQUAC(Ghanaei)模型(AAD为5.41%),优于其他4种模型。
(2) 评价结果表明,9种改进的模型均优于3种原始相平衡模型。根据计算结果可以看出,在P-UNIQUAC(Ghanaei)模型中增加DIPPR固液相焓差修正项后的改进模型,对固相分率的计算结果最准确。
(3) 当体系温度高于或低于熔点温度时,固液两相的焓差显著影响K值模型的计算。在K值模型中加入固液相焓差修正项,可以提高固液相平衡中固相分率计算结果的精度,这对模型的改进十分必要。
因多组分非电解质固液相平衡的文献实验数据相对较少,本研究涉及的模型仅对非电解质中正构烷烃体系的混合物组分进行了评价与测试,未来将基于其他例如芳烃、醇、酯等体系进行研究和模型改进,使其应用范围及计算精度得到提升。
符号说明:
AAD
—平均绝对偏差,%
—组分i的有序固相到无序固相转化温度,K
AD
—绝对偏差,%
Vi
—组分i的摩尔体积,m3⋅mol−1
a4, a5
—焓差修正项参数
—组分i在液相中的摩尔分数
Cli~ C5i
— DIPPR热容关联式的系数
—组分i在固相中的摩尔分数
—液相摩尔定压热容,J⋅mol⋅K−1
Z
—配位数
—固相摩尔定压热容,J⋅mol⋅K−1
γ
—活度系数
—组分i的熔化焓,J⋅mol−1
δ
—溶解度参数
—组分i的升华焓,J⋅mol−1
—平均溶解度参数
—组分i的有序固相到无序固相转化焓,J⋅mol−1
—平均表面积分数
—非电解质固液相平衡常数
—平均体积分数
MAD
—最大绝对偏差,%
λij
—二元分子键能交互作用参数
Mr, i
—组分i的相对分子质量
τ ij, τ ji, τkj
nC, i
—组分i的碳原子个数
—二元能量交互作用参数
qi
—组分i的表面积参数
上标
R
—普适气体常数,8.314 J⋅mol−1⋅K−1
S, L
—固相相态,液相相态
ri
—组分i的体积参数
下标
T
—温度,K
i, j
—组分
—组分i的熔点温度,K
| [1] |
WON K W. Thermodynamics for solid solution-liquid-vapor equilibria: Wax phase formation from heavy hydrocarbon mixtures[J]. Fluid Phase Equilibria, 1986, 30(4): 265-279. |
| [2] |
PEDERSEN K S, SKOVBORG P, RONNINGSEN H P. Wax precipitation from north sea crude oils. 4. Thermodynamic modeling[J]. Energy & Fuels, 1991, 5(6): 924-932. |
| [3] |
ZUO J Y, ZHANG D D, NG H J. An improved thermodynamic model for wax precipitation from petroleum fluids[J]. Chemical Engineering Science, 2001, 56(24): 6941-6947. DOI:10.1016/S0009-2509(01)00338-4 |
| [4] |
陈五花. 原油中石蜡沉积的热力学研究[D]. 大连: 大连理工大学, 2006. CHEN W H. Thermodynamic study of paraffin deposition in crude oil [D]. Dalian: Dalian University of Technology, 2006. |
| [5] |
杨居衡. 多相体系蜡析出计算模型研究[D]. 北京: 中国石油大学, 2018. YANG J H. Study on calculation model of wax precipitation in polyphase system [D]. Beijing: China University of Petroleum, 2018. |
| [6] |
COUTINHO J A P, KNUDSEN K, ANDERSEN S I, et al. A local composition model for paraffinic solid solutions[J]. Chemical Engineering Science, 1996, 51(12): 3273-3282. DOI:10.1016/0009-2509(95)00397-5 |
| [7] |
COUTINHO J A P, STENBY E H. Predictive local composition models for solid-liquid equilibrium in n-alkane systems: Wilson equation for multicomponent systems[J]. Industrial & Engineering Chemistry Research, 1996, 35(3): 918-925. |
| [8] |
COUTINHO J A P. Predictive UNIQUAC: A new model for the description of multiphase solid-liquid equilibrium in complex hydrocarbon mixtures[J]. Industrial & Engineering Chemistry Research, 1998, 37(12): 4870-4875. |
| [9] |
COUTINHO J A P. Predictive local composition models: NRTL and UNIQUAC and their application to model solid-liquid equilibrium of n-alkanes[J]. Fluid Phase Equilibria, 1999, 158(2): 447-457. |
| [10] |
COUTINHO J A P, MIRANTE F, PAULY J. A new predictive UNIQUAC for modeling of wax formation in hydrocarbon fluids[J]. Fluid Phase Equilibria, 2006, 247(1/2): 8-17. |
| [11] |
JI H Y, TOHIDI B, DANESH A, et al. Wax phase equilibria: Developing a thermodynamic model using a systematic approach[J]. Fluid Phase Equilibria, 2004, 216(2): 201-217. DOI:10.1016/j.fluid.2003.05.011 |
| [12] |
GHANAEI E, ESMAEILZADEH F, FATHIKALAJAHI J, et al. Wax formation from paraffinic mixtures: A simplified thermodynamic model based on sensitivity analysis together with a new modified predictive UNIQUAC[J]. Fuel, 2012, 99(3): 235-244. |
| [13] |
DA SILVA V M, DO CARMO R P, FLEMING F P, et al. Paraffin solubility and calorimetric data calculation using Peng-Robinson EoS and modified UNIQUAC models[J]. Journal of Petroleum Science and Engineering, 2017, 156(3): 945-957. |
| [14] |
PEREIRA E, JUNQUEIRA F T, MEIRELLES A J D, et al. Prediction of the melting behavior of edible fats using UNIFAC and UNIQUAC models[J]. Fluid Phase Equilibria, 2019, 493(6): 58-66. |
| [15] |
MAHABADIAN M A, CHAPOY A, TOHIDI B. A new thermodynamic model for paraffin precipitation in highly asymmetric systems at high pressure conditions[J]. Industrial & Engineering Chemistry Research, 2021, 85(5): 238-248. DOI:10.3969/j.issn.1673-5641.2021.05.117 |
| [16] |
PAULY J, DAUPHIN C, DARIDON J L. Liquid-Solid equilibria in a decane plus multi-paraffins system[J]. Fluid Phase Equilibria, 1998, 158(4): 845-857. |
| [17] |
陈五花. 降凝剂对含蜡油石蜡析出过程影响的实验与模型化研究[D]. 大连: 大连理工大学, 2009. CHEN W H. Experimental and modeling study on the effect of pour point depressant on paraffin precipitation in waxy oil [D]. Dalian: Dalian University of Technology, 2009. |




