2. 浙江大学衢州研究院, 浙江 衢州 324000;
3. 浙江中烟工业有限责任公司, 浙江 杭州 310024
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China;
3. Technology Center, China Tobacco Zhejiang Industrial Co. Ltd., Hangzhou 310024, China
干冰膨胀烟丝(DIET)技术是烟草工业中普遍使用的工艺技术。这项技术的研究始于20世纪70年代[1-2],其原理是用液态二氧化碳浸泡干烟丝,然后减压,形成干冰烟丝,再与高温工艺气体接触,干冰升华导致烟丝体积急速膨胀,从而增大烟丝的填充性能,由此可降低单箱卷烟的烟丝消耗量、减少焦油等危害性成分释放量、提升烟气透发性[3-4]。
国内外关于DIET技术研究已有不少报道,主要涉及工艺改进、设备改造和膨胀前后化学组分变化等。Utsch等[5],de la Burde等[6]在其专利中提出了以下工艺:用液态二氧化碳浸润烟丝,然后快速冷却使二氧化碳固化,再通过加热使二氧化碳升华,促使烟丝细胞膨胀,并对设备进行了详细介绍。在此基础上,Cho等[7]提出了DIET生产的具体流程和完整设备的设计方案,使其适用于高堆积密度的烟丝处理过程。Enzell等[8]对膨胀后烟丝组分的研究表明,膨胀后烟丝中焦油等有害有机物和卷烟的抽吸次数均有所降低。Halter等[9]比较了二氧化碳、氨气和氟利昂等3种烟丝膨胀方法,结果表明,3种方法得到的烟丝膨胀率依次降低。Theophilus等[10]对DIET进行毒理学研究,发现DIET与传统的三氯氟甲烷膨胀后的烟丝具有相似的生物活性。王志华等[11]对二氧化碳浸渍缸进行了优化设计,使浸渍后的烟草较松散、不易结块,从而减少碎丝率,保证膨胀后烟丝的品质。姜建平[12]对二氧化碳膨胀升华管的设计进行了改良,使整丝率提高了8.4%、碎丝率降低了1.54%。崇黎明等[13]以烟丝的感官评价为评价指标,研究了运行参数对评价指标的影响。资文华等[14]指出膨胀后烟丝含水率w2(质量分数,下同)对膨胀烟丝感官质量有显著影响,当w2为8.0% 时,感官评吸结果最好。韩金民[15]通过Fluent软件对“Z”型膨胀塔进行了数值模拟,得到干冰烟丝在膨胀塔内运动的物流模型。然而,目前大部分研究以实验为主,缺少对DIET过程的相关数学模型研究,导致实际生产中难以对w2进行精准控制,例如出现w2逐步降低的异常现象。
本研究通过建立DIET过程的数学模型,着重分析工艺条件对w2这一重要技术指标的影响,以期为改进生产工艺提供相关理论依据。
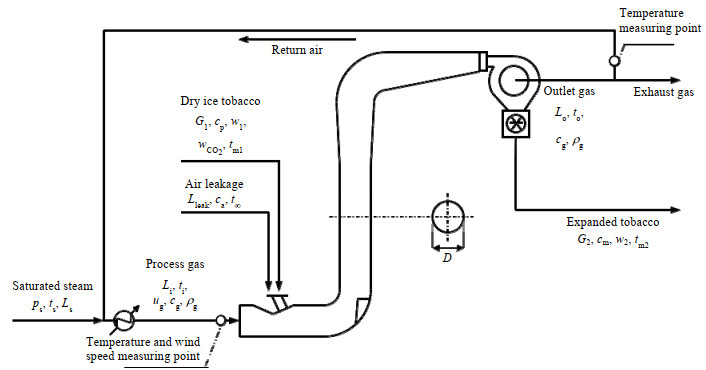
2 数学模型如图 1所示,DIET过程膨胀段的主要流程为:饱和蒸气与回风(循环废气)混合后加热到300 ℃左右,形成工艺气体(其中水蒸气质量分数yw约为76.4%,空气质量分数ya约为23.6%),工艺气体进入膨胀管;干冰烟丝(其中含水率w1为18.9%,湿基干冰含量wCO2为5.6%,均为质量分数,下同)与工艺气体在膨胀管中进行气流干燥;之后经旋风分离器进行气、固分离,出口工艺气体废气(质量流量为图 1中的Lo)部分循环作为回风,膨胀后的烟丝则进入下一工序,此时w2降至8% 左右,烟丝体积膨胀率为70%~100%。为确保烟丝能够顺利进入膨胀管,管内需要维持一定的负压(约为−1kPa),这会导致烟丝进口处吸进一部分空气(质量流量为图 1中的Lleak)。在实际操作中,每天需先对膨胀管系统进行一段时间的吹扫,然后再进料,1个操作周期约为5 h。一般情况下1 d的总操作时长大约10 h,即2个周期。
|
图 1 DIET过程膨胀段流程示意图 Fig.1 Schematic diagram of the expansion section in the DIET process |
DIET过程本质上是一个过热蒸气气流干燥过程。烟丝在膨胀管内的停留时间很短[16],分别经历了干冰升华和烟丝干燥除去水分等2个阶段。第1阶段,烟丝中的干冰升华,烟丝体积迅速增大、温度恒定为−78.5 ℃(干冰升华温度),干冰烟丝湿基干冰含量由5.6% 降至0;第2阶段,烟丝升温的同时进行干燥以除去水分,烟丝含水率由18.9% 降至8% 左右。由烟丝的干燥特性[17]可知,烟丝干燥过程主要为恒速干燥。若将膨胀后的烟丝(w2=8%)视为一个物质,且忽略设备热损失、膨胀过程中的烟丝比热容变化,2个阶段中烟丝吸收的热量Qt可表示为:
| $ Q_{\mathrm{t}}=M_{\mathrm{CO}_2} \gamma_{\mathrm{CO}_2}+W \gamma_{\mathrm{w}}+G_2 c_{\mathrm{m}}\left(t_{\mathrm{m} 2}-t_{\mathrm{m} 1}\right) $ | (1) |
式中:烟丝干冰升华量MCO2=G1wCO2,烟丝干燥去除的总水量W=G1w1− G2w2。
再由烟丝进、出系统的总物料衡算可得:
| $ G_1=G_2+W+M_{\mathrm{CO}_2}=G_2+\left(G_1 w_1-G_2 w_2\right)+G_1 w_{\mathrm{CO}_2} $ | (2) |
整理式(2)可得绝干烟丝质量流量Gc表达式:
| $ G_{\mathrm{c}}=G_1\left(1-w_1-w_{\mathrm{CO}_2}\right)=G_2\left(1-w_2\right) $ | (3) |
烟丝由计量带送入膨胀塔,故G1由计量带频率f和计量带上烟丝高度H控制,为烟丝密度ρp、烟丝流股截面宽度、H和带速等4者之积,其中前2者为定值,带速与f呈正比,因此,G1可用常数ϕ(计量带流量系数)与H、f之积来表示:
| $ {G_1} = \phi Hf $ | (4) |
热风干燥下工艺气体与烟丝间传热方式主要为对流传热,故Qt亦可表示为:
| $ Q_{\mathrm{t}}=\alpha S \Delta t $ | (5) |
式中:工程实际中,气体与烟丝间的平均传热温差∆t可采用算术平均,即
| $ \Delta t=\frac{\left(t_{\mathrm{i}}-t_{\mathrm{m} 1}\right)+\left(t_{\mathrm{o}}-t_{\mathrm{m} 2}\right)}{2} $ | (6) |
联立式(1) ~(6)可得:
| $ w_2=1-\frac{\phi H f \times\left(1-w_1-w_{\mathrm{CO}_2}\right)\left[\gamma_{\mathrm{w}}-c_{\mathrm{m}}\left(t_{\mathrm{m} 2}-t_{\mathrm{m} 1}\right)\right]}{\phi H f \times\left[w_{\mathrm{CO}_2} \gamma_{\mathrm{CO}_2}+\left(1-w_{\mathrm{CO}_2}\right) \gamma_{\mathrm{w}}\right]-\frac{\alpha S\left(t_{\mathrm{i}}+t_{\mathrm{o}}-t_{\mathrm{m} 1}-t_{\mathrm{m} 2}\right)}{2}} $ | (7) |
由式(7)可知,需先确定气体与烟丝间的对流传热系数α、传热面积S、膨胀后烟丝出口温度tm2、工艺气体出口温度to等物理量数值,才能得到w2的数学模型。
2.1 对流传热系数α及传热面积S 2.1.1 对流传热系数α设每天开始进料的时刻为0时刻,此时的对流传热系数记作初始对流传热系数α0,可用白丽青[18]和Lee等[19]总结的公式进行计算:
| $ \alpha_0=\frac{N u \cdot \lambda_{\mathrm{g}}}{d_{\mathrm{e}}}=\frac{\lambda_{\mathrm{g}}}{d_{\mathrm{e}}}\left(2+0.74 {Re}_{\mathrm{r}}^{1 / 2} {Pr}^{1 / 3}\right)$ | (8) |
式中:
| $ \rho_{\mathrm{g}}=y_{\mathrm{w}} \rho_{\mathrm{w}}+y_{\mathrm{a}} \rho_{\mathrm{a}} $ | (9) |
| $\mu_{\mathrm{g}}=\frac{y_{\mathrm{w}} \mu_{\mathrm{w}} M_{\mathrm{w}}^{1 / 2}+y_{\mathrm{a}} \mu_{\mathrm{a}} M_{\mathrm{a}}^{1 / 2}}{y_{\mathrm{w}} M_{\mathrm{w}}^{1 / 2}+y_{\mathrm{a}} M_{\mathrm{a}}^{1 / 2}} $ | (10) |
| $ \lambda_{\mathrm{g}}=\frac{y_{\mathrm{w}} \lambda_{\mathrm{w}} M_{\mathrm{w}}^{1 / 3}+y_{\mathrm{a}} \lambda_{\mathrm{a}} M_{\mathrm{a}}^{1 / 3}}{y_{\mathrm{w}} M_{\mathrm{w}}^{1 / 3}+y_{\mathrm{a}} M_{\mathrm{a}}^{1 / 3}} $ | (11) |
| $ c_{\mathrm{g}}=y_{\mathrm{w}} c_{\mathrm{w}}+y_{\mathrm{a}} c_{\mathrm{a}} $ | (12) |
Rer计算式中的烟丝颗粒的运动速度up可由烟丝单颗粒的自由沉降速度ut(式(13))按式(14)~(16)修正得到。
对于气流干燥,其雷诺数一般为1~500,属过渡流状态,故ut计算公式为[24]:
| $ u_{\mathrm{t}}=1.195 d_{\mathrm{p}}\left[\frac{\left(\rho_{\mathrm{p}}-\rho_{\mathrm{g}}\right)^2}{\rho_{\mathrm{g}} \mu_{\mathrm{g}}}\right]^{\frac{1}{3}} $ | (13) |
干冰烟丝膨胀过程属于烟丝颗粒群在工艺管道内的气力输送,直接使用式(13)估算up误差较大,因此需对其进行以下几方面修正。
(1) 竖直管内过渡流状态下,考虑到颗粒群对烟丝运动的影响,可将式(13)中的ut修正为式(14)中的u'p [24]:
| $ u_{\mathrm{p}}^{\prime}=\frac{1}{1.5}\left[1-\left(\frac{u_{\mathrm{t}}}{u_{\mathrm{g}}}\right)^{1.5}\right] \cdot u_{\mathrm{g}} $ | (14) |
(2) 考虑到管壁对烟丝的运动速度也会产生影响,可将式(14)中的up′修正为式(15)中的
| $ u_{\mathrm{p}}^{\prime \prime}=\left[1-\left(\frac{d_{\mathrm{e}}}{D}\right)^{1.5}\right] \cdot u_{\mathrm{p}}^{\prime} $ | (15) |
(3) 其他修正:烟丝为丝状柔性细长颗粒,在运动中会发生“结绳现象”[26],另外,被二氧化碳浸渍形成的干冰烟丝会发生部分结块,以上2个原因均会导致烟丝平均粒径增大。此外,烟丝颗粒在经过弯管时,会发生聚集并贴壁流动,壁面会对颗粒产生摩擦阻力,同时烟丝在弯管处撞击壁面导致其运动轨迹不再是直线,十分复杂[16]。以上各影响因素均会导致烟丝的实际运动速度降低,本研究将这些影响用1个小于1的修正系数θ表示,于是式(15)中的up″修正如下:
| $u_{\mathrm{p}}=\theta u_{\mathrm{p}}^{\prime \prime} $ | (16) |
由于干冰烟丝在膨胀过程中会产生碎丝[12],且旋风分离器无法完全分离粒径较小的碎丝颗粒,部分碎丝颗粒会随废气进入回风,所以在1天两个操作周期内,设备中的工艺气体里的碎丝颗粒含量会逐渐变大,而碎丝颗粒含量的增大又会增大颗粒群间的撞击频率,引起α增大[27]。所以本研究认为,在1天两个操作周期内,α是逐步增大的,可表示为:
| $ \alpha = {\alpha _0} + \sigma \tau $ | (17) |
式(17)中,烟丝颗粒停留时间τ=0时,α =α0,表示工艺气体中只有气相不含碎丝。联立式(8)~(17)可得:
| $ \alpha=\frac{\lambda_{\mathrm{g}}}{d_{\mathrm{e}}}\left\{2+0.74\left[\frac{d_{\mathrm{e}}\left(u_{\mathrm{g}}-u_{\mathrm{p}}\right) \rho_{\mathrm{g}}}{\mu_{\mathrm{g}}}\right]^{1 / 2} \cdot\left(\frac{c_{\mathrm{g}} \mu_{\mathrm{g}}}{\lambda_{\mathrm{g}}}\right)^{1 / 3}\right\}+\sigma \tau $ | (18) |
式中:up由式(13)~(16)整理得到,
S为塔内烟丝的总外表面积,等于烟丝颗粒数N乘以单个烟丝颗粒的外表面积Sp,计算式为:
| $ S=N \cdot S_{\mathrm{p}} $ | (19) |
式中:N可由烟丝的总质量(G1τ)除以入口处单个烟丝颗粒质量m0求取(见式(20)),Sp则按烟丝颗粒为片状来估算(见式(21))。
| $ N=\frac{G_1}{m_0} \cdot \tau=\frac{G_1}{\frac{1}{6} \mathtt{π} d_{\mathrm{e}}^3 \rho_{\mathrm{p}}} \cdot \tau $ | (20) |
| $S_{\mathrm{p}}=2\left(l_{\mathrm{p}} b+l_{\mathrm{p}} \delta+b \delta\right) $ | (21) |
烟丝颗粒在膨胀管中的流动可分为加速段和匀速段,由于加速段比匀速段要短得多,所以近似认为颗粒在膨胀塔内只做匀速运动,故式(18)、(20)中τ的表达式为:
| $ \tau=l / u_{\mathrm{p}} $ | (22) |
将式(4)、式(20)~(22)代入式(19)可得:
| $ S=\frac{12\left(l_{\mathrm{p}} b+l_{\mathrm{p}} \delta+b \delta\right) \cdot \phi H f}{\pi d_{\mathrm{e}}^3 \rho_{\mathrm{p}}} \cdot \frac{l}{u_{\mathrm{p}}} $ | (23) |
在实际生产中,tm2的监控十分困难,所以需要给出其计算式,以便估计其数值。以下计算假设:单个烟丝颗粒的几何尺寸很小,可近似认为颗粒内部温度分布均匀;烟丝中的干冰升华完全后才进行干燥;为简化计算,α采用不含碎丝时的α0。
(1) 对于干冰升华段:
| $ -\gamma_{\mathrm{CO}_2} \frac{\mathrm{d} m_{\mathrm{p}}}{\mathrm{d} \tau}=\alpha_0 S_{\mathrm{p}}\left(t_{\mathrm{g}}-t_{\mathrm{m} 1}\right) $ | (24) |
式(24)的初始条件为:τ=0时,
(2) 对于烟丝干燥过程:
| $\alpha_0 S_{\mathrm{p}}\left(t_{\mathrm{g}}-t\right)=-\gamma_{\mathrm{w}} \frac{\mathrm{d} m_{\mathrm{p}}}{\mathrm{d} \tau}+m_{\mathrm{p}} c_{\mathrm{m}} \frac{\mathrm{d} t}{\mathrm{d} \tau} $ | (25) |
由于烟丝干燥过程为恒速干燥,故dmp/dτ=k为定值,代入式(25)得:
| $ \alpha_0 S_{\mathrm{p}}\left(t_{\mathrm{g}}-t\right)=-k \gamma_{\mathrm{w}}+m_{\mathrm{p}} c_{\mathrm{m}} \frac{\mathrm{d} t}{\mathrm{~d} \tau} $ | (26) |
式(26)的定解条件为:τ=τ1时,mp=m0(1−wCO2),t=tm1。
从工程角度看,tg可取为工艺气体的出、入口温度的算术平均值:
| $ t_{\mathrm{g}}=\frac{\overline{t_{\mathrm{i}}}+\overline{t_{\mathrm{o}}}}{2} $ | (27) |
由以上微分方程组可得式(28),通过式(28)可求取烟丝出口温度tm2。
| $ \left\{\begin{array}{l} t=t_{\mathrm{m} 1} \quad\left(\tau \leqslant \tau_1\right) \\ t=t_{\mathrm{g}}-\frac{k \gamma_{\mathrm{w}}}{2 \alpha_0\left(l_{\mathrm{p}} b+l_{\mathrm{p}} \delta+b \delta\right)}+a\left[\frac{1}{6 k} \mathtt{π} d_{\mathrm{e}}^3 \rho_{\mathrm{p}}\left(1-w_{\mathrm{CO}_2}\right)-\tau\right]^{\frac{2 \alpha_0\left(l_{\mathrm{p}} b+l_{\mathrm{p}} \delta+b \delta\right)}{k c_{\mathrm{m}}}} \quad\left(\tau>\tau_1\right) \end{array}\right. $ | (28) |
式中:
回风温度可近似视为与to相同。根据整个系统的热量衡算可得:
| $ L_{\mathrm{i}} c_{\mathrm{g}} t_{\mathrm{i}}+L_{\text {leak }} c_{\mathrm{a}} t_{\infty}+\left(G_2 c_{\mathrm{m}}+M_{\mathrm{CO}_2} c_{\mathrm{d}}+W c_{\text {ice }}\right) t_{\mathrm{m} 1}=L_{\mathrm{o}} c_{\mathrm{g}} t_{\mathrm{o}}+G_2 c_{\mathrm{m}} t_{\mathrm{m} 2}+M \gamma_{\mathrm{CO}_2}+W \gamma_{\mathrm{w}}+Q_1 $ | (29) |
再由干燥过程总物料衡算式
| $ L_{\mathrm{o}}=L_{\mathrm{i}}+M_{\mathrm{CO}_2}+W+L_{\text {leak }} $ | (30) |
式中:Li=ρgugπD2/4,Lleak可由烟丝进口管道尺寸与壁内风速估算出来,正常工况下约为219 kg⋅h−1或0.0608 kg⋅s−1。为简化运算,式(29)的等号左侧的W和式(30)中的W按式(31)计算:
| $ W = {G_1}{w_1} - {G_2}{w_2} $ | (31) |
由热量衡算可知,式(29)中的膨胀塔管壁与环境之间的热损失Ql,与工艺气体与污垢层间的对流传热量、污垢层内的导热量、金属管壁内的导热量、保温层内的导热量、保温层外壁与环境之间的对流传热量均相等,于是得到总传热方程为:
| $ Q_1=K_{\mathrm{o}} \cdot \mathtt{π} D_2 l \cdot\left(t_{\mathrm{g}}-t_{\infty}\right) $ | (32) |
式中:Ko的表达式为
| $ K_{\mathrm{o}}=\frac{1}{\frac{1}{\alpha_{\text {in }}} \cdot \frac{D_2}{D}+R_{\text {si }} \cdot \frac{D_2}{D}+\frac{D_1-D}{\lambda_{\text {wall }}} \cdot \frac{D}{D_{\mathrm{m}}}+\frac{D_2-D_1}{\lambda_{\text {ins }}} \cdot \frac{D}{D_{\text {m }}}+\frac{1}{\alpha_{\text {out }}}} $ | (33) |
式中:管内工艺气体与污垢层间的对流传热系数αin可用齐德-泰特公式[28](式(34))计算、保温层外壁与环境之间的对流传热系数αout可用经验公式(式(35))计算[28]:
| $ \alpha_{\mathrm{in}}=\frac{\lambda_{\mathrm{g}}}{D} N u=\frac{\lambda_{\mathrm{g}}}{D} \cdot\left[0.027 {Re}_{\mathrm{g}}^{0.8} {Pr}^{1 / 3}\left(\frac{\mu_{\mathrm{g}}}{\mu_{\mathrm{w}}}\right)^{0.14}\right]$ | (34) |
| $ \alpha_{\text {out }}=9.8+0.052\left(t_{\text {out }}-t_{\infty}\right) $ | (35) |
式中:Reg=Dugρg/μg,(μ/μw)0.14=0.95。
联立式(24)~(35)可得到to表达式:
| $ t_{\mathrm{o}}=\frac{1}{B}\left[A t_{\mathrm{i}}+C-\frac{C+(A+B) t_{\mathrm{i}}-2 B t_{\infty}}{\frac{2 B}{\pi D_2 l}\left(\frac{1}{\alpha_{\text {in }}} \cdot \frac{D_2}{D}+R_{\mathrm{si}} \cdot \frac{D_2}{D}+\frac{D_1-D}{\lambda_{\mathrm{w}}} \cdot \frac{D}{D_{\mathrm{m}}}+\frac{D_2-D_1}{\lambda_{\text {ins }}} \cdot \frac{D}{D_{\mathrm{m}}}+\frac{1}{\alpha_{\text {out }}}\right)+1}\right]$ | (36) |
式中:
将式(18)、(23)、(28)、(36)代入式(7),可得到w2的最终数学模型,其中,θ和σ作为拟合参数需通过实验数据拟合得到。
3 模型参数的标定 3.1 DIET实验数学模型需要的设备结构参数、烟丝和工艺气体等物性参数以及膨胀烟丝实验的工艺条件列于表 1。
|
|
表 1 数学模型需要的设备结构参数、物性参数与工艺条件 Table 1 Structural parameters, physical properties and process conditions used in the mathematical model |
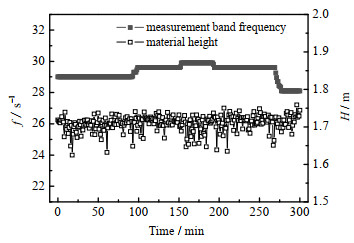
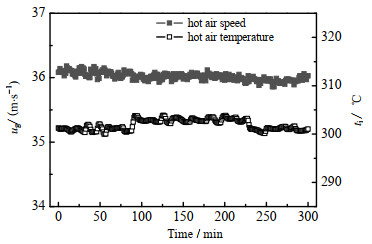
由表 1可见,工艺条件t∞、tout、Lleak、w1、wCO2、tm1均为定值,而DIET实验中属于操作控制的工艺条件f、H、ug、ti在1个操作周期(5 h即300 min)内的变化情况如图 2、3所示。由图 2可见,f为28~30 s−1、H为1.60~1.76 m;由图 3可见,ug为35.9~36.2 m⋅s−1、ti为300~305 ℃。生产过程中,每10 s取1组数据点;处理数据时,每6个点即1 min取1个均值,共监控300 min即300个数据点。
|
图 2 f与H随操作时间变化图 Fig.2 Profiles of f and H as a function of processing time |
|
图 3 ug与ti随操作时间变化图 Fig.3 Profiles of ug and ti as a function of processing time |
|
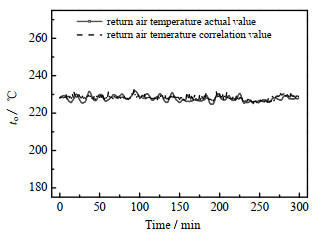
图 4 to的关联值和实际值 Fig.4 Comparison of correlation and experimental values of to |
|
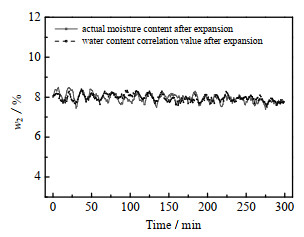
图 5 w2的关联值和实际值 Fig.5 Comparison of correlation and experimental values of w2 |
结合图 2、3及表 1中的参数与工艺条件,使用Matlab软件、调节拟合参数θ和σ,对实验数据进行拟合,求出过程目标函数F的最小值,即可得到最佳θ和σ。F表达式为:
| $ F=\frac{1}{N_{\mathrm{p}}} \sum\limits_{i=1}^{N_{\mathrm{p}}}\left\{\frac{\left[\left(\hat{w}_2\right)_i-\left(w_2\right)_i\right]^2}{\left(w_2\right)_i^2}+\frac{\left[\left(\hat{t}_{\mathrm{o}}\right)_i-\left(t_{\mathrm{o}}\right)_i\right]^2}{\left(t_{\mathrm{o}}\right)_i^2}\right\}$ | (37) |
最终拟合结果为:当θ为0.992 2、σ为1.833×10−7 kW⋅(m2⋅℃⋅s)−1时模型效果最好。
对实验中点(第150 min)的数据应用第2节得到的数学模型,计算得到
|
|
表 2 第150 min时实验值与关联值比较 Table 2 Comparison of experimental and correlation values at 150 min |
使用平均绝对误差(MAPE)来评估通过数学模型计算出的关联值
| $ \mathrm{MAPE}_{t_{\mathrm{o}}}=\frac{100 \%}{N_{\mathrm{p}}} \sum\limits_{i=1}^{N_{\mathrm{p}}} \frac{\left|\left(\hat{t}_{\mathrm{o}}\right)_i-\left(t_{\mathrm{o}}\right)_i\right|}{\left(t_{\mathrm{o}}\right)_i} $ | (38) |
| $ \mathrm{MAPE}_{w_2}=\frac{100 \%}{N_{\mathrm{p}}} \sum\limits_{i=1}^{N_{\mathrm{p}}} \frac{\left|\left(\hat{w}_2\right)_i-\left(w_2\right)_i\right|}{\left(w_2\right)_i} $ | (39) |
评估结果为:对于to,MAPE为0.24%,最大误差为0.83%;对于w2,MAPE为1.99%,最大误差为6.33%。可见,to和w2的拟合精度都较好,同时
本研究针对卷烟厂制丝车间DIET工艺,基于物料衡算和热量衡算,推导出了τ、f、ug、ti等操作条件与tm2、to、w2之间的数学模型。to和w2的MAPE分别为0.24% 和1.99%,表明模型关联值与实验值吻合良好,能较准确地估算干冰烟丝膨胀前、后的含水率变化值,对DIET工艺过程w2的控制具有较好的指导意义。
符号说明:
A — 式(36)中的指代量 to — 工艺气体出口或回风温度,℃
a — 式(28)中的指代量
B — 式(36)中的指代量
b — 烟丝颗粒宽度,m tout — 保温层外壁温度,℃
C — 式(36)中的指代量 ts — 饱和蒸气温度,℃
ca — 空气的比热容,kJ⋅kg−1⋅℃−1 t∞ — 环境空气温度,℃
cd — 干冰的比热容,kJ⋅kg−1⋅℃−1 ∆t — 气体与烟丝间的平均传热温差,℃
cg — 工艺气体的比热容,kJ⋅kg−1⋅℃−1 ug — 工艺气体风速,m⋅s−1
cice — 冰的比热容,kJ⋅kg−1⋅℃−1 up — 烟丝颗粒运动速度,m⋅s−1
cm — 不含干冰的烟丝比热容,kJ⋅kg−1⋅℃−1 up′ — 第一次修正后竖直管颗粒群的运动速度,m⋅s−1
cp — 干冰烟丝比热容,kJ⋅kg−1⋅℃−1 up″ — 第二次修正后竖直管颗粒群的运动速度,m⋅s−1
cw — 水蒸气比热容,kJ⋅kg−1⋅℃−1 ut — 烟丝颗粒自由沉降速度,m⋅s−1
D — 膨胀塔内径,m W — 烟丝干燥总水量,kg⋅s−1
D1 — 膨胀塔外径,m w1 — 入口处干冰烟丝含水率
D2 — 保温层外径,m
Dm — 膨胀塔平均直径,m w2 — 出口处膨胀后烟丝含水率
de — 烟丝颗粒的当量直径,m
dp — 颗粒直径,m
F — 目标函数 wCO2 — 入口处干冰烟丝湿基干冰含量,无因次
f — 计量带频率,s−1 ya — 工艺气体含空气率,无因次
G1 — 入口处干冰烟丝质量流量,kg⋅s−1 yw — 工艺气体含水率,无因次
G2 — 出口处膨胀后烟丝质量流量,kg⋅s−1 α — 气体与烟丝间的对流传热系数,kW⋅m−2⋅℃−1
Gc — 绝干烟丝质量流量,kg⋅s−1 α0 — 气、固两相间的初始对流传热系数,kW⋅m−2⋅℃−1
H — 计量带上的烟丝高度,m αin — 气体与内壁间的对流传热系数,kW⋅m−2⋅℃−1
Ko — 膨胀塔总传热系数,kW⋅m−2⋅℃−1 αout — 保温层与环境间的对流传热系数,kW⋅m−2⋅℃−1
k — 烟丝的质量变化率,kg⋅s−1 δ — 烟丝颗粒厚度,m
Li — 进风量,kg⋅s−1 ϕ — 计量带流量系数,kg⋅m−1
Lleak — 设备漏风量,kg⋅s−1 γCO2 — 干冰升华热,kJ⋅kg−1
Lo — 回风量,kg⋅s−1 γw — 水的相变热(包括融化与汽化),kJ⋅kg−1
Ls — 入口饱和蒸气流量,kg⋅s−1 λa — 空气的导热系数,kW⋅m−1⋅℃−1
l — 膨胀塔长度,m λg — 工艺气体的导热系数,kW⋅m−1⋅℃−1
lp — 烟丝颗粒长度,m λins — 保温层的导热系数,kW⋅m−1⋅℃−1
MAPE — 绝对百分比误差,无因次 λwall — 金属管壁的导热系数,kW⋅m−1⋅℃−1
Ma — 空气的摩尔质量,kg⋅mol−1 λw — 水蒸气的导热系数,kW⋅m−1⋅℃−1
MCO2 — 烟丝干冰升华量,kg⋅s−1 μa — 空气的黏度,Pa⋅s
Mw — 水的摩尔质量,kg⋅mol−1 μg — 工艺气体的黏度,Pa⋅s
mp — 单个烟丝颗粒质量,kg μw — 水蒸气的黏度,Pa⋅s
m0 — 入口处单个干冰烟丝颗粒质量,kg θ — 烟丝颗粒运动速度修正系数,无因次
N — 膨胀塔中烟丝的颗粒数,无因次 ρa — 空气密度,kg⋅m−3
NP — 数据总量,无因次 ρg — 工艺气体密度,kg⋅m−3
Nu — 努塞尔数,无因次 ρp — 烟丝密度,kg⋅m−3
n — 每秒进入膨胀塔的烟丝颗粒数,s−1 ρw — 水蒸气密度,kg⋅m−3
Pr — 普朗特数,无因次 σ — 对流传热系数变化速率,kW⋅m−2⋅℃−1⋅s−1
ps — 入口饱和蒸气压力,kPa τ — 烟丝颗粒停留时间,s
Ql — 过程热损失,kW τ1 — 干冰升华时间,s
Qt — 烟丝吸收的热量,kW 下标
Reg — 工艺气体的雷诺数,无因次 a — 空气
Rer — 烟丝颗粒的真实雷诺数,无因次 g — 工艺气体
Rsi — 内壁污垢热阻,m2⋅℃⋅kW−1 in — 塔壁内侧
S — 塔内烟丝的总外表面积即传热面积,m2 out — 保温层外侧
Sp — 单个烟丝颗粒的外表面积,m2 p — 烟丝颗粒
t — 烟丝温度,℃ s — 饱和蒸气
tg — 工艺气体平均温度,℃ w — 水蒸气
ti — 工艺气体入口温度,℃ d — 干冰
tm1 — 干冰烟丝进口温度,℃ ^ — 关联值
tm2 — 膨胀后烟丝出口温度,℃ — — 平均值
| [1] |
张美华, 黄岳元, 赵兴昌, 等. 二氧化碳膨化烟丝研究[J]. 西北大学学报, 1991, 21(1): 49-55. ZHANG M H, HUANG Y Y, ZHAO X C, et al. Research bulletin of expanding tobacco by carbon dioxide[J]. Journal of Northwest University, 1991, 21(1): 49-55. |
| [2] |
WHITHAM S. Recent advance in tobacco expansion[J]. Tobacco Reporter, 1970, 97(1): 31-35. |
| [3] |
THEOPHILUS E H, PENCE D H, MECKLEY D R, et al. Toxicological evaluation of expanded shredded tobacco stems[J]. Food and Chemical Toxicology, 2004, 42(4): 631-639. DOI:10.1016/j.fct.2003.11.008 |
| [4] |
GREEN C R, SCHUMACHER J N, RODGMAN A. The expansion of tobacco and its effect on cigarette mainstream smoke properties[J]. Beitrage zur Tabakforschung International, 2007, 22(5): 317-345. |
| [5] |
UTSCH F V, DE LA BURDE R Z, AUMENT P E. Carbon dioxide impregnation of tobacco by super cooling: US, 4 250 898A [P]. 1981-02-17.
|
| [6] |
DE LA BURDE R Z, AUMENT P E. Expanding tobacco: US, 4 340 073A [P]. 1985-07-20.
|
| [7] |
CHO K H, CLARKE T J, DOBBS J M, et al. Process and apparatus for impregnation and expansion of tobacco: US, 5 799 665A [P]. 1998-09-01.
|
| [8] |
ENZELL C R, DALHAMN T, JOHNSON W H. Chemical and ciliotoxic studies of smoke[J]. Beitrage zur Tabakforschung International, 1971, 6(1): 129-135. |
| [9] |
HALTER H M. Effect of tobacco reconstitution and expansion process on smoke composition[J]. Recent Advance of Tobacco Science, 1978, 32(4): 113-132. |
| [10] |
THEOPHILUS E H, POINDEXTER D B, MECKLEY D R, et al. Toxicological evaluation of dry ice expanded tobacco[J]. Toxicology Letters, 2003, 145(2): 107-119. DOI:10.1016/S0378-4274(03)00235-2 |
| [11] |
王志华, 李根宝. 液体二氧化碳膨胀烟草的改良工艺及装置: CN, 1 063 208A [P]. 1992-08-05. WANG Z H, LI G B. Improved technology and equipment for expanding tobacco with liquid carbon dioxide: CN, 1 063 208A [P]. 1992-08-05. |
| [12] |
姜建平. 二氧化碳膨胀升华管的改进设计[J]. 甘肃科技, 2010, 26(7): 14-16, 105. JIANG J P. Improved design of carbon dioxide expansion sublimation tube[J]. Gansu Science and Technology, 2010, 26(7): 14-16, 105. |
| [13] |
崇黎明, 芦渊, 蒋广. 膨胀工艺对烟丝质量的影响[J]. 食品与机械, 2020, 36(8): 195-200, 228. CHONG L M, LU Y, JIANG G. Effects expansion process on tobacco quality[J]. Food & Machinery, 2020, 36(8): 195-200, 228. |
| [14] |
资文华, 王慧, 番绍军, 等. 干冰膨胀烟丝加工过程参数优化研究[J]. 烟草科技, 2008(1): 8-11, 18. ZI W H, WANG H, FAN S J, et al. Optimization of parameters in CO2 expanded cut tobacco processing[J]. Tobacco Science & Technology, 2008(1): 8-11, 18. |
| [15] |
韩金民. 数值模拟在膨胀塔结构研究和优化设计中的应用[D]. 北京: 华北电力大学, 2008. HAN J M. The application of numerical simulation to structure research and optimize design of sublimator [D]. Beijing: North China Electric Power University, 2008. |
| [16] |
刘广文. 干燥设备设计手册[M]. 北京: 机械工业出版社, 2009. LIU G W. Drying equipment design manual[M]. Beijing: China Machine Press, 2009. |
| [17] |
张欣. 塔式烘丝机烟丝烘干特性的实验与仿真研究[D]. 湘潭: 湘潭大学, 2018. ZHANG X. Experimental and simulation research study on drying characteristics of comas tower dryer [D]. Xiangtan: Xiangtan University, 2018. |
| [18] |
白丽青. 用过热蒸汽干燥酒精糟的实验研究[D]. 郑州: 郑州大学, 2008. BAI L Q. Experimental research on drying the distiller's grain with superheated steam [D]. Zhengzhou: Zhengzhou University, 2008. |
| [19] |
LEE K, RYLEY D J. The evaporation of water droplets in superheated steam[J]. ASME Journal of Heat and Mass Transfer, 1968, 90(4): 445-451. |
| [20] |
湿气体的密度和体积的计算[J]. 建筑技术通讯(暖通空调), 1980(4): 15-21. MA G D. Calculation of density and volume of wet gas[J]. Heating Ventilating & Air Conditioning, 1980(4): 15-21. |
| [21] |
纯气体、混合气体及液体粘度的计算[J]. 化肥设计, 1997, 35(6): 9-13. TIAN L N. Viscosity calculation of pure gas, gas mixture and liquid[J]. Chemical Fertilizer Design, 1997, 35(6): 9-13. |
| [22] |
纯气体、混合气体及液体导热系数的计算[J]. 氮肥设计, 1996, 34(4): 19-22. TIAN L N. Calculation of thermal conductivity of pure gas, mixed gas and liquid[J]. Chemical Fertilizer Design, 1996, 34(4): 19-22. |
| [23] |
多组分气体热物性参数的计算方法[J]. 动力工程学报, 2010, 30(10): 772-776. CHANG Y Q, CAO Z D, ZHAO Z X, et al. Calculation method for thermal properties of multi-component gas[J]. Journal of Chinese Society of Power Engineering, 2010, 30(10): 772-776. |
| [24] |
杨伦, 谢一华. 气力输送工程[M]. 北京: 机械工业出版社, 2006. YANG L, XIE Y H. Pneumatic conveying engineering[M]. Beijing: China Machine Press, 2006. |
| [25] |
ANANTHARAMAN A, CAHYADI A, HADINOTO K, et al. Impact of particle diameter, density and sphericity on minimum pickup velocity of binary mixtures in gas-solid pneumatic conveying[J]. Powder Technology, 2016, 297: 311-319. |
| [26] |
李永祥, 杨文超, 邱晓峰. 膨胀塔结构改进及提高膨丝质量: 上海市烟草专卖局2007年度获奖论文集[C]. 上海: 上海市烟草学会, 2008. LI Y X, YANG W C, QIU X F. Structure improvement of expansion tower and improvement of expansion quality: Proceedings of the 2007 Annual Academic Conference of Shanghai Tobacco Society[C]. Shanghai: Shanghai Tobacco Society, 2008. |
| [27] |
气固两相流强化传热研究进展[J]. 化工学报, 2014, 65(7): 2485-2494. LIU C P, LI C, LI Y L, et al. Heat transfer enhancement in gas-solid flow[J]. CIESC Journal, 2014, 65(7): 2485-2494. |
| [28] |
何潮洪, 刘永忠, 窦梅, 等. 化工原理[M]. 3版. 北京: 科学出版社, 2017. HE C H, LIU Y Z, DOU M, et al. Principles of chemical engineering[M]. 3rd ed. Beijing: Science Press, 2017. |




