高分子材料是现代工业和高新技术的重要基石,已成为国民经济的重要基础性产业和国家战略性新型产业[1-2]。我国高分子材料的生产主要以低端材料为主,同发达国家相比,在高端材料的研发上仍有一定距离[3]。加强产品质量控制,实现技术独立自主是突破高端装备制造和战略新兴产业发展瓶颈的关键。
在体现高分子材料性能及质量差异的诸多因素中,微观质量指标具有关键作用——直接决定了聚合物产品的最终用途和特性[4-6]。聚合物的微观质量指标包括链长分布(chain length distribution,CLD)、相对分子质量分布(molecular weight distribution,MWD)、化学组成分布(chemical composition distribution,CCD)、序列分布(sequence length distribution,SLD)、支链分布(branching distribution)等[7-8]。获取聚合物在聚合反应过程中各个阶段的微观信息,提供分子层面的产品分析,有助于提高高分子材料的产率与性能。然而,准确并快速地预测出聚合物的微观质量指标是一大难点。通过实验手段得到聚合物的微观指标,所需时间较长[9];构建机理模型表征微观过程需要准确地描述出反应机理和速率,计算复杂性高。
计算聚合物微观质量指标主要分为确定性方法和统计性方法(也称随机性方法)[10-12]。求解基于物料守恒的平衡方程获得微观信息是典型的确定性方法[13-17]。该方法具有求解快,结果确定性高的特点,但难以应用于复杂聚合过程。蒙特卡洛(Monte Carlo)方法[18-21]隶属于统计性方法,无需大量的数学求解,往往是对具体聚合反应的直接模拟,模型化方法简单且易于理解。但是,蒙特卡洛方法的随机性要求样本数必须足够多,大大延长了模拟的时间[22]。根据蒙特卡洛模拟过程是否具有时间维度,又可分为稳态蒙特卡洛模拟和动态蒙特卡洛模拟。为快速预测聚合物微观信息,不同的蒙特卡洛模拟加速方法被相继提出。在此基础上,本文将对蒙特卡洛方法在聚合反应工程领域中的研究和应用进行综述及展望。
2 蒙特卡洛方法概述蒙特卡洛方法是一种数值计算方法,通过生成随机数,在所有可能发生的事件集合中根据概率选择下一个要发生的事件。随着实验数据量的增大,蒙特卡洛方法得到的结果也越精确,经典的蒲丰投针实验就是蒙特卡洛方法的一个典型问题[23]。蒙特卡洛方法已广泛应用于金融[24]、生物医学[25]、计算物理[26]、项目管理[27]、材料科学[28]、分子模拟[29]等诸多领域。随着计算机技术的高速发展,以蒙特卡洛方法为代表的概率模型的建立和求解变得更加高效快捷。
以求解圆周率π为例,简要说明蒙特卡洛方法的基本原理。如图 1所示,半径为1的圆位于边长为2的正方形中,向正方形内均匀随机地撒点,计算落在圆内点与所有点个数的比值并乘以4,便可得到π值,计算过程如图 2所示。撒的点越多,得到的π值越精确。蒙特卡洛方法计算圆周率的模拟次数与计算结果见表 1,计算得到的π值为10次不同实验下的平均值。从表 1可以看出,随着模拟量的增加,计算得到的π值更接近真实值。

|
图 1 蒙特卡洛方法计算圆周率 Fig.1 Calculation of PI via the Monte Carlo method |
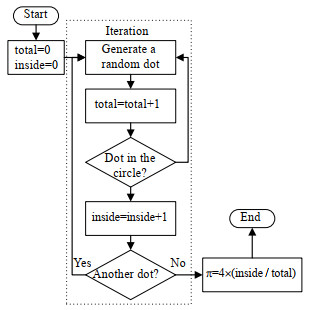
|
图 2 蒙特卡洛方法计算圆周率的流程示意图 Fig.2 Flow chart of calculation of PI via the Monte Carlo method |
|
|
表 1 蒙特卡洛方法计算圆周率:模拟次数与计算结果 Table 1 Calculation of PI via the Monte Carlo method: the number of simulated times and the corresponding calculated PI value |
与分子动力学结合,蒙特卡洛方法可以模拟聚合反应过程并获得聚合物的微观信息。在上述计算圆周率的例子中,若每落下一个点看作一个事件,那么在聚合反应过程的模拟中,每条反应的发生(如链引发反应、链增长反应、链终止反应等)可视为一个事件。蒙特卡洛方法模拟聚合反应过程的简要流程如图 3所示。在当前状态下生成随机数,根据各个事件在当前系统状态下的概率进行选择后更新系统。模拟不断迭代直至满足终止条件,最终获得聚合物的微观质量指标。结果准确度和模拟时间均与迭代次数正相关[30]。

|
图 3 蒙特卡洛方法模拟聚合反应过程 Fig.3 Monte Carlo simulation of polymerization process |
根据聚合反应系统状态是否随着时间改变而发生变化,聚合反应过程中的蒙特卡洛方法可分为稳态蒙特卡洛方法与动态蒙特卡洛方法[31]。
3.1 稳态蒙特卡洛方法稳态蒙特卡洛模型(steady-state Monte Carlo model)用于模拟计算聚合物微观质量指标时一般不具有反应时间维度信息,常应用于连续反应下的聚合物微观结构信息的计算[32]。
如表 2所示为三元聚合反应的化学反应机制,表中P0为活性位点;A、B、C为三元聚合中的3个不同类型的单体;Pl, 1、Pl, x、Pl, x+1 (l
|
|
表 2 三元聚合反应的化学反应机制 Table 2 Chemical mechanism of ternary polymerization |
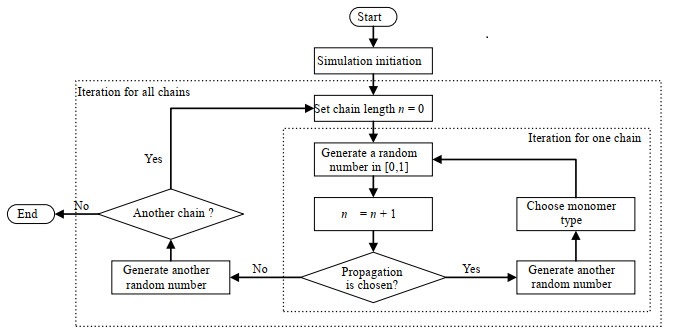
|
图 4 稳态蒙特卡洛方法模拟三元聚合反应的流程图 Fig.4 Flow chart for steady-state Monte Carlo simulation of ternary polymerization |
蒙特卡洛方法可以给出复杂聚合反应体系下的分子静态行为。Beigzadeh等[33]通过稳态蒙特卡洛方法模拟聚合物的长链支化并得到了聚乙烯树脂的支化结构。Simon等[34-35]研究了链行走机理下的乙烯聚合,并提出用稳态蒙特卡洛方法得到短支链分布结果。Tobita[36]通过蒙特卡洛方法计算得到加入交联和降解反应后的聚合物分子量分布。Alshaiban等[31]应用蒙特卡洛方法建立了一种丙烯聚合反应过程模型,描述了聚合物的MWD以及序列分布等。
3.2 动态蒙特卡洛方法当系统状态随着反应时间而改变时,动态蒙特卡洛(dynamic Monte Carlo, DMC)模型可以描述聚合反应过程的动态变化。区别于稳态蒙特卡洛方法,动态模拟具有反应时间维度信息,即除了要完成稳态模型中所必需的反应选择,还需要在每次事件选择后更新反应系统状态并重新计算各个反应事件的概率。DMC方法可以记录任意时刻下的反应系统状态,实时追踪反应过程中聚合物的结构特征,对于复杂反应的模拟和复杂微观质量指标的预测具有优势。对比DMC方法,基于物料守恒的平衡方程求解[37]和矩方法难以完整地表征出聚合物的微观细节信息[11, 38]。
DMC应用于聚合反应过程,需要进行宏观量到微观量的转换[39]:
| $ {k}_{\rm{Mic}}={k}_{\rm{Mac}}(反应为一级反应)$ | (1) |
| $ {k}_{\rm{Mic}}={k}_{\rm{Mac}}/(V\times {N}_{\rm{A}})(不同反应物种类下的二级反应)$ | (2) |
式中:
Gillespie[40]最早提出了应用于分子动力学中的随机模拟算法(stochastic simulation algorithm, SSA),该算法是DMC模拟化学反应过程的算法基础[41]。SSA关注2个问题:1)下一个反应何时发生,2)下一个发生的是哪一个反应。为了回答这2个问题,定义参数对(τ,μ),其中τ为反应时间步进;μ (
| $ \begin{array}{l}{a}_{\mu }\equiv 给定时间t下的系统状态({X}_{1}, \mathrm{...}, {X}_{N}), 在V中的时\\ 间间隔(t, t+{\rm{d}}t)内反应R{e}_{\mu }会发生的概率(\mu \rm{=}1, \mathrm{...}, M)\end{array}$ | (3) |
式中:
| $ \begin{array}{l}P(\tau , \mu )\equiv 给定时间t下的系统状态({X}_{1}, \mathrm{...}, {X}_{N}), 在V中无限小的\\ 时间间隔(t+\tau , t+\tau +\rm{d}\tau )内下一个发生的反应是R{e}_{\mu }的概率\end{array}$ | (4) |
最终可以得到
| $P(\tau , \mu ){\rm{ = }}{a_\mu }\exp {\rm{ }}( - {a_0}\tau )$ | (5) |
式中:a0为所有反应倾向函数之和,即
| ${a_0}{\rm{ = }}\sum\limits_{\mu = 1}^M {{a_\mu }} $ | (6) |
SSA通过每次模拟一个反应事件达到模拟聚合反应过程的目的,根据计算参数对(τ, μ)方法的不同,主要分为直接计算法(the direct method)、第一反应法(the first reaction method)以及下一反应法(the next reaction method)等。
直接计算法[40]通过在每一次迭代中单独生成两个[0, 1]间均匀分布的随机数rnd1和rnd2来计算系统时间步进τ以及下一个要发生的反应Reμ:
| $\tau = (1/{a_0}) \times \ln {\rm{ }}(1/{\rm{rn}}{{\rm{d}}_1})$ | (7) |
| $\sum\limits_{\gamma = 1}^{\mu - 1} {{a_\gamma }} < {\rm{rn}}{{\rm{d}}_2} \times {a_0} \leqslant \sum\limits_{\gamma = 1}^\mu {{a_\gamma }} $ | (8) |
式中:
(1) 系统初始化:输入反应系统的初始状态,将计数器counter和当前反应时间t置0,并设置随机数生成器种子;
(2) 计算倾向函数:计算当前系统状态下每条反应的倾向函数aμ, (μ=1, …, M)以及所有倾向函数之和a0;
(3) 计算时间步进并选择反应:生成[0, 1]间均匀分布的随机数rnd1和rnd2,根据式(7)和(8)计算系统时间步进τ以及选择反应Reμ;
(4) 更新系统状态:更新反应时间t(t=t+τ);更新计数器counter(counter=counter+1);根据所选反应,更新系统状态,即所选反应中反应物的个数相应减少,生成物的个数相应增加。
(5) 判断迭代结束:判断模拟是否结束;如果结束,退出,否则返回(2);
步骤(5)中的模拟结束条件可以是反应时间或转化率到达指定值。步骤(2)-步骤(3)-步骤(4)可认为是DMC在直接计算法下的一次模拟迭代。
Chung[42]将直接计算法用于研究自由基调聚反应过程,成功表征了调节聚合中聚合物的CLD指标。Al-Harthi等[43]通过直接计算法,建立了半间歇操作下的原子转移自由基聚合反应DMC模型,预测得到了梯度共聚物的平均链重、多分散性指数以及MWD、CLD等微观质量指标。Tongtummachat等[44]用直接计算法建立了与停留时间分布结合的DMC模型,模拟连续搅拌釜下的链穿梭聚合反应并得到了烯烃嵌段共聚物的微观结构。Agarwal等[45]结合直接计算法提出了一种蒙特卡洛集成方法,用于模拟单中心催化剂存在下的溶液共聚反应,成功描述了聚合物的流变和结晶行为。Wang等[46]通过建立基于动力学蒙特卡洛的通用计算框架来追踪梯度共聚物中的每个分子链,预测了共聚物的显性序列。He等[47]采用直接计算法对多功能引发剂存在下的超支化共聚物进行研究,模拟得到超支化共聚物的MWD、支化点比率和支化度。
如表 3所示为均聚反应的化学机制,表中,P0为活性位点;Mo为单体;Px和Px+1分别为链长为x和x+1的活链;Dx为链长x的死链。以该反应机制为例对直接计算法应用于聚合反应过程模拟做更具体地说明。其中的模拟参数值列于表 4,系统中的氢气浓度c(H2)和单体浓度c(Mo)为定值。此时倾向函数为各个反应的微观反应速率:
| ${R_{{\rm{Mic, i}}}} = {k_{{\rm{Mac, i}}}} \times c(Mo) \times {n_{{p^0}}}$ | (9) |
| ${R_{{\rm{Mic, p}}}} = {k_{{\rm{Mac, p}}}} \times c(Mo) \times {n_p}$ | (10) |
| ${R_{{\rm{Mic, t}}}} = {k_{{\rm{Mac, t}}}} \times c({{\rm{H}}_2}) \times {n_p}$ | (11) |
|
|
表 3 均聚反应的化学反应机制 Table 3 Chemical mechanism of homopolymerization |
|
|
表 4 均聚反应机制的初始参数值 Table 4 Initial parameter values of the homopolymerization mechanism |
式中:
时间步进为
| $\tau {\rm{ = }}\frac{1}{{{R_{{\rm{Mic, i}}}} + {R_{{\rm{Mic, p}}}} + {R_{{\rm{Mic, t}}}}}} \times \ln {\rm{ }}(\frac{1}{{{\rm{rn}}{{\rm{d}}_{\rm{1}}}}})$ | (12) |
对表 3中的反应机制设置不同的反应时间和反应体积,进行2次模拟,得到的聚合物CLD如图 5所示,其中图 5(a)表示反应时间为0.5 s,初始的P0数量为106的模拟结果,计算模拟所需时长约34 min;图 5(b)表示反应时间为30 min,初始的P0数量为104的模拟结果,计算模拟所需时长约17 h。DMC模拟耗时与反应时间正相关。模拟的分子数量越多,DMC方法得到的结果越精确,但计算模拟时间也相应延长。
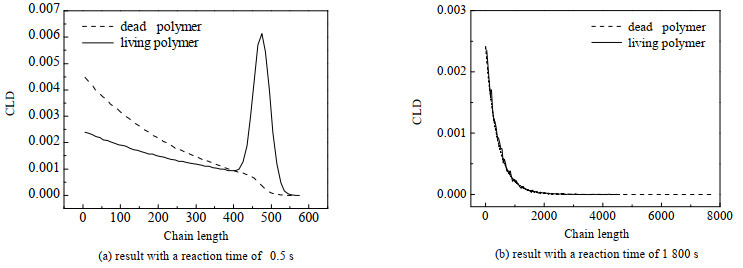
|
图 5 模拟均聚反应得到的分子链长分布结果 Fig.5 Simulation result of chain length distribution for the homopolymerization mechanism |
区别于直接计算法,第一反应法[48]在计算参数对(τ, μ)上有所不同。第一反应法通过生成与反应个数相同数量的[0, 1]间均匀分布的随机数来计算时间步进τ
| ${\tau _\mu }{\rm{ = }}\frac{1}{{{a_\mu }}} \times \ln {\rm{ }}(\frac{1}{{{\rm{rn}}{{\rm{d}}_\mu }}});{\rm{ }}\mu = 1, ..., M$ | (13) |
| $\tau {\rm{ = }}\min {\rm{ }}\{ {\tau _1}, ..., {\tau _M}\} $ | (14) |
其中具有最小τ值的反应Reμ为被选定的反应事件。第一反应法通过生成多个随机数来确定参数对(τ, μ)的值,其算法可描述如下:
(1) 系统初始化:确定反应系统的初始状态,将计数器counter和当前反应时间t置0,初始化随机数生成器;
(2) 计算倾向函数:计算每条反应的倾向函数aμ, (μ=1, …, M)以及所有倾向函数之和a0;
(3) 计算时间步进并选择反应:生成M个[0, 1]间均匀分布的随机数,计算τμ, (μ=1, …, M)。根据式(13)和(14)计算τ,并选择反应Reμ;
(4) 更新系统状态:更新反应时间t(t=t+τ);更新计数器counter(counter=counter+1);根据上步所选反应,更新系统状态;
(5) 判断迭代结束:判断模拟是否结束,如果结束,退出,否则返回(2)。
第一反应法与直接计算法得到的模拟结果一致,但由于第一反应法每步迭代中浪费(M-1)个随机数,模拟效率较低。在第一反应法的基础上,Gibson等[49]改进了数据处理策略并提出了下一反应法,在每一步的反应事件选择和系统状态更新中仅需要生成一个随机数,模拟效率明显提升。Rubenstein等[50]基于直接计算法和下一反应法获得了成核聚合反应过程(nucleated polymerization)中的聚合物动态特性。
值得注意的是,下一反应法在提高模拟效率的同时对计算机存储,尤其是CPU存储能力有较高要求。为进一步提高计算效率,Cao等[51]提出了优化直接法(optimized direct method);McCollum等[52]提出了分类直接法(sorting direct method)。将这一系列随机算法与聚合反应过程结合,模拟预测聚合物性质时,应针对具体的反应机制、反应参数以及应用需求等,权衡数据存储与数据计算时间,选择合适的方法用于反应模拟[53]。
4 蒙特卡洛模拟加速方法当模拟复杂系统时,每步迭代仅模拟一个反应事件的方法效率较低。即便很多学者提出了模拟效率高于直接计算法的改进SSA方法,但受限于“一步一个反应”,依旧无法完成快速的聚合反应过程模拟。蒙特卡洛模拟的计算时间和结果精度严格依赖于系统中的分子数以及发生的反应事件次数,Al-Harthi等[54]研究了动态蒙特卡洛方法模拟自由基聚合反应过程,并比较了不同反应体积下得到的MWD结果。当模拟体积过小时,MWD结果曲线有明显的锯齿状,随机波动严重;当模拟体积增加1 000倍后,得到的模拟结果精确的同时模拟时间增加17 308倍。很多学者提出了基于计算机算力提升和以牺牲结果精确度为代价换取模拟效率的加速方法,主要包括τ跳跃方法(τ-leaping method)及其改进算法、缩放方法(scaling method)、混合方法(hybrid method)、并行方法等。
4.1 τ跳跃方法传统的SSA在时间步进τ内,有且仅有一个反应发生。这种方法的优点在于可以完整地记录系统在时间维度上的所有状态信息,但大量依次发生的反应事件导致计算时间过长。考虑到时间维度上完整的系统状态信息并非完全必要,Gillespie[55]提出了τ跳跃方法,允许在时间间隔内发生一定数量的多个反应。如图 6所示,τ跳跃方法将时间维度划分为多个子时间间隔[t,t+τleap),计算在各个子时间间隔内反应事件的发生次数以及事件类型。在模拟过程中,τ跳跃方法只需确定这些子时间间隔内的系统状态变化,这种“一步多个反应”的方法,计算效率较高。
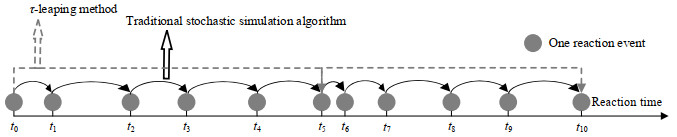
|
图 6 传统随机模拟算法与τ跳跃方法对比 Fig.6 Comparison between the traditional stochastic simulation algorithm and τ-leaping method |
对τ跳跃方法进行数学描述,首先定义概率函数Q:
| $ \begin{array}{l}Q({K}_{1}, \mathrm{...}, {K}_{2}, {K}_{M}|{\tau }_{l\rm{eap}};\boldsymbol{x}, t)\equiv 给定系统状态 \boldsymbol{X}(t)=\boldsymbol{x}, 在时间间\\ 隔[t, t+{\tau }_{\rm{leap}})内, 反应R{e}_{\mu }刚好发生了{K}_{\mu }次的概率(\mu =1, \mathrm{...}, M)\end{array}$ | (15) |
式中:K1, K2, …, KM分别为第1, 2, …, M个反应在时间间隔内的发生次数。对于(K1, K2, …, KM)这M个整数随机变量,定义:
| $ \begin{array}{l}{K}_{\mu }({\tau }_{\rm{leap}};\boldsymbol{x}, t)\equiv 给定系统状态 \boldsymbol{X}(t)=\boldsymbol{x}, 在时间间\\ 隔[t, t+{\tau }_{\rm{leap}})内, 反应R{e}_{\mu }发生的次数(\mu =1, \mathrm{...}, M)\end{array}$ | (16) |
为确定Q(K1, K2, …, KM |τleap; x, t)中的τleap值,反应系统需要满足跳跃条件(leap condition):τleap (τleap > 0)值不能让时间间隔[t, t+τleap)内倾向函数aμ(x)的变化过于明显。当满足跳跃条件后,式(16)可表示为
| ${K_\mu }({\tau _{{\rm{leap}}}};\boldsymbol{x}, t) = \mathcal{P}({a_\mu }(\boldsymbol{x}), {\tau _{{\rm{leap}}}})$ | (17) |
式中:
| $ \boldsymbol{\lambda} {\rm{ = }}\sum\limits_{\mu = 1}^M {{K_\mu }{\nu _{\mu i}}} $ | (18) |
式中:
总结τ跳跃方法的算法过程:选择满足跳跃条件的τleap (τleap > 0)值后,通过泊松随机变量
τleap值的确定对τ跳跃方法的发展起到关键作用,而以往靠经验选择的τleap值无法高效模拟反应过程并得到系统状态及分子微观结构。Gillespie等[56]对τ跳跃方法进行扩展,提出τleap值的选择策略。此外,由于各个反应在反应系统中的发生频率可能会有很大的差别,出现频率少的反应在τ跳跃方法中很难被采样到,从而导致最终结果发生偏差,这类偏差问题称为“系统刚性问题”。Rathinam等[57]针对τ跳跃方法导致的系统刚性问题提出了隐性τleap值计算方法。Cao等[58-59]在已有工作的基础上对泊松τ跳跃方法中的负值问题进行修正,并提出了最大τleap值的选择方法以加速模拟。Brand?o等[41]分别用直接计算法和τ跳跃方法模拟伴随长支链形成的共聚反应过程,同样的反应时间和系统体积下,τ跳跃方法的计算效率明显高于直接计算法。
4.2 缩放方法(scaling method)将蒙特卡洛方法应用于模拟聚合反应过程并计算聚合物的分子量分布、记录各个分子链的单体序列等微观结构信息时,为了能准确地表征出反应过程,至少需要一定数量的分子数。缩放方法可以有效缩放模拟的分子数量和反应速率常数,从而减少模拟耗时。Gao等[60]推导了共聚反应的显性表达式计算模拟所需的分子数下限以及缩放因数,通过对丙烯酸酯共聚机制进行模拟得到了聚合物的MWD以及序列分布,模拟效率提升明显。Lin等[61]提出了部分缩放法(partial scaling),可以对反应系统进行动态缩放:考虑系统中的每一个单独反应,若放缩尺度小于提前设置的阈值,则对系统进行缩放。该方法为每一个反应计算出各自的缩放因数,对“刚性系统”的模拟准确率和效率提升明显。
4.3 并行策略近几年来计算集群、工作站的搭建,给并行算法提供了算力支持。将并行策略应用于蒙特卡洛方法,为加速预测聚合物微观质量指标提供了新思路。蒙特卡洛方法应用于聚合反应过程,模拟结果依赖于系统分子量。并行计算策略通过将各个模拟或迭代任务分布在不同的计算节点上,实现了加速模拟。Chaffey-Millar等[62]通过分布式策略以及CPU多核多线程并行策略,将计算数据分配到不同的计算机节点上并行处理,加速了聚合物微观质量指标的模拟。Li等[63]提出了一种离散随机模拟算法来预测无法通过确定性算法获取到的分子动态行为,并结合基于图像处理单元(graphics processing unit platform,GPU)的并行策略,得到了较好的加速效果。Weng等[64]在GPU上进行多核并行编程,完成了稳态蒙特卡洛预测共聚物微观质量指标的加速。该方法结合GPU的高性能并行运算,将每条分子链的模拟任务分配到不同的GPU线程中,实现了和GPU核数相同数量级的大规模并行,准确得到了聚合物微观信息的同时,模拟加速效果明显。Ma等[65]结合GPU并行技术和蒙特卡洛方法预测了聚合物的CCD,并提出由自适应模拟算法与连续边界收缩算法组成的内嵌蒙特卡洛模型的系统化优化方法,该方法加快了优化过程中的模拟计算。此外,Lemarchand等[66]将并行算法与分子动力学结合,对生成的长聚合物链进行模拟;De Buyl等[67]将并行算法应用于逐步聚合反应过程与链增长聚合反应过程的模拟;Zhang等[68]建立了一个并行多尺度模拟框架,克服了传统方法模拟慢的问题,并成功应用于具有超支化的复杂聚合反应;Liu等[69]结合不同的聚合反应机制和硬件架构,提出了基于不同硬件平台的动态蒙特卡洛模拟加速算法。
4.4 混合方法(hybrid method)混合方法结合了确定性模型和统计性模型的优点,通过确定性方法求解聚合物基本信息,再结合蒙特卡洛方法模拟得到具体的聚合物微观性质。混合方法在获得聚合物微观质量指标的同时模拟量大大减少。Schuette等[70]提出了混合伽辽金-蒙特卡洛算法(hybrid Galerkin-Monte Carlo method),将伽辽金法确定性求解和蒙特卡洛统计性方法同时应用于模拟计算分子链长分布;He等[71]用混合方法模拟了活性自由基聚合中的CLD,在交换反应平衡的假设下,用解析表达表征活化及失活交换反应,用蒙特卡洛方法模拟链增长反应和不可逆的链终止反应。Tripathi等[72]提出了一种应用在自由基聚合反应中的高效率混合算法,明显缩短了聚合物微观结构信息的计算时间,同时还能保证结果的准确性与完整性。在该方法中,原来在动态蒙特卡洛方法中占据大量模拟时间的链增长反应由微分方程处理,而对于链终止反应和链引发反应则使用统计性方法处理。Ozcam等[73]在已有研究的基础上,提出了新的混合方法——逐链蒙特卡洛方法(chain-by-chain Monte Carlo method),先用矩方法获得聚合物的整体信息,再将其与蒙特卡洛方法结合,得到分子链的细节信息。
5 结论以蒙特卡洛方法为代表的统计性模型(随机性模型)具有建模简单、适用于复杂聚合反应过程模拟等优点,在化学工程以及高分子领域的应用愈发广泛。针对聚合物微观质量指标的预测,蒙特卡洛方法可以在时间及空间维度下得到聚合物分子内和分子间完整的微观结构信息,对高端高分子材料产品的生产及质量提升有着深刻影响。
蒙特卡洛方法应用在以产品结构优化为技术导向的高端材料研究领域意义重大,聚合反应过程中的蒙特卡洛方法在精细化建模、基于统计性模型的加速优化、模拟过程中的数据存储优化、复杂聚合反应过程模拟、多样性微观质量指标的预测等方向有很大的探索空间。另外,随着机器学习的快速发展,蒙特卡洛方法还有望与强化学习、深度学习等技术整合,优化生产流程以及聚合产品性能。
| [1] |
乔金樑. 我国高分子材料产业转型发展的思考[J]. 石油化工, 2015, 44(9): 1033-1037. QIAO J L. Further development of polymer industry in china[J]. Petrochemical Technology, 2015, 44(9): 1033-1037. DOI:10.3969/j.issn.1000-8144.2015.09.001 |
| [2] |
崔毅杰, 宋盛菊, 屈小中, 等. 中国制造2025视野下高分子材料产业发展的再思考与展望[J]. 工程研究-跨学科视野中的工程, 2017, 9(6): 568-576. CUI Y J, SONG S J, QU X Z, et al. Rethinking and outlook on the development of polymeric materials industry under the view of "made in China 2025"[J]. Journal of Engineering Studies, 2017, 9(6): 568-576. |
| [3] |
王瑜鑫. 我国高分子材料产业发展现状与前景——以塑料橡胶为例[J]. 环渤海经济瞭望, 2018, 286(7): 68-68. WANG Y X. The development status and prospects of polymer materials industry in China——taking plastics and rubber as an example[J]. Economic Outlook the Bohai Sea, 2018, 286(7): 68-68. |
| [4] |
张晨. 基于分子量分布的聚合过程建模、优化与流程重构[D]. 杭州: 浙江大学, 2016. ZHANG C. Modeling, optimization, and flowsheet reconfiguration of polymerization process with embedded molecular weight distribution[D]. Hangzhou: Zhejiang University, 2016 |
| [5] |
翁金祖. 基于微观质量指标的聚合过程模拟与优化方法研究[D]. 杭州: 浙江大学, 2016. WENG J Z. Microstructure-based simulation and optimization methods for polymerization processes[D]. Hangzhou: Zhejiang University, 2016 |
| [6] |
马彦楠. 面向微观结构质量优化的模型重构与求解加速方法研究[D]. 杭州: 浙江大学, 2019. MA Y N. Model reconstruction and optimization acceleration with microstructural quality indices[D]. Hangzhou: Zhejiang University, 2019. |
| [7] |
RIAHINEZHAD M, MCMANUS N, PENLIDIS A. Effect of monomer concentration and pH on reaction kinetics and copolymer microstructure of acrylamide/acrylic acid copolymer[J]. Macromolecular Reaction Engineering, 2015, 9(2): 100-113. DOI:10.1002/mren.201400053 |
| [8] |
LUTZ J F, JAHED N, MATYJASZEWSKI K. Preparation and characterization of graft terpolymers with controlled molecular structure[J]. Journal of Polymer Science Part A-Polymer Chemistry, 2004, 42(8): 1939-1952. DOI:10.1002/pola.20043 |
| [9] |
SHAN C, SOARES J, PENLIDIS A. Ethylene/1-octene copolymerization studies with in situ supported metallocene catalysts: Effect of polymerization parameters on the catalyst activity and polymer microstructure[J]. Journal of Polymer Science Part A-Polymer Chemistry, 2002, 40(24): 4426-4451. DOI:10.1002/pola.10533 |
| [10] |
童伟达, 陆建明, 孙猛, 等. 自由基聚合反应的Monte Carlo模拟方法[J]. 高等学校化学学报, 1991, 12(7): 979-982. TONG W D, LU J M, SUN M, et al. Monte Carlo simulation method of radical polymerization[J]. Chemical Journal of Chinese University, 1991, 12(7): 979-982. DOI:10.3321/j.issn:0251-0790.1991.07.024 |
| [11] |
MASTAN E, ZHU S. Method of moments: A versatile tool for deterministic modeling of polymerization kinetics[J]. European Polymer Journal, 2015, 68: 139-160. DOI:10.1016/j.eurpolymj.2015.04.018 |
| [12] |
CHEN X, SHAO Z, GU X, et al. Process intensification of polymerization processes with embedded molecular weight distributions models: An advanced optimization approach[J]. Industrial & Engineering Chemistry Research, 2019, 58(15SI): 6133-6145. |
| [13] |
ZHANG C, SHAO Z, CHEN X, et al. Simulation and optimization of polymer molecular weight distribution with nonideal reactors[J]. Computers & Chemical Engineering, 2017, 106: 744-757. |
| [14] |
KANG J, SHAO Z, CHEN X, et al. Fast and reliable computational strategy for developing a rigorous model-driven soft sensor of dynamic molecular weight distribution[J]. Journal of Process Control, 2017, 56: 79-99. DOI:10.1016/j.jprocont.2017.05.006 |
| [15] |
ZHANG C, SHAO Z, CHEN X, et al. Optimal flowsheet configuration of a polymerization process with embedded molecular weight distributions[J]. AIChE Journal, 2016, 62(1): 131-145. DOI:10.1002/aic.15040 |
| [16] |
WENG J, CHEN X, BIEGLER L T. A multi-thread parallel computation method for dynamic simulation of molecular weight distribution of multisite polymerization[J]. Computers & Chemical Engineering, 2015, 82(2): 55-67. |
| [17] |
ZHANG C, SHAO Z, CHEN X, et al. Kinetic parameter estimation of HDPE slurry process from molecular weight distribution: estimability analysis and multistep methodology[J]. AIChE Journal, 2014, 60(10): 3442-3459. DOI:10.1002/aic.14527 |
| [18] |
陆建明, 孙猛, 杨玉良. 不等活性缩聚反应动力学及其分子量分布Monte Carlo模拟[J]. 高分子学报, 1994, 1(5): 565-572. LU J M, SUN M, YANG Y L. Monte Carlo studies on the condensation polymerization of unequal functional group reactivity[J]. Acta Polymerica Sinica, 1994, 1(5): 565-572. |
| [19] |
杨玉良, 张红东. 高分子科学中的Monte Carlo方法[M]. 上海: 复旦大学出版社, 1993. YANG Y L, ZHANG H D. Monte Carlo method in polymer science[M]. Shanghai: Fudan University Press, 1993. |
| [20] |
LYU J, GAO Y, ZHANG Z, et al. Monte Carlo simulations of atom transfer radical (homo)polymerization of divinyl monomers: applicability of Flory-Stockmayer theory[J]. Macromolecules, 2018, 51(17): 6673-6681. DOI:10.1021/acs.macromol.8b01630 |
| [21] |
ZHAO Y R, MCAULEY K B, IEDEMA P D, et al. Advanced Monte Carlo modeling using weight-based selection of arborescent polyisobutylene molecules in a batch reactor[J]. Macromolecular Theory and Simulations, 2016, 25(2): 134-154. DOI:10.1002/mats.201500059 |
| [22] |
张胜, 骆德莘, 杨玉良, 等. 三元共聚反应序列分布的Monte Carlo模拟[J]. 功能高分子学报, 1993, 6(1): 41-45. ZHANG S, LUO D X, YANG Y L. Monte Carlo simulation of sequence distribution of terpolymerization[J]. Functional Polymer, 1993, 6(1): 41-45. |
| [23] |
黄朝霞. 蒲丰投针问题研究[J]. 集美大学学报(自然科学版), 2005, 10(4): 381-384. HUANG Z X. Study on Buffon throwing-pin problem[J]. Journal of Jimei University (Natural Science), 2005, 10(4): 381-384. DOI:10.3969/j.issn.1007-7405.2005.04.021 |
| [24] |
AVRAMIDIS A N, L'ECUYER P. Efficient Monte Carlo and quasi-Monte Carlo option pricing under the variance gamma model[J]. Management Science, 2006, 52(12): 1930-1944. DOI:10.1287/mnsc.1060.0575 |
| [25] |
WANG L H, JACQUES S L, ZHENG L Q. MCML-Monte-Carlo modeling of light transport in multilayered tissues[J]. Computer Methods and Programs in Biomedicine, 1995, 47(2): 131-146. DOI:10.1016/0169-2607(95)01640-F |
| [26] |
司瑞芳, 杜永清. 蒙特卡洛方法在高能核物理研究中的一些应用[J]. 太原师范学院学报(自然科学版), 2010, 9(2): 84-86. SI R F, DU Y Q. Some applications of Monte Carlo method in investigations of high energy nuclear physics[J]. Journal of Taiyuan Normal University (Natural Science Edition), 2010, 9(2): 84-86. DOI:10.3969/j.issn.1672-2027.2010.02.024 |
| [27] |
VAN DORP J R, DUFFEY M R. Statistical dependence in risk analysis for project networks using Monte Carlo methods[J]. International Journal of Production Economics, 1999, 58(1): 17-29. DOI:10.1016/S0925-5273(98)00081-4 |
| [28] |
SERGEI P, KRUZ K, YOUSRA N, et al. Large scale hybrid Monte Carlo simulations for structure and property prediction[J]. NPJ Computational Materials, 2018, 4: 80. DOI:10.1038/s41524-018-0137-0 |
| [29] |
MEIMAROGLOU D, KIPARISSIDES C. Review of Monte Carlo methods for the prediction of distributed molecular and morphological polymer properties[J]. Industrial & Engineering Chemistry Research, 2014, 53(22): 8963-8979. |
| [30] |
REGO A S C, BRANDAO A L T. General method for Speeding up kinetic Monte Carlo simulations[J]. Industrial & Engineering Chemistry Research, 2020, 59(19): 9034-9042. |
| [31] |
ALSHAIBAN A, SOARES J B P. Mathematical modeling of the microstructure of poly(propylene) made with Ziegler-Natta catalysts in the presence of electron donors[J]. Macromolecular Reaction Engineering, 2011, 5(2): 96-116. DOI:10.1002/mren.201000036 |
| [32] |
BRANDÃO A L T, SOARES J B P, PINTO J C, et al. When polymer reaction engineers play dice: Applications of Monte Carlo models in PRE[J]. Macromolecular Reaction Engineering, 2015, 9(3): 141-185. DOI:10.1002/mren.201500020 |
| [33] |
BEIGZADEH D, SOARES J B P, DUEVER T A, et al. Analysis of branching structure in polyethylene resins synthesized with constrained-geometry catalyst systems, using monte carlo simulation[J]. Polymer Reaction Engineering, 1999, 7(2): 195-205. DOI:10.1080/10543414.1999.10744507 |
| [34] |
SIMON L C, SOARES J, DE SOUZA R F. Monte-Carlo simulation of branching distribution in Ni-diimine catalyzed polyethylene[J]. AIChE Journal, 2000, 46(6): 1234-1240. DOI:10.1002/aic.690460615 |
| [35] |
SIMON L C, WILLIAMS C P, SOARES J, et al. Effect of polymerization temperature and pressure on the microstructure of Ni-diimine-catalyzed polyethylene: parameter identification for Monte-Carlo simulation[J]. Chemical Engineering Science, 2001, 56(13): 4181-4190. DOI:10.1016/S0009-2509(01)00086-0 |
| [36] |
TOBITA H. Simulation model for the modification of polymers via crosslinking and degradation[J]. Polymer (Guilford), 1995, 36(13): 2585-2596. DOI:10.1016/0032-3861(95)91205-L |
| [37] |
RIVERO P, HERRERA R. Modeling the kinetics of anionic polymerization in cyclohexane as a non-complexing solvent[J]. Journal of Polymer Research, 2011, 18(4): 519-526. DOI:10.1007/s10965-010-9444-y |
| [38] |
AL-HARTHI M, SOARES J B P, SIMON L C. Dynamic Monte Carlo simulation of ATRP with bifunctional initiators[J]. Macromolecular Reaction Engineering, 2007, 1(1): 95-105. DOI:10.1002/mren.200600004 |
| [39] |
HE J, ZHANG H, YANG Y. Monte Carlo simulation of chain length distribution in radical polymerization with transfer reaction[J]. Macromolecular Theory and Simulations, 1995, 4(4): 811-819. DOI:10.1002/mats.1995.040040414 |
| [40] |
GILLESPIE D T. Exact stochastic simulation of coupled chemical-reactions[J]. Journal of Physical Chemistry, 1977, 81(25): 2340-2361. DOI:10.1021/j100540a008 |
| [41] |
BRANDÃO A L T, SOARES J B P, PINTO J C, et al. Comparison of different dynamic Monte Carlo methods for the simulation of olefin polymerization[J]. Macromolecular Symposia, 2016, 360(1): 160-178. DOI:10.1002/masy.201500111 |
| [42] |
CHUNG I. Monte Carlo simulation of free radical telomerization[J]. Polymer, 2000, 41(15): 5643-5651. DOI:10.1016/S0032-3861(99)00772-7 |
| [43] |
AL-HARTHI M, KHAN M J, ABBASI S H, et al. Gradient copolymers by ATRP in semibatch reactors: Dynamic Monte Carlo simulation[J]. Macromolecular Reaction Engineering, 2009, 3(4): 148-159. DOI:10.1002/mren.200800055 |
| [44] |
TONGTUMMACHAT T, ANANTAWARASKUL S, SOARES J B P. Dynamic Monte Carlo Simulation of olefin block copolymers (OBCs) produced via chain-shuttling polymerization: Effect of kinetic rate constants on chain microstructure[J]. Macromolecular Reaction Engineering, 2018, 12(4): 1800021. DOI:10.1002/mren.201800021 |
| [45] |
AGARWAL U, DEN DOELDER J. Integrated kinetic Monte Carlo-structure-rheology model for solution copolymerization of ethylene and α-olefins[J]. Macromolecules, 2018, 52(1): 292-310. |
| [46] |
WANG L, BROADBELT L J. Explicit sequence of styrene/methyl methacrylate gradient copolymers synthesized by forced gradient copolymerization with nitroxide-mediated controlled radical polymerization[J]. Macromolecules, 2009, 42(20): 7961-7968. DOI:10.1021/ma901298h |
| [47] |
HE X, LIANG H, PAN C. Monte Carlo simulation of hyperbranched copolymerizations in the presence of a multifunctional initiator[J]. Macromolecular Theory and Simulations, 2001, 10(3): 196-203. DOI:10.1002/1521-3919(20010301)10:3<196::AID-MATS196>3.0.CO;2-J |
| [48] |
GILLESPIE D T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions[J]. Journal of Computational Physics, 1976, 22(4): 403-434. DOI:10.1016/0021-9991(76)90041-3 |
| [49] |
GIBSON M A, BRUCK J. Efficient exact stochastic simulation of chemical systems with many species and many channels[J]. The Journal of Physical Chemistry A, 2000, 104(9): 1876-1889. DOI:10.1021/jp993732q |
| [50] |
RUBENSTEIN R, GRAY P C, CLELAND T J, et al. Dynamics of the nucleated polymerization model of prion replication[J]. Biophysical Chemistry, 2007, 125(2/3): 360-367. |
| [51] |
CAO Y, LI H, PETZOLD L. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems[J]. Journal of Chemical Physics, 2004, 121(9): 4059-4067. DOI:10.1063/1.1778376 |
| [52] |
MCCOLLUM J M, PETERSON G D, COX C D, et al. The sorting direct method for stochastic simulation of biochemical systems with varying reaction execution behavior[J]. Computational Biology and Chemistry, 2006, 30(1): 39-49. DOI:10.1016/j.compbiolchem.2005.10.007 |
| [53] |
LECCA P. Stochastic chemical kinetics: A review of the modelling and simulation approaches[J]. Biophysical Reviews, 2013, 5(4): 323-345. DOI:10.1007/s12551-013-0122-2 |
| [54] |
AL-HARTHI M, SOARES J B P, SIMON L C. Dynamic Monte Carlo simulation of atom-transfer radical polymerization[J]. Macromolecular Materials and Engineering, 2006, 291(8): 993-1003. DOI:10.1002/mame.200600155 |
| [55] |
GILLESPIE D T. Approximate accelerated stochastic simulation of chemically reacting systems[J]. Journal of Chemical Physics, 2001, 115(4): 1716-1733. DOI:10.1063/1.1378322 |
| [56] |
GILLESPIE D T, PETZOLD L R. Improved leap-size selection for accelerated stochastic simulation[J]. Journal of Chemical Physics, 2003, 119(16): 8229-8234. DOI:10.1063/1.1613254 |
| [57] |
RATHINAM M, PETZOLD L R, CAO Y, et al. Stiffness in stochastic chemically reacting systems: The implicit tau-leaping method[J]. Journal of Chemical Physics, 2003, 119(24): 12784-12794. DOI:10.1063/1.1627296 |
| [58] |
CAO Y, GILLESPIE D T, PETZOLD L R. Avoiding negative populations in explicit Poisson tau-leaping[J]. Journal of Chemical Physics, 2005, 123(5): 54104. DOI:10.1063/1.1992473 |
| [59] |
CAO Y, GILLESPIE D T, PETZOLD L R. Efficient step size selection for the tau-leaping simulation method[J]. Journal of Chemical Physics, 2006, 124(4): 044109.1-044109.11. |
| [60] |
GAO H, OAKLEY L H, KONSTANTINOV I A, et al. Acceleration of kinetic Monte Carlo method for the simulation of free radical copolymerization through scaling[J]. Industrial & Engineering Chemistry Research, 2015, 54(48): 11975-11985. |
| [61] |
LIN Y T, FENG S, HLAVACEK W S. Scaling methods for accelerating kinetic Monte Carlo simulations of chemical reaction networks[J]. Journal of Chemical Physics, 2019, 150(24): 244101.1-244101.17. |
| [62] |
CHAFFEY-MILLAR H, STEWART D, CHAKRAVARTY M M T, et al. A parallelised high performance Monte Carlo simulation approach for complex polymerisation kinetics[J]. Macromolecular Theory and Simulations, 2007, 16(6): 575-592. DOI:10.1002/mats.200700028 |
| [63] |
LI H, PETZOLD L. Efficient parallelization of the stochastic simulation algorithm for chemically reacting systems on the graphics processing unit[J]. International Journal of High Performance Computing Applications, 2010, 24(2): 107-116. DOI:10.1177/1094342009106066 |
| [64] |
WENG J, CHEN X, YAO Z, et al. Parallel Monte Carlo simulation of molecular weight distribution and chemical composition distribution for copolymerization on a graphics processing unit platform[J]. Macromolecular Theory and Simulations, 2015, 24(5): 521-536. DOI:10.1002/mats.201500021 |
| [65] |
MA Y, CHEN X, BIEGLER L T. Monte-Carlo-simulation-based optimization for copolymerization processes with embedded chemical composition distribution[J]. Computers & Chemical Engineering, 2018, 109: 261-275. |
| [66] |
LEMARCHAND C A, BOUSQUET D, SCHNELL B, et al. A parallel algorithm to produce long polymer chains in molecular dynamics[J]. Journal of Chemical Physics, 2019, 150(22): 224902.1-224902.16. |
| [67] |
DE BUYL P, NIES E. A parallel algorithm for step- and chain-growth polymerization in molecular dynamics[J]. Journal of Chemical Physics, 2015, 142(13): 134102. DOI:10.1063/1.4916313 |
| [68] |
ZHANG Z, KRAJNIAK J, SAMAEY G, et al. A parallel multiscale simulation framework for complex polymerization: ab2-type monomer hyperbranched polymerization as an example[J]. Advanced Theory and Simulations, 2018, 2(2): 1800102. |
| [69] |
LIU R, ARMAOU A, CHEN X. Adaptable parallel acceleration strategy for dynamic Monte Carlo simulations of polymerization with microscopic resolution[J]. Industrial & Engineering Chemistry Research, 2021, 60(17): 6173-6187. |
| [70] |
SCHUETTE C, WULKOW M. A hybrid Galerkin-Monte-Carlo approach to higher-dimensional population balances in polymerization kinetics[J]. Macromolecular Reaction Engineering, 2010, 4(9/10): 562-577. |
| [71] |
HE J P, ZHANG H D, CHEN J M, et al. Monte Carlo simulation of kinetics and chain length distributions in living free-radical polymerization[J]. Macromolecules, 1997, 30(25): 8010-8018. DOI:10.1021/ma9614858 |
| [72] |
TRIPATHI A K, SUNDBERG D C. A hybrid algorithm for accurate and efficient Monte Carlo simulations of free-radical polymerization reactions[J]. Macromolecular Theory and Simulations, 2015, 24(1): 52-64. DOI:10.1002/mats.201400062 |
| [73] |
OZCAM D D, TEYMOUR F. Chain-by-chain Monte Carlo simulation: A novel hybrid method for modeling polymerization. Part I. Linear controlled radical polymerization systems[J]. Macromolecular Reaction Engineering, 2017, 11(1): 1600042.1-160042.22. |




